Open Access Article
Open Access ArticleSelf-healing polymer dielectric exhibiting ultrahigh capacitive energy storage performance at 250 °C†
Wenhan
Xu‡
 ,
Fei
Yang‡
,
Guodong
Zhao
,
Shixian
Zhang
,
Fei
Yang‡
,
Guodong
Zhao
,
Shixian
Zhang
 ,
Guanchun
Rui
,
Muchen
Zhao
,
Lingling
Liu
,
Long-Qing
Chen
and
Qing
Wang
,
Guanchun
Rui
,
Muchen
Zhao
,
Lingling
Liu
,
Long-Qing
Chen
and
Qing
Wang
 *
*
Department of Materials Science and Engineering, The Pennsylvania State University, University Park, Pennsylvania 16802, USA. E-mail: wang@matse.psu.edu
First published on 15th October 2024
Abstract
Polymer dielectrics capable of operating at elevated temperatures are essential components in advanced electronics and electrical power systems. However, dielectric polymers generally display significantly deteriorated capacitive performance at high temperatures because of exponential growth of electrical conduction. Here we design and prepare the cross-linked copolymers with interrupted translational symmetry and the use of local disorder-induced electron localization (i.e., Anderson localization) to impede electrical conduction of the copolymers. Consequently, the copolymer exhibits state-of-the-art discharged energy density of 3.5 J cm−3 with a charge–discharge efficiency of 90% at 250 °C. The copolymer also displays much more stable capacitive energy storage performance in the temperature range of 25 to 250 °C compared to existing dielectric polymers. With the demonstrated breakdown self-healing ability and excellent cyclability of the copolymer, this work sheds a new light on the design of high-temperature high-energy-density polymer dielectrics.
Broader contextPolymers are the preferred materials for high-energy-density energy storage capacitors due to their high breakdown strength and facile processability. However, the performance of existing dielectric polymers is compromised under extreme conditions and fails to meet the growing demands in electric vehicles, aerospace systems, and power grids. In this work, we utilize the broken translational symmetry in the crosslinked copolymers to reduce leakage current and conduction loss, leading to the dielectric polymers with excellent energy densities and stable capacitive performance from room temperature to 250 °C. We further describe the self-healing ability of the polymers that can restore dielectric properties and capacitive performance after electrical breakdown. This approach establishes a new paradigm for the structural design of polymer dielectrics to address the critical needs of high-temperature electrical energy storage. |
1. Introduction
In line with the continuous progress of electrification and the evolving requirements of the internet of things (IoT), dielectric capacitors, which are fundamental components in advanced electrical power systems and electronic devices, are demanded to exhibit reliable functionality across a diverse spectrum of operational scenarios.1–7 Polymer film capacitors, widely chosen for their outstanding breakdown strength, unique self-healing capabilities, ease of processing and scalability, confront several challenges when deployed in extreme environments.8–13 Biaxially oriented polyethylene films (BOPP), recognized as the best commercially available polymer dielectric, typically operate at temperatures below ∼85 °C. When temperature is above 85 °C, they have a 30–50% voltage derating due to deterioration in the breakdown strength and lifetime of the films.4,14 To enable the use of BOPP at high temperatures, the additional cooling units are brought in, e.g., electric vehicles, to reduce the capacitor temperature, which unfortunately adds complexity to the system and decreases fuel efficiency. In the fields such as oil and gas exploration and aerospace systems, where spatial constraints hinder the integration of refrigeration systems for capacitors, there is a pressing demand for the capacitors constructed with high-temperature dielectrics that are capable of maintaining consistent performance across a broad temperature range (Table S1, ESI†).15,16High-temperature polymer dielectrics have been extensively developed over the last decade to meet the urgent needs, in which electrical conduction is identified as the main loss mechanism.1,3,16–24 The exponential increase in electrical conduction with the applied electric fields and temperatures leads to substantially decreased discharge energy density (Ud) and charge–discharge efficiency (η) of polymer dielectrics compared to those obtained at ambient temperature.1,3Ud directly impacts the size, compactness and modernization of electrical power systems, while η is indicative of dielectric loss and affects lifetime and reliability of dielectric materials during continuous operation. The addition of inorganic fillers with wide bandgaps, such as boron nitride,2,25 alumina,15,26 and silicon dioxide,27,28 which can effectively impede the electrical conduction, has been utilized in the creation of high-temperature dielectric polymer composites. Similarly, high-temperature dielectric polymers have been designed based on the incorporation of high-electron-affinity units into high-glass-transition (Tg) polymers and the modulation of bandgaps of the aromatic polymers.29–32 While these approaches are effectively in improving Ud and η at elevated temperatures, most of the current high-temperature polymer dielectric still suffer from relatively large variations of the capacitive performance over temperature. For instance, the best high-temperature polymer films such as polyetherimides (PEI) and fluorene polyester (FPE), their η decreases >50% with increasing temperature from 25 °C to 200 °C. Moreover, most research on high-temperature dielectric polymers is focused on temperatures below 200 °C, and expanding the operating temperature range to higher temperature of dielectric polymer remains a challenge. In addition to the parameters such as Ud, η and Weibull breakdown strength (Eb), self-healing capability, i.e., the ability of a metallized capacitor to clear a fault area and restore its capacitance prior to catastrophic failure, is a key metric for evaluating the reliability of metallized film capacitors and assessing the suitability of new polymer dielectrics for practical applications. However, because of high ratios of carbon atoms in the aromatic structures such as PEI, polyimides, and poly(ether ether ketone), only a few aromatic polymers have been shown the breakdown self-healing ability.33,34
In this work, we design and synthesize the cross-linked copolymer based on divinyltetramethyldisiloxane-bis(benzocyclobutene) (cBCB) as high-temperature dielectrics. In particular, by introducing methanesulfonic acid modified norbornene (N-4-aminophenyl sulfonylmethyl-norbornene imide, SNI) to break the translational symmetry of the polymer network, the local disorder-induced electron localization (i.e., Anderson localization), for the first time, is applied to reduce the hopping distance and electrical conduction of the polymer dielectrics at elevated temperatures and high applied fields. Remarkable capacitive energy storage performance, i.e., an Ud of 3.5 J cm−3 at 250 °C and stable η > 90% at an applied field of 475 MV m−1 in the temperature ranging from 25–250 °C, has been demonstrated in the copolymer, which outperforms the current high-temperature polymer and polymer composite dielectrics. Moreover, Ue exhibits modest variation with temperature, with only −1.9% from 25 °C to 200 °C and −9.8% to 250 °C. The demonstration of self-healing ability and outstanding cyclic stability in the copolymer further suggests the promise of this structural design in the development of high-energy-density dielectric polymers for wide temperature range applications.
2. Result and discussion
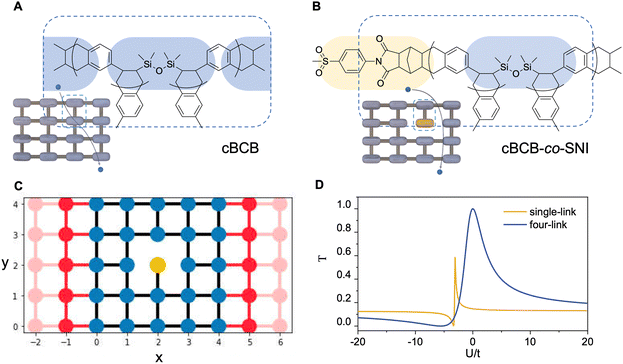
2.1 Design of polymer dielectric with Anderson localization
The conduction model of the hopping motion of localized electrons with distribution function is the underlying mechanism responsible for the electric conduction of dielectrics. While this single-particle hopping model is similar to the one for mesoscopic transport behavior,35 an effective strategy to reduce the conductivity in the field of the mesoscopic transport is to utilize the Anderson disorder localization, a fundamental phenomenon of the electric-conductivity reduction by local disorder as a consequence of the breaking of the translational symmetry.35 To investigate the applicability of this effect in polymer dielectrics, we use tetra-functionality of BCB to prepare the cross-linked cBCB and also introduce a small amount of monofunctional SNI into the network as internal disorder sites (Fig. 1a and b). Topologically, this structure is equivalent to a two-dimensional single-particle hopping model within the field of the mesoscopic transport (shown in Fig. 1c and Fig. S1, ESI†),35 in which the Hamiltonian H of electrons can be expressed as: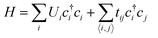 | (1) |
The field of the mesoscopic transport concerns the electron transmission coefficient (T), which describes the probability of the transmitted electron to that of the incident electron, i.e., the probability of electron tunneling/hopping through a potential barrier or well.
For the structure in Fig. 1c, we calculate T around a single local disorder within the framework of the Landauer–Buttiker approach,35 and the numerical results are presented in Fig. 1d. For illustration, we first artificially set a four-link connection of the SNI (blue curve) into the cross-linked network. As seen from the figure, the increase in the difference of the on-site potential energies between disorder site and normal site from zero remarkably reduces transmission coefficient T no matter whether this difference is positive or negative. This is because for a positive energy difference, the hopping electrons need to cross a potential barrier with the possibility of the reflection/back-scattering whereas for a negative difference, the potential well due to the local disorder provides the possibility of the electron trapping. Both are detrimental to the electron transmission. We next consider the single-link connection of SNI. It is noted that there are two cases for the remaining link along and perpendicular to the transport direction. We therefore calculate the average of transmission coefficient T for both cases (yellow curve). As seen from the figure, a sharp anti-resonance of the transmission coefficient T emerges in the regime of negative U. This is because for single-link connection, the localized state due to a negative U on a local disorder has a strong localization character, and the existence of the strongly localized state provides the discrete channel to interfere with the conducting channel, leading to a characteristic, asymmetric line shape in the transmission spectroscopy, known as the Fano-type anti-resonance.36,37 It is noted that, as a consequence of the single-link connection (i.e., Fano effect), the peak of the electron transmission gets suppressed in comparison with the case for the four-link connection, which suppresses the localization character due to a stronger connection to the normal sites.
Consequently, for the structure shown in Fig. 1c, besides the on-site potential energy, the monofunctional monomer SNI brings an additional translational-symmetry breaking: a single-link connection to the cross-linked network, differing from the four-link one of cBCB. Both origins can lead to a remarkable reduction in transmission coefficient T. Moreover, as a consequence of the Anderson disorder localization via the unique translational-symmetry breaking by SNI, the resulted transmission coefficient T is very robust against structure distortion (i.e., fluctuation of hopping or on-site energy on normal sites) and disturbance by external fields as well as thermal fluctuation, making this design highly feasible for high-temperature high-field dielectric applications.
2.2 Electrical and dielectric characteristics
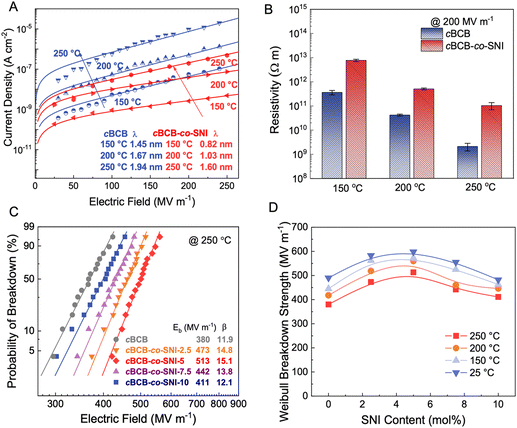
The leakage current density of cBCB-co-SNI with different contents of SNI are measured at high temperatures. As shown in Fig. S2 and S3 (ESI†), cBCB-co-SNI with 5 mol% SNI consistently exhibits the lowest leakage current density and the smallest charge carrier hopping distance. The larger leakage current at >5 mol% SNI is attributable to higher conduction of SNI relative to that of cBCB. Fig. 2a compares the leakage current and resistivity of cBCB and cBCB-co-SNI (in which SNI constitutes 5 mol%, unless otherwise specified) measured at high temperatures as a function of the applied electric fields. Consistent with theoretical predictions, the leakage current of the copolymer film is found to be notably smaller compared to that of pristine cBCB. Specifically, at 200 MV m−1 and 200 °C, the leakage current is decreased more than an order of magnitude from 4.76 × 10−7 A cm−2 of cBCB to 3.96 × 10−8 A cm−2 of cBCB-co-SNI. Comparatively, state-of-the-art polymer dielectrics like PSBNP-co-PTNI0.02 and sc-PEENA exhibit relatively higher leakage currents, reported as 5.56 × 10−8 A cm−2 and 2.42 × 10−7 A cm−2, respectively, under the same condition.1,32 At 200 MV m−1 and 250 °C, the copolymer shows an exceptionally low leakage current of only 1.94 × 10−7 A cm−2 which is the smallest leakage current reported so far in polymer and composite dielectrics.Based on the hopping conduction equation,
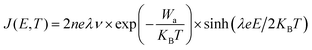 | (2) |
| λ = veτ | (3) |
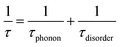 | (4) |
We also calculate the effect of the SNI ratio x in the copolymer on the conductivity. At finite but small x, one can apply the random phase approximation where the collision rate 1/τdisorder of electrons with disorder is proportional to the disorder concentration, i.e., 1/τdisorder = x/τ0disorder with τ0disorder being the collision time of electrons by single disorder. Then, considering the ratio cBCB (1 − x), from eqn (2)–(4), one finds that the electric conductance at small x reads
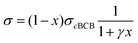 | (5) |
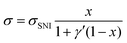 | (6) |
The dielectric spectra of cBCB and cBCB-co-SNI are presented in Fig. S5 and S6 (ESI†). It is evident that the dielectric constant of the copolymers increases with the SNI content, e.g., from 2.76 of cBCB to 3.10 of cBCB-co-SNI, while the dissipation loss essentially remains unchanged. The dielectric constant and dissipation factor of cBCB and cBCB-co-SNI are highly stable over a wide range of temperature from 25–250 °C and frequency from 102–106 Hz.
2.3 Capacitive energy storage performance
We examine the breakdown strength of the dielectric films utilizing Weibull statistics at various temperatures as summarized in Fig. 2c, d and Fig. S7 (ESI†). The cumulative probability of electric breakdown P(E) is represented by the equation:| P(E) = 1 − exp(−E/Eb)β | (7) |
Fig. 3a and b compare the Ud and η of cBCB-co-SNI with those of the current high-performance dielectric polymers, including cBCB, BOPP, PEI, FPE, and PI-CF3-iso,29 measured at 250 °C. cBCB-co-SNI delivers the maximal Ud of 3.8 J cm−3 compared with 1.8 J cm−3 of cBCB, 2.7 J cm−3 of PI-CF3-iso, 0.3 J cm−3 of FPE and 0.2 J cm−3 of PI at 250 °C. The best Ud achieved in cBCB-co-SNI is apparently benefited from its much-reduced conduction and higher Eb which is attributed to its unique crosslinked structure with local disorder-induced electron localization. Indeed, the copolymer displays a superior η of 86.4% to 61% of PI-CF3-iso and all other high-temperature dielectric polymers at 250 °C and 500 MV m−1. It is noteworthy that cBCB-co-SNI exhibits highly stable η of over 90% up to the applied field of 475 MV m−1 at 250 °C. The achieved Ud of 3.5 J cm−3 at η ≥ 90% also represents the state-of-the-art in dielectric polymers measured at 250 °C, improving the current performance record by over 50%. Specifically, we increased the maximum energy storage density from 2.2 J cm−3 of PI-CF3-iso to 3.5 J cm−3 of cBCB-co-SNI at over 90% efficiency (as shown in Fig. S8, ESI†). The P–E loops, along with Ud and η, of the copolymers with different compositions, are presented in Fig. S9 and S10 (ESI†). cBCB-co-SNI-5 exhibits the best overall capacitive performance.
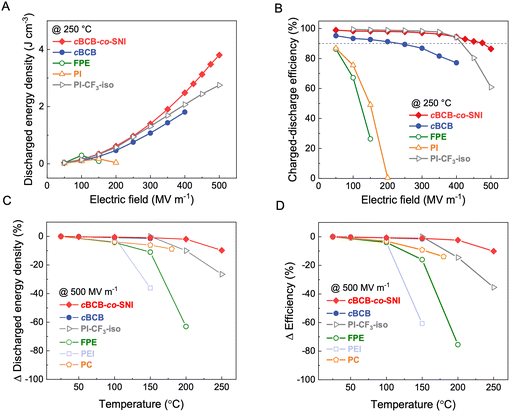 | ||
| Fig. 3 Capacitive energy storage performance. (A) Discharged energy density and (B) charge–discharge efficiency of cBCB-co-SNI, PI-CF3-iso29 and other high-temperature dielectric polymers as a function of the applied electric field at 250 °C. (C) and (D) Change in (C) discharged energy density and (D) charge–discharge efficiency of the dielectric polymers as a function of temperature measured at 500 MV m−1. | ||
We further compare the Ud and η of the copolymer with the current high-temperature polymer dielectrics measured 500 MV m−1 as a function of temperature to assess their temperature stability. As summarized in Fig. 3c and d, cBCB-co-SNI clearly has much better stability of Ud and η, i.e., ΔUd of −9.8% and Δη of −10.1% compared to ΔUd of −26.5% and Δη of −35.4% of PI-CF3-iso with increasing temperature from 25 to 250 °C and ΔUd of −11% and Δη of −16% observed in FPE in the temperature range from 25 to 150 °C, which is again attributed to the fact that the increase of the conductivity of cBCB-co-SNI with temperature is much less pronounced.
2.4 Self-healing ability and cyclability
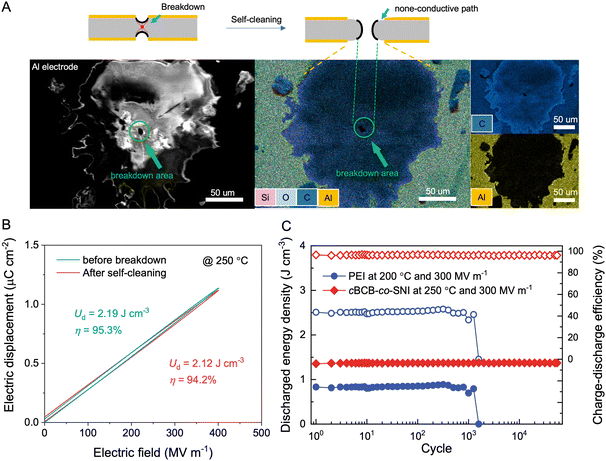
While the theoretical link between chemical composition and the self-healing capability of dielectric polymers remains elusive, empirical observations suggest that, for polymers with a general formula of CαHβOγNδSθ, a low ratio of (α + δ + θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) to (β + γ) usually correlates well with potential for the self-healing ability. Interestingly, cBCB-co-SNI has a ratio of ∼0.72 that is much lower than PSBNP-co-PTNI0.02 of 0.971 and other high-temperature polymer dielectrics such as PEI (1.3), PI (1.6), and PET (0.83). The scanning electron microscopy/energy dispersive X-ray spectroscopy (SEM EDS) analysis of the cBCB-co-SNI film, depicted in Fig. 4a, reveals the vaporization of the electrode in the area where dielectric breakdown occurs. The destruction of the electrodes during the so-called self-cleaning process allows the spontaneous extinction of a local electrical arc and thus would prevent catastrophic failure for continuing the operation of the capacitor films. The dielectric constant and dissipation factor of the films show no significant variation before and after breakdown, indicating no conductive pathway formation (Fig. S16, ESI†). Consequently, as shown in Fig. 4b, minimal loss in the Ud and η measured at 400 MV m−1 and 250 °C is found in the dielectric films after self-cleaning.
) to (β + γ) usually correlates well with potential for the self-healing ability. Interestingly, cBCB-co-SNI has a ratio of ∼0.72 that is much lower than PSBNP-co-PTNI0.02 of 0.971 and other high-temperature polymer dielectrics such as PEI (1.3), PI (1.6), and PET (0.83). The scanning electron microscopy/energy dispersive X-ray spectroscopy (SEM EDS) analysis of the cBCB-co-SNI film, depicted in Fig. 4a, reveals the vaporization of the electrode in the area where dielectric breakdown occurs. The destruction of the electrodes during the so-called self-cleaning process allows the spontaneous extinction of a local electrical arc and thus would prevent catastrophic failure for continuing the operation of the capacitor films. The dielectric constant and dissipation factor of the films show no significant variation before and after breakdown, indicating no conductive pathway formation (Fig. S16, ESI†). Consequently, as shown in Fig. 4b, minimal loss in the Ud and η measured at 400 MV m−1 and 250 °C is found in the dielectric films after self-cleaning.
Fig. 4c compares the cyclic performance of cBCB-co-SNI to that of PEI under an applied field of 300 MV m−1. In contrast to commercial capacitor-grade PEI films that fail after less than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles at 200 °C, the cBCB-co-SNI film exhibits stable Ud and η up to 50
000 cycles at 200 °C, the cBCB-co-SNI film exhibits stable Ud and η up to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles at 250 °C. Curiously, the excellent stability of the copolymer cannot be credited to its mechanical properties since PEI has much greater mechanical strength (i.e., Young's modulus of 1.1 GPa at 200 °C) than the copolymer with the Young's modulus of 0.49 GPa at 200 °C. On the other hand, at an applied field of 300 MV m−1, the copolymer has remarkably lower conduction loss (i.e., 2.9% at 250 °C) compared to PEI (6.6% at 150 °C and 56.4% at 200 °C). Therefore, it can be assumed that much less Joule heat resulting from lower loss in the copolymer is highly beneficial to long-term stability of dielectric films.
000 cycles at 250 °C. Curiously, the excellent stability of the copolymer cannot be credited to its mechanical properties since PEI has much greater mechanical strength (i.e., Young's modulus of 1.1 GPa at 200 °C) than the copolymer with the Young's modulus of 0.49 GPa at 200 °C. On the other hand, at an applied field of 300 MV m−1, the copolymer has remarkably lower conduction loss (i.e., 2.9% at 250 °C) compared to PEI (6.6% at 150 °C and 56.4% at 200 °C). Therefore, it can be assumed that much less Joule heat resulting from lower loss in the copolymer is highly beneficial to long-term stability of dielectric films.
3. Conclusions
We strategically introduce monofunctional monomers to disrupt the translational symmetry of the cross-linked polymer and leverage the Anderson localization effect to effectively hinder the electrical conduction of the polymers at high electric fields and elevated temperatures. This design principle is different from the current approaches to high-temperature dielectric polymers. As a consequence of radically reduced conductivity resulting from the Anderson localization, the copolymer reported in this work displays outstanding Ud and η at 250 °C, far exceeding the current polymer and composite dielectrics. More impressively, η of over 90% is maintained up to the applied field of 475 MV m−1 at 250 °C. The copolymer also exhibits significantly more stable capacitive energy storage performance over a wide temperature range from 25 to 250 °C than the current polymer and composite dielectrics. In addition, breakdown self-healing ability and excellent cyclability have been demonstrated in the copolymer. This work successfully improves the effective operating temperature of dielectric polymers from 200 to 250 °C and opens a new avenue for high-temperature dielectric polymers for their potential applications in electronics and power systems under extreme conditions.Author contributions
Q. W. and W. X. conceived the idea. Q. W. and W. X. designed the experiments. W. X. and M. Z. conducted polymer synthesis. W. X. and L. L. prepared device samples for measurements. W. X., S. Z., and G. R. carried out electrical, thermal and optical measurements under the supervision of Q. W. F. Y. and G. Z. performed all simulations and theoretical part under the supervision of L. C. W. X. carried out SEM-EDS studies. W. X., S. Z., L. L., M. Z., G. R., and F. Y. analysed the data. Q. W., W. X., and F. Y. wrote the manuscript all authors discussed the results and provided inputs to the manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no competing interests.Acknowledgements
This research was supported by the US Office of Naval Research (N000142312267). The theoretical analysis based on the Anderson Location Model was supported by as part of the Computational Materials Sciences Program funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award No. DE-SC0020145 (F. Y. and L. Q. C.). L. Q. C. also acknowledges the support by the Hamer Foundation through the Hamer Professorship.Notes and references
- J. Chen, Y. Zhou, X. Huang, C. Yu, D. Han, A. Wang, Y. Zhu, K. Shi, Q. Kang, P. Li, P. Jiang, X. Qian, H. Bao, S. Li, G. Wu, X. Zhu and Q. Wang, Nature, 2023, 615, 62–66 CrossRef CAS
.
- Q. Li, L. Chen, M. R. Gadinski, S. Zhang, G. Zhang, H. U. Li, E. Iagodkine, A. Haque, L.-Q. Chen, T. N. Jackson and Q. Wang, Nature, 2015, 523, 576–579 CrossRef CAS PubMed
.
- J. Pei, L. Yin, S. Zhong and Z. Dang, Adv. Mater., 2023, 35, 2203623 CrossRef CAS
.
- D. Tan, L. Zhang, Q. Chen and P. Irwin, J. Electron. Mater., 2014, 43, 4569–4575 CrossRef CAS
.
- A. A. Deshmukh, C. Wu, O. Yassin, A. Mishra, L. Chen, A. Alamri, Z. Li, J. Zhou, Z. Mutlu, M. Sotzing, P. Rajak, S. Shukla, J. Vellek, M. Arab Baferani, M. Cakmak, P. Vashishta, R. Ramprasad, Y. Cao and G. Sotzing, Energy Environ. Sci., 2022, 15, 1307–1314 RSC
.
- G. Wang, Z. Lu, Y. Li, L. Li, H. Ji, A. Feteira, D. Zhou, D. Wang, S. Zhang and I. M. Reaney, Chem. Rev., 2021, 121, 6124–6172 CrossRef CAS PubMed
.
- X. Wu, A. Karlin, V. Beilin, G. E. Shter, G. S. Grader, Y. Ivry, S. Lin and D. Q. Tan, Adv. Mater., 2024, 2401597 CrossRef CAS PubMed
.
- J. Chen, Y. Wang, H. Li, H. Han, X. Liao, R. Sun, X. Huang and M. Xie, Chem. Mater., 2018, 30, 1102–1112 CrossRef CAS
.
- X. Li, B. Liu and J. Wang,
et al.
, Nat. Commun., 2024, 15, 6655 CrossRef CAS
.
- B. Chu, X. Zhou, K. Ren, B. Neese, M. Lin, Q. Wang, F. Bauer and Q. M. Zhang, Science, 2006, 313, 334–336 CrossRef CAS PubMed
.
- J. Wei and L. Zhu, Prog. Polym. Sci., 2020, 106, 101254 CrossRef CAS
.
- H. Li, B. S. Chang, H. Kim, Z. Xie, A. Lainé, L. Ma, T. Xu, C. Yang, J. Kwon, S. W. Shelton, L. M. Klivansky, V. Altoé, B. Gao, A. M. Schwartzberg, Z. Peng, R. O. Ritchie, T. Xu, M. Salmeron, R. Ruiz, K. B. Sharpless, P. Wu and Y. Liu, Joule, 2023, 7, 95–111 CrossRef CAS
.
- X. Wu, X. Chen, Q. M. Zhang and D. Q. Tan, Energy Storage Mater., 2022, 44, 29–47 CrossRef
.
- M. Rabuffi and G. Picci, IEEE Trans. Plasma Sci., 2002, 30, 1939–1942 CrossRef CAS
.
- T. Zhang, X. Chen, Y. Thakur, B. Lu, Q. Zhang, J. Runt and Q. M. Zhang, Sci. Adv., 2020, 6, eaax6622 CrossRef CAS PubMed
.
- Z. Zhang, D. H. Wang, M. H. Litt, L.-S. Tan and L. Zhu, Angew. Chem., 2018, 130, 1544–1547 CrossRef
.
- Y. Zhou, Y. Zhu, W. Xu and Q. Wang, Adv. Energy Mater., 2023, 13, 2203961 CrossRef CAS
.
- C. Zhou, W. Xu, B. Zhang, Y. Zhang, C. Shen, Q. Xu, X. Liu, F. Bertram, J. Bernholc, Z. Jiang, Y. Shang and H. Zhang, Chem. Mater., 2022, 34, 2333–2341 CrossRef CAS
.
- A. Alamri, C. Wu, A. Mishra, L. Chen, Z. Li, A. Deshmukh, J. Zhou, O. Yassin, R. Ramprasad, P. Vashishta, Y. Cao and G. Sotzing, Chem. Mater., 2022, 34, 6553–6558 CrossRef CAS
.
- J. Dong, R. Hu, X. Xu, J. Chen, Y. Niu, F. Wang, J. Hao, K. Wu, Q. Wang and H. Wang, Adv. Funct. Mater., 2021, 31, 2102644 CrossRef CAS
.
- Z. Dai, Z. Bao, S. Ding, C. Liu, H. Sun, H. Wang, X. Zhou, Y. Wang, Y. Yin and X. Li, Adv. Mater., 2022, 34, 2101976 CrossRef CAS
.
- M. Yang, H. Li, J. Wang, W. Shi, Q. Zhang, H. Xing, W. Ren, B. Sun, M. Guo, E. Xu, N. Sun, L. Zhou, Y. Xiao, M. Zhang, Z. Li, J. Pan, J. Jiang, Z. Shen, X. Li, L. Gu, C.-W. Nan, X. Wang and Y. Shen, Nat. Energy, 2024, 9, 143–153 CrossRef CAS
.
- H. Li, E. Vargo, Z. Xie, L. Ma, P. F. Pieters, S. W. Shelton, A. P. Alivisatos, T. Xu and Y. Liu, Adv. Mater., 2024, 2401954 CrossRef CAS
.
- M. Dai, J. Sun and Q. Fang, Mater. Today Sustainability, 2023, 24, 100557 CrossRef
.
- A. Azizi, M. R. Gadinski, Q. Li, M. A. AlSaud, J. Wang, Y. Wang, B. Wang, F. Liu, L.-Q. Chen, N. Alem and Q. Wang, Adv. Mater., 2017, 29, 1701864 CrossRef PubMed
.
- H. Li, D. Ai, L. Ren, B. Yao, Z. Han, Z. Shen, J. Wang, L.-Q. Chen and Q. Wang, Adv. Mater., 2019, 31, 1900875 CrossRef
.
- Y. Zhou, Q. Li, B. Dang, Y. Yang, T. Shao, H. Li, J. Hu, R. Zeng, J. He and Q. Wang, Adv. Mater., 2018, 30, 1805672 CrossRef
.
- G. Rui, J. (Jerry) Bernholc, S. Zhang and Q. Zhang, Adv. Mater., 2024, 2311739 CrossRef PubMed
.
- R. Wang, Y. Zhu, J. Fu, M. Yang, Z. Ran, J. Li, M. Li, J. Hu, J. He and Q. Li, Nat. Commun., 2023, 14, 2406 Search PubMed
.
- Z. Ran, R. Wang, J. Fu, M. Yang, M. Li, J. Hu, J. He and Q. Li, Adv. Mater., 2023, 35, 2303849 CrossRef CAS PubMed
.
- H. Li, B. S. Chang, H. Kim, Z. Xie, A. Lainé, L. Ma, T. Xu, C. Yang, J. Kwon, S. W. Shelton, L. M. Klivansky, V. Altoé, B. Gao, A. M. Schwartzberg, Z. Peng, R. O. Ritchie, T. Xu, M. Salmeron, R. Ruiz, K. B. Sharpless, P. Wu and Y. Liu, Joule, 2023, 7, 95–111 CrossRef CAS
.
- W. Xu, C. Zhou, W. Ji, Y. Zhang, F. Bertram, Z. Jiang, Y. Shang, H. Zhang and C. Shen, Angew. Chem., Int. Ed., 2024, e202319766 CAS
.
- J. S. Ho and S. G. Greenbaum, ACS Appl. Mater. Interfaces, 2018, 10, 29189–29218 CrossRef CAS
.
- H. Li, Y. Zhou, Y. Liu, L. Li, Y. Liu and Q. Wang, Chem. Soc. Rev., 2021, 50, 6369–6400 RSC
.
-
S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, Cambridge, 1995 Search PubMed
.
- U. Fano, Phys. Rev., 1961, 124, 1866–1878 CrossRef CAS
.
- A. E. Miroshnichenko, S. Flach and Y. S. Kivshar, Rev. Mod. Phys., 2010, 82, 2257–2298 CrossRef CAS
.
- V. Ambegaokar, B. I. Halperin and J. S. Langer, Phys. Rev. B: Solid State, 1971, 4, 2612–2620 Search PubMed
.
- P. Coleman, P. W. Anderson and T. V. Ramakrishnan, Phys. Rev. Lett., 1985, 55, 414–417 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee03705g |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |