Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Measuring heat transfer processes in gully pots for real-time estimation of accumulated sediment depths†
Manuel
Regueiro-Picallo
 *a,
Antonio
Moreno-Rodenas
*a,
Antonio
Moreno-Rodenas
 b and
Francois
Clemens-Meyer
b and
Francois
Clemens-Meyer
 cd
cd
aWater and Environmental Research Team (GEAMA), Centro de Innovación Tecnolóxica en Edificación e Enxeñaría Civil (CITEEC), Universidade da Coruña, 15071 A Coruña, Spain. E-mail: manuel.regueiro1@udc.es
bHydraulic Engineering Unit, Deltares, 2629 HV Delft, The Netherlands
cDepartment of Civil Engineering, Faculty of Engineering, Norwegian University of Science and Technology, 7491 Trondheim, Norway
dSkillsInMotion B.V., Esdoornlaan 11, 3454 HH De Meern, The Netherlands
First published on 16th July 2024
Abstract
The accumulation of sediments in stormwater systems negatively affects their functioning. For example, the re-suspension of these sediments can lead to serious pollution of surface water bodies through combined sewer overflows (CSOs). In addition, the persistent accumulation of sediments reduces the storage and hydraulic capacity of stormwater systems, resulting in an increased risk of flooding. Stormwater managers spend considerable resources cleaning these systems, but we still lack reliable and easy-to-use monitoring methods to provide information on the location, volume and composition of sediments. This study explores the use of temperature sensors combined with the analysis of heat transfer processes to measure sediment depth in sand trap gully pots. To this end, a laboratory-scale experimental campaign was carried out using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 scale gully pot model, with different sediment types, hydrographs and inflow temperature conditions. The experiments were designed using field measurements to reproduce the temperature changes in gully pots and thus the heat transfer processes. The results showed maximum differences between reference measurements and estimated depths of less than 30 mm. Finally, the use of temperature sensors as a cost-effective solution for monitoring sediment accumulation is discussed.
1 scale gully pot model, with different sediment types, hydrographs and inflow temperature conditions. The experiments were designed using field measurements to reproduce the temperature changes in gully pots and thus the heat transfer processes. The results showed maximum differences between reference measurements and estimated depths of less than 30 mm. Finally, the use of temperature sensors as a cost-effective solution for monitoring sediment accumulation is discussed.
Water impactSediment collectors, e.g. gully pots, prevent the overloading of particles in urban drainage systems by inducing their sedimentation. We present a temperature-based system that uses pioneering measurements of heat transfer processes in sediment collectors to estimate sediment accumulation. This system was tested on a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 scale model of a gully pot using organic and surrogate sediments. 1 scale model of a gully pot using organic and surrogate sediments.
|
1. Introduction
The discharge of runoff generated in urban areas into stormwater systems is controlled by gully pots, also known as catch basins or catchpits, which are elements of infrastructure that convey street runoff volumes to the drainage pipes. The gully pots are also expected to control and mitigate water depths and overland flow velocities at the inlet of the stormwater pipe networks. In addition, they retain small floating objects and prevent large solid objects that can cause blockages from entering the underground stormwater systems. Finally, they also reduce the load of sediments and their associated pollutants so as to prevent the accumulation of these materials in drainage systems and the transport to downstream receiving waters. The current paper focuses on the latter function, more specifically the trapping of sediment by gully pots. As sediments accumulate in gully pots over time, regular cleaning is required to ensure a minimum hydraulic capacity and to reduce the risk of flooding.1,2Traditionally, cleaning operations are scheduled on a regular basis, with gully pots in residential areas typically cleaned out about once a year, while those in specific locations with high solid loads, such as marketplaces, are cleaned between two and four times annually.3,4 However, recent studies suggest that this approach may be questioned in terms of its effectiveness. Post et al.5 show that a stable sediment depth can develop in gully pots within just a few months, suggesting that the sediment retention capacity of these infrastructures can be lost before a new round of cleaning is undertaken. This in turn means that sediments can freely enter stormwater systems over a significant time period, leading to a potential loss of hydraulic capacity and (avoidable) environmental damage.
A further finding of previous studies is that there is a notable spatial and temporal variability (and even indications of chaotic process characteristics) in the sediment accumulation rate in gully pots, even for small service areas.2,5 In addition, cleaning programmes do not usually cover all gully pots in an urban area. The number of gully pots emptied in a given year usually represents a small percentage of the whole, e.g. 5% was reported in the municipality of Oslo, Norway.6 This hinders the task of formulating effective and efficient cleaning strategies by the responsible asset manager. Ideally, information on the status of (groups of) gully pot(s) would lead to the formulation of a successful maintenance strategy (either a cost- or risk-based one).
Measurements of sediment accumulation rates in gullies reported in the literature have usually been carried out using manual methods,7 which require the availability of substantial material and personal resources, while the results obtained prove to be only limited transferable to a ‘real world’ system. To the authors' knowledge, no reliable, continuous monitoring solution that is both practical and scales well in terms of cost is currently available. Such a measurement technique would ideally have the following characteristics: i) low-cost, since each municipal area covers thousands of structures; ii) robust to clogging and changing environmental conditions, such as build-up of debris; iii) low-power and relatively maintenance free, thus not requiring constant maintenance and battery swaps; and iv) with an acceptable level of accuracy to measure the sediment depth.
The present study considers the use of passive-temperature sensors as an inexpensive monitoring solution for sediment accumulation in gully pots. This idea derives from a method developed to measure sediment depths in sewers by using temperature sensors and the analysis of heat transfer processes.8 Such a method is based on establishing a relationship between the attenuation and time lag of the temperature time series in the water and sediment layers and the sediment depth itself. For this purpose, the heat transfer triggered by temperature fluctuations should be significant in order to estimate the sediment accumulation. However, the heat transfer processes in gully pots differ from those in sewer pipes,9,10 and thus further development and refinement of this method is necessary. Unlike temperature time series in sewer pipes, which follow a cyclical pattern,8,11 temperature fluctuations in gully pots are triggered when rainfall occurs, similar to retention ponds.12 Therefore, the approach to gully pots is based on analysing the heat transfer towards the sediment layer caused by the temperature gradient between the runoff entering the gully pot and the inner standing water to estimate the sediment accumulation.
This study aims to describe the heat transfer processes in gully pots and to develop a method to estimate sediment depths based on passive temperature measurements. To this end, preliminary field measurements were performed to design a lab-scale experimental campaign. Experiments were performed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 scaled gully pot model to determine the main variables that influence heat transfer processes and to evaluate the method to estimate the sediment depths. The temperature-based system showed high performance when comparing the sediment depth estimations with reference measurements, setting a baseline for the potential application in field measurements. The use of temperature sensors, then, emerges as a promising solution towards optimising the monitoring and cleaning strategies for gully pots while ensuring their efficient performance, as well as investigating sediment build-up processes.
1 scaled gully pot model to determine the main variables that influence heat transfer processes and to evaluate the method to estimate the sediment depths. The temperature-based system showed high performance when comparing the sediment depth estimations with reference measurements, setting a baseline for the potential application in field measurements. The use of temperature sensors, then, emerges as a promising solution towards optimising the monitoring and cleaning strategies for gully pots while ensuring their efficient performance, as well as investigating sediment build-up processes.
2. Materials
2.1. Experimental setup
The experimental setup consisted of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 scaled gully pot model located in the Hydro Hall facilities at Deltares (Delft, The Netherlands). The gully pot model was made of polymethyl methacrylate (PMMA) and the inner dimensions were 350 × 350 × 1010 mm. In addition, the model had a grated lateral inflow, and a flow outlet opening located 390 mm from the bottom. Sediment layers were poured at the bottom and were covered by a water layer up to the outlet opening. Further details on the gully pot geometry can be found in the research performed by Rietveld.4
1 scaled gully pot model located in the Hydro Hall facilities at Deltares (Delft, The Netherlands). The gully pot model was made of polymethyl methacrylate (PMMA) and the inner dimensions were 350 × 350 × 1010 mm. In addition, the model had a grated lateral inflow, and a flow outlet opening located 390 mm from the bottom. Sediment layers were poured at the bottom and were covered by a water layer up to the outlet opening. Further details on the gully pot geometry can be found in the research performed by Rietveld.4
The gully pot was placed inside a tank with inner dimensions of 450 × 840 × 950 mm. The outer tank was used as a stable boundary condition mimicking the soil temperature and to control the initial temperature conditions in the gully pot. For this purpose, the outer tank was filled with deionised water while a temperature control system was built by using a NESLAB RTE-211 recirculating water bath (ThermFisher Scientific, The Netherlands).
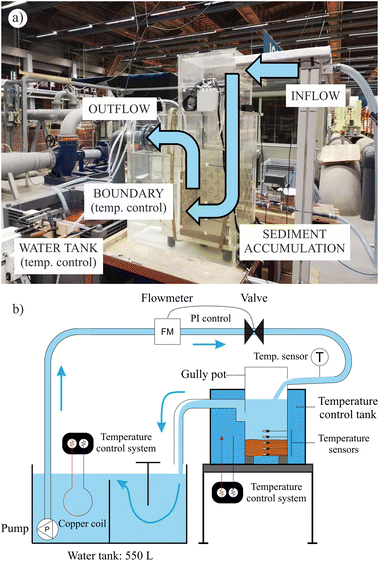
A system of PVC pipes and connectors carried the outflow from the gully pot to a water tank of 550 L which acted as a reservoir. This second water tank also included a temperature control system to set the temperature gradient with respect to the initial temperature in the gully pot. For this purpose, a NESLAB ThermoFlex2500 recirculating chiller (ThermFisher Scientific, The Netherlands) was installed. In addition, the 550 L water tank also included a deflector to induce the sedimentation of the resuspended particles flushed out of the gully pot, and a hydraulic pump with a discharge capacity of 4500 L h−1. The setup was operated in a closed loop by pumping the water from the 550 L water tank to the gully pot inlet. Fig. 1 shows an image and a schematic overview of the experimental setup.
2.2. Instrumentation
A total of 23 temperature sensors were installed in the experimental setup to measure the heat transfer processes inside the gully pot, as well as to control the boundary and initial conditions. Inside the gully pot, four sensors were placed at the bottom, plus two sensors at the middle section of the walls every 50 mm from the bottom up to 300 mm. Additionally, two sensors were placed at ∼500 mm from the bottom to measure the temperature of the water layer, and one sensor was installed at the inlet to measure the inflow temperature. Outside the gully pot, one sensor was placed inside the outer tank to measure the contour temperature, one sensor inside the 550 L water tank to establish and control the initial temperature, and two sensors to measure the room temperature. A graphical description of the sensor distribution can be found in the ESI.†
The PI control system was implemented using LabVIEW software that controlled an analogue input and output module (IO module) of the flowmeter and valve positioner signals. First, a predefined hydrograph was uploaded before executing the software, including flow rate setpoints with a time resolution of 0.1 s. The LabVIEW software started by reading the analogue input from the flow meter, using the IO module. The PI control system then computed the voltage output, and subsequently opened or closed the solenoid valve. The proportional (P) and integral (I) gain coefficients that controlled the PI system were 0.15 and 0.007, respectively. Finally, the software read the next flow rate setpoint from the predefined hydrograph.
2.3. Experimental procedure
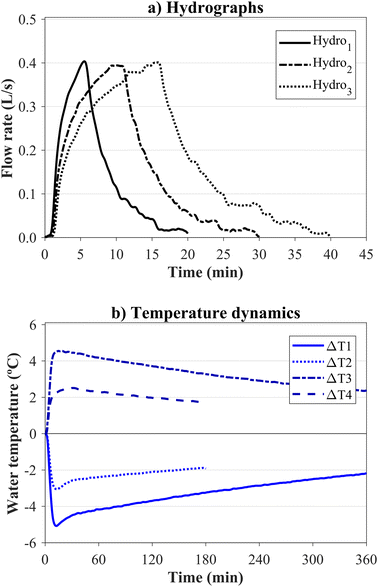
Fifty-six experiments were performed by combining the following features. A table summarising the test configurations is provided in the dataset related to the lab-scale experimental campaign (see Data availability).17Field observations showed temperature gradients (ΔT) of the standing water when rainfall-runoff events occurred, where the temperature gradient was defined as the difference between the initial and the maximum or minimum temperatures of the standing water during a rainfall-runoff period (positive and negative gradients, respectively). For this purpose, a rainfall-runoff event was considered when the rainfall accumulation exceeded 1.5 mm in a one hour period without constraints in the preceding dry weather periods. Negative temperature gradients ranging from −0.4 °C to −7.0 °C were observed in most of the rainfall during the measuring period, i.e., the temperature of the standing water was initially warmer than the runoff inflow. Only a few events were observed where the runoff inflow caused positive temperature gradients. See section 4.1.1. for further information related to field temperature observations.
As a result of the field measurements, two negative temperature gradients (ΔT1 = −5.0 °C and ΔT2 = −3.0 °C) were selected for the experimental campaign with the aim of analysing the influence of the water temperature gradient on the diffusion of heat through the sediment layer to estimate the sediment depth. The temperature gradients were established by the difference between the water temperature in the 550 L tank and the initial temperature of the standing water inside the gully pot, which was mainly conditioned by the outer tank temperature control system. Additionally, six experiments were performed under positive-gradient conditions (ΔT3 = +5.0 °C and ΔT4 = +3.0 °C) for inorganic sediments.
Temperature measurements were stored using local data loggers. The measurement sampling frequency ranged from 1 s to 60 s during the experimental campaign to monitor initial temperature changes. A common sampling frequency of 60 s was selected in the analysis of the heat transfer processes.
The durations of the setpoint hydrographs were 20, 30, and 40 min, respectively. After the hydrograph duration was exceeded, data collection continued to monitor the heat recovery in the laboratory-scale gully pot. The overall experiment duration was defined based on the temperature gradient. Thus, experiments with a temperature gradient of ±5.0 °C (ΔT1 and ΔT3) and ±3.0 °C (ΔT2 and ΔT4) lasted 6 and 3 hours, respectively. Fig. 2 provides an overview of the hydraulic and thermal experimental conditions.
3. Methods
3.1. Heat transfer model
Heat transfer in gully pots during rainfall is mainly governed by advection and dispersion processes in the water layer and diffusion processes in the sediment layer. A uniform distribution of the temperature in the water layer was assumed due to fast mixing induced by high-turbulent conditions. In addition, the heat transfer in the sediment layer caused by changes in the water temperature can be addressed by the partial differential equation (PDE) governing the heat diffusion. For the squared geometry of the gully pot, the sensor locations in the model, and assuming isotropic and homogenous thermal properties of the sediment layer, the 2D heat diffusion equation with no heat generation can be expressed as follows: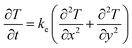 | (1) |
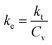 | (2) |
| Tw = f(t) | (3) |
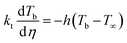 | (4) |
 is the outward normal derivative (°C m−1), T∞ is the ambient soil temperature, which corresponds to the water temperature in the outer tank surrounding the gully pot (°C), and h is the convective heat transfer coefficient (W m−2 °C−1), which depends on the gully pot model material, i.e., PMMA, and can be expressed as h = ktPMMA/e, where ktPMMA is the thermal conductivity of the PMMA and e is the thickness of the gully pot wall.
is the outward normal derivative (°C m−1), T∞ is the ambient soil temperature, which corresponds to the water temperature in the outer tank surrounding the gully pot (°C), and h is the convective heat transfer coefficient (W m−2 °C−1), which depends on the gully pot model material, i.e., PMMA, and can be expressed as h = ktPMMA/e, where ktPMMA is the thermal conductivity of the PMMA and e is the thickness of the gully pot wall.
A MATLAB® subroutine was coded to implicitly solve eqn (1) using the finite difference method, with a node-centred and rectangular discretisation of the sediment layer and a mesh size of 50 mm on the x-axis and 1 mm on the y-axis. Note that the validity of the reduction to two spatial dimensions is stated in the Discussion section. As a result, sediment temperatures could be simulated and compared with the experimental observations at the locations where the sensors were installed. The code is available in ZENODO and can be run on MATLAB® R2017a or later versions.17
3.2. Sediment depth estimation
The comparison between the experimental and simulated temperature time series in the sediment layer was used to estimate the sediment depth. For this purpose, the 2D heat diffusion model was applied considering the following input variables: i) the temperature time series in the water layer (Tw) and outside the gully pot domain (T∞); ii) the sediment thermal properties (kt and Cv); iii) the heat loss at the left, right and bottom boundaries, defined by the convective heat transfer coefficient (h), and iv) the sediment depth (hsed).Since a homogeneous temperature in the water layer was assumed, Tw was obtained by a spatial averaging of the measurements of the sensors above the water–sediment interface. Additionally, T∞ was considered to be equal to the time average of the temperature measurements at the outer tank due to the stability of the temperature control system (±0.1 °C). kt and Cv were measured with a thermal property sensor (TP01) by analysing sediment subsamples and considering the average values of each sediment as the model input. The h-value was defined by the thermal conductivity of the PMMA (ktPMMA) and the thickness (e) of the gully pot wall (see section 3.1). The wall thickness of the gully pot was 18 mm and the ktPMMA for worn PMMA can be ranged between 0.15–0.25 W m−1 °C−1.20 A value of ktPMMA = 0.23 W m−1 °C−1 was assumed after averaging the best fitting ktPMMA-values between the simulated and experimental sediment-bed temperature time series (see ESI†). Consequently, the convective heat transfer coefficient was h = 12.8 W m−2 °C−1. Finally, sediment depth was introduced as an iterative variable (hsedi) that converges when the minimum difference between the experimental measurements and numerical simulations was obtained. A constant sediment depth during each rainfall-runoff event was assumed for the simulations, i.e., no sediment deposition during the inflow. Although the runoff inflow is the main source of sediments entering gully pots, this assumption was supported by the low sediment accumulation rates observed in field campaigns in The Netherlands with maximum rates of 0.94 L per day,4 which correspond to accumulation rates of ∼8 mm for a gully pot cross-section of 350 × 350 mm2. Consequently, the methodology was designed to capture long-term dynamics of sediment build-up.
Sediment temperatures were simulated (Tssimulated) and compared to the experimental measurements (Ts). Average temperature time series of the two sensors buried in the sediment layer and closest to the water–sediment interface were selected for comparison. Temperature measurements from sensors located deeper in the sediment layer were not used because they showed a large temperature attenuation and time lag, thus introducing considerable uncertainties in the sediment depth estimation method. A MATLAB® subroutine based on the Nonlinear Least-Squares algorithm was coded to obtain the sediment depth with the best fit. For this purpose, a Least-Squares objective function was programmed to minimise errors between the simulated temperatures and the experimental measurements in those locations in the sediment layer close to the water–sediment interface. Additionally, model performance was assessed by calculating the absolute error between the sediment depth estimated using the temperature-fit model (hsedm) and that measured with the SfM or using measuring tapes (hsedr), ε = |hsedm − hsedr|. Fig. 3 summarises the input variables to iteratively estimate the sediment depths and perform the model assessment.
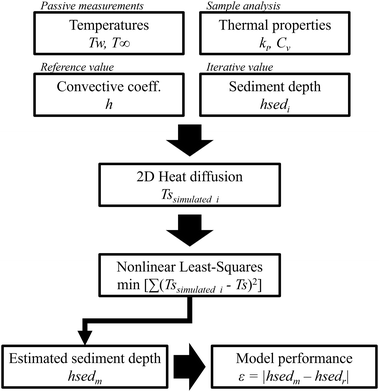 | ||
| Fig. 3 Scheme to estimate sediment depths using the temperature-based model and evaluate its performance. | ||
4. Results
4.1. Heat transfer dynamics in gully pots
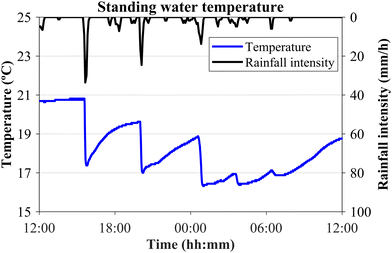 | ||
| Fig. 4 24 hour temperature time series measured in the standing water layer of a gully pot at the Deltares campus. Rainfall intensity data were downloaded from the Met Office Weather Observations Network.19 | ||
The temperature gradients in GP1 were all negative, between −0.4 to −7.0 °C, with a median value of −2.6 °C. Conversely, negative (−0.5 to −6.4 °C) and positive (+0.4 to +1.7 °C) gradients were observed in GP2, with median values of −1.7 and +1.2 °C, respectively. Overall, only 16.7% of the rainfall led to positive gradients. The oscillation between positive and negative temperature gradients was related to the initial standing water temperature of the gully pot, which is influenced mainly by the thermal inertia of the soil. Moreover, the largest temperature gradients occurred when the antecedent dry weather period was greater than 24 hours, thus excluding consecutive rainfalls. Under these circumstances, the median temperature gradients were slightly higher, −3.7 °C in GP1, and −2.7 and +1.7 °C in GP2. The rainfall and temperature gradient field observations are summarised in the ESI† (Table S1).
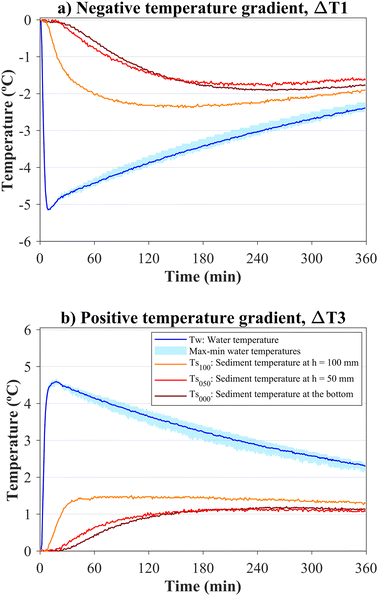
Fig. 5 shows the temperature time series of sensors located in the water layer compared to those at different locations within the sediment layer. The temperature time series of the sediment layer were attenuated compared to the water layer, which was influenced by the inflow temperature into the gully pot. In addition, the temperature attenuation increased in terms of how deep the sensors were placed compared to the water–sediment interface. For instance, the temperature time series influenced by negative gradients, as shown in Fig. 5a, yielded rs-values between the temperature in the water layer and in the sediment layer at heights of 100, 50 and 0 (bottom) mm of 0.01, to −0.65 and −0.78, respectively, highlighting a progressive attenuation of temperatures through the sediment layer. The same pattern was observed for the positive temperature gradients shown in Fig. 5b, with rs-values decreasing from 0.40, to −0.71 and −0.82, respectively. Considering the relative differences in rs-values, the temperature attenuation within the sediment layer was not linear, i.e., the attenuation was higher in those areas closer to the water–sediment interface than those observed between the areas near the bottom of the gully pot. Hence, the deeper the sediment layer, the more challenging it was to observe significant differences in temperature attenuation. For this reason, only the closest sensors to the water–sediment interface were considered for estimating the sediment depth.
Furthermore, no temperature stratification was observed in the water layer due to the uniformity of the outer temperatures established by the temperature control system in the outer tank. The differences between the temperature time series measured at various heights showed absolute deviations less than 0.35 °C, with the largest deviations occurring in the experiments with the lowest sediment depth, i.e., hsed = 50 mm (see ESI,† Fig. S4). Consequently, the mean of the sensor measurements was considered to reflect the reference temperature of the water layer.
| Sediment typea | Volatile contentb (%) | Volumetric water contentc (%) | Bulk densityb(kg m−3) | Thermal conductivityc (W m−1 °C−1) | Volumetric heat capacityc (MJ m−3 °C−1) |
|---|---|---|---|---|---|
| a Submerged conditions. b Laboratory-based measurements in triplicate. c Sensor-based measurements. | |||||
| Sand | 0 | 42.2 ± 0.2 | 1598 ± 26 | 2.168 ± 0.018 | 3.029 ± 0.089 |
| Mixture | 2.2 ± 0.2 | 34.3 ± 3.2 | 1377 ± 20 | 1.739 ± 0.031 | 2.868 ± 0.213 |
| Organic | 14.1 ± 1.9 | 48.1 ± 2.5 | 468 ± 46 | 0.808 ± 0.055 | 3.277 ± 0.163 |
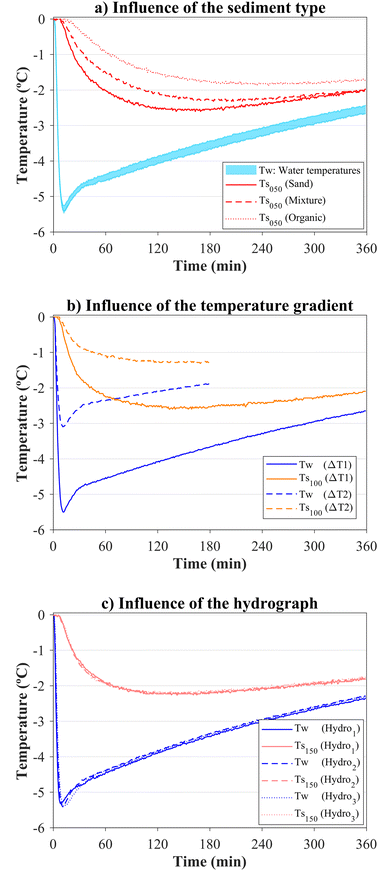
Fig. 6a shows the temperature time series according to sediment type, highlighting the temperature attenuation between the water layer and the sediment at a depth of 50 mm below the water–sediment interface, resulting in rs-values of −0.01, −0.41 and −0.71 for sand, composite mixture, and organic sediments, respectively. This trend indicates that the lower the thermal diffusivity of the sediments, the greater the attenuation of temperatures, i.e., sand, ke = 0.72 mm2 s−1, showed a lower temperature attenuation than the composite mixture, ke = 0.61 mm2 s−1, and the organic sample, ke = 0.25 mm2 s−1.
The influence of temperature gradients and hydrographs on heat transfer processes is related to the temperature of inputs into the water layer. Fig. 6b shows the heat transfer between the water layer and the sediment layer considering the temperature gradients dT1 = −5.0 °C and dT2 = −3.0 °C. High heat transfer to the sediment layer was obtained for high absolute temperature gradients. In the experiments performed with different inflow hydrographs, similar temperature time series were obtained for Hydro1, Hydro2 and Hydro3 conditions (Fig. 6c). Differences were only observed in the negative peaks of the water temperatures, which were time-lagged according to the peak flowrate. However, this peak flow effect was attenuated by the heat transfer to the sediment layer and, consequently, had no influence on sediment depth estimation.
Finally, the sediment depth also influenced the temperature attenuation. Although the distance between the water–sediment interface and the top pair of sensors buried in the sediment layer was similar in all tests, approximately 50 mm, the distance from the bottom boundary, i.e. the depth, affected on the water temperature diffusion in the sediment layer. Fig. 6 qualitatively shows that the attenuation between water and sediment temperatures was similar for depths of 100, 150 and 200 mm, sand-type sediment, temperature gradient ΔT1, and Hydro2 flow conditions. Under these experimental conditions, the rs-values were −0.01, 0.11 and 0.11, respectively, highlighting a similar attenuation between the temperature in the water and the sediment-buried sensors close to the interface. Conversely, the temperature attenuation under the same experimental conditions and a sediment depth of 50 mm was lower than the experiments mentioned above, with a rs-value of 0.47. Therefore, the bottom boundary barely affected on the water temperature diffusion process in the sediment bed for depths greater than 100 mm.
4.2. Sediment depth estimations
.The sediment depth was obtained by estimating the distance between the temperature sensors buried in the sediment layer and the water–sediment interface and adding the reference height at which the sensors were installed. The sediment temperature measurements closest to the sediment–water interface (Ts) were iteratively compared to simulated temperatures (Tssimulated) to obtain the sediment depth of best fit, see examples in the ESI† (Fig. S5). Consequently, sediment depth estimation was influenced by the vertical sensor spacing.Fig. 7 shows the comparison between reference sediment depths measured with the SfM methodology (sand) and measuring tapes (organic and composite mixture) and those estimated with the temperature-based model. The absolute errors between the reference values and the estimated measurements were less than 30 mm in all cases, and the median absolute deviation (MAD) was less than 4 mm. The largest deviations (greater than ±15 mm) were obtained for the composite mixture and reference sediment depths of 200 mm and 250 mm, and for the sand experiment with a positive temperature gradient and a reference sediment depth of 150 mm.
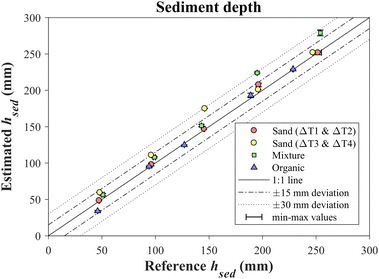 | ||
| Fig. 7 Comparison of the sediment depths estimated with the temperature-based system and the reference measurements obtained by the SfM technique and visual observations. | ||
The deviations were generally more significant for the experiments using organic sediments or composite mixtures than for those performed with sand under negative temperature gradient conditions. The main reason could be the uncertainty of the reference sediment depths measured with the measuring tapes due to the difference between the point measurements and the average sediment depth (±5 mm error). Despite the sediment surface was manually flattened, its uniformity could not be evaluated due to the water turbidity caused by fine particles from the organic sediments. Conversely, the comparison between the estimated sediment depths and the reference measurements with the SfM method for sand resulted in errors of less than 14 mm. The SfM method was used to verify the uniformity (flatness) of the sand surface. As a result, the uniformity coefficients 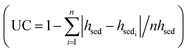 of the sediment depths for the sand experiments ranged from 94 to 99%. Another possible reason why depth estimations for organic sediments and composite mixtures showed larger deviations than sand could be the spatial variability of sediment properties.
of the sediment depths for the sand experiments ranged from 94 to 99%. Another possible reason why depth estimations for organic sediments and composite mixtures showed larger deviations than sand could be the spatial variability of sediment properties.
The sand-depth estimations between experiments with negative and positive temperature gradients were similar (differences of less than 15 mm), except for the sediment depth of 150 mm, in which the estimated value of the positive temperature gradient deviated 30 mm from the reference value. On analysing the temperature series of negative and positive temperature gradient experiments for a sand-depth of 150 mm (Fig. 5a and b), a greater temperature attenuation in the sediment layer was observed in the experiment with the positive temperature gradient, since a significant difference of 0.5 °C between the temperature in the outer tank (T∞) and the initial temperature in the sediment layer was measured. Additionally, deviations in the sediment depth estimations for composite mixtures were positive, which is probably related to the sediment thermal properties and their disposition at the bottom of the gully pot model. Because this sediment was a composite mixture of the sand and organic compounds with different densities (Table 1), the disposition at the bottom might have turned out to be slightly heterogeneous, and as a consequence yield different thermal properties from the laboratory-based measurements.
5. Discussion
Temperature-based systems appear to be a solution to the monitoring of sediment build-up processes in collectors of urban drainage systems, such as gully pots, thus ensuring their efficiency. The methodology was developed based on lab-scale experiments and reference field measurements on gully pots and can be potentially extended to other conditions. The following discussion, then, addresses two main issues: i) the influence of the assumptions of the experimental campaign on the sediment depth estimation, and; ii) the practical applications of temperature-based systems to monitor urban sediment collectors.5.1. Influence of the experiment conditions on the sediment depth estimation
Uniform temperatures could be assumed in the water layer while runoff flowed into the gully pots due to the turbulent mixing processes. However, this assumption is not necessarily met once the runoff inflow stops or under high inflow conditions to cause short flow paths, leaving the water layer without a complete mixing of temperatures. Standing water temperatures remained uniform after the inflow hydrograph in the experimental campaign, in that the absolute temperature deviations at different vertical locations were less than 0.35 °C. The uniformity of the water temperature was indirectly induced by the wall boundary condition. A nearly constant boundary temperature was established using the thermal control system on the wall contours, although real gully pots are influenced by the soil thermal inertia, which may lead to a vertical temperature stratification and, consequently, a transfer of temperature to the water layer of the gully pot once the runoff inflow has stopped. Thus, assuming a uniform temperature in the water layer, when the boundary condition is influenced by a vertical temperature distribution, this may lead to deviations of sediment depth estimations.
Under temperature stratification conditions of the water layer, measuring the water temperature close to the water–sediment interface would be required to determine the top-boundary condition of the heat diffusion model and, subsequently, to estimate the sediment depth accurately. For this purpose, a vertical distribution of temperature sensors is crucial, as well as to know their locations during the installation process and ensure that they remain in the same position during the measurement period. Sensors submerged in the water layer would show a short-term shift in temperatures during inflow, while the temperature signal would be attenuated for sensors buried in the sediment layer. Alternatively, water stratification process could be included in the simulation of heat transfer processes to estimate the sediment depth. However, simulating the water temperature stratification would increase the complexity and computational cost of the heat transfer model by taking into account convective processes in the water layer and air-water interface conditions, as well as measuring water depths.
Sediment type, which is mainly characterised by the organic matter content, was also seen to constitute a sensitive feature in the heat transfer processes due to its relation to thermal properties. Organic gully pot sediments showed higher temperature attenuations than the sand and the composite mixture. Consequently, detecting sediment accumulation at low depths will be easier when the sediments show a high volatile content compared to those inorganic sediments. Nevertheless, estimating large depths will lead to uncertain values, i.e., the depth estimation range is smaller for organic sediments than for sand layers. This has implications for sensor spacing optimisation, which can be quantified using the thermal relaxation time, expressed as t = L2/ke, which relates time-scales (t), distance scales (L) and material properties (thermal diffusivity, ke). In terms of the thermal properties measured for the sand and the organic sediment under a constant time-scale, the following relationship holds: Lsand ∼ 1.7Lorganic, meaning that heat diffusion develops at a distance scale 70% greater in sand layers than in organic sediments and, therefore, spacing of sensors in sand layers can be wider than in organic sediments.
Moreover, significant differences were observed between the thermal properties of sand and organic sediments, e.g. the thermal diffusivity is 2.9 times greater for sand than for organic sediments. Therefore, sediment thermal properties should be determined to accurately estimate the sediment depth. Likewise, the spatial variability of sediment properties should be also considered. These variations may be due to different types of particles transported by runoff, as well as seasonal variations in sediment sources.22 As a solution, laboratory-based measurements were performed to determine sediment thermal properties for the lab-scale experimental campaign. Alternatively, thermal properties could be also measured in situ by including a dual-probe heat-pulse (DPHP) system, similar to Regueiro-Picallo et al.8
Finally, a minor influence of the inflow hydrographs was observed in the water and sediment temperature time series. However, a high variability of rainfall intensities is likely to occur under field conditions, and as a consequence multiple hydrograph scenarios that influence gully pot inflow temperatures come in play. The hydrograph does not have a direct influence on the sediment depth estimation, but does impact the temperature changes of the water layer, which is the top-boundary condition of the heat diffusion model. Therefore, hydrograph variability is captured by the temperature measurements, and no flow measurement is required to perform depth estimations. Furthermore, determining the duration of the inflow hydrograph influence on heat transfer processes is challenging due to the remaining conditions, i.e., sediment properties, wall boundaries, sensor locations, etc. Thus, a fixed event duration must be established to evaluate the heat transfer processes. For example, periods of 3 and 6 hours starting from the entry of the flow into the gully pot were established in the lab-scale experimental campaign (Fig. 2b).
Moreover, flat-bed conditions were established to accurately determine sediment depth using a temperature-based system. However, turbulent processes, especially during heavy rainfall, can resuspend/disturb deposited materials in large sediment depths and lead to bed forms on the sediment surface due to the flow currents from the impinging jet direction and the outflow location (see Rietveld et al.2). Assuming a constant sediment bed, then, constitutes a source of inherent systematic uncertainty in depth estimations when measuring at a single position on the sediment bed surface.
5.2. Practical applications of temperature-based systems to estimate sediment depths in gully pots
Temperature-based systems can be used in field applications to optimise cleaning tasks in gully pots, sediment traps or similar urban drainage infrastructures. The sensor setup used in the lab-scale experimental campaign consisted of temperature sensors attached to the wall with a horizontal orientation, i.e. parallel to the bottom. This configuration might be problematical if, for example, vacuum cleaner systems are used to clean the gully pots. In such cases, a vertical configuration was designed and tested (data in Regueiro-Picallo et al.17), and this can be installed in corners so that it is protected from cleaning and maintenance activities. A corner installation may require a 3D thermal diffusion model to estimate the sediment depth, and potentially would result in a lower sensitivity to changes in depth due to the stronger influence of the wall-boundaries. Alternatively, dismountable systems could be designed so that they could be removed during the cleaning tasks.The methodology could be simplified to a comparison of temperature time series to reduce the complexity of field measurements, where millimetre accuracy is not required, such as determining whether a gully pot should be cleaned to prevent malfunction. For this purpose, temperature measurements from sensors that are submerged in the water layer could be compared with temperatures from sensors close to the bottom. The sediment level would then be obtained by identifying the water–sediment interface position between the pair of sensors that show a high temperature attenuation and time-offset, similar to Sebok et al.23 Consequently, depth measurements could be discretised by installing temperature sensors along the vertical axis of the infrastructure. A high temperature resolution demands a narrower spacing of sensors, thus the addition of more thermal sensors. The number of sensors could be reduced by establishing a threshold depth for cleaning purposes. Alternatively, simplified surrogate models could be developed to increase the accuracy of depth measurements from the temperatures of the water-submerged sensor and the sediment-buried sensor close to the interface, thus monitoring the build-up processes. For this purpose, features of the temperature time series should be defined, similar to Regueiro-Picallo et al.24
Other alternative monitoring techniques include distributed temperature sensing (DTS) systems, such as those used to detect illicit connections in sewer pipes.25 However, the DTS system is not scalable in terms of installation, maintenance costs, and energy consumption for application in multiple gully pots. Active heat-pulse systems could also provide information on the sediment depth by applying methodologies similar to those used to determine the thermal properties of soils and urban sediments.8,26,27 However, depth estimations using active heat-pulse systems would be highly power intensive,8 thus requiring access to a continuous power source or the use of impractically large batteries and chargers. Other potential techniques are laser sensors, such as LiDAR, or acoustic sensors, but they are sensitive to clogging, e.g., spider webs, and therefore are maintenance intensive.
The passive temperature system proposed in the present study is cost-scalable, in that it consists of low-cost sensors with low power consumption. In addition, the technique uses a time-scale for analysis similar to the sediment accumulation processes, which might result in limitations in dry-weather basins where sediments may initiate the rainfall process completely dry, i.e., sediment saturation conditions and therefore thermal properties will change during rainfall-runoff events. Temperature-based systems only provide sediment depth monitoring of those gully pots where they were installed, which is itself a breakthrough for resolving this problem. However, there are thousands of gully pots or sediment traps in urban areas. Therefore, a strategy should be defined to optimise the cost of monitoring and cleaning by establishing a threshold to determine whether a specific gully pot tends to lose sediment retention efficiency in light of all the inherent uncertainties in the measurement. To this end, additional improvements should be made to the temperature-based system, such as data transfer modules for online monitoring of these urban drainage systems.
6. Conclusions
Sediment accumulation in gully pots can reduce the hydraulic capacity of drainage systems during rainfall, causing flooding in urban areas. A methodology based on temperature measurements and the analysis of heat transfer processes was developed to monitor sediment depths. For this purpose, a lab-scale experimental campaign was performed on a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 scale gully pot model, which was designed using reference field measurements. The results of this study show that passive temperature-based systems can be implemented to monitor sediment build-up processes. The main conclusions are as follows:
1 scale gully pot model, which was designed using reference field measurements. The results of this study show that passive temperature-based systems can be implemented to monitor sediment build-up processes. The main conclusions are as follows:
• Field measurements at two gully pots showed that runoff volumes cause thermal gradients in the standing water layer. The observed envelope of temperature gradients ranged from −7.0 °C for negative gradients, and +1.7 °C for positive gradients during the summer season in The Netherlands. Field measurements were used as a reference for the design of a lab-scale experimental campaign, in which two temperature control systems were set up to reproduce temperature patterns.
• The results of the experimental campaign showed that the temperature gradients in the standing water layer were diffused through the sediment layer depending on the sediment thermal properties, the gully pot walls and the bottom boundary conditions (defined by the material and the soil temperature), and the amplitude of the temperature gradient.
• A method for estimating sediment depth from passive temperature measurements and prior knowledge of sensor positions was developed and evaluated. Depth estimations were obtained by iteratively comparing temperature measurements in the sediment layer with simulations of a 2D diffusion heat transfer model. The maximum and median absolute deviations between depth estimations and reference measurements were 30 mm and 4 mm, respectively.
• This technology uses low-cost passive sensors, which require minimal maintenance and are easily scalable to establish sediment monitoring systems in urban drainage systems. No flow measurements are required because its impact is directly captured by the temperature sensors in the standing water layer.
• Further data are still required: i) to describe heat transfer processes in sediment collectors with a wider range of properties, considering anisotropic effects on thermal properties induced by stratified macro-elements in the sediment layer, such as plastics or decomposing leaves; ii) to analyse sediment depth uncertainties based on non-uniform sediment beds; iii) to estimate the performance of temperature sensors installed in the corners of pots, thus facilitating cleaning operations; and iv) to study the economic scalability of the temperature-based technology, since the unit cost is influenced by the optimisation of sensor spacing.
Data availability
The data collected in the laboratory-scale experimental campaign is openly accessible in ZENODO and available in these in-text data citation references: Regueiro-Picallo et al.,17 with a license Creative Commons Attribution 4.0 International (CC BY-NC 4.0). https://doi.org/10.5281/zenodo.10226224.Author contributions
M. R.-P.: investigation, methodology, formal analysis, data curation, writing – original draft; A. M.-R.: funding acquisition, resources, investigation, writing – review & editing; F. C.-M.: funding acquisition, resources, supervision, writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The work developed by Manuel Regueiro-Picallo is funded within the postdoctoral fellowship programmes from the Xunta de Galicia (Consellería de Cultura, Educación e Universidade, ED481B-2021-082 and ED481D-2024-023). This work includes the results from a joint research activity funded by the EU under the Horizon 2020 INFRAIA program (Co-UDlabs project. GA No. 101008626). The authors are also indebted to the members of the ESF department of Deltares, in special Danko Boonstra, Christian van Nieuwenhuizen, Jelle Molenaar, Gerard Vaalburg, Richard Boele, Ben Boon and Jos Ooms, for their support during the experimental campaign. Funding for open access charge: Universidade da Coruña/CISUG.References
- A. Bolognesi, A. Casadio, A. Ciccarello, M. Maglionico and S. Artina, Experimental study of roadside gully pots efficiency in trapping solids washed off during rainfall events, presented in part at 11th International Conference on Urban Drainage, Edinburgh, Scotland, 2008 Search PubMed.
- M. Rietveld, F. Clemens and J. Langeveld, Solids dynamics in gully pots, Urban Water J., 2020, 17(7), 669–680, DOI:10.1080/1573062X.2020.1823430.
- J. A. E. Ten Veldhuis and F. H. L. R. Clemens, The efficiency of asset management strategies to reduce urban flood risk, Water Sci. Technol., 2011, 64(6), 1317–1324, DOI:10.2166/wst.2011.715.
- M. W. J. Rietveld, On the build-up of storm water solids in gully pots, PhD thesis, Delft University of Technology, The Netherlands, 2021 Search PubMed.
- J. A. B. Post, I. W. M. Pothof, J. Dirksen, E. J. Baars, J. G. Langeveld and F. H. L. R. Clemens, Monitoring and statistical modelling of sedimentation in gully pots, Water Res., 2016, 88, 245–256, DOI:10.1016/j.watres.2015.10.021.
- H. Wei, T. M. Muthanna, L. Lundy and M. Viklander, An assessment of gully pot sediment scour behaviour under current and potential future rainfall conditions, J. Environ. Manage., 2021, 282, 111911, DOI:10.1016/j.jenvman.2020.111911.
- M. W. J. Rietveld, F. H. L. R. Clemens and J. G. Langeveld, Monitoring and statistical modelling of the solids accumulation rate in gully pots, Urban Water J., 2020, 17(6), 549–559, DOI:10.1080/1573062X.2020.1800760.
- M. Regueiro-Picallo, J. Langeveld, H. Wei, J.-L. Bertrand-Krajewski and J. Rieckermann, Combining a daily temperature pattern analysis and a heat-pulse system to estimate sediment depths in sewer systems, Environ. Sci.: Water Res. Technol., 2024, 10, 922–935, 10.1039/D3EW00825H.
- A. Figueroa, B. Hadengue, J. P. Leitão, J. Rieckermann and F. Blumensaat, A distributed heat transfer model for thermal-hydraulic analyses in sewer networks, Water Res., 2021, 204, 117649, DOI:10.1016/j.watres.2021.117649.
- M. Abdel-Aal, S. Tait, M. Mohamed and A. Schellart, Using long term simulations to understand heat transfer processes during steady flow conditions in combined sewers, Water, 2021, 13(4), 570, DOI:10.3390/w13040570.
- M. Regueiro-Picallo, A. Schellart, H. Jensen, J. Langeveld, M. Viklander and L. Lundy, Flow rate influence on sediment depth estimation in sewers using temperature sensors, Water Sci. Technol., 2024, 89(11), 3133–3146, DOI:10.2166/wst.2024.193.
- E. T. Hester and K. S. Bauman, Stream and retention pond thermal response to heated summer runoff from urban impervious Surfaces, J. Am. Water Resour. Assoc., 2013, 49(2), 328–342, DOI:10.1111/jawr.12019.
- M. Regueiro-Picallo, J. Suárez, E. Sañudo, J. Puertas and J. Anta, New insights to study the accumulation and erosion processes of fine-grained organic sediments in combined sewer systems from a laboratory scale model, Sci. Total Environ., 2020, 716, 136923, DOI:10.1016/j.scitotenv.2020.136923.
- 3DF Zephyr 7.5: User manual, https://www.3dflow.net/technology/documents/3df-zephyr-documentation/, (accessed 19 March 2024) Search PubMed.
- P. Cignoni, M. Callieri, M. Corsini, M. Dellepiane, F. Ganovelli and G. Ranzuglia, Meshlab: an open-source mesh processing tool, presented in part at Proceedings of the Eurographics Italian chapter conference, Salerno, Italy, 2008, pp. 129–136 Search PubMed.
- APHA, AWWA, WEF, Standard Methods for the Examination of Water and Wastewater, American Public Health Association/American Water Works Association/Water Environment Federation, Washington DC, USA, 20th edn, 1998 Search PubMed.
- M. Regueiro-Picallo, A. Moreno-Rodenas and F. Clemens-Meyer, Measuring sediment deposits in gully pots from temperature signals, ZENODO, 2023, DOI:10.5281/zenodo.10226224.
- M. Rietveld, F. Clemens and J. Langeveld, The mismatch between long-term monitoring data and modelling of solids wash-off to gully pots, Urban Water J., 2022, 19(2), 183–194, DOI:10.1080/1573062X.2021.1986079.
- The UK Met Office Weather Observation Website (WOW), https://wow.metoffice.gov.uk/observations/details/20230130qobp94fyiwe65gsryyb96smpma, (accessed 20 February 2023) Search PubMed.
- Omnexus: The material selection platform, Thermal conductivity, https://omnexus.specialchem.com/polymer-property/thermal-insulation, (accessed 2 April 2024) Search PubMed.
- K. Kim, A. M. Thompson and G. Botter, Modeling of thermal runoff response from an asphalt-paved plot in the framework of the mass response functions, Water Resour. Res., 2008, 44(11), W11405, DOI:10.1029/2007WR005993.
- H. Wei, T. M. Muthanna, L. Lundy and M. Viklander, An evaluation of temporal changes in physicochemical properties of gully pot sediments, Environ. Sci. Pollut. Res., 2022, 29(43), 65452–65465, DOI:10.1007/s11356-022-20341-8.
- E. Sebok, P. Engesgaard and C. Duque, Long-term monitoring of streambed sedimentation and scour in a dynamic stream based on streambed temperature time series, Environ. Monit. Assess., 2017, 189(9), 1–15, DOI:10.1007/s10661-017-6194-x.
- M. Regueiro-Picallo, J. Anta, A. Naves, A. Figueroa and J. Rieckermann, Towards urban drainage sediment accumulation monitoring using temperature sensors, Environ. Sci.: Water Res. Technol., 2023, 9, 3200–3212, 10.1039/D2EW00820C.
- M. Vosse, R. Schilperoort, C. de Haan, J. Nienhuis, M. Tirion and J. Langeveld, Processing of DTS monitoring results: automated detection of illicit connections, Water Pract. Technol., 2013, 8(3–4), 375–381, DOI:10.2166/wpt.2013.037.
- H. He, M. F. Dyck, R. Horton, T. Ren, K. L. Bristow, J. Lv and B. Si, Development and application of the heat pulse method for soil physical measurements, Rev. Geophys., 2018, 56(4), 567–620, DOI:10.1029/2017RG000584.
- M. Shehata, J. Heitman, J. Ishak and C. Sayde, High-resolution measurement of soil thermal properties and moisture content using a novel heated fiber optics approach, Water Resour. Res., 2020, 56(7), e2019WR025204, DOI:10.1029/2019WR025204.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ew00389f |
| This journal is © The Royal Society of Chemistry 2024 |