Doping-mediated excited state dynamics of diphosphine-protected M@Au12 (M = Au, Ir) superatom nanoclusters†
Wei
Pei
 *a,
Lei
Hou
a,
Jing
Yang
a,
Si
Zhou
*bc and
Jijun
Zhao
*a,
Lei
Hou
a,
Jing
Yang
a,
Si
Zhou
*bc and
Jijun
Zhao
 *bc
*bc
aCollege of Physical Science and Technology, Yangzhou University, Yangzhou 225009, China. E-mail: pwei@yzu.edu.cn
bGuangdong Basic Research Center of Excellence for Structure and Fundamental Interactions of Matter, Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, School of Physics, South China Normal University, Guangzhou 510006, China. E-mail: sizhou@m.scnu.edu.cn; zhaojj@dlut.edu.cn
cGuangdong-Hong Kong Joint Laboratory of Quantum Matter, Frontier Research Institute for Physics, South China Normal University, Guangzhou 510006, China
First published on 1st July 2024
Abstract
Doping heterometal atoms into ligand-protected gold superatom nanoclusters (Aun NCs) is proposed to further diversify their geometrical and electronic structures and enhance their photoluminescence properties, which is attributed to the mixing and effects between atoms. However, the fundamental principles that govern the optoelectronic properties of the doped Aun NCs remain elusive. Herein, we systematically explored two prototypical 8-electron Aun (n = 11 and 13) NCs with and without Ir dopant atoms using comprehensive ab initio calculations and real-time nonadiabatic molecular dynamics simulations. These doped Aun NCs maintain their parent geometrical structures and 8-electron superatomic configuration (1S21P6). Strong core–shell (Ir–Aun) electronic coupling significantly expands the energy gap, resulting in a weak nonadiabatic coupling matrix element, which in turn increases the carrier lifetime. This increase is mainly governed by the low-frequency vibration mode. We uncovered the relationship between electronic structures, electron–vibration, and carrier dynamics for these doped Aun NCs. These calculated results provide crucial insights for the atomically precise design of metal NCs with superior optoelectronic properties.
1. Introduction
Ligand-protected gold nanoclusters (Au NCs) hold immense promise as nanoscale functional materials owing to their size-specific physicochemical properties, which can be tailored by the manipulation of their composition, size, and ligands,1,2 rendering them akin to atoms. This analogy extends to magic-sized Au NCs, prized for their atom-like characteristics, where metal atoms mimic nucleons and valence electrons imitate atomic electrons.3–5 This unique behavior opens up diverse applications in luminescence, biomedicine, sensing, photonics, and photo-relative fields.6,7 However, highly luminescent Au NCs remain rare, primarily due to nonradiative relaxation dominating the excited state, resulting in low photoluminescence (PL) quantum yields (<1%), presenting obstacles for practical applications. To address these challenges, several strategies have been explored,8 including core etching and alloying,9 capped-ligand engineering,9 heteroatom doping, aggregation-induced emission (AIE), and surrounding medium.10Among them, atomically precise doping-induced enhancement emerges as a standout strategy for fine-tuning the performance of ligand-protected Au NCs.8,11,12 This approach not only enables the adjustment of the emission properties of Au NCs, but also provides valuable atomic-level insight into the origin of their emission. Through experimentation, Tsukuda et al. synthesized a series of diphosphine-protected M@Au12 (M = Pt, Ir, Ru, Rh, Pd) NCs with PL quantum yields of 46%–67%.13 This dramatic enhancement of PL was attributed to the expansion of the energy gap by the upshifted 1P 8-electron (8e) superatomic orbitals,14 which retarded the nonradiative decay of the photoexcited state by decoupling it from the excited state to the ground state, resulting in a longer excited-state lifetime.15,16 Jin and Ramakrishna et al. demonstrated that thiolate-protected M@Au24 NCs [M@Au24(SR)18] with an 8e superatomic configuration possess a longer excited-state lifetime (50–200 ns) compared to the non-8e configuration of M@Au24(SR)18 (<5 ps).17,18 This phenomenon was attributed to the introduction of heteroatoms, which triggered strong core–shell electron coupling, thereby regulating the distribution and configuration of the valence electron wave function to stabilize the excited state of ligand-protected Au NCs and determine their carrier dynamics behavior.19 Existing experimental measurements to directly observe the relaxation of atoms, electrons and energy in the excited state dynamics of ligand-protected Au NCs remain challenging, hindering the elucidation of the origin of their emission.
Based on the time-dependent density functional theory (TD-DFT), the Aikens group conducted extensive theoretical investigations focusing on the thiolate-protected Au25 NCs and phosphine-protected Au13 NCs,20,21 both exhibiting emissions originating from Au13 core-based transitions, i.e., superatomic 1D → 1P transitions, regardless of different ligands. The tuning of these transition channels is achieved through dopant–Aun cage interactions, which determine the degree of electron–hole overlap, thereby regulating emission energy and intensity for phosphine-protected M@Au12 NCs. Additionally, ab initio real-time nonadiabatic molecular dynamics (NAMD) simulations provide a means to address complex photoexcited phenomena and reveal intricate photoinduced processes at the atomic level.21–24 Recent research has demonstrated that the distinct excited-state behavior of M@Au24(SR)18 NCs is doubly modulated by the sp–d and d–d orbital hybridization strengths of M dopants and the Au13 core in radiative dynamics.25 The configuration of Aun core packing in Aun(SR)m NCs plays a crucial role in tuning electron–phonon couplings, determining the lifetime of excited states.26,27 Compared to thiolate ligands, understanding the mechanisms of the doping effect in phosphine-protected Au NCs remains elusive, as comprehensive calculations combining TD-DFT with NAMD have yet to establish an explicit correlation between the electronic structures and emission properties.
As prototypical phosphine-protected Au NCs, Au11 and Au13 NCs exhibit 1S21P6 configurations based on the jellium model and serve as vital basic building blocks for forming larger or alloyed Aun NCs. Herein, we systematically explored the geometrical, electronic, and absorption properties, and excited-state dynamics of Aun NCs when the central Au atom is replaced by an Ir atom. The interfacial electronic coupling between dopant atoms and the Aun cage plays a crucial role in renormalizing the Kohn–Sham orbital arrangement and tuning the dynamic behavior of photogenerated carriers. Through elucidating the relationship among the carrier lifetime, electronic structures, and electron–vibration coupling, we pave the way for the rational design of ligand-protected metal NCs with targeted optoelectronic properties.
2. Computational methods
All the ground states (S0) and excited states (Sn, n is the number of excited states) were fully optimized using DFT and TD-DFT calculations, as employed in the Gaussian 09 software package.28 According to our previous studies,29 the LANL2DZ and 6-311+G(d) basis sets were used for metal and non-metal atoms, respectively. The optical absorption spectra involve at least 300 possible transition channels. The analysis of electronic structures including charge density distribution of the frontier orbital, transition channel, and natural orbital population was conducted using Multiwfn3.8,30 and the results were visualized using Visual Molecular Dynamics (VMD) software.31 The adaptive natural density partition (AdNDP) method was employed to reveal the multicenter chemical bonding patterns of the ligand-protected Au NCs.32The excited-state dynamics of ligand-protected Au NCs was simulated with Hefei-NAMD implemented in the Vienna ab initio simulation package (VASP)33,34 using a plane-wave basis set with an energy cutoff of 500 eV, projector augmented wave (PAW) potentials,35 and the generalized gradient approximation parameterized by Perdew, Burke, and Ernzerhof (GGA-PBE) for the exchange–correlation functional.36 The ligand-protected Au NCs were placed in a cubic supercell with a lattice constant of 30 Å and their Brillouin zone was sampled using a 1 × 1 × 1 uniform k-point grid.37 We used a velocity rescaling algorithm to maintain the temperature of the system at around 300 K. After that, a 2 ps microcanonical ab initio MD trajectory was generated with a 1 fs time step. The NAMD results were obtained by averaging over 50 different initial configurations randomly selected from the MD trajectory based on the classical path approximation.
3. Results and discussion
3.1 Geometrical structures and orbital analysis
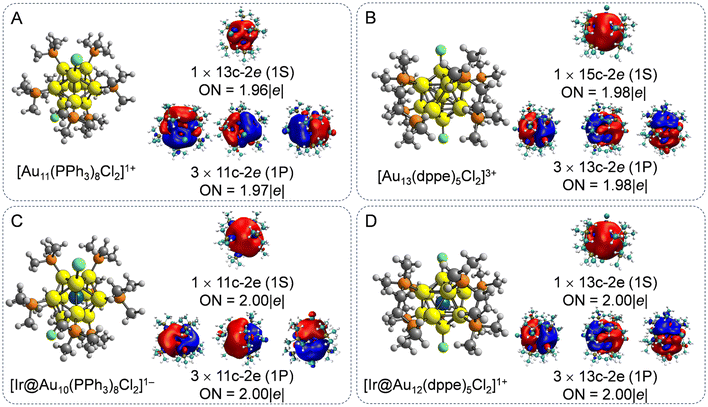
In the laboratory, atomically precise Au NCs with 8e superatomic configurations have been widely synthesized,1,2,8,11,13,38,39 owing to their excellent stabilities and unique molecule-like electronic structures. We first examined the atomic structures of phosphine halide-protected Au11 and Au13 NCs, as the two prototypical 8e Aun NCs. To simplify our models and improve computational efficiency, the –triphenylphosphine (–PPh3) and –diphosphine (–dppe) ligands were replaced by –P(CH3)3 and –PCH2(CH3)2 ligands, respectively. This ligand simplification strategy has been successfully employed to explore the evaluation of geometrical and electronic structures of ligand-protected Aun NCs in the theoretical simulation.39,40 As shown in Fig. 1A and B, the [Au11(PPh3)8Cl2]1+ NCs were composed of an incomplete centered icosahedral Au11 core with C2v symmetry with eight PPh3 ligands and two chloride atoms, while Au13 NCs have a prefect icosahedral Au13 core with D5 symmetry protected by five dppe ligands and two chloride atoms. For the ligand-protected Au–alloy NCs, the center Au atoms were substituted with an Ir atom, possessing reversible redox characteristics between the 1+ and 2+ charge states15 to regulate the electron configuration. Overall, the Ir-doped Aun (n = 10 and 12) NCs maintain their parent configuration well with an average bond length between the Ir atoms and the Au atoms of 2.65–2.79 Å, indicating typical covalent bond interactions.29 Consequently, the Ir@Au10 and Ir@Au12 cores exhibit higher symmetry, corresponding to D4d and Ih, respectively, compared to the C2v and D5 symmetries of undoped Au11 and Au13 NCs(Fig. 1C and D).To deeply understand the chemical bonding interaction of ligand-protected Au NCs with and without Ir dopant atoms, AdNDP analysis was employed to describe multicenter bonding interactions, as shown in Fig. 1. The AdNDP analysis reveals four 11c–2e and 13c–2e σ-aromatic islands in both the doped and undoped Au11 and Au13 NCs, respectively, consistent with the 8e count fulfilling a 1S21P6 electronic shell structure based on the empirical sphere jellium model.41 The aromatic character of these ligand-protected Au NCs originates from the [Au11]3+, [Ir@Au10]1+, [Au13]5+, and [Ir@Au12]3+ cores, further revealing the enhanced stability of Au13-based NCs.42 This multicenter –2e binding pattern is in accordance with previous experimentally systemized [Au19(Hdppa)3(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CPh)9]2+,43 [Au25(SR)18]−,44 Au13Cu4(PPh2Py)3(SePh)9,45 and [Au13Cu2(PPh3)6(SR)6]+.46
CPh)9]2+,43 [Au25(SR)18]−,44 Au13Cu4(PPh2Py)3(SePh)9,45 and [Au13Cu2(PPh3)6(SR)6]+.46
3.2 Absorption spectrum and electronic structures
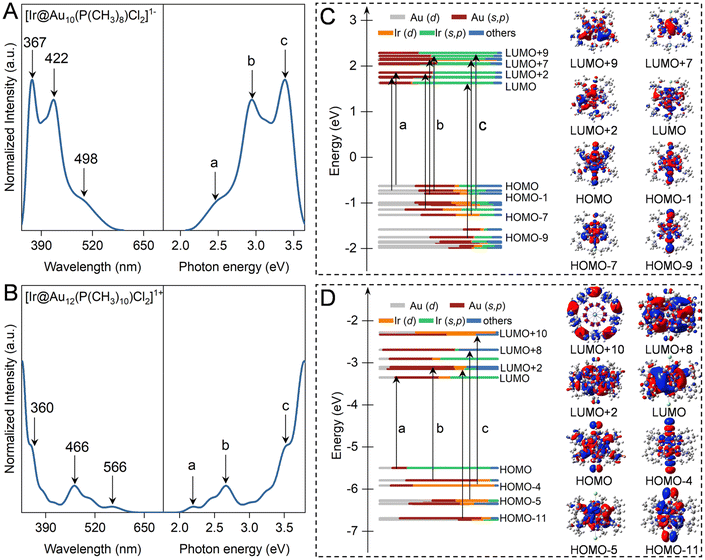
Fig. 2 and S1† illustrate the computed optical absorption spectrum of ligand-protected Aun NCs based on the TD-DFT framework. The undoped Au11 NCs exhibit three prominent peaks at 344 nm, 419 nm, and 477 nm, corresponding to excitation energies of 3.60 eV, 2.96 eV, and 2.60 eV, respectively, consistent with the experimental measurements at 312 nm, 416 nm, and 500 nm.47 According to the transition contribution map, these characteristic peaks of Au11 NCs originate from some discrete excitation states, i.e. HOMO−2 → LUMO (peak a at 477 nm), HOMO−6 → LUMO, HOMO−5 → LUMO+1, and HOMO−4 → LUMO+2 (peak b at 419 nm), and HOMO−9 → LUMO+4, HOMO−3 → LUMO+5, and HOMO−2 → LUMO+8 (peak a at 317 nm). In the Kohn–Sham orbital energy level diagram of ligand-protected Au11 NCs, the molecular orbitals involved in these transitions are mainly composed of 6s5p and 5d10 atomic orbitals.48 The absorption spectrum of [Au13(dppe)5Cl2]3+ NCs consists of prominent absorption peaks at 322 and 387 nm and a shoulder peak at 594 nm, in line with the experimental spectrum of the characteristic peaks of 300 nm, 390 nm, and 560 nm.21 The prominent and shoulder peaks belong to the HOMO−2 → LUMO+7 and HOMO → LUMO+9, respectively, mainly originating from the atomic orbitals of the Au13 core, regardless of ligand atoms. This explains why ligand simplification can be used to describe the light absorption properties of such clusters. According to the sphere jellium model, it is found that superatomic P → D and P → F transitions mainly contribute to the prominent and shoulder absorption peaks of ligand-protected Aun (n = 11 and 13) NCs (Fig. S1†).Replacing the central Au atom with an Ir atom leads to a modification of the jellium potential, resulting in an increased energy gap of Ir@Aun (n = 10 and 12) NCs to 2.16–2.26 eV compared to their parent NCs of 1.86–1.93 eV. This increase can be contributed to the Ir dopant atoms, which have a low electronegativity (∼2.2) and acquire electrons from the Aun cage, causing an upshift in the HOMO and LUMO levels. Moreover, the increase in the LUMO level is significantly greater than that of the HOMO level upon doping with Ir atoms, yielding wider HOMO–LUMO gaps. As shown in Fig. 2A and B, the first absorption peak of Ir@Aun (n = 10 and 12) NCs experiences an obvious blueshift to 498 nm and 566 nm from 530 nm and 594 nm for the undoped Aun (n = 11 and 13) NCs, respectively. The unoccupied d-orbital of Ir induces a strong core–shell interaction, leading to denser Kohn–Sham molecular orbitals near the front orbitals. This density allows for multiple excitations between many electronic states, resulting in broader absorption peaks. The unoccupied orbitals of [Ir@Au10(PPh3)8Cl2]1− NCs are composed of 6s5p orbitals of Ir and Au atoms, while the occupied ones are mixed composites with 5d and 6s5p of Ir and Au atoms. The contributions to the three strong absorption peaks of ligand-protected Ir@Au10 NCs come from electronic transitions between the 5d10 atomic orbitals of the Au10 cage and the 6s5p orbital of Ir atoms, involving a typical core–shell transition behavior (Fig. 2C). In contrast, the HOMOs of [Ir@Au12(dppe)5Cl2]1+ NCs are mainly composed of the 6s5p orbital of Ir atoms(Fig. 2D), which are excited to the Au12 cage and its d orbital to participate in electronic transitions. Therefore, heteroatom doping can redistribute the electronic charge within the nanocluster, influencing both radiative and non-radiative recombination processes. This redistribution can significantly affect the photoluminescence properties of the material, either enhancing or quenching it, depending on the nature of the dopant atoms and their positions within the cluster.
3.3 Excited state dynamics behavior
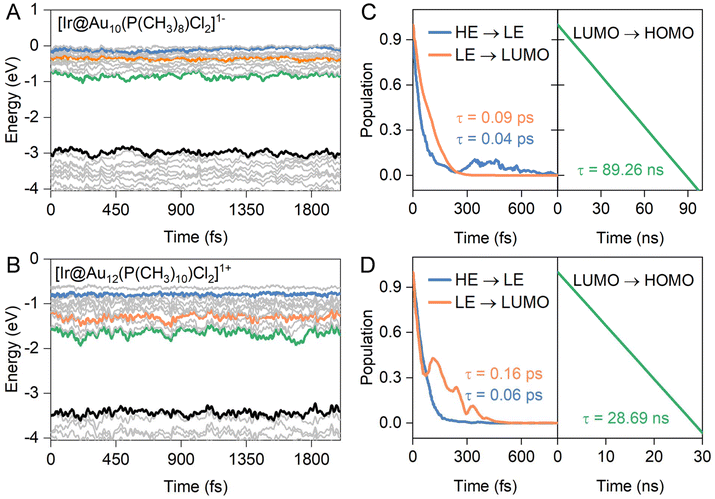
According to the experimental femtosecond transient absorption spectrum of ligand-protected Au NCs,49–51 the hot electrons in the high energy (HE)-excited states are first relaxed to the low-energy (LE) excited states and then to the position of the LUMO via a strong internal conversion, both of which are nonradiative processes. Subsequently, the electron in the LUMO experiences a weaker decay process to recombine with the hole in the HOMO, involving radiative transition, thereby yielding luminescence. To identify the key states involved in the dynamics and quantify the timescale of various processes, the HE and LE states for our ligand-protected Au NCs are presented as blue and orange lines in Fig. 3A and B, respectively, according to the orbital transition map of optical absorption combined with the orbital delocalization index. Therefore, we chose positions higher than LUMO ∼ 1.00 eV and ∼0.50 eV as the initial states of high- and low-excited states for hot electron relaxation, respectively. It should be noted that there are HE and LE states showing superatomic F and D characteristics, respectively, akin to typical superatomic fullerene clusters.52 The LUMO and HOMO constitute the initial and final states for the electron–hole (e–h) recombination across the energy gap for ligand-protected Au NCs. It is noteworthy that hot electron transitions between the HE and LE states, as well as between the LE and LUMO states, have a narrower energy gap, for which the fewest-switches surface-hopping (FSSH) method was employed.53 However, the e–h recombination experiences a wider energy gap within a range from 1.77 eV to 2.36 eV. Quantum decoherence significantly influences this dynamic process, and thus, the decoherence-induced surface hopping (DISH) method was selected for simulations.54Indeed, electron–phonon (e–p) interactions at finite temperature can exert a significant influence on the electronic structures of a system.55,56Fig. 3 and S2† depict the time-dependent evolution of the frontier orbitals for both undoped and doped ligand-protected Au11 and Au13 NCs calculated from ab initio molecular dynamics (AIMD) simulations within a micro-canonical ensemble for 2000 fs at 300 K. As a result, the high-energy excited state exhibits lower pronounced time-dependent oscillations, involving smaller vibration amplitudes within a range of 0.13–0.25 eV than that of the other three frontier orbitals (0.33–0.48 eV for LE, 0.38–0.56 eV for the LUMO, and 0.33–0.48 eV for the HOMO), irrespective of the presence of dopant atoms. The distinct e–p coupling-induced orbital renormalization is associated with the dynamics behavior of hot electrons in both carrier relaxation and recombination.26,56 As shown in Fig. S2C and S2D,† the excited electrons of high-energy states relax to LE states (HE → LE) within the range of 1.23–3.64 ps for the undoped ligand-protected Au NCs, slightly longer than that of the Ir-doped systems (0.09–0.16 ps in Fig. 3C and D). Similarly, the LE → LUMO process exhibits fast electron relaxation behavior, with short timescales of 0.04–0.06 ps and 0.21–1.31 ps for the doped and undoped Au NCs, respectively. This discrepancy may be attributed to the heteroatom-induced denser arrangement of energy levels, resulting in lower nonadiabatic coupling elements between the initial states and the final states of electron transitions (more on this later).
In contrast to the aforementioned processes, the presence of an Ir dopant significantly suppresses the e–h recombination, leading to a prolonged carrier lifetime (τ). The carrier lifetime of ligand-protected Ir@Au12 NCs is approximately ∼29 ns, nearly three times longer than that of Au13 NCs at ∼10 ns, consistent with experimental measurements where the photoluminescence lifetime of Ir@Au12 is reported to be 2–3 times higher than that of Au13.16 This trend is further highlighted by the calculated e–h recombination of ∼89 ns for Ir@Au10 NCs, showing the slowest decay time constant, much higher than that of undoped Au11 NCs at τ = ∼22 ns. These phosphine-protected Au NCs possess longer carrier lifetimes compared to those of thiolate-protected Au NCs [M@Au24(SR)18]− (M = Pd, Pt, Cd, Hg) of 0.1–8 ns based on the DISH method.25 In general, the lifetime of e–h recombination follows the sequence: Ir@Au10 > Ir@Au12 > Au11 > Au13. The overall trend of carrier lifetimes observed in the four NCs is in line with previous experimental reports based on the time-resolved photoluminescence decay of ligand-protected Au NCs.16,38 However, it is worth noting that the difference in carrier lifetimes between the NCs in our simulations is not as pronounced as observed in experimental studies. This discrepancy could be attributed to the experimental use of crystal structures of gold NCs, which introduces additional factors influencing carrier dynamics, including inter-cluster interactions and overall lattice symmetry.26,27
In previous theoretical studies based on NAMD simulations, the probability of hot electron relaxation is found to be sensitive to the nonadiabatic coupling (NAC) elements between the acceptor and donor states, which is defined as34,57
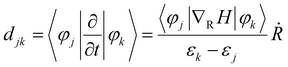 | (1) |
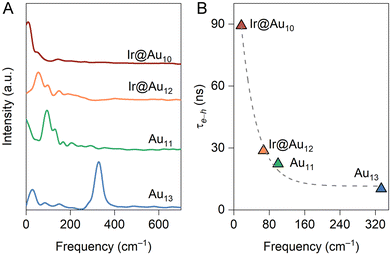
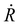 corresponds to nuclear velocity. Generally, a narrower energy gap and stronger e–p coupling lead to a larger NAC element, resulting in faster hot electron transition from the donor level to the acceptor level. Table 1 summarizes the average values of energy gap, NAC elements, and hot electron relaxation lifetimes of ligand-protected Aun NCs with and without Ir dopants for the three electron transition channels mentioned above. In both the processes of HE → LE and LE → LUMO, the NAC strength is enhanced upon Ir doping, corresponding to the range of 3.74–8.45 meV with regard to the undoped system in the range of 2.14–6.05 meV. This enhancement in inelastic electron–vibrational scattering leads to faster electron transitions for Ir@Aun (n = 10 and 12) NCs.58 The strong core–shell (Ir–Au10 and Ir–Au12) electronic coupling significantly increases the HOMO–LUMO gap,29 which results in weaker NAC elements (0.45–0.52 meV), suppressing the e–h recombination. We further explored the phonon excitations and e–p coupling via the Fourier transform of the autocorrelation functions of the HOMO–LUMO gap fluctuations (Fig. 4A). Except for the undoped Au13 NCs, the dominant phonon modes are low-frequency vibrational modes within a range of 0–200 cm−1, which can be assigned to the bending, stretching, and liberation modes of the Aun core unit.59 The Au13 NCs show an intermediate frequency vibrational mode of ∼333 cm−1, corresponding to the normal modes of Au–Cl and Au–P bonds.60 The low-frequency phonon modes are associated with the heavy atoms characterized by small nuclear velocities and weak electron–phonon interactions, resulting in a small NAC matrix element and a long carrier lifetime (Fig. 4B). These results suggest that the dopant-induced enhancement of the carrier lifetime of ligand-protected Au NCs can be attributed to both a stronger core–shell interaction resulting in a larger energy gap and tunable electron–vibration coupling determining the coupling of the frontier orbital.
corresponds to nuclear velocity. Generally, a narrower energy gap and stronger e–p coupling lead to a larger NAC element, resulting in faster hot electron transition from the donor level to the acceptor level. Table 1 summarizes the average values of energy gap, NAC elements, and hot electron relaxation lifetimes of ligand-protected Aun NCs with and without Ir dopants for the three electron transition channels mentioned above. In both the processes of HE → LE and LE → LUMO, the NAC strength is enhanced upon Ir doping, corresponding to the range of 3.74–8.45 meV with regard to the undoped system in the range of 2.14–6.05 meV. This enhancement in inelastic electron–vibrational scattering leads to faster electron transitions for Ir@Aun (n = 10 and 12) NCs.58 The strong core–shell (Ir–Au10 and Ir–Au12) electronic coupling significantly increases the HOMO–LUMO gap,29 which results in weaker NAC elements (0.45–0.52 meV), suppressing the e–h recombination. We further explored the phonon excitations and e–p coupling via the Fourier transform of the autocorrelation functions of the HOMO–LUMO gap fluctuations (Fig. 4A). Except for the undoped Au13 NCs, the dominant phonon modes are low-frequency vibrational modes within a range of 0–200 cm−1, which can be assigned to the bending, stretching, and liberation modes of the Aun core unit.59 The Au13 NCs show an intermediate frequency vibrational mode of ∼333 cm−1, corresponding to the normal modes of Au–Cl and Au–P bonds.60 The low-frequency phonon modes are associated with the heavy atoms characterized by small nuclear velocities and weak electron–phonon interactions, resulting in a small NAC matrix element and a long carrier lifetime (Fig. 4B). These results suggest that the dopant-induced enhancement of the carrier lifetime of ligand-protected Au NCs can be attributed to both a stronger core–shell interaction resulting in a larger energy gap and tunable electron–vibration coupling determining the coupling of the frontier orbital.
| HE → LE | LE → LUMO | LUMO → HOMO | |||||||
|---|---|---|---|---|---|---|---|---|---|
| System | ΔE (eV) | NAC (meV) | Time (ps) | ΔE (eV) | NAC (meV) | Time (ps) | ΔE (eV) | NAC (meV) | Time (ns) |
| Au11 | 0.57 | 2.68 | 1.23 | 0.62 | 6.05 | 0.21 | 1.86 | 0.57 | 22.33 |
| Ir@Au10 | 0.17 | 8.45 | 0.09 | 0.36 | 3.74 | 0.04 | 2.36 | 0.45 | 89.26 |
| Au13 | 1.18 | 1.98 | 3.64 | 0.71 | 2.14 | 1.31 | 1.77 | 0.71 | 10.21 |
| Ir@Au12 | 0.41 | 4.29 | 0.16 | 0.34 | 4.37 | 0.06 | 1.96 | 0.52 | 28.69 |
4. Conclusion
In summary, we systematically explored the excited state dynamics of two prototypical 8e Aun NCs (n = 11 and 13) with and without Ir dopant atoms using first-principles calculations combined with NAMD simulations. Owing to the strong core–shell (Ir–Aun) electronic coupling, the HOMO–LUMO gap of the doped Aun NCs was significantly increased, leading to an obvious blueshift in their absorption spectrum compared to that of pristine systems. The high-energy excited state possesses low pronounced time-dependent oscillation, having fast hot electron relaxation regardless of the presence of dopant atoms. In e–h recombination, Ir dopant atoms induced an obvious inhibiting effect, which was governed by both the value of the energy gap and the peak of low-frequency phonon modes between the LUMO and the HOMO. This systematic study provides a practically useful guide to tuning the electronic structures and phonon modes to regulate the excited-state dynamic behavior of ligand-protected Au NCs by heteroatom doping.Data availability
The data supporting the findings of this study are available within the article and its ESI.† Additional data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (12304300 and 12222403), the Natural Science Foundation of Jiangsu Province (No. BK20230555), the Natural Science Foundation of Jiangsu Higher Education Institutions of China (No. 23KJB140019), and the Outstanding Doctor Program of Yangzhou City ‘Lv Yang Jin Feng’ (No. YZLYJFJH2022YXBSO84).References
- M. R. Narouz, K. M. Osten, P. J. Unsworth, R. W. Y. Man, K. Salorinne, S. Takano, R. Tomihara, S. Kaappa, S. Malola, C.-T. Dinh, J. D. Padmos, K. Ayoo, P. J. Garrett, M. Nambo, J. H. Horton, E. H. Sargent, H. Häkkinen, T. Tsukuda and C. M. Crudden, Nat. Chem., 2019, 11, 419–425 CrossRef CAS.
- H. Hirai, S. Takano, T. Nakamura and T. Tsukuda, Inorg. Chem., 2020, 59, 17889–17895 CrossRef CAS.
- Z. Luo and A. W. Castleman, Acc. Chem. Res., 2014, 47, 2931–2940 CrossRef CAS.
- Z. Luo and S. Lin, Coord. Chem. Rev., 2024, 500, 215505 CrossRef CAS.
- B. D. Peter, W. Pei, G. N. Andrew, S. Zhou and Z. Luo, Nanoscale, 2024, 16, 8090–8095 RSC.
- L. Liu, P. Li, L.-F. Yuan, L. Cheng and J. Yang, Nanoscale, 2016, 8, 12787–12792 RSC.
- D.-e. Jiang and S. Dai, Inorg. Chem., 2009, 48, 2720–2722 CrossRef CAS.
- X. Kang and M. Zhu, Chem. Soc. Rev., 2019, 48, 2422–2457 RSC.
- H.-H. Deng, X.-Q. Shi, F.-F. Wang, H.-P. Peng, A.-L. Liu, X.-H. Xia and W. Chen, Chem. Mater., 2017, 29, 1362–1369 CrossRef CAS.
- L.-Y. Chen, C.-W. Wang, Z. Yuan and H.-T. Chang, Anal. Chem., 2015, 87, 216–229 CrossRef CAS.
- H. Qian, M. Zhu, Z. Wu and R. Jin, Acc. Chem. Res., 2012, 45, 1470–1479 CrossRef CAS.
- M. Ebina, T. Iwasa, Y. Harabuchi and T. Taketsugu, J. Phys. Chem. C, 2018, 122, 4097–4104 CrossRef CAS.
- H. Hirai, S. Takano, T. Nakashima, T. Iwasa, T. Taketsugu and T. Tsukuda, Angew. Chem., Int. Ed., 2022, 61, e202207290 CrossRef CAS PubMed.
- S. Takano, H. Hirai, T. Nakashima, T. Iwasa, T. Taketsugu and T. Tsukuda, J. Am. Chem. Soc., 2021, 143, 10560–10564 CrossRef CAS.
- H. Hirai, S. Takano, T. Nakamura and T. Tsukuda, Inorg. Chem., 2020, 59, 17889–17895 CrossRef CAS.
- H. Hirai, T. Nakashima, S. Takano, Y. Shichibu, K. Konishi, T. Kawai and T. Tsukuda, J. Mater. Chem. C, 2023, 11, 3095–3100 RSC.
- M. Zhou, C. Yao, M. Y. Sfeir, T. Higaki, Z. Wu and R. Jin, J. Phys. Chem. C, 2018, 122, 13435–13442 CrossRef CAS.
- V. D. Thanthirige, M. Kim, W. Choi, K. Kwak, D. Lee and G. Ramakrishna, J. Phys. Chem. C, 2016, 120(40), 23180–23188 CrossRef CAS.
- S. Maity, S. Kolay, S. Ghosh, S. Chakraborty, D. Bain and A. Patra, J. Phys. Chem. Lett., 2022, 13, 5581–5588 CrossRef CAS.
- R. D. Senanayake, A. V. Akimov and C. M. Aikens, J. Phys. Chem. C, 2017, 121, 10653–10662 CrossRef CAS.
- K. L. D. M. Weerawardene, P. Pandeya, M. Zhou, Y. Chen, R. Jin and C. M. Aikens, J. Am. Chem. Soc., 2019, 141, 18715–18726 CrossRef CAS.
- K. L. D. M. Weerawardene, E. B. Guidez and C. M. Aikens, J. Phys. Chem. C, 2017, 121, 15416–15423 CrossRef CAS.
- K. L. D. M. Weerawardene and C. M. Aikens, J. Phys. Chem. C, 2018, 122, 2440–2447 CrossRef CAS.
- R. D. Senanayake, E. B. Guidez, A. J. Neukirch, O. V. Prezhdo and C. M. Aikens, J. Phys. Chem. C, 2018, 122, 16380–16388 CrossRef CAS.
- X. Yu, Y. Sun, W.-w. Xu, J. Fan, J. Gao, X. Jiang, Y. Su and J. Zhao, Nanoscale Horiz., 2022, 7, 1192–1200 RSC.
- X. Yu, W. Pei, W.-w. Xu, Y. Zhao, Y. Su and J. Zhao, Inorg. Chem., 2023, 62, 20450–20457 CrossRef CAS PubMed.
- X. Yu, Y. Su, W.-w. Xu and J. Zhao, J. Phys. Chem. Lett., 2021, 12, 2312–2319 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, Wallingford Ct, 2009, vol. 2009.
- J. She, W. Pei, S. Zhou and J. Zhao, J. Phys. Chem. Lett., 2022, 13, 5873–5880 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- Q. Zheng, W. Chu, C. Zhao, L. Zhang, H. Guo, Y. Wang, X. Jiang and J. Zhao, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1411 CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- X.-J. Zhai, J.-H. Hu, J. Guan, Y. Si, X.-Y. Dong, P. Luo, F. Pan, Z. Yu, R. Han and S.-Q. Zang, Nano Res., 2023, 16, 11366–11374 CrossRef CAS.
- D. Yang, W. Pei, S. Zhou, J. Zhao, W. Ding and Y. Zhu, Angew. Chem., Int. Ed., 2020, 59, 1919–1924 CrossRef CAS.
- S. Zhao, N. Austin, M. Li, Y. Song, S. D. House, S. Bernhard, J. C. Yang, G. Mpourmpakis and R. Jin, ACS Catal., 2018, 8, 4996–5001 CrossRef CAS.
- S. B. Zhang, M. L. Cohen and M. Y. Chou, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 3455–3458 CrossRef CAS PubMed.
- N. Fedik, A. I. Boldyrev and A. Muñoz-Castro, Phys. Chem. Chem. Phys., 2019, 21, 25215–25219 RSC.
- X.-K. Wan, Q. Tang, S.-F. Yuan, D.-e. Jiang and Q.-M. Wang, J. Am. Chem. Soc., 2015, 137, 652–655 CrossRef CAS PubMed.
- J. J. Li, Z. J. Guan, Z. Lei, F. Hu and Q. M. Wang, Angew. Chem., 2019, 131, 1095–1099 CrossRef.
- Y. Song, Y. Lv, M. Zhou, T.-Y. Luo, S. Zhao, N. L. Rosi, H. Yu, M. Zhu and R. Jin, Nanoscale, 2018, 10, 12093–12099 RSC.
- H. Yang, Y. Wang, J. Lei, L. Shi, X. Wu, V. Mäkinen, S. Lin, Z. Tang, J. He and H. Häkkinen, J. Am. Chem. Soc., 2013, 135, 9568–9571 CrossRef CAS.
- L. C. McKenzie, T. O. Zaikova and J. E. Hutchison, J. Am. Chem. Soc., 2014, 136, 13426–13435 CrossRef CAS PubMed.
- M. Zhu, C. M. Aikens, F. J. Hollander, G. C. Schatz and R. Jin, J. Am. Chem. Soc., 2008, 130, 5883–5885 CrossRef CAS.
- W. Zhang, J. Kong, Y. Li, Z. Kuang, H. Wang and M. Zhou, Chem. Sci., 2022, 13, 8124–8130 RSC.
- M. Zhou, C. Zeng, M. Y. Sfeir, M. Cotlet, K. Iida, K. Nobusada and R. Jin, J. Phys. Chem. Lett., 2017, 8, 4023–4030 CrossRef CAS PubMed.
- Q. Li, M. Zhou, W. Y. So, J. Huang, M. Li, D. R. Kauffman, M. Cotlet, T. Higaki, L. A. Peteanu and Z. Shao, J. Am. Chem. Soc., 2019, 141, 5314–5325 CrossRef CAS.
- H. Guo, C. Zhao, Q. Zheng, Z. Lan, O. V. Prezhdo, W. A. Saidi and J. Zhao, J. Phys. Chem. Lett., 2018, 9, 3485–3490 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- H. M. Jaeger, S. Fischer and O. V. Prezhdo, J. Chem. Phys., 2012, 137, 22A545 CrossRef PubMed.
- W. Chu, Q. Zheng, O. V. Prezhdo, J. Zhao and W. A. Saidi, Sci. Adv., 2020, 6, eaaw7453 CrossRef CAS.
- W. Chu, W. A. Saidi, J. Zhao and O. V. Prezhdo, Angew. Chem., Int. Ed., 2020, 59, 6435–6441 CrossRef CAS.
- C. F. Craig, W. R. Duncan and O. V. Prezhdo, Phys. Rev. Lett., 2005, 95, 163001 CrossRef PubMed.
- C. Zhang, Y. Shi, Y. Si, M. Liu, L. Guo, J. Zhao and O. V. Prezhdo, Nano Lett., 2022, 22, 6334–6341 CrossRef CAS PubMed.
- M. Kato, Y. Shichibu, K. Ogura, M. Iwasaki, M. Sugiuchi, K. Konishi and I. Yagi, J. Phys. Chem. Lett., 2020, 11, 7996–8001 CrossRef CAS.
- A. Wing-Bocanegra and A. Tlahuice-Flores, Phys. Chem. Chem. Phys., 2019, 21, 23855–23864 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Optical absorption spectrum and time evolution of the Kohn–Sham molecular orbital of ligand-protected Au NCs. See DOI: https://doi.org/10.1039/d4nr02051k |
| This journal is © The Royal Society of Chemistry 2024 |