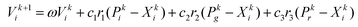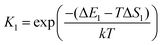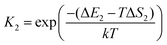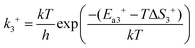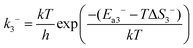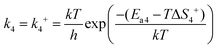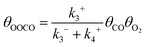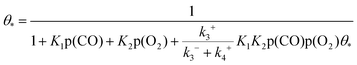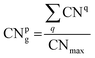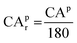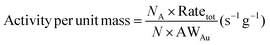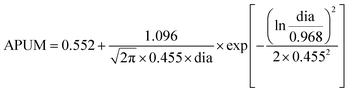DOI:
10.1039/D4NR02705A
(Paper)
Nanoscale, 2024,
16, 18871-18881
Size-dependent catalytic activity for CO oxidation over sub-nano-Au clusters†
Received
30th June 2024
, Accepted 5th September 2024
First published on 5th September 2024
Abstract
Gold (Au) nanocatalysts present outstanding activity for many reactions and have long attracted much attention, but the size effect of sub-nano-clusters on catalytic activity lacks systematic research. Using CO oxidation as a probe reaction, the size-dependent catalytic capability of sub-nano-Au clusters was explored. The global-minimum (GM) structures of AuN (N = 2–300, <2.5 nm) were obtained utilizing revised particle swarm optimization (RPSO) combined with density functional theory (DFT) calculations and the Gupta empirical potential. Geometric structural descriptors built a bridge among geometric features, adsorption energy, and the CO oxidation rate of each site of any given sub-nano-Au clusters, making it possible for high-throughput evaluation of the adsorption energy and catalytic activity of the whole sub-nano-Au cluster. The activity per unit mass of sub-nano-Au clusters shows a volcano-shaped relationship with the cluster size, where the sub-nano-Au clusters with a 0.75 nm diameter possess the highest CO2 formation rate per unit mass. The Edge and Kink sites have a higher turnover frequency (approximately 106) than the Face sites (approximately 102), which contribute the most to CO2 formation. The weak adsorption of CO and O2 was found to be a crucial factor determining the inferior activity of the Face site to the Kink and Edge sites. The adsorption process rather than the surface reaction step becomes the rate-determining step on the Face site, attributed to the decreased activity per unit mass of sub-nano-Au clusters. This work provides an in-depth mechanistic understanding of size-dependent catalytic activity for Au clusters at the sub-nano level.
1 Introduction
Gold (Au) had been considered chemically inert for a long time, until the discovery of Au clusters’ remarkable catalytic properties by Hutchings et al. in their pioneering works.1 Au clusters have exhibited extraordinarily high activities for various reactions,2 including low-temperature catalytic combustion, partial oxidation of hydrocarbons, selective reduction of nitrogen oxides,3etc. The high activity of these Au clusters could be partly attributed to their high surface-to-volume ratio, surface atom arrangement, low-coordinated atoms and so on.4 On the one hand, the constituent atoms of the Au clusters are arranged in a significantly different manner from that of bulk gold to reduce the surface energy. On the other hand, the electronic structures of Au clusters are quantized with an energy gap so that reactants can be activated via electron transfer.5
Donoeva et al.,2 Sh. K. Shaikhutdinov et al.,6 and G. R. Bamwenda et al.7 explored the CO catalytic activity of Au clusters at the nanoscale (at least 2.5 nm). In this range, only Au particles smaller than 5 nm are active in low-temperature CO oxidation,2 and a further increase in the cluster diameter above 3 nm leads to a decrease in the activity of Au clusters.7 Celine et al. for the first time reported the experimental evidence that nano-Au island films have the same CO adsorption behavior as both large Au particles and extended Au surfaces,8 which highlights the particularity of sub-nano-Au clusters. For sub-nano-structures, the ultra-small size induces strong electron energy quantization.4 Yamazoe et al. discovered that sub-nano-Au clusters less than 2 nm could show obvious catalytic effects in various aerobic oxidation reactions. In the hydrogenation processes, gold nanoparticles ranging from 1 to 2 nm exhibit good catalytic activity.9
The outstanding catalytic properties of Au clusters are highly dependent on their size.10,11 Size effects on adsorption and reactivity play a very important role in the excellent catalytic performance of Au clusters, a phenomenon that has been observed for decades.8 Goodman's group invoked the concept of quantum effects.3 The size-dependent catalytic activity could be attributed to the size-dependent adsorption behaviors, which are induced by the size-dependent electronic structures of Au clusters.12
The exploration of size-dependent catalytic activity through theoretical calculations has also been conducted. Nørskov et al. predicted that Au10 can be highly active for CO oxidation in the gas phase.13 Bernhardt et al. revealed the full reaction cycle of CO oxidation on Au2 and Au3 by performing ab initio calculations.14,15 Kaatz et al. studied larger Au clusters (2–6 nm) to conclude that low coordination leads to a higher turnover frequency.16 However, the size-dependent catalytic activity in lots of literature is limited to the nanoscale (>3 nm), and the Au cluster models are often established through highly symmetric polyhedral configurations or employing Wulff construction rules, which retain the atom arrangement of the Au bulk crystal structure. As for sub-nano-Au clusters (<3 nm) with GM structures tend to be irregular, neither the distribution of active sites nor size-dependent catalytic activity has long been a lack of attention, which hinders the construction of sub-nano-Au clusters with enhanced catalytic performance. The lack of both sub-nano-Au clusters’ GM configuration and detailed structure–activity research within this diameter range is not conducive to further progress of Au catalysts.
In this paper, using CO oxidation as a probe reaction, a comprehensive study of Au clusters at the sub-nano level was carried out, mainly focusing on Au clusters composed of 2 to 300 atoms with a diameter less than 2.5 nm. Their GM configurations were identified using the RPSO algorithm based on DFT calculations and the Gupta empirical potential. The elaborate description of size-dependent catalytic performance at each site one by one was achieved by the systematic classification of adsorption sites utilizing the generalized coordination number. A geometry–adsorption–activity relationship is built to analyze the size-dependent catalytic activity of sub-nano-Au clusters. Aided by a microkinetic model and electronic structure analysis, a detailed discussion of how the geometric coordination feature of reaction sites affects catalytic performance was conducted.
2 Computational details
2.1 Revised particle swarm optimization
Based on the particle swarm algorithm (PSO), which is an efficient method for global optimization, our group developed a revised particle swarm optimization (RPSO) algorithm in order to overcome the tendency of the original PSO to be easily trapped in local minima.17 RPSO consists of a random learning procedure, competition strategy, confusion policy, and mutation mechanism. These efforts make RPSO an outstanding algorithm for the global optimization of complex nonlinear systems. In the previous work,17 the global optimization of Lennard-Jones (LJ), elemental metal, and bimetallic clusters was conducted successfully, which strongly supports the efficiency. The evolution part of the RPSO could be explained by the following equation:| | 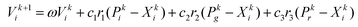 | (1) |
where Vki is the velocity of the particle i in the swarm at iteration k. ω remains the same as the original PSO standing for the inertia weight factor from 0.9 to 1. Besides c1 and c2 as acceleration constants, RPSO imports a new acceleration constant c3 to maintain population diversity. r, r2, and r3 are uniformly distributed random numbers between 0 and 1. The four parts on the right side of eqn (1) are named inertia, local, global, and random. The term random represents the random learning procedure that could boost the convergence speed.
2.2 Structural global optimization of Au clusters
The potential energy surface (PES) of Au clusters is explored using RPSO combined with first-principles calculations as well as the Gupta empirical potential. The RPSO method is capable of surmounting the high barrier on the PES and identifying GM structures. The capability of this method for exploring the PES has been demonstrated for both transition monometallic clusters like Ag18 and bimetallic Pt–Pd clusters.17 The Rosenbrock function of different dimensions17,19 and 15 benchmark functions in CEC17,20 served as test cases, and RPSO showed better performance in searching for the global best solution. Although RPSO is a global optimization method with high efficiency, its application with DFT calculations is still time-consuming. Therefore, Au clusters with more than 20 atoms are searched with RPSO at the Gupta empirical potential level to make a trade-off between precision and efficiency in this work. The empirical potential is much more efficient in generating highly symmetric Au structures with lower computational costs than ab initio methods.21,22 The Gupta potential in this work could enable a reasonable description of the metal clusters’ PES.23 Additionally, empirical potentials originate from the approximation of bulk materials and thus are prone to overestimating atomic interactions, which can affect the evaluation of system energy. Therefore, an energy correction step is necessary.
All calculations of freestanding Au clusters are carried out with a vacuum layer of at least 10 Å in all three directions to prevent interaction forces from influencing the results. All DFT calculations are performed using the VASP package.24 For the calculation of electronic energies, a kinetic energy cutoff of 400 eV and an electronic self-consistency criterion of 10−5 eV are used. In the application of the Gupta potential, the parameters of Au are listed in Table S1.†
2.3 Recognition of surface sites of sub-nano-Au clusters
Due to the complexity of the three-dimensional surfaces of clusters, previous theoretical exploration of catalytic reactions upon surfaces mainly focused on regular shaped surfaces or a few specific adsorption sites. In this paper, we employed the alpha shape algorithm, which traverses the atom set to construct triangulation sequentially, and the key parameter α is determined based on the radius of the outer sphere of the obtained spatial tetrahedron. The value of α regulates the shape of the concave package. A larger α corresponds to a rougher enclosure, and as α approaches infinity, the concave enclosure degenerates into a convex. Therefore, the binary search method can be used to determine the appropriate α value to suit different systems. This tactic could facilitate the identification and further exploration of all surface sites of large-scale complex structures. The ideal minimum concave is a polyhedral cover of a known atom set, which is also called an alpha shape (Fig. S1† shows an example). There have been mature implementations of finding alpha shapes and the open-source Python package Alphashape 1.3.1 was chosen in this work.25 Based on this method, all surface atoms that have the potential to participate in reactions could be identified successfully.
2.4 Microkinetic model of CO oxidation
CO oxidation was modeled with the L–H mechanism. The whole reaction could be divided into five steps, namely co-adsorption of CO and O2 ((R1) and (R2)), formation of OOCO intermediates (R3), dissociation of OOCO intermediates into CO2 and atomic oxygen (R4), and the reaction of the second CO molecule with the remaining adsorbed oxygen atoms to produce the second carbon dioxide molecule (R5).
The asterisk (*) indicates the adsorbed species. The experimental conditions for the CO oxidation reaction are as follows: the temperature denoted as T is 298 K, the partial pressure of CO is 0.01 bar, and the partial pressure of O2 is 0.21 bar. In the following equations, k represents Boltzmann's constant, and h represents Planck's constant. In (R1) and (R2), their reaction equilibrium constants are denoted as K1 and K2, respectively. ΔE1 = Ead(CO) stands for CO adsorption energy. ΔE2 = Ead(O2) stands for O2 adsorption energy. ΔS1 and ΔS2 represent the change of entropy in the adsorption process of the corresponding gas molecules. ΔS1 = −197.71 J mol−1 K−1 and ΔS2 = −205.1 J mol−1 K−1.
| | 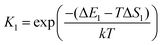 | (2) |
| | 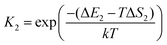 | (3) |
In reaction (R3), the adsorbed CO and O2 are close to each other and then overcome the first activation energy barrier (Ea1), reach the transition state 1 (TS1) and form the intermediate complex OOCO*. k3+ represents the forward reaction rate constant and k3− represents the reverse reaction rate constant. Assuming that the entropy of the adsorbate is zero, it follows that ΔS3 = 0. Ea3+ represents the forward reaction activation energy barrier, Ea3− represents the reverse reaction activation energy barrier, Eco-ad means the co-adsorption energy of the oxygen molecule and carbon monoxide, ETS-1 means the first transition state energy of the elementary reaction (R3), and EOOCO means the relative energies of intermediate states OOCO.
| | 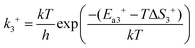 | (4) |
| | 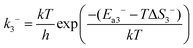 | (5) |
In reaction (R4), the unstable peroxide OOCO* intermediate is dissociated and overcomes the activation energy (Ea2) to reach the transition state 2 (TS2), resulting in a CO2 molecule and an adsorbed oxygen atom. k4 means the forward reaction rate constant. The same assumption implies that the entropy of adsorption is zero, so ΔS4 is still zero. Ea4 stands for the activation energy barrier. ETS-2 means the second transition state energy of the elementary reaction (R4).
| | 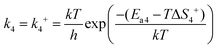 | (8) |
In reaction (R5), the adsorbed oxygen atom directly interacts with another CO molecule to form a second CO2. Since (R5) usually exhibits a very low activation energy barrier,26,27 this last reaction is not the rate-controlling step. The expression formula of OOCO coverage can be obtained by ignoring the weak influence of the non-speed control step (R5). The coverage of OOCO satisfies the following equation:
| | 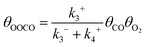 | (10) |
Given that the barrier of reaction (R5) is negligible, the coverage of the O atom is set to 0. Here in the microkinetic model of CO oxidation on Au clusters based on the L–H mechanism, the sum of all intermediates and free top adsorption sites is equal to 1.
| | | θ* + θCO + θO2 + θOOCO = 1 | (11) |
Based on the derivation of the above formulas, it can be obtained that the coverage rate of free adsorption sites satisfies the following equation:
| | 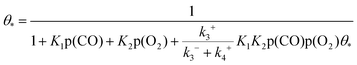 | (12) |
Finally, as the goal of the final kinetic analysis, the CO2 conversion rate is determined using the following formula:
| | | Rate = rate(R4) = k4+θOOCO | (13) |
Through the analysis of the above series of mathematical relations, six parameters affecting the oxidation rate of CO were obtained: Ead(CO), Ead(O2), ETS-1, ETS-2, Eco-ad, and EOOC. The first two parameters could be obtained through the geometry–adsorption relationship in the Results and discussion section. The last four parameters could be calculated through the following equations:
| | | Eco-ad = 1.51 × [Ead(O2) + Ead(CO)] + 0.08 | (14) |
| | | ETS-1 = 0.75 × Eco-ad − 0.12 | (15) |
| | | EOOCO = 1.49 × Eco-ad + 0.85 | (16) |
| | | ETS-2 = 0.71 × EOOCO − 0.16 | (17) |
3. Results and discussion
3.1 Structural global optimization of sub-nano-Au clusters
As shown in Fig. 1 and Fig. S2(a–c),† RPSO could filter out the global optimal structure of clusters. The bonding information and cluster diameter are shown in Fig. S3 and S4.† The analysis of energy is as follows. The cohesive energies for finite cluster sizes are defined as| | | Ecoh = (NEAu − Ecluster)/N | (18) |
where EAu denotes the electronic energy of the free Au atom and Ecluster denotes the total energy of the AuN cluster with N atoms. The calculated results of cohesive energy are well consistent with the previous work23,28 (see Table S2†). Most of the structures are consistent with the literature. Some biased structures, such as Au20, are different from their GM structures, but with only a small difference in energy. The disparity between the extrapolation intercept and bulk cohesive energy in Fig. 2(a) exposes a universal problem that DFT methods fail to accurately describe strongly correlated systems like Au bulk23 (also shown in Fig. S6†). Meanwhile, different DFT functionals characterize the binding situation differently and hence result in substantially different cohesive energies.28,29 Because the parameters used in the empirical potential were obtained by fitting the bulk properties,30 it is reasonable that the Gupta potential could properly reflect the tendency of larger systems but fail to describe the interactions among Au atoms in sub-nano-clusters, as shown in Fig. S5.† This also indicates the necessity of DFT corrective measures to structures at the Gupta level. Considering the common defects of nanostructures described by empirical potentials, the corrective measure is conducted when dealing with clusters optimized at the Gupta level, as shown in Fig. S5.† In the range of 21–300, some of the AuN structures were selected to perform self-consistent field DFT calculations. There is always a linear relationship between the total energy of the system and the number of atoms; thus using the selected data points to correct the whole line of original energy at the Gupta level is possible.
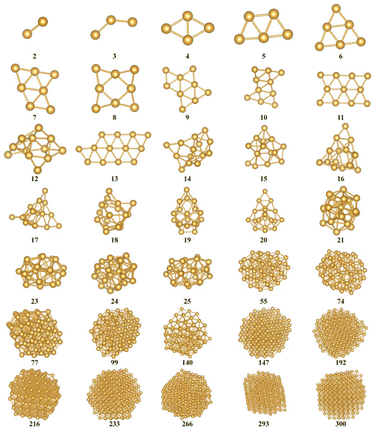 |
| | Fig. 1 Snapshots of some sub-nano-AuN clusters' (N = 2–300) GM structures obtained by RPSO. AuN (N = 2–20) structures are determined by RPSO at the DFT level. AuN (N = 21–300) structures are found by RPSO at the Gupta level. Other structures are shown in Fig. S2(a–c).† All coordinate files are provided in the ESI.† | |
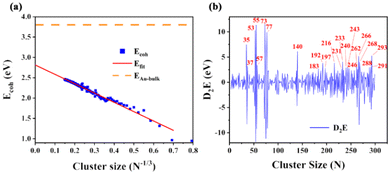 |
| | Fig. 2 (a) The calculated cohesive energy of AuN (N = 2–300) related to cluster size. The red line denotes extrapolation from N = 3–300. The orange dashed line indicates the observed cohesive energy of bulk gold, which is 3.8 eV.23 (b) D2E (second finite difference) of AuN (N = 2–300). Red label numbers correspond to sizes with significantly high values. | |
For GM structures screened by RPSO, a quantity to assess their cluster stability is the second finite difference (D2E). D2E could depict clusters’ stability relative to their N + 1 and N − 1 neighbors. It is calculated as follows:
| | | D2E = EN+1 + EN−1 − 2EN | (19) |
E
N
corresponds to the calculated total energy of AuN consisting of N atoms. Clusters with larger D2E have higher stability than their neighbors in Fig. 2(b). Those remarkably stable AuN clusters are consistent with previous works.31,32 It has been reported that these clusters at the pure DFT level are relatively stable (N = 4, 6, 8, 10, 12, 14, and 18),33,34 and the results in Fig. S7† are in good agreement with these findings, indicating the reliability of RPSO.
3.2 Geometry–adsorption relationship
The generalized coordination number (CNg) and relative curvature angle (CAr) serve as efficient geometric descriptors for the adsorption energy of CO/O2 on Au clusters. These two geometric descriptors are the basis of the geometry–adsorption correlation model in this paper.
The coordination number (CN) is used as an index to describe the coordination saturation of an atom. As shown in Fig. 3(a), the atom q is five-coordinated. The atom in bulk Au has the largest coordination number, with a single atom surrounded by its 12 closest neighbors. Au atoms with coordination numbers below 12 tend to form bonds to compensate for reduced coordination. Based on the definition of the traditional coordination number, the generalized coordination number (CNg) is adopted in this work to describe the trend of adsorption strength on Au clusters’ surface more precisely. The CNg of the atom p is calculated using the weighted sum of traditional coordination numbers of all the first nearest neighbor atoms through the following equation and also shown in Fig. 3(b):
| | 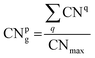 | (20) |
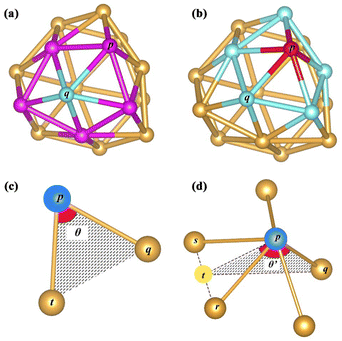 |
| | Fig. 3 (a) Coordination number of the blue atom q, which equals the number of pink atoms p. (b) The CNg of the red atom p is calculated according to the weighted average of the coordination numbers of blue atoms q. (c) The CAr of the blue atom p is denoted as θ when there are two nearest neighbors around p. (d) If the atom p has more than three atoms in the set of nearest neighbors, CAr is calculated according to the weighted average of θ′. Imaginary point t is located at the midpoint between the atom s and atom r. All displayed Au atoms are nearest neighbors of the blue atom p. | |
CNmax of 12 corresponds to the maximum coordination number achieved by a face-centered cubic Au structure. CNq represents the coordination number of the atom q, which comes from a collection of all nearest neighbors of the atom p. The bonding threshold of Au clusters is set to 3.3 Å, which is used to determine the bonding information of atoms.
The relative curvature angle of the atom p (CApr) is defined as follows. The first thing to do is to obtain the collection S consisting of all nearest neighbors of the atom p. The next step is to deal with the different cases of the set S. (1) When the number of elements in the set S does not exceed 1, then the curvature angle CAp is defined as 0. (2) When the number of elements in the set S is exactly equal to 2, the curvature angle CAp is defined as θ in Fig. 3(c). (3) The set S has more than 3 elements. As shown in Fig. 3(d), the curvature angle is calculated by averaging the sum of all θ′. Any atom q (q is the atom with the closest Euclidean distance to the atom p from the collection S) is randomly chosen. The straight line between the atom p and the atom q is denoted as the line pq. Any atom r in S except q is selected and then the atom s nearest to r except the atom q in S is selected, and these two atoms form a line sr. The imaginary point t is the midpoint of the line rs. The line between the atom p and point t is denoted as the line tp. θ′ is determined by the line pq and line tp. The atom q may have more than one choice (some atoms in S have the same distance as the target atom p), but after random selection, there would be only one certain atom selected. The atom q has at least two choices (the collection S has more than 3 members); meanwhile, the atom r and atom s have more combinations. Each of these different combinations will yield a value of θ′. After going through all these combinations, the average result of all θ′ is the curvature angle of the atom p, namely CAp. After discussing the above three cases, the curvature angle CAp of the atom p will be obtained. Finally, the relative curvature angle of the atom p (CApr) is then simply normalized using 180 degrees, as shown in the following equation:
| | 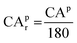 | (21) |
Based on previously defined geometric descriptors, the adsorption energies of CO and O2 on the top sites of freestanding sub-nano-Au clusters could be depicted systematically. Adsorption energies are defined as Eads = Eadsorbate+cluster − Eadsorbate − Ecluster. As shown in Fig. 4, there are linear relationships35,36 between geometric descriptors and adsorption energies. The data points in Fig. 4 were obtained from ref. 27, 28 and 37–44. It is credible that such an adsorption energy linear relationship has a certain universality based on lots of data coming from multiple references.
 |
| | Fig. 4 All data on adsorption energy are cited from ref. 27, 28 and 37–44. (a) The linear relationship between CO adsorption energies and CAr. (b) The linear relationship between O2 adsorption energies and CAr. (c) The linear relationship between CO adsorption energies and CNg. Auext represents the adsorption data of extended gold surfaces, including Au(100), Au(111), Au(110), Au(211), Au(321), and Au(553). The gray dashed line represents the trend of crystal surface adsorption energy, which is Ead(CO) = 0.2 × CNg − 1.76. (d) The linear relationship between O2 adsorption energies and CNg. The meaning of Auext and the gray dashed line remains the same as before. The crystal surface adsorption energy follows Ead(O2) = 0.23 × CNg − 1.39. | |
When CNg < 4, CAr is chosen to quantify the geometry effect on adsorption energies, as shown in Fig. 4(a) and (b). For atoms with CNg > 4, it is possible to deal with predicting adsorption energy using CNg. These linear relationships could serve as reliable and useful tools for evaluating trends in adsorption energy, as stated in Nørskov's previous research that lines are much more precise than points.45 All linear relationships were obtained by least squares fits using the Python package Numpy.46 As a result, the adsorption energies could be correlated with geometric descriptors via the following equations:
| | | Ead(CO) = 1.59CAr − 1.82 (CNg < 4) | (22) |
| | | Ead(O2) = 1.58CAr − 1.02 (CNg < 4) | (23) |
| | | Ead(CO) = 0.15CNg − 1.47 (CNg ≥ 4) | (24) |
| | | Ead(O2) = 0.14CNg − 0.83 (CNg ≥ 4) | (25) |
3.3 Size-dependent adsorption properties of sub-nano-Au clusters
When exploring the adsorption properties of clusters, the first thing to do is to determine which atoms could act as adsorbed sites. Because of the complexity of the surface environment of irregular sub-nano-clusters, it is almost impossible to manually find a large number of exposed surface atoms in a large set of complex structures. Top sites are taken into consideration for some simplification. Thus, each top site on the outer surface would be recognized, which provides a reasonable criterion for measuring catalytic activity.
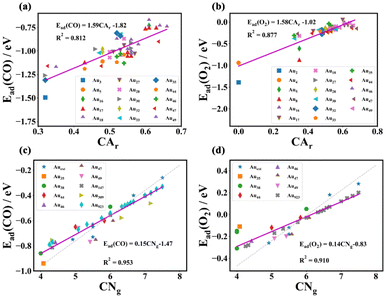
According to the linear relationship in Fig. 4, the CO and O2 adsorption energies of all studied sub-nano-AuN clusters (N = 2–300) can be evaluated. As shown in Fig. 5(a), with increasing cluster size, the adsorption energy of CO adsorbed on sub-nano-AuN clusters gradually approaches that of extended Au surfaces, namely Au(211), Au(100) and Au(111). It indicates that the atomic arrangement of surface sites of sub-nano-AuN clusters gradually achieves greater coordination saturation accompanied by a larger cluster size. The gradual increase in the coordination saturation of surface atoms leads to the adsorption behavior of sub-nano-AuN clusters approaching those of Au(211), Au(100), and Au(111) in sequence. It is the similarity of the local coordination environment that results in similar CO adsorption performance.
 |
| | Fig. 5 (a) The average adsorption energy of CO upon sub-nano-Au clusters. Dashed lines represent adsorption energy on the corresponding Au crystal faces respectively, cited from ref. 23 and 43. (b) The average adsorption energy of molecular O2 upon sub-nano-Au clusters. Dashed lines represent adsorption energy on the corresponding gold crystal face respectively, cited from ref. 27. (c) The d-band center (εd) of sub-nano-Au clusters. (d) The energy barrier of the elementary steps of CO oxidation as a function of the size of sub-nano-Au clusters. | |
A similar size-dependent adsorption trend also occurs when observing adsorbed O2 in Fig. 5(b). Since the atomic coordination environment on the surface of a given structure does not change, the corresponding relative relationship of adsorption energy is the same, which follows the law that the adsorption of the corresponding gas molecules becomes weaker with the increase of cluster size. Different from CO adsorption, the adsorption of molecular oxygen on extended crystal surfaces with high CNg (Au(111) and Au(100)) is much weaker than that of CO. As shown in Fig. 4(c and d), gray dashed lines represent the trend of adsorption energy on the crystal surface. The fitted lines of CO adsorption energy between clusters and crystal surfaces are closer, while there is a significant difference in the trend lines of O2 adsorption energy. Therefore, as the cluster size increases, the CO adsorption energy of clusters approaches the value of crystal surfaces, while the O2 adsorption energy deviates from that. The stronger reactant adsorption of sub-nano-Au clusters can to some extent explain their better catalytic activity compared to bulk gold. Adsorption as a function of the cluster diameter follows a linear logarithmic trend as shown in Fig. S8.†
For post-transition metals like Au, the lower the d band center, the weaker the adsorption strength.47,48 As the cluster size increases, the surface atoms become more tightly arranged and the coordination number is generally higher, resulting in enhanced d orbital interactions of gold atoms. The enhanced interaction of the orbitals is accompanied by the d orbitals occupying a wider energy range, namely a wider d bandwidth. Therefore, a lower d band center would appear in Fig. 5(c) and that is the reason why size-dependent adsorption behaves as scatters in Fig. 5(a) and (b). Naturally, when the cluster size increases to a certain extent, there is little room for the atoms to get more compact so the d band center no longer decreases continuously and fluctuates only in a very small range.
3.4 Size effect of sub-nano-Au clusters on CO oxidation reaction kinetics
According to the microkinetic analysis in section 2.4, (R3) and (R4) play the role of a rate controller. Their energy barriers are all plotted in Fig. 5(d). Ea1 is the energy barrier for (R3) and Ea2 is the energy barrier for (R4). Both of them conform to a single exponential decay distribution as follows. Ea1 yields an R2 value of 0.854 and Ea2 yields an R2 value of 0.856.| | | Ea1 = 0.5052 × exp(−N/29.1161) + 0.0852 | (26) |
| | | Ea2 = 0.7188 × exp(−N/29.1768) + 0.0419 | (27) |
On the basis of the L–H mechanism, the reaction energy barrier of the reaction pathway has not exceeded 0.5 eV (0.5 eV energy barrier is the upper limit for a facile reaction at room temperature), which verifies the hypothesis of dominating the L–H reaction mechanism. As the cluster size increases, the reaction energy barrier continuously decreases, suggesting that elementary reaction steps on the catalyst surface become facile and may not be rate-determining steps for sub-nano-Au clusters with increasing size.
Through the application of the newly established geometry–adsorption relationships, as well as the adsorption-barrier equations above, it is possible to predict the reaction rate of CO oxidation on different surface sites of sub-nano-Au clusters. In the rate-mapping color model in Fig. 6, it is clear that clusters with different sizes have distinct distributions of active sites. The maximum and minimum values of the reaction rate are decided based on the rate data set from AuN (2–300). Those atoms with the original golden color are inside the concave polyhedron of sub-nano-Au clusters, which are determined through the alpha shape algorithm.
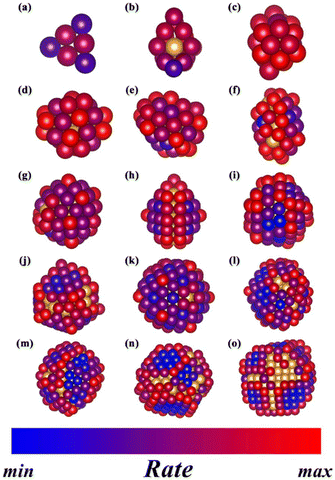 |
| | Fig. 6 Schematics of the reaction rate of CO oxidation on all surface sites of sub-nano-Au clusters, including (a) Au6, (b) Au19, (c) Au25, (d) Au35, (e) Au53, (f) Au55, (g) Au73, (h) Au77, (i) Au112, (j) Au140, (k) Au159, (l) Au199, (m) Au234, (n) Au293 and (o) Au300. | |
In Fig. 7, the activity (CO2 formation rate) per unit mass (APUM) is defined as follows:
| | 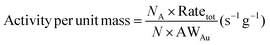 | (28) |
where AW
Au = 196.967 g mol
−1,
NA is Avogadro's constant and Rate
tot is calculated from the sum of CO
2 formation rates from all surface sites on one Au
N (
N = 2–300). The activity per unit mass could reflect the catalytic capacity in the CO oxidation reaction of certain sub-nano-Au clusters in
Fig. 7(a and b). The correlation between the APUM and the diameter of sub-nano-Au clusters is quantitatively investigated through log–normal distribution modeling with
R2 = 0.924 as follows:
| | 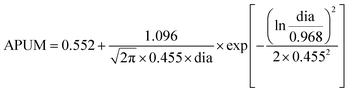 | (29) |
 |
| | Fig. 7 (a) Size-dependent activity (CO oxidation reaction rate) per unit mass of sub-nano-Au clusters, as a function of the number of Au atoms. (b) Size-dependent activity (CO oxidation reaction rate) per unit mass of sub-nano-Au clusters, as a function of the diameter of sub-nano-Au clusters. (c) Average CO oxidation rate at different surface sites (Kink, Edge, and Face) of sub-nano-Au clusters as a function of the number of Au atoms. (d) Contribution from Kink, Edge and Face sites to the overall CO oxidation reaction rate of sub-nano-Au clusters, as a function of the number of Au atoms. | |
The APUM trend as a function of particle diameter shows a volcano-shaped relationship, and it provides a reference for estimating the approximate optimal range of diameters for sub-nano-Au clusters. Extreme values appear when the cluster size is in the range from 21 to 30 atoms. Among them, Au25 displays the best catalytic performance. When the size surpasses 50 atoms, the APUM decreases as the cluster size increases. This result is consistent with the conventional view regarding the size–activity relationship of sub-nano-Au catalysts,2,6,44 further validating the underlying size-dependent catalytic performance of sub-nano-Au clusters.
As shown in Fig. S9,† the surface sites of sub-nano-Au clusters can be classified into three kinds according to their CNg, where Kink sites show the lowest CNg smaller than 4, Face sites have the highest CNg ranging from 6 to 8 and Edge sites correspond to medium CNg ranging from 4 to 6. Fig. S10† shows that the proportion of surface sites would decrease as the cluster size increases. Meanwhile, the ratio of active sites (Kink and Edge) among surface sites also does not increase, as shown in Fig. S11.† Before 0.75 nm (or 25 atoms), as shown in Fig. 7c, the average rate on Kink sites becomes larger, and at 0.75 nm (or 25 atoms), Edge sites with the highest average rate begin to take part in the reaction, which leads to the maximum APUM for sub-nano-Au clusters at around 0.75 nm (or 25 atoms). As shown in Fig. S10,† the proportion of surface sites participating in the reaction decreases as their size increases. Only very small sub-nano-Au clusters could form planar structures and these 2-dimensional (D) clusters’ size cannot exceed 13 atoms.30 As long as the size of clusters becomes larger, it is almost certain to get 3-D GM structures. Therefore, Au clusters with a size over 50 atoms would exhibit 3D polyhedral structures. For 3-D structures, the surface-to-volume ratio increases as the size increases,29 and more atoms inaccessible to the reaction would appear. These inner atoms would lower the APUM of a given sub-nano-Au cluster. More Face sites among surface sites participate in the reaction. Although there are an increasing number of Face sites in larger Au clusters, it can be clearly seen from Fig. 7(c) that the catalytic performance of Face sites is significantly weaker than that of other types of sites, which also results in the catalytic activity of sub-nano-Au clusters decreasing with the increase of cluster size.
In Fig. 7(d), the contribution of different surface sites is illustrated, respectively. It is obvious that Kink sites dominate the catalytic reaction at a very small size of Au clusters. When N > 50, more and more Face sites start to participate in the contribution of the whole cluster catalysis. Although Face sites show inferior catalytic performance in Fig. 7(c), the increasing number of Face atoms in relatively large clusters remarkably compensates for their poor individual ability. From 50 to 150 atoms, the APUM decreases with increasing cluster size due to the higher and higher contributors to the overall cluster catalytic rate from Face sites. After 150 atoms, although the contribution distribution and average rate of surface sites remain largely unchanged (Fig. 7d and Fig. S10†), the decreasing surface site percentage becomes the main reason for the reduction in the APUM. Meanwhile, the decreasing contribution of Kink sites with increasing cluster size does not mean that Kink sites are catalytically inactive. This phenomenon is attributed to the small number of Kink sites in large clusters because the shape of clusters becomes more regular when the size increases. Tatsuya et al.51 studied the aerobic oxidation of size-controlled Au clusters smaller than 2 nm, and they selected AuN (N = 10, 18, 25, 39, and 85) and fitted the TOF curve based on these 5 data points. Their experimental data have something in common with our computational results; the activity curve in their work decreases when N exceeds 50. A similar phenomenon also appears in Fig. 7(a), where Au clusters consisting of fewer than 50 atoms show better catalytic activity.
3.5 CO oxidation kinetics controlled by site-dependent adsorption on sub-nano-Au clusters
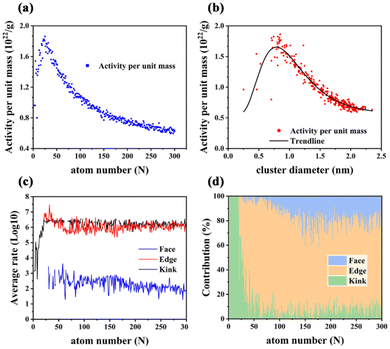
As the cluster size increases, the reaction phenomenon yields a paradox that despite the decreasing energy barrier in Fig. 5(d), the overall catalytic performance of clusters in Fig. 7(a and b) still deteriorates. The adsorption energy of all types of reaction sites is discussed in Fig. 8(a and b). For both CO and O2 adsorption, the Face sites show significantly weaker adsorption than other types of sites. In the adsorption of molecular oxygen, Face sites tend to produce positive adsorption energy, which is also consistent with the previous description that O2 cannot adsorb on these highly coordinated atoms. Due to the inability of these Face sites to adsorb the reactants efficiently, this leads to the poor catalytic performance of the Face sites to some extent. Although the reduction of the rate-controlled energy barrier makes the reaction easier to proceed, too weak adsorption of the reactants still makes it difficult to even start the reaction. Fig. 7(c and d) discuss the coverage of CO and O2 on the cluster surface. CO molecules show a high coverage at Kink sites, while showing a medium coverage at Edge sites. However, the coverage of CO on these two types of sites is far higher than that on Face sites, rationalizing the weak adsorption of Face sites leading to a low reaction rate. Compared with the CO coverage, the O2 coverage at the Face sites is significantly weaker by several orders of magnitude, which indicates that the adhesion of O2 at the Face sites of clusters is more difficult.50 Given the fact that the O2 coverage is extremely low, the coverage of the Face sites is still the lowest compared with other types of sites, which further explains the poor reaction performance of Face sites. Both Edge sites and Kink sites exhibit disparities in their CO coverage and O2 coverage, with Kink sites demonstrating much higher CO coverage characteristics but a much lower O2 coverage compared to Edge sites. David M. Rayner's group explored CO adsorption on Au clusters aided by infrared photodepletion spectroscopy to record the vibrational spectra of Au–CO complexes. Additionally, they use infrared reflectance measurements to find that low-coordinated Au atoms (Kink and Edge sites) tend to adsorb CO molecules at a low CO coverage because of their strong CO binding. CO binds preferentially to Au atoms in low coordination, whereas highly coordinated Au atoms (Face sites) are not reactive toward CO.52 Whetten's group studied molecular oxygen adsorption53–55 over Au clusters and established a binary-like adsorption behaviour (either zero or one O2 adsorbed), which could rationalize the simulated weak adsorption and low coverage of O2.
 |
| | Fig. 8 (a) The distribution of CO adsorption energy on different surface sites (Kink, Edge, and Face) of sub-nano-Au clusters as a function of the number of Au atoms. (b) The distribution of O2 adsorption energy on different surface sites of sub-nano-Au clusters as a function of the number of Au atoms. (c) The coverage of CO on different surface sites of sub-nano-Au clusters as a function of the number of Au atoms. (d) The coverage of O2 on different surface sites of sub-nano-Au clusters as a function of the number of Au atoms. (e) The CO reaction order on different surface sites of sub-nano-Au clusters as a function of the number of Au atoms. (f) The O2 reaction order on different surface sites of sub-nano-Au clusters as a function of the number of Au atoms. | |
The reaction orders determined by varying the partial pressures of CO and O2 respectively are shown in Fig. 8(e and f). So as to explore the size-dependent reaction order, some clusters are randomly selected with atom number as 19, 25, 35, 53, 77, 113, 140, 162, 199, 234, 293, and 300. The reaction order of Face sites remains zero no matter how the size of the cluster changes, which indicates that the variation of neither CO partial pressure nor O2 partial pressure has any effect on the activity of Face sites. In other words, Face sites are very insensitive to the external atmosphere, which indicates that these gas molecules have very weak adsorption at Face sites. In Fig. 8(e), Kink sites show negative reaction orders when changing the amount of CO, which could be attributed to extremely strong CO adsorption and excessively high CO coverage at Kink sites. Because of these reasons, when a continuous increase in the partial pressure of CO happens, Kink sites are poisoned and their reaction processing is hindered, and such similar results have also been reported in the previous work.43–45,49 The reaction order of Kink sites adsorbing O2 and all Edge sites is always positive when the size changes. In contrast to Face sites, the increase of the corresponding gas partial pressure promotes the reaction on these types of sites. This phenomenon can be attributed to the fact that the adsorption at Edge sites and the adsorption of O2 at Kink sites are far from reaching their saturation state. Therefore, increasing the corresponding partial pressure of CO or O2 will promote the adsorption of their respective reactants and thus play a positive role in boosting the CO oxidation reaction rate.
Based on the above discussions, the results of the rate-mapping color model in Fig. 6 could be interpreted reasonably. Observing the distribution of active sites in clusters of different sizes, it can be concluded that the Face site activity of large clusters is very low, while the Face site activity of small clusters is generally high but the Kink site activity is poor. These intuitive results conform well to the geometric features of surface sites, and only suitable adsorption and coverage facilitate an easy CO oxidation process. In small clusters such as Au6 and Au19, Kink sites exhibit too strong CO adsorption, which hinders the corresponding activity. Larger clusters such as Au293 and Au300 tend to possess surfaces consisting of Face sites, which generate a low coverage of the reactant and make it difficult to adsorb the reactant. In contrast, the Edge sites exhibit moderate adsorption strength and reactant coverage, which leads to their generally better catalytic performance.
4 Conclusions
In this paper, a systematic study of AuN (N = 2–300) sub-nano-clusters for CO oxidation is conducted, focusing on the size effect on their adsorption and catalytic activity. The RPSO method is used to screen out the globally optimal structure of the chosen sub-nano-Au clusters. Geometric descriptors, including CNg and CAr, are used to describe the geometric features of reaction sites, which help to build the geometric–adsorption–activity correlation and enable the evaluation of the reaction rate of each site for any given sub-nano-Au cluster. The distinctive catalytic performance of different geometric structural sites has also been discussed to rationalize the volcano-shaped relationship of size-dependent activity per unit mass. This volcano-shaped reactivity conforms well with the experimental result of Tatsuya's work.51 Due to the different local atom arrangements at the reaction sites of sub-nano-Au clusters of different sizes, the adsorption of CO and O2, the energy barrier of the surface elementary reaction, and the site contribution to the overall reaction all exhibit significant size effects. The interplay of these factors has resulted in the outcome that around Au25 (or 0.75 nm) is located at the volcano peak. Moreover, while similar adsorption behaviors have been observed in experiments, mostly focusing on limited sizes (<100), our work makes reasonable predictions for larger-scale adsorption.52–55 This study further explores the research paradigm of catalytic mechanisms at the site level, contributing to a fundamental understanding of size-dependent activity over sub-nano-Au catalysts. In the future, this type of precise site-level reaction simulation may further promote the development of catalytic science and boost the research progress of high-performance sub-nano-catalysts’ rational design.
Data availability
The data supporting this article have been included as part of the ESI.† The structure data for AuN (2–300) as XYZ files have been deposited at https://doi.org/10.1039/d4nr02705a.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (22278014 and 22078005) and Beijing Science and Technology New Star Program (20240484659).
References
- G. J. Hutchings, J. Catal., 1985, 96, 292–295 CrossRef CAS.
- B. G. Donoeva, D. S. Ovoshchnikov and V. B. Golovko, ACS Catal., 2013, 3, 2986–2991 CrossRef CAS.
- M. Valden, X. Lai and D. W. Goodman, Science, 1998, 281, 1647–1650 CrossRef CAS PubMed.
- G. Li and R. Jin, Acc. Chem. Res., 2013, 46, 1749–1758 CrossRef CAS PubMed.
- S. Yamazoe, K. Koyasu and T. Tsukuda, Acc. Chem. Res., 2014, 47, 816–824 CrossRef CAS PubMed.
- S. K. Shaikhutdinov, R. Meyer, M. Naschitzki, M. Bäumer and H.-J. Freund, Catal. Lett., 2003, 86, 211–219 CrossRef CAS.
- G. R. Bamwenda, S. Tsubota, T. Nakamura and M. Haruta, Catal. Lett., 1997, 44, 83–87 CrossRef CAS.
- C. Lemire, R. Meyer, S. Shaikhutdinov and H. Freund, Angew. Chem., Int. Ed., 2004, 43, 118–121 CrossRef PubMed.
- G. Li, D. Jiang, S. Kumar, Y. Chen and R. Jin, ACS Catal., 2014, 4, 2463–2469 CrossRef CAS.
- M. M. Kappes, P. Radi, M. Schär and E. Schumacher, Chem. Phys. Lett., 1985, 119, 11–16 CrossRef CAS.
- M. M. Kappes, R. W. Kunz and E. Schumacher, Chem. Phys. Lett., 1982, 91, 413–418 CrossRef CAS.
- Y. Zhang, P. Song, T. Chen, X. Liu, T. Chen, Z. Wu, Y. Wang, J. Xie and W. Xu, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10588–10593 CrossRef CAS PubMed.
- N. Lopez and J. K. Nørskov, J. Am. Chem. Soc., 2002, 124, 11262–11263 CrossRef CAS PubMed.
- D. M. Popolan and T. M. Bernhardt, J. Chem. Phys., 2011, 134, 091102 CrossRef PubMed.
- L. D. Socaciu, J. Hagen, T. M. Bernhardt, L. Wöste, U. Heiz, H. Häkkinen and U. Landman, J. Am. Chem. Soc., 2003, 125, 10437–10445 CrossRef CAS PubMed.
- F. H. Kaatz, D. Yu. Murzin and A. Bultheel, ACS Catal., 2021, 11, 9073–9085 CrossRef CAS.
- Y. Zhou, Z. Zhao and D. Cheng, Comput. Phys. Commun., 2020, 247, 106945 CrossRef CAS.
- Z. Deng, Y. Zhou, L. Zhao and D. Cheng, Mol. Simul., 2022, 48, 891–901 CrossRef CAS.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- CEC-Benchmark-Functions/CEC2017/CEC-Benchmark-Functions, https://github.com/tsingke/CEC-Benchmark-Functions/tree/master/CEC2017.
- F. Cleri and V. Rosato, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 22–33 CrossRef CAS PubMed.
- Y. Pei and X. C. Zeng, Nanoscale, 2012, 4, 4054 RSC.
- B. Assadollahzadeh and P. Schwerdtfeger, J. Chem. Phys., 2009, 131, 064306 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- alphashape·PyPI, https://pypi.org/project/alphashape/.
- B. Yoon, H. Häkkinen, U. Landman, A. S. Wörz, J.-M. Antonietti, S. Abbet, K. Judai and U. Heiz, Science, 2005, 307, 403–407 CrossRef CAS PubMed.
- H. Xu, D. Cheng, Y. Gao and X. C. Zeng, ACS Catal., 2018, 8, 9702–9710 CrossRef CAS.
- H. Li, L. Li, A. Pedersen, Y. Gao, N. Khetrapal, H. Jonsson and X. C. Zeng, Nano Lett., 2015, 15, 682–688 CrossRef CAS PubMed.
- O. D. Häberlen, S.-C. Chung, M. Stener and N. Rösch, J. Chem. Phys., 1997, 106, 5189–5201 CrossRef.
- L. Xiao, B. Tollberg, X. Hu and L. Wang, J. Chem. Phys., 2006, 124, 114309 CrossRef PubMed.
- A. Sebetci and Z. B. Güvenç, Modell. Simul. Mater. Sci. Eng., 2005, 13, 683–698 CrossRef CAS.
- S. Heiles, A. J. Logsdail, R. Schäfer and R. L. Johnston, Nanoscale, 2012, 4, 1109–1115 RSC.
- J. Wang, G. Wang and J. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035418 CrossRef.
- X.-B. Li, H.-Y. Wang, X.-D. Yang, Z.-H. Zhu and Y.-J. Tang, J. Chem. Phys., 2007, 126, 084505 CrossRef PubMed.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, P. Sautet and D. Loffreda, Angew. Chem., Int. Ed., 2014, 53, 8316–8319 CrossRef CAS PubMed.
- F. Calle-Vallejo, J. Tymoczko, V. Colic, Q. H. Vu, M. D. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. S. Bandarenka, Science, 2015, 350, 185–189 CrossRef CAS PubMed.
- X. Kuang, X. Wang and G. Liu, Phys. E, 2012, 44, 2132–2137 CrossRef CAS.
- J. L. C. Fajín, M. N. D. S. Cordeiro and J. R. B. Gomes, J. Phys. Chem. C, 2008, 112, 17291–17302 CrossRef.
- C.-C. Lee and H.-T. Chen, J. Phys. Chem., 2015, 119, 8547–8555 CrossRef CAS PubMed.
- B. Yoon, H. Häkkinen and U. Landman, J. Phys. Chem. A, 2003, 107, 4066–4071 CrossRef CAS.
- M. A. Dar and S. Krishnamurty, ACS Omega, 2019, 4, 12687–12695 CrossRef CAS PubMed.
- A. Hussain, D. Curulla Ferré, J. Gracia, B. E. Nieuwenhuys and J. W. Niemantsverdriet, Surf. Sci., 2009, 603, 2734–2741 CrossRef CAS.
- F. Mehmood, A. Kara, T. S. Rahman and C. R. Henry, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 075422 CrossRef.
- B. Hammer, Y. Morikawa and J. K. Nørskov, Phys. Rev. Lett., 1996, 76, 2141–2144 CrossRef CAS PubMed.
- A. J. Medford, J. Wellendorff, A. Vojvodic, F. Studt, F. Abild-Pedersen, K. W. Jacobsen, T. Bligaard and J. K. Nørskov, Science, 2014, 345, 197–200 CrossRef CAS PubMed.
- C. R. Harris, K. J. Millman, S. J. Van Der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. Van Kerkwijk, M. Brett, A. Haldane, J. F. Del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- B. Hammer and J. K. Norskov, Nature, 1995, 376, 238–240 CrossRef CAS.
- A. Ruban, B. Hammer, P. Stoltze, H. L. Skriver and J. K. Nørskov, J. Mol. Catal. A: Chem., 1997, 115, 421–429 CrossRef CAS.
- A. A. Koverga, S. Frank and M. T. M. Koper, Electrochim. Acta, 2013, 101, 244–253 CrossRef CAS.
- J. Kleis, J. P. Greeley, N. A. Romero, V. A. Morozov, H. Falsig, A. H. Larsen, J. Lu, J. J. Mortensen, M. Dułak, K. S. Thygesen, J. K. Nørskov and K. W. Jacobsen, Catal. Lett., 2011, 141, 1067–1071 CrossRef CAS.
- Y. Liu, H. Tsunoyama, T. Akita, S. Xie and T. Tsukuda, ACS Catal., 2011, 1, 2–6 CrossRef CAS.
- A. Fielicke, G. Von Helden, G. Meijer, D. B. Pedersen, B. Simard and D. M. Rayner, J. Am. Chem. Soc., 2005, 127, 8416–8423 CrossRef CAS PubMed.
- B. E. Salisbury, W. T. Wallace and R. L. Whetten, Chem. Phys., 2000, 262, 131–141 CrossRef CAS.
- W. T. Wallace and R. L. Whetten, J. Phys. Chem. B, 2000, 104, 10964–10968 CrossRef CAS.
- W. T. Wallace and R. L. Whetten, J. Am. Chem. Soc., 2002, 124, 7499–7505 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a
*a