Characterization of neutral metal hydride–hydroxide hydrogen-bonded clusters HMOH(H₂O)₂ (M = Al and Ga)

Abstract

Metal hydride–hydroxide hydrogen-bonded clusters HMOH(H₂O)_n are key intermediates in the reactions of metals with water. However, characterizing the structure of such neutral clusters is a challenging experimental goal due to the difficulty of size selection. Here, neutral HMOH(H₂O)₂ (M = Al and Ga) clusters were prepared by using a laser-vaporization source and characterized by size-specific infrared-vacuum ultraviolet spectroscopy combined with quantum chemical calculations and ab initio molecular dynamics simulations. The HMOH(H₂O)₂ (M = Al and Ga) clusters were found to have intriguing hydrogen-bonded network structures. The results indicate that the formation of HMOH(H₂O)₂ (M = Al and Ga) is both thermodynamically exothermic and kinetically facile in the gas phase. The present system serves as a model for capturing key intermediates in metal–water reactions and also opens up new avenues for systematic studies of a large variety of reactions between neutral metal atoms/clusters and small molecules.

---

Introduction

The reactions of metals with water are ubiquitous and play an important role in many fields (i.e., catalysis, energy, environment).^1,2 For instance, the reaction between aluminum and water finds applications in rocket propellants and explosives.^3–5 Gas-phase well-defined metal clusters have been demonstrated to be useful models for gaining molecular-level understanding of microscopic reaction mechanisms.^6,7 Extensive experimental studies of ionic Al–H₂O clusters have been carried out because charged species allow easy detection and mass-spectrometry-based size selection.^8–14 Al⁺(H₂O)_n (n = 1–10) clusters were investigated using single-photon ionization and photodissociation spectroscopy.⁸ Black-body radiation studies of Al⁺(H₂O)_n indicated that for n ≈ 11–24, the evaporation of water is accompanied by oxidation of the Al⁺ ion and the loss of H₂.⁹ Infrared photodissociation (IRPD) spectroscopy of Al⁺(H₂O)_n (n = 1–2) was used to identify the HAlOH⁺ ion core structure in [Al(H₂O)₂]⁺.¹¹ Photodissociation spectroscopy revealed the coexistence of Al⁺(H₂O)_n and HAlOH⁺(H₂O)_n−1 at n = 4–8 and the presence of HAlOH⁺(H₂O)_n−1 at n = 9 or 10.¹³ Integration of HAlOH into the hydrogen-bonded network of the cluster was found to be required for effective initiation of the hydrogen evolution reaction.¹⁴ Together with advanced theoretical calculations, these studies have provided significant information on the reaction mechanisms of ionic Al–H₂O systems.^8–23

In contrast, experimental studies of neutral Al–water systems have been scarce, because the absence of a charge makes size selection difficult. The solvated complex Al(H₂O) was observed by using single-photon zero electron kinetic energy (ZEKE) pulsed field ionization (PFI) spectroscopy.²⁴ The HAlOH and HAlOH(H₂O) complexes were detected in low-temperature matrices.^25–28 The HGaOH insertion structure was also characterized by using infrared (IR) and ultraviolet (UV)-vis spectroscopy.²⁹ Theoretical calculations indicated that the formation of HAlOH is unfavorable from the reaction of the neutral Al atom with just one water molecule.^30–32 Interestingly, additional water molecules can have a promotion effect on the Al + (n + 1)H₂O → HAlOH(H₂O)_n processes.^31,33 Even though the formation of HAlOH(H₂O)_n (n = 2–3) clusters was suggested to be favorable in the reactions of Al with a few water molecules,^31,33 none of these clusters has been observed experimentally.

Here, neutral HMOH(H₂O)₂ (M = Al and Ga) clusters were prepared using a laser-vaporization source and characterized by size-specific infrared-vacuum ultraviolet (IR-VUV) spectroscopy combined with quantum chemical calculations and ab initio molecular dynamics (AIMD) simulations. The HMOH(H₂O)₂ (M = Al and Ga) clusters were found to have intriguing hydrogen-bonded network structures. The results indicate that the formation of HMOH(H₂O)₂ (M = Al and Ga) is both thermodynamically exothermic and kinetically facile in the gas phase. The present system serves as a model for capturing key intermediates in the metal–water reactions.

Experimental and theoretical methods

The experimental IR spectra of HMOH(H₂O)₂ (M = Al and Ga) were obtained by using an IR-VUV device (see the ESI† for experimental details).^34,35 Neutral HMOH(H₂O)₂ (M = Al and Ga) clusters were produced by supersonic expansions of 0.2%He/H₂O mixtures using a laser vaporization source. An IR laser was used to excite neutral clusters via a KTP/KTA optical parametric oscillator/amplifier system (OPO/OPA, LaserVision) with a tuning wavelength range of 700–7000 cm⁻¹. VUV photoionization was performed at 193 nm generated using an ArF excimer laser (Coherent, GAMLAS EX5A) with a delay of 60 ns with respect to the IR laser. The experimental IR spectra were recorded using the depletion spectrum scheme. The IR power dependence of the signal was measured during the experiments to ensure that the predissociation yield was linear with the photon flux.

Quantum chemical calculations were performed using the Gaussian 16 package at the MP2/aug-cc-pVDZ (abbreviated as MP2/AVDZ) level of theory.³⁶ For the possible isomerization pathways, the initial structures of transition states were constructed manually and optimized using the Berny algorithm. The intrinsic reaction coordinates (IRC) of all the transition states were calculated to confirm that the transition states were connected to the initial and final states. The relative energies and energy barriers of 0 K structures were calculated, including zero-point vibrational energies. To account for systematic errors associated with the method, the harmonic vibrational frequencies were scaled with a coefficient of 0.959 and convoluted with a Gaussian linear shape function with a full width at half-maximum (FWHM) of 10 cm⁻¹.³⁷

AIMD simulations were carried out using the CP2K package.³⁸ The wave functions were expanded in a double zeta Gaussian basis set, while the electron density was expanded in Gaussians and auxiliary plane waves (GPW) with an energy cut-off of 450 Rydberg for the electron density. The atomic cores were modelled using Goedecker–Teter–Hutter (GTH)-type pseudopotentials. The exchange and correlation energies were calculated using the BLYP functional, with additional Grimme's dispersion corrections at the D3 level. A cluster was put at the center of a periodic cubic box, and the effects of the periodic charge density images were corrected using the decoupling technique developed by Martyna and Tuckerman.³⁹ The box length was 15 Å. The convergence criterion for the SCF electronic procedure was set to be 10⁻⁷ a.u. at each time step. For molecular dynamics, the temperature was controlled using a Nose–Hoover thermostat, with a time step of 0.5 fs. An equilibration period of up to 5 ps was performed first, with the temperature scaled to an interval of at least 10 K around the intended value. A data collection run was then followed in the microcanonical ensemble. For different simulated temperatures, the duration of a trajectory was 60 ps. Each trajectory was then cut into 10 ps intervals for Fourier transformation and then they were added to produce the dipole time-correlation function (DTCF) spectrum for a specific temperature.⁴⁰ Dynamic and anharmonic effects were automatically taken into account in such a scheme, although quantum effects at low temperature were not included. The AIMD-simulated anharmonic IR spectra were unscaled.

Results and discussion

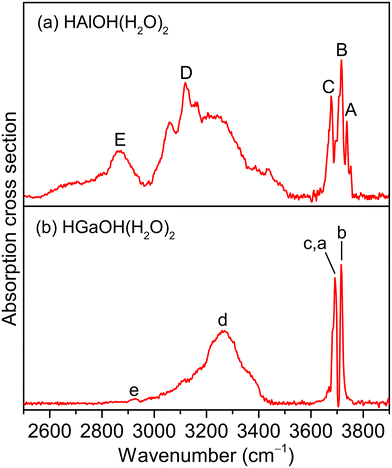
Fig. 1 shows the experimental IR spectra of HAlOH(H₂O)₂ and HGaOH(H₂O)₂, whose corresponding band positions are listed in Table 1. The experimental IR spectrum of HAlOH(H₂O)₂ (Fig. 1a) consists of five characteristic bands (labeled A–E), among which bands A, B, and C are sharply centered at 3737, 3717, and 3677 cm⁻¹, respectively. Bands D (3119 cm⁻¹) and E (2865 cm⁻¹) are broad features in the hydrogen-bonded OH stretch region, indicative of the large-amplitude motion of the water molecules. Similarly, the experimental IR spectrum of HGaOH(H₂O)₂ (Fig. 1b) shows two sharp characteristic bands (labeled c(a) and b) and two broad bands (labeled d and e) centered at 3692, 3716, 3269 and 2927 cm⁻¹, respectively. The broadening of band E (∼350 cm⁻¹) in HAlOH(H₂O)₂ is significantly larger than that of band e (50 cm⁻¹) in HGaOH(H₂O)₂.

Fig. 1 Experimental IR spectra of neutral HMOH(H₂O)₂ (M = Al and Ga) clusters.

Table 1 Comparison of the experimental band positions (cm⁻¹) of HMOH(H₂O)₂ (M = Al and Ga) with the calculated values of isomers 2-I and 2-i obtained at the MP2/aug-cc-pVDZ level of theory (the harmonic vibrational frequencies are scaled by a factor of 0.959). The atom labelling is indicated in Fig. 2

Species	Label	Exptl	Calcd	Mode
HAlOH(H2O)2	A	3737	3729	Stretching mode of the O(1)H(1) group
	B	3717	3714	Stretching mode of the O(2)H(2) group
	C	3677	3676	Stretching mode of the O(3)H(3) group
	D	3119	3168	Stretching mode of the O(2)H(2′) group
	E	2865	2893	Stretching mode of the O(3)H(3′) group
HGaOH(H2O)2	a	3692	3691	Stretching mode of the O(1)H(1) group
	b	3716	3719	Stretching mode of the O(2)H(2) group
	c	3692	3678	Stretching mode of the O(3)H(3) group
	d	3269	3145	Stretching mode of the O(2)H(2′) group
	e	2927	2975	Stretching mode of the O(3)H(3′) group

---

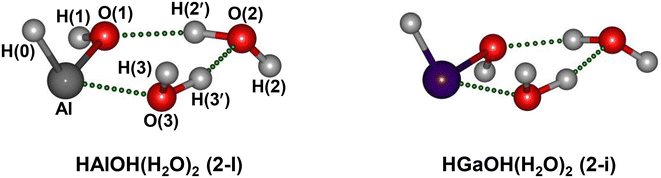
To assign the experimental IR spectra and identify the structures of HMOH(H₂O)₂ (M = Al and Ga), quantum chemical calculations were performed at the MP2/AVDZ level of theory. Similar structures were obtained for HMOH(H₂O)₂ (M = Al and Ga). The lowest-energy structures of HMOH(H₂O)₂ (M = Al and Ga) are illustrated in Fig. 2, denoted as isomers 2-I and 2-i hereafter. The structures of the other two low-lying isomers (2-II and 2-III) are representatively shown for HAlOH(H₂O)₂ in Fig. S3.† The MP2/AVDZ calculated harmonic IR spectra of isomers 2-I and 2-i were compared to the experimental IR spectra and are presented in Fig. 3 and S4,† respectively. Fig. S3† shows a comparison of the MP2/AVDZ calculated harmonic IR spectra of isomers 2-II and 2-III and the experimental IR spectrum of HAlOH(H₂O)₂.

Fig. 2 Identified structures of neutral HMOH(H₂O)₂ (M = Al and Ga) clusters calculated at the MP2/aug-cc-pVDZ level of theory (O, red; H, light gray; Al, gray; Ga, purple). The atoms are labeled for discussion.

Fig. 3 Comparison of the experimental IR spectrum of the neutral HAlOH(H₂O)₂ cluster (a), the MP2/aug-cc-pVDZ calculated harmonic IR spectrum of isomer 2-I (b) and AIMD-simulated anharmonic IR spectra at 50 K, 100 K, 200 K, and 225 K (c–f) of isomer 2-I.

In the structure of isomer 2-I of HAlOH(H₂O)₂, two water molecules connected by a hydrogen bond are bound to the hydroxyl group oxygen and the Al atom of a trans-HAlOH core, respectively, forming a hydrogen-bonded network. The structure of the trans-HAlOH core is consistent with previous matrix-isolation IR and EPR spectroscopic studies.^25,27 The 2-II isomer lies 14.6 kcal mol⁻¹ higher in energy above the 2-I isomer and consists of a hydrogen-bonded water dimer bound to the hydroxyl group oxygen and the hydroxyl group hydrogen of trans-HAlOH, respectively. The 2-III isomer lies 45.4 kcal mol⁻¹ higher in energy above 2-I and consists of an Al(H₂O)₃ solvated structure, in which a hydrogen-bonded water trimer is bound to the Al atom.

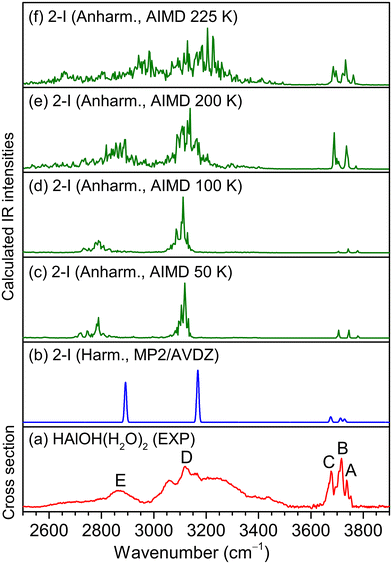
In the MP2/AVDZ calculated harmonic IR spectrum of isomer 2-I for HAlOH(H₂O)₂ (Fig. 3b), the bands at 3729, 3714, and 3676 cm⁻¹ are due to the stretching modes of the O(1)H(1), O(2)H(2), and O(3)H(3) groups (Table 1), respectively, which are consistent with experimental bands A, B, and C (3737, 3717, and 3677 cm⁻¹). The hydrogen-bonded OH stretching modes of the O(2)H(2′) and O(3)H(3′) groups are sharply predicted at 3168 and 2893 cm⁻¹, respectively, which are close to the center positions of experimental bands D and E (3119 and 2865 cm⁻¹). As shown in Fig. S3,† the simulated spectrum of isomer 2-II exhibits two sharp peaks at 3459 and 3479 cm⁻¹ that are not observed experimentally, indicative of a negligible contribution to the experimental spectrum. The 2-III isomer could lie too high in energy to be detected in the experiment. The overall agreement of the MP2/AVDZ simulated IR spectrum of isomer 2-I with the experimental one is reasonable to confirm the assignment of this isomer as responsible for HAlOH(H₂O)₂.

Analogous qualitative understanding of the experimental IR spectrum of HGaOH(H₂O)₂ was also obtained from MP2/AVDZ harmonic calculations (Fig. S4† and Table 1). The stretching modes of the O(1)H(1) and O(3)H(3) groups in HGaOH(H₂O)₂ were calculated to be close at 3691 and 3678 cm⁻¹, respectively, which are observed as one experimental band at 3692 cm⁻¹ (bands a and c). It can be seen from Fig. 3 and S4† that the peak intensities and broadening of experimental spectral features cannot be well reproduced by harmonic analysis based on stationary structures. As demonstrated previously,^41–43 understanding the IR spectra of flexible hydrogen-bonded clusters usually requires theoretical tools beyond harmonic approximation.

Previous studies indicated that AIMD simulations would help in understanding the dynamic fluctuation of hydrogen bonds, broadening of the corresponding IR spectra^42–44 and the size-dependent H₂ elimination mechanism of HAlOH⁺(H₂O)_n.¹⁶ Accordingly, AIMD simulations were carried out for HMOH(H₂O)₂ (M = Al and Ga) at a series of finite temperatures. The AIMD-simulated anharmonic IR spectra of HMOH(H₂O)₂ (M = Al and Ga) are shown in Fig. 3c–f and S4c–f,† respectively. For HAlOH(H₂O)₂, the AIMD 50 K spectrum (Fig. 3c) already shows a slight broadening of the hydrogen-bonded OH stretching modes (bands D and E). With an increase in simulation temperature, the bands in the AIMD spectra become broader. As shown in Fig. 3f, the AIMD 225 K spectrum yields a better agreement with the experimental spectrum throughout the spectral range for band positions and relative intensities. Similar results are also obtained for HGaOH(H₂O)₂ (Fig. S4c–f†), in which the AIMD 225 K spectrum agrees best with the experimental spectrum. As shown in Fig. S4,† the spectral features at around 3200 cm⁻¹ become narrower at 225 K. This could be rationalized as dynamic fluctuation of hydrogen bonds in the heavier cluster HGaOH(H₂O)₂ converging at 225 K. Upon further increase in AIMD simulation temperature, dissociation of HGaOH(H₂O)₂ could occur. As compared to the supersonic expansion of pure molecular beams, the utilization of a laser vaporization source under our present experiment conditions leads to additional heating during the reaction process, resulting in an elevated temperature. Note that the AIMD-simulated temperature does not really correspond to the experimental temperature, since zero-point vibrations and quantum effects are not taken into account during the AIMD simulations, but it does indicate the degree of atomic motion, since the temperature is calculated from the average kinetic energy.^38,45,46

Dynamic fluctuation of hydrogen bonds is an important factor in understanding the broadening of vibrational features.^{42–44,46–49} The temperature effects on the hydrogen-bond distances for HMOH(H₂O)₂ (M = Al and Ga) are shown in Fig. 4 and S4,† respectively. As shown in Fig. 4d, for HAlOH(H₂O)₂, the O(2)H(2′)⋯O(1) hydrogen-bond distance in the AIMD 225 K simulation varies from 1.40 to 2.10 Å. Such a large amplitude (∼0.70 Å) produces broad progression of the stretching mode of O(2)H(2′) in the range of 3000–3500 cm⁻¹, which is in the same OH stretching vibrational frequency region of experimental band D. The O(3)H(3′)⋯O(2) hydrogen-bond distance in the AIMD 225 K simulation varies from 1.40 to 1.90 Å (Fig. 4h), indicative of a smaller amplitude (∼0.50 Å) as compared to fluctuation of the O(2)H(2′)⋯O(1) hydrogen-bond distance and consequently smaller progression of the stretching mode of O(3)H(3′). This result is consistent with smaller broadening of experimental band E than of band D. Similar results are also obtained for the HGaOH(H₂O)₂ system (Fig. S5†). In addition, fluctuation of the O(3)H(3′)⋯O(2) hydrogen-bond distance in HAlOH(H₂O)₂ (∼0.50 Å, Fig. 4h) is larger than that in the heavier cluster HGaOH(H₂O)₂ (∼0.40 Å, Fig. S5h†), which is in accordance with the larger broadening of band E (∼350 cm⁻¹) in HAlOH(H₂O)₂ than of band e (50 cm⁻¹) in HGaOH(H₂O)₂.^43,44 In the AIMD 225 K simulation, the O(3)–H(3′) bond distance in HGaOH(H₂O)₂ (1.01 Å, Fig. S6h†) is slightly shorter than that in HAlOH(H₂O)₂ (1.02 Å, Fig. S7h†), indicating that the O(3)–H(3′) bond in the heavier cluster HGaOH(H₂O)₂ is slightly more robust than that in HAlOH(H₂O)₂. This is consistent with the higher frequency and weaker intensity of experimental band e (HGaOH(H₂O)₂) as compared to experimental band E (HAlOH(H₂O)₂) (Fig. 1).

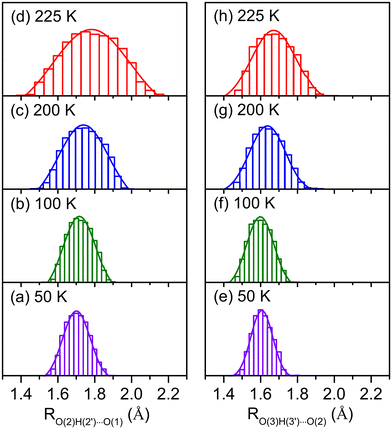Fig. 4 Normal distribution of O(2)H(2′)⋯O(1) and O(3)H(3′)⋯O(2) hydrogen-bond distances (R_{O(2)H(2′)⋯O(1)} and R_{O(3)H(3′)⋯O(2)}) during AIMD simulations of isomer 2-I for HAlOH(H₂O)₂ at 50 K, 100 K, 200 K, and 225 K. The atom labelling is indicated in Fig. 2.

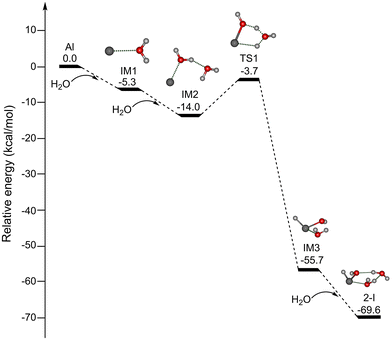
Since the reaction processes that occur under the plasma conditions of laser vaporization sources are very complex and difficult to characterize definitively, the possible formation mechanisms were explored by quantum chemical calculations at the MP2/AVDZ level of theory. Due to the spectral and structural similarity of HAlOH(H₂O)₂ and HGaOH(H₂O)₂, we mainly focus on discussion of the formation mechanisms of HAlOH(H₂O)₂. Since the reaction of the Al atom with one water molecule was predicted to be hindered by a substantial energy barrier,^30–32 the formation of HAlOH(H₂O)₂ from the reactions of the Al atom with two and three water molecules was explored in this work. Potential energy profiles of two pathways for the formation of HAlOH(H₂O)₂ (isomer 2-I) are shown in Fig. 5 and S8,† respectively, for which the thermodynamic data are listed in Table S1.†

Fig. 5 Potential energy profiles of pathway A for the formation of HAlOH(H₂O)₂ (isomer 2-I) calculated at the MP2/aug-cc-pVDZ level of theory. The abbreviation “IM” stands for the intermediate and “TS” for the transition state. The corresponding structures are shown in the inset (O, red; H, light gray; Al, gray).

As shown in Fig. 5, for pathway A, the addition of H₂O to Al forms the intermediate IM1 [Al(H₂O)], which is exothermic by 5.3 kcal mol⁻¹. IM1 could react with the second water molecule to form the solvated complex IM2 [Al(H₂O)₂], and this process releases 8.7 kcal mol⁻¹ of energy. IM2 is transformed into IM3 with an insertion HAlOH core via TS1 with an energy barrier of 10.3 kcal mol⁻¹, releasing 41.7 kcal mol⁻¹ of energy. Our results are consistent with previous UHF-(U)CCSD calculations.³³ IM3 combines with the third water molecule to form isomer 2-I, and this process is exothermic by 13.9 kcal mol⁻¹. Pathway A shows that the H–OH bond breaks after the Al atom is solvated with two water molecules.

As shown in Fig. S8,† for pathway B, the first and second processes are identical to those of pathway A (Fig. 5). Subsequently, the addition of the third water molecule to IM2 results in the formation of the solvated complex IM4 [Al(H₂O)₃], which is exothermic by 10.2 kcal mol⁻¹. IM4 could undergo isomerization to generate isomer 2-I, which releases 45.4 kcal mol⁻¹ of energy with a 8.9 kcal mol⁻¹ barrier (TS2), similar to the barrier calculated at the UHF-(U)CCSD level (8.7 kcal mol⁻¹).³³ Pathway B shows that the H–OH bond breaks after the Al atom is solvated with three water molecules.

It can be seen from Fig. 5 and S8† that the barrier for the Al(H₂O)₃ → HAlOH(H₂O)₂ isomerization (8.9 kcal mol⁻¹) is smaller than that for the Al(H₂O)₂ → HAlOH(H₂O) isomerization (10.3 kcal mol⁻¹), indicating that the formation of the HAlOH insertion complex becomes more favorable with increasing number of water molecules. The investigation of the mechanism of the metal–water reaction predicts the involvement of multiple intermediates, while small clusters serve as the building blocks for large clusters. Theoretical calculations suggest that HAlOH, HAlOH(H₂O), and HAlOH(H₂O)₂ are crucial precursors in the aluminum–water reaction system.^31–33 The studies of HAlOH are very extensive, and the spectral and structural information of HAlOH(H₂O) has been obtained by integrating the EPR spectra with the calculated data.^3,25,27 Our present experimental and theoretical characterization of HAlOH(H₂O)₂ and HGaOH(H₂O)₂ enrich the types of intermediates in the metal–water reactions.

Conclusion

We used the IR-VUV method to obtain infrared spectra of HMOH(H₂O)₂ (M = Al and Ga) in the OH stretch vibrational region of 2500–3900 cm⁻¹. Combined with quantum chemical harmonic calculations and AIMD anharmonic simulations, it is confirmed that the most stable isomer of HMOH(H₂O)₂ (M = Al and Ga) has a hydride–hydroxide core HMOH with the desired hydrogen-bonded network formed by two water molecules. The broadening of the experimental spectral bands of HMOH(H₂O)₂ (M = Al and Ga) was rationalized in the context of hydrogen-bond fluctuations via AIMD simulations. The formation of HMOH(H₂O)₂ (M = Al and Ga) from the reaction of metal atoms with two and/or three water molecules was theoretically predicted to be both thermodynamically exothermic and kinetically facile in the gas phase, which supports the experimentally observed features. It is hoped that the present results will stimulate further studies on the microscopic mechanisms of a large variety of reactions between metals and small molecules (i.e., CO, N₂, H₂O, CO₂, NH₃, CH₄, etc.).

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the Dalian Coherent Light Source (DCLS) for support and assistance. This work was supported by the National Natural Science Foundation of China (No. 22125303, 92361302, 92061203, 22103082, 22273101, 22288201, and 21327901), the National Key Research and Development Program of China (No. 2021YFA1400501), the Innovation Program for Quantum Science and Technology (No. 2021ZD0303304), the Dalian Institute of Chemical Physics (DICP I202437), the Chinese Academy of Sciences (No. GJJSTD20220001), and the International Partnership Program of CAS (121421KYSB20170012).

References

1. A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278.
2. T. Takata, J. Jiang, Y. Sakata, M. Nakabayashi, N. Shibata, V. Nandal, K. Seki, T. Hisatomi and K. Domen, Nature, 2020, 581, 411–414.
3. S. B. Oblath and J. L. Gole, J. Chem. Phys., 1979, 70, 581–582.
4. R. E. McClean, H. H. Nelson and M. L. Campbell, J. Phys. Chem., 1993, 97, 9673–9676.
5. A. L. Ramaswamy and P. Kaste, J. Energ. Mater., 2005, 23, 1–25.
6. D. K. Bohme and H. Schwarz, Angew. Chem., Int. Ed., 2005, 44, 2336–2354.
7. Z. Luo, A. W. Castleman, Jr. and S. N. Khanna, Chem. Rev., 2016, 116, 14456–14492.
8. F. Misaizu, K. Tsukamoto, M. Sanekata and K. Fuke, Z. Phys. D, 1993, 26, S177–S179.
9. M. Beyer, C. Berg, H. W. Görlitzer, T. Schindler, U. Achatz, G. Albert, G. Niedner-Schatteburg and V. E. Bondybey, J. Am. Chem. Soc., 1996, 118, 7386–7389.
10. M. Beyer, U. Achatz, C. Berg, S. Joos, G. Niedner-Schatteburg and V. E. Bondybey, J. Phys. Chem. A, 1999, 103, 671–678.
11. Y. Inokuchi, K. Ohshimo, F. Misaizu and N. Nishi, Chem. Phys. Lett., 2004, 390, 140–144.
12. M. K. Beyer, Mass Spectrom. Rev., 2007, 26, 517–541.
13. J. Heller, T. F. Pascher, C. van der Linde, M. Oncák and M. K. Beyer, Chem. – Eur. J., 2021, 27, 16367–16376.
14. J. Heller, W. K. Tang, E. M. Cunningham, E. G. Demissie, C. van der Linde, W. K. Lam, M. Oncák, C. K. Siu and M. K. Beyer, Angew. Chem., Int. Ed., 2021, 60, 16858–16863.
15. H. Watanabe and S. Iwata, J. Phys. Chem., 1996, 100, 3377–3386.
16. C. K. Siu, Z. F. Liu and J. S. Tse, J. Am. Chem. Soc., 2002, 124, 10846–10860.
17. R. J. Evans, J. R. Rustad and W. H. Casey, J. Phys. Chem. A, 2008, 112, 4125–4140.
18. S. Bogatko, J. Moens and P. Geerlings, J. Phys. Chem. A, 2010, 114, 7791–7799.
19. C. van der Linde and M. K. Beyer, Phys. Chem. Chem. Phys., 2011, 13, 6776–6778.
20. S. Álvarez-Barcia and J. R. Flores, Phys. Chem. Chem. Phys., 2016, 18, 6103–6112.
21. C. W. Bauschlicher and H. Partridge, J. Phys. Chem., 1991, 95, 9694–9698.
22. M. Sodupe and C. W. Bauschlicher, Chem. Phys. Lett., 1991, 181, 321–326.
23. B. M. Reinhard and G. Niedner-Schatteburg, J. Phys. Chem. A, 2002, 106, 7988–7992.
24. J. K. Agreiter, A. M. Knight and M. A. Duncan, Chem. Phys. Lett., 1999, 313, 162–170.
25. R. H. Hauge, J. W. Kauffman and J. L. Margrave, J. Am. Chem. Soc., 1980, 102, 6005–6011.
26. H. A. Joly, J. A. Howard, M. Tomietto and J. S. Tse, J. Chem. Soc., Faraday Trans., 1994, 90, 3145–3151.
27. F. D. Brunet and H. A. Joly, J. Phys. Chem. A, 2012, 116, 4267–4273.
28. X. Wang and L. Andrews, J. Phys. Chem. A, 2007, 111, 1860–1868.
29. V. A. Macrae and A. J. Downs, Phys. Chem. Chem. Phys., 2004, 6, 4571–4578.
30. S. Alvarez-Barcia and J. R. Flores, Chem. Phys. Lett., 2009, 470, 196–202.
31. S. Álvarez-Barcia and J. R. Flores, J. Chem. Phys., 2009, 131, 174307.
32. S. Álvarez-Barcia and J. R. Flores, Chem. Phys., 2011, 382, 92–97.
33. S. Álvarez-Barcia and J. R. Flores, Chem. Phys., 2010, 374, 131–137.
34. B. B. Zhang, Y. Yu, Z. J. Zhang, Y. Y. Zhang, S. K. Jiang, Q. M. Li, S. Yang, H. S. Hu, W. Q. Zhang, D. X. Dai, G. R. Wu, J. Li, D. H. Zhang, X. M. Yang and L. Jiang, J. Phys. Chem. Lett., 2020, 11, 851–855.
35. G. Li, C. Wang, H. J. Zheng, T. T. Wang, H. Xie, X. M. Yang and L. Jiang, Chin. J. Chem. Phys., 2021, 34, 51–60.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A. 03, Wallingford, CT, 2016.
37. R. D. Johnson, NIST computational chemistry comparison and benchmark database. In https://cccbdb.nist.gov/, 2006.
38. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
39. G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 1999, 110, 2810–2821.
40. D. McQuarrie, Statistical Mechanics, Harper Collins Publishers, New York, NY, 1976.
41. K. R. Asmis, N. L. Pivonka, G. Santambrogio, M. Brummer, C. Kaposta, D. M. Neumark and L. Woste, Science, 2003, 299, 1375–1377.
42. S. K. Jiang, M. Z. Su, S. Yang, C. Wang, Q. R. Huang, G. Li, H. Xie, J. Y. Yang, G. R. Wu, W. Q. Zhang, Z. J. Zhang, J. L. Kuo, Z. F. Liu, D. H. Zhang, X. M. Yang and L. Jiang, J. Phys. Chem. Lett., 2021, 12, 2259–2265.
43. L. Jiang, S. T. Sun, N. Heine, J. W. Liu, T. I. Yacovitch, T. Wende, Z. F. Liu, D. M. Neumark and K. R. Asmis, Phys. Chem. Chem. Phys., 2014, 16, 1314–1318.
44. S. T. Sun, L. Jiang, J. W. Liu, N. Heine, T. I. Yacovitch, T. Wende, K. R. Asmis, D. M. Neumark and Z. F. Liu, Phys. Chem. Chem. Phys., 2015, 17, 25714–25724.
45. A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843.
46. H. Y. Li, X. T. Kong, L. Jiang and Z. F. Liu, J. Phys. Chem. Lett., 2019, 10, 2162–2169.
47. X. T. Kong, S. T. Sun, L. Jiang and Z. F. Liu, Phys. Chem. Chem. Phys., 2018, 20, 4571–4578.
48. H. Y. Li, X. T. Kong, L. Jiang and Z. F. Liu, Phys. Chem. Chem. Phys., 2018, 20, 26918–26925.
49. S. J. Gui, L. Jiang and Z. F. Liu, J. Comput. Chem., 2021, 42, 1514–1525.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03440f

---