Open Access Article
Open Access ArticleResolving molecular frontier orbitals in molecular junctions with kHz resolution†
Yuji
Isshiki
a,
Enrique
Montes
 b,
Tomoaki
Nishino
b,
Tomoaki
Nishino
 a,
Héctor
Vázquez
a,
Héctor
Vázquez
 *b and
Shintaro
Fujii
*b and
Shintaro
Fujii
 *a
*a
aDepartment of Chemistry, School of Science, Tokyo Institute of Technology, 2-12-1 W4-10 Ookayama, Meguro-ku, Tokyo 152-8551, Japan. E-mail: fujii.s.af@m.titech.ac.jp
bInstitute of Physics, Czech Academy of Sciences, Cukrovarnická 10, Prague, CZ-162 00, Czech Republic. E-mail: vazquez@fzu.cz
First published on 23rd September 2024
Abstract
Designing and building single-molecule circuits with tailored functionalities requires a detailed knowledge of the junction electronic structure. The energy of frontier molecular orbitals and their electronic coupling with the electrodes play a key role in determining the conductance of nanoscale molecular circuits. Here, we developed a method for measuring the current–voltage (I–V) characteristics of single-molecule junctions with a time resolution that is two orders of magnitude higher than previously achieved. These I–V measurements with high temporal resolution, together with atomistic simulations, enabled us to characterize in detail the frontier molecular states and their evolution in sub-angstrom stretching of the junction. For a series of molecules, changes in the electronic structure were resolved as well as their fluctuations prior to junction breakdown. This study describes a new methodology to determine the key frontier MO parameters at single-molecule junctions and demonstrates how these can be mechanically tuned at the single-molecule level.
Introduction
Characterizing and controlling frontier molecular orbitals (MOs) at interfaces between metals and organic molecules is a key requirement for designing tailored single-molecule junctions (SMJs). The alignment of MOs and metallic electrode states is one of the factors determining the charge transport efficiency of the metal–molecule interface, which has been studied in detail for bulk surfaces using spectroscopic methods1–6 and local charge transport through the metal–molecule interface at the nanoscale and has been characterized using the scanning probe method.7–10 At the molecular scale, the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) levels of SMJs can be changed by introducing chemical functional groups into the molecular backbone11–13 or by changing the type of electrode.14 Furthermore, fine energy tuning of the MO levels has been examined in recent years, and it has been demonstrated that the energy level arrangement between a molecule and metal electrodes can be tuned at a single-molecule level by mechanical stretching of SMJs formed between metal electrodes (Fig. 1a and b).15–24 Recent advances in single-molecule technology have made it possible to experimentally control the interface and electronic structure between individual molecules and metal electrodes using break junction (BJ) methods, but only a few studies have demonstrated the controllability of electronic structure, including metal–molecule energy level alignment. Due to the difficulty of routinely manipulating a single molecule in a junction and making current–voltage (I–V) measurements of SMJs with remarkably short lifetimes (10–100 ms) under increased bias conditions (∼1 V),25 these studies have typically been limited to a few selected compounds, hindering better understanding of the modulation of molecular orbitals at the single-molecule scale.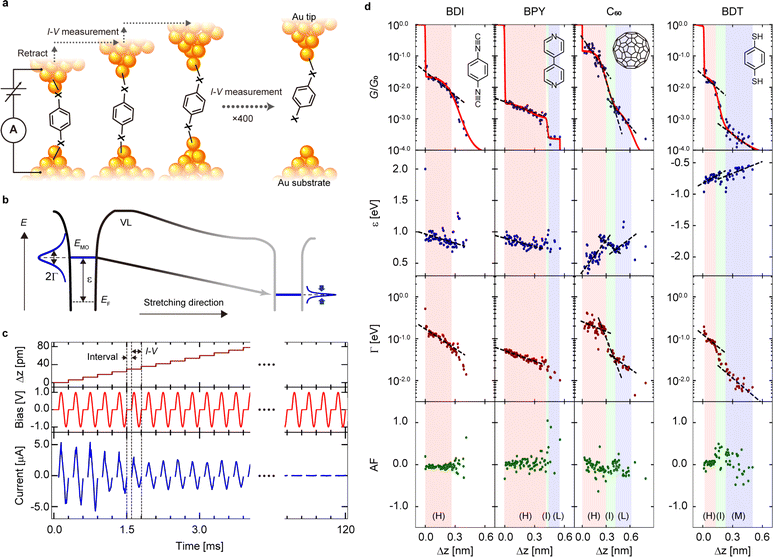 | ||
| Fig. 1 (a) Schematic illustration showing one cycle of repeated current–voltage (I–V) curve measurement during the junction stretching process. (b) Shift of molecular orbital level (ε) and electronic coupling (Γ) during molecule junction stretching. (c) Time course of Δz, bias voltage applied to the junction, and measured current in the magnified time region, in which a molecular junction forms. Here, the zero point of Δz is redefined as the display starting point. (d) Conductance (G), ε, Γ and asymmetric factor (AF) with junction elongation for BDI, BPY, BDT, and C60. The ε, Γ, and AF values are obtained by analyzing I–V curves measured during the junction stretching process in (c). See main text for details. Blue, blue, red, and green dots indicate G, ε, Γ, and AF, respectively. The labels of (H) and (L) indicate the high and low conductance states, and (I) indicates intermediate states between H (M) and L states. The regions of the H, T and L (M) states are filled in red, green, and blue, respectively. See ESI Section 3† for the method used to determine the region of each state. The dotted lines represent the results of a linear fit of the experimental data for each region. | ||
In this study, we developed a spectroscopic approach to describe in detail the electronic structure of various SMJs during the junction stretching process. This spectroscopic approach is based on I–V using a customized program based on field-programmable gate array (FPGA) technology, which has sub-angstrom distance resolution and can routinely collect I–V curves at a time resolution of 5 kHz, corresponding to a single I–V curve acquisition time of 0.2 ms. The temporal resolution surpasses that of conventional BJ methods by approximately two orders of magnitude.26 In addition to the standard analysis of conductance (G) of SMJs, the statistical analysis of I–V curves based on the single-level model27 gives the parameters, the MO level (ε) and the metal–molecule electronic coupling (Γ), which are essential for understanding the electronic structure of SMJs.28 Together with atomistic simulations of the junctions, which verify the trends found by experiment, this combined analysis of G, ε and Γ in the stretching process of SMJs demonstrated the manipulation of the electronic structure by stretching. These trends in electronic structure obtained from fitting measured I–V curves are supported by conductance simulations based on DFT. In order to investigate a series of HOMO- and LUMO-conducting junctions, this method was applied to SMJs of 1,4-benzenediisocyanide (BDI), 4,4′-bipyridine (BPY), fullerene (C60), and 1,4-benzenedithiol (BDT), which are paradigmatic molecules used in charge transport studies. Our study reveals the temporal evolution of junction electronic structure with unprecedented temporal resolution and how it can be mechanically modulated and tuned at the single molecule level by simply displacing the electrodes.
Results and discussion
Fig. 1c shows a part of the I–V measurement during a stretching process of a BDI junction and the time course of the junction current when an AC bias of 1.0 V in amplitude and 5 kHz in frequency is applied from 0.0 ms to 120 ms, in which the time is set to 0 when the SMJ is formed (ESI, Section 1†). This I–V measurement procedure has a relatively low junction stretching rate (20 nm s−1) and two orders of magnitude higher time resolution than previous studies,23,26 allowing us to track detailed changes in the I–V curve due to junction elongation that have previously been hidden by time averaging. In order to investigate different molecular backbones, this I–V measurement procedure was also applied to BPY, C60, and BDT (ESI, Section 2†). Measured I–V curves were interpreted within the single-level model (Fig. 1b). The model considers transport mediated by molecular resonance, characterized by energy ε with respect to the Fermi level (EF), and electronic couplings to the left and right electrodes given by ΓL and ΓR, respectively. At a low bias regime, transmission at the Fermi level is given by the Lorentzian function:| T(E) = Γ2/((E − ε)2 + Γ2), | (1) |
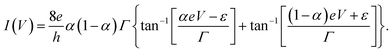 | (2) |
The parameter α describes the asymmetry of electronic coupling with the electrodes, α = ΓR/(ΓR + ΓL). By fitting the measured I–V curves with eqn (2), the electronic structure (i.e., ε and Γ values) of the SMJ was determined (ESI, Section 3†). To evaluate the structural asymmetry of the junction that is asymmetry of the I–V shape, the asymmetric factor (AF) was defined where AF is the ratio of G values (AF = log10(Gp/Gn)) where Gp and Gn are G at positive and negative bias ranges. When AF > 0 (AF < 0), larger current values are shown on the tip (substrate) side. Fig. 1d shows representative traces of G, ε, Γ, and AF with respect to tip displacement Δz for the junction stretching. The conductance value G is determined from the slope of the I–V curve within the bias range 475–525 mV. With this time-resolved I–V measurement, detailed modulations with sub-angstrom distance resolution were obtained for ε, Γ, and AF, in addition to G during the junction stretching process. The G traces in Fig. 1d reproduce well the typical electronic states formed during the junction stretching reported earlier for BDI,29 BPY,30 C60,26 and BDT.31 It had been previously shown that SMJs exhibit multiple conductance states such as high (H), medium (M), and low (L) conductance states depending on the geometry of the metal–molecule interface structure26,28,32,33 (i.e., binding modes between the metal and the molecule) for BPY, C60, and BDT. The states that appear during the transition between the H and L (M) states are denoted as intermediate (I) states in our work. The H, I, and L states are defined based on the results of fitting the G trace with a sigmoid function (ESI, Section 3†). Notably, the high temporal resolution of I–V measurement carried out in this study was able to capture the I state that appears during the transition from the H state to the L (M) state for C60 (BDT), which had not been confirmed before. The formation, evolution, breakdown, or transitions of each electronic state during junction stretching, measured as stepwise changes in G, are found to correlate with changes in the values of ε, Γ, and AF (Fig. 1d) measured simultaneously with G. The conduction MO that carries electronic charges through the SMJs has been confirmed to be the LUMO for BDI,29,34 BPY,35 and C60,36 and HOMO for BDT.37 For the H states of BDI, BPY and BDT, the MO level approaches the EF; in contrast, the LUMO level moves away from the EF for the H states of C60 due to the junction stretching (Fig. 1d). The MO level of C60 exhibits a non-monotonic energy change during the H → I → L state transition with a decrease, increase, and decrease in the LUMO level (Fig. 1d). While ε exhibits a variety of energy changes, the metal–molecule electronic coupling Γ is monotonically weakened by the junction stretching (Fig. 1d). Information of the structural symmetry during the junction stretching can be obtained by examining the AR values (Fig. 1d).38 Compared with other molecules, BDI exhibits a symmetric interface structure with the junction stretching (AF = log10(Gp/Gn) ∼ 0), which agrees with the result that the BDI forms a well-defined metal–molecule interface structure whose conductance ranges from 10−3 to 10−2G0.29 On the other hand, BDT and C60 show variable metal–molecule interface structures26,31 with G ranging from 10−5 to 10−1G0 with the junction stretching. The junction stretching changes the metal–molecule interface structure, forming an asymmetric junction structure, which is responsible for the relatively large changes in the AF values (σAF = 0.04–0.05) for C60 and BDT than that of BDI (σAF = 0.003). Here σAF is calculated as a standard deviation of a histogram of the AF values at a given electrode separation (ESI, Section 4†).
To quantitatively evaluate the modulation of ε and Γ traces due to the junction stretching of Δz, one-dimensional (1D) G histograms and 2D histograms of ε–Δz and Γ–Δz traces were created from hundreds to thousands of traces (Fig. 2a and b), which shows a clear distribution of the H and I states. In the 2D histograms, distributions of the L or M states of BPY, C60, and BDT were obscured due to the low generation probabilities and the low conductance near the lower conductance limit of the measurement system (G = 2 × 10−4G0). The variation of the electronic structure in the H and I states with respect to stretching distance Δz (i.e., ∂ε/∂z, and ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z) was determined by linear fits of the slope of the distributions (Table 1 and ESI, Section 4†). The H states of BDI and BPY display a negative ∂ε/∂z of −0.5 to −0.3 eV nm−1, while the H states of C60 and BDT show positive ∂ε/∂z of 0.9 eV nm−1 and 0.3 eV nm−1, respectively. The I states of C60 and BDT display negative and positive ∂ε/∂z of −0.2 eV nm−1 and 0.3 eV nm−1, respectively. In contrast to ∂ε/∂z, ∂
Γ/∂z) was determined by linear fits of the slope of the distributions (Table 1 and ESI, Section 4†). The H states of BDI and BPY display a negative ∂ε/∂z of −0.5 to −0.3 eV nm−1, while the H states of C60 and BDT show positive ∂ε/∂z of 0.9 eV nm−1 and 0.3 eV nm−1, respectively. The I states of C60 and BDT display negative and positive ∂ε/∂z of −0.2 eV nm−1 and 0.3 eV nm−1, respectively. In contrast to ∂ε/∂z, ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z is always negative regardless of the molecules and the conductance states (Table 1). Interestingly, the I states exhibit larger negative ∂
Γ/∂z is always negative regardless of the molecules and the conductance states (Table 1). Interestingly, the I states exhibit larger negative ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z than the H states, and Γ is reduced significantly in the intermediate states due to the junction stretching (Table 1). Repeated I–V measurement with improved time resolution allowed us to capture statistical changes in the junction-electronic structure that were previously inaccessible, and to resolve the peculiar fluctuation of the MO levels prior to the breakdown of the junctions. We would like to emphasize again that with this I–V approach, we were able to visualize the distance evolution of the electronic structure (i.e., ε and Γ), which was not possible with conventional G measurements.
Γ/∂z than the H states, and Γ is reduced significantly in the intermediate states due to the junction stretching (Table 1). Repeated I–V measurement with improved time resolution allowed us to capture statistical changes in the junction-electronic structure that were previously inaccessible, and to resolve the peculiar fluctuation of the MO levels prior to the breakdown of the junctions. We would like to emphasize again that with this I–V approach, we were able to visualize the distance evolution of the electronic structure (i.e., ε and Γ), which was not possible with conventional G measurements.
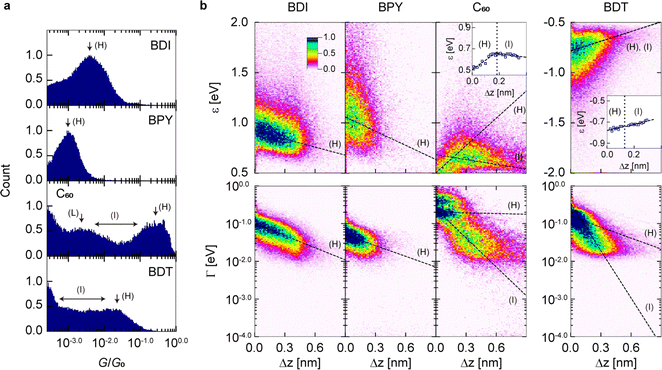 | ||
| Fig. 2 Statistical analysis of the mechanical tuning of the electronic structures. (a and b) 1D histograms of G and 2D histograms of ε–Δz traces and Γ–Δz traces for BDI, BPY, C60, and BDT constructed from 1278, 889, 513, and 2033 junction-stretching processes, respectively (see Fig. 1d for examples of individual traces). Bin sizes of 0.02, 12 pm, 0.0075 eV, and 0.02, are used for G, Δz, ε, and Γ, respectively. The dashed lines in the 2D histograms are the results of linear fitting. Representative values of ε and Γ were determined as a Gaussian peak of the distributions in each bin (see ESI Section 4† for further details). The insets of BDT and C60 plot the representative ε values as a function of Δz. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G/∂z, ∂ε/∂z, ∂ε/∂zDFT, ∂
G/∂z, ∂ε/∂z, ∂ε/∂zDFT, ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z, ∂
Γ/∂z, ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂zDFT, and full width at half maximum of AF (wAF) for BPY, BDI, C60 and BDT in Fig. 2 (see also ESI Section 4)
Γ/∂zDFT, and full width at half maximum of AF (wAF) for BPY, BDI, C60 and BDT in Fig. 2 (see also ESI Section 4)
| BDI(H) | BPY(H) | C60(H) | C60(T) | BDT(H) | BDT(I) | |
|---|---|---|---|---|---|---|
| G peak/G0 | 10−2.39 | 10−3.04 | 10−0.60 | 10−2.69 | 10−1.67 | 10−2.8 |
| ε peak [eV] | 0.87 | 1.02 | 0.60 | 0.64 | 0.76 | 0.71 |
| Γ peak [eV] | 0.06 | 0.04 | 0.22 | 0.04 | 0.14 | 0.03 |
∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G/∂z [nm−1] G/∂z [nm−1] |
−1.64 | −1.21 | −2.40 | −5.15 | −2.24 | −7.75 |
| ∂ε/∂z [eV nm−1] | −0.27 | −0.47 | 0.91 | −0.16 | 0.31 | 0.33 |
| ∂ε/∂zDFT [eV nm−1] | −1.47 | −2.72 | 1.88 | N.A. | 2.28 | N.A. |
∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z [nm−1] Γ/∂z [nm−1] |
−1.07 | −0.95 | −0.06 | −2.56 | −0.97 | −4.18 |
∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂zDFT [nm−1] Γ/∂zDFT [nm−1] |
−4.99 | −5.05 | −2.75 | N.A. | −0.97 | N.A. |
| w AF | 0.20 | 0.29 | 0.40 | 1.02 | 0.61 | 0.93 |
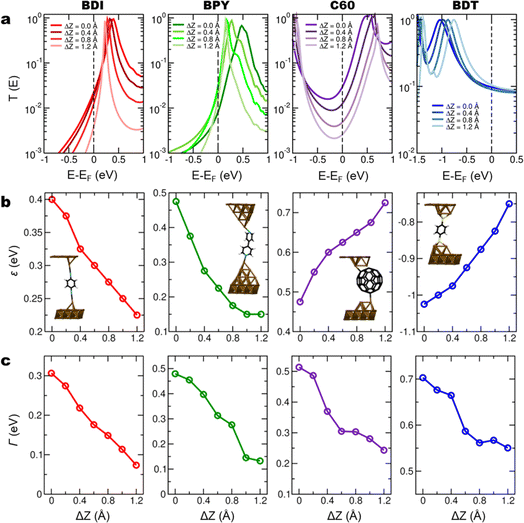
To understand the observed behaviour, transport calculations were performed within the DFT-NEGF formalism for BDI, BPY, C60, and BDT. These calculations focus on the evolution of molecular levels in the final stages prior to the breaking of the junction. Junctions were built where individual molecules were placed between several Au(111) layers. Molecules were bonded to both electrodes via Au tip structures. For each molecular species, the conducting properties were calculated for a range of electrode separations close to the junction rupture. At every inter-electrode separation, the junction geometry was optimized and the transmission spectrum was calculated. The top electrode was then displaced upwards and the junction geometry optimization and subsequent conductance calculation were repeated. Fig. 3a shows the computed transmission spectra of the BDI, BPY, C60, and BDT junctions for a range of electrode separations, depicting the elongation of structures from equilibrium, obtained as the elongation which minimizes the junction energy. For this range of elongations, the calculated conductance is in the range 3.8 × 10−3 to 2.2 × 10−2G0 for BDI, 1.1 × 10−3 to 1.8 × 10−3G0 for BPY, 9.7 × 10−2 to 1.4 × 10−1G0 for BDT, and 2.5 × 10−3 to 2.9 × 10−2G0 for C60. These results agree well with previously reported values based on DFT calculations: 4.8 × 10−2G0 for BDI,39 4.0 × 10−3G0 for BPY,35 2.7 × 10−2G0 for C60,40 and 2.4 × 10−2G0 for BDT.37 The calculated conducting properties reproduce experimental findings well. BDI, BPY and C60 junctions are LUMO-conducting while BDT is HOMO-conducting, as previously reported.23,29 Fig. S17† shows the spectra of all junctions replotted over a wide energy range (ESI, Section 6†). As the electrodes are separated, molecular frontier resonance energies change. At each electrode separation, values of ε and Γ were obtained from the calculated spectra by fitting the relevant transmission peak to a Lorentzian. Fig. 3b shows the calculated energy ε of the frontier molecular orbital, given as the peak position in the transmission spectra of Fig. 3a. For BDI and BPY junctions, the LUMO resonance shifts towards EF as the electrode retracts. In these cases, the Au contact atoms come closer to the benzene nodal planes during junction elongation, decreasing the electronic coupling of molecular π states. A similar behaviour is obtained for BDT and the calculated HOMO resonance moves towards EF as the junction is broken. In C60, unoccupied resonances shift towards higher energies as the junction is elongated. For BDT and C60, there are no significant changes in junction geometry with elongation, and the distance to the electrodes (or to just one electrode, in the case of C60) increases. This reduction of the metal–molecule hybridization results in molecular resonance energies being driven away from the Fermi level with increasing electrode separation.
A linear fit to the results of Fig. 3b yields the slope of the frontier molecular orbital with distance, reported as ∂ε/∂zDFT in Table 1. Discrete molecular states broaden out in energy when coupled with the electrodes. In the absence of energy-dependent metal electronic states, this broadening follows a Lorentzian line shape, whose full width at half maximum (Γ) depends on the strength of the metal–molecule electronic coupling.27 Under these conditions, peaks in transmission spectra arising from molecular resonances also follow this Lorentzian line shape. Molecular resonances in DFT-based transmission spectra approximately exhibit a Lorentzian character near the peaks, although the line shape can be affected by the presence of other molecular resonances near the Fermi level, or of gap states. Fig. 3c shows the calculated electronic coupling Γ, obtained as the full width at half maximum of a Lorentzian fit to the transmission peaks of Fig. 3a. DFT transmission spectra include several phenomena such as energy-dependent Au states or other molecular orbitals, which introduce deviations with respect to the single-level approximation. As such, DFT spectra deviate from simple Lorentzian profiles41 (for example for C60). This leads to quantitative differences between calculated and measured parameters, as we find here. Despite these limitations, however, Lorentzian fits to DFT transmission spectra have been carried out as they allow for trends to be inferred and compared with those in measured quantities.24,35,42–44 In all cases, the coupling Γ decreases with junction stretching, as seen in the experiment. For both ∂ε/∂z and ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z, the sign of measured and calculated quantities always agrees. In Table 1, the calculated values differ from measured ones, reflecting the fact that the exhaustive DFT calculations performed here correspond to a series of optimized geometries with increasing junction length. This contrasts with the values in the experiment, where measurements average over many conformations. DFT calculations yield the largest variations with increasing junction length for BDI and BPY. In the simulations of these junctions, the molecule changed its orientation slightly becoming more vertical as the junction was elongated. Junction geometries for different electrode separations are shown in Fig. S18.† This led to a decrease in the π-Au electronic coupling with the electrode in BDI and BPY and a transition toward coupling through σ bonds along the long molecular axis. In contrast, simulations of BDT showed that adsorption in the hollow site of the tip structures was energetically favourable. This enabled out-of-plane π-Au coupling to be preserved throughout the junction elongation, and the BDT junction yields the smallest decrease in ∂
Γ/∂z, the sign of measured and calculated quantities always agrees. In Table 1, the calculated values differ from measured ones, reflecting the fact that the exhaustive DFT calculations performed here correspond to a series of optimized geometries with increasing junction length. This contrasts with the values in the experiment, where measurements average over many conformations. DFT calculations yield the largest variations with increasing junction length for BDI and BPY. In the simulations of these junctions, the molecule changed its orientation slightly becoming more vertical as the junction was elongated. Junction geometries for different electrode separations are shown in Fig. S18.† This led to a decrease in the π-Au electronic coupling with the electrode in BDI and BPY and a transition toward coupling through σ bonds along the long molecular axis. In contrast, simulations of BDT showed that adsorption in the hollow site of the tip structures was energetically favourable. This enabled out-of-plane π-Au coupling to be preserved throughout the junction elongation, and the BDT junction yields the smallest decrease in ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z. In the C60 junction there is a small rotation of the cage which seems to contribute to the reduction of the electronic coupling. Qualitative trends in calculated and measured parameter changes best match in BDI and BPY, while differences are more prominent in BDT and, especially, C60. We speculate that this may be due to limitations in the applicability of the single-level model for the C60 junction.
Γ/∂z. In the C60 junction there is a small rotation of the cage which seems to contribute to the reduction of the electronic coupling. Qualitative trends in calculated and measured parameter changes best match in BDI and BPY, while differences are more prominent in BDT and, especially, C60. We speculate that this may be due to limitations in the applicability of the single-level model for the C60 junction.
In the above discussion, we examined the averaged global trend of stretch-induced modulation of ε in molecular junctions for the stochastically significant conductance states identified in the 2D histograms of G, ε, and Γ vs. z traces (Fig. 2b). Besides the global trend of the stretch-induced modulation of ε, we focus here on local small fluctuations of ε and Γ measured in the experiment. Fig. 4a shows examples of ε–Δz and Γ–Δz traces with peculiar fluctuation of ε and Γ for the H states of BDT. In addition to the global trend of the HOMO level ε approaching EF (see also Fig. 2b), there are local fluctuations where the HOMO level drops and rises. We observe that the fluctuations in ε are correlated with those in Γ. To clarify the local small variation of ε and Γ in individual traces, we determined ∂ε/∂z and ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z by dividing individual experimental traces into multiple segments (Fig. 4a and ESI, Section 4†) and created 2D plots (Fig. 4b). Distribution in the ∂|ε|/∂z vs. ∂
Γ/∂z by dividing individual experimental traces into multiple segments (Fig. 4a and ESI, Section 4†) and created 2D plots (Fig. 4b). Distribution in the ∂|ε|/∂z vs. ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z 2D plots indicates that the smaller the value of ∂
Γ/∂z 2D plots indicates that the smaller the value of ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z, the smaller the value of ∂|ε|/∂z. The relationship between ε and Γ can be confirmed by the rotation angles of the distributions fitted by the two-dimensional Gaussian distributions (see circles in Fig. 4b and ESI, Section 4†). Analysis of the fluctuations in the distributions shows that for BPY and BDT, ∂ε/∂z is associated with a gradual change in ∂
Γ/∂z, the smaller the value of ∂|ε|/∂z. The relationship between ε and Γ can be confirmed by the rotation angles of the distributions fitted by the two-dimensional Gaussian distributions (see circles in Fig. 4b and ESI, Section 4†). Analysis of the fluctuations in the distributions shows that for BPY and BDT, ∂ε/∂z is associated with a gradual change in ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z. On the other hand, for C60 and BDI, small changes of ∂ε/∂z are related to large fluctuations in ∂
Γ/∂z. On the other hand, for C60 and BDI, small changes of ∂ε/∂z are related to large fluctuations in ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z. Thus, the analysis of the ∂ε/∂z–∂
Γ/∂z. Thus, the analysis of the ∂ε/∂z–∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z histograms shows that the ∂ε/∂z fluctuations exhibit different behaviour in different molecules.
Γ/∂z histograms shows that the ∂ε/∂z fluctuations exhibit different behaviour in different molecules.
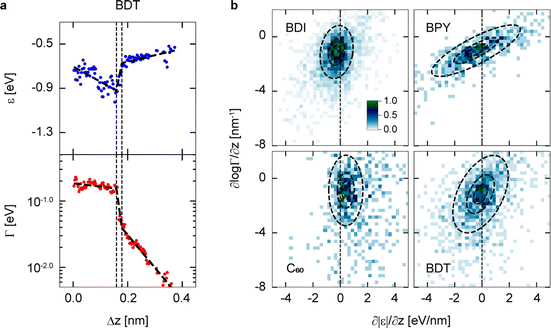 | ||
Fig. 4 Fluctuations of ε and Γ. (a) Example of evaluation of ∂ε/∂z and ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z in a segmented trace of BDT. ε and Γ were linearly fitted in three segments as seen in dashed lines. (b) 2D ∂ε/∂z–∂ Γ/∂z in a segmented trace of BDT. ε and Γ were linearly fitted in three segments as seen in dashed lines. (b) 2D ∂ε/∂z–∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ/∂z histograms for BDI, BPY, C60 and BDT. The dashed circles are the result of fitting with a 2D Gaussian distribution (see ESI Section 4†). Γ/∂z histograms for BDI, BPY, C60 and BDT. The dashed circles are the result of fitting with a 2D Gaussian distribution (see ESI Section 4†). | ||
Conclusions
We found that the MO levels can be mechanically gated on the order of −0.5 to 0.9 eV nm−1 by stretching junctions for a series of standard molecules. While electrostatic (field-effect) gating requires microfabrication techniques to build single-molecule device structures with transistor-type electrode configurations, mechanical gating does not require the fabrication of complex device structures and has relatively high gating rates, making it one of the more useful approaches to control the MO levels of SMJs. The I–V measurement procedure established in this study is applicable to the evaluation of the electronic structure of short-lived molecular junctions, where the molecule–electrode interaction is weak and/or a temperature gradient exists across the junction, providing opportunities to comprehensively characterize and understand the charge transport properties of various single molecules.Materials and methods
Sample preparation
The Au(111) electrode was prepared by thermal evaporation of Au on mica under high vacuum conditions. The Au(111) was flame annealed and cleaned with ethanol (Kanto Chemical, purity > 99.5%) before use. Mechanically cut Au wire (Nilaco, diameter approximately 0.3 mm, purity > 99.9%) was used as the tip. The target molecule was deposited on the Au(111) electrode by immersing the tip or substrate in a solution of the molecule. Ethanol was used as a solvent for the BPY (Wako Pure Chemical Industries, purity > 97.0%) and BDT (Tokyo Chemical Industry, purity > 98%), tetrahydrofuran for the BDI (Sigma-Aldrich, purity > 97%), and toluene for the C60 (Tokyo Chemical Industry, purity > 99.0%). Solutions of 1 mM for BDT and 10 mM for BPY, BDI, and C60 were prepared. The samples of BPY, BDT, BDI, and C60, which have strong bonding strength, were prepared by immersing a mechanically cut Au tip for one second.Experimental
A commercially available scanning tunnelling microscopy (STM) apparatus was used with a signal access module III (Bruker, Multimode STM), in which the current amplifier and piezo driver were replaced by an SR570 (Stanford Research System) and E-663 (Physik Instrumente), respectively. The feedback loop for the STM operation was controlled using a custom-made program based on an FPGA (National Instrument, PCIe 7852R), which has an analogue-to-digital conversion sampling rate of 750 kHz. Meanwhile, the I–V measurement rate was 5 kHz (for further details, see ESI Sections 1 and 5†). The sampling rate determines the frequency at which data points are collected, while the measurement rate refers to the frequency at which I–V curves are repeatedly recorded.The SMJs were formed using the BJ method based on STM.45 First, the Au STM tip is brought close to the Au(111) electrode where the target molecule is adsorbed, while monitoring electronic current (I) between the Au tip and the Au electrode at a bias voltage V = 50 mV. When a point contact between the Au tip and the Au electrode is made, G (= I/V) between the tip and electrode increases to more than 10G0. Then, the Au tip is pulled away from the Au electrode to form an atomic contact at a tip displacement velocity of 20 nm s−1. When G of the point contact falls below 10G0 (G0 = 2e2/h), the application of sinusoidal voltage is started and the point contact is gradually extended with a tip displacement velocity of 1 nm s−1. This elongation broke the point contact and formed a nanogap between the Au tip and the Au electrode. When the conductance falls below 0.8G0 and a single molecule was trapped in this nanogap and an SMJ was formed, the tip was further moved away from the Au electrode in 6 pm steps at a tip displacement velocity of 20 nm s−1. After each 6 pm-stretching within 2 μs, an I–V curve of the junction was measured within 0.2 ms, followed by a 0.1 ms wait. This one cycle of I–V measurement with the total data acquisition time of ca. 0.3 ms (0.302 ms) was repeated 400 times. After the 400 cycles of I–V measurement, the tip was pulled up to 10–40 nm and then returned to the initial position. All the feedback control of the STM tip positions was programmed using the FPGA technology. A lifetime of a molecular junction measured at room temperature has been reported to be 100–1000 s at low bias voltages of ∼0.2 V, while it is as low as 10–100 ms at high bias voltages of ∼1 V.25 Therefore, fast I–V measurements are essential to repeatedly record a large number of I–V characteristics within the ±1 V bias range for a molecular junction. Indeed, the time resolution of the present I–V measurement of 0.5 ms is much faster than the junction lifetime and allows detailed tracking of the time evolution of the I–V characteristics of molecular junctions. Eqn (2), which was used to fit the experimental I–V curves, did not consider the effect of temperature on the I–V characteristics26 because, as shown in a previous study, the effect of temperature at 300 K is known to be less than a few percent.46
Transport calculations
Electron transport calculations were performed for BDI, BPY, BDT and C60 junctions using the DFT-NEGF formalism as implemented in SIESTA and TranSIESTA.47,48 Unit cells containing the molecule, pyramidal tip structures, and several Au(111) layers were prepared. Each Au(111) layer contained 16 atoms. The stretching of the molecular junction was simulated by increasing the inter-electrode separation in successive steps of 0.2 Å. At each electrode separation, the geometry of the junction was optimized by allowing the coordinates of molecular and tip atoms to relax with a force cutoff of 0.02 eV Å−1. Transmission spectra were calculated at optimized geometries by pasting additional Au layers. A single- (double-)zeta polarized basis was used for molecular (gold) atoms. A real-space grid was defined with an equivalent cut-off energy of 250 Ry. Exchange–correlation was described using the Perdew–Burke–Ernzerhof (PBE) implementation of the generalized gradient approximation (GGA). Reciprocal space was sampled using 2 × 2 × 1, 5 × 5 × 1, and 15 × 15 × 1 Monkhorst–Pack grids for geometry optimization, the calculation of electronic structure and Green's function, and the calculation of transmission spectra, respectively.Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported in part by JST SICORP (JPMJSC22C2), JSPS KAKENHI (no. JP23K04517), the Czech Science Foundation (GAČR) under project 23-05891S, and the Ministry of Education, Youth and Sports (MŠMT) under grant number 8I23002. Computational resources were supplied by the project “e-Infrastruktura CZ” (e-INFRA LM2018140) provided within the program Projects of Large Research, Development and Innovation Infrastructure.References
- H. Ishii, K. Sugiyama, E. Ito and K. Seki, Energy Level Alignment and Interfacial Electronic Structures at Organic/Metal and Organic/Organic Interfaces, Adv. Mater., 1999, 11, 605–625 CrossRef CAS.
- D. Cahen and A. Kahn, Electron Energetics at Surfaces and Interfaces: Concepts and Experiments, Adv. Mater., 2003, 15, 271–277 CrossRef CAS.
- N. Koch, Energy Levels at Interfaces between Metals and Conjugated Organic Molecules, J. Phys.: Condens. Matter, 2008, 20, 184008 CrossRef.
- G. Heimel, L. Romaner, E. Zojer and J.-L. Bredas, The Interface Energetics of Self-Assembled Monolayers on Metals, Acc. Chem. Res., 2008, 41, 721–729 CrossRef CAS PubMed.
- S. Braun, W. R. Salaneck and M. Fahlman, Energy-Level Alignment at Organic/Metal and Organic/Organic Interfaces, Adv. Mater., 2009, 21, 1450–1472 CrossRef CAS.
- J. Hwang, A. Wan and A. Kahn, Energetics of Metal–Organic Interfaces: New Experiments and Assessment of the Field, Mater. Sci. Eng., R, 2009, 64, 1–31 CrossRef.
- A. Salomon, D. Cahen, S. Lindsay, J. Tomfohr, V. B. Engelkes and C. D. Frisbie, Comparison of Electronic Transport Measurements on Organic Molecules, Adv. Mater., 2003, 15, 1881–1890 CrossRef CAS.
- V. B. Engelkes, J. M. Beebe and C. D. Frisbie, Length-Dependent Transport in Molecular Junctions Based on SAMs of Alkanethiols and Alkanedithiols: Effect of Metal Work Function and Applied Bias on Tunneling Efficiency and Contact Resistance, J. Am. Chem. Soc., 2004, 126, 14287–14296 CrossRef CAS PubMed.
- J. M. Beebe, B. Kim, J. W. Gadzuk, C. D. Frisbie and J. G. Kushmerick, Transition from Direct Tunneling to Field Emission in Metal-Molecule-Metal Junctions, Phys. Rev. Lett., 2006, 97, 026801 CrossRef PubMed.
- B. Kim, S. H. Choi, X. Y. Zhu and C. D. Frisbie, Molecular Tunnel Junctions Based on π-Conjugated Oligoacene Thiols and Dithiols between Ag, Au, and Pt Contacts: Effect of Surface Linking Group and Metal Work Function, J. Am. Chem. Soc., 2011, 133, 19864–19877 CrossRef CAS PubMed.
- L. Venkataraman, Y. S. Park, A. C. Whalley, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Electronics and Chemistry: Varying Single-Molecule Junction Conductance Using Chemical Substituents, Nano Lett., 2007, 7, 502–506 CrossRef CAS PubMed.
- J. A. Ivie, N. D. Bamberger, K. N. Parida, S. Shepard, D. Dyer, A. Saraiva-Souza, R. Himmelhuber, D. V. McGrath, M. Smeu and O. L. A. Monti, Correlated Energy-Level Alignment Effects Determine Substituent-Tuned Single-Molecule Conductance, ACS Appl. Mater. Interfaces, 2021, 13, 4267–4277 CrossRef CAS PubMed.
- L. Yuan, C. Franco, N. Crivillers, M. Mas-Torrent, L. Cao, C. S. S. Sangeeth, C. Rovira, J. Veciana and C. A. Nijhuis, Chemical Control over the Energy-Level Alignment in a Two-Terminal Junction, Nat. Commun., 2016, 7, 12066 CrossRef CAS PubMed.
- K. Sun and S. Kawai, Strength of Electronic Decoupling of Fullerene on an AuSiX Layer Formed on Au(111), Phys. Chem. Chem. Phys., 2021, 23, 5455–5459 RSC.
- R. Frisenda and H. S. J. van der Zant, Transition from Strong to Weak Electronic Coupling in a Single-Molecule Junction, Phys. Rev. Lett., 2016, 117, 126804 CrossRef CAS.
- C. Bruot, J. Hihath and N. Tao, Mechanically Controlled Molecular Orbital Alignment in Single Molecule Junctions, Nat. Nanotechnol., 2012, 7, 35–40 CrossRef CAS PubMed.
- M. L. Perrin, C. J. O. Verzijl, C. A. Martin, A. J. Shaikh, R. Eelkema, J. H. van Esch, J. M. van Ruitenbeek, J. M. Thijssen, H. S. J. van der Zant and D. Dulić, Large Tunable Image-Charge Effects in Single-Molecule Junctions, Nat. Nanotechnol., 2013, 8, 282–287 CrossRef CAS.
- S. Y. Quek, M. Kamenetska, M. L. Steigerwald, H. J. Choi, S. G. Louie, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, Mechanically Controlled Binary Conductance Switching of a Single-Molecule Junction, Nat. Nanotechnol., 2009, 4, 230–234 CrossRef CAS PubMed.
- M. Tsutsui, T. Morikawa and Y. He, High Thermopower of Mechanically Stretched Single-Molecule Junctions, Sci. Rep., 2015, 5, 11519 CrossRef CAS.
- L. Rincón-García, A. Ismael and C. Evangeli, et al., Molecular Design and Control of Fullerene-Based Bi-Thermoelectric Materials, Nat. Mater., 2016, 15, 289–293 CrossRef PubMed.
- Y.-H. Kim, H. S. Kim, J. Lee, M. Tsutsui and T. Kawai, Stretching-Induced Conductance Variations as Fingerprints of Contact Configurations in Single-Molecule Junctions, J. Am. Chem. Soc., 2017, 139, 8286–8294 CrossRef CAS PubMed.
- T. Morikawa, M. Tsutsui, Y. Komoto, K. Yokota and M. Taniguchi, Dependence of Molecular Diode Behaviors on Aromaticity, J. Phys. Chem. Lett., 2022, 13, 6359–6366 CrossRef CAS PubMed.
- S. Fujii, E. Montes, H. Cho, Y. Yue, M. Koike, T. Nishino, H. Vázquez and M. Kiguchi, Mechanically Tuned Thermopower of Single-Molecule Junctions, Adv. Electron. Mater., 2022, 8, 2200700 CrossRef CAS.
- M. Lokamani, F. Kilibarda, F. Günther, J. Kelling, A. Strobel, P. Zahn, G. Juckeland, K. V. Gothel, E. Scheer, S. Gemming and A. Erbe, Stretch Evolution of Electronic Coupling of the Thiophenyl Anchoring Group with Gold in Mechanically Controllable Break Junctions, J. Phys. Chem. Lett., 2023, 14, 5709–5717 CrossRef CAS.
- M. Tsutsui, M. Taniguchi and T. Kawai, Local Heating in Metal-Molecule-Metal Junctions, Nano Lett., 2008, 8, 3293–3297 CrossRef CAS PubMed.
- Y. Isshiki, S. Fujii, T. Nishino and M. Kiguchi, Fluctuation in Interface and Electronic Structure of Single-Molecule Junctions Investigated by Current versus Bias Voltage Characteristics, J. Am. Chem. Soc., 2018, 140, 3760–3767 CrossRef CAS PubMed.
- J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific, Singapore, 2010, vol. 1 Search PubMed.
- Y. Komoto, S. Fujii, H. Nakamura, T. Tada, T. Nishino and M. Kiguchi, Resolving Metal-Molecule Interfaces at Single-Molecule Junctions, Sci. Rep., 2016, 6, 26606 CrossRef CAS PubMed.
- A. Vladyka, M. L. Perrin, J. Overbeck, R. R. Ferradás, V. García-Suárez, M. Gantenbein, J. Brunner, M. Mayor, J. Ferrer and M. Calame, In situ Formation of One-Dimensional Coordination Polymers in Molecular Junctions, Nat. Commun., 2019, 10, 262 CrossRef PubMed.
- M. Kamenetska, S. Y. Quek, A. C. Whalley, M. L. Steigerwald, H. J. Choi, S. G. Louie, C. Nuckolls, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, Conductance and Geometry of Pyridine-Linked Single-Molecule Junctions, J. Am. Chem. Soc., 2010, 132, 6817–6821 CrossRef CAS PubMed.
- Y. Kim, T. Pietsch, A. Erbe, W. Belzig and E. Scheer, Benzenedithiol: A Broad-Range Single-Channel Molecular Conductor, Nano Lett., 2011, 11, 3734–3738 CrossRef CAS PubMed.
- S. Bilan, L. A. Zotti, F. Pauly and J. C. Cuevas, Theoretical Study of the Charge Transport through C60-Based Single-Molecule Junctions, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 205403 CrossRef.
- X.-Q. Shi, M. A. van Hove and R.-Q. Zhang, Survey of Structural and Electronic Properties of C60 on Close-Packed Metal Surfaces, J. Mater. Sci., 2012, 47, 7341–7355 CrossRef CAS.
- A. Tan, J. Balachandran, S. Sadat, V. Gavini, B. D. Dunietz, S.-Y. Jang and P. Reddy, Effect of Length and Contact Chemistry on the Electronic Structure and Thermoelectric Properties of Molecular Junctions, J. Am. Chem. Soc., 2011, 133, 8838–8841 CrossRef CAS PubMed.
- T. Kim, P. Darancet, J. R. Widawsky, M. Kotiuga, S. Y. Quek, J. B. Neaton and L. Venkataraman, Determination of Energy Level Alignment and Coupling Strength in 4,4’-Bipyridine Single-Molecule Junctions, Nano Lett., 2014, 14, 794–798 CrossRef CAS PubMed.
- C. Evangeli, K. Gillemot, E. Leary, M. T. González, G. Rubio-Bollinger, C. J. Lambert and N. Agraït, Engineering the Thermopower of C60 Molecular Junctions, Nano Lett., 2013, 13, 2141–2145 CrossRef CAS PubMed.
- P. Reddy, S.-Y. Jang, R. A. Segalman and A. Majumdar, Thermoelectricity in Molecular Junctions, Science, 2007, 315, 1568–1571 CrossRef CAS.
- Y. Isshiki, D. Li, M. Kiguchi, T. Nishino, F. Pauly and S. Fujii, Structural Asymmetry of Metallic Single-Atom Contacts Detected by Current–Voltage Characteristics, ACS Appl. Mater. Interfaces, 2022, 14, 11919–11926 CrossRef CAS PubMed.
- W. Lee, K. Kim, W. Jeong, L. A. Zotti, F. Pauly, J. C. Cuevas and P. Reddy, Heat Dissipation in Atomic-Scale Junctions, Nature, 2013, 498, 209–212 CrossRef CAS PubMed.
- S. Kaneko, E. Montes, S. Suzuki, S. Fujii, T. Nishino, K. Tsukagoshi, K. Ikeda, H. Kano, H. Nakamura, H. Vázquez and M. Kiguchi, Identifying the Molecular Adsorption Site of a Single Molecule Junction through Combined Raman and Conductance Studies, Chem. Sci., 2019, 10, 6261–6269 RSC.
- V. Delmas, V. Diez-Cabanes, C. van Dyck, E. Scheer, K. Costuas and J. Cornil, On the Reliability of Acquiring Molecular Junction Parameters by Lorentzian Fitting of I/V Curves, Phys. Chem. Chem. Phys., 2020, 22, 26702–26706 RSC.
- Z.-F. Liu and J. B. Neaton, Voltage Dependence of Molecule–Electrode Coupling in Biased Molecular Junctions, J. Phys. Chem. C, 2017, 121, 21136–21144 CrossRef CAS.
- T. Yelin, R. Korytár, N. Sukenik, R. Vardimon, B. Kumar, C. Nuckolls, F. Evers and O. Tal, Conductance Saturation in a Series of Highly Transmitting Molecular Junctions, Nat. Mater., 2016, 15, 444–449 CrossRef CAS PubMed.
- S. Y. Quek, H. J. Choi, S. G. Louie and J. B. Neaton, Thermopower of Amine−Gold-Linked Aromatic Molecular Junctions from First Principles, ACS Nano, 2011, 5, 551–557 CrossRef CAS PubMed.
- B. Xu and N. J. Tao, Measurement of Single-Molecule Resistance by Repeated Formation of Molecular Junctions, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- R. Matsuhita, M. Horikawa, Y. Naitoh, H. Nakamura and M. Kiguchi, Conductance and SERS Measurement of Benzenedithiol Molecules Bridging Between Au Electrodes, J. Phys. Chem. C, 2013, 117, 1791–1795 CrossRef CAS.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, The SIESTA Method for Ab Initio Order-N Materials Simulation, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- N. Lorente, T. Frederiksen, A. García and M. Brandbyge, Improvements on Non-Equilibrium and Transport Green Function Techniques: The Next-Generation Transiesta, Comput. Phys. Commun., 2017, 212, 8–24 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the measurement system, frequency response of the measurement system, I–V measurement and analysis, statistical analysis of I–V curves, statistical analysis of junction length, calculated transmission spectra and junction geometries. See DOI: https://doi.org/10.1039/d4sc05285d |
| This journal is © The Royal Society of Chemistry 2024 |