Statistical optimization of cell–hydrogel interactions for green microbiology – a tutorial review

Abstract

In this tutorial mini-review, we explore the application of Design of Experiments (DOE) as a powerful statistical tool in biotechnology. Specifically, we review the optimization of hydrogel materials for diverse microbial applications related to green microbiology, the use of microbes to promote sustainability. Hydrogels, three-dimensional polymers networks with high water retention capabilities, are pivotal in the immobilization of microorganisms and provide a customizable environment essential for directing microbial fate. We focus on the application of DOE to precisely tailor hydrogel compositions for a range of fungi and bacteria either used for the sustainable production of chemical compounds, or the elimination of hazardous substances. We examine a variety of DOE design strategies such as central composite designs, Box–Behnken designs, and optimal designs, and discuss their strategic implementation across diverse hydrogel formulations. Our analysis explores the integral role of DOE in refining hydrogels derived from a spectrum of polymers, including natural and synthetic polymers. We illustrate how DOE facilitates nuanced control over hydrogel properties that cannot be achieved using a standard one factor at a time approach. Furthermore, this review reveals a conserved finding across different materials and applications: there are significant interactions between hydrogel parameters and cell behavior. This highlights the intricacies of cell–hydrogel interactions and the impact on hydrogel material properties and cellular functions. Lastly, this review not only highlights DOE's efficacy in streamlining the optimization of cell–hydrogel processes but also positions it as a critical tool in advancing our understanding of cell–hydrogel dynamics, potentially leading to innovative advancements in biotechnological applications and bioengineering solutions.

---

Conor G. Harris

Conor Harris is a Chemical Engineering PhD candidate at Oregon State University in the School of Chemical, Biological, and Environmental Engineering. His research focuses on polymer science and non-Newtonian fluid mechanics with applications in 3D printing material development, wax deposition in subsea oil pipelines, and biomaterial development for bioremediation.

Lewis Semprini

Lewis Semprini is a University Distinguished Professor of Environmental Engineering, in the School of Chemical, Biological, and Environmental Engineering. His research focuses on biological processes for the treatment of hazardous wastes, and on the fate and transport of organic contaminants in the environment. He specializes in field, laboratory, and modeling studies of both aerobic and anaerobic processes for treating chlorinated solvents, polycyclic aromatic hydrocarbons and emerging contaminants.

Willie E. Rochefort

Skip Rochefort is an Associate Professor of Chemical Engineering at Oregon State University, in the School of Chemical, Biological, and Environmental Engineering. His research focus is on polymer science and engineering, including the operation of a polymer laboratory with capability for rheological, thermal, molecular, and surface characterization of materials and polymer processing; 3D filament printing and 3D printing materials development; and biomaterials. Other activities include K-12 outreach and engineering education.

Kaitlin C. Fogg

Kaitlin Fogg is an Assistant Professor in the School of Chemical, Biological, and Environmental Engineering. Her research focuses on using statistical optimization to engineer hydrogels for a wide array of bioengineering applications, specializing in designing 3D models of gynecological tissues.

---

Sustainability spotlight

Green microbiology provides environmental sustainability through the use of microorganisms to produce chemical goods and eliminate hazardous waste. Microbial immobilization via hydrogels enhances the applications of green microbiology by providing a suitable microenvironment for microbes. In addition, the statistical optimization tool, Design of Experiments, offers sustainable practices by generating empirical models with a smaller number of experiments compared to a one-factor-at-a-time approach. Research groups dedicated to optimizing immobilized microbial processes via Design of Experiments help to achieve UN Sustainable Development Goals: (6) Clean Water and Sanitation and (12) Responsible Consumption and Production. This tutorial review provides concepts for Design of Experiments and microbial immobilization for the production of chemical compounds and elimination of hazardous materials.

Introduction

Green microbiology includes the use of microorganisms in the production of chemical compounds and elimination of hazardous compounds and promotes environmental sustainability.¹ The microenvironment that microorganisms inhabit affects microbial processes, such as the capability to proliferate, differentiate, and communicate.² To better understand and utilize microorganisms, we must understand how their surrounding microenvironment motivates them. With advances in biomaterials and polymer science, we can design and tailor microenvironments with materials called hydrogels to study and apply microbes for more sustainable practices. Hydrogels are a unique group of materials formed from hydrophilic, three-dimensional (3D) networks of crosslinked polymers with the distinct capability to absorb and retain high amounts of aqueous solvents.³ Hydrogels can be formed from natural and/or synthetic polymers and biophysical cues can be tuned based on material properties to control cell fate.

Microbial or cell immobilization via hydrogels is used across a variety of applications, including, but not limited to, enzyme systems, production of biofuels, and bioremediation. Immobilization is the process of confining cells in or onto a matrix whilst retaining their viability and catalytic functions.^4–7 Several reviews compiled literature regarding the enhancement of bioremediation with hydrogels to immobilize cells.^4,8–10 However, there is currently not a review that summarizes how these hydrogels can be engineered to optimize microbial processes.

Despite the existence of models to describe cell–hydrogel interactions, there is a need to validate them with experimental and computational work.¹¹ To further develop and validate such mechanistic models, more empirical data is required to describe these cell–hydrogel interactions. Thus, if we want to identify a hydrogel formulation that optimizes microbes for a particular application, we need to develop and use empirical models. One of the most useful techniques to develop an empirical model and optimize cell interactions in hydrogels is the statistical technique Design of Experiments (DOE).^12–14

DOE is a statistical optimization technique used across many fields.¹⁵ DOE provides empirical models that sufficiently describe the behavior of cell–hydrogel interactions while reducing the number of required experiments. By purposefully selecting the experimental conditions that capture the effects of all of the input variables and their potential significant interactions, DOE enables researchers to statistically determine the contributions of individual factors and their interactions on given outputs with significantly fewer experiments, as illustrated in Fig. 1. This can be especially important for processes such as cell culture that are time and cost intensive.¹⁷

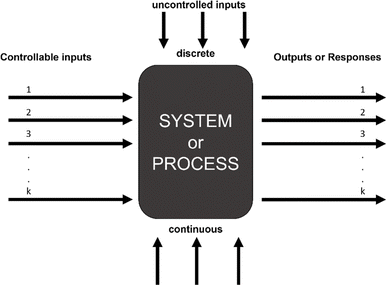Fig. 1 Black box representation of DOE.¹⁶

Although work on cell immobilization started in the mid-1970s, the number of publications has increased over time, with the highest number of publications occurring in 2020 (Fig. 2A). Even with the latest works, there is a need to better understand the interactions that occur between immobilized cells and the hydrogel carrier.¹¹ Similarly, the number of publications that includes DOE continues to rise over the past 80 years, demonstrating the potential and popularity of this statistical method (Fig. 2B).

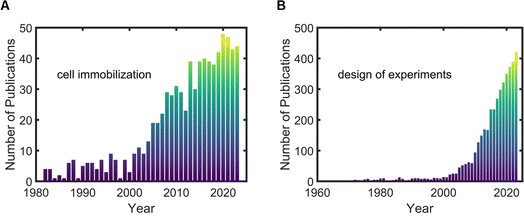Fig. 2 Results by publication year from PubMed based on searches for (A) “cell immobilization” and (B) “design of experiments.”

The objective of this review is to highlight the utility of DOE in identifying parameters that affect the fate and function of the hydrogels and cells immobilized within them. To achieve this objective, we will provide readers with a brief overview of the most commonly used designs in DOE for optimization. We will then delve into the application of these designs to optimize cell–hydrogel interactions based on the hydrogel polymer backbone.

Experimental designs used for optimizing hydrogels with immobilized cells

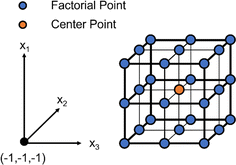
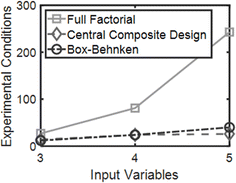
DOE is a statistical optimization technique that was introduced by Dr George E. P. Box in the 1950s.¹⁸ The objective of DOE is to find where maximums and minimums occur for a given response, or dependent variable, based on selected inputs, or independent variables. Responses can be visualized as a surface with at least two inputs that vary over three levels (x₁, x₂ = {−1, 0, 1}). Thus, DOE is also known as response surface methodology. If we consider hydrogels with immobilized cells a system or process, the black box representation of DOE from the National Institute of Standards and Technology (NIST) demonstrates how experimental design accepts i inputs and returns m responses for any system or process with any number of uncontrolled inputs.¹⁶ Here, i ranges from 2 to infinity and m ranges from 1 to infinity. At least 2 inputs are required to form a response surface, but a single response can be evaluated to optimize the system.

Consider three variables evaluated at three levels (x₁, x₂, x₃ = {−1, 0, 1}). If we plot these experimental conditions in a 3-dimensional space we form a cube that represents our full factorial design with number of levels, n = 3, and number of factors, k = 3 (Fig. 3). The number of experimental conditions required to generate a response model is dependent on both n and k, and the full factorial consists of n^k experimental conditions. As the number of input variables increases, k increases and the number of experimental conditions for a full-factorial design increases exponentially. For instance, for 5 factors with 3 levels, evaluating 243 experimental conditions would be necessary, which would be costly and impractical for some applications. In contrast, by using statistical designs, the number of experimental conditions required to identify the optimal conditions can be reduced by a factor of 6 or more with the total number of runs somewhere between 24 to 40, depending on the design. The most common statistical designs are Central Composite Design, Box–Behnken, and D-optimal, all of which consist of significantly less experimental conditions compared to a full factorial design (Fig. 4).

Fig. 3 3-Dimensional depiction of a full factorial design for three variables and three levels (x₁, x₂, x₃ = {−1, 0, 1}). Blue and yellow points represent the factorial and center points, respectively.

Fig. 4 Experimental conditions as a function of input variables for full factorial (squares, solid line), central composite designs (diamonds, dashed line), and Box–Behnken (circles, dashed-dotted lines) designs.

Central composite and Box–Behnken designs

Central composite designs consist of selected factorial points with a center point and a group of axial (or star) points.¹⁹ In coded units, the distance of the factorial points from the center equal ±1, and the distance between the axial points, α, and center is |α| ≥ 1 (Table 1).^16,20 There are several types of central composite designs, such as Central Composite Circumscribed (CCC), Central Composite Inscribed (CCI), and Central Composite Face Centered (CCF or FCCD), each with different applications and properties.²¹ Circumscribed designs are spherical, near-rotatable designs with |α| > 1. The axial points for CCC designs occur at the extremes of the design and cannot be used if the system is confined to within the design factorial points. For designs with such constraints, CCF designs are non-rotatable and cubed, and the augment points appear on the vertices of the cube. CCI designs are spherical, near-rotatable design with the augmented points positioned at |α| = 1 and the factorial points set within the bounds of those points. Lastly, Box–Behnken designs (BBD) are rotatable or near rotatable designs with points that form a cube centered at the origin.²² BBD designs do not contain experimental conditions at the vertices of the design space cube and may be useful in avoiding experiments under extreme conditions where unsatisfactory results might occur.

Table 1 General terminology of center, factorial, axial, and edge points used in DOE and RSM

Point type	Definition	Purpose	Distance from center	Example
Center point	Point at the center of the design space	Used for estimating experimental error and checking for curvature	0	N/A
Factorial points	Represents all combinations of factor levels at their high (+1) and low (−1) settings	Used to explore linear and interaction effects	+1, −1	In a two-factor experiment (k = 2), the factorial points would be at (−1, −1), (−1, +1), (+1, −1), and (+1, +1)
Axial points (star points)	Represents points located on the axes of the design space (axial) that can extend beyond factorial points and are crucial for fitting a quadratic model	Used to estimate the curvature and allow for the modeling of quadratic effects, which more thoroughly explore the space around the central point and assist in identifying optimal settings of the factors	Typically represented by α, where |α| ≥ 1	In a two-factor experiment (k = 2), axial points might be at positions such as (±α, 0) and (0, ±α) if using a central composite design
Edge points	Points located on edge of the factorial cube but are not included in a full-factorial design and occur only in optimal designs	Used to estimate curvature and allow for modeling of quadratic effects	Dependent on optimal design	In a three-factor experiment (k = 3), edge points might be at positions (0.333, 1, −1) or (−1, 1, −0.333)

---

Optimal designs

Optimal designs, collectively known as alphabetical designs. (A – average, D – determinant, E − eigen value), use computational algorithms to select experimental criteria that reduce the size of confidence intervals for model coefficients. The D-optimal design is one example of an optimal design that minimizes width of confidence intervals for model coefficients.^23,24 This design can be helpful when including qualitative factors or binary variables in the experimental design.

Comparisons between statistical designs

Between the designs examined in this tutorial mini-review, there can be differences in the structure, point types used, efficiency, model fit and flexibility of each design (Fig. 5).²⁵ Further, each design has advantages and disadvantages when compared against one another. CCDs are ideal when a comprehensive exploration of the response surface is needed, given that the experimental conditions allow for it. BBD is more efficient with fewer runs and is better suited for situations where extreme conditions are not practical or possible. In addition, BBD is not efficient for only two factors whereas CCD and optimal designs can handle two factors. Finally, optimal designs provide the most flexibility and efficiency compared to CCD or BBD, especially when dealing with complex models, constraints, or cost considerations in experimental settings.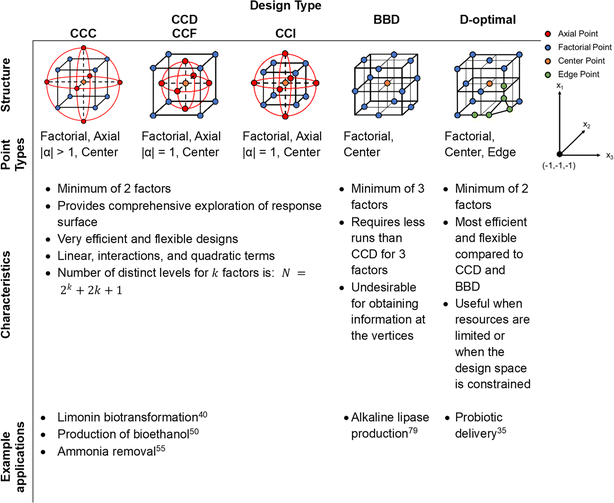

Fig. 5 Statistical designs for three factors and three levels, with details on structure, point types, characteristics, and example applications.²⁵ For all designs, the red, blue, orange, and green dots correspond to axial, factorial, center, and edge points, respectively.

Hydrogel materials used for cell immobilization

Hydrogels used for cell immobilization must generally be permeable to oxygen and nutrient transport and promote cell viability and function.⁵ Immobilization methods with hydrogels include adhesion, entrapment, and encapsulation; all of which have been documented in previous reviews.^4–6,8 Natural polysaccharides such as agarose, alginate, chitosan, gellan gum, κ-carrageenan and xanthan gum are commonly used for cell immobilization.^4,26–31 Polysaccharides offer unique biocompatibility properties that promote cell adhesion and proliferation, can be procured inexpensively, and are biodegradable. Synthetic polymers such as poly(vinyl alcohol) are also commonly used for cell immobilization.³² While the material properties of synthetic polymers can be more easily controlled, in most cases they must be coupled with natural polymers or modified to promote cell adhesion and biocompatibility.

We have organized DOE inputs and outputs variables in tables based on the hydrogel material (tabulated alphabetically) with information on the cell type, statistical optimization design, specific application, inputs, outputs, significant factors and the reference (Tables 2–9). These are further detailed for each hydrogel material below.

Alginate

Alginate is a polysaccharide that occurs from harvested brown seaweeds.³³ The backbone of alginate is comprised of two monomers: a linear 1,4 β-D-mannuronic acid (M) and α-L-guluronic acid (G). The structure of alginate can contain blocks of either consecutive or alternating monomers and the distribution of these blocks is important when forming gels. The polymer is regarded for qualities such as biocompatibility, low cost, and low toxicity. Overall, the vast amount of research surrounding alginate makes it one of the most popular carrier for cell immobilization.²⁶

Immobilization itself can be the goal of the DOE. Maximizing the number of cells immobilized into hydrogel complexes can increase product yield and contamination removal with less overall material used. Trabelsi et al. used a Box–Behnken experimental design to optimize the microencapsulation yield (%) of Lactobacillus plantarum in alginate beads coated in chitosan based on the hardening time (15–45 min), biomass concentration (10⁸–10¹⁰ CFU mL⁻¹), and CaCl₂ concentration (0.25–0.75 M).³⁴ The optimization goal was set to maximize the microencapsulation yield, and this was achieved by setting the hardening time, CaCl₂ concentration, and biomass concentration to 30 min, 0.45 M, and 10¹⁰ CFU mL⁻¹, respectively. Popović et al. optimized the microencapsulation of a potential probiotic strain, Lactobacillus reuteri B2, with a D-optimal design based on the input variables, concentration of alginate (0.5–2.5%) and starch maleate (2.0–6.0%). The authors evaluated and sought to maximize the encapsulation yield (%) and found the optimal conditions were 2.0% alginate and 3.0% starch maleate.³⁵ Other examples include the immobilization of recombinant Escherichia coli, immobilization of Bacillus subtilis natto, and pharmocobiotic entrapment.^36–38 Taken together, these articles found that polymer concentration, crosslinking concentration, and cell concentration, as well as the interaction terms between these terms, significantly affected immobilization or microencapsulation efficiency.

The removal of toxic or unwanted compounds from processes or aquatic environments via cells immobilized in alginate hydrogels has been optimized with DOE. The work of Surabhi and Elzagheid optimized an alginate immobilization method for sulfide oxidation by immobilized Thiobacillus species via DOE and a CCD.³⁹ Surabhi and Elzagheid optimized the sulfide oxidation (%) by Thiobacillus species in response to the variables: alginate concentration (1–5%, w/v), CaCl₂ concentration (1–5%, v/v), inoculum size (2–10%), and agitation speed involved in the immobilization method (50–250 rpm). Interestingly, the authors reported no significance of the interaction between alginate concentration and inoculum size for their particular process. Still, they found that the interaction between CaCl₂ concentration and inoculum size, which may have a similar effect, due to the fact that CaCl₂ concentration can directly influence gel properties, such as crosslinking density. Other studies have used DOE to enhance limonin biotransformation or remove a endocrine disrupting chemical, 17α-ethinylestradiol, from aquatic environments.^40,41 In addition, environmental factors, such as initial substrate concentration or pH, have been optimized using DOE for the removal of compounds.^42,43 Altogether, these works demonstrate how alginate concentration, crosslinking concentration, and cell concentration can significantly influence the transformation of unwanted compounds in aquatic environments with microorganisms, all which can be useful for applications in bioremediation.

Production of compounds with immobilized cells has been optimized via DOE based on hydrogel formula parameters. The immobilization of Gluconobacter oxydans in alginate gels for the production of benzaldehyde in a biphasic system was optimized via DOE and a BBD by Wu et al.⁴⁴ They measured the activity yields of benzaldehyde (g L⁻¹) and stability of beads (OD₆₀₀) in response to changes in the experimental variables: alginate concentration (2–4%, w/v), cell load (35–55 g L⁻¹), and bead diameter (2.2–3.2 mm). Wu et al. determined the optimal conditions by maximizing activity yield and minimizing stability responses (lower values of OD₆₀₀ correspond to a higher stability) and found the optimal solution with parameter values: 2.55%, w/v alginate concentration, 49.26 g L⁻¹ cell load, and 2.2 mm bead diameter. A calcium-alginate immobilization method was optimized for the production of alkaline protease by Bacillus licheniformis NCIM-2042 with central composite design.⁴⁵ Potumarthi et al. sought to optimize the alkaline protease response (U mL⁻¹) and selected four parameters of the alginate immobilization method: alginate concentration (1–5%, w/v), CaCl₂ concentration (1–5%, v/v), inoculum size (2–10%), and agitation speed involved in the immobilization method (50–250 rpm). With this model, the following optimum conditions were selected and validated to maximize the protease production: alginate concentration at 2.78%, CaCl₂ concentration at 2.15%, inoculum size at 8.10%, and agitation speed at 139 rpm. Again, the interaction between alginate concentration and cell loading (inoculum size) was determined to be significant for a different compound production and different cell type. An interesting study was conducted by Seifan et al. to induce and optimize calcium carbonate precipitation from two bacterial strains, Bacillus sphaericus NZRM 4381 and Bacillus licheniformis ATCC 9789, immobilized in calcium alginate beads via DOE.⁴⁶ The researchers identified the response variable, calcium carbonate (g L⁻¹), as a function of the two input variables, alginate concentration (1–3%, w/v) and CaCl₂ concentration (0.1–0.3 M). They reported the optimum conditions based on the goal to maximize the concentration of calcium carbonate as 1.38% w/v alginate concentration and 0.13 M CaCl₂ concentration. Both Wu et al. and Seifan et al. report the alginate content as significant for the production of their target compound, while the work dedicated to alkaline protease production by Potumarthi et al. did not. Similarly, Seifan et al. reported the calcium chloride concentration significant, whereas Potumarthi et al. did not find the same parameter significant. While not all the same parameters were reported significant for each specific compound yield, both Wu et al. and Potumarthi et al. found that the interaction between the polymer content and cell content input variables significantly affected the production of the target compound. Other literature on the production of compounds consists of the optimization of isomaltulose (palatinose) production or the optimization of environmental factors on the production of compounds.^47–51 In summary, research dedicated to the production of compounds from immobilized cells can be optimized using the hydrogel formula via DOE.

In conclusion, the majority of papers that evaluated both hydrogel material properties and cell loading determined that there was a significant interaction term between the polymer content and cell loading or crosslinking concentration and cell loading. This could suggest that there is competition between the number of cells and pore size in the hydrogel, especially as some found that the optimal conditions of cell loading are near the “low” levels (−1) in order to achieve high activity. Additionally, it could suggest that enough polymer content must be available for adhesion, as many articles determined optimal conditions near the center point (0) of polymer content. Altogether, the alginate immobilization method has been optimized for numerous applications with many different cell types and strains. Further characterization between the interactions between cells and hydrogels is needed, possibly with microscopy to evaluate how cells reside in the hydrogel complex, or with more mechanical tests to determine if or how the hydrogel properties is changed by immobilized cells initially and over time.

Chitosan

Chitosan is the polysaccharide derivative of the chitin polymer, synthesized from the shells of species such as crabs and shrimp.⁵² Chitosan contains N-acetyl-β-D-glucosamine chains that have been deacetylated at least by 50% or more, and the degree of deacetylation influences the physical, mechanical, and biological properties. Unlike many other natural polymers, chitosan is a polycation, and can easily form complexes between polyanion polymers. As such, we have already seen a chitosan coated alginate encapsulation method (Alginate section). Even with such unique properties, chitosan has been used to immobilize whole cells.

Reaction conditions and environmental factors have been optimized for two specific processes with cells immobilized in chitosan beads. Jyoti et al. optimized the nitrilase activity of a Rhodococcus pyridinivorans NIT-36 strain immobilized in chitosan beads based on the temperature (20–50 °C), pH (6–8), and substrate concentration (100–300 mM), yet optimal conditions are not reported specifically.⁵³ Uranium (U(VI)) biosorption via Pseudomonas putida PTCC 1694 immobilized in chitosan beads was optimized with DOE based on the environmental factors and cell loading.⁵⁴ The work entailed a design matrix designed with a CCD with the response U(VI) biosorption capacity (mg g⁻¹) and independent variables, pH (2–5), initial concentration of U(VI) (100–500 mg L⁻¹), biosorbent dosage (0.40–3.00 g L⁻¹), and bacteria (0.0–30.0 wt%). The optimal condition was set at a pH of 5, with an initial concentration of 500 mg L⁻¹, biosorbent dosage at 0.4 g L⁻¹, and a bacteria concentration of 20 wt%. They concluded that there were synergistic effects between cells and chitosan, and that chitosan could be used as both a carrier and adsorbent.

Hydrogel formulation parameters have also been optimized via DOE to remove unwanted compounds with cells immobilized in chitosan mixed with alginate beads. Guo et al. identified optimized ammonia nitrogen removal efficiency with chitosan–alginate hydrogels used to immobilize bacteria from biological sludge, of which 99.6% was identified as Bacillus subtilis.⁵⁵ They modified sodium alginate dosage (0.4–1.6%, m V⁻¹), chitosan dosage (0.1–0.8%, m V⁻¹), and embedding time (20–50 min) and measured the response of ammonia nitrogen removal efficiency (%) with an experimental matrix designed via CCD. The authors determined the optimal conditions to maximize ammonia nitrogen removal efficiency such that the sodium alginate dosage was 0.84% m V⁻¹, chitosan dosage was 0.22% m V⁻¹, and embedding time was 32 min. They suggested that sodium alginate provided the structural characteristics of the beads, whereas chitosan provided the biocompatibility of the beads. Further, the interaction between sodium alginate and chitosan revealed that when sodium alginate was at its center point, increased amounts of chitosan increased the ammonia nitrogen removal efficiency. However, when sodium alginate was at its maximum, increasing chitosan provided unsatisfactory results and suggests that alginate and chitosan compete for space in the bead.

Several papers have identified parameters in the use of chitosan hydrogels for immobilization. We have compiled the results of optimized environmental factors, demonstrating that temperature and pH are significant on immobilized microbial activity. Further, the results demonstrate immobilized cells can tolerate higher temperatures than free cells. An interesting finding for multi-polymer hydrogel beads is that the interaction between the two polymer types (chitosan polymer and alginate polymer) were significant. More information is needed on the network that forms between two or more polymers, especially when cells are present.

Gellan gum

Gellan gum is an exopolysaccharide, consisting of repeating units of β-1,3-D-glucose with acetate and glycerate groups, β-1,4-D-glucuronic acid, β-1,3-D-glucose, and α-1,4-L-rhamnose, produced by the bacteria Sphingomonas paucimobilis ATCC 31461.³¹ Gellan gum hydrogels occur by physical (thermal) crosslinking with the addition of chemical crosslinking with either monovalent or divalent cations.⁵⁶ Gellan gum properties include biocompatibility, biodegradability, and ductility.⁵⁷ The prevalence of gellan gum in the pharmaceutical and biomedical fields has endorsed its biocompatibility, making it a popular choice for cell immobilization applications.⁵⁸

Muliadi et al. demonstrated the optimization of gel characteristics, environment factors, and processing parameters using BBD for a metanil yellow (MY) decolorizing mixed culture, named FN3, immobilized in gellan gum beads.⁵⁹ The authors evaluated the MY dye decolorization (%) with a BBD based on the inputs, dye concentration (100–350 mg L⁻¹), gellan gum concentration (0.75–1.5%), number of beads (10–50), and beads size (0.3–0.6 cm). The optimum conditions set to maximize the decolorization was predicted and suitably validated with a dye concentration of 130 mg L⁻¹, a gellan gum concentration of 1.478%, with a number of beads of 50, and beads size of 0.6 cm. Karamba et al. optimized the biodegradation of cyanide (%) based input parameters gellan gum concentration (0.36–1.04 g), number of beads (−3.64–63.64), and beads size (0.10–0.60 cm) on using CCD for bacteria cells in a gellan gum hydrogel.⁶⁰ First, we must recognize the importance of selecting an experimental design, as the number of beads minimum was reported below zero and is physically impossible. CCD uses the axial points to evaluate extreme cases, and if the user is not careful, can fall outside the physical boundaries of the experiment. The goal to maximize the biodegradation of cyanide determined the optimal conditions: gellan gum concentration of 0.7%, number of beads at 30, and beads size of 0.3 cm. Between these articles, both authors found that polymer content (linear and quadratic), number of beads (linear and quadratic), and bead size (quadratic) significantly affected their specific output. While these studies have evaluated pure gellan gum hydrogels, combinations of polymer types could be explored, due to the synergistic qualities between gellan gum and other biopolymers.^61,62 Further, while other biopolymer crosslinker concentrations have been optimized with DOE and deemed significant, crosslinker concentration was not explored in these examples and could be important for future studies.

Poly(vinyl alcohol)

Poly(vinyl alcohol) (PVA) is a synthetic semicrystalline polymer, usually generated from the continuous hydrolysis of polyvinyl acetate in ethanol with potassium hydroxide.^63,64 Thus, PVA consists of a carbon chain with hydroxyl groups on alternating carbons. The characteristics of PVA include good mechanical properties and good biocompatibility, making it suitable for many cell immobilization and biomaterial applications.^65,66 PVA can be chemically crosslinked with multiple compounds (boric acid, maleic acid, glutaraldehyde, etc.) or physically crosslinked with a “freeze-thawing” method.⁶⁷

Lactic acid production by immobilized cells in PVA beads has been optimized based on processing and hydrogel formula parameters. Wang et al. optimized the lactic acid yield from Lactobacillus pentosus ATCC 8041 immobilized in alginate–PVA beads was completed on processing parameters for lactic acid production.⁶⁸ This work used a BBD to effectively modify the effects of the bead diameter (2–4 mm), pH (2–7), initial glucose concentration (100–120 g L⁻¹), and biomass (200–400) and measuring the lactic acid yield. From the model, the authors estimated optimal conditions to maximize lactic acid yield, where the bead diameter was 2.0 mm, the pH was 5.99, initial glucose concentration was 101.19 g L⁻¹ and biomass was 204.6 mg. Another demonstration of the power of DOE was completed by the Liu lab, with a more complex immobilization method including alginate, PVA, and chitosan to immobilize Lactobacillus pentosus ATCC 8041 for lactic acid production.⁶⁹ In this work, two responses, lactic acid yield and lactic acid production rate, were evaluated as functions of the sodium alginate concentration (1–5% w/v), PVA concentration (4.0–7.0% w/v), chitosan concentration (90–120 g L⁻¹), fructose concentration (90–120 g L⁻¹), temperature (31–39 °C), and pH (5–7). The optimal conditions set to maximize the lactic acid yield and production rate were 2.809% w/v sodium alginate, 5.253% w/v PVA, and 0.478% w/v chitosan, 107.396 g L⁻¹ fructose, 36.363 °C, and 6.084 pH. Overall, the results from this paper can demonstrate the power of DOE. Many factors (6) were evaluated with only 54 experimental runs, and the results generated powerful models that identified significant individual and interaction terms and an optimized condition that performed better than previous designs. In all, these works demonstrate the capability of DOE to determine input and interaction effects of polymer content, cell loading, environmental effects, as well as additional polymer supports on cell behavior for compound production.

Biodegradation for some compounds with immobilized cells in PVA beads has been optimized with DOE. Hsu et al. utilized a CCD to optimize the parameters to reduce sulfate and remove copper from the environment using a sulfate reducing bacterial culture immobilized in a PVA matrix.⁷⁰ They optimized the quantity of immobilized cell culture in solution (19–235 volatile suspended cells (VSS) per L) and the concentration of the copper (10–100 mg L⁻¹) based on the dependent variables, copper removal by bioprecipitation and sulfate reduction rate. Optimal conditions were not presented in this work. Biodegradation of p-nitrophenol (PNP) with activated sludge immobilized in PVA–alginate cryogel beads has been optimized using DOE and a CCD.⁷¹ Sam et al. identified the effects of bead size (1–5 mm), PVA concentration (2–10%), alginate concentration (0.5–2.0%), CaCl₂ concentration (1–5%), and number of freeze–thaw cycles (2–6 cycles) on the responses rate of PNP transformation and breakage of beads (mechanical stability). The optimal conditions to maximize the PNP transformation rate and minimize the breakage were 3.659 mm bead size, 8.0 wt% PVA concentration, 1.411 wt% alginate concentration, 3.012 wt% CaCl₂ concentration, and 3 freeze-thawing cycles. Our previous work involved the biodegradation of cis-1,2-dichloroethylene with a Rhodococcus rhodochrous ATCC 21198 bacteria cell and a slow-release compound immobilized in a poly(vinyl alcohol)–alginate hydrogel bead.⁷² In this work, the hydrogel compressive modulus and the cell oxygen uptake rate at days 1 and 30 were optimized using a CCD based on the PVA concentration (1–3% w/v), alginate concentration (1–2% w/v), and crosslinking time (14–135 min). The optimal conditions set to maximize the compressive modulus and minimize the oxygen uptake rate at both days 1 and 30 were 3.2% w/v PVA concentration, 2.0% w/v alginate concentration, and 110 min crosslinking time. We identified significant individual and interaction terms for all models which demonstrate how hydrogel formulae can impact both material properties and cell response in multi-component hydrogel systems. In general, these works can provide evidence for the capability of DOE to evaluate multiple factors and provide the experimental design to capture significant effects.

Production of some compounds by immobilized cells in PVA has also been optimized with DOE. Wei et al. optimized the immobilization of Escherichia coli AST3 for cadaverine production.⁷³ The work involved measuring the relatively activity of immobilized cells in PVA–alginate beads based on the parameters sodium alginate concentration (0.5–6.5%), PVA concentration (0–8%), CaCl₂ concentration (0.5–6.5%), calcification time (0–24 h), and freezing time at −80 °C (0–24 h) with experiments designed using a CCD. The optimal conditions to maximize the relative activity of the immobilized cells were 3.62% alginate, 4.71% PVA, 4.21% CaCl₂, 12 h calcification time, and 16 h freeze time. Nonthasen et al. optimized the entrapment of a Kluyveromyces marxianus strain DBKKUY-103 fungal cell to produce ethanol from sweet sorghum juice.⁷⁴ They modified the sodium alginate concentration (1.32–4.68% w/v), PVA concentration (8.32–11.68% w/v), and sodium sulfate concentration (0.16–0.84 M) and measured the response variable, ethanol concentration after 84 h. Optimal conditions were provided and validated to maximize the ethanol concentration, set such that the alginate concentration was 3.39% w/v, the PVA concentration was 10.09% w/v, and the sodium sulfate concentration was 0.30 M. The significant interaction observed between alginate concentration and sodium sulfate concentration is interesting, due to the fact that sodium sulfate is used as a crosslinker for PVA, not alginate. Overall, these articles utilized DOE to optimize compound production from immobilized cells in PVA hydrogels and found that all of the variables they tested were significant for their specific compound.

In summary, optimization models were generated to evaluate transformation or production of products from several different cell lines in PVA hydrogels. As expected for diffusion limitations, polymer content was a significant variable in the majority of the models discussed. However, cell behavior was not usually discussed in the context of these papers, and there could be interesting works regarding how cells interact with PVA or the intermixing of two or more polymers. In addition, PVA comes in many molecular weight ranges. The molecular weight can change the properties of PVA hydrogels;⁷⁵ and the concentration where polymers interact such that crosslinks can form (overlap concentration) changes based on the molecular weight.^76,77 Thus, we see several different ranges of PVA concentration throughout the papers discussed, and it might be advantageous to evaluate the concentration of PVA as a concentration over its overlap concentration.

Other polymers

While alginate, chitosan, collagen, fibrin, gellan gum, and PVA hydrogels have been optimized for cell immobilization by multiple groups, there exists additional hydrogels that have only been optimized by a select few. These include agarose, κ-carrageenan, pectin, and xanthan gum.

Agarose is a carbohydrate polymer, classified as a biocompatible polysaccharide, that has been used for many tissue engineering applications.⁷⁸ Extracted from marine red algae, agarose polymer chains consist of repeated agarobiose (disaccharide of D-galactose and 3,6-anhydro-L-galactopyranose) units. Agarose gels occur via hydrogen bonding and electrostatic interaction, to form a thermo-reversible gel without the need of a chemical crosslinking agent. Bisht et al. optimized the immobilized conditions of agarose gels for alkaline lipase production by Pseudomonas aeruginosa mutant cells using a Box–Behnken design matrix.⁷⁹ They optimized the independent variables agarose concentration (1.0–3.0%), inoculum size (3.0–5.0 g), cell concentration (0.6–1.0 g), and incubation time (20–28 h) with the output variable enzyme activity (U mL⁻¹). The optimal conditions were set to maximize the lipase production and were determined as agarose concentration, 1.96%; inoculum size, 4.06 g; cell concentration, 0.81 g; and incubation time, 22.54 h. In this work, the authors reported significant interactions related to polymer and cell content, a reoccurring interaction term found throughout this review.

κ-Carrageenan is one of the three carrageenan polysaccharides, which is water-soluble and obtained by extraction from Rhodophyceae red algae.^52,80,81 The structure of the κ-carrageenan polymer is composed with alternating 3-linked β-D-galactopyranose and 4-linked 3,6-anhydro-α-D-galactopyranose units, and one sulphate group per repeating diad.³⁰ The gel is a thermoreversible gel, formed via physical crosslinking in the presence of monovalent cations (K⁺, Rb⁺, Cs⁺, and NH₄⁺).The optimization of the immobilization method of bacteria into κ-carrageenan hydrogels using CCD has been demonstrated by Pan et al. In their work, they immobilized Escherichia coli BL21(DE3) that contained a cis-epoxysuccinate hydrolase, into κ-carrageenan for the formation of D(−)-tartaric acid. They optimized the response variables, enzyme activity (%) and gel strength (g cm⁻²), as a function of the concentration of biomass (25.9–54.1 g L⁻¹) and the κ-carrageenan concentration (8.3–33.7 g L⁻¹).⁸² The optimized parameters used to maximize the enzyme activity and gel strength were 23.6 g L⁻¹ and 43.4 g L⁻¹ for the biomass and κ-carrageenan concentration, respectively. While other studies have observed significant interactions between biomass concentration and polymer concentration for enzymatic transformations, Pan et al. report this interaction is insignificant. This suggests that further studies on different carrier types and cells may be necessary to understand if and when cells interact with the polymer to provide greater enzyme activity. In addition, the authors report that the biomass concentration and the interaction between biomass concentration and κ-carrageenan concentration had a negative linear relationship with the gel strength. This might be due to changes in the gel matrix with more biomass around, as biomass could potentially inhibit crosslinks to form, though more evidence is required to understand this behavior.

Pectin is a naturally occurring component of all terrestrial plants, but is primarily extracted from citrus peel or apple pomace, that is used as a gelling, thickening, stabilizing and emulsifying agent.⁸³ As a highly complex polymer type, pectin has 18 different distinct monomers connected by 20 different linkages!⁸⁴ To immobilize cells, low methoxy (LM) pectin is typically used, due to the capability for divalent cations to crosslink LM pectin chains near instantaneously. The encapsulating matrix of LM pectin with calcium is generally called calcium pectinate. Microencapsulation efficiency and lysozyme production via immobilized cells has been optimized for pectin hydrogels. Parra et al. optimized alginate or pectin hydrogels based on the qualitative parameter, polymer type (alginate or pectate), polymer concentration (2–4% w/v), inoculum concentration (20–33% v/v), and CaCl₂ concentration (2.0–3.5% w/v), using CCD for lysozyme production with a genetically engineered Aspergillus niger strain.⁸⁵ The optimum design predicted to maximize the lysozyme production was set as with a pectate polymer type, 2% (w/v) polymer concentration, 33% (w/v) inoculum concentration, and 3.5% w/v CaCl₂ concentration. Both articles found that the polymer concentration significantly affected the outputs, besides the swelling degree response in Zhao et al. While identifying the differences between alginate and pectin and their concentrations is important, the incorporation of both polymers could improve characteristics of gels compared to single polymer gels and is recommended for future studies.

Xanthan gum is a high molecular weight polysaccharide produced by fermentation with Xanthomonas campestris.⁸⁶ Xanthan gum consists of β-1,-4-D-glucopyranose glucan repeating units, with mannose (β-1,4), glucuronic acid (β-1,2) and terminal mannose branched side chains.⁸⁷ Xanthan gum can form hydrogels either by physical or chemical crosslinking used to immobilize cells. BBD was employed by Shu et al. to optimize xanthan gum–chitosan microcapsules to encapsulate the bacteria Bifidobacterium bifidum BB01 used as a probiotic.⁸⁸ In their work, they optimized the chitosan concentration (0.80–1.0 g mL⁻¹), ratio between xanthan gum/chitosan (1 : 7–1 : 9), and stirring time used to generate the microcapsules (40–60 min), and measured two response variables, a maximum viable count of the immobilized cells and encapsulation yield. The results of both models generated optimal conditions to maximize the viable counts and encapsulation yield, with a chitosan concentration of 0.84 g mL⁻¹, a ratio of xanthan gum to chitosan of 1 : 9, and a stirring time of 60 minutes. The results demonstrate the interesting effects of polymer concentration. Viable counts increased and then decreased as chitosan concentration and ratio to xanthan gum to chitosan concentration increased. This could indicate how gels can support cell communities, and more polymer content can promote greater cell adhesion, until a certain point, which then the hydrogel stiffness exceeds the stiffness where cells can effectively proliferate.⁸⁹

To conclude, many hydrogel types have been optimized through DOE, yet several still need more data to ascertain unique interactions and input variables specific to gel types. This could include different cell lines, or different applications of immobilized cells in the hydrogels in this section. In addition, these unique polymer types could be combined with each other or other polymer types (i.e. alginate) to overcome disadvantages related to a single polymer type. Overall, the papers above can provide a starting point for certain polymer types and the related variables to test.

Conclusions

Numerous studies have optimized hydrogel systems with immobilized cells for a wide range of diverse applications related to the sustainable production of chemical compounds or elimination of hazardous compounds. This tutorial review particularly highlights the extensive work done on hydrogels for immobilizing bacteria. An interesting observation across different applications of immobilized cells is that significant interactions often occur between polymer content and cell loading on multiple response variables. While DOE cannot elucidate the mechanisms of cell–hydrogel interactions, it is highly effective for initial evaluations of these complex processes, optimizing processes where cell–hydrogel interactions are important. In addition, many sources have utilized CCDs and BBDs to optimize cell immobilization for green microbiology, however the number of optimal design studies is currently lacking when compared to CCD and BBD. Therefore, future studies could include optimal designs to optimize parameters or compare optimal designs to other DOE designs. Our review also notes a tendency to focus more on cell functionality compared to material properties. However, there's a growing need for studies that simultaneously evaluate both aspects to gain deeper insights into how hydrogel properties influence diverse cellular behaviors. This necessitates a multidisciplinary approach, combining expertise from material science, microbiology, and bioengineering. In conclusion, DOE is a powerful tool for advancing the fields of biomaterials, bioprocess engineering, and bioremediation. We encourage collaboration across disciplines to fully leverage DOE's capabilities, paving the way for groundbreaking developments in cell-based technologies and therapeutic applications.

List of abbreviations

3D	Three-dimensional
BBD	Box–Behnken design
CaCl2	Calcium chloride
CCC	Central Composite Circumscribed
CCF or FCCD	Central Composite Face Centered
CCI	Central Composite Inscribed
Cu(II)	Copper
DOE	Design of experiments
EE2	17α-ethinylestradiol
LM	Low methoxy
MY	Metanil yellow
NIST	National Institute of Standards and Technology
PNP	p-Nitrophenol
PVA	Poly(vinyl alcohol)
U(VI)	Uranium

Data availability

The authors declare that the data supporting the findings of this study are available within the paper.

Author contributions

C. H. was responsible for the conceptualization, analysis, and writing of the main manuscript text, K. F. contributed to the conceptualization of the manuscript, and reviewed and revised the manuscript, and K. F., L. S., and W. R. contributed to the allocation of resources and provided supervision. All authors reviewed the manuscript.

Conflicts of interest

The authors have no conflicts to declare.

Appendix

Table 2 Agarose immobilization methods optimization inputs and outputs^a

Cell type	Design	Application	Inputs				Outputs	Sig. inputs	Ref.
			x 1	x 2	x 3	x 4	y 1	y 1
a b = bacteria; BBD = Box–Behnken design; conc. = concentration.
b	BBD	Alkaline lipase production	Agarose conc. (1.0–3.0) [%]	Inoculum size (3.0–5.0) [g]	Cell concentration (0.6–1.0) [g]	Incubation time	Enzyme activity	x 1, x1^2, x2, x2^2, x3, x3^2, x4, x4^2, x1x2, x1x3, x2x3, x2x4	79

---

Table 3 Alginate immobilization methods optimization inputs and outputs^a

Cell type	Design	Application	Inputs				Outputs				Sig. inputs				Ref.
			x 1	x 2	x 3	x 4	y 1	y 2	y 3	y 4	y 1	y 2	y 3	y 4
a b = bacteria; f = fungus; BBD = Box–Behnken design; CCD = central composite design; conc. = concentration; Cu(II) = copper; CaCl2 = calcium chloride.
b	BBD	L-Ribulose production	CaCl2 conc. (0.05–0.15) [M]	Alginate conc. (1–3) [%]	Cell mass (33–67) [g L^−1]		Immobilization efficiency				x 1, x1^2, x3, x3^2, x1x2, x2x3				36
b	BBD	Probiotic survival	Hardening time (15–45) [min]	Biomass conc. (10^8–10^10) [CFU mL^−1]	CaCl2 conc. (0.25–0.75) [M]		Microencapsulation yield				x 1, x1^2, x3, x3^2, x2x3				34
b	CCD	Cell immobilization	Alginate conc. (1.5–3.5) [%]	Cells added (10–100) [million colonies per mL]			Immobilization efficiency [%]				x 1, x1^2, x2, x1x2				37
b	D-opt.	Probiotic delivery	Alginate conc. (0.5–2.5) [%]	Starch maleate (2.0–6.0) [%]			Encapsulation yield				x 1, x1^2, x2, x1x2				35
b	D-opt.	Drug and probiotic delivery	Alginate conc. (2–4) [% w/v]	CaCl2 conc. (1–3) [% w/v]	PEG 4000 conc. (5–20) [% w/v]	Stirring speed (100, 300) [rpm]	LAB entrapment [%]	GE entrapment [%]	Time for 50% GE release [min]	Time for 90% GE release [min]	x 1, x2, x3, x4, x2x3, x2x4, x3x4, x3^2	x 1, x2, x3, x4, x2x3, x2x4, x3^2	x 1, x2, x3, x4, x2x4, x1^2	x 1, x2, x3, x4, x1x4, x2x3, x2x4, x3x4, x1^2, x3^2	38
b	BBD	Removal of 17-alpha-ethinylestradiol	Alginate conc. (1–5) [%]	CaCl2 conc. (0.1–0.5) [M]	Curing time (1–6) [h]	Bead size (1.5–5) [mm]	Removal efficiency of EE2				x 1, x2, x3, x3^2, x4, x4^2, x1x4, x2x4				41
b	CCD	Limonin biotransformation	Alginate conc. (0.32–3.68) [% w/v]	Cell load (36.5–53.41) [mg mL^−1]	Bead diameter (1.16–2.84) [mm]		Limonin transformation [%]	Stability of beads [OD600 nm]			x 2, x3, x3^2, x1x2	x 1, x1^2, x2, x3, x3^2, x1x2, x1x3			40
b	CCD	Sulfide oxidation	Na–alginate conc. (1–5) [% w/v]	CaCl2 conc. (1–5) [% v/v]	Inoculum size (2–10) [%]	Agitation rpm (50–250) [rpm]	Sulfide oxidation				x 1, x2, x3^2, x4, x4^2, x2x3, x2x4, x3x4				39
b	BBD	Biodegradation of light crude oil	Inoculum size (5–15) [% v/v]	Crude oil conc. (1500–3500) [ppm]	NaCl conc. (0–30) [g L^−1]		Crude oil removal (%)				x 1, x2, x3, x3^2, x2x3				42
f	BBD	Copper (Cu(II)) biosorption	Adsorbent dosage (2–6) [g L^−1]	Initial pH of solution (2–6)	Initial Cu(II) concentration (250–750) [mg L^−1]		Cu(II) removal efficiency				x 1, x1^2, x2, x3, x3^2, x1x3, x2x3				43
b	BBD	Benzaldehyde production	Alginate conc. (2–4) [%]	Cell load (35–55) [g L^−1]	Bead diameter (2.2–3.2) [mm]		Activity yields	Stability (OD600)			x 1, x1^2, x2^2, x3, x3^2, x2x3	x 1, x1^2, x2, x3, x3^2			44
b	CCD	Alkaline protease production	Alginate conc. (1–5) [% w/v]	CaCl2 conc. (1–5) [% v/v]	Inoculum size (2–10) [%]	Agitation rpm (50–250) [rpm]	Protease production				x 3 ^2, x4^2, x1x3				45
b	CCD	Fermentation CaCO3 production	Alginate% (1–3) [% w/v]	CaCl2 conc. (0.1–0.3) [M]			CaCO3%				x 1, x1^2, x2, x2^2, x1x2				46
b	CCD	Palatinose production	Alginate conc. (4–6) [%]	Bead diameter (1.5–3) [mm]	Cell loading (15–18) [g L^−1]		Palstinose yield				x 1 ^2, x2^2, x3, x3^2, x1x3				47
b	CCD	Isomaltulose production	Alginate conc. (1.5–3.5) [%]	CaCl2 conc. (0.032–0.368) [M]	Transglutaminase conc. (0–1.5) [%]		Isomaltulose produced				x 1, x2^2, x3				48
b	CCD	α-Amylase production	Incubation period (4.4–76.4) [h]	pH (2.6–8.0)	Temp. (16.4–70) [°C]		Enzyme production				Not reported				49
b	CCD	Bioethanol production	Peptone conc. (0.2–9.8) [g L^−1]	Ammonium sulfate conc. (0.1–4.9) [g L^−1]	Citrate dehydrate conc. (0.1–2.9) [g L^−1]	Glycerol conc. (5–25) [g L^−1]	Production of bioethanol [g L^−1]				x 1, x1^2, x2, x3				50
f	CCD	Pullulan production	Initial pH (6.5–8.5)	Agitation speed (125–225) [rpm]	Incubation time (76–120) [h]		Pullulan production [g dm^−1]				x 1, x1^2, x2, x2^2, x3, x3^2, x1x2, x1x3, x2x3				51

---

Table 4 Chitosan immobilization methods optimization inputs and outputs^a

Cell type	Design	Application	Inputs				Outputs	Sig. inputs	Ref.
			x 1	x 2	x 3	x 4	y 1	y 1
a b = bacteria; CCD = central composite design; conc. = concentration.
b	CCD	Bioremediation of toxic nitrile compounds	Temp (20–50) [°C]	pH (6–8)	Substrate conc. (100–300) [mM]		Nitrilase activity	x 1, x1^2, x2, x2^2	53
b	CCD	Uranium U(VI) biosorption	pH (2–5)	Uranium U(VI) conc. (100–500) [mg L^−1]	Biosorbent dosage (0.40–3.00) [g L^−1]	Cell conc. (0.0–30.0) [wt%]	Biosorption capacity (mg g^−1)	x 1, x1^2, x2, x2^2, x3, x4, x4^2, x1x2, x1x3, x2x4	54
b	CCD	Ammonia removal	Alginate conc. (0.4–1.6) [% w/v]	Chitosan conc. (0.1–0.8) [% w/v]	Embedding time (20–50) [min]		Removal efficiency of ammonia nitrogen [%]	x 1, x1^2, x2, x2^2, x1x2, x1x3	55

---

Table 5 Gellan gum immobilization methods optimization inputs and outputs^a

Cell type	Design	Application	Inputs				Outputs	Sig. inputs	Ref.
			x 1	x 2	x 3	x 4	y 1	y 1
a b = bacteria; BBD = Box–Behnken design; CCD = central composite design; conc. = concentration.
b	BBD	MY dye decolorization	dye conc. (100–250) [mg L^−1]	Gellan gum conc. (0.75–1.5) [%]	Number of beads (10–50)	Beads size (0.3–0.6) [cm]	MY dye decolorization (%)	x 1, x1^2, x2, x2^2, x4^2	59
b	CCD	Cyanide biodegradation	Gellan gum conc. (0.36–1.04) [g]	Number of beads (−3.64–64.64)	Beads size (0.1–0.6) [cm]		Biodegradation of cyanide [%]	x 1, x1^2, x2, x2^2, x3, x3^2, x1x2, x1x3, x2x3	60

---

Table 6 κ-Carrageenan immobilization methods optimization inputs and outputs^a

Cell type	Design	Application	Inputs				Outputs			Sig. inputs			Ref.
			x 1	x 2	x 3	x 4	y 1	y 2	y 3	y 1	y 2	y 3
a b = bacteria; CCD = central composite design; conc. = concentration.
b	CCD	D(−)-Tartaric acid production	Biomass conc. (25.9–54.1) [g L^−1]	κ-Carrageenan conc. (8.3–33.7) [g L^−1]			Enzyme activity [%]	Gel strength [g cm^−2]		x 1, x2	x 1, x2, x1x2		82

---

Table 7 Pectin immobilization methods optimization inputs and outputs^a

Cell type	Design	Application	Inputs				Outputs			Sig. inputs			Ref.
			x 1	x 2	x 3	x 4	y 1	y 2	y 3	y 1	y 2	y 3
a b = bacteria; BBD = Box–Behnken design; CCD = central composite design; conc. = concentration.
f	CCD	Lysozyme production	Polymer type (alginate or pectate)	Polymer conc. (2–4) [% w/v]	Inoculum conc. (20–33) [% v/v]	CaCl2 conc. (2.0–3.5) [% w/v]	Lysozyme production			x 1, x2, x3			85

---

Table 8 Poly(vinyl alcohol) immobilization methods optimization inputs and outputs^a

Cell type	Design	Application	Inputs						Outputs				Sig. inputs				Ref.
			x 1	x 2	x 3	x 4	x 5	x 6	y 1	y 2	y 3	y 4	y 1	y 2	y 3	y 4
a b = bacteria; f = fungus; BBD = Box–Behnken design; CCD = central composite design; PVA = poly(vinyl alcohol); AG = alginate; conc. = concentration; CaCl2 = calcium chloride; E = compressive modulus; kO2 = oxygen uptake rate.
b	BBD	Lactic acid production	Bead diameter (2–4) [mm]	pH (2–7)	Initial glucose conc. (100–120) [g L^−1]	Biomass (200–400)			Lactic acid yield				x 1, x2, x2^2, x3, x3^2, x4^2, x2x3, x2x4, x3x4				68
b	BBD	L-Lactic acid production	AG conc. (1–5) [% w/v]	PVA conc. (4.0–7.0) [% w/v]	Chitosan conc. (90–120) [g L^−1]	Fructose conc. (90–120) [g L^−1]	Temp. (31–39) [°C]	pH (5–7)	Lactic acid yield	Lactic acid production rate			x 1, x1^2, x2,x2^2, x3, x3^2, x4, x4^2, x5, x5^2, x6, x6^2, x1x2, x1x3, x1x4, x1x5, x1x6, x2x3, x2x4, x2x5, x2x6, x3x4, x3x5, x3x6x4x5, x4x6, x5x6	x 1, x1^2, x2, x2^2, x3, x3^2, x4, x4^2, x5, x5^2, x6, x6^2, x1x2, x1x3, x1x4, x1x5, x1x6, x2x3, x2x4, x2x5, x2x6, x3x5, x3x6x4x5, x4x6, x5x6			69
b	CCD	Sulfate reduction and copper removal	Cell quantity (19–235) [VSS per L]	Copper conc. (10–100) [mg mL^−1]					Copper removal	Sulfate reduction rate			x 2	x 1, x1^2, x2, x2^2			70
b	CCD	p-Nitrophenol biodegradation	Bead size (1–5) [mm]	PVA conc. (2–10) [%]	AG conc. (0.5–2.0) [%]	CaCl2 conc. (1–5) [%]	Freeze–thaw cycles (2–6) [cycles]		PNP transformation rate	Breakage of beads			x 1, x1^2, x2, x2^2, x3, x3^2, x4, x4^2, x5, x5^2, x1x2, x1x3, x1x4, x1x5, x2x3, x2x4, x2x5, x3x4, x3x5, x4x5	x 1 ^2, x2, x2^2, x3, x3^2, x4, x1x2, x1x3, x1x4, x1x1x5, x2x3, x2x4, x2x5, x3x4, x3x5, x4x5			71
b	CCD	Chlorinated solvent bioremediation	PVA conc. (1–3) [% w/v]	AG conc. (1–2) [% w/v]	Crosslinking time (14–135) [min]				E (day 1)	E (day 30)	k O2 (day 1)	k O2 (day 30)	x 1, x2, x2^2, x3	x 1, x1^2, x2, x2^2, x3, x1x3	x 1, x2, x2^2, x3, x1x3	x 1, x2, x2^2, x3, x1x2, x1x3	72
b	CCD	Cadaverine production	AG conc. (0.5–6.5) [%]	PVA conc. (0–8) [%]	CaCl2 conc. (0.5–6.5) [%]	Calcification time (0–24) [h]	Freezing time (0–24) [h]		Relative activity				x 1, x1^2, x2, x2^2, x3, x3^2, x4, x4^2, x5, x5^2, x1x2, x1x3, x1x5, x1^2x2, x1^2x3, x1^2x5				73
f	CCD	Ethanol production	AG conc. (1.32–4.68) [% w/v]	PVA conc. (8.32–11.68) [% w/v]	Sodium sulfate conc. (0.16–0.84) [M]				Ethanol concentration				x 1, x1^2, x2, x2^2, x3, x3^2, x1x3				74

---

Table 9 Xanthan gum immobilization methods optimization inputs and outputs^a

Cell type	Design	Application	Inputs			Outputs			Sig. inputs		Ref.
			x 1	x 2	x 3	y 1	y 2	y 3	y 1	y 2
a b = bacteria; BBD = Box–Behnken design; conc. = concentration.
b	BBD	Dietary supplements in pure milk	Chitosan conc. (0.8–1.0) [g mL^−1]	XG/chitosan (1 : 7–1 : 9)	Stirring time (40–60) [min]	Viable counts of B. bifidum BB01 microcapsules	Microencapsulation yield of B. bifidum BB01 microcapsules		x 1, x2, x3, x1x2, x1x3, x2x3	x 1 ^2, x2, x2^2, x2x3	88

---

Acknowledgements

This review was funded by the National Institute of Environmental Health Sciences under grant NIH 5R01ES032707.

References

1. A. A. Akinsemolu, Principles of Green Microbiology: The Microbial Blueprint for Sustainable Development, Environ. Adv., 2023, 14, 100440,  DOI:10.1016/j.envadv.2023.100440.
2. R. M. Stubbendieck, C. Vargas-Bautista and P. D. Straight, Bacterial Communities: Interactions to Scale, Front. Microbiol., 2016, 7, 1234,  DOI:10.3389/fmicb.2016.01234.
3. Hydrogels: Recent Advances, Gels Horizons: from Science to Smart Materials, ed. Thakur, V. K. and Thakur, M. K., Springer Singapore, Singapore, 2018,  DOI:10.1007/978-981-10-6077-9.
4. A. Dzionek, D. Wojcieszyńska and U. Guzik, Natural Carriers in Bioremediation: A Review, Electron. J. Biotechnol., 2016, 23, 28–36,  DOI:10.1016/j.ejbt.2016.07.003.
5. A. C. Jen, M. C. Wake and A. G. Mikos, Review: Hydrogels for Cell Immobilization, Biotechnol. Bioeng., 2000, 50(4), 357–364,  DOI:10.1002/(SICI)1097-0290(19960520)50:4<357::AID-BIT2>3.0.CO;2-K.
6. M. J. Lapponi, M. B. Méndez, J. A. Trelles and C. W. Rivero, Cell Immobilization Strategies for Biotransformations, Curr. Opin. Green Sustainable Chem., 2022, 33, 100565,  DOI:10.1016/j.cogsc.2021.100565.
7. Immobilization Strategies: Biomedical, Bioengineering and Environmental Applications, Gels Horizons: from Science to Smart Materials, ed. Tripathi, A. and Melo, J. S., Springer Singapore, Singapore, 2021,  DOI:10.1007/978-981-15-7998-1.
8. M. B. Cassidy, H. Lee and J. T. Trevors, Environmental Applications of Immobilized Microbial Cells: A Review, J. Ind. Microbiol., 1996, 16(2), 79–101,  DOI:10.1007/bf01570068.
9. T. Mehrotra, S. Dev, A. Banerjee, A. Chatterjee, R. Singh and S. Aggarwal, Use of Immobilized Bacteria for Environmental Bioremediation: A Review, J. Environ. Chem. Eng., 2021, 9(5), 105920,  DOI:10.1016/j.jece.2021.105920.
10. Z. Bayat, M. Hassanshahian and S. Cappello, Immobilization of Microbes for Bioremediation of Crude Oil Polluted Environments: A Mini Review, Open Microbiol. J., 2015, 9, 48,  DOI:10.2174/1874285801509010048.
11. F. J. Vernerey, S. Lalitha Sridhar, A. Muralidharan and S. J. Bryant, Mechanics of 3D Cell–Hydrogel Interactions: Experiments, Models, and Mechanisms, Chem. Rev., 2021, 121(18), 11085–11148,  DOI:10.1021/acs.chemrev.1c00046.
12. L. Smith Callahan, Combinatorial Method/High Throughput Strategies for Hydrogel Optimization in Tissue Engineering Applications, Gels, 2016, 2(2), 18,  DOI:10.3390/gels2020018.
13. M. Darnell and D. J. Mooney, Leveraging Advances in Biology to Design Biomaterials, Nat. Mater., 2017, 16(12), 1178–1185,  DOI:10.1038/nmat4991.
14. Z. Wahid and N. Nadir, Improvement of One Factor at a Time through Design of Experiments, World Appl. Sci. J., 2013, 21(1), 56–61,  DOI:10.5829/idosi.wasj.2013.21.mae.99919.
15. R. E. Bruns, I. S. Scarminio and B. d. Barros Neto, Statistical Design--Chemometrics, Data Handling in Science and Technology, Elsevier, Amsterdam, Boston, 1st edn, 2006,  DOI:10.1016/s0922-3487(05)x2500-x.
16. W. F. Guthrie, NIST/SEMATECH E-Handbook of Statistical Methods, NIST Handbook 151, 2020,  DOI:10.18434/M32189.
17. T. Keskin Gündoğdu, İ. Deniz, G. Çalışkan, E. S. Şahin and N. Azbar, Experimental Design Methods for Bioengineering Applications, Crit. Rev. Biotechnol., 2016, 36(2), 368–388,  DOI:10.3109/07388551.2014.973014.
18. G. E. P. Box and H. L. Lucas, Design of Experiments in Non-Linear Situations, Biometrika, 1959, 46(1/2), 77–90,  DOI:10.2307/2332810.
19. P. Angelopoulos, H. Evangelaras and C. Koukouvinos, Small, Balanced, Efficient and near Rotatable Central Composite Designs, J. Stat. Plan. Inference, 2009, 139(6), 2010–2013,  DOI:10.1016/j.jspi.2008.09.001.
20. M. J. Anderson and P. J. WhitcombDesign of Experiments, in Kirk-Othmer Encyclopedia of Chemical Technology, John Wiley & Sons, Ltd, 2010; pp. pp. 1–22,  DOI:10.1002/0471238961.0405190908010814.a01.pub3.
21. Z. Zhang and B. Xiaofeng, Comparison about the Three Central Composite Designs with Simulation, in 2009 International Conference on Advanced Computer Control; IEEE, Singapore, Singapore, 2009; pp. pp. 163–167,  DOI:10.1109/ICACC.2009.48.
22. S. L. C. Ferreira, R. E. Bruns, H. S. Ferreira, G. D. Matos, J. M. David, G. C. Brandão, E. G. P. da Silva, L. A. Portugal, P. S. dos Reis, A. S. Souza and W. N. L. dos Santos, Box-Behnken Design: An Alternative for the Optimization of Analytical Methods, Anal. Chim. Acta, 2007, 597(2), 179–186,  DOI:10.1016/j.aca.2007.07.011.
23. R. Unal, R. Lepsch and M. McMillin, Response Surface Model Building and Multidisciplinary Optimization Using D-Optimal Designs, in 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, American Institute of Aeronautics and Astronautics, St. Louis, MO, U.S.A., 1998,  DOI:10.2514/6.1998-4759.
24. S. S. Ranade and P. Thiagarajan, Selection of a Design for Response Surface, IOP Conf. Ser.: Mater. Sci. Eng., 2017, 263, 022043,  DOI:10.1088/1757-899X/263/2/022043.
25. A. Witek-Krowiak, K. Chojnacka, D. Podstawczyk, A. Dawiec and K. Bubała, Application of Response Surface Methodology and Artificial Neural Network Methods in Modelling and Optimization of Biosorption Process, Bioresour. Technol., 2014, 160, 150–160,  DOI:10.1016/j.biortech.2014.01.021.
26. K. Y. Lee and D. J. Mooney, Alginate: Properties and Biomedical Applications, Prog. Polym. Sci., 2012, 37(1), 106–126,  DOI:10.1016/j.progpolymsci.2011.06.003.
27. I. Aranaz, A. R. Alcántara, M. C. Civera, C. Arias, B. Elorza, A. Heras Caballero and N. Acosta, Chitosan: An Overview of Its Properties and Applications, Polymers, 2021, 13(19), 3256,  DOI:10.3390/polym13193256.
28. K. B. Guiseley, Chemical and Physical Properties of Algal Polysaccharides Used for Cell Immobilization, Enzyme Microb. Technol., 1989, 11(11), 706–716,  DOI:10.1016/0141-0229(89)90119-1.
29. A. Dzionek, D. Wojcieszyńska and U. Guzik, Use of Xanthan Gum for Whole Cell Immobilization and Its Impact in Bioremediation - a Review, Bioresour. Technol., 2022, 351, 126918,  DOI:10.1016/j.biortech.2022.126918.
30. F. van de Velde, N. D. Lourenço, H. M. Pinheiro and M. Bakker, Carrageenan: A Food-Grade and Biocompatible Support for Immobilisation Techniques, Adv. Synth. Catal., 2002, 344(8), 815–835,  DOI:10.1002/1615-4169(200209)344:8<815::AID-ADSC815>3.0.CO;2-H.
31. I. Giavasis, L. M. Harvey and B. McNeil, Gellan Gum, Crit. Rev. Biotechnol., 2000, 20(3), 177–211,  DOI:10.1080/07388550008984169.
32. Polymer Gels: Science and Fundamentals, Gels Horizons: from Science to Smart Materials, ed. Thakur, V. K. and Thakur, M. K., Springer Singapore, Singapore, 2018,  DOI:10.1007/978-981-10-6086-1.
33. T. Andersen, P. Auk-Emblem and M. Dornish, 3D Cell Culture in Alginate Hydrogels, Microarrays, 2015, 4(2), 133–161,  DOI:10.3390/microarrays4020133.
34. I. Trabelsi, W. Bejar, D. Ayadi, H. Chouayekh, R. Kammoun, S. Bejar and R. Ben Salah, Encapsulation in Alginate and Alginate Coated-Chitosan Improved the Survival of Newly Probiotic in Oxgall and Gastric Juice, Int. J. Biol. Macromol., 2013, 61, 36–42,  DOI:10.1016/j.ijbiomac.2013.06.035.
35. M. Popović, M. Stojanović, Z. Veličković, A. Kovačević, R. Miljković, N. Mirković and A. Marinković, Characterization of Potential Probiotic Strain, L. Reuteri B2, and Its Microencapsulation Using Alginate-Based Biopolymers, Int. J. Biol. Macromol., 2021, 183, 423–434,  DOI:10.1016/j.ijbiomac.2021.04.177.
36. Y.-W. Zhang, P. Prabhu and J.-K. Lee, Alginate Immobilization of Recombinant Escherichia coli Whole Cells Harboring L-Arabinose Isomerase for L-Ribulose Production, Bioprocess Biosyst. Eng., 2010, 33(6), 741–748,  DOI:10.1007/s00449-009-0397-7.
37. H. T. Ho and H. T. Nguyen, Optimization of Bacillus subtilis Natto Immobilization Process on Alginate – Chitosan Complex and Its Application for Nattokinase Fermentation, Int. J. Pharm. Sci. Invent., 2016, 5(3), 25–30,  DOI:10.9790/6718.
38. P. K. Deol, P. Khare, D. P. Singh, G. Soman, M. Bishnoi, K. K. Kondepudi and I. P. Kaur, Managing Colonic Inflammation Associated Gut Derangements by Systematically Optimised and Targeted Ginger Extract-Lactobacillus acidophilus Loaded Pharmacobiotic Alginate Beads, Int. J. Biol. Macromol., 2017, 105, 81–91,  DOI:10.1016/j.ijbiomac.2017.06.117.
39. A. K. Surabhi and M. I. Elzagheid, Optimization of Na-Alginate Immobilization Method for Sulfide Oxidation Using Immobilized Thiobacillus Species, J. Environ. Waste Manage., 2018, 5(2), 275–282.
40. M. Malik and M. Ghosh, Immobilization Parameters Statistically Optimized for Whole Cells of Pseudomonas putida G7 to Enhance Limonin Biotransformation, J. Adv. Lab. Res. Biol., 2012, 3(4), 266–275.
41. T. N. Tran, D.-G. Kim and S.-O. Ko, Encapsulation of Biogenic Manganese Oxide and Pseudomonas putida MnB1 for Removing 17 α-Ethinylestradiol from Aquatic Environments, J. Water Proc. Eng., 2020, 37, 101423,  DOI:10.1016/j.jwpe.2020.101423.
42. E. Khanpour-Alikelayeh, A. Partovinia, A. Talebi and H. Kermanian, Enhanced Biodegradation of Light Crude Oil by Immobilized Bacillus licheniformis in Fabricated Alginate Beads through Electrospray Technique, Environ. Monit. Assess., 2021, 193(6), 328,  DOI:10.1007/s10661-021-09104-z.
43. A. Thirunavukkarasu and R. Nithya, Response Surface Optimization of Cu(II) Biosorption onto Candida tropicalis Immobilized Strontium Alginate Beads by Box-Behnken Experimental Design, Journal of Environment and Biotechnology Research, 2019, 8(2), 14–21,  DOI:10.5281/zenodo.2619835.
44. J. Wu, J.-L. Wang, M.-H. Li, J.-P. Lin and D.-Z. Wei, Optimization of Immobilization for Selective Oxidation of Benzyl Alcohol by Gluconobacter Gluconobacter oxydans Using Response Surface Methodology, Bioresour. Technol., 2010, 101(23), 8936–8941,  DOI:10.1016/j.biortech.2010.07.019.
45. R. Potumarthi, Ch. Subhakar, A. Pavani and A. Jetty, Evaluation of Various Parameters of Calcium-Alginate Immobilization Method for Enhanced Alkaline Protease Production by Bacillus licheniformis NCIM-2042 Using Statistical Methods, Bioresour. Technol., 2008, 99(6), 1776–1786,  DOI:10.1016/j.biortech.2007.03.041.
46. M. Seifan, A. K. Samani, S. Hewitt and A. Berenjian, The Effect of Cell Immobilization by Calcium Alginate on Bacterially Induced Calcium Carbonate Precipitation, Fermentation, 2017, 3(4), 57,  DOI:10.3390/fermentation3040057.
47. P. Mundra, K. Desai and S. S. Lele, Application of Response Surface Methodology to Cell Immobilization for the Production of Palatinose, Bioresour. Technol., 2007, 98(15), 2892–2896,  DOI:10.1016/j.biortech.2006.09.046.
48. P. H. Carvalho, H. Y. Kawaguti, W. F. C. de Souza and H. H. Sato, Immobilization of Serratia plymuthica by Ionic Gelation and Cross-Linking with Transglutaminase for the Conversion of Sucrose into Isomaltulose, Bioprocess Biosyst. Eng., 2021, 44(6), 1109–1118,  DOI:10.1007/s00449-021-02513-x.
49. S. Kar and R. C. Ray, Statistical Optimization of α-Amylase Production by Streptomyces erumpens MTCC 7317 Cells in Calcium Alginate Beads Using Response Surface Methodology, Pol. J. Microbiol., 2008, 57(1), 49,  DOI:10.1007/s12010-008-8248-6.
50. S. J. Lee, J. H. Lee, X. Yang, H. Y. Yoo, S. O. Han, C. Park and S. W. Kim, Re-Utilization of Waste Glycerol for Continuous Production of Bioethanol by Immobilized Enterobacter aerogenes, J. Cleaner Prod., 2017, 161, 757–764,  DOI:10.1016/j.jclepro.2017.05.170.
51. Z. Ürküt, S. Daǧbaǧlı and Y. Göksungur, Optimization of Pullulan Production Using Ca-Alginate-immobilized Aureobasidium pullulans by Response Surface Methodology, J. Chem. Technol. Biotechnol., 2007, 82(9), 837–846,  DOI:10.1002/jctb.1750.
52. L. Gasperini, J. F. Mano and R. L. Reis, Natural Polymers for the Microencapsulation of Cells, J. R. Soc., Interface, 2014, 11(100), 20140817,  DOI:10.1098/rsif.2014.0817.
53. Jyoti, K. Bhatia, K. Chauhan, C. Attri and A. Seth, Improving Stability and Reusability of Rhodococcus pyridinivorans NIT-36 Nitrilase by Whole Cell Immobilization Using Chitosan, Int. J. Biol. Macromol., 2017, 103, 8–15,  DOI:10.1016/j.ijbiomac.2017.05.012.
54. H. Sohbatzadeh, A. R. Keshtkar, J. Safdari and F. U. Fatemi, (VI) Biosorption by Bi-Functionalized Pseudomonas putida@Chitosan Bead: Modeling and Optimization Using RSM, Int. J. Biol. Macromol., 2016, 89, 647–658,  DOI:10.1016/j.ijbiomac.2016.05.017.
55. J. Guo, C. Chen, W. Chen, J. Jiang, B. Chen and F. Zheng, Effective Immobilization of Bacillus subtilis in Chitosan-Sodium Alginate Composite Carrier for Ammonia Removal from Anaerobically Digested Swine Wastewater, Chemosphere, 2021, 284, 131266,  DOI:10.1016/j.chemosphere.2021.131266.
56. G. Sworn, G. R. Sanderson and W. Gibson, Gellan Gum Fluid Gels, Food Hydrocolloids, 1995, 9(4), 265–271,  DOI:10.1016/S0268-005X(09)80257-9.
57. K. M. Zia, S. Tabasum, M. F. Khan, N. Akram, N. Akhter, A. Noreen and M. Zuber, Recent Trends on Gellan Gum Blends with Natural and Synthetic Polymers: A Review, Int. J. Biol. Macromol., 2018, 109, 1068–1087,  DOI:10.1016/j.ijbiomac.2017.11.099.
58. M. Das and T. K. Giri, Hydrogels Based on Gellan Gum in Cell Delivery and Drug Delivery, J. Drug Delivery Sci. Technol., 2020, 56, 101586,  DOI:10.1016/j.jddst.2020.101586.
59. F. N. A. Muliadi, M. I. E. Halmi, S. B. A. Wahid, S. S. A. Gani, K. Mahmud and M. Y. A. Shukor, Immobilization of Metanil Yellow Decolorizing Mixed Culture FN3 Using Gelling Gum as Matrix for Bioremediation Application, Sustainability, 2020, 13(1), 36,  DOI:10.3390/su13010036.
60. K. I. Karamba, S. A. Ahmad, A. Zulkharnain, N. A. Yasid, A. Khalid and M. Y. Shukor, Biodegradation of Cyanide and Evaluation of Kinetic Models by Immobilized Cells of Serratia marcescens Strain AQ07, Int. J. Environ. Sci. Technol., 2017, 14(9), 1945–1958,  DOI:10.1007/s13762-017-1287-1.
61. N. Zhang, X. Li, J. Ye, Y. Yang, Y. Huang, X. Zhang and M. Xiao, Effect of Gellan Gum and Xanthan Gum Synergistic Interactions and Plasticizers on Physical Properties of Plant-Based Enteric Polymer Films, Polymers, 2020, 12(1), 121,  DOI:10.3390/polym12010121.
62. Y. Han, L. Zhu, H. Zhang, T. Liu and G. Wu, Synergistic Effect of Gellan Gum and Guar Gum on Improving the Foaming Properties of Soy Protein Isolate-Based Complexes: Interaction Mechanism and Interfacial Behavior, Carbohydr. Polym., 2024, 339, 122202,  DOI:10.1016/j.carbpol.2024.122202.
63. R. Nagarkar and J. Patel, Polyvinyl Alcohol: A Comprehensive Study, Acta Sci. Pharm. Sci., 2019, 3(4), 34–44.
64. D. Wong and J. Parasrampuria, Polyvinyl Alcohol, in Analytical Profiles of Drug Substances and Excipients, ed. Brittain, H. G., Academic Press, 1996; vol. 24, pp. 397–441,  DOI:10.1016/S0099-5428(08)60699-1.
65. A. Kumar and S. S. Han, PVA-Based Hydrogels for Tissue Engineering: A Review, Int. J. Polym. Mater. Polym. Biomater., 2017, 66(4), 159–182,  DOI:10.1080/00914037.2016.1190930.
66. S. Moulay, Review: Poly(Vinyl Alcohol) Functionalizations and Applications, Polym.-Plast. Technol. Eng., 2015, 54(12), 1289–1319,  DOI:10.1080/03602559.2015.1021487.
67. E. Marin, J. Rojas and Y. Ciro, A Review of Polyvinyl Alcohol Derivatives: Promising Materials for Pharmaceutical and Biomedical Applications, Afr. J. Pharm. Pharmacol., 2014, 8(24), 674–684,  DOI:10.5897/AJPP2013.3906.
68. J. Wang, J. Huang, H. Laffend, S. Jiang, J. Zhang, Y. Ning, M. Fang and S. Liu, Optimization of Immobilized Lactobacillus pentosus Cell Fermentation for Lactic Acid Production, Bioresources and Bioprocessing, 2020, 7(1), 15,  DOI:10.1186/s40643-020-00305-x.
69. J. Wang, H. Guo, J. Huang, S. Jiang, S. Hou, X. Chen, H. Lv, X. Bi, M. Hou, H. Lin, Y. Lu, J. Qiao, R. Yang and S. Liu, L-Lactic Acid Production from Fructose by Chitosan Film-Coated Sodium Alginate-Polyvinyl Alcohol Immobilized Lactobacillus pentosus Cells and Its Kinetic Analysis, Bioresources and Bioprocessing, 2021, 8(1), 27,  DOI:10.1186/s40643-021-00380-8.
70. H.-F. Hsu, Y.-S. Jhuo, M. Kumar, Y.-S. Ma and J.-G. Lin, Simultaneous Sulfate Reduction and Copper Removal by a PVA-Immobilized Sulfate Reducing Bacterial Culture, Bioresour. Technol., 2010, 101(12), 4354–4361,  DOI:10.1016/j.biortech.2010.01.094.
71. S. P. Sam, R. Adnan and S. L. Ng, Statistical Optimization of Immobilization of Activated Sludge in PVA/Alginate Cryogel Beads Using Response Surface Methodology for p-Nitrophenol Biodegradation, J. Water Proc. Eng., 2021, 39, 101725,  DOI:10.1016/j.jwpe.2020.101725.
72. C. G. Harris, H. K. Gedde, A. A. Davis, L. Semprini, W. E. Rochefort and K. C. Fogg, The Optimization of Poly(Vinyl)-Alcohol-Alginate Beads with a Slow-Release Compound for the Aerobic Cometabolism of Chlorinated Aliphatic Hydrocarbons, RSC Sustainability, 2024, 2(4), 1101–1117,  10.1039/d3su00409k.
73. G. Wei, W. Ma, A. Zhang, X. Cao, J. Shen, Y. Li, K. Chen and P. Ouyang, Enhancing Catalytic Stability and Cadaverine Tolerance by Whole-Cell Immobilization and the Addition of Cell Protectant during Cadaverine Production, Appl. Microbiol. Biotechnol., 2018, 102(18), 7837–7847,  DOI:10.1007/s00253-018-9190-3.
74. K. Nonthasen, W. Piyatheerawong and P. Thanonkeo, Efficient Entrapment of Kluyveromyces marxianus DBKKUY-103 in Polyvinyl Alcohol Hydrogel for Ethanol Production from Sweet Sorghum Juice, Turk. J. Biol., 2015, 39(1), 119–128,  DOI:10.3906/biy-1405-43.
75. Y. Chen, J. Li, J. Lu, M. Ding and Y. Chen, Synthesis and Properties of Poly(Vinyl Alcohol) Hydrogels with High Strength and Toughness, Polym. Test., 2022, 108, 107516,  DOI:10.1016/j.polymertesting.2022.107516.
76. Physical Properties of Polymers Handbook, ed. Mark, J. E., Springer New York, New York, NY, 2007,  DOI:10.1007/978-0-387-69002-5.
77. Q. Ying and B. Chu, Overlap Concentration of Macromolecules in Solution, Macromolecules, 1987, 20(2), 362–366,  DOI:10.1021/ma00168a023.
78. P. Zarrintaj, S. Manouchehri, Z. Ahmadi, M. R. Saeb, A. M. Urbanska, D. L. Kaplan and M. Mozafari, Agarose-Based Biomaterials for Tissue Engineering, Carbohydr. Polym., 2018, 187, 66–84,  DOI:10.1016/j.carbpol.2018.01.060.
79. D. Bisht, S. K. Yadav and N. S. Darnwal, Optimization of Immobilization Conditions by Conventional and Statistical Strategies for Alkaline Lipase Production by Pseudomonas aeruginosa Mutant Cells: Scale-up at Bench-Scale Bioreactor Level Level, Turk. J. Biol., 2013, 4(3), 392–404,  DOI:10.3906/biy-1209-19.
80. G. A. De Ruiter and B. Rudolph, Carrageenan Biotechnology, Trends Food Sci. Technol., 1997, 8(12), 389–395,  DOI:10.1016/S0924-2244(97)01091-1.
81. K. M. Zia, S. Tabasum, M. Nasif, N. Sultan, N. Aslam, A. Noreen and M. Zuber, A Review on Synthesis, Properties and Applications of Natural Polymer Based Carrageenan Blends and Composites, Int. J. Biol. Macromol., 2017, 96, 282–301,  DOI:10.1016/j.ijbiomac.2016.11.095.
82. H. Pan, W. Bao, Z. Xie, J. Zhang and Y. Li, Immobilization of Escherichia coli Cells with Cis-Epoxysuccinate Hydrolase Activity for D(−)-Tartaric Acid Production, Biotechnol. Lett., 2010, 32(2), 235–241,  DOI:10.1007/s10529-009-0134-y.
83. Pectin: Technological and Physiological Properties, ed. Kontogiorgos, V., Springer International Publishing, Cham, 2020,  DOI:10.1007/978-3-030-53421-9.
84. D. Mohnen, Pectin Structure and Biosynthesis, Curr. Opin. Plant Biol., 2008, 11(3), 266–277,  DOI:10.1016/j.pbi.2008.03.006.
85. R. Parra, D. Aldred and N. Magan, A Novel Immobilised Design for the Production of the Heterologous Protein Lysozyme by a Genetically Engineered Aspergillus niger Strain, Appl. Microbiol. Biotechnol., 2005, 67(3), 336–344,  DOI:10.1007/s00253-004-1742-z.
86. J. Patel, B. Maji, N. S. H. N. Moorthy and S. Maiti, Xanthan Gum Derivatives: Review of Synthesis, Properties and Diverse Applications, RSC Adv., 2020, 10(45), 27103–27136,  10.1039/D0RA04366D.
87. J. D. Hinchliffe, A. Parassini Madappura, S. M. D. Syed Mohamed and I. Roy, Biomedical Applications of Bacteria-Derived Polymers, Polymers, 2021, 13(7), 1081,  DOI:10.3390/polym13071081.
88. G. Shu, Y. He, L. Chen, Y. Song, J. Meng and H. Chen, Microencapsulation of Bifidobacterium bifidum BB01 by Xanthan–Chitosan: Preparation and Its Stability in Pure Milk, Artif. Cells, Nanomed., Biotechnol., 2018, 46(1), 588–596,  DOI:10.1080/21691401.2018.1431652.
89. M. Ahearne, Introduction to Cell–Hydrogel Mechanosensing, Interface Focus, 2014, 4(2), 20130038,  DOI:10.1098/rsfs.2013.0038.

---