Open Access Article
Open Access Articleα-Synuclein interaction with POPC/POPS vesicles†
Marija
Dubackic
 *a,
Veronica
Lattanzi
*a,
Veronica
Lattanzi
 ab,
Yun
Liu
cd,
Michael
Haertlein
e,
Juliette M.
Devos
ab,
Yun
Liu
cd,
Michael
Haertlein
e,
Juliette M.
Devos
 e,
Emma
Sparr
e,
Emma
Sparr
 a,
Sara
Linse
a,
Sara
Linse
 b and
Ulf
Olsson
b and
Ulf
Olsson
 a
a
aPhysical Chemistry, Chemistry Centre, Lund University, SE-22100 Lund, Sweden. E-mail: majuskad@hotmail.com
bBiochemistry and Structural Biology, Chemistry Centre, Lund University, SE-22100 Lund, Sweden
cCenter for Neutron Research, National Institute of Standards and Technology, 20878 Gaithersburg, Maryland, USA
dChemical and Biomolecular Engineering Department, University of Delaware, 19716, Newark, Delaware, USA
eLife Sciences Group, Institut Laue-Langevin, 38000 Grenoble, France
First published on 9th January 2025
Abstract
We have investigated the adsorption of the amyloid-forming protein α-Synuclein (αSyn) onto small unilamellar vesicles composed of a mixture of zwitterionic POPC and anionic POPS lipids. αSyn monomers adsorb onto the anionic lipid vesicles where they adopt an α-helical secondary structure. The degree of adsorption depends on the fraction of anionic lipid in the mixed lipid membrane, but one needs to consider the electrostatic shift of the serine pKa with increasing fraction of POPS. The vesicles with adsorbed αSyn monomers are kinetically stable. However, after fibrils have been formed, here triggered by the addition of a small concentration of pre-formed fibrils (seeds), we observed that the average vesicle size increased by approximately a factor of two. This increase in the vesicle size can be explained by vesicle fusion taking place during the fibril formation process.
1 Introduction
α-Synuclein (αSyn) is a 140 amino acid residues long, intrinsically disordered protein, abundantly present in neurons. Monomeric αSyn in solution has a random coil conformation. However, when associated with lipid membranes, a part of the protein molecule can adopt an α-helical structure1,2 and, under certain conditions, the protein can self-assemble into amyloid fibrils by arranging part of its sequence into β-strands.3,4 αSyn has been receiving significant attention since it has been associated with Parkinsons disease (PD), following the discovery that mutations in the SNCA gene are related to PD.5 The protein is moreover the main component of neuronal inclusions that are a hallmark of PD, so-called Lewy bodies (LBs),6 where αSyn is present in fibrillar form ref. 7.The αSyn sequence can be divided into three domains. The N-terminal domain, composed of the first 60 residues, has a positive net charge around neutral pH and has been found to adopt an α-helical structure upon association with negatively charged lipid membranes.8 It is believed that it is the presence of a repetitive KTKGEV sequence in the N-terminus, which allows αSyn to adopt an α-helical structure.9 The middle part of the αSyn sequence, the so-called non-amyloid-β component (NAC), consists of 34 residues that are mostly hydrophobic. The NAC region is believed to play a critical role in amyloid formation10 and is also implicated in the interaction with lipid moieties.1 The C-terminus contains mainly negatively charged residues, and it is unstructured also when the protein is adsorbed at lipid membranes11 as well as in amyloid fibrils.4
The physiological role of αSyn is not fully understood. However, it is implied in the interaction with lipids and lipid membranes,12–16 as well as in neurotransmission and the corresponding trafficking of synaptic vesicles.12,13 While the protein has been reported to facilitate vesicle fusion,17,18 a recent study highlights that fission or stable shape deformations are more likely scenarios.19 Furthermore, the presence of various lipids has been detected in LBs.20,21 Hence, as both the physiological function and possibly the role of αSyn in PD are related to interactions of the protein with lipid membranes, such interactions have been extensively studied in the past decades.22 It has been demonstrated that αSyn monomers adsorb to anionic lipid membranes,23–28 with its N-terminal domain forming an α-helix at the membrane interface1,2,29,30 which leads to increased acyl-chain ordering of the lipids in the bilayer and stabilization of the vesicles.31,32 It has also been shown that the number of residues in the N-terminus which adopts α-helical conformation depends on lipid-to-protein ratio.1,11,30,33,34 Due to the net positive charge of the N-terminus, attractive electrostatic interactions are considered to be an important driving force for adsorption35 in addition to a hydrophobic component.36 However, the role of the negative membrane charge may alternatively be to modulate and dampen the electrostatic repulsion between the positively charged N-termini in the adsorbed state.
The electrostatic contribution is expected to depend on the pH of the solution, in particular around the effective pKa of the anionic lipid and the isoelectric point (IP) of αSyn, which are not necessarily that far apart for the serine lipid headgroup and αSyn.
Fibril formation in the presence of various lipid membranes has been extensively studied,37–45 and it was shown that under some conditions the presence of vesicles during fibril formation may act as an aggregation catalyser.37–40 Protein-induced membrane remodeling has also been observed.22,46,47
In this work, we investigated how αSyn interacts with small unilamellar vesicles (SUVs), composed of a mixture of zwitterionic phospholipids 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine (POPC) and anionic 1-palimtoyl-2-oleoyl-sn-glycero-3-phosho-L-serine (POPS). The vesicle radii in this study were targeted to be similar to those of the synaptic vesicles, ≈15–20 nm.48 We investigated the adsorption of αSyn onto lipid membranes by determining the amount of membrane-bound α-helices using circular dichroism (CD), when the latter ones are composed of 10%, 15%, 20%, 30% and 50% charged lipids. We also calculated the number of lipid molecules per number of protein molecules, which are involved in binding at different fractions of anionic lipids (β). Using small-angle X-ray scattering (SAXS), we looked into the effect of αSyn on the vesicle scattering profile, and related the difference to the findings from CD experiments. We also investigated the end-state of the fibril formation in the presence of lipid vesicles by means of cryogenic transmission electron microscopy (cryo-TEM) and small-angle neutron scattering (SANS).
2 Materials and methods
2.1 α-Synuclein
Human αSyn was expressed in Escherichia coli from a synthetic gene with E. coli-optimized codons cloned into a Pet3a plasmid (purchased from Genscript, Piscataway) and purified as described previously in ref. 49. Protein monomers were isolated by size exclusion chromatography (SEC) in 10 mM MES buffer at pH = 5.5 using a 24 mL Superdex75 column (GE healthcare). Protein samples corresponding to the central region of the peak were collected. Following this, buffer salts were removed by desalting on a 5 ml HiTrap desalting (GE Healthcare) column. The protein concentration was determined by absorbance at 280 nm using an extinction coefficient 5800 M−1 cm−1. To obtain the high concentration required for scattering experiments, samples were lyophilised after being desalted.The matchout deuterated αSyn was produced in E. coli. Cell pellet containing matchout deuterated αSyn was prepared in the Deuteration Laboratory of the Institut Laue-Langevin in Grenoble, France using a modified protocol from the one described in ref. 2. A high cell density fed-batch culture using 85% deuterated Enfors minimal medium was grown at a temperature of 30 °C and pO2 at 30% saturation.50 The degree of deuteration was 75% as confirmed by mass spectrometry. Deuterated αSyn monomers were isolated by SEC as described above and lyophilised in order to obtain high concentration.
2.2 Lipid vesicles
The lipids used in this study were the zwitterionic POPC and anionic POPS. All lipids were obtained from Avanti Polar Lipids (Alabaster, AL, USA). In the preparation of mixed lipid vesicles, lipids were weighted and mixed at the desired proportion (β = 0.1, β = 0.15, β = 0.2, β = 0.3 and β = 0.5). The powder was dissolved in a chloroform/methanol (3/1 volume ratio) mixture. The solvent was evaporated under a stream of N2 gas, and the created lipid film was dried in a overnight under vacuum. The lipids were finally dispersed in the desired buffer (20 mM phosphate buffer (PB) at pH 6.0, 6.5, 7.0 and 7.4) and vortexed for a few minutes.SUVs were prepared via sonication. The sonication was performed for 15 min, 10 s on/off duty at 70% amplitude on ice. The lipid dispersions were then centrifuged for 10 min at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm in order to pellet any contaminating particles from the sonicator tip. The supernatant was collected and used as the vesicle dispersion.
000 rpm in order to pellet any contaminating particles from the sonicator tip. The supernatant was collected and used as the vesicle dispersion.
2.3 Sample preparation
For circular dichroism (CD) spectroscopy, protein monomers were collected after SEC in 20 mM PB, pH = 7.0. Subsequently, the monomeric protein solution was mixed with different amounts of vesicle dispersion to obtained the desired lipid-to-protein (L/P) ratios.For small-angle X-ray scattering (SAXS) and dynamic light scattering (DLS) samples were prepared using desalted and lyophilised αSyn. The protein powder was first dissolved in 1 mM NaOH at pH = 11.4 for half an hour, which ensures that we are starting from monomeric solution. Following this, the same volume of 40 mM PB at pH = 7.0 was added. Finally, the correct amount of vesicle dispersion in 20 mM PB at pH = 7.0 was added.
For small-angle neutron scattering (SANS) samples were prepared using the lyophilized protein powder containing buffer salts. The powder was resuspended in filtered D2O. Seeds, i.e. preformed αSyn fibrils, were added to a concentration corresponding to 5% of the total αSyn concentration in monomer units. Finally, a lipid vesicle dispersion was added. At the end, the final concentration of αSyn monomers was equal to 280 μM. The samples were prepared with a lipid concentration of 2.1 mM, which corresponds to a lipid to protein ratio of 7.5. All samples were incubated in Axygen low-binding tubes at 37 °C for 14 days under quiescent conditions.
2.4 Circular dichroism
CD spectra were recorded using a JASCO J-715 CD spectrometer in 1 mm path length quartz cuvette (Hellma 110-QS). The measurement settings were 1 nm bandwidth, 2 s response time and 20 nm min−1 scan rate. The measurements were performed at 25 °C and an average of 5 scans was used for each measurement. The protein concentration was 5 μM and the lipid concentration was varied. The data are presented as the mean residue ellipticity, [θ], which is calculated as where θ is the ellipticity in deg, l is the path length in cm, c is the protein concentration in dmol per cm3 and n is the number of residues.
where θ is the ellipticity in deg, l is the path length in cm, c is the protein concentration in dmol per cm3 and n is the number of residues.
2.5 Dynamic light scattering and electrophoretic mobility
The hydrodynamic radius of vesicles with adsorbed αSyn was monitored over time using 3D LS Spectrometer, LS Instruments, AG, equipped with λ = 660 nm Cobolt laser with maximum power of 100 mW. The correlation functions were recorded from 60° to 145° with 5° steps. The measurements were performed at 37 °C in 5 mm radius glass capillaries, emerged in a refractive index-matching liquid, decalin. A z-averaged decay rates, 〈Γz〉 were obtained by applying cumulant analysis on correlation functions measured at different angles, as described in ref. 51. 〈Γz〉 is further related to a collective diffusion coefficient, 〈Dc〉z through the relation 〈Γz〉 = 〈Dc〉zq2, where q = 4π/nλ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(θ/2) is the scattering vector magnitude, with n being the refractive index of solvent. Hence, extrapolating 〈Γz〉 to zero q we obtain the diffusion coefficient. Assuming non-interacting particles (infinite dilution) Dc = D0, where D0 is the self-diffusion coefficient which is related to the hydrodynamic radius, 〈RH〉z〉, via the Stokes–Einstein relation 〈D0〉z = kBT/(6πη〈RH〉z〉), where KB = 1.3810−23 J K−1 is the Boltzmann constant, T is temperature and η is the solvent viscosity.
sin(θ/2) is the scattering vector magnitude, with n being the refractive index of solvent. Hence, extrapolating 〈Γz〉 to zero q we obtain the diffusion coefficient. Assuming non-interacting particles (infinite dilution) Dc = D0, where D0 is the self-diffusion coefficient which is related to the hydrodynamic radius, 〈RH〉z〉, via the Stokes–Einstein relation 〈D0〉z = kBT/(6πη〈RH〉z〉), where KB = 1.3810−23 J K−1 is the Boltzmann constant, T is temperature and η is the solvent viscosity.
Other DLS experiments and electrophoretic mobility measurements were performed on a Zetasizer Nano ZS instrument (Malvern Instruments, Ltd, Worcestershire, UK) at θ = 173° using laser light of λ = 632.8 nm wavelength. The electrophoretic mobility, UE provides information about the ζ-potential, which tells us about the surface charge of the colloidal particles, via Henry's equation:  where ε and ε0 are dielectric constant of the solvent and vacuum permittivity, respectively, and η is the solvent viscostiy. The ζ-potential was calculated assuming the Smoluchowski approximation, which gives f(kRh) = 1.5.
where ε and ε0 are dielectric constant of the solvent and vacuum permittivity, respectively, and η is the solvent viscostiy. The ζ-potential was calculated assuming the Smoluchowski approximation, which gives f(kRh) = 1.5.
2.6 Small-angle X-ray scattering
SAXS experiments were performed on a SAXS-lab Ganesha pinhole instrument JJ X-ray System APS (JJ X-ray, Hoersholm, Denmark) with an X-ray microsource (Xenocs, Sassenage, France) and a two-dimensional 300k Pilatus detector (Dectris Ltd, Baden-Daettwil, Switzerland). Two sample-to-detector distances were used and the X-ray wavelength, λ, was 1.54 Å. The two-dimensional scattering pattern was always isotropic (circularly symmetric) and was therefore radially averaged to obtain the one-dimensional scattering function, I(q), where q = 4π/λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2) is the magnitude of the scattering vector, θ being the scattering angle. Absolute scaling of the scattered intensity was performed by using water as a calibration standard. Scattering from the buffer measured in the same capillary as the sample was subtracted.
sin(θ/2) is the magnitude of the scattering vector, θ being the scattering angle. Absolute scaling of the scattered intensity was performed by using water as a calibration standard. Scattering from the buffer measured in the same capillary as the sample was subtracted.
2.7 Small-angle neutron scattering
SANS experiments were performed at NIST Center for Neutron Research in Maryland, USA. The instrument used was NG7 SANS. Four sample to-detector distances (1 m, 4 m, 13 m and 15.3 m with lenses), and a neutron wavelength of 6.0 Å (sample-to-detector distances of 1 m, 4 m and 13 m) and 8.1 Å (15.3 m with lenses) were used to obtain a q range spanning from 0.001 Å−1 to 0.5 Å−1. The wavelength spread is approximately 12%.52 The data were reduced to the absolute scale using the Igor Pro software by following the standard protocol at NCNR to correct the effect of the background, empty cell, detector efficiency, and the transmission of each sample.53 Samples were measured in 1 mm path length cylindrical quartz cells. Measurements were performed at T = 20 °C, 30 °C, 37 °C, 50 °C and 80 °C.2.8 Cryogenic transmission electron microscopy
Cryo-TEM experiments were performed using JEM-2200FS transmission electron microscope (JEOL) at the National Center for High Resolution Electron Microscopy (nCHREM) at Lund University. The Schottky field-emission electron source is operated at an acceleration voltage of 200 kV. The filters and slits used were an in-column energy (omega) filter and a 25 eV slits. The images were recorded via SerialEM software under low-dose conditions onto a bottom-mounted TemCam-F416 camera (TVIPS).Samples were prepared by depositing 4 μL droplets on carbon-coated Ted Pella grids, which were then blotted with filter papers. The grids were then plunged into liquid ethane at ca. −184 °C. The plunging was performed in an automatic plunge-freezer system (Leica EM GP) with the environmental chamber operated at 20.0 °C and 90% relative humidity. The grids were stored in liquid nitrogen at −196 °C before imaging.
3 Results and discussion
3.1 Adsorption of monomeric αSyn onto small unilamellar vesicles (SUVs)
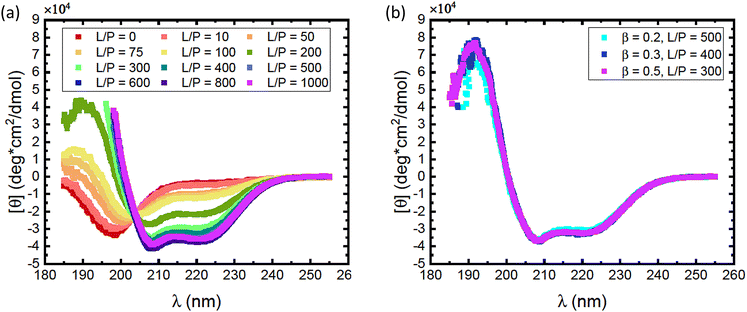
As αSyn undergoes a transition from a random coil to a large fraction of α-helical structure when it adsorbs to anionic lipid membranes,1,2 it is possible to follow the adsorption using CD spectroscopy.38 Here we have focused on the adsorption of αSyn to SUVs composed of a mixture of the zwitterionic lipid POPC and the anionic lipid POPS, at different fractions of the anionic lipid, β. The radii of vesicles at different β values varies between 25 nm and 27 nm. CD experiments were performed on solutions containing 5 μM αSyn and varying concentrations of lipids in 20 mM PB, pH = 7.0, at 25 °C. Results are shown in Fig. 1 where the lipid concentrations are presented as the lipid-to-protein molar ratio, L/P. In Fig. 1a we present CD spectra at different L/P for β = 0.3. For L/P = 0, we see the typical CD spectrum from proteins with a random coil conformation.54 With addition of lipid vesicles we observe the emergence of two minima at λ ≈ 208 nm and λ ≈ 222 nm, which are signatures of an α-helical conformation.54 At high L/P values, the CD spectrum no longer changes, indicating that adsorption is saturated and essentially all protein molecules have adsorbed onto vesicles with the maximum amount of α-helix of almost 100 residues. The L/P value above which saturation is observed we refer to as (L/P)sat. At β = 0.3, we estimate (L/P)sat = 400.It has been shown that αSyn adsorbs to negatively charged membranes with its net positively charged N-terminus which adopts an α-helical conformation, while the net negatively charged C-terminus remains disordered and protrudes into the bulk solution.1,30 The fraction of the molecule that adopts an α-helical conformation can vary.1,11,30,33,34 Typically this fraction is smaller at low L/P and involves a maximum of ≈100 residues at saturation.1,30 Thus, the CD spectrum at saturation is expected to represent a mixture of approximately 2/3 α-helix and 1/3 random coil. These saturation spectra were essentially identical for β = 0.2, 0.3 and 0.5, as shown in Fig. 1b. The noisy data at low wavelengths are caused by significant scattering from vesicles which are present in high concentrations at these L/P ratios.
Consistent with an earlier study,26 we note that the variation with L/P shows an isodichroic point at λ ≈ 203 nm, indicating the coexistence of two states that are populated to varying degree. In fact, the CD spectra at different L/P, here presented as the mean residue ellipticity, [θ], are well described by a linear combination of the random coil spectrum at L/P = 0, [θ]L/P=0, and the spectrum obtained at saturation, [θ]sat.55 This can be seen in Fig. 2a, where we compare data with linear combinations for a few selected L/P in the lipid system with β = 0.3. The linear combination was calculated as
| [θ] = (1 − f)[θ]L/P=0 + f[θ]sat | (1) |
 | ||
| Fig. 2 (a) CD spectra obtained for different L/P, for the case of vesicles with composition β = 0.3 at pH = 7.0. The protein concentration was cP = 5 μM. Solid black lines are best fits of linear combinations as described by eqn (1), from which values of the fraction f were obtained. (b) The fraction f plotted versus L/P for different lipids compositions β as indicated in the figure. The protein concentration was cP = 5 μM. The saturation points, i.e. the minimum L/P values for which f = 1 were evaluated. The saturation points estimated were (L/P)sat = 500 for β = 0.2, (L/P)sat = 400 for β = 0.3, and (L/P)sat = 300 for β = 0.5. (c) Estimated adsorbed amount Γ = 1/(L/P)sat plotted versus the fraction of anionic lipid, β. Data from the present work (pH = 7.0) are shown with black square symbols. For comparison we also plot similar data from ref. 23, obtained at pH = 5.5. Solid lines are merely guides to the eye. | ||
Saturation with respect to α-helical signal (f = 1) is concluded by no further changes in the CD spectra with increasing L/P ratio. Here we can identify an adsorbed amount as Γ = 1/(L/P)sat, where (L/P)sat is estimated from Fig. 2b as the L/P value where f reaches 1. For β = 0.2, we estimate Γ = 1/500, for β = 0.3 we estimate Γ = 1/400 and for β = 0.5 we estimate Γ = 1/300. By linear extrapolation we also estimate Γ = 1/1200 for β = 0.15, with reasonable accuracy. For β = 0.1 extrapolation becomes more uncertain, but if we assume a linear dependence, we obtain Γ = 1/1800. These Γ-values are plotted against β in Fig. 2c. The fact that an increased amount of POPS leads to an increase in Γ implies that the adsorption is, to a large extent, governed by an electrostatic attraction between the net positively charged N-terminal part of αSyn and the negatively charged membrane.24,25 Additionally, the observed increase in Γ with β appears to level off at higher β values.
With the goal of gaining further insight into how electrostatic interactions govern the adsorption process, it is useful to compare our findings with the recent work of Andersson et al.,23 who also investigated αSyn adsorption onto a lipid membrane system while varying the fraction of anionic lipids, but at a lower pH of 5.5. The lipid systems used in both studies are nearly identical, with a slight difference reflected in the fact that Andersson et al. used 1,2-dioleoyl-sn-glycero-3-phospho-L-serine (DOPS) as the anionic lipid. However, the difference between DOPS and POPS, used in the current study, is considered negligible. Furthermore, it has been shown that changes in headgroup chemistry do not affect αSyn binding to vesicles, provided that the charge of the headgroups remains unchanged.56 As a result, the response to changes in pH is expected to be similar in the two studies compared.
In Fig. 2c we have included how Γ = 1/(L/P)sat varies with β taken from the data presented in Fig. 2b of ref. 23. As can be seen, αSyn has a significantly stronger affinity for the PC/PS membrane at pH = 5.5 compared to at pH = 7.0. Furthermore, at pH = 5.5, Γ appears to level off to a plateau at Γ = Γmax = 0.005 for β ≥ 0.2.
A similar strong difference in adsorption between pH = 7.0 and pH = 5.5 has been reported for the case of POPC/POPS vesicles.26 Furthermore, Middleton and Rhoades studied the adsorption of αSyn onto POPC/POPS (β = 0.5) vesicles at pH = 5.0 and found saturation at an L/P as low as ≈40.27 We note also that our observed L/Psat at pH = 7.0 for β = 0.5 is very similar to that observed by Lokappa and Ulmer at pH = 7.4.28
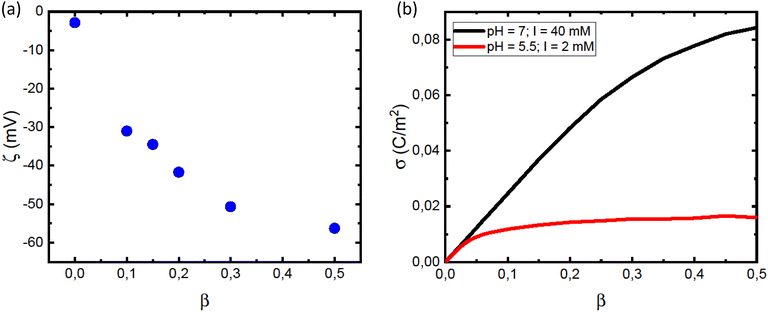
The leveling off of Γ at higher values of L/P could be due to a state of saturation being reached, where the vesicles are completely covered with protein and there is no room for more. Another possibility is that the net surface charge density, σ, varies linearly with β for low POPS fractions, but approaches a saturation at higher β-values. This is indeed indicated by the data in Fig. 3a where we have plotted the ζ potential as a function of β. The ζ-potential decreases to negative values when β increases. However, the slope decreases with increasing β. At pH = 7 we are well above the intrinsic pKa of the carboxylate group of the POPS headgroup.57 However, with increasing β the interface is becoming increasingly negatively charged, leading to an increase of the pKa, which is expected to significantly shift the acid–base equilibrium towards the acid state as also observed in highly charged proteins and protein aggregates.58,59 We illustrate this effect below by estimating how the surface charge density, σ, depends on β.
The pKa depends on the surface potential, ψs, according to ref. 60.
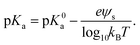 | (2) |
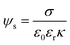 | (3) |
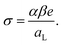 | (4) |
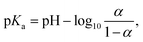 | (5) |
We conclude that αSyn adsorbs with higher surface coverage to the anionic vesicles at pH = 5.5 compared to pH = 7.0, even though the estimated membrane charge density appears to be significantly lower. There is clearly an attractive electrostatic component to the adsorption as this is promoted by anionic lipids, and there is likely also an attractive hydrophobic interaction.36 However, in addition, there is the unfavorable electrostatic repulsion between the disordered negatively charged C-termini that lowers the coverage. One should also keep in mind that there is a repulsive electrostatic component to the coverage as a result of the overall protein net charge, which is pH dependent. For αSyn, IP ≈ 4.7. The net charge of monmomeric αSyn at pH 5.5 is ≈−5 as calculated based on the reported pKa values of His50 and all acidic groups,62 while at pH = 7.0, the protein charge is close to −9.63,64 The higher surface coverage at pH = 5.5 we therefore ascribe to the lower negative charge of the protein that lowers the repulsive protein–protein interactions at the lipid membrane interface, as well as the repulsive electrostatic component of the protein–membrane interaction. Moreover, the net charge of the protein is reduced in fibrils due to a pKa value upshift of ca one unit upon assembly, an effect also expected upon surface adsorption of the protein on vesicles. We note that for pH = 5.5, σ essentially levels off to a plateau for β > 0.2 (Fig. 3b). This correlates well with the observed plateau in the adsorption, Γ, for β > 0.2 (Fig. 2c), and is consistent with the view that it is mainly the negative charges on the membrane that attract αSyn molecules.
It is also useful to consider the density of αSyn helices on the vesicle surfaces, and their possible packing. Several αSyn-binding modes have been reported.11,30,33,34 On lipid vesicle membranes, αSyn can adsorb with a short helix, involving approximately the first 25 residues, an intermediate helix, involving approximately 50 first residues34 or a long helix involving residues 1–97.11 On the other hand, upon binding to small SDS micelles, αSyn adopts a broken helical form with 2 almost equally long anti-parallel helical segments, involving residues 3–37 and 45–92, respectively, connected by a short linker.33 These different modes are schematically illustrated in Fig. 4. More recently it has been reported that αSyn for low L/P can also form long helix with only a part docking to the lipid membrane and the remaining part extending into the bulk.65 This can be seen as an alternative to the short α-helix, while at the same time the structure resembles the broken helix with only the N-terminal part in contact with the membrane.
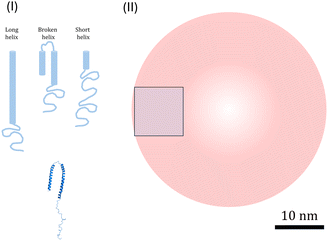 | ||
| Fig. 4 (I) Illustration of three possible modes of α-helices (light blue): long, broken and short, and the PDB structure of broken helix taken from ref. 33 (darker blue). (II) Illustration of R = 20 nm vesicles (red) and 100 nm2 square (blue) corresponding to an average membrane area occupied by one αSyn molecule at saturation for β = 0.5. The scale bar (10 nm) refer to all illustrations. | ||
CD spectra obtained at saturation are expected to represent the state of αSyn adsorbed via a long helix. The CD spectra at saturation for β = 0.2, 0.3 and 0.5, respectively, presented in Fig. 1b are strikingly similar. As can be seen, they are essentially identical and show a significant contribution from α-helical signal. A typical α-helix far UV CD spectrum shows a positive band at λ = 193 nm and two negative bands of similar amplitude at 208 nm and 222 nm, respectively, where the positive amplitude of the 193 nm band is approximately twice the negative amplitudes of the 208 nm and 222 nm bands.66,67 In terms of mean residue ellipticity, [θ]λ, the typical values for α-helix are [θ]helix(193 nm) ≈ 8 × 104 deg cm2 dmol−1 and [θ]helix(208 nm) ≈ [θ]helix(222 nm) ≈ −4 × 104 deg cm2 dmol−1. This is in fact close to what we actually observe in Fig. 1b, and we conclude from this that, at saturation, a major part of the adsorbed αSyn molecules must have adopted an α-helix conformation.
We can also consider the density of the αSyn molecules on the vesicle surface at the saturation. For the highest fraction of POPS investigated here, β = 0.5, we find Γ = 1/300 (see Fig. 2b). Since there are approximately the same number of lipids in the two monolayers, this means that there is one αSyn molecule adsorbed per 150 lipid molecules in the outer monolayer. With an area per lipid of aL = 0.65 nm2, this corresponds to one αSyn molecule per circa 100 nm2. To visualize this we show a 10 nm × 10 nm square in Fig. 4. A vesicle with R = 20 nm has a bilayer area of ca. 1300 nm2, hence we expect circa 13 adsorbed αSyn molecules per vesicle for β = 0.5 at saturation.
A typical α-helix has 3.6 residues per turn, with 0.54 nm rise per turn, and has a diameter of approximately 1.2 nm. The long 97 residue extended α-helix of αSyn is thus circa 15 nm long. We note first that this length is similar to the vesicle radius of ≈20 nm. In Fig. 4 we have also drawn a 20 nm radius vesicle on scale together with the different forms of α-helix-containing αSyn. The Figure also illustrates the average area occupied by a single αSyn molecule at saturation for β = 0.5. From these simple geometrical considerations, we can conclude that αSyn can adopt either of the possible helical states under the conditions investigated. In fact, Lokappa and Ulmer has suggested that αSyn populates both elongated and broken helix states on small unilamellar vesicles.28
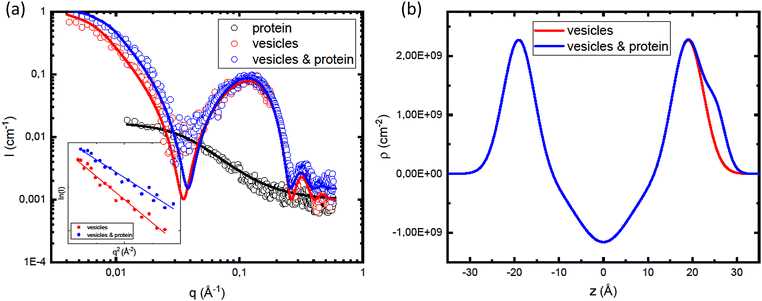
In order to gain further insight in the αSyn adsorption, we investigated how the presence of protein influences the vesicle structure utilizing SAXS.68 Due to the overall low lipid–water X-ray contrast, which results in relatively low scattered intensity at lower q-values, we used higher lipid concentrations compared to the CD experiments. In Fig. 5a, we compare SAXS data from vesicle samples in the presence and absence of αSyn. The lipid concentration was cL = 42 mM, with β = 0.3, and the protein concentration was cP = 0.14 mM, corresponding to L/P = 300. As the signature of the bilayer scattering, a broad peak at q ≈ 0.1 Å−1, is essentially the same in both cases, we can conclude that the protein adsorption does not affect the bilayer structure. However, there is an increase in forward scattering when the vesicles are coated with protein.
In Fig. 5a, we are also showing the scattering curve from a sample containing only protein monomers. A protein concentration of 0.14 mM is sufficiently low for protein–protein interactions to be neglected, and the scattered intensity, I(q), of protein monomers can be written as
| I(q) = I(0)Pm(q). | (6) |
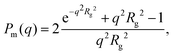 | (7) |
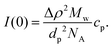 | (8) |
The bilayer contribution to the scattering profile of vesicles, both in the presence and absence of protein, was modeled using an approach proposed by Pabst et al.70 The model takes into account strong electron density variation across the z direction of the bilayer (Fig. 5b), which is responsible for the appearance of the broad peak in the scattering profiles at q ≈ 0.1 Å−1. The advantage of this model is that the electron density profiles are described with Gaussian distributions, taking into account the diffuse scattering of bilayer. Separating the contribution of all three lipid regions (inner and outter head group and hydrocarbon regions), the bilayer form factor can be written as
| F(q) = 2FHG + FT | (9) |
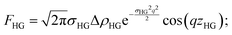 | (10) |
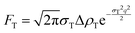 | (11) |
To include contribution of the scattering of vesicles as whole, we combined the bilayer form factor (eqn (9)) with the Guinier–Porod model.71 The Guinier–Porod model assumes that scattering profiles are composed of two regions: Guinier region where  and Porod region where
and Porod region where 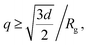 d being the Porod exponent. The Porod exponent describes the roughness of the surface of the scattering particles, and d = 2 for the 2-dimensional surface of the lipid vesicles. The scattering intensity in the Guinier (IG) and the Porod (IP) regions are given with the following expressions
d being the Porod exponent. The Porod exponent describes the roughness of the surface of the scattering particles, and d = 2 for the 2-dimensional surface of the lipid vesicles. The scattering intensity in the Guinier (IG) and the Porod (IP) regions are given with the following expressions
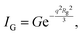 | (12) |
| IP = Dq−d | (13) |
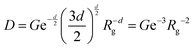 is the Porod scaling factor.
is the Porod scaling factor.
In Fig. 5b, we are showing the obtained electron density distribution. As expected, the head group region and αSyn have higher electron density compared to water, unlike the hydrocarbon region with electron density lower than that of water. The fitting parameters used in the models shown in the Fig. 5a are summarized in Table 1.
| Fitting parameters | Values |
|---|---|
| z HG | 19.0 Å |
| z P | 25.5 Å |
| σ HG | 3.5 Å |
| σ T | 6.2 Å |
| σ P | 2.1 Å |
| ΔρHG | 2.0 × 1010 cm−2 |
| ΔρT | −1.8 × 1010 cm−2 |
| ΔρP | 0.4 × 1010 cm−2 |
| R g vesicles alone | 20.0 nm |
| R g vesicles and protein | 16.0 nm |
In the inset in Fig. 5a we are showing the Guinier plots, id est ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I(q) vs. q2, from which we are able to estimate Rg and I(0) directly. As was obtained from the model fitting, αSyn adsorption leads to a decreases in Rg from 18 nm to 16. On the other hand, there is an increase of the forward scattering from 0.8 cm−1 to 1.0 cm−1 upon the addition of the protein.
I(q) vs. q2, from which we are able to estimate Rg and I(0) directly. As was obtained from the model fitting, αSyn adsorption leads to a decreases in Rg from 18 nm to 16. On the other hand, there is an increase of the forward scattering from 0.8 cm−1 to 1.0 cm−1 upon the addition of the protein.
For a particle system, the forward scattering intensity can be written as
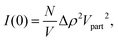 | (14) |
In the presence of protein, a fraction, Pb, of αSyn molecules adsorbs onto the vesicles. If this occurs at a constant number of vesicles, N/V, it changes the vesicle contribution to I(0) by a change in the average contrast, and by a small increase in Vpart. When the protein is in excess, Pb < 1, every vesicle is covered by the maximum adsorbed amount of αSyn molecules. Denoting the forward scattering ILP(0) we write
 | (15) |
| Δρav = (ϕLρL + PbϕPρP)/(ϕL + Pbϕp) − ρs. | (16) |
Assuming that for the corresponding solvent conditions and for β = 0.3 all protein molecules are adsorbed with a long helical segment at L/Psat = 400 (Fig. 2b), we obtain the fraction of residues in helical conformation in the current case (L/P = 300) to be Pb = 0.75. By simple geometrical analysis, we can estimate the maximum amount of the protein molecules that can be adsorbed onto vesicle. DLS measurements of vesicle suspensions yield the average vesicle radius of 24.6 nm, which allows for estimation of the average vesicle surface area of AV = 7.6 × 103 nm2. From the literature values for area per lipid HG of aL = 0.65 nm2, we can estimate the amount of lipid molecules per vesicle to be 2AV/aL = 2.3 × 104 (1.17 × 104 lipid molecules per outer layer). Knowing that 400 lipid molecules bind 1 αSyn molecule, we can estimate the maximum amount of αSyn molecules per vesicle adsorbed with a maximal helical segment to be nP = 58. Furthermore, considering the length of a lipid molecule to be lL = 2 nm,72 we can calculate the volume of a lipid molecule vL = aL × lL = 1.3 nm3 and the volume of a protein molecule can be calculated as vP = Mw/(dP × NA) = 17 nm3. The volume fractions can be calculated from molecular weight, mass concentration and mass density as ϕ = (Mwc)/d. Finally, assuming lipid mass density of 1 mg ml−1 gives SLD equal to ρL = 9.42 × 1010 cm−2. Inserting these values in eqn (14)–(16), we obtain the following values for the forward intensities: IL = 0.26 and ILP = 0.46. The ratio of these intensities of 1.5 is in a good agreement with the experimental ratio of 1.8 obtained for low-q data, as is the difference of ΔI = 0.2 cm−1.
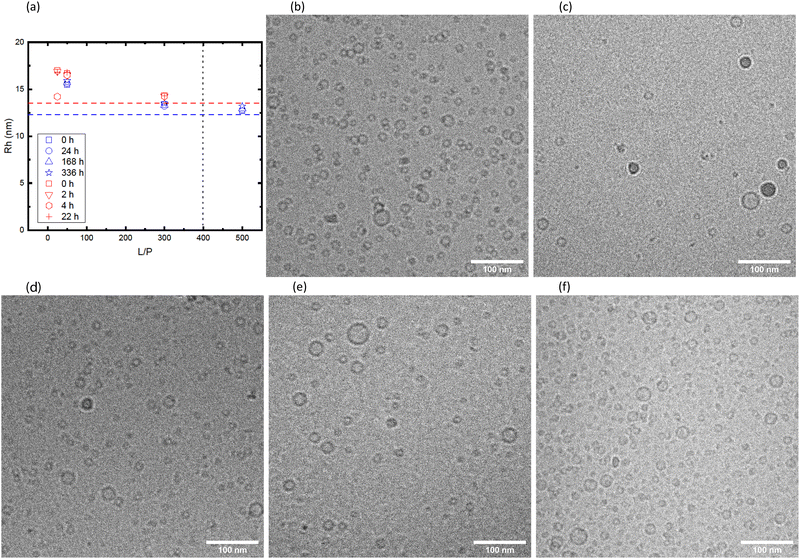
The vesicles with adsorbed αSyn are kinetically stable. This is seen from Fig. 6 where we have plotted the hydrodynamic radii obtained from DLS as function of time, for samples with different L/P and β = 0.3. The data shown in the figure are coming from two different sample preparation and were measured with two different instruments. The horizontal dashed lines are illustrating the size of vesicles without adsorbed αSyn for each of the cases, and the vertical line illustrates the saturation point for the given β. We can see from the Fig. 6a that there is essentially no variation with time during the 14 days timescale. It can also be observed that the apparent size of vesicles is biggest at intermediate L/P. As has been proposed earlier,1,30 at L/P lower than L/Psat, αSyn adsorbs only with a small segment (ca. 20 amino acids) and the rest of the protein is extending from the vesicle surface as a random coil, leading to increase in the vesicles' hydrodynamic radius. The increase of ≈3 nm at intermediate L/P is in good agreement with what is expected for ca. 120-amino-acid-long protein (the radius of gyration for the whole protein is estimated to be 4 nm as shown in Fig. 5a), and the increase of 1 nm around the saturation point can be explained by 40 amino acid residues at the C-terminus that extend as the random coil. It is also important to note that fibril formation did not occur under these conditions, as demonstrated in Fig. S1 (ESI†), where we are showing CD spectra obtained at different time points.
The samples shown in red in Fig. 6a were also imaged with cryo-TEM (rest of Fig. 6). The samples were vitrified ≈15 min after sample preparation. The observed size distributions are consistent with the DLS results. We also note that the vesicle shapes remain spherical after adsorption of αSyn. Significant deformations in the shape of vesicles after adsorption of αSyn have recently been observed with small unilamellar vesicles composed of DOPC/DOPS.19 The vesicles in the present system are in fact very small which might explain their stronger resistance to deformation.
4 Fibril formation induces vesicle fusion
Having established that vesicles are kinetically stable also with adsorbed αSyn monomers, we now turn to the fate of the lipid vesicles after the formation of αSyn fibrils has occured in their presence. We have recently shown, using small angle X-ray scattering (SAXS), that POPC/POPS vesicles in the presence of αSyn retained locally their bilayer membrane structure also after the protein has formed fibrils.3 However the SAXS pattern was at lower q-values dominated by fibril scattering and it was not possible to investigate any potential membrane remodelling. Here, we have therefore turned to neutron scattering and contrast variation, SANS. SANS experiments were performed using deuterated αSyn and protonated lipids in D2O buffer. The deuterated αSyn is almost completely contrast matched to the solvent, with a negligible contribution to the scattering pattern.The vesicle dispersion was tip-sonicated to produce small unilamellar vesicles, yielding a z-averaged mean radius of 〈R〉z = 24.8 ± 0.3 nm, as measured by DLS. The fibril formation of 280 μM monomeric αSyn in the presence of vesicles (cL = 2.1 mM, β = 0.3) was initiated by adding 14 μM fibril seeds. The samples were then incubated for 14 days at 37 °C in a pH 7.0 buffer.
Fig. 7a compares the scattering profiles of the pure vesicle dispersion and vesicles in the presence of α-Syn fibrils. As can be seen, the two scattering patterns essentially overlap for q > 0.01 Å−1. However, they deviate in the low q regime. Here, the scattering intensity is significantly higher in the sample with fibrils, demonstrating that the vesicles are larger after fibril formation had taken place in their presence. The data were fitted using the same model that was used to analyze the SAXS data (eqn (9)–(13)). The neutron scattering densities used in the model73 are presented in Table 2. The best fits are shown as solid lines. For the vesicles alone, we obtain an average radius of 22 nm, while in the sample fibrils the average radius had increased to twice the size, approximately 44 nm.
| Fitting parameters | Values |
|---|---|
| z HG | 19.0 Å |
| σ HG | 3.5 Å |
| σ T | 6.2 Å |
| ΔρHG | 3.9 × 1010 cm−2 |
| ΔρT | −6.8 × 1010 cm−2 |
| R g vesicles alone | 22.0 nm |
| R g vesicles and protein | 44.0 nm |
The twofold increase in vesicle size was confirmed by cryo-TEM. A representative image is shown in Fig. 7b, where we observe that αSyn fibrils coexist with lipid vesicles with radii in the range 20–40 nm. The representative image of a pure vesicle dispersion is shown in ESI† (Fig. S3g). From the histogram constructed by analysis of 388 vesicles in the presence of fibrils at pH = 7.0, shown in Fig. 7c, we find average size of vesicle radius to be ≈23 nm, while that of vesicles without adsorbed protein is ≈11 nm (see ESI†). Since we have shown that the initial small vesicles are kinetically stable over time (Fig. 6), the results indicate that a small finite number of fusion events have occurred during the process of fibril formation. The two-fold increase observed by SANS and cryo-TEM in the radius corresponds to a four-fold increase of the bilayer area per vesicle, and hence three fusion events occurred during fibril formation.
The same SANS and cryo-TEM experiments were repeated at three different pH values, pH = 6.0, 6.5 and 7.4, respectively, with essentially identical results. The results from these experiments are presented in ESI,† Fig. S2 and S3. In Fig. S2 (ESI†), the SANS patterns are also compared with a calculated scattering pattern from deuterated αSyn fibrils, confirming that the deuterated αSyn fibrils do not contribute significantly to the SANS patterns.
5 Conclusions
We have investigated the interactions of αSyn with POPC/POPS small unilamellar lipid vesicles at pH = 7.0. As has been reported frequently in the literature,23–28 αSyn monomers readily adsorb onto anionic lipid vesicles, and this was also observed here. The adsorbed amount increased with increasing fraction of the negatively charged POPS in the membrane, but with a tendency to level off at highest POPS fraction investigated.A comparison with similar studies23,27 conducted at lower pH values (5.5 and 5.0) offers new insights into the electrostatic interactions between αSyn and lipid vesicles, clarifying the mechanisms that govern the adsorption process. This further extends our understanding of how factors such as vesicle charge, pH, and ionic strength influence protein adsorption. We show that the saturation point is pH dependent, as demonstrated in Fig. 3b, where we show that σ saturates for lower β values at pH = 5.5 compared to pH = 7.0. This correlates with the up-shift of the carboxyl group pKa value with increasing charge density of the membrane, resulting in that the membrane charge density approaches a plateau at higher POPS fractions. Additionally, the adsorbed amount is shown to be strongly pH dependent, decreasing with increasing pH, even though the membrane charge density increases with increasing pH. We ascribe this to the increased protonation of the proteins acidic residues. Lowering the pH from 7.0 to 5.0 makes the N-terminus increasingly positively charged, thus increasing its electrostatic attraction to negatively charged surfaces. Furthermore, it makes the C-terminus less negatively charged decreasing the lateral protein–protein repulsion in the adsorbed state.
Moreover, we show that small POPC/POPS vesicles, with size similar to those of synaptic vesicles, are found to be kinetically stable over the course of 14 days, both with and without adsorbed monomeric αSyn. However, when fibril formation, here induced by the addition of small amounts of preformed fibril seed, occurs in their presence, the vesicle size increases by approximately a factor of two. While it remains unclear exactly when this thermodynamic drive for fusion arises, it is certain that a small number of fusion events occurred during fibril formation.
Author contributions
MD, ES, SL and UO designed research; MD performed SANS experiments with help of VL and YL; MH and JMD produced the deuterated protein; MD analysed data; MD wrote the paper with input from all other co-authors.Data availability
Data for this article are now available at https://docs.google.com/spreadsheets/d/19nbgLK_HnAgfCpWh-8iA49P1qGpIqj_N/edit?usp=drive_link&ouid=109662728783235682590rtpof=truesd=true.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Swedish Foundation for Strategic Research through the national Graduate School SwedNessESS (GSn15-0008), the Swedish Research Council VR (SL 2015-00143) and the Knut and Alice Wallenberg Foundation grant (ES, SL, UO 2016.0074). We would like to acknowledge the work of Anna Carnerup and Crispin Hetherington who performed cryo-TEM experiments, and Katja Bernfur for the help with mass spectrometry. Certain commercial equipment, instruments, or software are identified in this paper to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.References
- G. Fusco, A. D. Simone, T. Gopinath, V. Vostrikov, M. Vendruscolo, C. M. Dobson and G. Veglia, Nat. Commun., 2014, 5, 3827 CrossRef CAS PubMed
.
- E. Hellstrand, M. Grey, M. L. Ainalem, J. Ankner, V. T. Forsyth, G. Fragneto, M. Haertlein, M. T. Dauvergne, H. Nilsson, P. Brundin, S. Linse, T. Nylander and E. Sparr, ACS Chem. Neurosci., 2013, 4, 1339–1351 CrossRef CAS PubMed
.
- M. Dubackic, S. Linse, E. Sparr and U. Olsson, Front. Soft. Matter, 2022, 1, 741996 CrossRef
.
- Y. Li, C. Zhao, F. Luo, Z. Liu, X. Gui, Z. Luo, X. Zhang, D. Li, C. Liu and X. Li, Cell Res., 2018, 28, 897–903 CrossRef CAS
.
- M. H. Polymeropoulos, C. Lavedan, E. Leroy, S. E. Ide, A. Dehejia, A. Dutra, B. Pike, H. Root, J. Rubenstein, R. Boyer, E. S. Stenroos, S. Chandrasekharappa, A. Athanassiadou, T. Papapetropoulos, W. G. Johnson, A. M. Lazzarini, R. C. Duvoisin, G. D. Iorio, L. I. Golbe and R. L. Nussbaum, Science, 1997, 276, 2045–2047 CrossRef CAS PubMed
.
- M. G. Spillantini, M. L. Schmidt, V. M. Y. Lee, J. Q. Trojanowski, R. Jakes and M. Goedert, Nature, 1997, 388, 839–840 CrossRef CAS
.
- M. G. Spillantini, M. L. Schmidt, V. M. Y. Lee, J. Q. Trojanowski, R. Jakes and M. Goedert, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 6469–6473 CrossRef CAS PubMed
.
- F. N. Emamzadeh, J. Res. Med. Sci., 2016, 21, 29 CrossRef PubMed
.
- Y. Zarbiv, D. Simhi-Haham, E. Israeli, S. A. Elhadi, J. Grigoletto and R. Sharon, Neurobiol. Dis., 2015, 70, 90–98 CrossRef
.
- K. Ueda, H. Fukushima, E. Masliah, Y. Xia, A. Iwai, M. Yoshimoto, D. A. Otero, J. Kondo, Y. Ihara and T. Saitoh, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 11282–11286 CrossRef CAS
.
- C. R. Bodner, C. M. Dobson and A. Bax, J. Mol. Biol., 2009, 390, 775–790 CrossRef CAS
.
- J. Burre, J. Parkinson's. Dis., 2015, 5, 699–713 CAS
.
- M. Huang, B. Wang, X. Li, C. Fu, C. Wang and X. Kang, Front. Neurosci., 2019, 13, 28 Search PubMed
.
- J. Varkey, J. M. Isas, N. Mizuno, M. B. Jensen, V. K. Bhatia, C. C. Jao, J. Petrlova, J. C. Voss, D. G. Stamou, A. C. Steven and R. Langen, J. Biol. Chem., 2010, 285, 32486–32493 CrossRef CAS
.
- A. Adamczyk, M. Kacprzak and A. Kazmierczak, Folia Neuropathol., 2007, 45, 230–235 CAS
.
- J. Madine, A. J. Doig and A. D. Middleton, Biochemistry, 2006, 45, 5783–5792 CrossRef CAS PubMed
.
- R. Khounlo, B. J. D. Hawk, T.-M. Khu, G. Yoo, N. K. Lee, J. Pierson and Y.-K. Shin, Front. Cell Dev. Biol., 2021, 9, 663431 CrossRef PubMed
.
- R. K. Nellikkaa, B. R. Bhaskara, K. Sanghrajkaa, S. S. Patila and D. Das, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2021742118 CrossRef
.
- K. Makasewicz, S. Wennmalm, S. Linse and E. Sparr, QRB Discovery, 2022, e10, 1–9 Search PubMed
.
- S. Fanning, D. Selkoe and U. Dettmer, npj Parkinson’s Dis., 2020, 6, 3 CrossRef CAS
.
- H. A. Lashuel, Neurobiol. Dis., 2020, 141, 104876 CrossRef CAS PubMed
.
- K. Makasewicz, S. Wennmalm, B. Stenqvist, M. Fornasier, A. Andersson, P. Jönsson, S. Linse and E. Sparr, ACS Chem. Neurosci., 2021, 12, 2099–2109 CrossRef CAS PubMed
.
- A. Andersson, S. Linse, E. Sparr, M. Fornasier and P. Jonsson, Biophys. Chem., 2024, 305, 107143 CrossRef CAS
.
- M. Stockl, P. Fischer, E. Wanker and A. Herrmann, J. Mol. Biol., 2008, 375, 1394–1404 CrossRef
.
- V. V. Shvadchak, L. J. Falomir-Lockhart, D. A. Yushchenko and T. M. Jovin, J. Biol. Chem., 2008, 286, 13023–13032 CrossRef
.
- Z. Jiang, S. K. Hess, F. Heinrich and J. C. Lee, J. Phys. Chem. B, 2015, 119, 4812–4823 CrossRef CAS
.
- E. R. Middleton and E. Rhoades, Biophys. J., 2010, 99, 2279–2288 CrossRef CAS
.
- S. B. Lokappa and T. S. Ulmer, J. Biol. Chem., 2011, 286, 21450–21457 CrossRef CAS PubMed
.
- C. Pfefferkorn, F. Heinrich, A. J. Sodt, A. Maltsev, R. Pastor and J. Lee, Biophys. J., 2012, 102, 613–621 CrossRef CAS
.
- C. C. Jao, A. Der-Sarkissian, J. Chen and R. Langen, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 8331–8336 CrossRef CAS PubMed
.
- B. Nuscher, F. Kamp, T. Mehnert, S. Odoy, C. Haass, P. J. Kahle and K. Beyer, JBC, 2004, 279, 21966–21975 CrossRef CAS PubMed
.
- F. Kamp and K. Beyer, JBC, 2006, 281, 9251–9259 CrossRef CAS
.
- T. S. Ulmer, A. Bax, N. B. Cole and R. L. Nussbaum, J. Biol. Chem., 2005, 280, 9595–9603 CrossRef CAS
.
- K. Makasewicz, G. Carlström, O. Stenström, K. Bernfur, S. Fridolf, M. Akke, S. Linse and E. Sparr, Cell Rep. Phys. Sci., 2024, 102309 CrossRef
.
- E. Jo, J. McLaurin, C. M. Yipi, P. S. George-Hyslop and P. E. Fraser, J. Biol. Chem., 2000, 275, 34328–34334 CrossRef CAS
.
- E. Rhoades, T. F. Ramlall, W. W. Webb and D. Eliezer, Biophys. J., 2006, 90, 4692–4700 CrossRef CAS PubMed
.
- C. Galvagnion, A. K. Buell, G. Meisl, T. C. T. Michaels, M. Vendruscolo, T. P. J. Knowles and C. M. Dobson, Nat. Chem. Biol., 2015, 11, 229–234 CrossRef CAS PubMed
.
- C. Galvagnion, J. Parkinson's Dis., 2017, 7, 433–450 CAS
.
- M. Grey, C. J. Dunning, R. Gaspar, C. Grey, P. B. E. Sparr and S. Linse, J. Biol. Chem., 2015, 11, 2969–2982 CrossRef
.
- R. Gaspar, J. Pallbo, U. Weininger, S. Linse and E. Sparr, Biochim. Biophys. Acta, Proteins Proteomics, 2019, 1866, 1062–1072 CrossRef PubMed
.
- E. Hellstrand, A. Nowacka, D. Topgaard, S. Linse and E. Sparr, PLoS One, 2013, 8, e77235 CrossRef CAS
.
- A. van Maarschalkerweerd, V. Vetri, A. E. Langkilde, V. Fodera and B. Vestergaard, Biomacromolecules, 2014, 15, 3643–3654 CrossRef CAS PubMed
.
- N. P. Reynolds, A. Soragni, M. Rabe, D. Verdes, E. Liverani, S. Handschin, R. Riek and S. Seeger, J. Am. Chem. Soc., 2011, 133, 19366–19375 CrossRef CAS PubMed
.
- C. Galvagnion, D. Topgaard, K. Makasewicz, A. K. Buell, S. Linse, E. Sparr and C. M. Dobson, J. Phys. Chem. Lett., 2019, 10, 7872–7877 CrossRef CAS PubMed
.
- R. Gaspar, I. Idini, G. Carlström, S. Linse and E. Sparr, Front. Cell Dev. Biol., 2021, 9, 266 CrossRef PubMed
.
- Z. Shi, J. N. Sachs, E. Rhoades and T. Baumgart, Phys. Chem. Chem. Phys., 2015, 17, 15561–15568 RSC
.
- A. West, B. E. Brummel, A. R. Braun, E. Rhoades and J. N. Sachs, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 1594–1609 CrossRef CAS
.
- T. Schikorski and C. F. Stevens, J. Neurosci., 1997, 17, 5858–5867 CrossRef CAS PubMed
.
- M. Grey, S. Linse, H. Nilsson, P. Brundin and E. Sparr, J. Parkinsons Dis., 2011, 1, 359–371 CrossRef CAS PubMed
.
- M. Haertlein, M. Moulin, J. Devos, V. Laux, O. Dunne and V. Forsyth, Methods Enzymol., 2016, 566, 113–157 CAS
.
- D. E. Koppel, J. Chem. Phys., 1972, 57, 4814–4820 CrossRef CAS
.
- C. J. Glinka, J. G. Barker, B. Hammouda, S. Krueger, J. J. Moyert and W. J. Orts, J. Appl. Crystallogr., 1998, 31, 430–445 CrossRef CAS
.
- S. R. Kline, J. Appl. Crystallogr., 2006, 39, 895–900 CrossRef CAS
.
-
T. Engel, G. Drobny and P. Reid, Physical Chemistry for the Life Sciences, Pearson Education, Upper Saddle River NJ, 2008 Search PubMed
.
-
M. Dubackic, PhD thesis, Lund University, Lund, Sweden, 2021
.
- R. Gaspar, J. Pallbo, U. Weininger, S. Linse and E. Sparr, Biochim. Biophys. Acta, Proteins Proteomics, 2018, 1866, 1062–1072 CrossRef CAS PubMed
.
- F. C. Tsui, D. M. Ojcius and W. L. Hubbell, Biophys. J., 1986, 49, 459–468 CrossRef CAS PubMed
.
- T. Kesvatera, B. Jönsson, E. Thulin and S. Linse, Proteins, 2001, 45, 129–135 CrossRef CAS
.
- T. Pálmadóttir, A. Malmendal, T. Leiding, M. Lund and S. Linse, J. Am. Chem. Soc., 2021, 143, 7777–7791 CrossRef
.
-
D. F. Evans and H. Wennerström, The Colloidal Domain: Where Physics, Chemistry, Biology, and Technology Meet, Wiley, 2nd edn, 1999 Search PubMed
.
- N. Kucerka, M.-P. Nieh and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2761–2771 CrossRef CAS PubMed
.
- R. L. Croke, S. M. Patil, J. Quevreaux, D. A. Kendall and A. T. Alexandrescu, Protein Sci., 2011, 20, 256–269 CrossRef CAS
.
- B. Pogostin, S. Linse and U. Olsson, Langmuir, 2019, 35, 16536–16544 CrossRef CAS PubMed
.
- A. K. Buell, C. Galvagnion, R. Gaspar, E. Sparr, M. Vendruscolo, T. P. J. Knowles, S. Linse and C. M. Dobson, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 7671–7676 CrossRef CAS PubMed
.
- S. J. Roeters, K. Strunge, K. B. Pedersen, T. W. Golbek, M. Bregnhoj, Y. Zhang, Y. Wang, M. Dong, J. Nielsen, D. E. Otzen, B. Schiott and T. Weidner, Nat. Commun., 2023, 14, 5731 CrossRef CAS PubMed
.
- N. Sreerama and R. W. Woody, Methods Enzymol., 2004, 383, 318–351 CAS
.
- N. J. Greenfield and G. D. Fasman, Biochemistry, 1969, 8, 4108–4116 CrossRef CAS
.
- J. E. Nielsen, V. R. Koynarev and R. Lund, COCIS, 2023, 66, 101709 CAS
.
- P. Debye, J. Phys. Colloid Chem., 1947, 51, 18–32 CrossRef CAS
.
- G. Pabst, M. Rappolt, H. Amenitsch and P. Laggner, Phys. Rev. E, 2000, 62, 4000–4009 CrossRef CAS
.
- B. Hammouda, J. Appl. Crystallogr., 2010, 43, 716–719 CrossRef CAS
.
- P. Jurkiewicz, L. Cwiklik, A. Vojtiskova, P. Jungwirth and M. Hof, Biochim. Biophys. Acta, 2012, 1818, 609–616 CrossRef CAS
.
- W. T. Heller, Biomolecules, 2022, 12, 1591 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01036a |
| This journal is © The Royal Society of Chemistry 2025 |