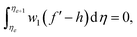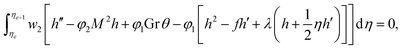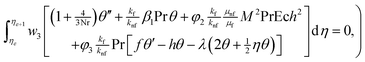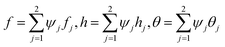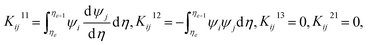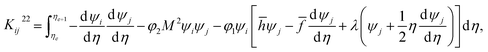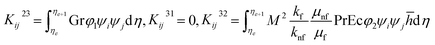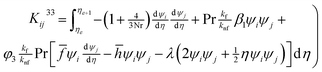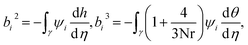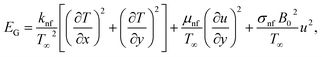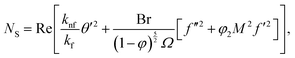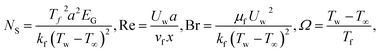DOI:
10.1039/C8RA03825B
(Paper)
RSC Adv., 2018,
8, 38324-38335
Computational fluid dynamic simulations for dispersion of nanoparticles in a magnetohydrodynamic liquid: a Galerkin finite element method
Received
4th May 2018
, Accepted 6th November 2018
First published on 14th November 2018
Abstract
This investigation studies the effects of the thermo-physical properties of four types of nano-metallic particles on the thermo-physical properties of radiative fluid in the presence of buoyant forces and Joule heating (ohmic dissipation). The Galerkin finite element algorithm is used to perform computations and simulated results are displayed in order to analyze the behavior of velocity and temperature of copper, silver, titanium dioxide and aluminum oxide-nanofluids. All the simulations are performed with ηmax = 6 computational tolerance 10−6 for 200 elemental discretizations. Due to the dispersion of nano-sized particles in the base fluid, an increase in the thermal conduction is noticed. This study also predicts future improvements in the thermal systems. Due to magnetic field and fluid flow interaction, the electrical energy converts into heat. This is undesirable in many thermal systems. Therefore, control of Joule heating in the design of thermos systems is necessary. However, this dissipation of heat may be desirable in some biological fluid flows. An increase in energy losses is noted as magnetic intensity is increased.
1 Introduction
Technologists and engineers have a major concern in enhancing the efficiency of thermal systems like hydronic heating and cooling in buildings, heating and cooling processes of transportation in the petro-chemical industry, pulp and textile manufacturing etc.1 Several methods to enhance the efficiency of thermal systems have been used for this purpose. These methods include active methods and passive methods.2 As mentioned in ref. 2, active methods include external agents like a mechanical input or magnetic field etc. whereas passive methods include treated surfaces, insert extended surfaces, boiling, condensation, twisted tape, wire coils2 etc. Combinations of active and passive methods are called compound methods. Although, the above mentioned methods are very effective and have been used for the enhancement of heat transfer, recent advancements in technology have opened the doors to new techniques and methods. One of these methods is the dispersion of nano-metallic particles in pure liquid. This inclusion of particles increases the thermal conductivity of the resulting mixture. Consequently, rate of heat transfer is enhanced. Several theoretical studies on this technique are published. For example Masuda et al.3 confirmed that the dispersion of ultrafine particles in the base fluid increases its ability to conduct more heat as compared to the pure fluid. Although this work reconfirms the enhancement in the process of transfer of heat due to inclusion of nanoparticles in liquids, this analysis is carried out in a limiting sense i.e. Joule heating, thermal radiation, buoyancy effects and heat generation are not considered. The work by Buongiorno4 introduced some empirical models for the thermophysical properties of nanofluids and formulated the mathematical relationships between the physical properties of solid particles, pure fluid and mixtures of pure fluid and nano-particles create a potential for theoretical studies on transport of heat by liquid as a coolant containing metal particles of very small size, but this work does not consider Joule heating and buoyancy effects. Transfer of heat in nanofluids over a stretching surface was studied by Khan and Pop.5 They investigated thermophoretic and Brownian motion in the flow of nanofluids. However, this work does not consider the heating generation and Joule heating effects simultaneously. Nadeem et al.6 analyzed the effects of Brownian motion and thermophoresis in the flow of Maxwell fluid. In fact this work does not consider the inclusion of nano-particles rather than thermophoresis and Brownian motion. Das et al.7 numerically investigated the effects of different types of nano-particles on the entropy generation of MHD flow over convective by heat surface boundary conditions. Although this work considers more than one effect simultaneously but it does not consider Joule heating, thermal radiation, buoyancy and heat generation effects simultaneously. The effect of space dependent magnetic field on free convection flow of Fe3O4–water nanofluid was studied by Sheikholeslami and Rashidi.8 It is important to mention that dispersion of Fe3O4 nano-particles in the water is considered i.e. Cu, Ag, Al2O3 and TiO2 are not considered. In another study, Rashidi et al.9 investigated the behavior of nano-particles on the thermal conductivity of the base fluid through Lie group approach but heat generation, Joule heating and buoyancy force are not taken into account. Nadeem and Saleem10 studied mixed convection flow of nanofluid over a rotating cone in the presence of magnetic fluid. Nawaz and Hayat11 studied heat transfer characteristics in an axisymmetric flow of nanofluid over a radially stretching surface. Nawaz and Zubair12 analyzed the effects of different types of nano-particles in the flow of blood over a surface moving with space dependent velocity. This work considers only two types of nano-particles (Cu and Ag). Other than this, convective type boundary condition and the entropy generation are not considered in this study.12 Ahmed et al.13 studied the effects of the shape of nanoparticles on mixed convection flow over a disk rotating with time dependent angular velocity. However, this work does not consider Joule heating, heat generation and buoyancy effects simultaneously. These effects will be considered in the present work.
There are various models (empirical formulae) which describe correlations between viscosities of the base fluid and metallic nano-particles and effective viscosities of nanofluids. These models include Einstein model,14 Brinkman model,15 Batchelor model,16 Graham model,17 model adopted by Wang et al.,18 model of Masoumi et al.19 Einstein model is valid for very low volume fraction (volume fraction < 0.002) and does not consider Brownian motion of nano-particles. Brinkman model is the modified form of the Einstein model and valid for average volume fraction whereas Batchelor model is the modification of Einstein model and considers Brownian motion of nano-particles.20 The model used by Wang et al.18 expresses the effective viscosity as a quadratic function of volume fraction. The model used by Masoumi et al.19 involves Brownian motion effects. It is also important to note that the models discussed in ref. 14–19 give correlations of effective viscosities. Studies on nanofluid show that dispersion of nano-particles impact thermal conductivity. Therefore, different correlations for effective thermal conductivity proposed. Detailed review on analytical models of effective thermal conductivity is given in ref. 20. It is noted that studies14–20 do not consider model of effective electrical conductivity of nano-fluid. As the present work considers magnetohydrodynamic flow of nanofluid and model for effective electrical conductivity is unavoidable. The correlations for effective electrical conductivity, effective thermal conductivity and effective viscosity are used by Das et al.7 The model used by Das et al.7 had dual characteristics of effective thermal viscosity and effective thermal conductivity as well as analytical model for effective electrical conductivity. This model is given by
| |
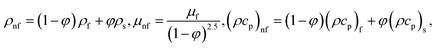 | (1) |
| |
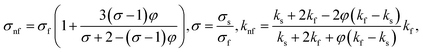 | (2) |
where
ρ,
k,
σ,
φ and
cp, respectively, are density, thermal conductivity, electrical conductivity, volume fraction and specific heat. The subscripts f, nf and s stands for fluid, nanofluid and solid particles (nano-particles) respectively.
Minimization of the entropy generation in the thermal system is a major concern as wastage of energy causes a great disorder. Therefore, the control of the entropy generation during the heat transfer has been investigated extensively in the last few years. Bejan21 was first to work on the minimization of the entropy generation. After his work on the entropy generation, several studies have been published. But, here some recent investigations are described. For instance, Bhatti et al.22 investigated the effects of magnetic field on the entropy generation of nonlinear transport of heat and mass in the boundary layer flow. Numerical investigation of the entropy generation during the heat transfer in the cavity flow was carried out by Armaghani et al.23 Vincenzo et al.24 analyzed the effects of the entropy generation due to temperature difference and viscous losses/friction loses in the flow.
The aim of this work is three fold. First, to study heat transfer enhancement in nanofluids in the presence of applied magnetic field, buoyancy force, thermal radiation and heat generation/absorption using correlation of effective electrical conductivity together with the correlations of effective thermal conductivity and effective viscosity based volume fraction and second is to investigate the effects of dispersion of nano-particles on entropy generation whereas third one is to implement finite element method to two-dimensional hydrothermal flow in the presence of buoyancy force and electromagnetic radiation.
2 Problem description
2.1 Physical situation
We consider the enhancement of heat transfer in water through four types of nano-particles (Cu, Ag, Al2O3 and TiO2) in an incompressible flow of an electrically conducting fluid over a vertical stretching sheet with space and time dependent velocity Uw(x,t) = ax/(1 − ct). A constant magnetic field [0,B0,0] is applied along y-axis normal to the sheet. The variation of the temperature of sheet is due to the variation of hot fluid occupying half space y < 0. The temperature of hot fluid below the sheet is varying as Tw(x,t) = T∞ + ax/(1 − ct)2 where T∞ is the ambient temperature, a and c are constants. There is no applied electric field and the effects of polarization and induced magnetic field are negligible. Thermo-physical properties (viscosity, density, thermal conductivity, specific heat etc.) are constant. The transport of heat nanofluid (occupying half space y > 0) is due to convection from the hot fluid (occupying half space y < 0) of temperature Tw(x,t) = T∞ + ax/(1 − ct)2. The buoyant force under Boussinesq approximation is significant.
2.2 Governing boundary layer equations
Applying boundary layer approximation to full two-dimensional conservation laws, one obtains the following boundary layer equations| |
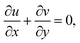 | (3) |
| |
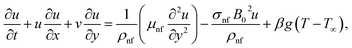 | (4) |
| |
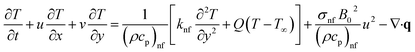 | (5) |
where (u, v) are the velocity component, β is the volumetric expansion coefficient, Q = Q0(1 − ct)−1 is the heat generation/absorption coefficient, T is the temperature of the fluid and q is the radiative heat flux vector which is defined by Stefan–Boltzmann law q = −(4σ*/3k*)∇(T4 − T∞4), where σ*is the Stefan–Boltzmann constant and k* is the mean absorption coefficient.
The associated conditions are
| |
u = v = 0,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T = T∞, ∀ x, y, t < 0 T = T∞, ∀ x, y, t < 0
| (6) |
| |
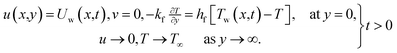 | (7) |
2.3 Dimensional analysis
In view of the importance of the results obtained from the dimensionless form of conservation equations, the following transformations are introduced| |
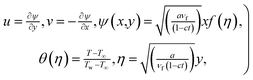 | (8) |
where ψ(x,y) is the stream function, f(η) and θ(η) is the dimensionless form of stream function and temperature, η is independent similarity variable.
The continuity eqn (3) is identically satisfied and eqn (4) and (5) and conditions are reduced to
| |
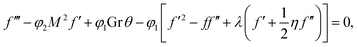 | (9) |
| | |
f(0) = 0, f′(0) = 1, f′ → 0,
| (10) |
| |
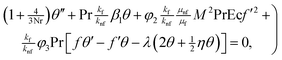 | (11) |
| | |
θ′(0) = −Bi(1 − θ(0)), θ → 0 as η →∞,
| (12) |
where
| |
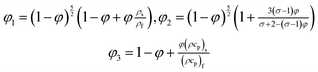 | (13) |
and
| |
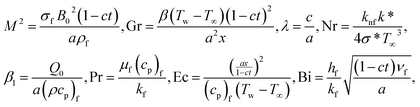 | (14) |
are, respectively, the Hartmann number, the Grashof number, the unsteadiness parameter, the radiation parameter, heat generation/absorption parameter, the Prandtl number, the Eckert number and the Biot number. The prescribed wall temperature case can be recovered as Bi → ∞. Also note that
φ = 0 is the case when fluid is pure and nano-particles are not dispersed, [the case of Butt and Ali
25 and for Gr = 0,
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
Nr = 0 and Ec = 0, the problem reduces to the case of Das
et al.7 with heat generation/absorption. The case of
M2 = 0,
λ = 0,
φ = 0 and Bi → ∞ is also considered by Abolbashari
et al.26 and Das
et al.7. The numerical values of thermo-physical properties used in this study are (
Table 1).
Table 1 Thermo-physical properties of water and nanoparticles7
| Physical property |
Base fluid |
Cu |
Ag |
Al2O3 |
TiO2 |
| ρ/(kg m−3) |
997.1 |
8933 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
3970 |
4250 |
| cp/(J kg−1 K−1) |
4179 |
385 |
235 |
765 |
686.2 |
| k/(W m−1 K−1) |
0.13 |
401 |
429 |
40 |
8.9538 |
| φ |
0.00 |
0.05 |
0.10 |
0.15 |
0.20 |
| σ/(s m−1) |
5.5 × 10−5 |
59.6 × 106 |
6.6 × 10−7 |
35 × 106 |
2.6 × 106 |
3 Galerkin finite element formulation
Following studies12,27–29 weighted residual approximations (WRA) for the system defined in eqn (9)–(12) are given below
where f′ = h, the dependent variables are approximated in term of unknown nodal values in the following way
where w1, w2, w3 = wi are weight functions. For Galerkin approach where wi = ψi.
3.1 Computation for stiffness matrix
Using the Galerkin finite element scheme, the following elements of stiffness matrix are calculated
where ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) = ψj
= ψj![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) j and
j and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = ψj
= ψj![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) j.
j. ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) j and
j and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) j are nodal values at previous iteration.
j are nodal values at previous iteration.
4 Results and discussion
Galerkin finite element algorithm is implemented to study the effects of thermo-physical properties of nano-sized metallic particles on unsteady two dimensional flows in the presence of buoyant force, thermal radiation and Joule heating. Non-linear stiffness matrix is linearized using Picards linearization scheme and system of algebraic equations are solved iteratively with tolerance 10−5. Several numerical experiments are done to search ηmax and grid independent studied is also carried out. Through extensive experiments, we have noted that the computed results converges with tolerance 10−5 when ηmax = 6 and domain [0,ηmax] is discretized into 200 elements.
4.1 Velocity profiles
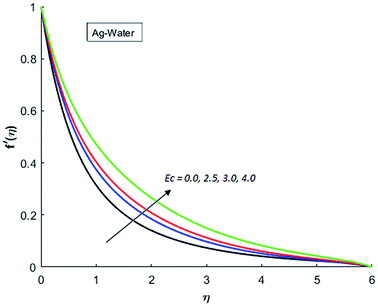
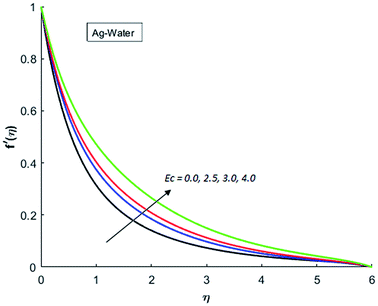
Fig. 1–4 display the effects of Eckert number Ec on the dimensional velocity of Cu, Ag, Al2O3 and TiO2-nanofluids when Gr > 0. These figures demonstrate that dimensionless velocity f′ increases as Eckert number Ec is increased. Ec is the ratio of kinetic energy to enthalpy and an increase in Ec results an increase in the kinetic energy. This increase in kinetic energy temperature of the fluid rises. This rise in temperature causes density differences which results an increase in the magnitude of buoyancy force. Due to this, as Eckert number is the coefficient of term (in energy eqn (11)) due to Joule heating and an increase in Ec corresponds to an increase in temperature. Grashof number (Gr) is the ratio of buoyancy force to the inertial force and it varies through positive values for downward flow and hence flow is accelerated by gravitational force and therefore, significant increase in the velocity is observed. For evidence, Fig. 5–8 are displayed. Thus by increasing Grashof number (Gr), a significant increase in velocity can be observed from Fig. 5–8. In qualitative sense, the buoyancy force has similar effects on the flow of Cu-nanofluid and TiO2-nanofluid. It is also observed that the momentum boundary layer thickness increases when Grashof number (Gr) is increased. During numerical simulations and numerical experiments, it is also noted that the velocity motion of nanofluid decelerates when Gr is varied through negative values. Gr is negative when flow is vertically upward and is opposed by the negative gravity. For the case of negative gravity, fluid motion slows down and a significant reduction in momentum boundary layer thickness is observed for (Gr < 0). The fluid under discussion has a property of emitting thermal radiations in the form of electromagnetic waves. The emission of electromagnetic waves from the fluid regime carries heat energy away which results a significant decrease in the temperature. In order to examine the effects of thermal radiation on the temperature of four types of nanofluids, simulations are carried out and are recorded in Fig. 9–12. It is found from simulations displayed by Fig. 9–12 that the motion of nanofluids slows down due to a reduction in buoyancy force. This is due to the fact that the temperature decreases when Gr > 0. Hence it is concluded that the emission of thermal radiation from the nanofluid of a decrease in the temperature of nanofluid. This decrease in temperature causes a density difference and hence favorable buoyancy force becomes weak. Consequently, fluid motion slows down. It is also observed that momentum boundary thickness is decreased by thermal radiation when gravity is positive. However, opposite behavior is observed for opposing gravitational force. The effects of different nanoparticles on the motion of nanofluids are simulated and are displayed by Fig. 13. This figure reflects that the velocity of Cu-nanofluid is smaller (in magnitude) than the velocities of Ag, Al2O3 and TiO2-nanofluids.
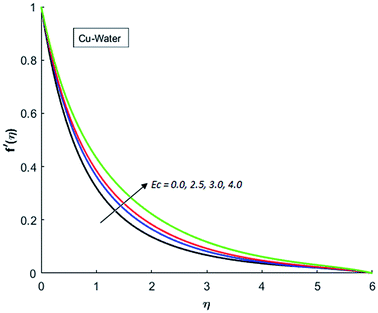 |
| | Fig. 1 Velocity distribution for various value of Ec when M = 0.5, Pr = 0.3, Gr = 5, Nr = 0.2 and λ = 1. | |
 |
| | Fig. 2 Velocity distribution for various value of Ec when M = 0.5, Pr = 0.3, Gr = 5, Nr = 0.2 and λ = 1. | |
 |
| | Fig. 3 Velocity distribution for various value of Ec when M = 0.5, Pr = 0.3, Gr = 5, Nr = 0.2 and λ = 1. | |
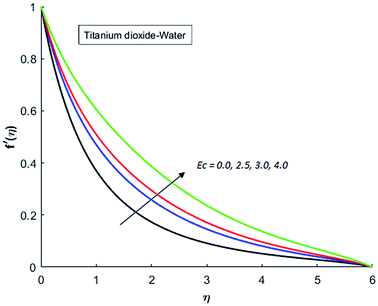 |
| | Fig. 4 Velocity distribution for various value of Ec when M = 0.5, Pr = 0.3, Gr = 5, Nr = 0.2 and λ = 1. | |
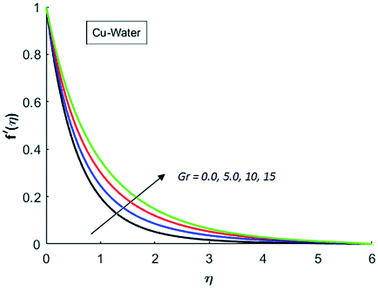 |
| | Fig. 5 Velocity distribution for various value of Gr when M = 1, Pr = 0.3, Ec = 0.1, Nr = 0.2 and λ = 1. | |
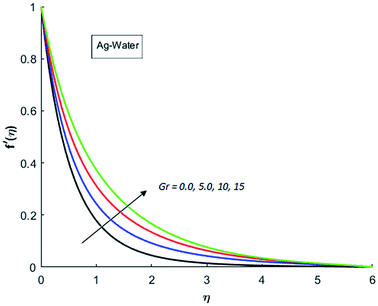 |
| | Fig. 6 Velocity distribution for various value of Gr when M = 1, Pr = 0.3, Ec = 0.1, Nr = 0.2 and λ = 1. | |
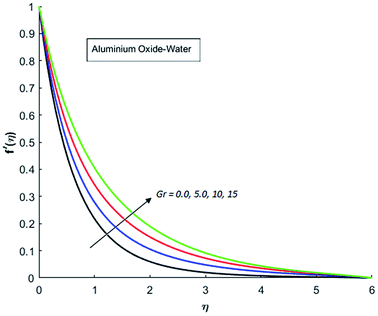 |
| | Fig. 7 Velocity distribution for various value of Gr when M = 1, Pr = 0.3, Ec = 0.1, Nr = 0.2 and λ = 1. | |
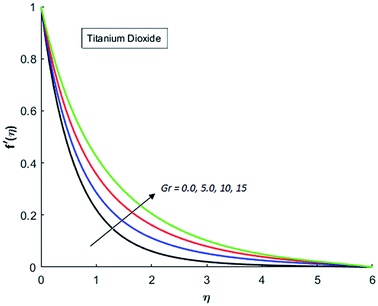 |
| | Fig. 8 Velocity distribution for various value of Gr when M = 1, Pr = 0.3, Ec = 0.1, Nr = 0.2 and λ = 1. | |
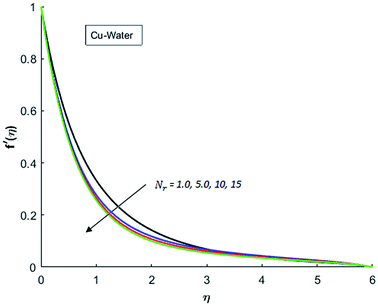 |
| | Fig. 9 Velocity distribution for various value of Nr when M = 0.5, Pr = 0.3, Gr = 0.5, Ec = 0.1 and λ = 1. | |
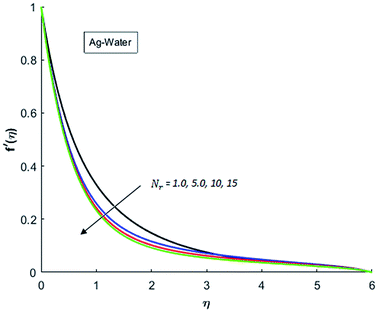 |
| | Fig. 10 Velocity distribution for various value of Nr when M = 0.5, Pr = 0.3, Gr = 0.5, Ec = 0.1 and λ = 1. | |
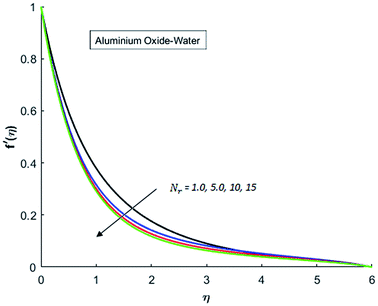 |
| | Fig. 11 Velocity distribution for various value of Nr when M = 0.5, Pr = 0.3, Gr = 0.5, Ec = 0.1 and λ = 1. | |
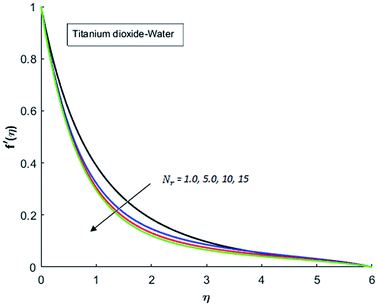 |
| | Fig. 12 Velocity distribution for various value of Nr when M = 0.5, Pr = 0.3, Gr = 0.5, Ec = 0.1 and λ = 1. | |
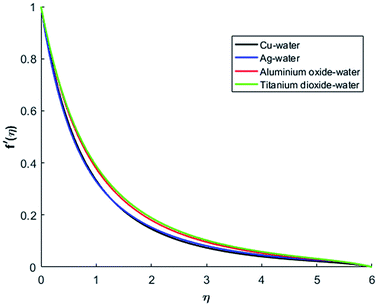 |
| | Fig. 13 Velocity profiles for different nanofluids when M = 0.5, Pr = 0.3, Ec = 0.1, Gr = 5, Nr = 0.2 and λ = 1. | |
4.2 Temperature profiles
The effects of dispersion of nanoparticles (Cu, Ag, Al2O3 and TiO2) buoyancy force and thermal radiations on the transport of heat in the flow of nanofluid are simulated and results are displayed by the Fig. 14–26. Respectively, Fig. 14 depicts that the temperature of Al2O3-nanofluid is high as compare to the temperature of Cu, Ag and TiO2-nanofluids and vice versa for Cu-nanofluid. The effects of Joule heating phenomenon on the temperature of four types of nanofluids are displayed in Fig. 15–18. These figures reflects that the temperature of the nanofluids increases as Eckert number Ec is increased. This increase in temperature (for four types of nano-particles) is due to the fact that Ec and M are the coefficient of Joule heating term in the dimensionless form of energy equation. An increase in Ec means that the effect of Joule heating becomes more and more strong and correspond to the generation of more heat due to ohmic dissipation of the fluid. Consequently, this heat adds to the fluid and hence temperature rises. Comparative study of Fig. 15–18 also shows that in TiO2-nanofluid highest amount of heat dissipates. It is already mentioned that the three types of modes of heat transfer (convection, conduction and thermal radiation) are considered. Further, opposing and favorable buoyant force is considered. In case of positive buoyant force (Gr > 0), flow experiences a favorable force due to which convection phenomenon becomes significant and process of carrying heat from hot wall to the fluid speeds up. Hence temperature of the fluid rises (see figures). This fact is completely in agreement with the physics of fluid flow (see Fig. 19–22). The four type of nanoparticles are dispersed in the fluid which is capable of radiating heat in the form of the electromagnetic waves as heat passes through it. Here in this study the effect of radiative nature is examined through radiation parameter Nr. An increase in the radiation parameter Nr represents the situation for which more electromagnetic waves carry heat energy away from the fluid. That is why temperature of nanofluid (four types of nanofluids) decreases with an increase in the radiation parameter Nr as shown in Fig. 23–26.
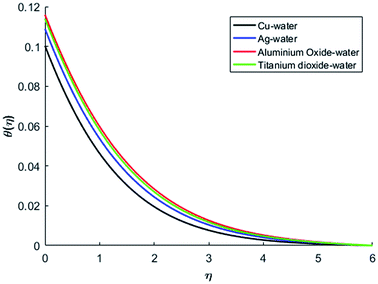 |
| | Fig. 14 Temperature curves for different nanofluids when M = 0.5, Pr = 0.3, Nr = 0.2, Ec = 0.1, Gr = 0.5 and λ = 1. | |
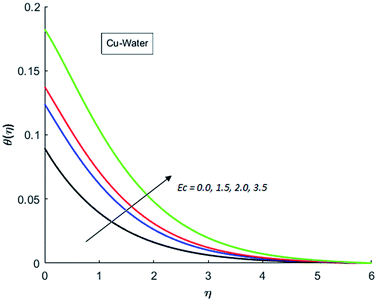 |
| | Fig. 15 Temperature curves for various value of Ec when M = 0.5, Pr = 0.3, Gr = 5, Nr = 0.2 and λ = 1. | |
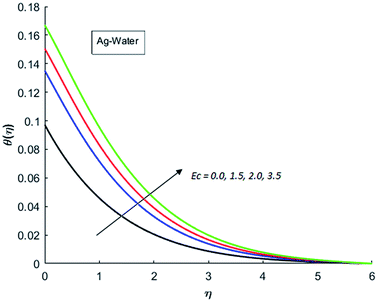 |
| | Fig. 16 Temperature curves for various value of Ec when M = 0.5, Pr = 0.3, Gr = 5, Nr = 0.2 and λ = 1. | |
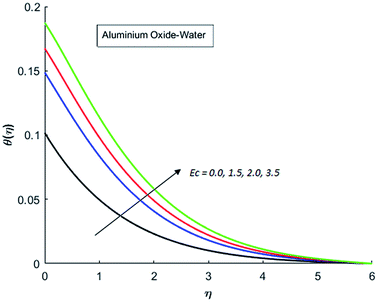 |
| | Fig. 17 Temperature curves for various value of Ec when M = 0.5, Pr = 0.3, Gr = 5, Nr = 0.2 and λ = 1. | |
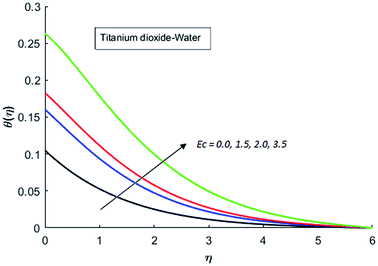 |
| | Fig. 18 Temperature curves for various value of Ec when M = 0.5, Pr = 0.3, Gr = 5, Nr = 0.2 and λ = 1. | |
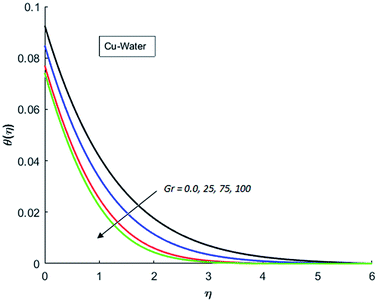 |
| | Fig. 19 Temperature curves for various value of Gr when M = 0.5, Pr = 0.3, Ec = 0.5, Nr = 0.2 and λ = 1. | |
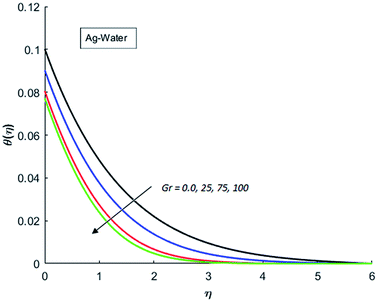 |
| | Fig. 20 Temperature curves for various value of Gr when M = 0.5, Pr = 0.3, Ec = 0.5, Nr = 0.2 and λ = 1. | |
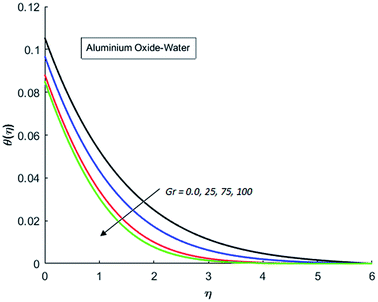 |
| | Fig. 21 Temperature curves for various value of Gr when M = 0.5, Pr = 0.3, Ec = 0.5, Nr = 0.2 and λ = 1. | |
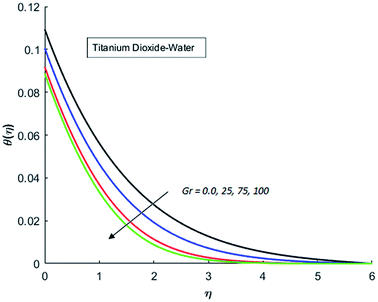 |
| | Fig. 22 Temperature curves for various value of Gr when M = 0.5, Pr = 0.3, Ec = 0.5, Nr = 0.2 and λ = 1. | |
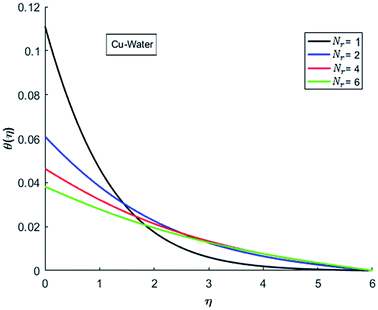 |
| | Fig. 23 Temperature curves for various value of Nr when M = 0.5, Pr = 0.3, Ec = 0.1, Gr = 0.5 and λ = 1. | |
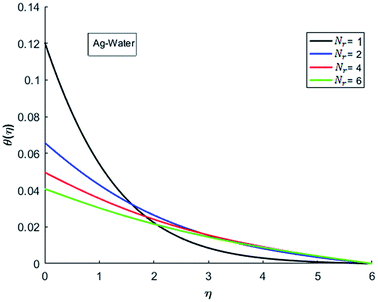 |
| | Fig. 24 Temperature curves for various value of Nr when M = 0.5, Pr = 0.3, Ec = 0.1, Gr = 0.5 and λ = 1. | |
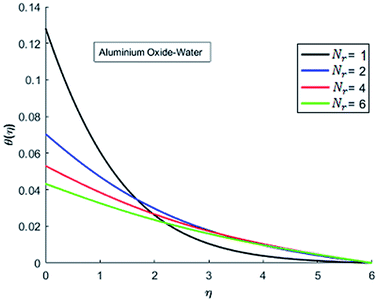 |
| | Fig. 25 Temperature curves for various value of Nr when M = 0.5, Pr = 0.3, Ec = 0.1, Gr = 0.5 and λ = 1. | |
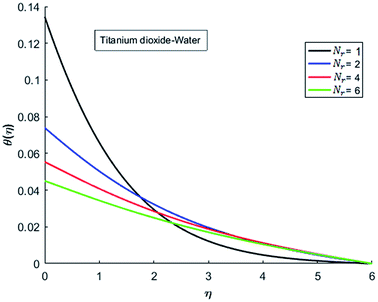 |
| | Fig. 26 Temperature curves for various value of Nr when M = 0.5, Pr = 0.3, Ec = 0.1, Gr = 0.5 and λ = 1. | |
4.3 Entropy analysis
The entropy generation due to temperature gradient, viscous dissipation and Joule heating is defined by
Using the similarity transformations given in eqn (8), one obtains the following dimensionless form of the entropy generation
where,
and, respectively, are called dimensionless the entropy generation number, the Reynolds number, the Brinkman number and the non-dimensionless temperature difference number.
4.4 Entropy generation profiles
The behavior of dimensionless entropy under the variation of Eckert number Ec, Grashof number Gr, unsteadiness parameter M and Biot number Bi is displayed in Fig. 27–31. Fig. 27 represents that rate of the entropy generation increases when Ec is increased. Therefore, it can be advised to use the fluid exhibiting less dissipation in order to avoid losses of heat energy in magneto-thermal system. This recommendation is both for nano and pure fluid. Despite of the advantage of magnetic fluid to control the momentum boundary layer thickness, it is not recommended to use electrically conducting fluid when the reduction of losses of heat energy is of high concern. The effect of buoyancy force on the entropy generation is also simulated and the simulated results are graphed in Fig. 28. This figure reflects that favorable buoyancy force causes an increase in the energy losses. These losses can be controlled by introducing the opposing buoyancy force i.e. considering downward flow on vertical sheet. Fig. 28 also demonstrates that losses of heat energy are significant for nanofluid as compare to the pure fluid. The entropy generation in steady and unsteady flow of both nanofluids and regular fluids is represented in Fig. 29. It is noted from Fig. 29 that the entropy generation is high in steady flow as compare to unsteady flow. The effect of Joule heating on the entropy generation is displayed in Fig. 30. This figure depicts that there is significant increase in the entropy generation when heat losses due to dissipation caused by the external magnetic field. This behavior is same for both pure and nanofluid. Therefore, it is advised not to use electrically conducting fluid. Alternatively, magnetic intensity of the fluid be adjusted in such a way that losses of heat energy should be minimum. This is for both nano and regular fluids. The entropy generation in nano-magnetohydrodynamic flow is high as compare to nano-hydrodynamic flow (see Fig. 30). The effect of convection boundary condition on the entropy generation is displayed in Fig. 31 is noted from this figure shows that there is a significant effect of Biot number (dimensionless number due to convective boundary conduction) on the entropy generation.
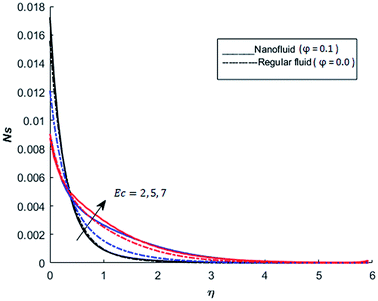 |
| | Fig. 27 The effect of Eckert number Ec on the entropy generation when Pr = 0.3, M = 1, Bi = 0.1, Nr = 0.2, Gr = 5, λ = 1, Re = 1, Br = 1 and Ω = 1. | |
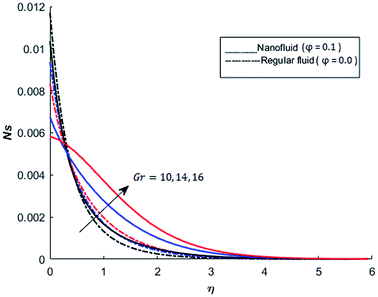 |
| | Fig. 28 The effect of Grashof number Gr on the entropy generation when Pr = 0.3, M = 1, Bi = 0.1, Nr = 0.2, Ec = 0.5, λ = 1, Re = 1, Br = 1 and Ω = 1. | |
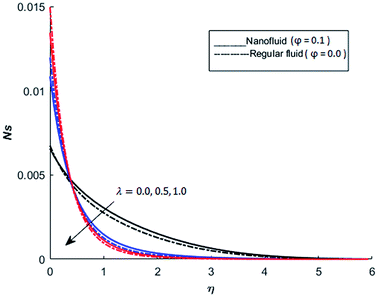 |
| | Fig. 29 The effect of λ on the entropy generation when Pr = 0.3, M = 1, Bi = 0.1, Nr = 0.2, Gr = 5, Ec = 0.5, Re = 1, Br = 1 and Ω = 1. | |
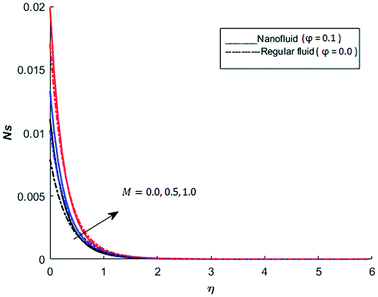 |
| | Fig. 30 The effect of M on the entropy generation when Pr = 0.3, Bi = 0.1, Nr = 0.2, Gr = 5, Ec = 0.5, λ = 1, Re = 1, Br = 1 and Ω = 1. | |
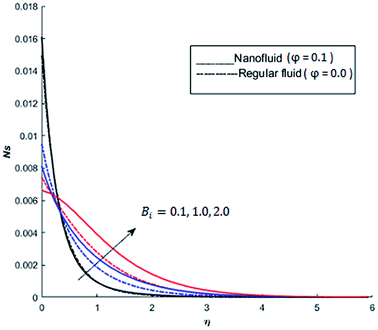 |
| | Fig. 31 The effect of Biot number Bi on the entropy generation when Pr = 0.3, Nr = 0.2, Gr = 5, Ec = 0.5, λ = 1, Re = 1, Br = 1 and Ω = 1. | |
5 Conclusion
In this paper, the effects of four types of nano-particles (Cu, Ag, Al2O3 and TiO2) on the transport of heat in unsteady two-dimensional boundary layer flow of a radiative fluid over a convectively heated surface in the presence of Joule heating, heat absorption/generation and buoyant force are investigated. It is observed that dispersion of nano-particles in the pure fluid increases the thermal conductivity of the resulting mixture which may play a vital role in the thermal systems. For favorable buoyant force the velocity of the mixture (mixture of nanoparticles and radiative fluid) increases which causes an increase in the thermal and momentum boundary layer thicknesses. However, in case of opposing buoyant force, a reverse mechanism regarding momentum and thermal boundary layer thicknesses is observed. The magnetic field intensity and ohmic dissipation are directly proportional with each other. Hence an increase in the intensity of the magnetic field converts more electrical energy into heat (due to ohmic dissipation process). It is also observed that an increase in the intensity of the magnetic field retards the flow and reduces the momentum boundary thicknesses. Therefore, it is advised that an external magnetic field may be applied to control the flow and momentum boundary layer thickness. However, it should be in mind that an increase in the imposition of external magnetic field has opposite effect on the thermal boundary layer thicknesses due to Joule heating mechanism. It is also important to mention that momentum boundary layer thickness for hydrodynamic flow is higher than that of the magnetohydrodynamic flow. However, thermal boundary layer thickness of hydrodynamic flow is less than that of the magnetohydrodynamic flow. During numerical computations, it is studied that the velocity of TiO2-nanofluid is higher than the velocity of Al2O3, Ag and Cu-nanofluids. Due to magnetic field and fluid flow interactions, the electrical energy converts into heat. This may undesirable in many thermal systems. Therefore, control of Joule heating in the design of thermal system is necessary. However, this dissipation of heat may be desirable in some biological fluid flows. Moreover, an increase in the intensity of the magnetic field causes an increase in the entropy generation. The positive buoyancy force enhances the entropy generation. However, opposing buoyancy force reduces energy losses. Energy losses in steady flow are high as compare to the unsteady flow. The key observations are listed below:
• The buoyant force is responsible for the influence of thermal radiations on the flow of nanofluid. It is observed that if buoyant force is not considered, then there is no effect of thermal radiations on the flow and hence momentum boundary layer thickness. As the buoyant force is significant in vertical flows, therefore, it is recommended that horizontal arrangement of physical model (sheet) should be taken if no impact of thermal radiations on the flow of nanofluid is desired.
• The magnetic field decelerates the fluid motion due to hindrance caused by the Lorentz force. Therefore, it is recommended to apply external magnetic field perpendicular to the plane of sheet if momentum boundary layer thickness is to be controlled.
• Convectively heated surface causes more entropy generation. Therefore, it is recommended not to use the convectively heated surface in thermal systems.
• Imposition of external magnetic field increases the entropy generation and is responsible of great energy loses. Therefore, thermal systems work efficiently without loses of energy if external magnetic field is not imposed.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Authors Miss Shafia Rana and Dr M. Nawaz are thankful to the Higher Education Commission (HEC) of Pakistan for the financial support under NRPU-vide 5855/Federal/NRPU/R&D/HEC/2016. Authors are also thankful to the referees for their useful comments regarding earlier version of this manuscript.
References
- A. Dewan, P. Mahanta, K. S. Raju and P. S. Kumar, Review of passive heat transfer augmentation techniques, J. Power Energy, 2018, 2004, 509–527 Search PubMed.
- T. Sonawane, P. Patil, A. Chavhan and B. M. Dusane, A review on heat transfer enhancement by passive methods, Int. Res. J. Eng. Tech., 2016, 3(9), 1567–1574 Search PubMed.
- H. Masuda, A. Ebata, K. Teramaeand and N. Hishinuma, Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles, Netsu Bussei, 1993, 7(4), 227–233 CrossRef CAS.
- J. Buongiorno, Convective transport in nanofluids, J. Heat Transfer, 2006, 128(3), 240–250 CrossRef.
- W. A. Khan and I. Pop, Boundary-layer flow of a nanofluid past a stretching sheet, Int. J. Heat Mass Transfer, 2010, 53, 11–12 Search PubMed.
- S. Nadeem, R. Ul-Haqa and Z. H. Khan, Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nano-particles, J. Taiwan Inst. Chem. Eng., 2014, 45(1), 121–126 CrossRef CAS.
- S. Das, S. Chakraborty, R. N. Jana and O. D. Makinde, Entropy analysis of unsteady magneto-nanofluid flow past accelerating stretching sheet with convective boundary condition, Appl. Math. Mech., 2015, 36(12), 1593–1610 CrossRef.
- M. Sheikholeslami and M. M. Rashidi, Effect of space dependent magnetic field on free convection of Fe2O3–water nanofluid, J. Taiwan Inst. Chem. Eng., 2015, 56, 6–15 CrossRef CAS.
- M. M. Rashidi, E. Momoniat, M. Ferdowa and A. Basiriparsa, Lie group solution for free convection flow of a nanofluid past a chemically reacting horizontal plate in a porous media, Math. Probl. Eng., 2014, 239082 Search PubMed.
- S. Nadeem and S. Saleem, Unsteady mixed convection flow of nanofluid on a rotating cone with magnetic field, Appl. Nanosci., 2014, 4, 405–414 CrossRef CAS.
- M. Nawaz and T. Hayat, Axisymmetric stagnation-point flow of nanofluid over a stretching surface, Adv. Appl. Math. Mech., 2014, 6(2), 220–232 CrossRef.
- M. Nawaz and T. Zubair, Finite element study of three dimensional radiative nano-plasma flow subject to Hall and ion slip currents, Results Phys., 2017, 7, 4111–4122 CrossRef.
- A. Zeeshan, M. Hassan, R. Ellahi and M. Nawaz, Shape effect of nanosize particles in unsteady mixed convection flow of nanofluid over disk with entropy generation, J. Process Mech. Eng., 2016, 231(4), 871–879 CrossRef.
- A. Einstein, Eineneue Bestimmung der Molekul-dimensionen, Ann. Phys., 1906, 19, 289–306 CrossRef CAS.
- H. C. Brinkman, The viscosity of concentrated suspensions and solutions, J. Chem. Phys., 1952, 20(4), 571–581 CrossRef CAS.
- G. K. Batchelor, The effect of Brownian motion on the bulk stress in a suspension of spherical particles, J. Fluid Mech., 1977, 83(1), 97 CrossRef.
- Y. Mori and N. Ototake, On the viscosity of suspensions, Chemical Engineering, 1956, 20(9), 488–494 CrossRef CAS.
- X. Wang, X. Xu and S. U. S. Choi, Thermal conductivity of nanoparticle.fluid mixture, J. Thermophys. Heat Transfer, 1999, 13(4), 474–480 CrossRef CAS.
- N. Masoumi, N. Sohrabi and A. Behzadmehr, A new model for calculating the effective viscosity of nanofluids, J. Phys. D: Appl. Phys., 2009, 42(5), 55501 CrossRef.
- S. H. Ayber, M. Sharfpur, M. R. Azizian, M. M. Josua, P. Meyer and S. H. Aybar, A Review of thermal conductivity models for nanofluids, Heat Transfer Eng., 2015, 36(13), 1085–1110 CrossRef.
- A. Bejan, Entropy generation minimization, The new thermodynamics of finite-size devices and finite-time processes, J. Appl. Phys., 1996, 79, 1191–1218 CrossRef CAS.
- M. M. Bhatti, M. M. Rashidi and I. Pop, Entropy Generation with nonlinear heat and mass transfer on MHD boundary layer over a moving surface using SLM, Nonlinear Engineering, 2017, 6, 43–52 Search PubMed.
- T. Armaghani, A. Kasaeipoora, N. Alavib and M. M. Rashidic, Numerical investigation of water-alumina nanofluid natural convection heat transfer and entropy generation in a baffled L-shaped cavity, J. Mol. Liq., 2016, 223, 243–251 CrossRef CAS.
- V. Bianco, S. Nardini and O. Manca, Enhancement of heat transfer and entropy generation analysis of nanofluids turbulent convection flow in square section tubes, Nanoscale Res. Lett., 2011, 6, 252 CrossRef PubMed.
- A. S. Butt and A. A. Ali, Computational study of entropy generation in magnetohydrodynamic flow and heat transfer over an unsteady stretching permeable sheet, Eur. Phys. J. Plus, 2014, 129, 1–13 CrossRef.
- M. H. Abolbashari, N. Freidoonimehr, F. Nazari and M. M. Rashidi, Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid, Powder Technol., 2014, 267, 256–267 CrossRef CAS.
- I. H. Qureshi, M. Nawaz, S. Rana and T. Zubair, Galerkin finite element study on the effects of variable thermal conductivity and variable mass diffusion conductance on heat and mass transfer, Commun. Theor. Phys., 2018, 70(1), 49–59 CrossRef.
- I. H. Qureshi, M. Nawaz, S. Rana, U. Nazir and A. J. Chamkha, Investigation of variable thermo-physical properties of viscoelastic rheology: A Galerkin finite element approach, AIP Adv., 2018, 8, 075027 CrossRef.
- M. Nawaz, S. Rana, I. H. Qureshi and T. Hayat, Three-dimensional heat transfer in the mixture of nanoparticles and micropolar MHD plasma with Hall and ion slip effects, AIP Adv., 2018, 8(10), 105109 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Shafia Rana and
Imran Haider Qureshi
*,
Shafia Rana and
Imran Haider Qureshi
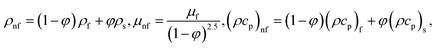
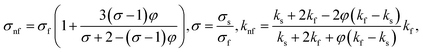
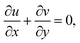
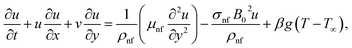
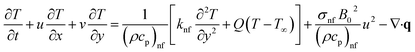
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T = T∞, ∀ x, y, t < 0
T = T∞, ∀ x, y, t < 0
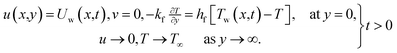
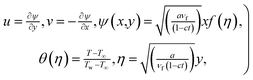
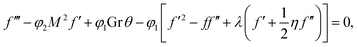
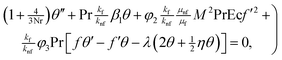
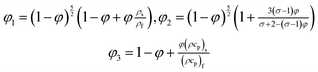
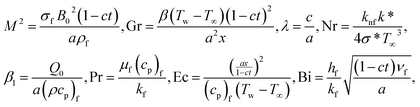
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nr = 0 and Ec = 0, the problem reduces to the case of Das et al.7 with heat generation/absorption. The case of M2 = 0, λ = 0, φ = 0 and Bi → ∞ is also considered by Abolbashari et al.26 and Das et al.7. The numerical values of thermo-physical properties used in this study are (Table 1).
Nr = 0 and Ec = 0, the problem reduces to the case of Das et al.7 with heat generation/absorption. The case of M2 = 0, λ = 0, φ = 0 and Bi → ∞ is also considered by Abolbashari et al.26 and Das et al.7. The numerical values of thermo-physical properties used in this study are (Table 1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500
500![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) = ψj
= ψj![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) j and
j and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = ψj
= ψj![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) j.
j. ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) j and
j and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) j are nodal values at previous iteration.
j are nodal values at previous iteration.