Biomimetic liquid lenses actuated by a laser beam: effects of evaporation and orientation to gravity
Alexandr
Malyuk
 and
Natalia
Ivanova
and
Natalia
Ivanova
 *
*
Photonics and Microfluidics Laboratory, University of Tyumen State, 625000, Russia. E-mail: n.ivanova@utmn.ru
First published on 9th July 2020
Abstract
Liquid lenses actuated by thermocapillary and solutocapillary forces via heating with a laser beam demonstrate a high level of adaptability. The focal length and the optical aperture are tuned by the variation of the refracting surface curvature and the base diameter of a liquid droplet in response to the change of the laser intensity. Depending on the properties of liquids and the actuating forces, the lenses can operate in both converging and diverging modes. However, evaporation caused by heating, and high sensitivity to gravity may restrict applicability of the lenses in complex optical devices. This paper presents an experimental study of the optical characteristics of lenses consisting of ethylene glycol and a binary mixture of ethylene glycol and ethyl alcohol under conditions of long-term operation, performing multiple focal adjustments and arbitrary orientation of the optical axis. We have shown that stable continuous lens operation with a constant focus and continuous switching between two values of the focal length lasts for several tens of minutes after accommodation depending on the laser power and the driving forces. Then, evaporation leads to an irreversible change in the optical characteristics of the lens. We have also established that liquid lenses retain their optical characteristics and stable position when tilted to the horizon to several tens of degrees. The results obtained give a reason to believe that the studied lenses have high potential for applications in consumer and industrial optical devices.
Design, System, ApplicationWe demonstrate liquid lenses replicating accommodation and pupil light reflexes of the eye in response to changing laser beam intensity. The lenses represent miniature sessile droplets of low-volatile organic compounds such as benzyl alcohol and ethylene glycol and binary mixtures of miscible low-volatile and volatile alcohols. The liquids used allow for the dynamic manipulation of curvature of the refractive interface in positive and negative ranges. The manipulation principle is based on the variation of surface tension of liquids with temperature and concentration of the liquid mixture components resulting from heating with a laser beam. The applicability of the proposed lens design is determined by the gravitational stability and the stability of the optical parameters during long-term operation. We have shown that evaporation of liquids caused by the long heating limits the lens operation time causing irreversible changes of the optical properties. The sensitivity of the lens position and its shape to tilt to the horizon restricts the arbitrary orientation of the lens when being used. We have suggested possible approaches to improve the stability of the proposed concept of liquid lenses that allow development of multifunctional optical devices for a wide range of applications. |
Introduction
Bio-inspired optical devices
Nowadays, a significant surge of interest in the development of bio-inspired optical elements and imaging systems takes place. This is related to the fact that today's challenges faced by humans in the area of imaging and control of light have been solved by nature over millions of years of evolution. Sparkling examples are the development of a new generation of optics mimicking compound eyes of insects consisting of a large number of ommatidia.1–4 These kinds of optical systems provide a wide angular field and support the collection of a panoramic image. There are more specialized bio-inspired optical devices and elements aimed to solve specific tasks. For instance, a camera with a light sensitivity enhancer imitates the eye of elephant-nose fish.5 The outstanding feature of this device is a large number of tapered light-harvesting waveguides through which light goes to light-sensitive elements, which is similar to light in the eyes of elephant-nose fish passing through crystalline tapered waveguides. This feature allows concentrating incident light on photo-elements and enhancing the sensitivity of the device. Another example is an imaging sensor giving information about spectra and polarization of light and mimicking the ommatidia of arthropods, such as the mantis shrimp.6 Shu Yang et al.7 presented a lens array with integrated pores through which a dyed pumping liquid is used as a diaphragm. Such design provides the control of light transmittance in a range from zero to 100%. This device is inspired by the vision system of a brittle star having a lens array with surrounding pores through which pumps chromatophore cells that allows to regulate the configuration of vision in this way.Many bio-mimetic optical devices rely on imitation of human and vertebrate eyes, especially the lens.8–14 Since the eye lens is a bi-convex transparent body which changes optical characteristics by varying the curvature of the refracting surface, most bio-mimetic lenses consist of a liquid as a lens body and imitate the same principle of the focal length tunability. Using liquids provides advantages compared to their solid counterparts as a naturally smooth refracting surface, such as the easy conformation of the lens shape under applied external stimuli,15–28 and the ability to perform any number of cycles without any wear and loss of its optical parameters.
One of the important properties of liquids is the interfacial tension at the liquid–air or the liquid–liquid interface, which is extremely sensitive to electrical, thermal, and concentration fields applied to the system. This fact gives a wide variety of methods to control the shape of the surface, i.e., the focal length of a liquid lens, and consequently, allows the design of adaptive optical devices on demand.
To date, a large number of bio-mimetic lenses based on the electrowetting effect have been developed,15–19 where the surface energy varies depending on the applied voltage. Fast response times with respect to the voltage changing and the stability of the refracting surface shape with respect to a change in the orientation of the lens optical axis relative to the gravitational vector made it possible to develop bio-mimetic optical devices for industrial use.
Recently, we have proposed two types of adaptive liquid lenses29,30 actuated by surface tension forces, which are generated by laser-induced thermal gradients and concentration gradients of solutes on the liquid surface. Such lenses have a wider range of functionalities compared to the electrowetting lenses by imitating not only accommodation reflex but also the pupil and the optokinetic reflexes, which allow for control of the amount of light and focusing on moving objects.
Note that in our previous studies,29,30 potential weak sides of these lenses related to the process of liquid evaporation during the heating and the shape stability to tilt its base surface to the horizon have not been considered. However, evaporation, which is an inherent part of the control mechanism, can lead to an irreversible change in the optical characteristics of the lenses during a prolonged operation due to loss of the lens volume.
In this paper, we present the results of the study of the stability of operating liquid lenses actuated by the thermocapillary and the solutocapillary forces generated on the free surface of a liquid by the thermal action of a laser beam.
Experimental
Materials
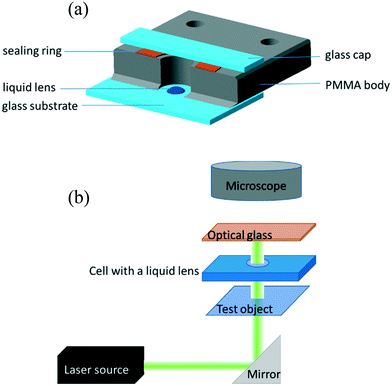
To form liquid lenses, we used pure ethylene glycol (EG), a binary mixture of EG and ethyl alcohol (EA) at a weight concentration of 50% ethylene glycol, and pure benzyl alcohol (BA). In order to enhance the absorption of laser irradiation, the liquids were dyed with crystal violet dye to an extent that the extinction coefficient was about 15 mm−1 for all liquids used. The main properties of the liquids are summarized in Table 1, where ρ, μ, and γ are the density, viscosity and surface tension, respectively; Pv and n0 are the saturated vapor pressure and the refractive index, respectively;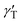 and nT are the thermal coefficients of surface tension and refraction, respectively. A small amount of liquid was deposited onto the bottom of a closed cell, which was made of two glass slides separated with a polymethyl methacrylate spacer, Fig. 1(a). The cell was used to prevent a loss of liquids due to the evaporation and influence of surrounding airflows. It is important to note that the wettability and thermal diffusivity of the glass substrate significantly influences the performance of liquid lenses. The wettability of the substrate determines the initial shape of a liquid droplet and, hence, affects the range of the focal length variation. The thermal diffusivity of the substrate affects the magnitude and the rate of temperature growth as well as the spatial distribution of the surface temperature gradient because it serves as a heat sink.
and nT are the thermal coefficients of surface tension and refraction, respectively. A small amount of liquid was deposited onto the bottom of a closed cell, which was made of two glass slides separated with a polymethyl methacrylate spacer, Fig. 1(a). The cell was used to prevent a loss of liquids due to the evaporation and influence of surrounding airflows. It is important to note that the wettability and thermal diffusivity of the glass substrate significantly influences the performance of liquid lenses. The wettability of the substrate determines the initial shape of a liquid droplet and, hence, affects the range of the focal length variation. The thermal diffusivity of the substrate affects the magnitude and the rate of temperature growth as well as the spatial distribution of the surface temperature gradient because it serves as a heat sink.
| Liquid | ρ, kg m−3 | μ, mPa s | γ, mN m−1 | , mN m−1 K−1 | P v, Pa | n 0 | n T, K−1 |
|---|---|---|---|---|---|---|---|
| BA | 1041.1 (ref. 31) | 5.474 (ref. 31) | 38.5 (ref. 32) | −0.094 (ref. 35) | 15 (ref. 31) | 1.54 (ref. 31) | −5.1 × 0−4 (ref. 34) |
| EG | 1113.5 (ref. 31) | 16.1 (ref. 31) | 47.99 (ref. 31) | −0.078 (ref. 35) | 7 (ref. 36) | 1.43 (ref. 31) | −2.6 × 10−4 (ref. 33) |
| EA | 785.1 (ref. 32) | 1.1 (ref. 32) | 21.9 (ref. 32) | −0.068 (ref. 32) | 12.4 × 103 ( ref. 36) | 1.36 (ref. 31) | −4 × 10−4 (ref. 33) |
Methods
A droplet of liquid was deposited onto the substrate with a precise syringe and then was mechanically spread over the surface to increase the base diameter and decrease the thickness of the droplet. This allows reducing the diffusion of the thermal field in the droplet bulk, i.e., to localize the heat flux produced with the laser beam in the central part of the droplet. The volumes of liquid placed in the cell ranged from 0.3 to 1 μl.The experimental setup is shown in Fig. 1(b). A laser beam (diameter of 0.8 mm and wavelength of 530 nm) with a Gaussian intensity distribution is directed with a mirror vertically through a test object (a metal grid with an element size of 0.4 × 0.4 mm) to the cell containing a liquid lens. An orange light filter cuts off a part of laser irradiation passed through the lens. A microscope equipped with a CCD-camera was used to take images of the test object obtained using the liquid lens. The power of the laser beam was varied stepwise from 2 to 125 mW. The focal length F of the liquid lens was calculated using the thin lens equation:
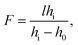 | (1) |
To study the operation stability of a liquid lens with respect to the inclination of its optical axis to the horizon, the microscope stage with the cell was tilted relative to the horizontal plane with steps of 10° from 0 to 60°, ensuring that the laser beam is incident onto the center of the lens. The shape and position of the droplet lens (50 wt% EG) on the substrate was monitored using images of the test grid formed by this lens. The measurements were carried out at a laser beam power varying from 2 to 30 mW.
Results and discussion
Liquid lenses actuated by thermocapillary forces
As mentioned above, external stimuli are necessary to achieve the variation in surface tension of a liquid. In our work, we used a laser beam to generate an axisymmetric temperature gradient along the liquid surface, which results in a surface tension gradient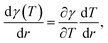 | (2) |
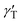 is the thermal coefficient of surface tension, which is negative for the used liquids, and dT/dr is the radial temperature gradient. The surface tension gradient is balanced by the viscous stresses in the bulk liquid. As a result, the radially outward thermocapillary flow removes liquid from the heated spot producing a concave deformation on the liquid surface.37–42 A negative capillary pressure arising below the concave surface generates a reverse flow resulting in the closed convective vortex.
is the thermal coefficient of surface tension, which is negative for the used liquids, and dT/dr is the radial temperature gradient. The surface tension gradient is balanced by the viscous stresses in the bulk liquid. As a result, the radially outward thermocapillary flow removes liquid from the heated spot producing a concave deformation on the liquid surface.37–42 A negative capillary pressure arising below the concave surface generates a reverse flow resulting in the closed convective vortex.
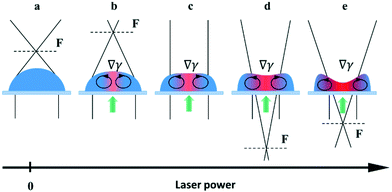
We used sessile droplets of pure ethylene glycol and benzyl alcohol as lenses driven by the laser-induced thermocapillary forces. The operating principle is shown in Fig. 2. When no power is applied, a sessile droplet represents a plane-convex lens with a short initial focal length, Fig. 2(a). When the laser is on, the thermocapillary flows reduce the droplet curvature in the heating area that leads to an increase in the focal length, Fig. 2(b). Raising the laser beam power results in the focal length increasing until it reaches infinity, when the lens surface becomes a plane, Fig. 2(c). Further increasing the power produces a thermocapillary dimple in the heated spot. Hereafter, the sessile droplet serves as a plano-concave diverging lens with a negative focal length, Fig. 2(d), the absolute value of which decreases with the laser beam power, Fig. 2(e).
The reduction of the power results in a reversible change of surface geometry, and when the laser is off, the droplet reverts to the initial shape of a plano-convex lens. It is important to note that the base diameter of the droplet remains constant, while the refractive surface curvature changes. This is related to the pinning of the contact line of the droplet caused by the non-uniform wettability of the substrate.
Liquid lenses actuated by solutocapillary forces
Liquid mixtures of ethylene glycol and ethyl alcohol were used to demonstrate the lenses actuated by the laser-induced solutocapillary forces. Ethyl alcohol has a higher saturated vapor pressure and lower surface tension compared to ethylene glycol (see Table 1); hence, the heating with the laser beam leads to a decrease in the concentration of ethyl alcohol in the heated area due to evaporation. In this case, the surface tension gradient along the liquid surface is a function of both temperature and concentration: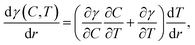 | (3) |
Focal length of a liquid lens as a function of the laser power
Fig. 4 shows the dependencies of the focal length of the liquid lenses of 1 μl in volume on the laser beam power for pure ethylene glycol and its 50% mixture with ethyl alcohol. The focal length corresponding to each value of the laser beam power was calculated using eqn (1). In the case of pure ethylene glycol, due to its high surface tension, the initial shape of the liquid lens represents a sessile droplet30 with an initial focal length of 15 mm. When the laser beam is incident to the droplet, its focal length increases nonlinearly and reaches 40 mm at the maximum power of 85 mW. The thermocapillary forces drive the focal length variation and tend to flatten the droplet.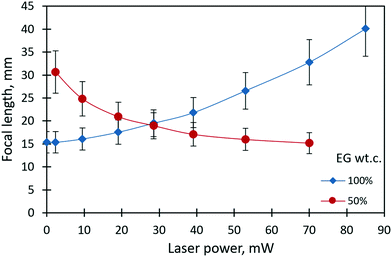 | ||
| Fig. 4 The focal length of the liquid lenses (1 μl in volume) of pure ethylene glycol and its 50% mixture with ethyl alcohol vs. the power of the laser beam. | ||
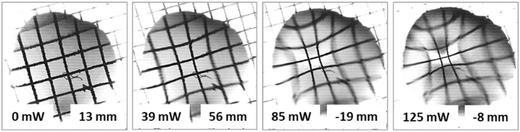
In the case of liquid mixtures, the dependency of the focal length on the power of the laser beam takes on an opposite trend according to the governing solutocapillary mechanism. In the initial state, when the laser beam is off, the lens has a shape close to a pancake due to the better wetting of the substrate by the liquid mixture with a lower surface tension compared to pure ethylene glycol. In this case, the focal length tends to reach infinity. The values of the focal length at a laser power higher than 70 mW for the 50% mixture were not possible to measure. The reason for this limitation is the intensification of the convective flows in the bulk of the lens that leads to oscillatory instability of the lens shape and the lens position in the laser beam. Fig. 5 presents images obtained with the solutocapillary lens, where the focal length and corresponding laser power are specified.
 | ||
| Fig. 5 Images of the test grid obtained with the solutocapillary lens (50% ethylene glycol, 1 μl) at different laser beam powers. | ||
The focal lengths as a function of the laser beam power for benzyl alcohol and ethylene glycol droplets of 0.3 μl are shown in Fig. 6. Images of the test object obtained with the thermocapillary lens based on benzyl alcohol are presented in Fig. 7. Experimental results (Fig. 6) can be approximated with the function 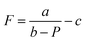 , where P – is the laser beam power, and a, b and c – are empirical constants. The approximation allows for definition of the threshold power of the laser beam at which the lens becomes flat (F ≈ ∞) and the operating mode changes from “converging” to “diverging”. As Fig. 6 shows, the threshold power for benzyl alcohol and ethylene glycol lenses takes on values of around 23 and 82 mW, respectively. This difference is caused mainly by the difference in surface tensions of both liquids (see Table 1). A droplet of ethylene glycol with a higher surface tension compared to benzyl alcohol has a larger wetting angle on the substrate; hence, the height of the droplet is higher and the base diameter is smaller. This promotes convective and diffusion dispersion of the localized heat source inside the bulk droplet; consequently, the temperature gradient on the droplet surface decreases.
, where P – is the laser beam power, and a, b and c – are empirical constants. The approximation allows for definition of the threshold power of the laser beam at which the lens becomes flat (F ≈ ∞) and the operating mode changes from “converging” to “diverging”. As Fig. 6 shows, the threshold power for benzyl alcohol and ethylene glycol lenses takes on values of around 23 and 82 mW, respectively. This difference is caused mainly by the difference in surface tensions of both liquids (see Table 1). A droplet of ethylene glycol with a higher surface tension compared to benzyl alcohol has a larger wetting angle on the substrate; hence, the height of the droplet is higher and the base diameter is smaller. This promotes convective and diffusion dispersion of the localized heat source inside the bulk droplet; consequently, the temperature gradient on the droplet surface decreases.
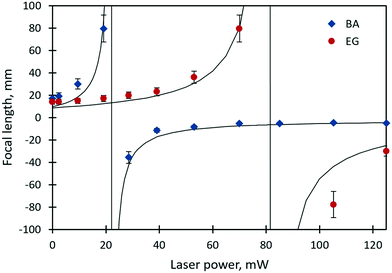 | ||
| Fig. 6 The focal length of the ethylene glycol and benzyl alcohol lenses (0.3 μl in volume) vs. the power of the laser beam. Vertical solid lines are asymptotes. | ||
 | ||
| Fig. 7 Images of the test grid obtained with the thermocapillary lens (benzyl alcohol, 0.6 μl) at different laser beam powers.30 | ||
The stability of the liquid lens operation
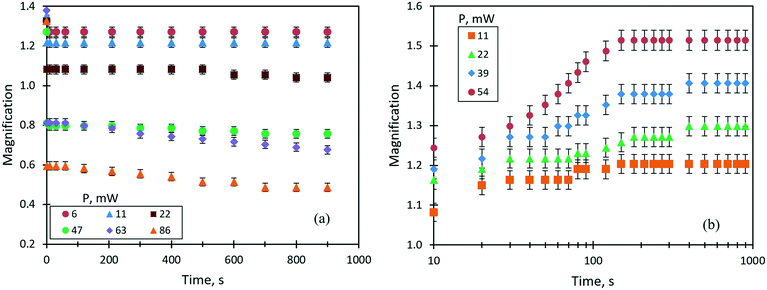
One of the important parameters of liquid lenses is the stability of the optical characteristics (the focal length or the magnification) during continuous operation for a long time. This is related to the fact that the lens operation is ensured by a continuous supply of heat flux into the liquid, which, in turn, can lead to a change in the optical parameters due to the loss of liquid caused by evaporation. Note that a change in the focal length caused by a variation of the refractive index of the liquid due to an increase in temperature or a change in the concentration of components is insignificant (within the measurement error) compared to that due to a change in the curvature of the lens surface. A study of the stability of the thermocapillary lens was performed for a droplet of benzyl alcohol (0.6 μl in volume, an initial focal length of 23 mm) at different values of the laser beam power. In this case, as an optical parameter of the lens, it was convenient to use the linear magnification, M. Fig. 8(a) shows the time dependencies of the linear magnification in the liquid lenses controlled by the thermocapillary forces at different powers of the laser beam. Our previous study30 showed that the accommodation time of the thermocapillary lens in response to the applied laser beam power is determined by attaining a stationary temperature gradient along the free surface of the lens, and is less than 1 s. Therefore, in the current study, we do not pay attention to this period of time. As can be seen in Fig. 8(a), at low values of the laser beam power from 6 to 22 mW, the lens operates in focusing mode with M > 1, and no changes in its optical characteristics are observed within up to 15 minutes of the irradiation. With an increase in the beam power above 47 mW, the linear magnification becomes M < 1; that is, the droplet works as a diverging lens. In this case, a stable M value is observed for about 100 s of operation, and then the focal length begins to increase. This is associated with a decrease in the curvature of the lens surface in the area of the thermocapillary concave deformation due to the evaporation of benzyl alcohol. After the laser was turned off, the thermocapillary lens took on a sessile droplet shape as it was before the experiment, but its focal length increased in comparison with the initial state. The latter means that, due to the pinned contact line of the droplet, the curvature of its surface decreased due to the evaporation.Thus, one may conclude that for the given conditions, the stable continuous operation of the thermocapillary lens is possible for no more than 2 minutes; after that, its optical characteristics irreversibly change.
Note that for a lens based on hygroscopic ethylene glycol, the increase in the focal length was observed already at an early stage within the first minute of irradiation due to the evaporation of the water contained. Thus, ethylene glycol is not a suitable candidate for the development of a thermocapillary liquid lens.
The steady operation of a liquid lens actuated by the solutocapillary forces was studied for the 50% liquid mixture (ethylene glycol and ethyl alcohol) of 1 μl in volume. It is important to note that the dynamic equilibrium between the rate of evaporation of ethyl alcohol from the heated area and the rate of its condensation at the droplet edge is the basis of the mechanism of the steady long-term lens operation. Fig. 8(b) shows the evolution of the lens magnification at different laser powers. As can be seen, M evolution is the opposite to that of the lens tuned by the thermocapillary forces. For the powers ranging from 11 to 39 mW, two stages of stable operation of the lens characterized by two accommodation times are identified, Fig. 8(b). The first stage lasts for around 1 min and the lens accommodation time takes on values of 10–20 s after the start of irradiation, then the focal length begins to decrease (M increases in Fig. 8(b)) and, in around 120 s of accommodation, it reaches the second stationary stage, which lasts for more than 12 minutes.
Note that according to our previous study,29 during the first stable stage, due to the balance of evaporation and condensation fluxes, loss of the lens volume caused by the evaporation is negligible. However, further heating results in an increase in the droplet edge temperature and condensation occurs predominantly on the cell walls and the top glass. In addition, due to the insufficient hermeticity of the junction between the top glass and the cell, leakage of the ethanol vapor over time occurs.
Indeed, when turning off the laser beam, the lens does not take on the initial pancake shape but becomes a sessile droplet, since the evaporation of ethanol increases the surface tension of the initial mixture, and the droplet does not wet the surface well.
Thus, we can conclude that for a liquid mixture of ethylene glycol and ethyl alcohol, continuous stable operation of the lens is possible for about 1 minute after accommodation, and then its optical parameters are irreversibly changed.
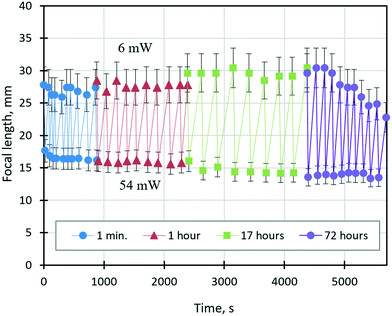
The ability of a varifocal liquid lens to change reversibly (without hysteresis) its focal length in response to a change in the beam power over a long time is crucial for its application in industrial processes where continuous autofocusing is required. Fig. 9 shows the time dependence of the focal length of the lens tuned by solutocapillary forces at cyclically changing power values of the laser beam between 6 and 54 mW. Experiments started at 6 mW, and the focal length was measured upon reaching the first stable stage (20–50 s after the laser was turned on). Then, the power was increased to 54 mW and the focal length was measured again. After about 10 such cycles of measurements, the laser was turned off, and new measurement series were repeated in 1, 17, and 72 hours. These periods of time can be considered as sleep modes when no power is applied to the lens.
To analyze the dependency shown in Fig. 9, we introduce the focal length adjustment parameter, ΔFi = Fmax − Fmin, where i is the series number, and Fmax and Fmin are the focal lengths corresponding to 6 and 54 mW, respectively. As can be seen in Fig. 9, ΔFi does not change significantly during the first two series of experiments and averaged ΔF1 = 10.7 ± 0.5 mm and ΔF2 = 11.8 ± 0.7 mm, which are within the measurement error. However, after 17 hours, ΔF expanded to ΔF3 = 14.8 ± 1.2 mm, and the focal length changed for both values of the beam power. This behavior is caused by free evaporation of ethyl alcohol from the liquid mixture and its condensation on the substrate away from the droplet during the long sleep mode. As a result, the lens volume decreased, and the curvature increased due to an increase in surface tension, which led to a decrease in the focal length at 54 mW. On the other hand, at 6 mW, the focal length increased, which is related to improving the wettability caused by an ethyl alcohol film condensed on the substrate near the lens. The dramatically decreasing ΔF4 from 16.1 to 9.3 mm during the last series is related to the decrease of Fmax values at 6 mW, Fig. 9. The latter is probably associated with free continuous evaporation of ethyl alcohol during the 72 hours of sleep mode and its leakage because of the poor hermeticity of the cell. A significant lowering of the ethyl alcohol fraction in the lens volume leads to the shrinkage of the lens aperture and the increase in its surface curvature and consequently the decrease in the focal length. However, more studies, including numerical experiments, are required.
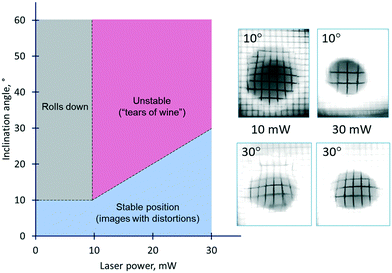
One of the crucial requirements for liquid lenses is the stability of their position and shape with respect to disturbances caused by the action of gravitational force and orientation of the lens in a gravity field. Whereas the gravitational effect on the thermocapillary lens was not detected due to its small size and the pinning of the contact line, its impact on the solutocapillary lens is notable. The stability diagram of the solutocapillary lens at different angles of inclination and powers of the laser beam is shown in Fig. 10. At powers up to 10 mW and an inclination up to 10°, the lens doesn't roll down and saves the ability of focus alteration, but its surface undergoes deformation resulting in some distortion of the obtained images. At larger angles of inclination, the lens rolls down, i.e., it is not retained in the laser beam. The increase of the laser beam power allows expansion of the inclination angle interval where the lens retains its operating ability. At 30 mW, the lens keeps its position in the laser beam even at 30° of inclination but again, its shape is deformed which is clearly seen on the distorted images of the grid mesh.
Thus, the area of the diagram limited by the values of angles in the range from 10 to 30° can be considered as the region of stable operation of the lens in the whole range of the laser beam power despite some image distortions.
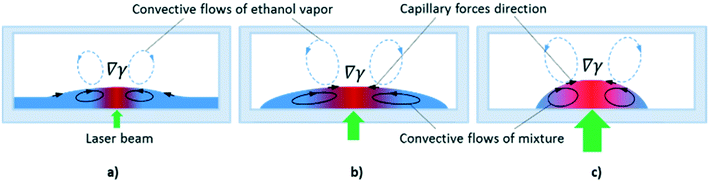
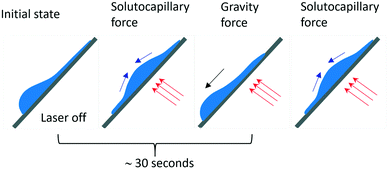
At the powers higher 10 mW, an increase in the inclination angles above the range of the stability boundary gives an interesting effect similar to the tears of wine phenomenon.45,46 When the laser beam is off, the liquid starts to move down leaving a thin liquid film on the substrate, Fig. 11. When the laser beam is incident to the film, the concentration of ethyl alcohol in the heated spot decreases resulting in the solutocapillary flows, which create the lens in the form of a sessile droplet. The stable position of the lens in the laser beam is determined by the competition between the solutocapillary forces and gravitational forces, Fig. 11. When the solutocapillary forces dominate, the lens is held in the beam spot. As the size of the lens grows, the gravitational forces begin to prevail over the solutocapillary forces and the lens moves down, like a droplet of wine on the wall of a wineglass. This process lasts for no more than 30 s, and then the solutocapillary mechanism starts to dominate, and the lens is formed again. This area in the diagram is called the area of unstable operation of the lens.
Potential improvements and applications
Despite the high level of adaptability of the proposed liquid lenses, their further application still requires overcoming a number of problems. As the present study shows, the weak points are associated with (i) evaporation of liquids that affects the stability of the lens performance and its durability and (ii) instability of the shape and position of the liquid lens caused by changing the lens orientation in the gravity field that limits its applicability.The solution to the mentioned challenges could be as follows. The long-term operation of the lens actuated by thermocapillary forces, which is limited by evaporation, can be achieved by using non-volatile liquids with a high surface tension, e.g., cinnamaldehyde and benzothiazole.47 Another way is adding a sealing immiscible liquid with a density identical to a working liquid, similar to electrowetting-driven lenses.17,18 Using such an immiscible liquid–liquid system, in turn, will also improve the stability of the lens to tilt to the horizon.
In the case of the lens actuated by solutocapillary forces, evaporation of a volatile liquid component of the mixture is a key mechanism of the lens performance. Therefore, reducing evaporation intensity may result in a decrease in the driving surface tension gradient; hence, another approach should be used. Such an approach could be the processing of internal surfaces of the housing of the cell aimed at improving the wettability, which allows reducing some of the irrevocable condensate accumulating on the internal surfaces during the laser heating.
The position stabilization of the solutocapillary lens when tilting to the horizon is a sophisticated problem since the use of two immiscible liquids of equal density is not possible. In this case, a possible solution might be applying a complex approach that combines reducing the size of a droplet, a special local surface treatment to increase the contact angle hysteresis, etc.
Nevertheless, we believe that the presented concept of liquid lenses, controlled by laser-induced surface tension forces, may be useful for some applications. These include the automatic readout of bar and QR codes in conveyor lines without mechanically shifting lenses for focusing, the design of small sized optical devices, such as endoscope cameras and benchtop optical systems to automatically control the coaxiality of light beams and optical elements, and artificial models for gaining a better understanding of the biomechanics of the human and vertebrate eyes.
Conclusions
We presented biomimetic liquid varifocal lenses actuated by laser-induced thermocapillary and solutocapillary forces. The focal length tuning is achieved by the change in the curvature of the refracting surface of a liquid in response to the change of the laser beam power. Depending on the composition of the working liquid (pure liquids or liquid mixtures) and the type of the actuating forces, the lens is able to operate in converging and diverging modes. Taking into account the thermal effect of the laser beam, which causes unavoidable evaporation of liquids, the study of the stability of the liquid lens operating for a long time is of great importance for its application as a part of complex biomimetic optical systems and artificial eyes.It was found that for the benzyl alcohol lens controlled by thermocapillary forces for about 100 s of continuous operation, evaporation is negligible, regardless of the beam power. During this time, a reversible change in the focal length is possible without changing its optical characteristics. Further irradiation leads to an irreversible decrease in its volume and a corresponding irreversible increase in focal length. However, the problem of evaporation for these lenses can be solved by using non-volatile liquids or adding a sealing liquid as in the case of electrowetting lenses.
For lenses based on a mixture of ethylene glycol and ethyl alcohol, stable operation of the lens was observed for about 1 minute after its accommodation, i.e. after the formation of a lens with a constant curvature of the refractive surface. During this time interval, the dynamic equilibrium of the evaporation and condensation fluxes of ethyl alcohol takes place and results in the reversible (without hysteresis) focal length tuning in response to the laser beam power. However, with prolonged heating, evaporation begins to dominate and the lens volume changes, which leads to an irreversible decrease in the focal length. We have also established that for the solutocapillary lens consisting of a 50% mixture of ethylene glycol and ethyl alcohol, continuous switching between two values of the focal length is possible for about 40 minutes. Note that when utilizing the solutocapillary mechanism for controlling the focal length of a liquid lens, the main problem in the present work is the poor tightness of the cell, which leads to leakage of the volatile component over long operating times. Another problem requiring a solution is distortion of the lens shape and the lens position instability in the laser beam when tilting the optical axis relative to the gravity vector. Although the lens remains in the laser beam at a tilt up to 30°, its shape is distorted causing image distortion.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was partially performed using resources from the Research Resource Center “Natural Resource Management and Physico-Chemical Research” (University of Tyumen) with the financial support of the Ministry of Science and Higher Education of the Russian Federation (contract no. 05.594.21.0019, unique identification number RFMEFI59420X0019).References
- K.-H. Jeong, J. Kim and L. P. Lee, Science, 2006, 312, 557–561 CrossRef CAS PubMed.
- L. Lun, H. Yongping and L. Fengli, 2nd International Conference on Image, Vision and Computing, 2017, pp. 592–596 Search PubMed.
- D. Shin, T. Huang, D. Neibloom, M. A. Bevan and J. Frechette, ACS Appl. Mater. Interfaces, 2019, 11, 34478–34486 CrossRef CAS PubMed.
- T. O. Kilinc, Z. Hayran, H. Kocer and H. Kurt, Proceedings Volume 10404: Infrared Sensors, Devices, and Applications VII, 2017, vol. 104040I Search PubMed.
- H. Liu, Y. Huang and H. Jiang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 3982–3985 CrossRef CAS PubMed.
- M. Garcia, T. Davis, R. Marinov, S. Blair and V. Gruev, Proc. SPIE 10655, Polarization: Measurement, Analysis, and Remote Sensing XIII, 2018, vol. 106550C Search PubMed.
- S. Yang, G. Chen, M. Megens, C. K. Ullal, Y.-J. Han, R. Rapaport, E. L. Thomas and J. Aizenberg, Adv. Mater., 2005, 17, 435–438 CrossRef CAS.
- D. Liang, K. Xiang, J.-W. Du, J.-N. Yang and X.-Y. Wang, Opt. Eng., 2014, 53(10), 105101 CrossRef.
- J.-M. Choi, H.-M. Son and Y.-J. Lee, Opt. Express, 2009, 17, 8152–8164 CrossRef PubMed.
- K. Yin, C.-Y. Lai, J. Wang, S. Ji, J. Aldridge, J. Feng, A. Olah, E. Baer and M. Ponting, Opt. Eng., 2018, 57(2), 027101 Search PubMed.
- J. Charmet, R. Barton and M. Oyen, Bioinspiration Biomimetics, 2015, 10, 046004 CrossRef PubMed.
- E. Förster, M. Stürmer, U. Wallrabe, J. Korvink and R. Brunner, Opt. Express, 2015, 23, 929–942 CrossRef PubMed.
- J. W. Bae, E.-J. Shin, J. Jeong, D.-S. Choi, J. E. Lee, B. U. Nam, L. Lin and S.-Y. Kim, Sci. Rep., 2017, 7, 2068 CrossRef PubMed.
- C. DeBoer, J. Lee, B. Wheelan, C. Cable, W. Shi, Y.-C. Tai and M. Humayun, IEEE Trans. Biomed. Eng., 2016, 63, 1129–1134 Search PubMed.
- B. Berge and J. Peseux, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 3, 159–163 CrossRef CAS.
- T. Krupenkin, S. Yang and P. Mach, Appl. Phys. Lett., 2003, 82, 316–318 CrossRef CAS.
- C. Li and H. Jiang, Appl. Phys. Lett., 2012, 100, 231105 CrossRef PubMed.
- S. Kuiper and B. Hendriks, Appl. Phys. Lett., 2004, 85, 1128–1130 CrossRef CAS.
- O. Supekar, M. Zohrabi, J. Gopinath and V. Bright, Langmuir, 2017, 33, 4863–4869 CrossRef CAS PubMed.
- C. Cheng, C. Chang and J. Yeh, Opt. Express, 2006, 14, 4101–4106 CrossRef PubMed.
- C. Cheng and J. Yeh, Opt. Express, 2007, 15, 7140–7145 CrossRef PubMed.
- S. Xu, H. Ren, Y. Liu and S. Wu, J. Microelectromech. Syst., 2011, 20, 297–301 Search PubMed.
- Q. Chen, T. Li, Y. Zhu, W. Yu and X. Zhang, Opt. Express, 2018, 26, 6532–6541 CrossRef CAS PubMed.
- K. Jeong, G. Liu, N. Chronis and L. Lee, Opt. Express, 2004, 12, 2494–2500 CrossRef PubMed.
- D. Zhang, V. Lien, Y. Berdichevsky, J. Choi and Y. Lo, Appl. Phys. Lett., 2003, 82, 3171–3172 CrossRef CAS.
- D. Zhang, N. Justise and Y. Lo, Appl. Phys. Lett., 2004, 84, 4194–4196 CrossRef CAS.
- H. Oku, K. Hashimoto and M. Ishikawa, Opt. Express, 2004, 12, 2138–2149 CrossRef PubMed.
- Y. Fuh, M. Lin and S. Lee, Opt. Lasers Eng., 2012, 50, 1677–1682 CrossRef.
- A. Malyuk and N. Ivanova, Opt. Commun., 2017, 392, 123–127 CrossRef CAS.
- A. Malyuk and N. Ivanova, Appl. Phys. Lett., 2018, 112, 103701 CrossRef.
- D. Lide, CRC Handbook of Chemistry and Physics, Internet version, 2005 Search PubMed.
- K. Chen, Y. Lin and C. Tu, J. Chem. Eng. Data, 2012, 57, 1118–1127 CrossRef CAS.
- S. Tang, B. Mayers, D. Vezenov and G. Whitesides, Appl. Phys. Lett., 2006, 88, 061112 CrossRef.
- H. Liu, Y. Shi, L. Liang, L. Li, S. Guo, L. Yin and Y. Yang, Lab Chip, 2017, 17, 1280–1286 RSC.
- S. Azizian and N. Bashavard, J. Chem. Eng. Data, 2005, 50, 709–712 CrossRef CAS.
- Engineering Tool Box, Vapour Pressure common Liquids, 2006, Access: https://www.engineeringtoolbox.com/vapor-pressure-d_312.html Search PubMed.
- G. Da Costa and J. Calatroni, Appl. Opt., 1978, 17, 2381–2385 CrossRef CAS PubMed.
- J. Calatroni and G. Da Costa, Opt. Commun., 1982, 42, 5–9 CrossRef.
- H. Helmers and W. Witte, Opt. Commun., 1984, 49, 21–23 CrossRef.
- D. L. Hitt and M. K. Smith, Phys. Fluids A, 1993, 5, 2624–2632 CrossRef CAS.
- J. Longtin, K. Hijikata and K. Ogawa, Int. J. Heat Mass Transfer, 1999, 42, 85–93 CrossRef CAS.
- B. A. Bezuglyi and O. A. Tarasov, Opt. Spectrosc., 2002, 92(4), 609–613 CrossRef CAS.
- K. Tatosova, A. Malyuk and N. Ivanova, Colloids Surf., A, 2016, 521, 22–29 CrossRef.
- N. A. Ivanova, A. V. Tatosov and B. A. Bezuglyi, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38(6), 60 CrossRef PubMed.
- M. Loewenthal, Philos. Mag., 1931, 12, 462 Search PubMed.
- D. C. Venerus and D. N. Simavilla, Sci. Rep., 2015, 5, 16162 CrossRef CAS PubMed.
- N.-T. Nguyen, Biomicrofluidics, 2010, 4, 031501 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2020 |