Experimental measurement and prediction of ionic liquid ionisation energies

Abstract

Ionic liquid (IL) valence electronic structure provides key descriptors for understanding and predicting IL properties. The ionisation energies of 60 ILs are measured and the most readily ionised valence state of each IL (the highest occupied molecular orbital, HOMO) is identified using a combination of X-ray photoelectron spectroscopy (XPS) and synchrotron resonant XPS. A structurally diverse range of cations and anions were studied. The cation gave rise to the HOMO for nine of the 60 ILs presented here, meaning it is energetically more favourable to remove an electron from the cation than the anion. The influence of the cation on the anion electronic structure (and vice versa) were established; the electrostatic effects are well understood and demonstrated to be consistently predictable. We used this knowledge to make predictions of both ionisation energy and HOMO identity for a further 516 ILs, providing a very valuable dataset for benchmarking electronic structure calculations and enabling the development of models linking experimental valence electronic structure descriptors to other IL properties, e.g. electrochemical stability. Furthermore, we provide design rules for the prediction of the electronic structure of ILs.

---

Kevin R. J. Lovelock

Kevin Lovelock has been selected as a PCCP Emerging Investigator. He held an Imperial College London Junior Research Fellowship from 2012 to 2015, followed by a year as a stay-at-home dad. In 2016 he was awarded a Royal Society University Research Fellowship, hosted by the University of Oxford; in 2017 he switched his fellowship to the University of Reading. His current research interests include studying ions in solution and at interfaces for energy applications using both laboratory and synchrotron X-ray spectroscopy.

---

1. Introduction

Ionisation energy, E_i, is a key descriptor for chemical, photochemical and electrochemical reactivity,^1–5 especially any application that involves exchange of electrons, particularly formal donation of an electron (ionisation) or donation of electron density (partial ionisation). For ionic liquids (ILs), these potential applications include: electrochemical energy storage; gas capture/separation/storage; as solvents for catalysis and metal extraction/separation.^6–11 The identity of the most readily ionised valence state, often called the highest occupied molecular orbital (HOMO),¹² is also a reactivity descriptor, particularly for ILs given the HOMO could come from the anion or from the cation. Furthermore, given their importance, E_i and the HOMO identity can be used for quantitative validation of calculations of ILs.¹³E_i can be used to validate methods, e.g. choice of functional/basis set in density functional theory (DFT) can be benchmarked.¹³ HOMO identity can be used to validate the ability of calculations to capture the solvation effects of ions in liquid phase. However, for ILs there is limited experimental data on electronic structure, including E_i and HOMO identity.

Most measurements of E_i have been made using non-resonant X-ray photoelectron spectroscopy (XPS) and ultraviolet photoelectron spectroscopy (UPS).¹⁴ Almost all E_i values for ILs, E_i(IL), have been measured on vaporised gas phase neutral ion pairs.^15–26 Whilst measuring E_i is relatively facile in the gas phase, a major problem is that most ILs are very tricky to vaporise without significant thermal decomposition occurring/dominating, meaning many IL ion pairs cannot be easily studied in the vapour phase;^27–32 furthermore, vapour phase ion pairs do not have the complete solvation environment of the liquid phase. A major hurdle for measuring reliable, reproducible, and comparable binding energies (E_B)¹⁴ and E_i for liquid phase ILs is dealing with sample charging during XPS measurements, which is not understood.^33,34 A widely-used, very robust method of charge referencing XP spectra for ILs is using E_B(C_alkyl 1s) = 285 eV for ILs with relatively long alkyl chains, usually –C₈H₁₇.^33,35–48E_B values of valence states using this charge referencing method have been reported, e.g. E_B(HOMO), E_B(cation HOFO) and E_B(anion HOFO), where the ion HOFOs are the highest occupied fragment orbital of each ion (one of which is the IL HOMO).⁴⁸ However, all of these E_B values were effectively charge referenced to an apparent Fermi level for the alkyl chains, not the vacuum level. Reporting of experimental E_i(IL) values (by definition, charge referenced to the vacuum level) for liquid phase ILs have been very limited, with little or no mention of charge referencing given;^49–51 these studies were published before IL sample charging was an acknowledged problem. Recently, E_i(C_C–C/C–H 1s) = 289.58 ± 0.14 eV was given as a reference to the vacuum level for C–C/C–H carbon adsorbed on conducting metal surfaces,^52–56 although this value has not been applied to IL XPS data to date.

A key challenge is to identify the valence states for ILs. Most importantly, which of the cation and the anion gives rise to the HOMO? For traditional salts such as NaCl, the anion is very clearly the HOMO, with the Na 2p cation HOFO valence state ∼26 eV larger E_B than the Cl 3p anion HOFO.⁵⁷ However, for ILs E_B of the cation HOFO and anion HOFO are far more similar. Furthermore, ILs have a relatively large number of valence electrons per the cation–anion molecular unit. Water and NaCl both have eight valence electrons and therefore the valence states are relatively easy to identify using XPS.^57–60 In contrast, common ILs can have between 50 and 300 valence electrons.⁶¹ Therefore, ILs have many valence states at similar E_B. Compounding this problem, the large range of ion solvation environments in the liquid phase is expected to give a significant range of E_B for the nominally the same valence state, as demonstrated for Cl⁻ ion solvated in water.⁶² Consequently, valence XP spectra of ILs often have many overlapping contributions, making the separation of cation and anion contributions very difficult. The most common laboratory-based XPS apparatus employs Al Kα radiation at hν = 1486.6 eV, giving non-resonant XPS. Valence XPS data from hν = 1486.6 eV has been analysed using a visual fingerprint method and subtraction,⁴⁸ although this approach is difficult when using results measured on different apparatus. Furthermore, for XPS measured at hν = 1486.6 eV the most important contributors to cation-based valence states, C 2p and N 2p, have very low photoionisation cross-sections relative to many of the common anion-based valence states, e.g. Cl 3p, S 3p, making identification of cationic-based valence states very challenging in particular. Measuring photoelectron spectroscopy with a second hν, e.g. hν = 21.2 eV from He(I) giving non-resonant UPS, helps valence state identification due to variation in photoionisation cross-sections with varying hν.^48,63–68 However, most valence state identification for ILs to date has relied on comparisons to calculations; this situation is less than ideal when trying to use experimental data to validate calculations. Valence state identification for ILs has mostly been limited to ILs comprised of [C_nC₁Im]⁺ (1-alkyl-3-methylimidazolium), with a small selection of commonly studied anions, particularly cyano-based anions and [NTf₂]⁻ (bis[(trifluoromethane)sulfonyl]imide).^48,63–73 A recent development has been the use of resonant Auger electron spectroscopy (RAES, also known as resonant XPS, RXPS), which allows identification of valence states, particularly those states with strong π-bonding contributions, e.g. imidazolium ring, cyano-based anions.⁴⁸ Using an approach combining variable hν XPS and RXPS, key values for 37 ILs were determined: E_B(HOMO), E_B(cation HOFO) and E_B(anion HOFO).⁴⁸ ΔE_B(ion HOFO) = E_B(cation HOFO) − E_B(anion HOFO) has been used as the key variable for judging IL HOMO identity.⁴⁸ For [C_nC₁Im][A] ILs (where [A]⁻ = anion), XPS data charge referenced to E_B(C_alkyl 1s) = 285.0 eV gave E_B(cation HOFO) = 4.8 ± 0.4 eV (independent of [A]⁻) and the [C_nC₁Im]⁺ HOFO (at least for n ≤ 8) was composed of N 2p and C 2p contributions from the imidazolium ring.⁴⁸ For the ILs [C_nC₁Im][BF₄], [C₄C₁Im][PF₆] and [C₆C₁Im][B(CN)₄] the cation (rather than the anion) has been identified as giving rise to the HOMO.^{48,49,74–76}

The possibility, out of the potentially vast number of ILs, that an ideal IL exists for a particular application is an appealing prospect. The challenge of synthesising, characterising and testing a large number of potential ILs for an application is daunting and makes screening using predictions hugely advantageous. One important question for understanding and predicting IL properties is: how independent is the electronic structure of the cation from the anion and vice versa? Using XPS it has been demonstrated implicitly, i.e. by studying core state E_B for elements located specifically in the cation, that the anion influenced the valence electronic structure of the cation (for the cations imidazolium,^35,37 pyridinium,^41,45 ammonium (linear³⁹ and cyclic^36,44) and phosphonium³⁹). Anions with larger Kamlet–Taft β solvent parameters gave lower E_B, e.g. E_B(N_cation 1s) and E_B(C_ring 1s) for [C₈C₁Im][A], and vice versa.^35,37,77 Furthermore, using XPS it has been demonstrated that the cation influenced the electronic structure of the anion; [C₈C₁Im][A] gave larger core state E_B for elements located specifically in the anion (denoted here as E_B(element_anion core)) than [P_6,6,6,14][A] when [A]⁻ was the same.⁷⁸ However, to date no experimental studies have been published to explicitly demonstrate the influence of cation–anion interactions on IL valence states.

Quantitative comparisons of IL electronic structure experimental descriptors to other experimentally measured physical properties are very limited, principally due to a lack of IL electronic structure experimental descriptors. A positive correlation was found between E_B(HOMO) from XPS and anodic stability for [C₂C₁Im][A] where [A]⁻ = [N(CN)₂]⁻, [C(CN)₃]⁻ and [B(CN)₄]⁻; both E_B(HOMO) and the anodic stability were largest when [A]⁻ = [B(CN)₄]⁻ and smallest when [A]⁻ = [C(CN)₃]⁻.⁶⁹ Gas phase E_i(IL) have been compared to electrochemical stability for a number of ILs (the IL choice being limited to those ILs that can be vaporised).²⁵

Comparisons exist between liquid phase experimental XP/UP spectra for ILs and calculated data, but the structural range of ILs studied is limited.^{24,49,64–70,72–76,79} Calculations showed the HOMO came from the cation for [C_nC₁Im][BF₄] (n = 1, 2, 4),^24,80–82 [C₄C₁Im][PF₆],^24,81,82 [C₂C₁Im][B(CN)₄],^73,83 which matched well to experimental HOMO identification,^{48,49,74–76} demonstrating that for this limited range of ILs the calculations captured the solvation of the cation and anion acceptably. E_i(IL) values have been calculated, e.g. ref. 84–87. Absolute comparisons of calculated E_i(IL) and experimental E_B values are unsatisfactory due to the calculated data being charge referenced to the vacuum level and the experimental data being charge referenced to a Fermi level (of e.g. metal substrate or alkyl carbon). Therefore, a lack of experimental E_i(IL) data means validation of calculated IL electronic structure, e.g. functional/basis set choices, has not been possible to date.

Calculated IL electronic structure descriptors, e.g. E_i(IL), have been used to predict other properties, e.g. electrochemical stability^{82–84,86–91} and thermal stability.^92,93 For a very small number of ILs a linear correlation between anodic stability and calculated E_i was identified, showing promise for such comparisons;⁸⁸ such comparisons should be made against experimental data measured on inert electrodes to minimise the importance of specific chemical reactivity with the electrode materials.⁸⁴ For quantitative structure–property relationships (QSPR), IL electronic structure descriptors such as E_i have been used to understand and predict IL properties.⁹⁴ Importantly, the accuracy of these calculated electronic structure descriptors is not routinely validated against IL experimental electronic structure data, most likely due to a lack of available experimental data.

In this article, we investigate IL valence electronic structure using experimental methods, without the aid of calculations. Key ions studied are given in Fig. 1; all 60 ILs studied in this paper are given in ESI,† Table S1. All 60 ILs were liquid at room temperature, making XPS experiments relatively straightforward, as no heating was required for any IL studied here. Compared to the ILs studied in ref. 48, two new cation cores were studied here, [C_nC₁Pyrr]⁺ and [C_nPy]⁺. Furthermore, 20 new anions were studied, with a variety of properties/reasons to study; how the new anions were chosen is given in ESI,† Section S1. We have studied a total of 60 ILs using laboratory-based XPS; 37 ILs from ref. 48 and 23 ILs newly published here. 18 of these ILs were studied using synchrotron resonant XPS (also known as RAES); 7 ILs from ref. 48 and 11 ILs newly published here. We have measured E_i for all 60 ILs using a combination of our E_B(HOMO) values and applying a charge referencing method that is new to ILs. Furthermore, we have identified the HOMO for all 60 ILs and have quantified the electronic effect of the cation on the anion, and vice versa. Finally, we have predicted E_i and the HOMO identity for a further 516 ILs.

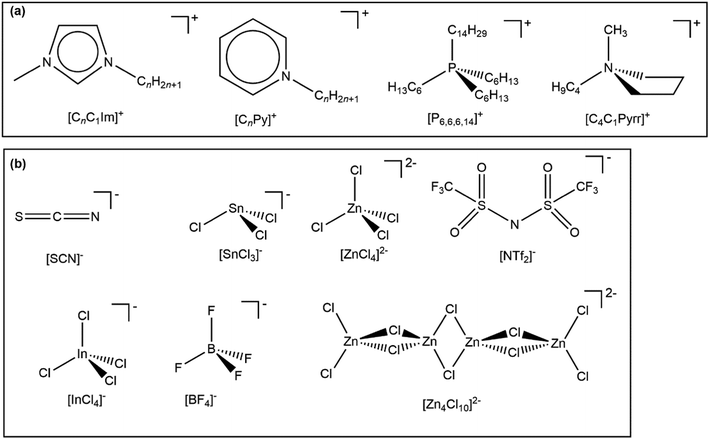Fig. 1 Key ions studied in this paper. A full list of ILs studied is given in the ESI,† Table S1.

2. Experimental

2.1. IL synthesis

Details of IL synthesis are given in the ESI,† Section S1.

2.2. Laboratory XPS

Laboratory-based XPS was carried out using four separate XP spectrometers for the 23 ILs studied here. In general, a drop of IL was placed directly onto a stainless steel sample plate (one IL was studied on a glass substrate). This sample was placed in a loadlock and the pressure reduced to 10⁻⁷ mbar by pumping down for >6 hours. After attaining the required pressure, the IL was transferred to the analysis chamber. Etching (where necessary) was carried out using a 500 eV Ar⁺ ion gun (∼10 minutes per sample). Acquisition parameters were matched where possible to give comparable energy resolution; generally, a pass energy of 20 eV was used for core states and ∼40 eV for valence states.

(i) Non-resonant XPS of 16 ILs were recorded at University College London on a Thermo Scientific K-alpha monochromated Al Kα source (hν = 1486.6 eV) spectrometer. Charge compensation was achieved using a dual beam flood gun which applied both electrons and low energy Ar⁺ ions to the sample.

(ii) Non-resonant XPS of 16 ILs were recorded at University College London on a Thermo Scientific Theta Probe monochromated Al Kα source (hν = 1486.6 eV) spectrometer. Charge compensation was achieved using a dual beam flood gun which applied both electrons and low energy Ar⁺ ions to the sample.

(iii) Non-resonant XPS of four ILs were recorded at the University of Nottingham on a Kratos Axis Ultra equipped with a monochromatic Al Kα source (hν = 1486.6 eV). The core states were published already in ref. 36 and 41–43. Charge compensation was achieved using a flood gun which applied low energy Ar⁺ ions to the sample.

(iv) Non-resonant XPS of one IL was recorded at Harwell XPS using a Kratos Axis Ultra DLD equipped with a monochromatic Al Kα source (hν = 1486.6 eV). The X-ray source was operated at 150 W (10 mA × 15 kV). Charge compensation was achieved using a flood gun which applied low energy Ar⁺ ions to the sample.

2.3. Synchrotron XPS and resonant XPS

Synchrotron XPS and resonant XPS were carried out using two separate beamlines, I09 and B07 at Diamond Light Source. In both cases a thin IL film was spread from less than 0.1 ml droplet on a tantalum sample holder so no drop could be observed by eye.

The soft synchrotron XPS for [C₈C₁Im][SnCl₃] was performed on the I09 beamline at Diamond Light Source (UK).⁹⁵ The XP spectra and RXP/RAE spectra were acquired using a VG Scienta EW4000 HAXPES analyser, which had an angular acceptance of ±30°. The analyser was mounted with its lens axis approximately 90° away from the direction of the incident X-ray light in a horizontal plane; the analyser slits (and thus the angular acceptance direction) were also in the horizontal plane. Due to significant observable beam damage/sample charging (ESI,† Section S2), the flux of the synchrotron light was decreased by first defocussing the incident light ∼20 fold and by detuning the undulator (i.e. offsetting the undulator gap) away from the maximum intensity so as to detune the flux a further 100-fold. Prior to XPS measurements the sample was Ar⁺ sputtered for 30 minutes at a voltage of 500 V.

The soft synchrotron XPS for 10 ILs was performed on the B07 beamline at Diamond Light Source (UK).⁹⁶ A thin film (less than 0.1 ml, essentially so no drop could be observed) of the IL sample was placed on a tantalum sample holder. For the T-cup apparatus, nine ILs were measured at the N 1s edge. Due to significant observable beam damage, the flux was reduced by using the 1200 l mm⁻¹ grating (T-cup apparatus only). For the T-pot apparatus, one IL was measured at the C 1s edge. Due to significant observable beam damage, the sample was rastered continually perpendicular to the analyser entrance nozzle during X-ray irradiation (T-pot apparatus only); this rastering allowed a higher flux (400 l mm⁻¹ grating) to be used than for the T-cup apparatus.

The RXPS/RAES data were acquired across the N 1s edge (hν ∼ 402 eV) or the C 1s edge (hν ∼ 285 eV); at each hν a RXP spectrum was acquired. Partial electron yield near edge X-ray absorption fine structure (NEXAFS) spectra for the N 1s and C 1s edges were recorded by summing the recorded RAE/RXPS intensity at each hν.

2.4. Analysing XP spectra

All non-resonant XP spectra were fitted using the CASAXPS™ software. Fitting was carried out using a Shirley background and GL30 line shapes (70% Gaussian, 30% Lorentzian). The peak constraints used for core XP spectra are outlined ESI,† Section S3 and peak constraints used for valence XP spectra are outlined ESI,† Section S4. The purity of the ILs studied here is demonstrated in the ESI,† Section S7.

2.5. Charge referencing methods for XP spectra

All XP spectra for ILs were effectively charge referenced to C–C/C–H carbon for long alkyl chains. Two different values of E_B(C_alkyl 1s) were used.

(a) E_B(C_alkyl 1s) = 285.00 eV, which is equivalent to charge referencing to the Fermi level for long alkyl chains. This E_B value is standard in the IL literature.^33,35–48

(b) E_i(C_alkyl 1s) = 289.58 eV,^52–56 which is equivalent to charge referencing to the vacuum level for long alkyl chains. Adding the work function⁹⁷ for long alkyl chains would convert E_B to E_i.¹⁴ The C–C/C–H carbon contribution to adventitious carbon has been found to match the vacuum level when setting E_i(C_alkyl 1s) = 289.58 ± 0.14 eV.^52–56 For our measurements, this value effectively means the work function was 289.58 − 285.00 = 4.58 eV. This value for the effective work function of alkyl carbon matches to expected work functions, which often range from 4 eV to 5 eV.⁹⁸ Therefore, to produce E_i values referenced to the vacuum level from our E_B values charge referenced to E_B(C_alkyl 1s) = 285.0 eV, we added 4.58 eV (Table 1). This charge referencing approach has not been used for ILs to date.

Table 1 How key valence electronic structure descriptors were determined

Descriptors referenced to Fermi level	How determined	Descriptors referenced to vacuum level	How determined	Descriptors for which the reference level does not matter	How determined
E B(anion HOFO)	Peak fitting and/or estimation	E i(anion)	E B(anion HOFO) + 4.58 eV
E B(cation HOFO)	Peak fitting and/or estimation	E i(cation)	E B(cation HOFO) + 4.58 eV
E B(HOMO)	Lowest value of EB(anion HOFO) and EB(cation HOFO)	E i(IL)	E B(HOMO) + 4.58 eV	ΔEB(ion HOFO)	E B(cation HOFO) − EB(anion HOFO)
E B(anion onset)	Onset method and/or estimation	E th(anion)	E B(anion onset) + 4.58 eV
E B(cation onset)	Onset method and/or estimation	E th(cation)	E B(cation onset) + 4.58 eV
E B(IL onset)	Lowest value of EB(anion onset) and EB(cation onset)	E th(IL)	E B(IL onset) + 4.58 eV	ΔEB(ion onset)	E B(cation onset) − EB(anion onset)
E B(cation HOFO,pred.) for [CnC1Im][A]	E B(Ncation 1s) − 397.1 eV	E i(cation,pred.) for [CnC1Im][A]	E B(cation HOFO,pred.) + 4.58 eV
E B(cation,pred.) for [CnC1Im][A]	E B(cation onset,pred.) − 1.1 eV	E th(cation,pred.) for [CnC1Im][A]	E i(cation,pred.) − 1.1 eV
				HOMO identity	ΔEB(ion HOFO), ΔEB(ion onset) and visual assessment

---

For the 60 ILs studied here, six different charge referencing methods were used to charge reference to E_B(C_alkyl 1s); all charge referencing was carried out after the measurements were completed.

(i) 36 ILs had a sufficiently long alkyl chain that a fitted component for E_B(C_alkyl 1s) for long alkyl chains was used for charge referencing all XP spectra. This approach to charge reference to E_B(C_alkyl 1s) has a very high confidence, with an error of less than ±0.1 eV.

(ii) 16 [C_nC_mIm][A] (where n ≤ 4 and m = 1 or 0) ILs where [C₈C₁Im][A] IL with the same anion had already been studied, so E_B(N_cation 1s) or E_B(element_anion core) was used for charge referencing all XP spectra, effectively charge referenced to E_B(C_alkyl 1s) for long alkyl chains. This approach has a very high confidence, with an error of less than ±0.1 eV.

(iii) 1 IL, [C₄C₁Im][MeSO₄], E_B(N_cation 1s) for [C₄C₁Im][OcSO₄] was used to charge reference all XP spectra. As both anions are alkylsulfate, the same functional group was interacting with the countercations; hence, this approach to effectively charge reference to E_B(C_alkyl 1s) has a very high confidence, with an estimated error of less than ±0.1 eV.

(iv) 1 IL, [C₄C₀Im][HSO₄] with a protic cation, E_B(C_alkyl 1s) for [C₄C₁Im][HSO₄] was used to charge reference all XP spectra. As n = 4, based on data in ref. 33, this approach to effectively charge reference to E_B(C_alkyl 1s) has an estimated error of ±0.2 eV.

(v) 4 ILs with relatively short alkyl chains, where an IL with the same anion and a different cation with a long alkyl chain had already been studied (i.e. ILs from charge referencing method i) but the cation was new for XPS studies, so E_B(element_anion core) from [C₈C₁Im][A] was used for charge referencing all XP spectra. Based on data for [C][A] (where [C]⁺ = cation) where the cation was varied (all with sufficiently long alkyl chains) and the anion kept constant, E_B(element_anion core) varied by a maximum of 0.4 eV.⁷⁸ Therefore, this approach to effectively charge reference to E_B(C_alkyl 1s) has an error of ±0.2 eV.

(vi) 2 [C_nC₁Im][A] (where n ≤ 4) ILs where the anion had not been studied for [C₈C₁Im][A] previously, so E_B(N_cation 1s) = 401.9 eV was used for charge referencing all XP spectra as an average E_B(N_cation 1s) value. Almost all [C₈C₁Im][A] ILs gave 401.7 eV < E_B(N_cation 1s) < 402.1 eV;^33,35 therefore, this approach to effectively charge reference to E_B(C_alkyl 1s) has an error of ±0.2 eV.

Details of the charge referencing method applied to the synchrotron XP spectra are given in ESI,† Section S5.

2.6. Determining key valence electronic structure descriptors

The onset method used to determine E_B(anion onset), E_B(cation onset) and E_B(IL onset) is explained in ref. 48. Threshold energies, E_th(IL), were obtained by adding 4.58 eV to E_i(IL onset), the IL onset energy charge referenced to the vacuum level); these E_th(IL) values are compared to literature values.

The valence electronic structure descriptors charge referenced to the Fermi level are given in column 1 of Table 1, and how they were determined in column 2. Values for valence electronic structure descriptors charge referenced to the Fermi level are given: E_B(HOMO) (ESI,† Table S5), E_B(anion HOFO) and E_B(anion onset) (ESI,† Tables S5 and S6), E_B(cation HOFO) and E_B(cation onset) (ESI,† Tables S5 and S7), E_B(cation HOFO,pred.) (Table 4 and ESI,† Table S8).

The valence electronic structure descriptors charge referenced to the vacuum level are given in column 3 of Table 1, and how they were determined in column 4. Values for valence electronic structure descriptors charge referenced to the vacuum level are given: E_i(IL) values (Table 3), E_i(anion) and E_i(cation) (ESI,† Tables S6 and S7 respectively) and E_i(cation,pred.) (Table 4 and ESI,† Table S8).

The valence electronic structure descriptors for which the reference level does not matter are given in column 5 of Table 1, and how they were determined in column 6. Values for valence electronic structure descriptors for which the reference level does not matter are given: ΔE_B(ion HOFO), ΔE_B(ion onset) and HOMO identity in Table 3 and ESI,† Table S5.

3. Experimental results

3.1. Determining E_B and E_i

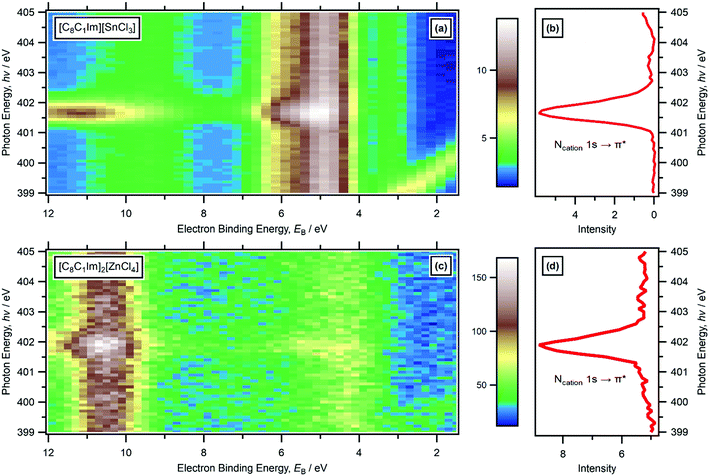
For five ILs studied here ([C₈C₁Im][BF₄], [C₄C₁Im][PF₆], [C₂C₁Im][FAP], [C₈C₁Im][SbF₆] and [C₈Py][BF₄]) the lowest E_B feature due to cationic valence states in the non-resonant valence XP spectra was observable at 4 eV < E_B < 7 eV (Fig. 2 and ESI,† Fig. S9f, S12f, S13f, S14f, S15f). However, for 18 ILs studied here, features due to cationic valence states were not readily observed in non-resonant valence XP spectra recorded at hν = 1486.6 eV due to features from the anion valence states dominating (ESI,† Fig. S10–S32); the photoionisation cross-sections of N 2p and C 2p atomic orbitals (AOs) are much lower than many of the anion-based AOs, e.g. Cl 3p.⁹⁹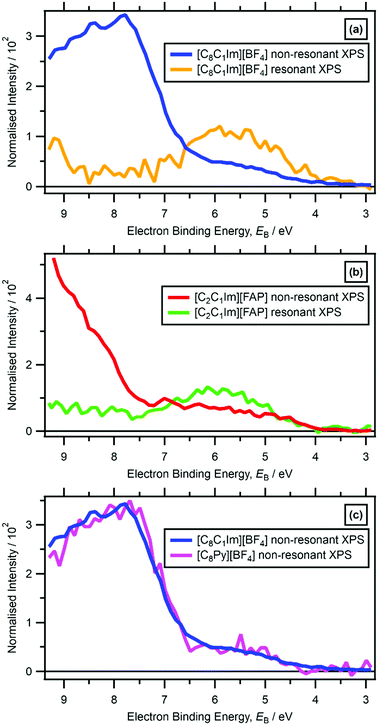

Fig. 2 Subtracted N_cation RXP spectrum and non-resonant laboratory valence XPS at hν = 1486.6 eV for: (a) [C₈C₁Im][BF₄], (b) [C₂C₁Im][FAP]. (c) Non-resonant laboratory valence XPS at hν = 1486.6 eV for [C₈C₁Im][BF₄] and [C₈Py][BF₄]. These RXPS traces were produced by subtraction of resonant XP spectrum minus non-resonant XP spectrum using the procedure outlined in ref. 48. All electron spectra were charge referenced using methods outlined in Section 2.4.

For RXPS of the 15 [C_nC₁Im]⁺-based ILs reported here and in ref. 48, including for [C₈C₁Im][SnCl₃] and [C₈C₁Im]₂[ZnCl₄], a broad feature due to resonant enhancement was observed at hν ≈ 402 eV and 3.5 eV < E_B(N_cation RXPS) < 7.5 eV (Fig. 3a, c, 4 and ESI,† Fig. S44). hν ≈ 402 eV corresponded to X-ray absorption from the N_cation 1s core state to imidazolium ring π* unoccupied valence state(s) (Fig. 3b and d).^48,100 The feature at 3.5 eV < E_B(N_cation RXPS) < 7.5 eV was from participator Auger transitions involving valence states with good overlap with the N_cation 1s core hole. Consequently, for [C_nC₁Im]⁺-based ILs, valence states at 3.5 eV < E_B(N_cation RXPS) < 7.5 eV had strong contributions from N_cation in the imidazolium ring, i.e. from N_cation 2p-based AOs. The anion charge ([A]⁻ or [A]²⁻) did not have a strong effect on E_B(N_cation RXPS) (Fig. 4). The average E_B(N_cation 2p) for [C₈C₁Im][A] was estimated as E_B ∼ 5.7 eV (Fig. 4). Based on results presented in ESI,† Fig. S45 and ref. 48, the lowest E_B(C_cation 2p) for [C₈C₁Im][A] was at ∼0.9 eV lower than the feature at E_B ∼ 5.7 eV for E_B(N_cation 2p) and represents the cation HOFO, as summarised in ESI,† Fig. S47 and the accompanying text. Therefore, for [C₈C₁Im][A] and [C₈C₁Im]₂[A] charge referenced to E_B(C_alkyl 1s) = 285.0 eV, E_B(cation HOFO) = 4.8 ± 0.4 eV, independent of the identity of the anion [A]⁻ or [A]²⁻. For two of the [C_nC₁Im]⁺-based ILs studied here, [C₈C₁Im][BF₄] and [C₂C₁Im][FAP], the nitrogen and carbon RXPS features matched very well to the lowest E_B feature in the non-resonant valence XP spectra (Fig. 2a and b). This observation demonstrated that our use of RXPS to identify E_B(cation HOFO) was very reliable. A similar analysis can be made for [C_nPy][A] (see ESI,† Section S8 for more details). Overall, when charge referenced to E_B(C_alkyl 1s) = 285.0 eV, E_B(cation HOFO) = 5.3 ± 0.6 eV for [C_nPy][A].

Fig. 3 RXPS N 1s edge data. [C₈C₁Im][SnCl₃]: (a) heat map of hν against E_B for the N 1s edge; (b) partial electron yield NEXAFS spectrum for the N 1s edge. [C₈C₁Im]₂[ZnCl₄]: (c) heat map of hν against E_B for the N 1s edge; (d) partial electron yield NEXAFS spectrum for the N 1s edge. These RXPS plots represent the raw data, with no subtraction performed. All electron spectra were charge referenced using methods outlined in Section 2.4. The features at 399 eV < hν < 401 eV and 0 eV < E_B < 3 eV were due to N 1s photoemission from 2nd order light.

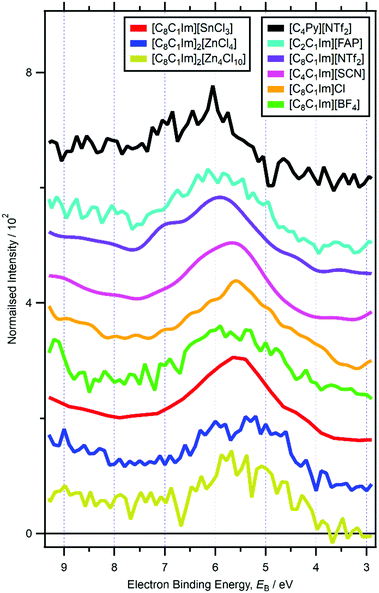Fig. 4 Subtracted RXP spectra for N_cation for nine ionic liquids (hν ∼ 402 eV). These RXPS traces were produced by subtraction of resonant XP spectrum minus non-resonant XP spectrum using the procedure outlined in ref. 48. All electron spectra were charge referenced using methods outlined in Section 2.4.

For ILs with quaternary cations (e.g. [N_4,1,1,0][HSO₄], [N_8,8,8,1][NTf₂], [P_6,6,6,14][A]), the number of alkyl carbons had a dramatic effect on E_B(cation HOFO). For [N_4,1,1,0][HSO₄] E_B(cation HOFO) = 6.5 eV and for [N_8,8,8,1][NTf₂] and [P_6,6,6,14][A] E_B(cation HOFO) = 5.0 eV (ESI,† Table S5), demonstrating that longer alkyl chain lengths gave smaller E_B(cation HOFO). At this stage, the relationship between the number alkyl carbons/length of alkyl chain and E_B(cation HOFO) is unclear. For imidazolium-based ILs where a feature from cationic valence states were readily observed in non-resonant XPS (i.e. [C₈C₁Im][BF₄], [C₈C₁Im][SbF₆], [C₆C₁Im][B(CN)₄], [C₄C₁Im][PF₆], [C₂C₁Im][FAP]), there was no clear effect of the alkyl chain length on E_B(cation HOFO). This observation is most likely because the cation HOFO was from the imidazolium ring and not from the alkyl chain. E_B(cation HOFO) was much lower for [N_{2OH,2OH,2OH,1}][TfO] compared to [N_4,1,1,0][HSO₄] (1.7 eV lower), certainly more than any effect due to the different counteranions or number of CH₂ groups; adding OH groups will lower E_B(cation HOFO) versus alkyl groups. In ref. 48, E_B(cation HOFO) for [N_8,1,1,0]⁺ was estimated to match that of [N_4,1,1,0]⁺. However, based on this effect of the alkyl chain length on E_B(cation HOFO), the E_B(cation HOFO) value for [N_8,1,1,0]⁺ was re-evaluated as 6.0 eV.

3.2. Quantifying the effect of counterions on E_B and E_i

3.2.1. Quantifying the effect of countercation on anion E_B and E_i. A quantitative countercation effect on E_B(anion HOFO) was observed when charge referenced to E_B(C_alkyl 1s) = 285.0 eV (Fig. 5a) for [C₈C₁Im][A] versus [P_6,6,6,14][A] where the anion [A]⁻ was the same (Fig. 5b and Table 2). E_B(anion HOFO) were between 0.2 eV and 0.4 eV larger for [C₈C₁Im][A] than E_B(anion HOFO) for [P_6,6,6,14][A] for five different anions (Table 2 and ESI,† Fig. S49–S52). These observations can be further confirmed by qualitative visual comparisons.

Fig. 5 Non-resonant laboratory XPS at hν = 1486.6 eV for [C₈C₁Im]₂[ZnCl₄] and [P_6,6,6,14]₂[ZnCl₄]: (a) C 1s, (b) valence. XP spectra were charge referenced to E_B(C_alkyl 1s) = 285.00 eV (i.e. using method 1 outlined in Section 2.5).

Table 2 Quantifying the effect of the countercation on anion E_B

IL	E B(elementanion core) charge referenced to EB(Calkyl 1s) = 285.0 eV/eV	E B(anion HOFO) charge referenced to EB(Calkyl 1s) = 285.0 eV/eV	E B(anion HOFO) for [C8C1Im][A] − EB(anion HOFO) for [P6,6,6,14][A]/eV
All values were recorded to two decimal places, but the values are reported here to one decimal place; hence, the subtracted values do not appear to match the original values for some ILs.
[C8C1Im]2[ZnCl4]	198.2 (Cl 2p3/2)	4.1	0.3
[P6,6,6,14]2[ZnCl4]	197.8 (Cl 2p3/2)	3.8
[C8C1Im]Cl	197.0 (Cl 2p3/2)	3.5	0.4
[P6,6,6,14]Cl	196.6 (Cl 2p3/2)	3.1
[C8C1Im]Br	67.4 (Br 3d5/2)	3.1	0.2
[P6,6,6,14]Br	67.1 (Br 3d5/2)	2.9
[C4C1Im][N(CN)2]	398.4 (Nterminal 1s)	3.5	0.3
[P6,6,6,14][N(CN)2]	398.0 (Nterminal 1s)	3.2
[C8C1Im][NTf2]	398.5 (Nanion 1s)	5.0	0.2
[P6,6,6,14][NTf2]	398.3 (Nanion 1s)	4.8

---

Table 3 E _i(IL) and HOMO identity

Ionic liquid	E i(IL)/eV	HOMO identity
[C8C1Im]2[FeCl4]	6.0 ± 0.3	Anion
[C6C1Im]I	7.2 ± 0.2	Anion
[C8C1Im]2[CoBr4]	7.3 ± 0.3	Anion
[C8C1Im][C(CN)3]	7.4 ± 0.2	Anion
[P6,6,6,14]Br	7.5 ± 0.2	Anion
[C8C1Im]2[CoCl4]	7.5 ± 0.3	Anion
[C4C1Im][SCN]	7.5 ± 0.2	Anion
[C8C1Im][SCN]	7.5 ± 0.2	Anion
[C8C1Im][I3]	7.5 ± 0.3	Anion
[P6,6,6,14]Cl	7.7 ± 0.2	Anion
[C8C1Im][SnCl3]	7.7 ± 0.2	Anion
[C8C1Im]Br	7.7 ± 0.2	Anion
[P6,6,6,14][N(CN)2]	7.8 ± 0.4	Anion
[C8C1Im]2[NiCl4]	7.9 ± 0.3	Anion
[P6,6,6,14][NO3]	8.1 ± 0.4	Anion
[C8C1Im]2[ZnBr4]	8.1 ± 0.3	Anion
[C4C1Im][N(CN)2]	8.1 ± 0.4	Anion
[C8C1Im]Cl	8.1 ± 0.2	Anion
[C8C1Im]2[ZnCl2Br2]	8.2 ± 0.3	Anion
[P6,6,6,14]2[ZnCl4]	8.4 ± 0.3	Anion
[C8C1Im]2[Zn2Br6]	8.4 ± 0.3	Anion
[C8C1Im]2[ZnCl4]	8.7 ± 0.3	Anion
[C8C1Im]2[Zn3Br8]	8.7 ± 0.3	Anion
[C8C1Im]2[Zn4Br10]	8.8 ± 0.3	Anion
[C8C1Im]2[Zn2Cl6]	9.0 ± 0.3	Anion
[C4C1Im][HSO4]	9.1 ± 0.4	Anion
[C8C1Im][HSO4]	9.1 ± 0.4	Anion
[C4C0Im][HSO4]	9.1 ± 0.4	Anion
[C4C1Im][MeSO4]	9.1 ± 0.4	Anion
[C4C1Im][OcSO4]	9.1 ± 0.4	Anion
[C2C1Im][MeSO3]	9.1 ± 0.4	Anion
[C4C1Im][Me2PO4]	9.1 ± 0.4	Anion
[N4,1,1,0][HSO4]	9.1 ± 0.4	Anion
[N8,1,1,0][HSO4]	9.1 ± 0.4	Anion
[C4C1Im][TfO]	9.4 ± 0.4	Cation/anion
[C8C1Im][TfO]	9.4 ± 0.4	Cation/anion
[C4C1Im][NTf2]	9.4 ± 0.4	Cation/anion
[C6C1Im][NTf2]	9.4 ± 0.4	Cation/anion
[C8C1Im][NTf2]	9.4 ± 0.4	Cation/anion
[C2C0Im][NTf2]	9.4 ± 0.4	Cation/anion
[C4C0Im][NTf2]	9.4 ± 0.4	Cation/anion
[C8C1Im]2[Co(NTf2)4]	9.4 ± 0.4	Cation/anion
[N2OH,2OH,2OH,1][TfO]	9.4 ± 0.4	Cation/anion
[C8C1Im]2[Zn4Cl10]	9.4 ± 0.4	Cation/anion
[C8C1Im][InCl4]	9.4 ± 0.4	Cation
[C6C1Im][B(CN)4]	9.4 ± 0.4	Cation
[C8C1Im][BF4]	9.4 ± 0.4	Cation
[C4C1Im][PF6]	9.4 ± 0.4	Cation
[C2C1Im][FAP]	9.4 ± 0.4	Cation
[C8C1Im][SbF6]	9.4 ± 0.4	Cation
[C4Py][NTf2]	9.6 ± 0.4	Cation/anion
[P6,6,6,14][NTf2]	9.6 ± 0.4	Cation/anion
[N8,8,8,1][NTf2]	9.6 ± 0.4	Cation/anion
[N2,2,1,0][TfO]	9.6 ± 0.4	Anion
[C4C1Pyrr][NTf2]	9.6 ± 0.4	Anion
[N4,1,1,1][NTf2]	9.6 ± 0.4	Anion
[N3,2,1,1][NTf2]	9.6 ± 0.4	Anion
[S2,2,2][NTf2]	9.6 ± 0.4	Anion
[S2,2,1][NTf2]	9.6 ± 0.4	Anion
[C8Py][BF4]	9.9 ± 0.6	Cation

---

Table 4 Predictions for [C_nC₁Im][A] ILs of E_B(cation HOFO) and E_i(cation) using E_B(cation HOFO,pred.) = E_B(N_cation 1s) − 397.1 eV and E_i(cation) = E_B(cation HOFO) + 4.58 eV. The error in E_B(N_cation 1s) is ±0.1 eV, and the errors in E_B(cation HOFO,pred.) and E_i(cation,pred.) are both ±0.2 eV

Ionic liquid	E B(Ncation 1s)/eV	E B(cation HOFO,pred.)/eV	E i(cation,pred.)/eV
[C8C1Im]Cl	401.7	4.6	9.2
[C8C1Im]2[ZnCl4]	401.8	4.7	9.3
[C4C1Im][SCN]	401.9	4.8	9.4
[C8C1Im][BF4]	402.0	4.9	9.5
[C8C1Im][SnCl3]	402.0	4.9	9.5
[C8C1Im]2[Zn4Cl10]	402.1	5.0	9.5
[C8C1Im][NTf2]	402.1	5.0	9.6
[C8C1Im][InCl4]	402.2	5.1	9.7
[C2C1Im][FAP]	402.3	5.2	9.8

---

No countercation effect on E_B(anion HOFO) was observed for [C₈C₁Im][NTf₂] versus [C₈Py][NTf₂] versus [N_8,8,8,1][NTf₂] or for [C₄Py][BF₄] versus [C₈Py][BF₄] (ESI,† Table S5), when effectively charge referenced to E_B(C_alkyl 1s) = 285.0 eV.

3.2.2. Quantifying the effect of counteranion on cation E_B and E_i. Given the dominance of anion features in the non-resonant valence XP spectra recorded at hν = 1486.6 eV,⁴⁸ investigating the effect of the counteranion on the cation contributions to valence XP spectra is very challenging. However, E_B(N_cation RXPS) potentially can be used to probe the effect of the counteranion on E_B(cation HOFO). E_B(N_cation RXPS) showed some variation with respect to the anion identity (Fig. 4). There was a link between E_B(N_cation RXPS) (i.e. E_B(N_cation 2p)) and E_B(N_cation 1s); for [C₈C₁Im][NTf₂] both E_B(N_cation 2p) and E_B(N_cation 1s) were relatively large compared to E_B(N_cation 2p) and E_B(N_cation 1s) for [C₈C₁Im]Cl. This variation was not easy to discern given uncertainty that was principally from the subtraction process. These tentative observations suggest a linear correlation between E_B(N_cation 2p) and E_B(N_cation 1s) for [C_nC₁Im][A] ILs; ΔE_B(N_correlation) = E_B(N_cation 1s) − E_B(N_cation 2p) ≈ 401.9–5.7 eV ≈ 396.2 eV (where 5.7 eV represents the average E_B(N_cation 2p) for [C₈C₁Im][A]). This observation is backed up by correlations for [C_nC₁Im][A] ILs when dissolved in molecular solvents, e.g. water.¹⁰¹

For features at E_B > 12 eV (ESI,† Fig. S48), the dominant contributions were from spectator Auger transitions (i.e. not from participator Auger transitions). When charge referenced to E_B(N_cation 1s) (ESI,† Fig. S48), the subtracted N_cation traces (which include peaks due to both participator and spectator Auger transitions) for [C_nC₁Im][A] where the anion was varied were the same (ESI,† Fig. S48). The main features appeared at the same E_B for all [C_nC₁Im][A] ILs. These findings demonstrate that cationic E_B differences were the same (within experimental error) for both valence and core levels, irrespective of the identity of the anion.

For [P_6,6,6,14][A], linear/cyclic ammoniums ([C₈Pyrr][A], [N_6,6,6,14][A], [C₈C₁Pip][A]) and [C₈Py][A], the central group 15 N (or P) atom showed E_B(N_cation 1s) (or E_B(P_cation 2p_3/2)) differences due to the counteranion when charge referenced to E_B(C_alkyl 1s) = 285.0 eV.^36,39,41,44 At present, it is not clear if this counteranion effect on the cation core state translates to any counteranion effect on the cation valence states, i.e. E_B(cation HOFO). Given the lack of strong cation participator features for many of these ILs⁴⁸ and the significant impact of the alkyl chain length on E_B(cation HOFO) for these ILs, observing any counteranion effect on the cation valence states appears very challenging.

3.2.3. Quantifying the effect of counterions E_B and E_i: summary. Countercations affect the anion electronic structure and counteranions affect the cation electronic structure. For the ILs studied here, these solvation (i.e. counterion) effects were not due to interactions between individual cation valence states and individual anion valence states, but can best be described as arising from electrostatic, non-specific interactions affecting anionic valence states relative to cationic valence states.

3.3. HOMO identification

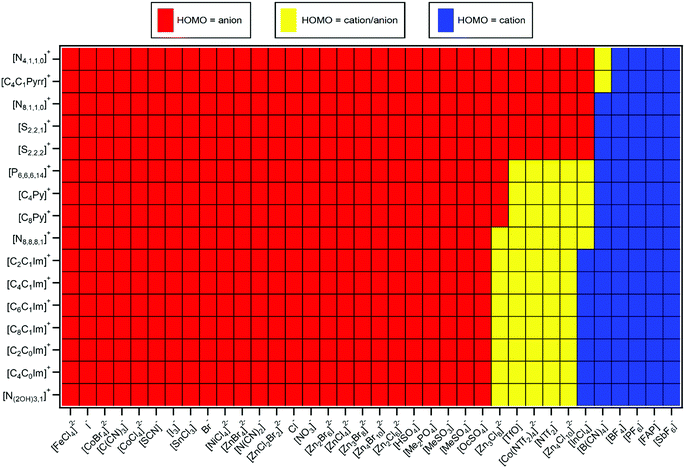
The HOMO identity was judged mainly using ΔE_B(ion HOFO) = E_B(cation HOFO) − E_B(anion HOFO) and ΔE_B(ion onset) = E_B(cation onset) − E_B(anion onset), in combination with a visual assessment of the both resonant and non-resonant valence XP spectra (Table 1). For example, for [C₈C₁Im][SnCl₃] ΔE_B(ion onset) = 1.6 ± 0.5 eV and ΔE_B(ion HOFO) = 1.7 ± 0.6 eV; no peak due to resonant enhancement was observed at E_B(anion HOFO) = 3.1 eV (i.e. only the same non-resonant XPS contribution can be observed at all hν values, Fig. 3a), demonstrating that the peak at lowest E_B for [C₈C₁Im][SnCl₃] was from the [SnCl₃]⁻ anion. Therefore, for [C₈C₁Im][SnCl₃] the HOMO was from the [SnCl₃]⁻ anion (Table 3).

For the 60 ILs studied here and in ref. 48, 39 ILs had the anion as the HOMO, 7 ILs had the cation as the HOMO, and for 14 ILs the HOMO was either the cation or the anion as it was too close to judge (Table 3 and ESI,† Table S5). Unambiguously, a significant number of ILs had the cation as the HOMO.

4. Predictions

The consistent E_B shift of all valence states when varying the counterion demonstrates that IL valence electronic structure can be predicted, as the non-specific, electrostatic-based E_B shift can be applied.

For [C_nC₁Im][A], [C_nPy][A], and [ammonium][A] the effect of the countercation on the anion was relatively small, so no changes to E_B(anion HOFO) were needed for these cations. For [C_nC₁Im][A] versus [P_6,6,6,14][A] the effect of the countercation on E_B(anion HOFO) was significant, with E_B(anion HOFO) for [P_6,6,6,14][A] ∼0.3 eV lower on average than E_B(anion HOFO) for [C_nC₁Im][A] (Table 2). Therefore, for predictions of ΔE_B(ion HOFO) and E_i(IL), E_B(anion HOFO) was set 0.3 eV lower for [P_6,6,6,14][A] compared to E_B(anion HOFO) for [C_nC₁Im][A]. For example, for [P_6,6,6,14][SCN] E_B(anion HOFO) = 2.6 eV whereas for E_B(anion HOFO) = 2.9 eV for [C₈C₁Im][SCN].

ΔE_B(N_correlation) ≈ 396.2 eV was used to predict E_B(cation HOFO,pred.), E_i(cation,pred.) and E_th(cation,pred.) for 36 [C_nC₁Im][A] ILs (Table 4 for select ILs, ESI,† Table S8 for all 36 ILs). However, the effect of the counteranion on E_B(cation HOFO) for [P_6,6,6,14]⁺, [C_nPy]⁺, ammonium or [S_2,2,n]⁺ has not been determined. Therefore, for predictions given in Fig. 6–8, no effects of the counteranion on E_B(cation HOFO) were included, i.e. E_B(cation HOFO) for each cation was kept constant whatever the identity of the anion, e.g. for all imidazolium-based ILs E_B(cation HOFO) = 4.8 ± 0.4 eV was used for the predictions presented in Fig. 6–8.

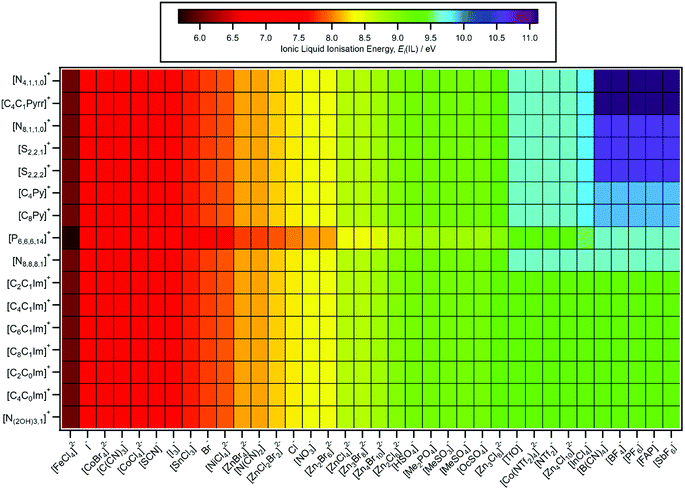Fig. 6 Predicted IL ionisation energies, E_i(IL,pred.). The errors in E_i(IL,pred.) generally range from ±0.2 eV to ±0.4 eV.

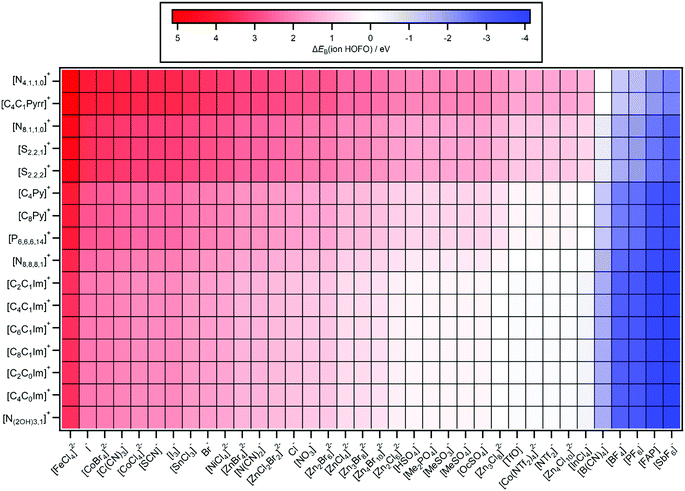Fig. 7 Predicted ΔE_B(ion HOFO,pred.) = E_B(cation HOFO,pred.) − E_B(anion HOFO,pred.) = E_i(cation,pred.) − E_i(anion,pred.). The errors in ΔE_B(ion HOFO,pred.) generally range from ±0.4 eV to ±0.6 eV.

Fig. 8 Predicted HOMO identity, judged mainly using ΔE_B(ion HOFO,pred.).

Predictions of E_i(IL), ΔE_B(ion HOFO) and HOMO identity for 576 ILs are presented in Fig. 6–8 respectively; 60 ILs for which experimental data exists and 516 ILs for which experimental data has not been measured. For these predictions, the IL might not be liquid at room temperature, unlike the 60 ILs studied experimentally here. Furthermore, for some cation–anion combinations, the speciation of the metal complex may be affected by the cation identity.

4.1. E _i(IL) predictions

The predicted E_B(cation HOFO) and E_B(cation HOFO) values were used to obtain E_i(cation), E_i(anion) and E_i(IL) (Fig. 6). As with the experimentally determined values of E_i(IL), the lowest value of E_i(cation) and E_i(anion) for each IL represents E_i(IL).

4.2. HOMO identity predictions

ΔE_B(ion HOFO) = E_B(cation HOFO) − E_B(anion HOFO) = E_i(cation) − E_i(anion) was calculated for 576 ILs to produce Fig. 7. Positive ΔE_B(ion HOFO) values (red in Fig. 7) represent the anion as the HOMO, whereas negative ΔE_B(ion HOFO) values (blue in Fig. 7) represent the cation as the HOMO; the ILs represented by near white have the cation/anion as the HOMO. The decision over which category (HOMO = anion, cation/anion or cation) each IL was placed into to produce Fig. 8 was based mainly on the predicted ΔE_B(ion HOFO) value for that IL, although the experimental data was also taken into account for e.g. the alkylsulfate-based ILs. For most ILs, the choice was easy, but for a few ILs the judgement was trickier. This area is expanded upon in the discussion section. Overall, of the 576 ILs, 431 were predicted to have an anion HOMO, 59 were predicted to have a cation/anion HOMO, and 86 were predicted to have a cation HOMO.

5. Discussion

5.1. Electrostatic effects of counterions on E_B and E_i

The electronic structure of the cation was not independent from the identity of the counteranion, and vice versa; non-specific, electrostatic interactions dominated and specific, directional ion–ion interactions were not important. In comparison, for the NaI dissolved in water, solvation effects on the water caused changes to some valence states of the water but not to other valence states of the water, i.e. the solvation effects were due to specific, directional ion–water interactions between individual water valence states and iodide anion valence states.¹⁰²

5.2. Design rules for tuning E_i and HOMO identity

Given the structural diversity of 36 anions and 16 cations studied here, gathering the anions and cations into groups is very challenging. All anions with E_i(anion) larger than Cl⁻ (i.e. E_i(anion) > 8.1 eV) are defined as superhalogen anions, demonstrating the relative stability of IL anions in general with respect to ionisation.^81,103

A design rule for producing (closed shell) anions with relatively small E_i(anion) values is the central atom having a formal lone pair, i.e. the anion HOFO is formed from ligand AOs only; conversely, for relatively large E_i(anion) values the central atom should have no formal lone pair. For example, the two cyano-containing ILs with the central atom having a lone pair (using Lewis structures), [N(CN)₂]⁻ and [C(CN)₃]⁻, both gave relatively small E_i(anion) values, whereas [B(CN)₄]⁻, for which the central B atom does not have a formal lone pair, gave a relatively large E_i(anion), i.e. the anion HOFO for [B(CN)₄]⁻ was formed from cyano ligand AOs only. Furthermore, the [SnCl₃]⁻ anion also contains a formal lone pair.⁷⁹ For [SCN]⁻, the central atom is carbon, but for this design rule the key atom is sulfur, which contains two formal lone pairs in the most favoured Lewis structure. One outlier to this design rule was [NTf₂]⁻, which has two formal lone pairs (or one lone pair, depending on the resonance structure drawn¹⁰⁴) on the central N atom but gave a relatively large E_i(anion) value. This design rule has also been observed for anions with F and O ligands.¹⁰⁵ A number of the anions with the smaller E_i(anion) values with a formal lone pair on the key atom also contained the soft and polarisable elements S and I; I⁻, [I₃]⁻, [SCN]⁻.

A design rule for producing (closed shell) anions with relatively large E_i(anion) values is the presence of fluorine, e.g. [SbF₆]⁻, [PF₆]⁻, [BF₄]⁻, [FAP]⁻, [NTf₂]⁻ and [TfO]⁻. All ILs containing a fluorinated anion gave a relatively large E_i(anion). Atomic fluorine has a relatively large E_B(F 2p) = 18.7 eV (compared to E_B(N 2p) = 13.2 eV to E_B(C 2p) = 10.7 eV),¹⁰⁶ showing the influence of atomic E_B values on E_B(anion HOFO) and E_i(anion). Only three anions with E_i(anion) > 9.5 eV contained no F atoms: [B(CN)₄]⁻, [InCl₄]⁻ and [Zn₄Cl₁₀]²⁻.

The dianions where the central atom was a transition metal (i.e. open shell) gave relatively small E_i(anion) values; indeed, the anion that gave the smallest E_i(anion) value was [FeCl₄]²⁻. However, having a dianion does not guarantee a small E_i(anion); [Zn₄Cl₁₀]²⁻ gave relatively a large E_i(anion) value.

A design rule for producing relatively small E_i(cation) values is either: (a) aromatic cations with readily ionised π systems (e.g. imidazolium and pyridinium) or (b) very long alkyl chains (e.g. [P_6,6,6,14]⁺). Conversely, a design rule for producing relatively large E_i(cation) values is a non-aromatic cation with short alkyl chains (e.g. [N_4,1,1,0]⁺, [S_2,2,2]⁺ and [S_2,2,1]⁺). The identity of the central atom does not appear to be hugely impactful on the E_i(cation) value; the relatively soft, polarisable S atom in the sulfonium cations has a formal lone pair, but this lone pair still does not lead to a low E_i(cation) value. Therefore, the design rule developed for anions based on the central atom does not hold for cations.

A design rule for obtaining large or small E_i(IL) is to use the design rules for cations and anions. For example, [C₈Py][BF₄] gave the largest E_i(IL) measured here, E_i(IL) = 9.9 eV, larger than E_i(IL) for [C₈C₁Im][BF₄], demonstrating that E_i(IL) can be tuned by selection of both the cation and the anion. The largest E_i(IL,pred.) = 11.1 eV for five [N_4,1,1,0][A] and five [C₄C₁Pyrr][A], where [A]⁻ = [B(CN)₄]⁻ and four of the fluorinated anions. The smallest E_i(IL,pred.) = 5.7 eV for [P_6,6,6,14]₂[FeCl₄]. A further design rule is that the [P_6,6,6,14][A] ILs give smaller E_i(IL,pred.) than ILs with other cations, i.e. any anion put with a [P_6,6,6,14]⁺ cation would give a lower E_i value than with other cations such as [C_nC₁Im]⁺.

5.3. Ionisation: competition between cation and anion

For two thirds of the anions studied here and in ref. 48, the anion was comfortably the HOMO. An electron was more readily removed from the anion than the cation, i.e. easier to remove an electron from the already negatively charged anion to form a neutral species, [A]⁻ → A˙, rather than remove an electron from the positively charged cation to form a dicationic ion, [C]⁺ → [C]²⁺.

∼10% of the ILs studied here gave the cation as the HOMO. Using the design rules laid out in Section 5.2, a combination of a cation with π-bonding/long alkyl chains and fluorinated anion/anion with no lone pair on central atom will likely give the cation as the HOMO, e.g. [C₈C₁Im][SbF₆], [C₂C₁Im][FAP] and [C₈Py][BF₄]. For [C₈C₁Im][InCl₄] this result was a surprise, given that the anion is a metal complex; it was easier to remove an electron from the +1 cation, [C]⁺ → [C]²⁺, than it was from the −1 anion, [A]⁻ → [A]˙. Furthermore, [C₄C₁Pyrr][PF₆] was predicted to have the cation as the HOMO, validating calculations for [C₃C₁Pyrr][PF₆].⁸²

∼20% of ILs studied here the HOMO could be from the cation or the anion; it was too close to tell, given both the experimental errors involved and the contribution from the IL sample to the variability in E_B(anion HOFO) and E_B(cation HOFO). There will be a significant variation in the valence state energies due to the large range of ion solvation environments in the liquid phase, as observed for high quality calculations of the Cl⁻ ion solvated in water⁶² and demonstrated here. In this work we identify the average E_B and E_i values, but it is important to consider the variability in these E_B and E_i values when attempting to identify the HOMO. This variability in E_B and E_i values is important when considering rare events such as chemical reactions, as ions in the liquid phase with extremes of E_B and E_i values are the ions that are likely to undergo reactions. One of the ILs for which the origin of the HOMO was uncertain was [C₈C₁Im]₂[Zn₄Cl₁₀], a stunning result; it required similar energy to remove an electron from the +1 cation, [C]⁺ → [C]²⁺, and from the −2 dianion, [A]²⁻ → [A]⁻.

5.4. Comparisons of E_i with other data sources

From UPS measurements of a microscopically thick but macroscopically thin film of [C₈C₁Im][BF₄] produced using physical vapour deposition, the work function was 4.2 eV and the first peak came at approximately 5.5 eV from visually judging the UP spectra.¹⁰⁷ Therefore, E_i(IL) using this approach was E_i(IL) = 4.2 eV + 5.5 eV = 9.7 eV.¹⁰⁷E_i(IL) = 9.4 eV from this work for [C₈C₁Im][BF₄], an excellent match to the E_i(IL) value derived from data in ref. 107.

For [C₄C₁Im][BF₄], [C₄C₁Im][PF₆] and [C₄C₁Im][NTf₂] using liquid phase external photoelectron emission spectroscopy, E_th = 7.8 eV, 7.9 eV and 8.1 eV respectively;⁵⁰ for [C₈C₁Im][BF₄], [C₄C₁Im][PF₆] and [C₄C₁Im][NTf₂], E_th(IL) = 8.3 eV from this work, a good match. Furthermore, for [C₄C₁Im]I E_th(IL) = 6.2 eV;⁵⁰E_th(IL) = 6.3 eV from this work for [C₆C₁Im]I, as excellent match. Lastly, for [N_3,1,1,1][NTf₂] E_th(IL) > 9.2 eV;⁵⁰E_th(IL) = 8.6 eV for the very similar IL [C₄C₁Pyrr][NTf₂] for our work gave a reasonable match. For [C₄C₁Im][BF₄], [C₄C₁Im][PF₆] and [C₄C₁Im][NTf₂] using liquid phase UPS, E_th(IL) = 6.6 eV, 7.8 eV and 7.8 eV respectively.⁴⁹ The E_th(IL) value for [C₄C₁Im][BF₄] from ref. 49 was significantly lower than E_th(IL) = 7.8 eV for [C₄C₁Im][BF₄] from ref. 50 and E_th(IL) = 8.3 eV for [C₈C₁Im][BF₄] from our work, strongly suggesting a problem with the charge referencing for the data in ref. 49.

Using gas phase UPS of neutral ion pairs, E_th(ion pair) values were measured by two groups, Leone and co-workers^15–18 and Kuusik and co-workers.^19–25 Most of these E_th(ion pair) values were for a combination of imidazolium cations and an imide anion, e.g. [NTf₂]⁻; E_th(ion pair) ∼ 8.5 eV for these ILs, which matches well to our E_th(IL,pred.) = 8.5 eV. Kuusik and co-workers have also published E_th(ion pair) values for a small selection of other ILs. For [C₄C₁Pyrr][PF₆] E_th(ion pair) = 10.5 eV, a good match to E_th(IL,pred.) = 11.2 eV; these values are very large, highlighting the very large E_i(IL) values for ILs with short alkyl chain ammonium cations and fluorinated anions.

Lastly, for comparisons to a molecular liquid, E_i = 11.16 eV for liquid phase water.¹⁰⁸ This value is significantly larger than any of the E_i(IL,exp.) values presented here, although a small selection of E_i(IL,pred.) values were similar, e.g. for [N_4,1,1,0][BF₄] E_i(IL,pred.) = 11.1 eV.

For optical spectroscopies of [C_nC₁Im][A] ILs, the lowest absorption energy was between ∼3.4 eV and 6.0 eV.^109–113 The smaller values were observed for [A]⁻ = halide ion, likely due to anion–cation charge transfer transitions not observed with [A]⁻ other than the halide ions.¹¹³ For [tetraalkylammonium][NTf₂] ILs the lowest absorption energy was ∼8.3 eV.^111,113 From N 1s resonant X-ray emission spectroscopy for [C₂C₁Im]Br and [C₂C₁Im][NTf₂], the energy transfer between N 2p-based occupied valence state and N 2p-based unoccupied valence state for the [C₂C₁Im]⁺ cation for both ILs was 6.9 eV (401.9 − 395.0 eV).¹¹⁴ By comparison, E_i(cation,pred.) = 9.2 eV for [C₈C₁Im]Br and E_i(cation,pred.) = 9.6 eV for [C₈C₁Im][NTf₂] (Table 4). E_i(IL) was always larger than these absorption energies (and transfer energies) from absorption spectroscopy (and resonant X-ray emission spectroscopy), demonstrating that the transitions in both absorption and resonant X-ray emission spectroscopies were to bound states; in the case of [C_nC₁Im][A] ILs the bound states were likely from the cationic ring. From N 1s resonant X-ray emission spectroscopy for [C₂C₁Im][NTf₂], N 2p-based occupied valence state to N 2p-based unoccupied valence state for the [NTf₂]⁺ anion was 9.5 eV (403.5 − 394.0 eV).¹¹⁴E_i(IL) = 9.4 eV for [C_nC₁Im][NTf₂], suggesting that the transition measured using N 1s resonant X-ray emission spectroscopy was to an unbound state.

These measurements of valence XPS for liquid phase halometallate anions and dianions serve as an excellent complement to gas phase measurements of halometallate anions and dianions; many of the anions and dianions studied here would not be stable enough to be studied in the gas phase, e.g. [FeCl₄]²⁻.¹¹⁵

5.5. Relationships of E_i with other IL properties

Comparing our data to electrochemical stability, our ILs with very large E_i(IL,pred), e.g. [C₄C₁Pyrr][PF₆], would be predicted to have excellent electrochemical stability. This prediction matches to experience, where tetraalkylammonium cations and highly fluorinated anions, e.g. [N_4,4,4,4][PF₆] or [N_4,4,4,4][BF₄], are used as supporting electrolytes, which need to be very electrochemically stable.¹¹⁶ Further comparisons to electrochemical stability data are challenging at this stage, given the tricky task of finding an experimental electrochemical dataset to test against, as the IL selection needs to be sufficiently diverse as a test set, but also a relatively inert electrode must have been used. We believe we have produced an excellent experimental dataset of IL valence electronic structures for which comparisons can be made in the future. It is a similar story with respect to comparisons of experimental electronic structure and thermal stability; is there an experimental thermal stability dataset of sufficient IL diversity to provide a high-quality test of our electronic structure data? One significant challenge is quantifying thermal stability; there are a number of different metrics, e.g. onset temperature at a certain % of mass loss, activation energy.^117,118

A pyridinium-based cation in an IL can act as an electron donor to a neutral dye solute.¹¹⁹ This study demonstrates that the cation has been considered as an electron donor in ILs, but the full potential and importance has not yet been considered.

6. Conclusions and future work

We have successfully measured valence electronic structure descriptors for 60 ILs, most importantly, E_i and the HOMO identity. Measuring E_i for such a structurally diverse set of ILs represents a significant step forward in the understanding of the valence electronic structure of ILs. The structurally diverse range of cations and anions studied allow us to provide qualitative design rules linking ion structure to valence electronic structure. The electronic influence of the countercation on the anion valence electronic structure (and vice versa) was demonstrated to be dominated by non-specific, electrostatic interactions; the largest effect was 0.6 eV, although most effects were much smaller than that. Given that the cation–anion effects were relatively predictable, we were able to make predictions of both E_i and the HOMO identity for a further 516 ILs.

∼10% of the ILs have the cation rather than the anion as the HOMO. The cation must be considered as a possible electron donor (or partial electron donor, when donating electron density rather than a formal electron pair) in such ILs in particular, especially for neutral solutes where electrostatic ion-solute interactions are expected to be less dominant.

Adding new anions to the dataset should be relatively facile if studied on a standard lab apparatus, given most anions dominate non-resonant XP spectra recorded at hν = 1486.6 eV; suitable charge referencing is achievable for any new IL. Adding new cations to the dataset will prove far more of a challenge, given the multiple experimental difficulties, especially those caused by the normally dominant anionic contributions to non-resonant XP spectra recorded at hν = 1486.6 eV.

Given our significant experimental and predicted data of valence electronic structure descriptors, the development of models linking experimental valence electronic structure descriptors to other IL properties, e.g. electrochemical stability and thermal stability, is now possible. Furthermore, our dataset will provide a very valuable benchmark for validation of electronic structure calculations.

Both qualitative comparisons (e.g. visual) and quantitative comparisons (e.g. peak E_B separation) of liquid phase and gas phase photoelectron spectra have great potential to provide insight into the effect of solvation on electronic structure. In the gas phase, a standard [C][A] IL has only one counterion, whereas in the liquid phase each ion is fully solvated. ILs that gave the cation as the HOMO, e.g. [C_nC₁Im][FAP], would be ideal candidates, given the cationic contributions to the valence electronic structure can be readily identified along with the anionic contributions, allowing any phase-related E_B shifts to be observed.

Author contributions

CJC synthesised the samples (where necessary). JMS, EG, AL, CJC, PL, DAD, PF, FV, RAB, RGP and KRJL performed the XPS/RXPS experiments. JMS, RMF and KRJL analysed the results. The manuscript was written by JMS and KRJL with the help from other authors. KRJL proposed and initiated the project, and supervised the investigation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

KRJL acknowledges support from a Royal Society University Research Fellowship (URF\R\150353). JMS acknowledges support from a Royal Society University Research Fellowship Enhancement Award (RGF\EA\180089). EG acknowledges support from a Royal Society Research Grant for Research Fellows (RGF\R1\180053). AL acknowledges part funding for a studentship from Johnson Matthey plc. PL acknowledges support from the EPSRC (EP/K005138/1 and EP/P013341/1). We acknowledge Diamond Light Source for time on Beamline I09 under Proposal SI20463 and Beamline B07 (VERSOX) under Proposals SI24304 and SI25929. Georg Held and Matthijs Van Spronsen are acknowledged for beamtime support on Proposal SI25929. XP spectra for [C₂C₁Im][FAP] were recorded by the EPSRC National Facility for Photoelectron Spectroscopy (HarwellXPS), operated by Cardiff University and UCL under contract number PR16195. Mark Isaacs is acknowledged for recording the HarwellXPS results.

References

1. I. Fleming, Molecular Orbitals and Organic Chemical Reactions, Wiley, Chichester, 2010.
2. K. Fukui, Angew. Chem., Int. Ed. Engl., 1982, 21, 801–809.
3. R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1982, 21, 711–724.
4. R. G. Pearson, Inorg. Chem., 1988, 27, 734–740.
5. R. G. Pearson, J. Org. Chem., 1989, 54, 1423–1430.
6. M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629.
7. D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232–250.
8. D. R. MacFarlane, M. Forsyth, P. C. Howlett, M. Kar, S. Passerini, J. M. Pringle, H. Ohno, M. Watanabe, F. Yan, W. J. Zheng, S. G. Zhang and J. Zhang, Nat. Rev. Mater., 2016, 1, 15005.
9. E. W. Castner and J. F. Wishart, J. Chem. Phys., 2010, 132, 120901.
10. E. W. Castner, C. J. Margulis, M. Maroncelli and J. F. Wishart, Annu. Rev. Phys. Chem., 2011, 62, 85–105.
11. B. J. Mincher and J. F. Wishart, Solvent Extr. Ion Exch., 2014, 32, 563–583.
12. In the calculation community, the HOMO usually refers to the lowest energy valence state in the ground state of the molecule or ion. In the experimental XPS community, the HOMO often represents the most readily ionised valence state of the molecule or ion ( A. Kahn, Mater. Horizons, 2016, 3, 7–10 ). In this article, we use the latter convention.
13. E. I. Izgorodina, Z. L. Seeger, D. L. A. Scarborough and S. Y. S. Tan, Chem. Rev., 2017, 117, 6696–6754.
14. In this article, ionisation energies, E_i, are charge referenced to the vacuum level; binding energies, E_B, are charge referenced to the alkyl carbon Fermi level.
15. D. Strasser, F. Goulay, M. S. Kelkar, E. J. Maginn and S. R. Leone, J. Phys. Chem. A, 2007, 111, 3191–3195.
16. D. Strasser, F. Goulay, L. Belau, O. Kostko, C. Koh, S. D. Chambreau, G. L. Vaghjiani, M. Ahmed and S. R. Leone, J. Phys. Chem. A, 2010, 114, 879–883.
17. S. D. Chambreau, G. L. Vaghjiani, A. To, C. Koh, D. Strasser, O. Kostko and S. R. Leone, J. Phys. Chem. B, 2010, 114, 1361–1367.
18. S. D. Chambreau, G. L. Vaghjiani, C. J. Koh, A. Golan and S. R. Leone, J. Phys. Chem. Lett., 2012, 3, 2910–2914.
19. I. Kuusik, M. Tarkanovskaja, J. Kruusma, V. Reedo, R. Valbe, A. Lohmus, V. Kisand, E. Lust, E. Kukk and E. Nommiste, RSC Adv., 2015, 5, 6834–6842.
20. I. Kuusik, M. Tarkanovskaja, J. Kruusma, V. Kisand, A. Tonisoo, E. Lust and E. Nommiste, J. Mol. Liq., 2016, 223, 939–942.
21. I. Kuusik, M. Berholts, J. Kruusma, V. Kisand, A. Tonisoo, E. Lust and E. Nommiste, RSC Adv., 2018, 8, 30298–30304.
22. I. Kuusik, M. Kook, R. Parna, A. Kivimaki, T. Kaambre, L. Reisberg, A. Kikas and V. Kisand, J. Mol. Liq., 2019, 294, 111580.
23. I. Kuusik, M. Berholts, J. Kruusma, A. Tonisoo, E. Lust, E. Nommiste and V. Kisand, RSC Adv., 2019, 9, 33140–33146.
24. J. M. Kahk, I. Kuusik, V. Kisand, K. R. J. Lovelock and J. Lischner, npj Comput. Mater., 2020, 6, 148.
25. I. Kuusik, M. Kook, R. Parna and V. Kisand, ACS Omega, 2021, 6, 5255–5265.
26. A. Deyko, K. R. J. Lovelock, P. Licence and R. G. Jones, Phys. Chem. Chem. Phys., 2011, 13, 16841–16850.
27. K. R. J. Lovelock, J. P. Armstrong, P. Licence and R. G. Jones, Phys. Chem. Chem. Phys., 2014, 16, 1339–1353.
28. C. J. Clarke, S. Puttick, T. J. Sanderson, A. W. Taylor, R. A. Bourne, K. R. J. Lovelock and P. Licence, Phys. Chem. Chem. Phys., 2018, 20, 16786–16800.
29. S. D. Chambreau, J. A. Boatz, G. L. Vaghjiani, C. Koh, O. Kostko, A. Golan and S. R. Leone, J. Phys. Chem. A, 2012, 116, 5867–5876.
30. S. D. Chambreau, A. C. Schenk, A. J. Sheppard, G. R. Yandek, G. L. Vaghjiani, J. Maciejewski, C. J. Koh, A. Golan and S. R. Leone, J. Phys. Chem. A, 2014, 118, 11119–11132.
31. V. Volpe, B. Brunetti, G. Gigli, A. Lapi, S. V. Ciprioti and A. Ciccioli, J. Phys. Chem. B, 2017, 121, 10382–10393.
32. C. J. Clarke, N. D. Richardson, A. E. J. Firth, J. P. Hallett and P. Licence, ACS Sustainable Chem. Eng., 2020, 8, 16386–16390.
33. I. J. Villar-Garcia, E. F. Smith, A. W. Taylor, F. L. Qiu, K. R. J. Lovelock, R. G. Jones and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 2797–2808.
34. A. Foelske-Schmitz and M. Sauer, J. Electron Spectrosc. Relat. Phenom., 2018, 224, 51–58.
35. T. Cremer, C. Kolbeck, K. R. J. Lovelock, N. Paape, R. Wölfel, P. S. Schulz, P. Wasserscheid, H. Weber, J. Thar, B. Kirchner, F. Maier and H. P. Steinrück, Chem. – Eur. J., 2010, 16, 9018–9033.
36. S. Men, K. R. J. Lovelock and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 15244–15255.
37. B. B. Hurisso, K. R. J. Lovelock and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 17737–17748.
38. A. W. Taylor, S. Men, C. J. Clarke and P. Licence, RSC Adv., 2013, 3, 9436–9445.
39. R. K. Blundell and P. Licence, Phys. Chem. Chem. Phys., 2014, 16, 15278–15288.
40. I. J. Villar-Garcia, K. R. J. Lovelock, S. Men and P. Licence, Chem. Sci., 2014, 5, 2573–2579.
41. S. Men, D. S. Mitchell, K. R. J. Lovelock and P. Licence, ChemPhysChem, 2015, 16, 2211–2218.
42. L. S. Longo, E. F. Smith and P. Licence, ACS Sustainable Chem. Eng., 2016, 4, 5953–5962.
43. S. A. Men, K. R. J. Lovelock and P. Licence, Chem. Phys. Lett., 2017, 679, 207–211.
44. S. Men, P. Licence, C. L. Do-Thanh, H. M. Luo and S. Dai, Phys. Chem. Chem. Phys., 2020, 22, 11976–11983.
45. S. Men, P. Licence, H. M. Luo and S. Dai, J. Phys. Chem. B, 2020, 124, 6657–6663.
46. R. M. Fogarty, R. P. Matthews, C. R. Ashworth, A. Brandt-Talbot, R. G. Palgrave, R. A. Bourne, T. V. Hoogerstraete, P. A. Hunt and K. R. J. Lovelock, J. Chem. Phys., 2018, 148, 193817.
47. R. M. Fogarty, R. Rowe, R. P. Matthews, M. T. Clough, C. R. Ashworth, A. Brandt, P. J. Corbett, R. G. Palgrave, E. F. Smith, R. A. Bourne, T. W. Chamberlain, P. B. J. Thompson, P. A. Hunt and K. R. J. Lovelock, Faraday Discuss., 2018, 206, 183–201.
48. R. M. Fogarty, R. G. Palgrave, R. A. Bourne, K. Handrup, I. J. Villar-Garcia, D. J. Payne, P. A. Hunt and K. R. J. Lovelock, Phys. Chem. Chem. Phys., 2019, 21, 18893–18910.
49. D. Yoshimura, T. Yokoyama, T. Nishi, H. Ishii, R. Ozawa, H. Hamaguchi and K. Seki, J. Electron Spectrosc. Relat. Phenom., 2005, 144, 319–322.
50. R. Katoh, J. Phys. Chem. B, 2008, 112, 14971–14975.
51. R. Katoh, Chem. Phys. Lett., 2009, 482, 259–262.
52. G. Greczynski and L. Hultman, ChemPhysChem, 2017, 18, 1507–1512.
53. G. Greczynski and L. Hultman, Appl. Surf. Sci., 2018, 451, 99–103.
54. D. R. Baer, K. Artyushkova, H. Cohen, C. D. Easton, M. Engelhard, T. R. Gengenbach, G. Greczynski, P. Mack, D. J. Morgan and A. Roberts, J. Vac. Sci. Technol., A, 2020, 38, 031204.
55. G. Greczynski and L. Hultman, Angew. Chem., Int. Ed., 2020, 59, 5002–5006.
56. G. Greczynski and L. Hultman, Prog. Mater. Sci., 2020, 107, 100591.
57. J. M. Thomas, I. Adams and M. Barber, Solid State Commun., 1971, 9, 1571–1573.
58. B. Winter and M. Faubel, Chem. Rev., 2006, 106, 1176–1211.
59. R. Seidel, S. Thürmer and B. Winter, J. Phys. Chem. Lett., 2011, 2, 633–641.
60. B. Winter, R. Weber, I. V. Hertel, M. Faubel, P. Jungwirth, E. C. Brown and S. E. Bradforth, J. Am. Chem. Soc., 2005, 127, 7203–7214.
61. [C₄C₁Im][SCN] has 72 valence electrons (1-butyl-3-methylimidazolium, [C₄C₁Im]⁺), [C₈C₁Im]Cl has 88 valence electrons (1-octyl-3-methylimidazolium, [C₈C₁Im]⁺), [C₈C₁Im][NTf₂] has 172 valence electrons ([NTf₂]⁻ = [(CF₃SO₂)₂N]⁻, bis[(trifluoromethane)sulfonyl]imide) and [P_6,6,6,14][NTf₂] has 292 valence electrons ([P_6,6,6,14]⁺ = tetradecyl(trihexyl)phosphonium).
62. L. Ge, L. Bernasconi and P. Hunt, Phys. Chem. Chem. Phys., 2013, 15, 13169–13183.
63. O. Höfft, S. Bahr, M. Himmerlich, S. Krischok, J. A. Schaefer and V. Kempter, Langmuir, 2006, 22, 7120–7123.
64. S. Krischok, R. Öttking, W. J. D. Beenken, M. Himmerlich, P. Lorenz, O. Höfft, S. Bahr, V. Kempter and J. A. Schaefer, Z. Phys. Chem.-Int. J. Res. Phys. Chem. Chem. Phys., 2006, 220, 1407–1416.
65. T. Ikari, A. Keppler, M. Reinmöller, W. J. D. Beenken, S. Krischok, M. Marschewski, W. Maus-Friedrichs, O. Höfft and F. Endres, e-J. Surf. Sci. Nanotechnol., 2010, 8, 241–245.
66. M. Reinmöller, A. Ulbrich, T. Ikari, J. Preiss, O. Höfft, F. Endres, S. Krischok and W. J. D. Beenken, Phys. Chem. Chem. Phys., 2011, 13, 19526–19533.
67. A. Ulbrich, M. Reinmöller, W. J. D. Beenken and S. Krischok, ChemPhysChem, 2012, 13, 1718–1724.
68. A. Ulbrich, M. Reinmöller, W. J. D. Beenken and S. Krischok, J. Mol. Liq., 2014, 192, 77–86.
69. D. Weingarth, I. Czekaj, Z. F. Fei, A. Foelske-Schmitz, P. J. Dyson, A. Wokaun and R. Kötz, J. Electrochem. Soc., 2012, 159, H611–H615.
70. S. Krischok, M. Eremtchenko, M. Himmerlich, P. Lorenz, J. Uhlig, A. Neumann, R. Öttking, W. J. D. Beenken, O. Höfft, S. Bahr, V. Kempter and J. A. Schaefer, J. Phys. Chem. B, 2007, 111, 4801–4806.
71. S. Krischok, A. Ulbrich, T. Ikari, V. Kempter, M. Marschewski and O. Höfft, Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. Atoms, 2014, 340, 51–57.
72. A. B. Biedron, E. L. Garfunkel, E. W. Castner and S. Rangan, J. Chem. Phys., 2017, 146, 054704.
73. S. Rangan, J. Viereck and R. A. Bartynski, J. Phys. Chem. B, 2020, 124, 7909–7917.
74. K. Kanai, T. Nishi, T. Iwahashi, Y. Ouchi, K. Seki, Y. Harada and S. Shin, J. Chem. Phys., 2008, 129, 224507.
75. T. Nishi, T. Iwahashi, H. Yamane, Y. Ouchi, K. Kanai and K. Seki, Chem. Phys. Lett., 2008, 455, 213–217.
76. K. Kanai, T. Nishi, T. Iwahashi, Y. Ouchi, K. Seki, Y. Harada and S. Shin, J. Electron Spectrosc. Relat. Phenom., 2009, 174, 110–115.
77. J. M. Seymour, C. J. Clarke, R. G. Palgrave, N. A. Besley and K. R. J. Lovelock, 2021, in preparation.
78. S. Men and P. Licence, Chem. Phys. Lett., 2017, 681, 40–43.
79. J. M. Seymour, E. Gousseva, R. M. Fogarty, L. Frankemoelle, R. Rowe, C. J. Clarke, D. A. Duncan, R. A. Bennett, R. G. Palgrave, P. A. Hunt and K. R. J. Lovelock, 2021, in preparation.
80. R. P. Matthews, C. Ashworth, T. Welton and P. A. Hunt, J. Phys.: Condens. Matter, 2014, 26, 284112.
81. A. K. Srivastava, A. Kumar and N. Misra, J. Phys. Chem. A, 2021, 125, 2146–2153.
82. S. P. Ong, O. Andreussi, Y. B. Wu, N. Marzari and G. Ceder, Chem. Mater., 2011, 23, 2979–2986.
83. K. B. Dhungana, L. F. O. Faria, B. N. Wu, M. Liang, M. C. C. Ribeiro, C. J. Margulis and E. W. Castner, J. Chem. Phys., 2016, 145, 024503.
84. S. P. Ong and G. Ceder, Electrochim. Acta, 2010, 55, 3804–3811.
85. J. B. Haskins, C. W. Bauschlicher and J. W. Lawson, J. Phys. Chem. B, 2015, 119, 14705–14719.
86. S. Kazemiabnavi, Z. C. Zhang, K. Thornton and S. Banerjee, J. Phys. Chem. B, 2016, 120, 5691–5702.
87. N. V. Ilawe, J. Fu, S. Ramanathan, B. M. Wong and J. Z. Wu, J. Phys. Chem. C, 2016, 120, 27757–27767.
88. V. R. Koch, L. A. Dominey, C. Nanjundiah and M. J. Ondrechen, J. Electrochem. Soc., 1996, 143, 798–803.
89. P. Ballone and R. Cortes-Huerto, Faraday Discuss., 2012, 154, 373–389.
90. Y. Zhang, C. J. Shi, J. F. Brennecke and E. J. Maginn, J. Phys. Chem. B, 2014, 118, 6250–6255.
91. C. Lian, H. L. Liu, C. Z. Li and J. Z. Wu, AIChE J., 2019, 65, 804–810.
92. E. Thomas, D. Thomas, K. P. Vijayalakshmi and B. K. George, RSC Adv., 2016, 6, 9421–9428.
93. E. Thomas, K. P. Vijayalakshmi and B. K. George, J. Mol. Liq., 2019, 276, 721–727.
94. S. Koutsoukos, F. Philippi, F. Malaret and T. Welton, Chem. Sci., 2021, 12, 6820–6843.
95. T. L. Lee and D. A. Duncan, Synchrotron Radiat. News, 2018, 31, 16–22.
96. G. Held, F. Venturini, D. C. Grinter, P. Ferrer, R. Arrigo, L. Deacon, W. Q. Garzon, K. Roy, A. Large, C. Stephens, A. Watts, P. Larkin, M. Hand, H. C. Wang, L. Pratt, J. J. Mudd, T. Richardson, S. Patel, M. Hillman and S. Scott, J. Synchrotron Radiat., 2020, 27, 1153–1166.
97. K. W. Kolasinski, Surface Science: Foundations of Catalysis and Nanoscience, Wiley, Chichester, 4th edn, 2020.
98. Surface Analysis: The Principal Techniques, ed. J. C. Vickerman and I. S. Gilmore, John Wiley & Sons, Chichester, 2009.
99. J. J. Yeh and I. Lindau, At. Data Nucl. Data Tables, 1985, 32, 1–155.
100. R. M. Fogarty, R. P. Matthews, M. T. Clough, C. R. Ashworth, A. Brandt-Talbot, P. J. Corbett, R. G. Palgrave, R. A. Bourne, T. W. Chamberlain, T. Vander Hoogerstraete, P. B. J. Thompson, P. A. Hunt, N. A. Besley and K. R. J. Lovelock, Phys. Chem. Chem. Phys., 2017, 19, 31156–31167.
101. J. M. Seymour, E. Gousseva, R. M. Fogarty, J. Werner, G. Öhrwall, O. Björneholm, D. Hein, G. Wartner, C. Kolbeck, B. Winter, R. Seidel and K. R. J. Lovelock, 2021, in preparation.
102. M. N. Pohl, E. Muchová, R. Seidel, H. Ali, S. Sršeň, I. Wilkinson, B. Winter and P. Slavíček, Chem. Sci., 2019, 10, 848–865.
103. J. Zhang, P. Yang, Z. R. Sun and X. B. Wang, J. Phys. Chem. A, 2014, 118, 8074–8080.
104. L. Péter and J. Arai, J. Appl. Electrochem., 1999, 29, 1053–1061.
105. G. L. Gutsev and A. I. Boldyrev, Chem. Phys., 1981, 56, 277–283.
106. J. B. Mann, T. L. Meek and L. C. Allen, J. Am. Chem. Soc., 2000, 122, 2780–2783.
107. K. L. Syres and R. G. Jones, Langmuir, 2015, 31, 9799–9808.
108. B. Winter, R. Weber, W. Widdra, M. Dittmar, M. Faubel and I. V. Hertel, J. Phys. Chem. A, 2004, 108, 2625–2632.
109. R. Katoh, Chem. Lett., 2007, 36, 1256–1257.
110. T. Miyata, M. Fukuyama, A. Hibara, E. Okunishi, M. Mukai and T. Mizoguchi, Microscopy, 2014, 63, 377–382.
111. K. Regeta, C. Bannwarth, S. Grimme and M. Allan, Phys. Chem. Chem. Phys., 2015, 17, 15771–15780.
112. I. Tanabe, Y. Kurawaki, Y. Morisawa and Y. Ozaki, Phys. Chem. Chem. Phys., 2016, 18, 22526–22530.
113. I. Tanabe, A. Suyama, T. Sato and K. Fukui, Analyst, 2018, 143, 2539–2545.
114. Y. Horikawa, T. Tokushima, O. Takahashi, H. Hoke and T. Takamuku, J. Phys. Chem. B, 2016, 120, 7480–7487.
115. T. Waters, X. B. Wang and L. S. Wang, Coord. Chem. Rev., 2007, 251, 474–491.
116. N. Elgrishi, K. J. Rountree, B. D. McCarthy, E. S. Rountree, T. T. Eisenhart and J. L. Dempsey, J. Chem. Educ., 2018, 95, 197–206.
117. F. Heym, B. J. M. Etzold, C. Kern and A. Jess, Phys. Chem. Chem. Phys., 2010, 12, 12089–12100.
118. F. Heym, B. J. M. Etzold, C. Kern and A. Jess, Green Chem., 2011, 13, 1453–1466.
119. B. N. Wu, M. Liang, N. Zmich, J. Hatcher, S. I. Lall-Ramnarine, J. F. Wishart, M. Maroncelli and E. W. Castner, J. Phys. Chem. B, 2018, 122, 2379–2388.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02441h

---