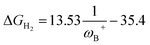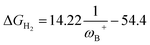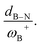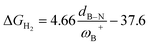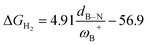Open Access Article
Open Access ArticleNew insights into H2 activation by intramolecular frustrated Lewis pairs based on aminoboranes: the local electrophilicity index of boron as a suitable indicator to tune the reversibility of the process†
César
Barrales-Martínez
 *a,
Rocío
Durán
*a,
Rocío
Durán
 a and
Pablo
Jaque
a and
Pablo
Jaque
 bc
bc
aInstituto de Investigación Interdisciplinaria (I3), Vicerrectoría Académica and Centro de Bioinformática, Simulación y Modelado (CBSM), Facultad de Ingeniería, Universidad de Talca, Campus Lircay, Talca 3460000, Chile. E-mail: cesar.barrales@utalca.cl
bDepartamento de Química Orgánica y Fisicoquímica, Facultad de Ciencias Químicas y Farmacéuticas, Universidad de Chile, Sergio Livingstone 1007, Independencia, Santiago, Chile
cCentro de Modelamiento Molecular, Biofísica y Bioinformática, CM2B2, Universidad de Chile, Sergio Livingstone 1007, Independencia, Santiago, Chile
First published on 3rd October 2023
Abstract
A large set of intramolecular aminoborane-based FLPs was studied employing density functional theory in the H2 activation process to analyze how the acidity and basicity of boron and nitrogen atoms, respectively, affect the reversibility of the process. Three different linkers were employed, keeping the C–C nature in the connection between both Lewis centers: –CH2–CH2–, –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–, and –C6H4–. The results show that significant differences in the Gibbs free energy of the process are found by considering all the combinations of substituents. Of the 75 systems studied, only 9 showed the ability to carry out the process reversibly (ΔGH2 in the range of −3.5 to 2.0 kcal mol−1), where combinations of alkyl/aryl or aryl/alkyl in boron/nitrogen generate systems capable of reaching reversibility. If the alkyl/alkyl or aryl/aryl combination is employed, highly exergonic (non-reversible H2 activation) and endergonic (unfeasible H2 activation) reactions are found, respectively. No appreciable differences in the linker were found, allowing us to continue the analysis with the most entropically favorable linker, the –C6H4– linker. From this, 25 different FLP systems of type 2-[bis(X)boryl]-(Y)aniline (X: H, CF3, C6F5, PFtB, FMes and Y: H, CH3, t-but, Ph, Mes) can be formed. By analyzing the electronic properties of each system, we have found that the condensed-to-boron electrophilicity index ωB+ is inversely related to the ΔGH2. Interestingly, two relationships were found; the first is for alkyl groups (Y: CH3 and t-but) and the second for aryl groups (Y: H, Ph, and Mes), which is intimately related to the proton affinity of each aniline. In addition, it is quite interesting when the frustration degree, given by B⋯N distance dB–N, is brought together with ωB+, since the
CH–, and –C6H4–. The results show that significant differences in the Gibbs free energy of the process are found by considering all the combinations of substituents. Of the 75 systems studied, only 9 showed the ability to carry out the process reversibly (ΔGH2 in the range of −3.5 to 2.0 kcal mol−1), where combinations of alkyl/aryl or aryl/alkyl in boron/nitrogen generate systems capable of reaching reversibility. If the alkyl/alkyl or aryl/aryl combination is employed, highly exergonic (non-reversible H2 activation) and endergonic (unfeasible H2 activation) reactions are found, respectively. No appreciable differences in the linker were found, allowing us to continue the analysis with the most entropically favorable linker, the –C6H4– linker. From this, 25 different FLP systems of type 2-[bis(X)boryl]-(Y)aniline (X: H, CF3, C6F5, PFtB, FMes and Y: H, CH3, t-but, Ph, Mes) can be formed. By analyzing the electronic properties of each system, we have found that the condensed-to-boron electrophilicity index ωB+ is inversely related to the ΔGH2. Interestingly, two relationships were found; the first is for alkyl groups (Y: CH3 and t-but) and the second for aryl groups (Y: H, Ph, and Mes), which is intimately related to the proton affinity of each aniline. In addition, it is quite interesting when the frustration degree, given by B⋯N distance dB–N, is brought together with ωB+, since the 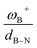 quotient has unit energy/length corresponding to unit force; concomitantly, a measure of the FLP strength in H–H bond activation can be defined. With this finding, a rational design of this kind of FLP can be performed by analyzing the acidity of boron through condensed-to-boron electrophilicity and knowing the nature of the substituent of nitrogen according to whether the Y is alkyl or aryl, optimizing the H2 reversible activation in a rational way, which is crucial to improve the catalytic performance.
quotient has unit energy/length corresponding to unit force; concomitantly, a measure of the FLP strength in H–H bond activation can be defined. With this finding, a rational design of this kind of FLP can be performed by analyzing the acidity of boron through condensed-to-boron electrophilicity and knowing the nature of the substituent of nitrogen according to whether the Y is alkyl or aryl, optimizing the H2 reversible activation in a rational way, which is crucial to improve the catalytic performance.
Introduction
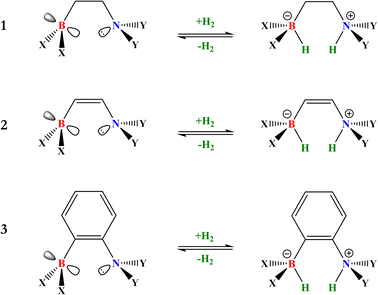
The activation of molecular hydrogen (H2), also known as dihydrogen, has attracted a great deal of attention from chemists in the last decade because H2 has been proposed as a new energetic vector that could replace current fossil fuel-based energy sources through the so-called hydrogen economy.1,2 H2 can be obtained from different sources, giving rise to the different types of hydrogen: gray, brown, blue, turquoise, and the most promising kind of hydrogen, green hydrogen,2,3 which can be obtained from water electrolysis and renewable energy sources. Safe and easy handling of H2 is a crucial step towards using this molecule as a fuel on a global scale, especially its storage and transport. In this sense, designing new, more environmentally friendly catalysts that can split and release this molecule under mild conditions is a great challenge since it is a difficult task due to its chemical inertness at room temperature (i.e., low polarizability and large dissociation energy). Over the years, transition metals have been employed in H2 activation;4 nevertheless, in 2006, Stephan reported the first reversible metal-free H2 activation using compounds called frustrated Lewis pairs (FLPs). FLPs consist of a molecular system containing a Lewis base (LB) and a Lewis acid (LA) center that can be prevented from forming the classic Lewis adduct because they have bulky substituents that hinder this process.5 This creates a cavity in which FLPs can donate and accept electrons, which favors the activation of very inert molecules such as H2, CO, and CO2, among others.6,7 Since this work, FLPs have been proposed to be employed for H2 activation, where the H–H bond is heterolytically split, generating a proton bonded to the LB and a hydride bonded to the LA, forming the zwitterion FLP-H+/H− system. Once the H2 is split, it can easily reduce polar and nonpolar unsaturated compounds. This procedure has gained increased attention in recent years, as it opens up the possibility of using these unsaturated compounds themselves to store and transport H2 more safely, which is a tremendous challenge in its use as a green fuel. For this purpose, the so-called liquid organic hydrogen carriers (LOHCs) term has been coined.8,9 In order to employ an FLP as a promising catalyst to activate H2 and hydrogenate LOHCs, it is necessary to optimize the H2 splitting process to generate labile protons and hydrides that can be easily transferred to the target molecule, i.e., the process should be neither too exergonic nor too endergonic. This is the basis for the concept of “reversibility” in H2 activation. Fig. 1 shows the general process of H2 activation by an FLP (Fig. 1a) and a general energetic scheme of the process (Fig. 1b), where according to the overall Gibbs free energy change, one can see non-reversible (ΔG° < 0), reversible (ΔG° ≈ 0), and thermodynamically unfeasible (ΔG° > 0) H2 activation.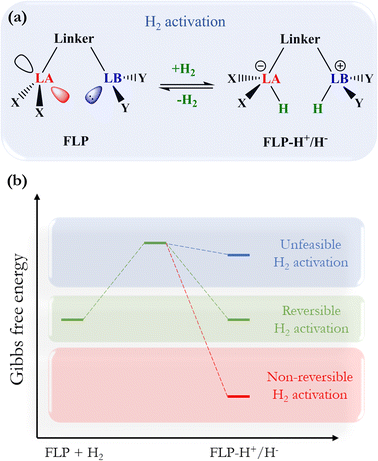 | ||
| Fig. 1 (a) General scheme of H2 activation by FLPs. (b) Energetic diagram for non-reversible, reversible, and a thermodynamically unfeasible H2 activation by FLPs. | ||
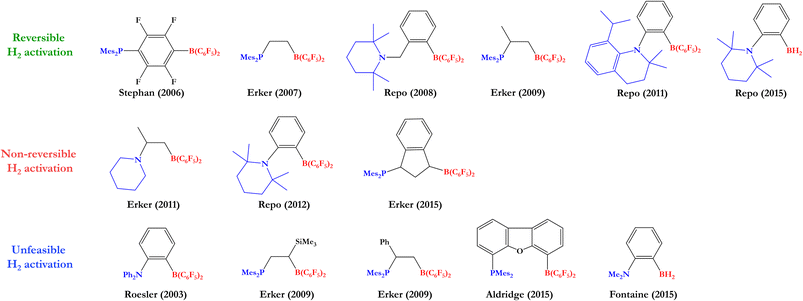
Based on this, many experimental and theoretical studies have been carried out to find the optimal FLP system that can reversibly cleave H2 and hydrogenate different polar and nonpolar unsaturated compounds. After the seminal studies of Stephan,10,11 various groups reached the reversible H2 activation by FLPs under ambient conditions, where to stand out the studies of Erker12–14 and Repo,15–17 which employed this activated H2 to reduce unsaturated compounds, such as benzaldehyde, enamines, and imines; however, among the FLPs tested, only a few of them were able to perform this process, indicating that the reversibility of H2 activation is strongly dependent on the electronic structure of the FLP (in some cases the H2 activation was non-reversible, and in others, H2 was not even activated by the FLPs employed). Like these, there are other examples of FLP systems tested as catalysts in the hydrogenation of unsaturated compounds from H2 activation.18–23 Some of the FLPs used in the studies mentioned above are shown in Fig. 2.
Theoretically and computationally, H2 activation by FLPs has been well-characterized from a different point of view. Two reactivity models have been proposed to be operating in this process: (i) the cooperative electron transfer (ET) proposed by Pápai et al.,24,25 which consists of the interaction between the lone pair of the base with the proton and the lone pair of the hydride with the empty p orbital of the acid center and (ii) the electron polarization (EP) by electric fields developed by Grimme et al.,26,27 consisting in the polarization of the H–H bond by the oscillating electric dipole generated in the cavity of the acid–base frustrated interaction. Based on ET, Pápai also developed a thermodynamic model to deeply analyze the H2 splitting by FLP systems,24 partitioning the Gibbs free energy change associated with the process in five elementary steps, thus rationalizing the H2 activation and allowing the control of the steric and electronic effects to reach the reversibility. In terms of the analysis of the reaction path, in 2016, Yepes et al.28 studied H2 activation by geminal aminoborane-based FLPs by using the activation strain model of reactivity,29 finding that electron-withdrawing groups (EWGs) in the borane center lead to a lowering of the activation barrier of the process as a consequence of stronger orbital and electrostatic interactions between reactants; in other words, the two effects described by both models (i.e., ET and EP) work in a complementary way to facilitate the process. In 2018, the same authors analyzed the hydrogenation of multiple polar bonds computationally by FLP-H+/H− complexes,30 indicating that, again, EWGs in the acid center kinetically favor the hydrogenation process and that an increase in the polarity of the unsaturated bond of the substrate also supports the feasibility of the process. In 2019, Wang et al.31 found, computationally based on previous experimental studies, that the frustration degree, taken as the distance between the acid and base centers of the FLP (dLA–LB), is a factor to be considered in the rational design of an FLP system for this purpose, with reversibility being achieved when dLA–LB is longer than 3.0 Å. In 2019, Liu et al.32 performed a comprehensive review of the mechanism of H2 activation by FLPs, showing that the kinetics is mainly affected by the strength of the LA, while the thermodynamics is significantly affected by the LB.
In addition to the experimental and theoretical evidence showing that intramolecular FLP systems are already capable of reversibly activating H2, it has also been found that slight modifications in Lewis centers' substituents or the linker can generate high variations in their reactivity, preventing even reversibility or simply avoiding the H2 splitting process; therefore, a thorough and systematic analysis of the electronic and steric effects in different FLP systems is essential to develop a more reliable guide for rational design of catalysts for the reversible activation of H2 that can be used to hydrogenate unsaturated compounds.
Recently, in a previous computational study,33 it has been found that the Lewis acidity of boron is inversely related to the overall Gibbs free energy change of H2 activation in an aminoborane type of FLP, i.e., a 2-[bis(R)boryl]-N,N-dimethylaniline-based FLP, where the R was varied from electron-donating groups to electron-withdrawing groups while the substitution on the N atom was retained and consequently, its Lewis basicity remained more or less unchanged. The Lewis acidity of the B atom was also shown to be inversely related to the catalytic activity of CO2 hydrogenation employing the FLP-H+/H− system, which was quantified using the computed turnover frequency (TOF) as proposed by Shaik et al.34 The Lewis acidity of boron was measured as the local electrophilicity index of the conceptual density functional theory (cDFT)35 condensed to the boron atom (ωB+), which proved to be a reliable indicator of boron acidity. Despite this interesting result, both the changes in the basicity of the nitrogen atom and the nature of the linker have not yet been studied in this direction. Consequently, in this work, we have centered our efforts on studying a broader set of systems in which both boron and nitrogen substituents have been modified to analyze how changes in boron acidity, nitrogen basicity, and the electronic nature of the linker affect the ωB+ ↔ ΔGH2 relationship recently found by us.33 For this, a series of electron-withdrawing groups (EWGs) were employed in boron (X) and electron-donating groups (EDGs) in nitrogen (Y) to be changed systematically. As EWGs, trifluoromethyl (CF3), pentafluorophenyl (C6F5), nonafluoro-tert-butyl, also known as perfluoro-tert-butyl (PFtB), and 2,4,6-tris(trifluoromethyl)phenyl (FMes) were considered, whereas as EDGs, methyl (CH3), tert-butyl (t-but), phenyl (Ph), and mesityl (Mes) were studied. Note that in both EWGs and EDGs there are two types of substituents that can be classified into two families: alkyl-based and aryl-based. Non-substituted boron and nitrogen (H) were also included as references. Moreover, to study the effect on the reversibility of H2 activation of the electronic and rigid nature of the linker that connects both Lewis centers, we considered the three linkers in the way shown in Fig. 3.
Theoretical background
Electrophilicity, Fukui function, and local electrophilicity index
Electrophilicity (ω) is defined within the cDFT framework as a global reactivity index.35,36 It measures the stabilization energy of a system when it is saturated with electrons from surroundings. Mathematically, in analogy to Ohm's law, it is expressed as: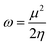 | (1) |
On the other hand, the Fukui function (f(r)) is defined as a local reactivity descriptor, which corresponds to the derivative of the electronic density with respect to N at a constant ν(r). Due to discontinuity in the electron number, f(r) is defined separately, taking the left-hand and right-hand derivatives, defining the f−(r) and f+(r) functions. The former and latter measure the most reactive sites in a molecule to undergo an electrophilic and nucleophilic attack, respectively. To obtain a numerical index of f(r), it can be integrated into any spatial region, where the most common partition employed is an atomic domain, allowing the most reactive atoms in a molecule to be obtained. Different atomic partitions can be applied; here we used the real-space partitioning of the electron density following the quantum theory of atoms in molecules (QTAIM) scheme,37,38 which allows defining atomic domains (ΩA) in a molecule from the analysis of the density gradient.
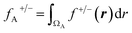 | (2) |
Taking the product of ω and fA+/− and following the concept of generalized philicity introduced by Chattaraj et al.39 it is possible to define respectively the local electrophilicity and nucleophilicity index (ωA+/−), which allows the most electrophilic and nucleophilic atom of a molecule to be obtained.
| ωA+/− = ωfA+/− | (3) |
In this case, they can be used as a measure of the Lewis acidity and basicity, respectively, of an atomic site in a molecule. Both global (μ and η) and local (f(r)) reactivity indices can be computed employing the frontier molecular orbital approximation (FMO) or the finite difference approximation (FDA). In the FMO, the reactivity indices are defined as: μ = 0.5(εHOMO + εLUMO), η = εLUMO − εHOMO, f−(r) ≈ ρHOMO and f+(r) ≈ ρLUMO, while in the FDA μ = 0.5(EN+1 − EN−1), η = EN+1 − 2EN + EN−1, f−(r) = ρN − ρN−1 and f+(r) = ρN+1 − ρN, which implies carrying out a ΔSCF procedure since single-point calculations are needed for the neutral (N), cation (N − 1), and anion (N + 1) systems. From these molecular properties, it is possible to characterize the intrinsic reactivity of any molecular system.
Computational details
Geometry optimization of stationary points was performed using the hybrid meta-GGA functional M06-2X40 combined with Pople's 6-31G(d,p) basis set. The nature of these structures on the potential energy surfaces was confirmed by harmonic frequency analysis, where no imaginary frequencies were found for reactants and products. The electronic energy was corrected using a larger basis set Def2-TZVP with the same functional. This methodology has been shown to successfully describe the reactivity of FLPs in activating small molecules, such as H2 and CO2.41 The implicit solvent effects were also included by using the self-consistent reaction field, employing the solvent density model (SMD),42 where benzene was chosen as solvent (ε = 2.2706). Therefore, the SMD/M06-2X/Def2-TZVP level of theory provides both the electronic and solvent contributions to the Gibbs free energy (EDef2-TZVPSMD), while the thermal (therm.) corrections were obtained in the gas phase (g) at the M06-2X/6-31G(d,p) level of theory (G6-31G(d,p)therm.,g), which were computed using statistical thermodynamics analysis at 298 K, employing the quasi-rotor-rigid-harmonic-oscillator (qRRHO) approximation, where frequencies lower than 100 cm−1 were treated as rigid rotors to avoid an overestimation in the vibrational contributions to entropy. In this way, the final reported Gibbs free energy was obtained as follows:| G = EDef2-TZVPSMD + G6-31G(d,p)therm.,g | (4) |
All electronic structure calculations were computed in the Gaussian09 package,43 while the q-RRHO calculations were performed employing the GoodVibes package.44,45 The reactivity indices from cDFT were calculated using the FMO approximation. The fA+/− values were given by integration of the f+/−(r) into the atomic basins defined within the QTAIM partition scheme, where the integration was performed in the Multiwfn 3.6 package.46
Results and discussion
Effect of substituents and linkers on the energetics of the H2 splitting process
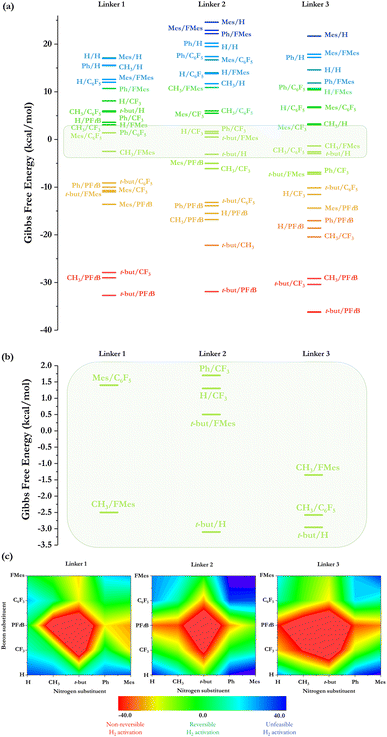
H2 activation was studied using each combination of substituents in the acid and base centers along with the variation of the linker, as is shown in Fig. 3. Based on the law of mass action for a chemical reaction at equilibrium at a given temperature and using stoichiometric amounts of FLP and H2, we employ the energy range from −3.5 to 2.0 kcal mol−1 to classify a reaction as quasi-ergoneutral to ensure a non-negligible amount of the species in thermal equilibrium at 298 K, i.e., 5% of either reactant (FLP and H2) or product (FLP-H+/H−); energetic differences outside this range imply either non-reversible (ΔG° < 0) or unfeasible (ΔG° > 0) activation of H2. The electronic and Gibbs free energy associated with the formation of FLP-H+/H− complexes are given in Table 1, where it can be noted that among the 75 FLP-H+/H− formed displayed in Fig. 4a, 27 do so following an exergonic process, 39 by an endergonic process and 9 by a quasi-ergoneutral process. Using the N-substituent/B-substituent notation, the near ergoneutral H2 activation reactions are carried out using the following substituent combinations: (i) for linker 1: CH3/FMes and Mes/C6F5 (experimentally tested by Erker et al.12,13 with a phosphoborane) (ii) for linker 2: H/CF3, t-but/H, t-but/FMes, and Ph/CF3, and (iii) for linker 3: CH3/C6F5, CH3/FMes, and t-but/H. It can be seen more clearly in the close-up of the selected energy range for quasi-ergoneutral, as shown in Fig. 4b.| LB center | LA center | Linker 1 | Linker 2 | Linker 3 | |||
|---|---|---|---|---|---|---|---|
| ΔEH2 | ΔGH2 | ΔEH2 | ΔGH2 | ΔEH2 | ΔGH2 | ||
| H | H | 5.7 | 17.0 | 5.8 | 19.5 | 1.0 | 14.6 |
| CF3 | −5.5 | 8.1 | −13.4 | 1.3 | −26.6 | −11.5 | |
| PFtB | −9.9 | 3.1 | −29.2 | −15.5 | −34.2 | −18.6 | |
| C6F5 | −0.7 | 12.0 | −1.3 | 13.8 | −8.0 | 6.7 | |
| FMes | −13.6 | 3.0 | −1.4 | 14.0 | −4.8 | 10.4 | |
| CH3 | H | 3.8 | 15.5 | −1.3 | 11.7 | −10.5 | 3.3 |
| CF3 | −9.8 | 3.1 | −20.4 | −6.1 | −35.4 | −20.4 | |
| PFtB | −45.2 | −29.0 | −32.5 | −16.8 | −44.9 | −29.2 | |
| C6F5 | −6.5 | 5.8 | −8.1 | 6.0 | −17.7 | −2.6 | |
| FMes | −18.5 | −2.5 | −4.2 | 10.9 | −16.9 | −1.4 | |
| t-but | H | −6.0 | 6.0 | −17.2 | −3.1 | −17.8 | −3.0 |
| CF3 | −42.8 | −27.9 | −36.8 | −22.2 | −46.0 | −30.4 | |
| PFtB | −49.0 | −32.7 | −47.6 | −31.9 | −52.5 | −36.2 | |
| C6F5 | −24.9 | −9.1 | −27.3 | −13.2 | −25.0 | −10.1 | |
| FMes | −27.1 | −11.0 | −15.5 | 0.5 | −23.6 | −7.2 | |
| Ph | H | 4.1 | 15.6 | 7.3 | 20.2 | 3.7 | 17.2 |
| CF3 | −9.2 | 3.6 | −12.2 | 1.7 | −22.6 | −6.9 | |
| PFtB | −25.4 | −10.0 | −28.9 | −13.9 | −33.0 | −17.0 | |
| C6F5 | −11.5 | 3.0 | 3.4 | 17.4 | −2.9 | 10.7 | |
| FMes | −5.5 | 10.7 | 7.8 | 22.2 | −3.7 | 11.8 | |
| Mes | H | 2.8 | 17.1 | 11.3 | 24.6 | 7.7 | 21.7 |
| CF3 | −26.0 | −10.7 | −8.4 | 5.5 | −12.3 | 3.0 | |
| PFtB | −29.6 | −13.6 | −20.6 | −5.0 | −29.7 | −14.4 | |
| C6F5 | −13.3 | 1.4 | 2.4 | 16.7 | −7.7 | 6.8 | |
| FMes | −4.2 | 12.6 | 8.9 | 22.9 | 2.9 | 17.9 | |
It is striking that the stiffer the linker (such as linker 3), the less frustration is needed to achieve reversible H2 activation. Fig. S1 (ESI†) shows the values of ΔGH2versus B substituents for each substituent attached to the N atom with the three linkers used here. When Y: t-but, Ph, and Mes, the trends are quite similar, indicating that in these cases, the thermodynamic driving force of the H2 activation process is almost independent of the nature of the linker; in contrast, when Y is H or CH3 (i.e., less steric hindrance) significant variations in ΔGH2 are observed, especially with linker 1 than with the rest of the linkers, generating an increase in ΔGH2 values (less exergonic), except when X: FMes. In this regard, for comparative purposes, all values of ΔGH2 for the two structurally similar linkers 1 and 2 are plotted against those of linker 3 and shown in Fig. S2a and b,† respectively. Both quantities are related to each other to different extents. While large deviations are found between the energy considering linkers 1 and 3 (see Fig S2a†), especially with the smaller systems as mentioned above, smaller deviations (see Fig. S2b†) are found considering linker 2, obtaining a good quality linear correlation (R2 = 0.93). In this case, the main difference between the reactions with linkers 2 and 3 is that, in the last case, the reactions are shifted towards the exergonic direction by about 6.4 kcal mol−1 (extracted from the intercept of the linear equation). These results can be explained by analyzing the electronic nature of the linker, where in the case of linkers 2 and 3, they can delocalize electron density across their π-system, conferring extra stabilization to an open FLP conformation. In contrast, linker 1 cannot stabilize an open conformation in less sterically hindered systems, since it leads to the classic Lewis adduct, making H2 activation less thermodynamically favorable.
Not only can systems achieve Lewis adduct conformation, but the more flexible the linker, the more conformational motifs they will have. In linker 1 a gauche/anti conformational change can occur; in linker 2 a Z/E isomerization can take place, while for linker 3, only a classical Lewis adduct formation can compete with the open or frustrated FLP conformation, which could indicate that this linker would be the most optimum to avoid catalyst quenching and/or any side reaction (these possible changes are shown in Fig. S3†). To confirm this, a conformational analysis was performed by evaluating the Gibbs energy of the different conformers with respect to their active conformation in each case. The energetic values and the percentage population according to the Boltzmann distribution are given in Table S1,† where the near ergoneutral reactions were analyzed to see if any conformational change could affect their reversibility. The gauche–anti change was studied for linker 1. As example, we took the ergoneutral CH3/FMes system. The Gibbs free energy difference between the two conformers is 1.9 kcal mol−1, indicating that the equilibrium is shifted towards gauche (96% of the sample is in the FLP conformer), whereas the equilibrium is displaced to the anti-conformer at 100% due to steric effects in the case of Mes/C6F5. On the other hand, Z/E isomerization was also analyzed for linker 2, taking the ergoneutral Ph/CF3 system, which presents an energy difference between both isomers of −8.6 kcal mol−1, indicating that the equilibrium is totally shifted towards the E isomer. The same trend is found for the rest of the systems, except for the H/CF3 system, where it is observed that the three conformers: Z (FLP), E, and Lewis adduct are in equilibrium at room temperature with a distribution of 1%, 66%, and 33%, respectively. Finally, in the case of linker 3 only the conformational change from the FLP to the classical Lewis adduct can occur. Both conformers in the CH3/C6F5 and t-but/H systems are in equilibrium but fully shifted towards the classical Lewis adduct (see Table S1†), whereas in CH3/FMes, the system is 100% in its frustrated form, indicating that a very bulky substituent, such as FMes, at a single center is sufficient to prevent the formation of the classical Lewis adduct. implying that less frustration may also trigger higher activity in H2 activation.47 These results make linker 3 the optimum to be employed; therefore, we will only consider linker 3 for the following analysis.
The most exergonic reactions are reached when the substituent in both acid and base centers is of the alkyl type, with exergonicity increasing as the size of the substituents also increases (the combination of t-but/PFtB attached to N and B atoms, respectively, generates more exergonic reactions for all the linkers). If one of the substituents is of the aryl type, the free energy of the process shifts quickly to a less exergonic direction. This can be seen more clearly in the RGB color code snapshots displayed in Fig. 4c, where changing the t-but/PFtB combination to Ph/PFtB or t-but/C6F5 generates a process that is about 20 kcal mol−1 less exergonic, regardless of the linker employed. The process becomes endergonic if both alkyl substituents t-but/PFtB are changed to the aryl type (to the Ph/C6F5 combination, for example). This feature is directly related to the stability of the isolated FLP provided by the aryl nature of both groups, promoting strong non-covalent interactions (e.g., donor–acceptor stacking) and, consequently, rearranging the electron density accumulated and depleted on nitrogen and boron, respectively, throughout the molecular system. If the size of these aryl substituents is increased, taking the Mes/FMes combination instead of Ph/C6F5, a highly endergonic process is found in all cases, which could be related to unfeasible H2 activation. From the in-depth analysis of Fig. 4c, ergoneutrality is clearly found around the bulkier t-but/PFtB combination, which is the region shown in green.
Based on previous experimental reports, we have performed a comparison between the reversibility of the process and our calculated Gibbs free energies. Fig. 5 shows some of the intramolecular FLPs (with different C–C connectors for LA and LB) experimentally employed to activate H2 with similar linkers used here by us. As we can see, the systems that show reversibility present a ΔGH2 value close to zero, while all non-reversible processes are exergonic (ΔGH2 < −9 kcal mol−1) and all the unreactive FLPs in front of H2 are endergonic reactions (ΔGH2 > 10 kcal mol−1), confirming that studying ΔGH2 and explaining the trends found is essential to gain new insights into the reversibility of the process and what factors control it. Notice that some of the experimentally tested FLPs shown are phosphoboranes (see Fig. 5); nevertheless, we have compared them with their analogous aminoboranes studied in this work.
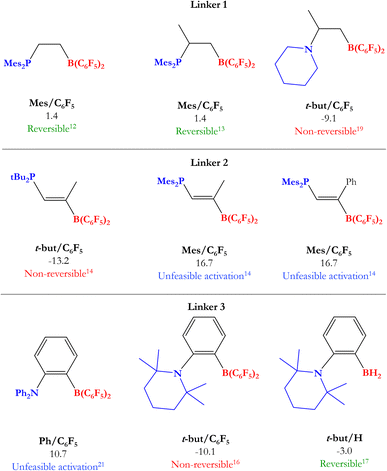 | ||
| Fig. 5 Some experimentally tested FLPs in H2 activation with C–C connectors for LA and LB. Their analogous systems to those studied in this work are mentioned below each FLP along with their Gibbs free energy from Table 1 and the experimental information about reversibility. | ||
Electronic properties of FLPs and their effect on the reversibility of H2 activation
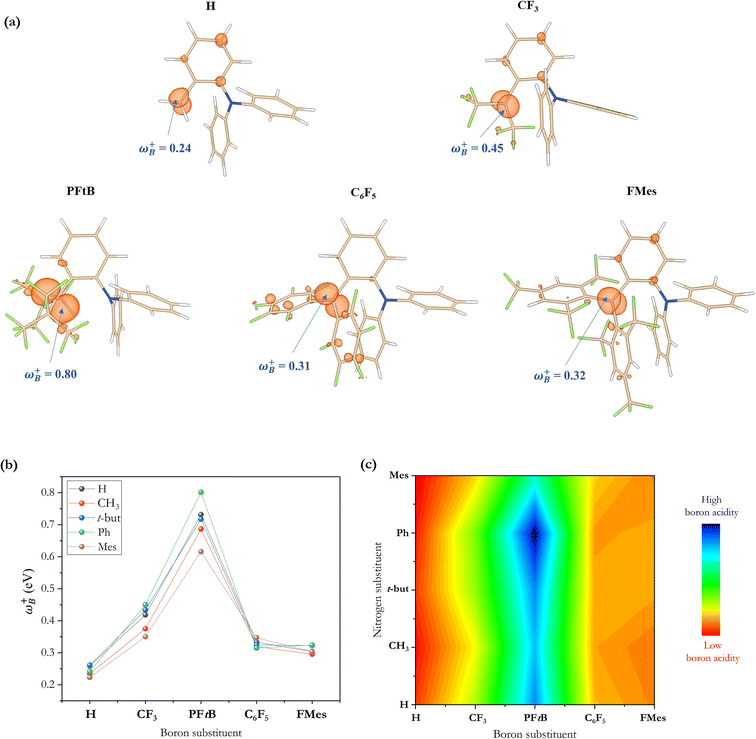
Recently, it has been shown that the local electrophilicity condensed on the boron atom (ωB+) is inversely related to the Gibbs free energy of the H2 activation using a 2-[bis(R)boryl]-N,N-dimethylaniline-based FLP,33i.e., the higher the ωB+ value, the more exergonic the process is, where ωB+ was then proposed as a measure of the Lewis acidity of the B atom. Note that in that study, the substitution of the N atom was not varied. Thus, to analyze the electronic effect that may be implied by changes in the substituent attached to the N atom of this type of aminoborane-based FLPs, we used the same local reactivity descriptor on the whole set of reactions with linker 3 studied in this work, although we discuss local properties on the N atom below. Table 2 summarizes the electronic properties (ω, fB+ and ωB+) of each FLP system and the boron–nitrogen internuclear distance in their active FLP conformation (dB–N) as a measure of the degree of frustration. At first glance, there are large differences among all systems. To see these results more clearly, the ωB+ values of all the substituent combinations employing linker 3 are plotted as shown in Fig. 6. Again, as in the analysis based on ΔGH2 data, we can observe that the higher values are found using the PFtB group on boron for all the cases, obtaining the highest value with the Ph group on the N atom. On the other hand, the lower values are observed with the H and FMes groups attached to B.| LB center | LA center | ω | f B + | ω B + | d B–N |
|---|---|---|---|---|---|
| H | H | 1.31 | 0.20 | 0.26 | 2.990 |
| CF3 | 1.91 | 0.22 | 0.42 | 3.049 | |
| PFtB | 2.05 | 0.36 | 0.73 | 3.112 | |
| C6F5 | 1.98 | 0.17 | 0.33 | 3.038 | |
| FMes | 2.02 | 0.15 | 0.30 | 2.963 | |
| CH3 | H | 1.22 | 0.19 | 0.23 | 3.017 |
| CF3 | 1.76 | 0.21 | 0.38 | 3.081 | |
| PFtB | 1.92 | 0.36 | 0.69 | 3.165 | |
| C6F5 | 1.91 | 0.17 | 0.32 | 2.976 | |
| FMes | 1.78 | 0.17 | 0.30 | 3.075 | |
| t-but | H | 1.32 | 0.20 | 0.26 | 2.973 |
| CF3 | 1.70 | 0.25 | 0.43 | 2.937 | |
| PFtB | 1.97 | 0.36 | 0.72 | 3.449 | |
| C6F5 | 1.86 | 0.17 | 0.32 | 2.998 | |
| FMes | 1.91 | 0.17 | 0.32 | 3.306 | |
| Ph | H | 1.33 | 0.18 | 0.24 | 3.001 |
| CF3 | 1.96 | 0.23 | 0.45 | 2.905 | |
| PFtB | 2.21 | 0.36 | 0.80 | 3.171 | |
| C6F5 | 1.94 | 0.16 | 0.31 | 3.054 | |
| FMes | 1.95 | 0.17 | 0.32 | 3.173 | |
| Mes | H | 1.20 | 0.19 | 0.22 | 3.004 |
| CF3 | 1.31 | 0.25 | 0.33 | 2.806 | |
| PFtB | 1.82 | 0.34 | 0.62 | 3.500 | |
| C6F5 | 1.87 | 0.19 | 0.35 | 3.159 | |
| FMes | 1.86 | 0.16 | 0.30 | 3.391 |
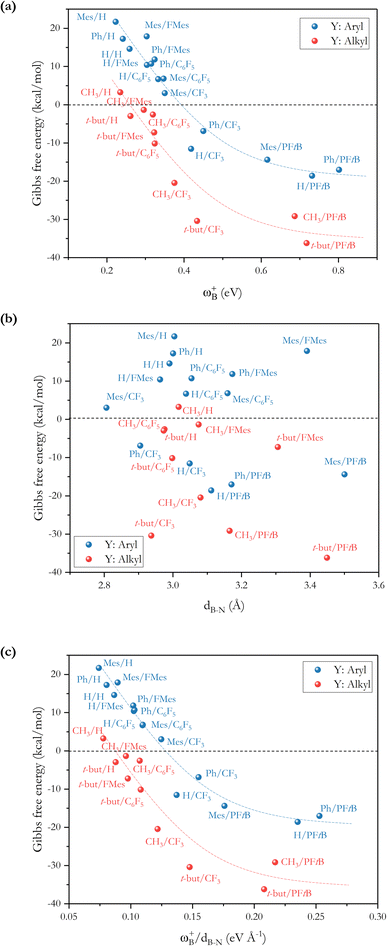
To analyze whether the relationship ωB+ ↔ ΔGH2 holds considering the whole set of reactions and thus move toward a generalized model in H–H bond activation, the values of ΔGH2 as a function of ωB+ are plotted as shown in Fig. 7a. As it can be seen, ΔGH2 correlates very well with ωB+ through an inverse relationship with two distinctive behaviors, thus confirming that as the Lewis acidity of B increases, it leads to more stable FLP-H+/H− zwitterions. The former is found for H, Ph, and Mes as substituents attached to the N atom (shown in blue circles), while the latter is found for CH3 and t-but (shown in red circles), i.e., there are two distinct relationships, one for aryl-type groups and one for alkyl-type groups attached to the N atom. Let us analyze the fitting parameters of each reciprocal function. First, the slopes are almost equal (13.53 vs. 14.22, being somewhat higher for alkyl-type substituents on the N atom), indicating that variations in the Lewis acidity of B given by ωB+ have a similar effect on the energetics of the H2 activation process with alkyl- and aryl-type groups. The most notable difference comes from the asymptotic value of the reciprocal function fitting procedure corresponding to the trend value for an extremely acidic FLP, which is considerably lower (more negative) for the alkyl group than for the aryl group (−54.4 vs. −35.4 kcal mol−1). This revealed fact is given by the nature of the substituent attached to the N atom; if this is aryl, such as Ph or Mes, at equal boron acidity, the process shifts toward an endoenergetic direction compared to if the substituent is alkyl, such as CH3 or t-but. In the latter case, extra stabilization of the product is generated, shifting the reaction in an exergonic direction. This feature is related to the Lewis base strength. Alkyl substituents tend to increase the basicity and, thus, the proton affinity (PA) of substituted anilines compared to aryl substituents. The experimental PAs of aniline, triphenylaniline, N,N-dimethylaniline, N,N-diethylaniline, and N,N-diisopropylaniline are 209.5,48 209.5,49 223.4,48 227.6,48 and 228.6,48 kcal mol−1, respectively (the first and second systems are analogous to H- and Ph-substituted FLPs, while the remnants are analogous to alkyl-substituted FLPs), i.e., PA(aniline) ≈ PA(triphenylaniline) < PA(N,N-dimethylaniline) ≈ PA(N,N-diethylaniline) ≈ PA(N,N-diisopropylaniline). Note that the PA of aniline is the same as that of triphenylaniline, which corroborates our findings that the unsubstituted (H/H) FLPs behave like those substituted at the N atom with aryl-type groups. Complementarily, we analyzed the local nucleophilicity values of the N atom as a measure of Lewis basicity of N for both an alkyl (CH3) and an aryl (Ph) substituent, which are reported in Table S2.† As can be seen, ωN− values are higher for the first type of substituent than the second, except for X: CF3. Furthermore, in Table S2† the standard deviations for the values of both ωB+ and ωN− are reported, which allows us to see the respective dispersions of the data. These show that Lewis acidity is more dispersed than Lewis basicity ensuring that our choice of ωB+ is an appropriate property to guide the design of these novel systems, since it is shown to be more sensitive to substitution in both LA and LB centers.
From the ωB+ ↔ ΔGH2 relationships, it is plausible to define the range of ωB+ where the “green window” that ensures reversible H2 activation falls. The case of aryl-type substituents attached to the N atom, which falls slightly slower than that corresponding to alkyl-type substituents, presents a wider range of ωB+ from 0.36 to 0.42 eV than that for alkyl-type substituents which ranges from 0.25 to 0.28 eV. We have tested the predictive value of these using some homologous systems shown in Fig. 5, finding satisfactory results that allow us to evaluate the robustness of the proposed relations as can be seen in Table S3.†
On the other hand, no relationship was found between the ΔGH2 and the degree of frustration given by the internuclear distance between the B and N atoms (dB–N) in the active form of the FLP, as shown in Fig. 7b. As mentioned above, the most acidic FLPs that give rise to the most stable FLP-H+/H− complexes are those substituted with the PFtB group on the B atom. This fact may be due to the high degree of frustration of these systems, since the B⋯N distance is slightly shorter than the sum of the van der Waals radii for B (1.92 Å)50 and N (1.55 Å),51i.e., 3.47 Å. Therefore, from this study, we verify that with lower frustration, reversible activation of H2 can be achieved.
It is striking that if ωB+ is divided by dB–N, (the degree of frustration), reciprocal relationships of higher quality are found again (see Fig. 7c), with distinct behaviors maintained for aryl- and alkyl-type substituents at the N atom. This suggests that both the Lewis acidity of boron (ωB+) and steric or frustration degree effects play a synergistic role, although the electronic effect is a predominant factor. It is quite interesting when dB–N is brought together with ωB+, since the 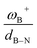 quotient has unit energy/length corresponding to unit force; concomitantly, it can be seen as a measure of the FLP strength in H–H bond activation, which to our knowledge is for the first time quantifiable in this field. Again, the slopes are more or less the same, while the asymptotic value of the reciprocal function fitting procedure is different depending on the type of substituent attached to the N atom, corresponding to the trend value for extremely strong FLPs, which is considerably lower (more negative) for the alkyl group than for the aryl group (−56.9 vs. −37.6 kcal mol−1) but similar to those obtained in the fitting procedure shown in Fig. 7a. This confirms that Lewis acidity is the predominant factor in the H2 activation process. Although we mentioned that changes in the nucleophilicity of the N atom are less sensitive to substituent changes in both LA and LB centers, the ratio between
quotient has unit energy/length corresponding to unit force; concomitantly, it can be seen as a measure of the FLP strength in H–H bond activation, which to our knowledge is for the first time quantifiable in this field. Again, the slopes are more or less the same, while the asymptotic value of the reciprocal function fitting procedure is different depending on the type of substituent attached to the N atom, corresponding to the trend value for extremely strong FLPs, which is considerably lower (more negative) for the alkyl group than for the aryl group (−56.9 vs. −37.6 kcal mol−1) but similar to those obtained in the fitting procedure shown in Fig. 7a. This confirms that Lewis acidity is the predominant factor in the H2 activation process. Although we mentioned that changes in the nucleophilicity of the N atom are less sensitive to substituent changes in both LA and LB centers, the ratio between 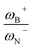 follows the same type of trend as that shown in Fig. 7c, following the same patterns between alkyl and aryl substitution as can be seen in Fig. S4.†
follows the same type of trend as that shown in Fig. 7c, following the same patterns between alkyl and aryl substitution as can be seen in Fig. S4.†
Thus, by knowing the acidity of the boron atom, through local electrophilicity, and the nature of the substituent attached to the N atom (aryl or alkyl), it is possible to estimate the performance of the FLP in the H2 activation process, allowing the rational design of FLPs to act as catalysts to be guided and to reach the reversibility of the process.
Finally, the comparison between the ΔGH2 ↔ ωB+ relationship found in this work with that found in the previous work33 to see differences when considering a larger set of reactions is discussed in more detail in the ESI.† Thus, it is recommended to use our new relationship between ΔGH2 and ωB+, which is a more general expression since it takes into account a larger set of systems, being valid for a wide range of ωB+ values.
Conclusions
In this work, a systematic study of H2 activation by 75 intramolecular aminoborane-based FLPs using different types of linkers shows that a large variation in the Gibbs free energy change of the process (from −36.2 to 24.6 kcal mol−1) is found by modifying the acidic and basic strengths of boron and nitrogen atoms, respectively. Thus, the reversibility of the process is only achieved in a few cases (12%), indicating that careful analysis of the acidity and basicity of both Lewis centers is crucial to obtain a reaction that meets this requirement.Variation in the linker, while maintaining the nature of the C–C connector between the LA and LB centers, does not generate considerable energetic differences using the same substituents, suggesting that the rigidity of the linker is the factor to be considered to improve the yields. In this regard, linker 3 proved to be more appropriate because it is less capable of undergoing conformational changes that may quench the catalyst.
The boron acidity, given by the condensed-to-boron electrophilicity index ωB+, correlates very well with the Gibbs free energy of the process, where two different relationships were found: one for aryl-type substituents on the N atom, including the non-substituted (i.e., H, Ph, and Mes) and another one for alkyl-type substituents on the N atom (i.e., CH3 and t-but). From the fitting functions, it was easy to confirm that alkyl substituents shift the process towards the exergonic direction, i.e., at equal boron acidity, H2 activation will be more exergonic with alkyl substituents on the N atom than with aryl substituents, including the non-substituted system. This result is directly related to the proton affinities of nitrogen, which are higher for alkyl-substituted anilines than for aryl-substituted ones. Furthermore, when the degree of frustration given by the B⋯N distance (dB–N) is brought together with ωB+ in this analysis as 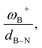 the quality of the above fitting function improves. This quotient has unit force and thus emerges as a measure of strength of FLPs, which, to our knowledge, is quantifiable for the first time. However, the thermodynamic driving force is dominated by the electron factors that are contained in ωB+.
the quality of the above fitting function improves. This quotient has unit force and thus emerges as a measure of strength of FLPs, which, to our knowledge, is quantifiable for the first time. However, the thermodynamic driving force is dominated by the electron factors that are contained in ωB+.
Finally, from the relationships found here and in previous reports, we can estimate the catalytic activity of these systems in the reduction of CO2 to formic acid, methanediol, and methanol. The present results showed that the more general relationship found in this work should be employed because it contains a considerably larger set of reactions than the previous work, finding a different dependence of ΔGH2 with respect to ωB+. This and the previously published articles open a new opportunity to guide the rational design of FLP-based systems to be employed in metal-free catalytic processes, optimizing the H2 reversible activation process in a rational way when this is crucial to improve the catalytic performance.
Data availability
Additional data can be found in the ESI file.†Author contributions
Investigation and validation: C. B.-M., R. D., and P. J. Conceptualisation, methodology, and supervision: C. B.-M. and P. J. Writing – original draft: C. B.-M., R. D., and P. J. Writing – review and editing: C. B.-M., R. D., and P. J.Conflicts of interest
There are no conflicts to declare.Acknowledgements
CBM and PJ acknowledge Fondecyt grants with projects no. 1181914 and 1231241, and RD acknowledges Fondecyt Iniciación project no. 11230753 for financial support.Notes and references
- P. P. Edwards, V. L. Kuznetsov and W. I. David, Philos. Trans. R. Soc., A, 2007, 365, 1043–1056 CrossRef CAS PubMed.
- W. W. Clark and J. Rifkin, Energy Policy, 2006, 34, 2630–2639 CrossRef.
- S. Atilhan, S. Park, M. M. El-Halwagi, M. Atilhan, M. Moore and R. B. Nielsen, Curr. Opin. Chem. Eng., 2021, 31, 100668 CrossRef.
- G. J. Kubas, J. Organomet. Chem., 2014, 751, 33–49 CrossRef CAS.
- D. W. Stephan, J. Am. Chem. Soc., 2015, 137, 10018–10032 CrossRef CAS PubMed.
- D. W. Stephan and G. Erker, Chem. Sci., 2014, 5, 2625–2641 RSC.
- D. W. Stephan, Acc. Chem. Res., 2015, 48, 306–316 CrossRef CAS PubMed.
- P. Preuster, C. Papp and P. Wasserscheid, Acc. Chem. Res., 2017, 50, 74–85 CrossRef CAS PubMed.
- M. Niermann, A. Beckendorff, M. Kaltschmitt and K. Bonhoff, Int. J. Hydrogen Energy, 2019, 44, 6631–6654 CrossRef CAS.
- G. C. Welch, R. R. S. Juan, J. D. Masuda and D. W. Stephan, Science, 2006, 314, 1124–1126 CrossRef CAS PubMed.
- P. A. Chase, G. C. Welch, T. Jurca and D. W. Stephan, Angew. Chem., Int. Ed., 2007, 46, 8050–8053 CrossRef CAS PubMed.
- P. Spies, G. Erker, G. Kehr, K. Bergander, R. Fröhlich, S. Grimme and D. W. Stephan, Chem. Commun., 2007, 5072 RSC.
- P. Spies, G. Kehr, K. Bergander, B. Wibbeling, R. Fröhlich and G. Erker, Dalton Trans., 2009, 1534 RSC.
- P. Spies, S. Schwendemann, S. Lange, G. Kehr, R. Fröhlich and G. Erker, Angew. Chem., Int. Ed., 2008, 47, 7543–7546 CrossRef CAS PubMed.
- V. Sumerin, F. Schulz, M. Atsumi, C. Wang, M. Nieger, M. Leskelä, T. Repo, P. Pyykkö and B. Rieger, J. Am. Chem. Soc., 2008, 130, 14117–14119 CrossRef CAS PubMed.
- K. Chernichenko, M. Nieger, M. Leskelä and T. Repo, Dalton Trans., 2012, 41, 9029 RSC.
- K. Chernichenko, B. Kótai, I. Pápai, V. Zhivonitko, M. Nieger, M. Leskelä and T. Repo, Angew. Chem., Int. Ed., 2015, 54, 1749–1753 CrossRef CAS PubMed.
- V. Sumerin, K. Chernichenko, M. Nieger, M. Leskelä, B. Rieger and T. Repo, Adv. Synth. Catal., 2011, 353, 2093–2110 CrossRef CAS.
- S. Schwendemann, R. Fröhlich, G. Kehr and G. Erker, Chem. Sci., 2011, 2, 1842 RSC.
- P. Moquist, G.-Q. Chen, C. Mück-Lichtenfeld, K. Bussmann, C. G. Daniliuc, G. Kehr and G. Erker, Chem. Sci., 2015, 6, 816–825 RSC.
- R. Roesler, W. E. Piers and M. Parvez, J. Organomet. Chem., 2003, 680, 218–222 CrossRef CAS.
- Z. Mo, E. L. Kolychev, A. Rit, J. Campos, H. Niu and S. Aldridge, J. Am. Chem. Soc., 2015, 137, 12227–12230 CrossRef CAS PubMed.
- M.-A. Courtemanche, A. P. Pulis, É. Rochette, M.-A. Légaré, D. W. Stephan and F.-G. Fontaine, Chem. Commun., 2015, 51, 9797–9800 RSC.
- T. A. Rokob, A. Hamza and I. Pápai, J. Am. Chem. Soc., 2009, 131, 10701–10710 CrossRef CAS PubMed.
- T. A. Rokob, I. Bakó, A. Stirling, A. Hamza and I. Pápai, J. Am. Chem. Soc., 2013, 135, 4425–4437 CrossRef CAS PubMed.
- S. Grimme, H. Kruse, L. Goerigk and G. Erker, Angew. Chem., Int. Ed., 2010, 49, 1402–1405 CrossRef CAS PubMed.
- B. Schirmer and S. Grimme, Chem. Commun., 2010, 46, 7942 RSC.
- D. Yepes, P. Jaque and I. Fernández, Chem.–Eur. J., 2016, 22, 18801–18809 CrossRef CAS PubMed.
- F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed.
- D. Yepes, P. Jaque and I. Fernández, Chem.–Eur. J., 2018, 24, 8833–8840 CrossRef CAS PubMed.
- K. Wang, Z. Pan, W. Xu, Z. Chen and X. Yu, J. Energy Chem., 2019, 35, 174–180 CrossRef.
- L. Liu, B. Lukose, P. Jaque and B. Ensing, Green Energy Environ., 2019, 4, 20–28 CrossRef.
- C. Barrales-Martínez, R. Durán and P. Jaque, Inorg. Chem. Front., 2023, 10, 2344–2358 RSC.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110 CrossRef CAS PubMed.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874 CrossRef CAS PubMed.
- R. G. Parr, L. v. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- P. K. Chattaraj, B. Maiti and U. Sarkar, J. Phys. Chem. A, 2003, 107, 4973–4975 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- F. Huang, J. Jiang, M. Wen and Z.-X. Wang, J. Theor. Comput. Chem., 2014, 13, 1350074 CrossRef.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Wallingford, CT, 2009 Search PubMed.
- G. Luchini, J. V. Alegre-Requena, I. Funes-Ardoiz and R. S. Paton, F1000Research, 2020, 9, 291 Search PubMed.
- I. Funes-Ardoiz and R. S. Paton, GoodVibes: version 2.0.3, Zenodo, 2018 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- M. V. Mane and K. Vanka, ChemCatChem, 2017, 9, 3013–3022 CrossRef CAS.
- S. G. Lias, J. A. A. Jackson, H. Argentar and J. F. Liebman, J. Org. Chem., 1985, 50, 333–338 CrossRef CAS.
- I. Kaljurand, R. Lilleorg, A. Murumaa, M. Mishima, P. Burk, I. Koppel, I. A. Koppel and I. Leito, J. Phys. Org. Chem., 2013, 26, 171–181 CrossRef CAS.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812 CrossRef CAS PubMed.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc03992g |
| This journal is © The Royal Society of Chemistry 2023 |