Microscopic insight into the shaping of MOFs and its impact on CO₂ capture performance

Abstract

The traditional synthesis method produces microcrystalline powdered MOFs, which prevents direct implementation in real-world applications which demand strict control of shape, morphology and physical properties. Therefore, shaping of MOFs via the use of binders is of paramount interest for their practical use in gas adsorption/separation, catalysis, sensors, etc. However, so far, the binders have been mostly selected by trial-and-error without anticipating the adhesion between the MOF and binder components to ensure the processability of homogeneous and mechanically stable shaped MOFs and the impact of the shaping on the intrinsic properties of the MOFs has been overlooked. Herein, we deliver a first systematic multiscale computational exploration of MOF/binder composites by selecting CALF-20, a prototypical MOF for real application in the field of CO₂ capture, and a series of binders that cover a rather broad spectrum of properties in terms of rigidity/flexibility, porosity, and chemical functionality. The adhesion between the two components and hence the effectiveness of the shaping as well as the impact of the overall porosity of the CALF-20/binder on the CO₂/N₂ selectivity, CO₂ sorption capacity and kinetics was analyzed. Shaping of CALF-20 by carboxymethyl cellulose was predicted to enable a fair compromise between excellent adhesion between the two components, whilst maintaining high CO₂/N₂ selectivity, large CO₂ uptake and CO₂ transport as fast as in the CALF-20. This multiscale computational tool paves the way towards the selection of an appropriate binder to achieve an optimum shaping of a given MOF in terms of processability whilst maintaining its high level of performance.

---

Introduction

Constructed from the assembly of metal ions/clusters with organic linkers, the so-called metal–organic frameworks (MOFs) have emerged as a novel class of porous materials with attractiveness owing to their high tunability in terms of topology/porosity and broad chemical diversity.^1–8 MOFs are promising candidates in different applications including gas storage, separation technologies, chemical sensing, catalysis, biomedicine and molecular electronics among others.^9–16 However, most MOF materials have been synthesized so far as small micron-size crystals with limited packing densities.^17–20 Specific crystal size, suitable three-dimensional shape, uniform morphology, and high mechanical strength are the key ingredients for real-world applications which MOF in powdered form usually lacks. Also, the pulverulent nature of powdered MOFs is a severe drawback for further applications in terms of the low mass transfer rate sometimes associated with a poor recyclability and low volumetric adsorption efficiency.^18,21 Therefore, successful deployment of this family of porous materials at the industrial level requires the engineering of MOF powders into well-shaped three-dimensional bodies while maintaining their inherent physical and chemical properties.

Substantial efforts have been made over the last few years to shape MOFs into films, pellets, spherical beads, foam, monolith granules, hollow structures, and honeycomb monoliths among others.^22–24 This has been realized by using a wide range of strategies including mechanical compression, granulation, extrusion, layer-by-layer decomposition and sol–gel methods.^18,25,26 Most of these shaping approaches have been inspired by the knowledge gained on shaping of conventional porous materials like zeolites or activated carbons. One of the most common shaping procedures is the mechanical pressure-induced pelletization.^27–30 However, this strategy severely impacts the crystallinity and textural properties of the pristine MOFs since the applied pressure narrows down the intermolecular voids, most of the time leads to amorphization and can even collapse the frameworks in some extreme cases. Deriving MOF monoliths via layer-by-layer decomposition or the sol–gel method is another approach which has also drawn prominent attention;^23,24 however, this process is not optimum owing to its operating complexity, timescale of gel formation, limited mechanical robustness and complicated scalable fabrication.

Alternatively, another shaping strategy has emerged where the MOF powder crystal is hybridized with external substrates, called binders, i.e., synthetic polymers in most cases, as well as ceramics, and nanoparticles, among others.^23,24 The resulting shaped materials in different forms (pellets, extrudates, etc.), commonly referred to as composites, offer potentially many advantages, e.g., high mechanical stability and improved processability.^25,31–33 So far, the binders associated with MOFs have been mostly selected by analogy with what has been considered for the inorganic zeolite materials.^34,35 Indeed, only a few commercially available binders have been tested and this choice has been mostly made by trial-and-error without anticipating (i) the nature of the MOF/binder interfaces that are of key importance for controlling the adhesion between the two components to ensure the processability of homogeneous and mechanically stable shaped MOFs and (ii) the structuring of the resulting composites, in particular, the pore network structuring at the MOF/binder interface that can play a pivotal role in the molecular adsorption and diffusion in the overall hybrid systems. Furthermore, understanding/rational analysis of the impact of the MOF shaping on its adsorption/separation performance compared to the powdered MOF has been overlooked. Indeed, the priority challenge for the MOF community is currently to promote this family of porous materials at the application level and many key applications at the industrial level require shaped materials to make decisive progress on the application side. Typically, our recent perspective article highlights the urgent need for precise control over MOF shaping to boost the integration of this class of materials in different practical applications.³⁶ Therefore, the challenge remains to select a priori optimum binders for shaping a given MOF with the objectives of ensuring good compatibility between the two components and maintaining a level of performance as close as possible to that of its powdered form for the target application.^37,38 This holds particularly true for the exploitation of MOF sorbents in industrial CO₂ capture adsorption processes, e.g., pressure swing adsorption (PSA) technology, that require shaped porous solids. To address this challenge, an unprecedented in-depth microscopic insight into the MOF/binder composite systems is required. As a proof-of-concept, our proposed multiscale computational approach integrating quantum calculation-based density functional theory (DFT) and force field molecular dynamics (MD) and Monte Carlo (MC) simulations was trained on the shaping of the prototypical Calgary Framework 20 (CALF-20) MOF. This MOF made of 1,2,4-triazolate bridged zinc(II) layers pillared by oxalate ions has been demonstrated recently as a benchmark CO₂ selective sorbent owing to its exceptionally high CO₂/N₂ selectivity and large CO₂ uptake under working conditions.^39,40 The shaping of this highly chemically stable and easily scalable MOF has been achieved with the use of a single binder, i.e., polysulfone; however, there is an associated loss of CO₂ sorption capacity as compared to its powdered form (about 20% loss).³⁹ This small pore MOF was selected to systematically assess the impact of the nature of the binders on the MOF/binder interfacial structuring and on the thermodynamic CO₂/N₂ separation and CO₂ kinetics performance of the resulting composite. Indeed, four different polymeric binders – carboxymethyl cellulose (CMC),⁴¹ poly(vinyl acetate) (PVA),⁴² poly(vinyl butyral) (PVB),⁴³ and poly(vinyl alcohol) (PVOH)⁴⁴ – were considered on account of their commercial availability, fabrication simplicity and their previous uses for shaping a range of porous materials. Further, these polymers cover a rather broad diversity in terms of rigidity/flexibility, porosity, and chemical functionality and this offers an opportunity to identify the features of the binder that most impact the nano-structuring and adsorption properties of the resulting MOF composites. Our multiscale computational approach was therefore deployed to construct in silico atomistic models for all composites and first gain insight into the MOF/binder composite in terms of interfacial interactions and structuring to assess the compatibility of the two components and hence the effectiveness of the shaping. An in-depth analysis of the overall porosity of the CALF-20/binder composite and its impact on the CO₂/N₂ selectivity as well as its CO₂ sorption capacity and CO₂ kinetics was further conducted. Shaping of CALF-20 by CMC was predicted to enable a compromise between good adhesion between the two components whilst maintaining high CO₂/N₂ selectivity, large CO₂ uptake and CO₂ transport as fast as in the CALF-20 MOF. From a broader perspective, our computational toolbox is expected to guide the experimental effort towards the selection of an appropriate binder to achieve an optimum shaping of a given MOF in terms of processability whilst maintaining a high level of selectivity.

Computational methodology

In this section, we present the methodology encompassing quantum calculation-based density functional theory and force field-based molecular dynamics that was employed to construct the atomistic models of both the binders and CALF-20 surface, along with CALF-20/binder composites. We also equally describe the details of the force field Monte Carlo and molecular dynamics approaches that were used to explore the gas adsorption and diffusion in these systems.

Construction of the polymeric binder models

The chemical structure of the constitutive monomers for the four binders (CMC, PVA, PVOH and PVB) is shown in Fig. 1a. The construction of the each of the individual atomistic binder models was accomplished by applying an in silico polymerization procedure as implemented in the Polymatic code.⁴⁵ The force-field parameters as well as the atomic partial charges for CMC, PVA and PVOH were considered from previous works^46–48 and are provided in the ESI (Tables S1–S3†). Regarding PVB, the non-bonded Lennard-Jones (LJ) parameters were taken from the TRAPPE united-atom force-field^49,50 as listed in Table S4† while the bonded parameters were considered from the GAFF force-field⁵¹ in a similar way to that previously implemented for other binder models. The partial charges for PVB were defined starting with the monomer first geometry optimized using the PBE functional and the 6-31+G(d,p) basis set as implemented in the Gaussian software.⁵² The corresponding CHELPG charges for the monomer were assessed⁵³ and listed in Table S4.† Details about the force-field and charges for all the binders can be found in the ESI (Fig. S1–S4 and Tables S1–S4†). Since most of the commercially shaped sorbent implies the use of 10–25 wt% binder,²¹ atomistic models were made of a polydisperse mixture of chains each containing from 10 to 50 monomers associated with a total mass of the binder required to achieve about 20 wt% in the MOF–binder composite. In order to ensure that the conclusions drawn on the MOF/binder composite constructed above are chain size and dispersity independent, additional simulations with different chain length distributions and system sizes have been conducted (Tables S5–S7, Fig. S5 and S6†).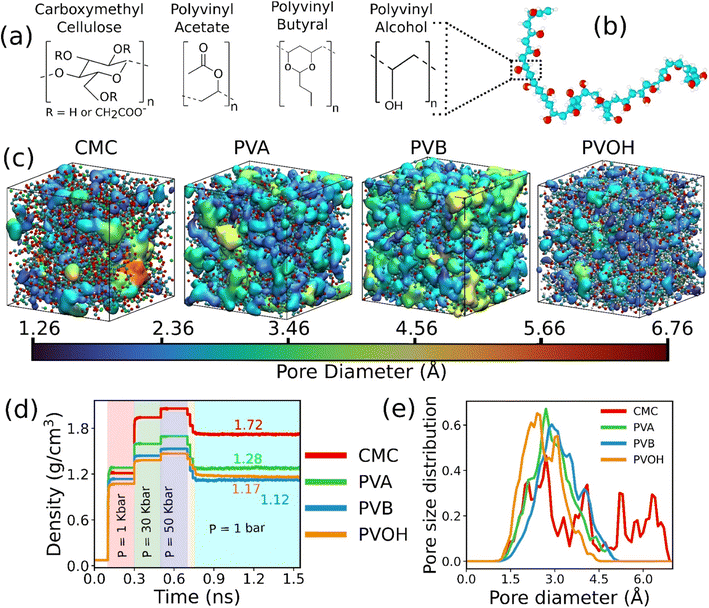

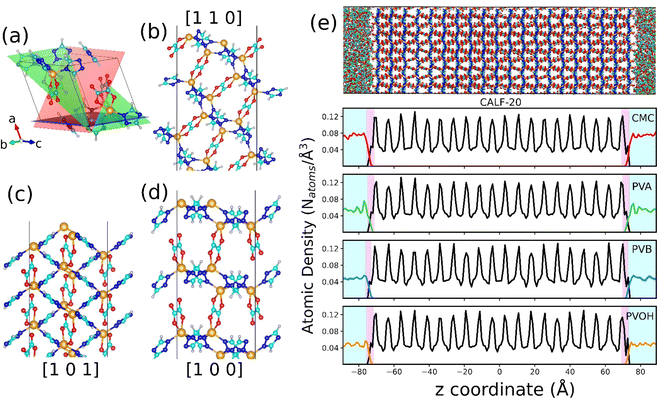
Fig. 1 Atomistic models of binders built by force field molecular dynamics simulations. (a) Nature of the constitutive monomers of all binders. (b) Schematic illustration of 1 long chain of PVOH. (c) Atomistic models for all binders after MD equilibration. Carbon, oxygen and hydrogen atoms are represented by cyan, red and white spheres respectively. The continuous media depicts the porosity of the binder. Different colors represent different pore diameters as shown in the scale. (d) Time evolution of the density of the binders during the 21-step equilibrium MD simulations with different pressure regions shown in different colors (see methods and ref. 73 for more details about the equilibration of the binder density). (e) Pore size distribution of all equilibrated binders.

The binder models were subjected to 21 MD step simulations with seven cycles of three MD simulations performed in NVT (T = 600 K), NVT (T = 300 K) and NPT (T = 300 K) ensembles. The value of the pressure in the NPT simulations was increased from 1 bar to 50 kbar in the first three cycles out of the seven cycles and then gradually decreased until it reached ambient pressure. Temperature and pressure were regulated by the Nosé-Hoover thermostat and barostat,^54,55 respectively. The coupling constant of both the thermostat and barostat was 0.1 ps. The time step of the simulation was chosen to be 1 fs. These MD simulations were performed using the LAMMPS simulation software.⁵⁶Fig. 1b reports an illustration of the equilibrated binder models along with the evolution of their density during the 21 step MD simulations as reported in Fig. 1c.

MOF surface generation

CALF-20 crystal structure. The pristine CALF-20 structure was first geometry optimized at the density functional theory (DFT) level, as implemented in the Vienna Ab initio Simulation Package (VASP, 5.4.4 version).⁵⁷ The projector augmented wave (PAW) method was utilized to describe the electron–ion interaction.⁵⁸ The generalized gradient approximation (GGA) Perdew–Burke–Ernzerhof (PBE)⁵⁹ functional and the electron wave functions were expanded using the plane waves with an energy cutoff of 520 eV. The DFT-D3 method of Grimme van der Waals correction was used to account for the long-range interactions.⁶⁰ The convergence of the total energy and the force between atoms were set to 10⁻⁵ eV and 0.01 eV Å⁻¹, respectively. The Brillouin zone was integrated with the Gaussian smearing method by using a smearing width of 0.02 eV. A Γ-centered Monkhorst–Pack k-mesh with a size of 3 × 3 × 3 was applied for the corresponding unit cell of CALF-20 structure.⁶¹ All atomic positions and lattice parameters were fully relaxed by using the conjugate gradient algorithm. The resulting DFT-optimized cell parameters were found to be in good agreement with the corresponding experimental data as reported in Table S9.†

CALF-20 surface slab models. To identify the MOF surface with the lowest energy, three surface models were cleaved from the DFT-optimized CALF-20 crystal structure along the [100], [101] and [110] crystallographic planes (Fig. 2a–d). These models are ∼50 Å in length along the z direction (∼5 times the cell size), which ensured that no interaction between the surfaces takes place in this direction. A vacuum box of 20 Å z-length was also added to avoid interactions between the slab and its periodic images in this direction. We also ensured that the net dipole moment is zero in the z-direction for all these slab models by rebuilding the surface accordingly. Theoretically, a wide range of surface types can be considered for a given MOF, including CALF-20. However, practically, only specific surface configurations are plausible and/or of interest. In the case of CALF-20, we focused our attention on MOF surfaces with channels exposed to the binders and subsequently to guest molecule adsorption/diffusion in the context of the applications. Indeed, the MOF surfaces exposed along the channels are those corresponding to the [100], [101], and [110] crystallographic planes that motivated our choice to restrict our studies to these 3 MOF surface slab models. All slab surfaces were terminated with water coordinated to Zn metals exposed at the CALF-20 surface in a similar way to how we previously proceeded to construct the slab models for UiO-66(Zr).⁶² Water molecules were chosen as a model solvent used in the MOF synthesis.³⁹ There is no direct experimental evidence available regarding the surface termination state of CALF-20. Herein, we chose a water termination of the MOF surface because the structured CALF-20 was formed by solvent/water exchange.³⁹ Indeed, it is highly probable that when we cut the slab models, the metal (Zn) sites exposed at the MOF surface are coordinated to water. This current strategy has already been applied to a series of MOF slab models for which water was used as solvent for the synthesis.^63,64 These MOF surface models were then DFT-geometry-optimized using the Quickstep module of the CP2K software⁶⁵ with the same level of theory and parameters as the optimization of the bulk CALF-20. This choice was made since CP2K is known to be particularly well-suited for handling the geometry optimization of large systems. Typically, we checked that the geometric features of the DFT-optimized CALF-20-[100] surface model obtained using both codes are identical (see Table S11†).

Fig. 2 DFT-optimized CALF-20 bulk structure and CALF-20 surface along with the composite combining the binders constructed by force field molecular dynamics simulations. (a) DFT optimized structure of CALF-20 with different surface cuts shown with a continuous plane. Planes with colors red, green and blue represent the planes with Miller indices [110], [101] and [100], respectively. (b–d) Illustration of the different DFT-optimized CALF-20 slab surfaces. (e) Atomic density profile of the CALF-20/binder composite plotted along the direction normal to the MOF surface. A representative illustration of the CALF-20/CMC composite is presented in the top panel of the figure with the CALF-20 surface located at Z = 0 at the center of the box. Color scheme: Zn, orange; O, red; N, blue; C, cyan; H, white; Na, green.

The surface energy E_surface for each MOF slab model was then calculated using the following equation:

where E_slab is the total energy of the slab model, N_slab is the total number of atoms in the slab model, A is area of the top or bottom face of the slab, and σ_bulk is the energy in the bulk crystal (energy per atom).

The atomic partial charges of each slab surface were calculated using the density derived electrostatic and chemical (DDEC6) method as implemented in the CHARGEMOL module.^66,67 The x- and y-dimensions of the resulting slab surface model were then expanded five times for further processing the construction of the MOF/binder composites at the force field level. The universal force-field (UFF) parameters⁶⁸ were selected to define the bonded and non-bonded terms of the MOF slab model. The force-field parameters of the MOF can be found in the ESI (Table S10†). Notably, a few equilibrium bond length parameters (Zn–O and Zn–N) of the UFF were tuned to ensure an excellent correspondence between the mean value of the bond distances, bending angles, and dihedral angles of the MD-equilibrated MOF slab structure and the corresponding geometric features obtained for the DFT optimized structure (Table S11†). The use of such a force field was demonstrated previously to lead to reliable structure models for many porous solids, including MOFs which do not contain any open metal sites^37,69 as is the case for all CALF-20 bulk and surface slab models used in this work.

Construction of the MOF–binder composite

In order to bring the binders into contact with the MOF, first, the simulation box of the binder was reshaped in the x- and y-dimensions to match the lattice parameters of the CALF-20 surface model. The binder coordinates were also unwrapped in the z direction, and the polymer was added on top of the MOF surface so that the z direction of the polymer is perpendicular to the MOF surface. Next, the resulting composite was subjected to 21 MD simulation cycles in the NVT and NP_zT ensembles as described above for the construction of the binder model (Table S13†). During this procedure, the MOF framework was kept rigid such that it acts as a piston on the binder and pressure was only applied in the z direction as the system expands/compresses only in this direction. This methodology that has been applied to create a series of MOF/polymer composites^37,70–73 enables an effective equilibration of the binder model at the MOF surface leading to a well-packed MOF/binder interface structuring. Three statistically independent MD simulations for each MOF/binder composite were performed for 20 ns and the geometric features of the composites were averaged over the last 10 ns of these 3 MD trajectories. In these MD simulations, the interaction between the binder and the MOF was taken as a summation of coulombic and LJ potential contributions, with cross interaction parameters computed according to the Lorentz–Berthelot mixing rules.⁴ All the MD simulations were performed using the LAMMPS software package.⁵⁶

Gas adsorption and diffusion simulations

Grand Canonical Monte Carlo (GCMC) simulations were performed to assess the single component CO₂, CH₄, and N₂ adsorption isotherms and the binary mixture of CO₂ : N₂ (molar concentration ratio of 15 : 85) of CALF-20 and its binder-based composites at 300 K in the pressure range of 0.001 to 5 bar. The GCMC simulations were performed with Complex Adsorption and Diffusion Simulation Suite (CADSS) code⁷⁴ with 10⁷ steps of equilibration followed by 10⁷ steps of production run for each point in the adsorption isotherm. CO₂ was modeled by a 3-site linear rigid LJ model,⁷⁵ CH₄ described by a single-site LJ model,⁴⁹ and N₂ treated as a 3-site linear rigid LJ model⁷⁶ – two sites for the nitrogen atoms and a third fictitious site for their center of mass. Short-range interactions were truncated at a cutoff radius of 12.5 Å. The long-range electrostatic interactions were handled using the Ewald summation technique.⁷⁷ The fugacity required for GCMC simulations was obtained from the Peng–Robinson equation of state⁷⁸ and adsorption enthalpies were computed using a revised Widom's test particle insertion method.⁷⁹

The self-diffusivity of CO₂ was further assessed in the CALF-20/CMC composite using equilibrium MD simulations. The initial configuration for the CO₂ loaded composite was generated by GCMC simulations performed for the single component adsorption of CO₂ at 1 bar and 300 K. Three statistically independent 200 ns long MD simulations were performed in the NVT ensemble, and the corresponding mean-square displacement (MSD) was calculated by using the following relation: MSD = 〈|r(t) − r(0)|²〉, where 〈…〉 indicates the average over all the CO₂ molecules and time origins and r(0) and r(t) are the reference position and the position of the molecule at time t, respectively. Self-diffusivity was then evaluated by using Einstein's relation⁸⁰ applied to the linear region of the MSD vs. time plot.

Results and discussion

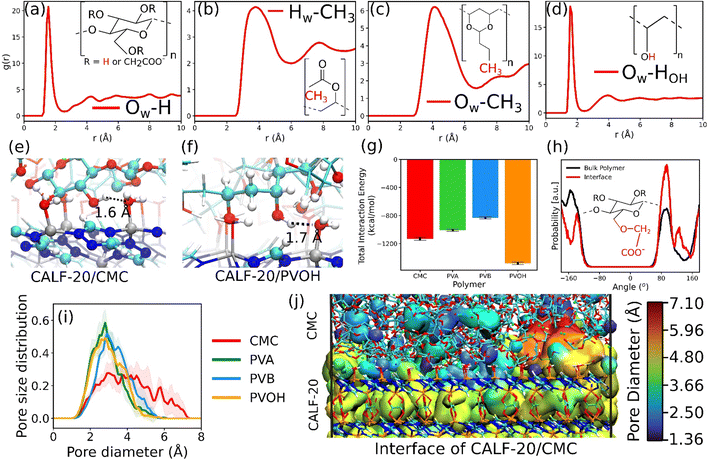
The in silico constructed atomistic models for the four binders are illustrated in Fig. 1c along with their resulting densities averaged over the MD run (Fig. 1d) that match well with their corresponding experimental values given in Table S7.† Typically, our simulated CMC model exhibits a density of 1.72 ± 0.005 g cm⁻³ which lies within the range of values (1.6 g cm⁻³ to 1.7 g cm⁻³) reported previously for different humidity and temperature conditions as well as diverse counterions.^41,81 Furthermore, the bulk and Young's moduli calculated for all binder models agree well with their corresponding experimental data (see Table S8†). Next, we analyzed the porosity of these binder atomistic models with Fig. 1e representing their pore size distributions. While the rigid-like and dense binder CMC was demonstrated to exhibit pores spanning up to 6–7 Å, the other 3 binders, i.e., PVB, PVA and PVOH, show very limited porosity (pores below 3 Å) hardly accessible by most of the common gas molecules. Poly-vinyl derivatives i.e., PVA, PVB, and PVOH are known to be very dense polymers and possess very low intrinsic porosity as described in the previous literature.⁸² Incorporating higher amounts of poly-vinyl derivatives in a composite generally yields a polymer matrix that is both highly dense and mechanically stable, owing to the low porosity and strong adhesive properties of these derivatives. On the other hand, the high porosity of CMC is a consequence of its highly branched and negatively charged polymer structure, which results in a three-dimensional network of voids and channels in aqueous solutions.⁴⁶ This network is further enhanced by the hydrophilic nature of the carboxymethyl groups, which allows CMC to absorb large amounts of water and increase its porosity.⁴⁶ This overall experimental–theoretical agreement validates the intra-molecular and inter-molecular force field parameters selected to describe this series of binders.

Illustrative snapshots of the bulk CALF-20 and the different DFT-optimized MOF surface slabs considered in this work are provided in Fig. 2a–d. The [100] surface of CALF-20 was found to be the most energetically stable one (Table S12†) and therefore selected as a representative slab model for this MOF. The surface of the MOF slab features outermost atoms of Zn coordinated to water molecules as well as exposed C–H groups of the 1,2,4-triazole that can both serve as potential anchoring sites for the binders. The surface contains small pockets that exist between consecutive water molecules, resulting in a “zig-zag” like structure. This structuring has the potential to aid the binder in optimally gripping the surface of the MOF. An illustration of the resulting geometry of the MOF surface is provided in Fig. S7.†

This MOF surface slab model was further combined with the different binders to create the corresponding composites by applying the force field-based MD methodology described above. An illustration of the MD-constructed atomistic model for the CALF-20/CMC composite is provided in Fig. 2e along with the density profile for all composites plotted along the direction normal to the MOF surface, namely the z-axis. In this representation, CALF-20 is located at the center of the simulation box with the binder on the left and right (see the corresponding illustration in Fig. 2e). We can observe that the atomic density of the binders fluctuates around a mean value at both ends of the simulation box in the region marked in cyan. In the proximity of the CALF-20 surface the atomic density of all binders decays to zero and we can define a zone where the binder and the MOF atoms overlap (pink region) due to the partial penetration of the binder into the MOF pocket. The associated overlap length was demonstrated to be a reliable metric to assess the affinity between the MOF and polymer in our previous studies on MOF/polymer mixed matrix membranes.^62,73 Table S14† summarizes the corresponding MOF/binder overlap length for all composites. This set of data evidence that CALF-20/CMC followed by CALF-20/PVOH shows overlap length significantly longer compared to the composites based on PVA and PVB. Although the CMC backbone is globally rigid, this binder can adopt a conformation in such a way that its carboxymethyl and –OH groups are enabled to interact strongly with the terminal Zn-coordinated water molecules which is at the origin of the relatively large overlap length. The sharp peak at 1.7 Å present in the radial distribution function (RDF) calculated between the hydroxyl groups of CMC and the oxygen atoms of the coordinated water at the CALF-20 surface confirms the existence of strong hydrogen-bond type interactions at the MOF/binder interface. Similarly, the –OH groups of the more flexible PVOH binder establish strong hydrogen bonds with the terminal Zn-coordinated water molecules which can be seen also from the RDF peak at a distance of around 1.6–1.7 Å. Illustrations of these interfacial MOF/binder interactions are shown in Fig. 3e and f. On the other hand, PVA and PVB binders do not contain any specific interacting sites resulting in a short MOF/binder overlap length. The first peak of the RDF of the methyl groups for both binders with the coordinated water molecules at the MOF surface lies within a distance of around 4 Å (Fig. 3b and c). Additional RDFs plotted between different MOF/binder atom pairs provided in the ESI (Fig. S9–S12†) confirmed this observation. We further assessed the interaction energy between the CALF-20 MOF surface and each binder in the composites from the equilibrium MD simulations (Fig. 3g). The corresponding data confirms that the CALF-20/CMC and CALF-20/PVOH composites are much more stabilized than the other composites, in line with the stronger hydrogen bond interactions at the MOF/binder interfaces as depicted by the RDF plots (Fig. 3a–d) and the larger MOF/binder overlap lengths discussed above (Table S14†). One intriguing feature is the adaptability of the rigid CMC binder to conform to the shape of the CALF-20 surface to favour optimum interfacial MOF/binder interactions. To gain further insight into the CMC structural behavior at the vicinity of the MOF surface, we analyzed the interfacial flexibility of its carboxymethyl groups by calculating the associated dihedral angle distribution averaged over the MD runs (inset of Fig. 3h and S13†). Compared to the bulk phase, the dihedral angle distribution of the interfacial CMC shows sharper peaks which signifies that the binder in the interfacial region becomes more rigid owing to the formation of a large number of hydrogen bonds. This directs CMC to tune its conformation compared to its bulk geometry thanks to the flexibility of its carboxymethyl groups in order to establish a good adhesion to the CALF-20 surface.

Fig. 3 Nano-structuring of the CALF-20/binder interface and interactions in play revealed by molecular dynamics simulations. (a–d) Radial distribution functions (RDFs) between the different chemical groups of the binder with the Zn-coordinated water molecules of CALF-20. The oxygen and hydrogen of the Zn-coordinated water are denoted by O_w and H_w respectively. The atom type of the binder is shown in the inset of the figure. (e and f) Illustration of the predominant interfacial interactions in (e) CALF-20/CMC and (f) CALF-20/PVOH. (g) Total non-bonded interaction energy calculated between the CALF-20 surface and all binders in the corresponding composites. (h) Dihedral angle distribution of the carboxymethyl groups of CMC at the interface of the composite and in the bulk region. (i) Pore size distribution of the interfaces of all MOF/binder composites. (j) Color mapping of the porosity at the interface of the CALF-20/CMC composite.

The pore size distribution of the overlap regions of the CALF-20/binder composite was further explored as illustrated in Fig. 3i. All composites show pores with size ranging from 3 to 4 Å except CALF-20/CMC that exhibits pores spanning up to 7 Å, in line with the intrinsic larger porosity of the CMC binder as bulk compared to the others. This interfacial pore structuring of CALF-20/CMC is expected to increase the overall CO₂ uptake of the composite and importantly to act as an effective bridge for fast diffusion of CO₂ from the binder to the MOF to prevent adsorption kinetic issues which is of utmost importance once shaped MOFs are required in the sorption-based process.

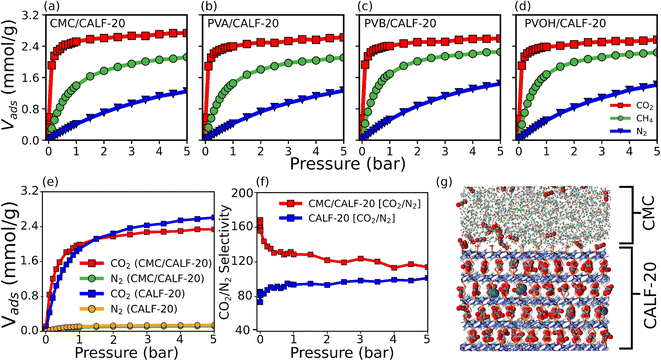
Grand canonical Monte Carlo (GCMC) simulations were further performed to predict the single component adsorption isotherms at 300 K for all MOF/binder composites (Fig. 4a–d) with force field parameters for both MOF/gas and binder/gas interactions that have been initially validated by a good agreement between the experimental and simulated adsorption isotherms for CO₂, N₂ and CH₄ in CALF-20 as well as in the four binders (see Fig. S15 and S16†). Fig. 4 shows that the amount of CO₂ adsorbed at 1 bar and 300 K is slightly larger for CALF-20/CMC (2.52 mmol g⁻¹) vs. CALF-20/PVA (2.4 mmol g⁻¹), CALF-20/PVB (2.4 mmol g⁻¹) and CALF-20/PVOH (2.38 mmol g⁻¹) composites, in line with the higher porosity of CMC that enables it to adsorb a slightly larger amount of CO₂ molecules in the binder region as well as at the MOF/CALF-20 interface as illustrated in Fig. S17.† Further, the CO₂ uptake of the CALF-20 crystal at 1 bar and 300 K, found to be 2.79 mmol g⁻¹, guarantees that binders maintain the adsorption properties of the pristine CALF-20. The steeper CO₂ adsorption isotherms calculated for all MOF/binder composites compared to the corresponding data for CH₄ and N₂ suggest that shaping of CALF-20 with these four binders maintains the intrinsic highest CO₂ affinity of CALF-20. Typically, this was confirmed by the much higher calculated adsorption enthalpy for CO₂ (−38.9 kJ mol⁻¹) vs. CH₄ (−27 kJ mol⁻¹) and N₂ (−22 kJ mol⁻¹) for CALF-20/CMC, in line with the energetics simulated for CALF-20 (CO₂ (−36.1 kJ mol⁻¹) vs. CH₄ (−24.7 kJ mol⁻¹) and N₂ (−20.5 kJ mol⁻¹)).

Fig. 4 Single component and binary mixture adsorption in the CALF-20/binder composites by Monte Carlo simulations. (a–d) GCMC simulated adsorption isotherms of CO₂, CH₄ and N₂ in all composites at 300 K. (e) Co-adsorption isotherm of CO₂/N₂ [15 : 85] at 300 K in CALF-20/CMC vs. pristine CALF-20. (f) Simulated CO₂/N₂ [15 : 85] thermodynamic selectivity as a function of pressure for CALF-20/CMC vs. pristine CALF-20. (g) GCMC representative snapshot showing the location of CO₂ and N₂ adsorbed in the CALF-20/CMC composite at 300 K and 1 bar.

Decisively, the CALF-20/CMC composite was further demonstrated by our CO₂/N₂ [15 : 85] binary mixture GCMC simulations to maintain the very high CO₂/N₂ selectivity of the pristine CALF-20 as shown in Fig. 4f. A representative snapshot of the co-adsorption scenario provided in Fig. 4g highlights that the CMC region hosts only CO₂ while a few N₂ molecules co-exist with CO₂ in the CALF-20 region. Interestingly, we can also see that the interfacial region hosts additional CO₂ molecules. The CO₂ molecules were shown to interact strongly with the hydroxyl groups of CMC and the coordinated water molecules present at the CALF-20 surface with characteristic O_CO2–H_CMC(OH) and C_CO2–H_CALF-20(H₂O) distances of 1.9 and 2.9 Å, respectively, as revealed by the corresponding RDF plots and illustrative snapshots (Fig. S17 and S18†). This overall observation emphasizes that the CO₂/N₂ selectivity remains comparable in the CALF-20/CMC composite vs. MOF itself (Fig. 4f).

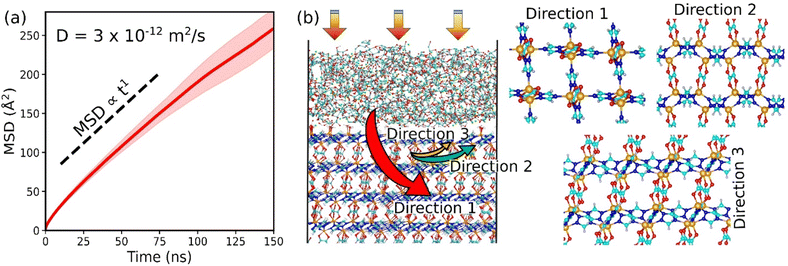
We finally examined the CO₂ kinetics in the CALF-20/CMC composite initially loaded by GCMC simulations performed at 1 bar and 300 K. The MSD for CO₂ averaged over 3 independent MD trajectories is plotted as a function of the simulation time in Fig. 5a. The self-diffusion coefficient (D_s) obtained from the linear regime of this MSD plot is found to be 3 × 10⁻¹² m² s⁻¹ (±10⁻¹⁵). This value is similar to the D_s simulated for CO₂ diffusing in CALF-20 (2.9 × 10⁻¹² m² s⁻¹ (±10⁻¹⁵)) (Fig. S19†). Interestingly, this observation emphasizes that shaping of CALF-20 with CMC is not expected to slow down the CO₂ transport in the overall composite which is of utmost importance for the target separation application. We further analyzed the diffusion path of CO₂ in the composite schematically as illustrated in Fig. 5b. CO₂ was found to follow a standard Fickian diffusion regime in both CMC and CALF-20 regions as well as in the interfacial zone since both components exhibit pore sizes large enough to enable CO₂ to diffuse. In the MOF region, we have observed that CO₂ can diffuse in the 3 directions moving from one channel to another since the separating pore aperture size (∼5 Å) enables sterically this jump for CO₂.

Fig. 5 CO₂ diffusion in the CALF-20/CMC composite by molecular dynamics simulations. (a) Mean-squared displacement of CO₂ in CALF-20/CMC for loading at 1 bar and 300 K. (b) Illustration of the diffusion mechanism with the CO₂ pathway along the three directions in CALF-20.

Conclusions

Shaping of MOF CALF-20 using binders was systematically assessed via molecular simulations integrating DFT and force field molecular dynamics/Monte Carlo calculations which enabled analysis all the way from the building of atomistic composite models to the exploration of their gas adsorption and diffusion properties. Atomistic models of four different binders were first constructed and validated by means of experimental data including density, mechanical properties and porosity. The most energetically stable slab surface of the MOF CALF-20 was further identified and combined with this series of binders to construct atomistic models for the corresponding composites. An in-depth structural and porosity analysis of these composites revealed that the CMC-based composite had the best adhesion between the MOF and the binder owing to strong interfacial hydrogen bond interactions between its OH-group and the coordinated water at the MOF surface along with the flexibility of the carboxymethyl group that enables CMC to conform to the shape of the MOF surface. This CALF-20/CMC was further demonstrated to maintain a thermodynamic CO₂/N₂ selectivity as high as that of the pristine CALF-20 while CO₂ diffusion was proven to be dominated by transport in CALF-20 with the binder playing no detrimental role in the gas kinetics. This computational prediction paves the way towards the optimum shaping of one of the most advanced MOFs envisioned for real industrial applications. From a broader perspective, our conclusions are expected to guide the experimental effort towards the selection of an appropriate binder to achieve an optimum shaping of a given MOF in terms of processability whilst maintaining a high level of performance. Furthermore, beyond the proof-of-concept delivered on the benchmark CALF-20 MOF, the multiscale methodology presented in this manuscript is fully transferable to any MOFs, zeolites and other porous materials for which shaping is also of key importance for many applications including pressure swing adsorption processes for the separation of many gases.

Data availability

All datasets used in this work are available in the present manuscript and ESI.† Additional data and codes related to this paper can be found on Github (https://github.com/supriyonaskar/MOF-Binder-Composite) and may be requested from the authors.

Code availability

The central codes used in this paper are VASP,⁵⁷ CP2K,⁶⁵ LAMMPS,⁵⁶ CADSS,⁷⁴ and Polymatic.⁴⁵ Detailed information related to the license and user guide are available in the referenced papers and on their websites.

Author contributions

S. N. and G. M. conceived the idea of the project, designed the simulation strategy, and wrote the manuscript. S. N. and D. F. performed the computational work under the supervision of G. M. A. G. participated in the implementation of the computational strategy. All authors contributed to the revision of the manuscript.

Conflicts of interest

The authors have no conflict of interest to declare.

Acknowledgements

For the computational work, access was granted to the HPC resources of CINES under the allocation A0120907613 made by GENCI.

References

1. A. J. Howarth, Y. Liu, P. Li, Z. Li, T. C. Wang, J. T. Hupp and O. K. Farha, Nat. Rev. Mater., 2016, 1, 15018.
2. O. M. Yaghi and H. Li, J. Am. Chem. Soc., 1995, 117, 10401–10402.
3. H. C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674.
4. S. Kitagawa, R. Kitaura and S. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375.
5. S. Horike and S. Kitagawa, Nat. Mater., 2022, 21, 983–985.
6. S. Kitagawa and R. Matsuda, Coord. Chem. Rev., 2007, 251, 2490–2509.
7. G. Maurin, C. Serre, A. Cooper and G. Férey, Chem. Soc. Rev., 2017, 46, 3104–3107.
8. G. Férey, Chem. Soc. Rev., 2008, 37, 191–214.
9. S. Wang and C. Serre, ACS Sustain. Chem. Eng., 2019, 7, 11911–11927.
10. P. Horcajada, R. Gref, T. Baati, P. K. Allan, G. Maurin, P. Couvreur, G. Férey, R. E. Morris and C. Serre, Chem. Rev., 2012, 112, 1232–1268.
11. Q. Qian, P. A. Asinger, M. J. Lee, G. Han, K. Mizrahi Rodriguez, S. Lin, F. M. Benedetti, A. X. Wu, W. S. Chi and Z. P. Smith, Chem. Rev., 2020, 120, 8161–8266.
12. J. M. Kolle, M. Fayaz and A. Sayari, Chem. Rev., 2021, 121, 7280–7345.
13. J. Yu, L. H. Xie, J. R. Li, Y. Ma, J. M. Seminario and P. B. Balbuena, Chem. Rev., 2017, 117, 9674–9754.
14. J. B. Decoste and G. W. Peterson, Chem. Rev., 2014, 114, 5695–5727.
15. L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. Van Duyne and J. T. Hupp, Chem. Rev., 2012, 112, 1105–1125.
16. M. D. Allendorf, R. Dong, X. Feng, S. Kaskel, D. Matoga and V. Stavila, Chem. Rev., 2020, 120, 8581–8640.
17. S. Yuan, L. Feng, K. Wang, J. Pang, M. Bosch, C. Lollar, Y. Sun, J. Qin, X. Yang, P. Zhang, Q. Wang, L. Zou, Y. Zhang, L. Zhang, Y. Fang, J. Li and H.-C. Zhou, Adv. Mater., 2018, 30, e1704303.
18. B. Yeskendir, J. P. Dacquin, Y. Lorgouilloux, C. Courtois, S. Royer and J. Dhainaut, Mater. Adv., 2021, 2, 7139–7186.
19. A. Terracina, L. N. McHugh, M. Mazaj, N. Vrtovec, S. Agnello, M. Cannas, F. M. Gelardi, R. E. Morris and G. Buscarino, Eur. J. Inorg. Chem., 2021, 2021, 2334–2342.
20. G. Férey, C. Serre, C. Mellot-Draznieks, F. Millange, S. Surblé, J. Dutour and I. Margiolaki, Angew. Chem., Int. Ed., 2004, 43, 6296–6301.
21. Y. Li, G. Wen, J. Li, Q. Li, H. Zhang, B. Tao and J. Zhang, Chem. Commun., 2022, 58, 11488–11506.
22. A. Permyakova, O. Skrylnyk, E. Courbon, M. Affram, S. Wang, U. H. Lee, A. H. Valekar, F. Nouar, G. Mouchaham, T. Devic, G. De Weireld, J. S. Chang, N. Steunou, M. Frère and C. Serre, ChemSusChem, 2017, 10, 1419–1426.
23. Z. Wang, L. Liu, Z. Li, N. Goyal, T. Du, J. He and G. K. Li, Energy Fuel., 2022, 36, 2927–2944.
24. X. M. Liu, L. H. Xie and Y. Wu, Inorg. Chem. Front., 2020, 7, 2840–2866.
25. A. Mallick, G. Mouchaham, P. M. Bhatt, W. Liang, Y. Belmabkhout, K. Adil, A. Jamal and M. Eddaoudi, Ind. Eng. Chem. Res., 2018, 57, 16897–16902.
26. R. Ding, Z. Li, Y. Dai, X. Li, X. Ruan, J. Gao, W. Zheng and G. He, Sep. Purif. Technol., 2022, 298, 121594.
27. K. W. Chapman, G. J. Halder and P. J. Chupas, J. Am. Chem. Soc., 2009, 131, 17546–17547.
28. A. L. Myers and P. A. Monson, Langmuir, 2002, 18, 10261–10273.
29. T. C. Wang, A. M. Wright, W. J. Hoover, K. J. Stoffel, R. K. Richardson, S. Rodriguez, R. C. Flores, J. P. Siegfried, N. A. Vermeulen, P. E. Fuller, M. H. Weston, O. K. Farha and W. Morris, ACS Appl. Mater. Interfaces, 2021, 13, 52106–52112.
30. G. W. Peterson, J. B. Decoste, T. G. Glover, Y. Huang, H. Jasuja and K. S. Walton, Microporous Mesoporous Mater., 2013, 179, 48–53.
31. Y. Chen, X. Huang, S. Zhang, S. Li, S. Cao, X. Pei, J. Zhou, X. Feng and B. Wang, J. Am. Chem. Soc., 2016, 138, 10810–10813.
32. B. M. Connolly, D. G. Madden, A. E. H. Wheatley and D. Fairen-Jimenez, J. Am. Chem. Soc., 2020, 142, 8541–8549.
33. J. Park, Y. S. Chae, D. W. Kang, M. Kang, J. H. Choe, S. Kim, J. Y. Kim, Y. W. Jeong and C. S. Hong, ACS Appl. Mater. Interfaces, 2021, 13, 25421–25427.
34. J. Caro, M. Noack, P. Kölsch and R. Schäfer, Microporous Mesoporous Mater., 2000, 38, 3–24.
35. D. Bastani, N. Esmaeili and M. Asadollahi, J. Ind. Eng. Chem., 2013, 19, 375–393.
36. V. Van Speybroeck and G. Maurin, Nat. Mater., 2023, 22, 12–13.
37. S. J. Datta, A. Mayoral, N. M. Srivatsa Bettahalli, P. M. Bhatt, M. Karunakaran, I. D. Carja, D. Fan, P. G. M. Mileo, R. Semino, G. Maurin, O. Terasaki and M. Eddaoudi, Science, 2022,(376), 1080–1087.
38. G. Dong, H. Li and V. Chen, J. Mater. Chem. A, 2013, 1, 4610–4630.
39. J. Bin Lin, T. T. T. Nguyen, R. Vaidhyanathan, J. Burner, J. M. Taylor, H. Durekova, F. Akhtar, R. K. Mah, O. Ghaffari-Nik, S. Marx, N. Fylstra, S. S. Iremonger, K. W. Dawson, P. Sarkar, P. Hovington, A. Rajendran, T. K. Woo and G. K. H. Shimizu, Science, 2021,(374), 1464–1469.
40. T. Al-Attas, S. K. Nabil, A. S. Zeraati, H. S. Shiran, T. Alkayyali, M. Zargartalebi, T. Tran, N. N. Marei, M. A. Al Bari, H. Lin, S. Roy, P. M. Ajayan, D. Sinton, G. Shimizu and M. G. Kibria, ACS Energy Lett., 2023, 8, 107–115.
41. C. C. Ruchhoft and C. Meckler, Ind. Eng. Chem., 1945, 37, 943–947.
42. A. R. Shultz, J. Am. Chem. Soc., 1954, 76, 3422–3430.
43. Y. Bai, Y. Chen, Q. Wang and T. Wang, J. Mater. Chem. A, 2014, 2, 9169–9177.
44. J. Du, Y. Wang, X. Lang and S. Fan, Energy Fuel., 2011, 25, 3204–3211.
45. L. J. Abbott, K. E. Hart and C. M. Colina, Theor. Chem. Acc., 2013, 132, 1–19.
46. O. Biermann, E. Hädicke, S. Koltzenburg and F. Müller-Plathe, Angew. Chem., Int. Ed., 2001, 40, 3822–3825.
47. X. Dong, X. Guan, Y. Jiang, J. Ma and M. Zhang, J. Mol. Liq., 2015, 209, 520–525.
48. R. Semino, J. P. Dürholt, R. Schmid and G. Maurin, J. Phys. Chem. C, 2017, 121, 21491–21496.
49. M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577.
50. S. J. Keasler, S. M. Charan, C. D. Wick, I. G. Economou and J. I. Siepmann, J. Phys. Chem. B, 2012, 116, 11234–11246.
51. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
52. A. Frisch, et al., Gaussian 09W Reference, Wallingford, USA, 2009, vol. 470, p. 25.
53. C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373.
54. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695.
55. S. Nosé, J. Chem. Phys., 1998, 81, 511.
56. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
57. J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078.
58. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
59. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
60. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
61. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
62. R. Semino, J. C. Moreton, N. A. Ramsahye, S. M. Cohen and G. Maurin, Chem. Sci., 2018, 9, 315–324.
63. A. Ozcan, R. Semino, G. Maurin and A. O. Yazaydin, Chem. Mater., 2020, 32, 1288–1296.
64. R. Semino, J. C. Moreton, N. A. Ramsahye, S. M. Cohen and G. Maurin, Chem. Sci., 2018, 9, 315–324.
65. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103.
66. T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2010, 6, 2455–2468.
67. T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801.
68. A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
69. M. Z. Ahmad, M. Navarro, M. Lhotka, B. Zornoza, C. Téllez, W. M. de Vos, N. E. Benes, N. M. Konnertz, T. Visser, R. Semino, G. Maurin, V. Fila and J. Coronas, J. Membr. Sci., 2018, 558, 64–77.
70. D. Fan, A. Ozcan, N. A. Ramsahye, G. Maurin and R. Semino, ACS Appl. Mater. Interfaces, 2022, 14, 16820–16829.
71. D. Fan, A. Ozcan, O. Shekhah, R. Semino, M. Eddaoudi and G. Maurin, J. Membr. Sci. Lett., 2022, 2, 100029.
72. D. Fan, A. Ozcan, N. A. Ramsahye, D. Zhao, G. Maurin and R. Semino, ACS Mater. Lett., 2021, 3, 344–350.
73. R. Semino, N. A. Ramsahye, A. Ghoufi and G. Maurin, ACS Appl. Mater. Interfaces, 2016, 8, 809–819.
74. Q. Yang and C. Zhong, J. Phys. Chem. B, 2006, 110, 17776–17783.
75. J. G. Harris and K. H. Yung, J. Phys. Chem., 1995, 99, 12021–12024.
76. J. J. Potoff and J. I. Siepmann, AIChE J., 2001, 47, 1676–1682.
77. P. P. Ewald, Ann. Phys., 1921, 369, 253–287.
78. D. Y. Peng and D. B. Robinson, Ind. Eng. Chem. Fund., 1976, 15, 59–64.
79. B. Wldom, J. Chem. Phys., 2004, 39, 2808.
80. R. Chitra and S. Yashonath, J. Phys. Chem. B, 1997, 101, 5437–5445.
81. H. Ma and Q. Ma, Adv. Mater. Sci. Eng., 2019, 2019, 1–8.
82. Z. Li, H. Tang, X. Liu, Y. Xia and J. Jiang, J. Membr. Sci., 2008, 312, 115–124.

---

Footnote

† Electronic supplementary information (ESI) available: Microscopic model and force-field parameters of the binders. DFT-optimized crystal structure of CALF-20. Surface energies of the different CALF-20 slabs. Force-field parameters used for CALF-20. Details of the MD simulated systems, and MD and GCMC simulation protocols. Density, porosity, and mechanical properties of the binders. Snapshots of the CALF-20 and their derived composites with binders. Additional radial distribution functions between MOF/binder atom pairs and dihedral angle distribution of the binders. See DOI: https://doi.org/10.1039/d3sc04218a

---