Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Velocity map images from surface-hopping; reactive scattering of OH (2Σ+) + H2 (1Σ+g)†
Christopher
Robertson
 * and
Martin J.
Paterson
* and
Martin J.
Paterson

School of Engineering & Physical Sciences, Heriot-Watt University, Edinburgh, Scotland EH14 4AS, UK. E-mail: m.j.paterson@hw.ac.uk
First published on 21st July 2022
Abstract
We study OH(Σ) + H2 → H2O(X) + H reactive scattering using two potential energy models found in the literature. We analyze the quenching channels and generate velocity map images (VMI) by simulating quantum-classical trajectories of the quenched products. The initial conditions attempt to simulate supersonic jet, molecular beam scattering experiments which we compare against. The simulated results are able to elucidate the mechanisms behind some of these experimental observations.
The Hydroxyl radical, a key oxidizing agent in atmospheric and combustion processes, has been the subject of intense experimental study.1–4 The presence of this radical is often monitored using Laser-induced fluorescence on the A2Σ+–X2Π band system. The electronically excited species can lead to significant energy release via quenching, as is the case with the Hydrogen molecule, where two competing quenching channels are available; OH(Σ+) + H2 → OH(Π) + H2 (non-reactive) or → H2O + H (reactive). Understanding the impact of this process in the OH(Σ+) lifetime is of importance. A complementary body of theoretical work has been also taken place,5–8 given the rich experimental data available. Much of this work culminated in two analytic models by Truhlar et al.6 and Yarkony et al.,7 and have more recently been used to perform dynamic simulations with them (Guo et al.8,9) to estimate a number of observables.
In this communication we generate velocity map images (VMI) and H product distributions, previously omitted.8,9 Velocity Map imagining is a mature and popular method for obtaining simultaneous angles and velocities (and a wealth of other implicit information) from scattering experiments.10 The popularity of this method makes it a natural choice for computational scientist to simulate, to effectively communicate results with experimentalist. We performed semi-classical trajectories on the potential energy surface (PES), used in similar systems to study quenching11,12 and angular and velocity distributions.13–16 Numerical quantum mechanical propagation and integration of these equations is a computationally intensive and hard to generalize. In contrast, for semi-classical trajectories the evaluation of velocity and scattering angles of particles can be done irrespective of the size of the system, using uniform phase-space binning procedures.17,18 Crossed-beams experimental work by Ortiz-Suarez et al.4 was done on the OH + D2 → HOD + D and obtained center of mass velocity map images from simulations fitted to experimental data. Also related, Lester et al.19,20 have performed Doppler profile measurements for the reaction products of these isotopically analogous systems under similar conditions. Finally, Brouard et al. have recently measured absolute cross-sections for the competing channels for this system, as well as several other experimental observables.3 Although this system is prototypical, being small and with competitive quenching channels, the PES description is nevertheless challenging. Although the models emphasize different mechanistic aspect of the scattering process, they are able to provide rich insight into some of the aforementioned experiments.
Two model PES are used here. A four-state diabatic PES developed by Malbon, Zhao, Guo and Yarkony (MZGY)7 and a three-state diabatic model developed by Shu, Bowman and Truhlar et al. (FWW2).8 At certain OH/H2 distances beyond 2.5 Å ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) we found in FWW2 a discontinuity of the OH stretch PE; at such distances we switched to FWW1,6 which matches FWW2 in most regions of the PES. Some PES cuts and couplings are provided in ESI.† Intersection seams connect the S2/S1 and S2/S0 along the H2 rotation in a planar configuration,6,7 where most quenching is expected.
we found in FWW2 a discontinuity of the OH stretch PE; at such distances we switched to FWW1,6 which matches FWW2 in most regions of the PES. Some PES cuts and couplings are provided in ESI.† Intersection seams connect the S2/S1 and S2/S0 along the H2 rotation in a planar configuration,6,7 where most quenching is expected.
We employed the SHARC code21 to integrate the equations of motion, in the adiabatic representation, using the fewest-switches algorithm22 on the non-adiabatic coupling provided by the models. We also applied energy based decoherence23 and post-hopping parallel velocity rescaling (further details in ESI†).
The internal and rotational degrees of freedom (DOF) are in their ground state. Given the afforded trajectories (∼25k per model) compared to similar examples13,15 we sample the orientations in fixed lattice points (used a Fibonacci sphere). We used 16 lattice points for OH and 9 for H2. For similar reasons we used regular lattice points for sampling the impact parameter (IP) b, spanning 10 bohr (9 lattice points). We used the Wigner distribuition obtained from the numerical integration of the stretch mode for each diatom (far from each other). These distributions where then sampled using Monte Carlo (MC) (16 samples per lattice point). Because this is a form of biased sampling (towards low IP), we weight the trajectories when constructing the resulting observables by the cross sectional area approximated by the bin width of that lattice point. An additional thousand trajectories were added to high IP lattice points. This results in 25k trajectories per model. A collisional energy of 0.05 eV was used, within a few factors of several experimental results discussed in the Discussions.
All trajectories were integrated until outgoing molecules where at least 6 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) apart. Approximately 2.5% of FWW2 trajectories lead to excessive energy changes during integration. Further detailed images, such as ro-vibrational spectra are offered as ESI,† as well as results for the FWW1 model.
apart. Approximately 2.5% of FWW2 trajectories lead to excessive energy changes during integration. Further detailed images, such as ro-vibrational spectra are offered as ESI,† as well as results for the FWW1 model.
Fig. 1 shows the branching ratio for the different channels for both models. The non-quenching channels are dominant and the quenched channels decrease as a function of IP. Integrating the bins that contain some quenching, we get 92% (MZGY) and 86% (FWW2) of the cross section results in non-quenching. Of the quenching channels, the non-reaction channel is 3.8 (MZGY) and 4.1 (FWW2) times greater than the reaction channel. By defining a OH/H2 intermolecular incoming distance of 2.5 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and outgoing distance 4.0 Å
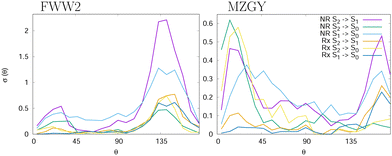
and outgoing distance 4.0 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) as cutoffs to measure the mean lifetime of the interacting complex. We found 155 (MZGY)/164 (FWW2) fs for non-reactive, 165/178 fs for reactive and 167/360 fs for OH nascent H. For FWW2, the incident H-facing OH (facing the incoming H2) compared to O-facing OH, has three times the expected lifetime (ESI† for details). Fig. 2 provides some insight into the initial quenching mechanisms by plotting the number of first instance hopping events weighted by the cross section as a function of the angle between the OH and H2 bond vectors, θ. The H2 vector is defined as always pointing away from the Oxygen. Zero degrees corresponds to the O-facing OH (facing the incoming H2), while 180° to H-facing OH. Each cells show the differential cross section as a function of θ for S2 → S1 | S0 and S1 → S0 transitions for the non-reaction (NR) and reaction channels (Rx). The first instance of a state transition (hop) from either transitions S2 → S1 → S0 or S1 → S0 is used.
as cutoffs to measure the mean lifetime of the interacting complex. We found 155 (MZGY)/164 (FWW2) fs for non-reactive, 165/178 fs for reactive and 167/360 fs for OH nascent H. For FWW2, the incident H-facing OH (facing the incoming H2) compared to O-facing OH, has three times the expected lifetime (ESI† for details). Fig. 2 provides some insight into the initial quenching mechanisms by plotting the number of first instance hopping events weighted by the cross section as a function of the angle between the OH and H2 bond vectors, θ. The H2 vector is defined as always pointing away from the Oxygen. Zero degrees corresponds to the O-facing OH (facing the incoming H2), while 180° to H-facing OH. Each cells show the differential cross section as a function of θ for S2 → S1 | S0 and S1 → S0 transitions for the non-reaction (NR) and reaction channels (Rx). The first instance of a state transition (hop) from either transitions S2 → S1 → S0 or S1 → S0 is used.
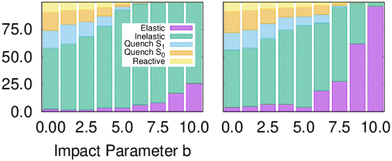 | ||
| Fig. 1 Branching ratios for the different channels as a function of impact parameter, models MZGY (left) and FWW2 (right). | ||
Both models suggest that quenching from the S2 (Σ) state occur preferentially at acute and obtuse angles. For MZGY, first S2 → S0 hop represent the largest cross section, and occur primarily at acute angles 15–20° (O-facing H2). S2 → S1 in contrast occurs at wider angles ≈160°, while S1 → S0 has a broad distribuition across all angles. The FWW2 model in contrast exhibits preferred hops at wide angles (H-facing OH) at ≈145° for most transitions, with exception to S1 → S0 which is also broad. A second minor peak at low acute angles is also present. ESI† offers more detailed images of the same account.
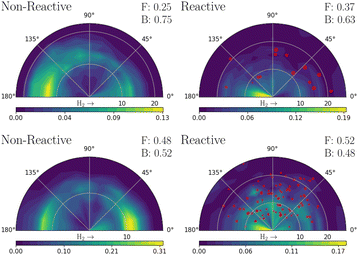
Fig. 3 shows the simulated velocity map images obtained from both models for the quenched H2 and H products. Zero degrees corresponds to the forward scattering hydrogens, in the same direction as the Hydrogen molecule's initial (z) velocity vector direction. The forward (“F”) and backward (“B”) fraction, as defined by the amount less or greater than π/2 angle respectively, is also shown in the figure. The red scattered points show the OH nascent H atoms, with a size proportional to their cross-section weight; these are ∼2% of H atoms in MZGY (21 trajectories), and 13% in FWW2. The VMI for IP greater (less) than 3 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) are provided as ESI,† and show an expectedly dominant forward (backward) distribuition. Forward scattering H products have a higher velocity; trajectories with angles <π/2 have an average of 14.5 (MZGY) 14.3 (FWW2) km s−1 compared to 12.8 (MZGY) 13.3 (FWW2) km s−1 for angles > π/2. By the time H2O and Hydrogen are away from the interaction region, the internal energy distribution of water is very similar for all 3 DOF and rotational energy. The mean H velocity as a function of b does not change substantially (∼12 km s−1 for MZGY, 13–15 km s−1 for FWW2). The spread of velocities is broad (see below), contrasting with the H2 maps, which exhibit in both models a high translational energy release. MZGY suggests an overall dominant backwards scattering of H2 (75% of H2 < π/2) and H (63%). In contrast, FWW2 slightly favours forward scattered H products (52%) while slight backward for H2 (52%). MZGY OH nascent H products favor a forward scattered angle, with a mean angle of 76° (80% occurring at low, <2.5 a0, IP) in contrast to a more isotropic distribution for FWW2 of 89° (a broader range of IP).
are provided as ESI,† and show an expectedly dominant forward (backward) distribuition. Forward scattering H products have a higher velocity; trajectories with angles <π/2 have an average of 14.5 (MZGY) 14.3 (FWW2) km s−1 compared to 12.8 (MZGY) 13.3 (FWW2) km s−1 for angles > π/2. By the time H2O and Hydrogen are away from the interaction region, the internal energy distribution of water is very similar for all 3 DOF and rotational energy. The mean H velocity as a function of b does not change substantially (∼12 km s−1 for MZGY, 13–15 km s−1 for FWW2). The spread of velocities is broad (see below), contrasting with the H2 maps, which exhibit in both models a high translational energy release. MZGY suggests an overall dominant backwards scattering of H2 (75% of H2 < π/2) and H (63%). In contrast, FWW2 slightly favours forward scattered H products (52%) while slight backward for H2 (52%). MZGY OH nascent H products favor a forward scattered angle, with a mean angle of 76° (80% occurring at low, <2.5 a0, IP) in contrast to a more isotropic distribution for FWW2 of 89° (a broader range of IP).
Fig. 4 shows the H product Kinetic Energy (KE) distribution of both models, with the distribution of OH nascent H atoms in green. Both models are qualitatively similar, with exception to the OH nascent H product, which for MZGY the maxima lies around 1.5 eV (modest number of 21 samples).
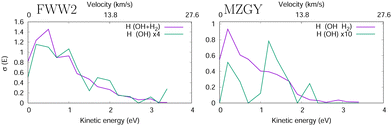 | ||
| Fig. 4 H product kinetic energy distribution in the FWW2 (left) and MZGY (right) models. The OH nascent H product also shown (green). | ||
Fig. 1 is semi-quantitatively similar to that found by ref. 8, for both models. By integrating until the last bin containing quenching trajectories, the non-quenching channels represent at least 86% of the cross section. This dominant non-quenching channel qualitatively agrees with experimental work by Brouard et al.;3 nevertheless, they suggests an approximate 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. One can expect that inclusion of Renner–Teller coupling, neglected by these models, would lead to an significant increase quenching further by a substantial factor, potentially putting in closer in line with experiments.11 The non-reaction channel is 3.8 (MZGY) and 4.1 (FWW2) times greater than the reaction channel, which is agreement with Collins et al.5 This contrasts with earlier estimated results by Lester et al.20,24 suggesting the opposite trend. Nevertheless, as argued elsewhere,9 their estimate was based on a poor estimate of the size of non-quenching channels; upon correction,3 the non-reaction channel becomes the dominant one. The reaction branching ratio decays more rapidly as a function of b in the MZGY model, making strongly forward scattered H product less likely (in contrast to the FWW2), as observed in Fig. 3.
1 ratio. One can expect that inclusion of Renner–Teller coupling, neglected by these models, would lead to an significant increase quenching further by a substantial factor, potentially putting in closer in line with experiments.11 The non-reaction channel is 3.8 (MZGY) and 4.1 (FWW2) times greater than the reaction channel, which is agreement with Collins et al.5 This contrasts with earlier estimated results by Lester et al.20,24 suggesting the opposite trend. Nevertheless, as argued elsewhere,9 their estimate was based on a poor estimate of the size of non-quenching channels; upon correction,3 the non-reaction channel becomes the dominant one. The reaction branching ratio decays more rapidly as a function of b in the MZGY model, making strongly forward scattered H product less likely (in contrast to the FWW2), as observed in Fig. 3.
The near co-linear C∞ν geometries are favored as the dominant quenching channel agrees with previously reported results.8,9 There is a long range (dipole-quadrapole) interaction at linear or perpendicular to H2 orientations depending on the atom OH face. Quenching in FWW2 model strongly prefers H-facing OH entrance channel which also dominates the mechanism leading the production of Hydrogen (Fig. 2). This is in disagreement with the recent simulations,8 which imply the opposite results. Its worth noting they used six times greater collisional energies. The long range potential is determined by FWW1, and although semi-quantitatively similar to FWW2, may well be over-emphasizing this channel. When hopping, the OH3 complex tends to form a rhombus complex structure with the oxygen at a long end, consistent with an angle of ≈145° (Fig. 2). In such orientations, S2 → S1 is the largest quenching channel (FWW2); from there, the broad distribuition of angles for S1 → S0 (for both models) show that by the time the transition takes place the H2 has already formed a chaotic, energetic complex with all hydrogens exchanging. The lifetime of incident H-facing OH complexes is estimated nearly 3 times greater than O-facing (see ESI†), increasing quenching. The MZGY model also shows this attractive entrance channel with H-facing hydroxide, but the dynamic steering effect is weaker, complex lifetime shorter (compared with FWW2), non-adiabatic coupling is comparatively absent (see ESI†) and consequently is not a dominant channel (Fig. 2). The S2 → S0 direct transfer to the ground state occurs largely at O-facing OH geometries. Particularly for MZGY, also being the mechanism for the OH nascent H product (see below).
A OH + D2 cross-beam VMI image by Ortiz-Suárez et al.4 is reproduced as ESI.† Mean collision energies are estimated at ≈0.16 eV, three times higher than in the simulations presented here. They observed two H product velocity distributions; a (likely low b) backward scattered channel representing 25% of the cross-section, and a dominant forward channel (75%). The KE distribuition of both channels are similar, peaking ≈0.5 eV with a long tail to the maximum available energy (≈4 eV), in broad agreement with other work.20 This is in qualitative disagreement with the MZGY and in only slight agreement with FWW2. Since forward scattering is clearly dominated by larger IP trajectories, the MZGY model may well not be characterizing the long range-interactions sufficiently. The OH nascent H product channel, which is largely forward scattered (Fig. 3) may also be underestimated. OH nascent H products of FWW2 arise from long-lived complexes, nearly twice as long as otherwise. This is a consequence of a strong randomization of the energy amongst the H atoms, which agrees with the models weak dependence of this processes as a function of IP, and the overall isotropic distribution. Visual inspection of trajectories also agrees with this assessment. Given the reactive cross section is most prominent for impact parameters b < 6a0, the collisional energy results in a typical orbit period for the system in the range of hundreds (<800 fs) of femtoseconds; the ∼160 fs the diatoms spend interacting is enough to result in an isotropic distribuition.
Lester et al.19,20 estimated two velocity distributions of the nascent H atoms with average KEs of 0.12 and 1.65 eV. OD + H2 scattering result in 75% HOD and 25% H2O products of the reaction cross section (60/40% for OH). The Nascent H atoms in OD + H2 → H + HOD, have a low average KE peaking at 0.15 eV, 2/3 with less than 0.5 eV and a long 4 eV tail. In contrast the D + H2O, product deuterium distribuition exhibits a second shoulder peaking at 1.8 eV, and more KE released into the translational DOF. This latter distribuition is naturally attributed to an insertion mechanism of the OH into the H2 molecule, likely at low IP. Collisional energies range in 0.005–0.05 eV, and appear qualitatively consistent.19,20 Together, the models used here may be able to partially flesh out some of these observations. The MZGY only gave a very limited number of OH nascent H product trajectories. Most of these (>90%) can be described as a H2 insertion mechanism and forward ejected OH nascent H product, which explains the second shoulder peak shown in Fig. 4. Although the OH nascent H product is underestimated by MZGY, it displays the correct channels when compared to experimental KE H product distributions.20 Although such an insertion mechanism is also present in the FWW2 model results, these comprise a small number (<15%) of the reactions (1.8 eV shoulder is weakly apparent in Fig. 4. Instead, the majority of OH nascent H product trajectories start with the OH H atom pointing towards the H2 (as discussed above); an attractive potential leads to a relatively long-lived (10 < t < 70 fs) configuration with all H3 shuffling while the complex rotates (leading to the isotropic distribution observed in Fig. 3) explaining why it has a similar distribuition in Fig. 4 for the overall nascent H products. In contrast with MZGY, where the OH nascent H via the H-facing OH entrance channel mechanism appears as a very minor, with only 3 trajectories with incident H-facing OH. The distributions of H products with energies below 1 eV (the dominant higher peak) in experiments20 could tentatively be assigned to the (incident H-facing) OH shuffling of H atoms in a long-lived complex. While the secondary, high energy peak can be attributed to the forward scattered OH nascent H product with a higher KE release via an insertion mechanism.
Two models, MZGY9 FWW28 where used to simulate molecular beam scattering experiments. Velocity maps, branching ratios, channel cross sections and H-product translational distributions where estimated. Results for branching ratios and cross sections are in semi-quantitative agreement with previous simulations. Both suggest the non-quenching to be dominant, albeit more than experimentally measured.3 The non-reactive channel is at least three times greater than the reactive channel, in agreement with experimental estimates.9,20,24 The FWW2 favors quenching around a H-facing OH orientation, while MZGY only if it quenches via S1 first (direct S0 prefers O-facing incoming OH). Experiments4 suggesting a dominant forward scattered H products is only modest agreement with FWW2 and weak disagreement with MZGY. Nevertheless, together both models describe reactive channels that might help explain the experimental observations. The models suggest that the low KE release of H is likely a result of energy redistribution during the (100–200 fs) lifetime of the OH3 complex. This complex may form from the dynamical steering of the OH at either H or O-facing the H2 molecule, the Hydrogen facing entrance channel leading to more chaotic behavior (more isotropic distribuition, and possibly, longer lived). An O-facing OH leads to a more likely insertion mechanism, with a higher KE release of the nascent H product, leading to the 1.8 eV second shoulder observed in experiments. This mechanism, as well as high impact parameter, abstraction reactions lead to a dominant forward scattered observed by experiments. Thanks to these models, the mechanism behind these experiments is beginning to come into focus.
Conflicts of interest
No conflicts of interest.Notes and references
- J. H. Lehman and M. I. Lester, Ann. Rev. Phys. Chem., 2014, 65, 537–555 CrossRef CAS PubMed
.
- B. L. Hemming and D. R. Crosley, J. Phys. Chem. A, 2002, 106, 8992–8995 CrossRef CAS
.
- M. Brouard, J. Lawlor, G. McCrudden, T. Perkins, S. A. Seamons, P. Stevenson, H. Chadwick and F. J. Aoiz, J. Chem. Phys., 2017, 146, 244313–244323 CrossRef CAS PubMed
.
- M. Ortiz-Suárez, M. F. Witinski and H. F. Davis, J. Chem. Phys., 2006, 124, 4–7 CrossRef PubMed
.
- M. A. Collins, O. Godsi, S. Liu and D. H. Zhang, J. Chem. Phys., 2011, 135, 234307–234314 CrossRef PubMed
.
- Y. Shu, J. Kryven, A. G. Sampaio De Oliveira-Filho, L. Zhang, G. L. Song, S. L. Li, R. Meana-Pañeda, B. Fu, J. M. Bowman and D. G. Truhlar, J. Chem. Phys., 2019, 151, 104311–104324 CrossRef PubMed
.
- C. L. Malbon, B. Zhao, H. Guo and D. R. Yarkony, Phys. Chem. Chem. Phys., 2020, 22, 13516–13527 RSC
.
- S. Han, A. G. de Oliveira-Filho, Y. Shu, D. G. Truhlar and H. Guo, ChemPhysChem, 2022, 23, 10064–10101 CrossRef PubMed
.
- B. Zhao, S. Han, C. L. Malbon, U. Manthe, D. R. Yarkony and H. Guo, Nat. Chem., 2021, 13, 909–915 CrossRef CAS PubMed
.
- J. N. Bull, J. W. Lee, S. H. Gardiner and C. Vallance, Eur. J. Mass Spectrom., 2014, 20, 117–129 CrossRef CAS PubMed
.
- T. Perkins, D. Herráez-Aguilar, G. McCrudden, J. Kłos, F. J. Aoiz and M. Brouard, J. Chem. Phys., 2015, 142, 144307–144315 CrossRef CAS PubMed
.
- H. Chadwick, M. Brouard, Y. P. Chang, C. J. Eyles, G. McCrudden, T. Perkins, S. A. Seamons, J. Kłos, M. H. Alexander, P. J. Dagdigian, D. Herráez-Aguilar and F. J. Aoiz, J. Chem. Phys., 2014, 140, 79–123 Search PubMed
.
- S. J. Greaves, E. Wrede, N. T. Goldberg, J. Zhang, D. J. Miller and R. N. Zare, Nature, 2008, 454, 88–91 CrossRef CAS PubMed
.
- S. J. Greaves, R. A. Rose, F. Abou-Chahine, D. R. Glowacki, D. Troya and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2011, 13, 11438–11445 RSC
.
- S. J. Greaves, D. Murdock, E. Wrede and S. C. Althorpe, J. Chem. Phys., 2008, 128, 0–10 Search PubMed
.
- C. Huang, W. Li and A. G. Suits, J. Chem. Phys., 2006, 125, 133107–133109 CrossRef PubMed
.
-
R. Bernstein, Atom-molecule collision theory, Plenum P., New York, 1979, ch. 16 Search PubMed
.
- M. B. Faist, J. Chem. Phys., 1976, 65, 5427–5435 CrossRef CAS
.
- D. T. Anderson, M. W. Todd and M. I. Lester, J. Chem. Phys., 1999, 110, 11117–11120 CrossRef CAS
.
- J. H. Lehman, J. L. Bertrand, T. A. Stephenson and M. I. Lester, J. Chem. Phys., 2011, 135, 144303–144309 CrossRef PubMed
.
-
S. Mai, M. Richter, M. Heindl, M. F. S. J. Menger, A. Atkins, M. Ruckenbauer, F. Plasser, L. M. Ibele, S. Kropf, M. Oppel, P. Marquetand and L. Gonzalez, SHARC2.1: Surface Hopping Including Arbitrary Couplings, http://sharc-md.org, 2019 Search PubMed
.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS
.
- G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111–134119 CrossRef PubMed
.
- L. P. Dempsey, C. Murray, P. A. Cleary and M. I. Lester, Phys. Chem. Chem. Phys., 2008, 10, 1424–1432 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available: Simulated data for FWW1 model, PES, and rovibrational spectrum. See DOI: https://doi.org/10.1039/d2cc03368b |
| This journal is © The Royal Society of Chemistry 2022 |