Open Access Article
Open Access ArticleImproving machine learning performance on small chemical reaction data with unsupervised contrastive pretraining†
Mingjian
Wen
 a,
Samuel M.
Blau
a,
Xiaowei
Xie
a,
Samuel M.
Blau
a,
Xiaowei
Xie
 bc,
Shyam
Dwaraknath
d and
Kristin A.
Persson
bc,
Shyam
Dwaraknath
d and
Kristin A.
Persson
 *ef
*ef
aEnergy Technologies Area, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
bCollege of Chemistry, University of California, Berkeley, CA 94720, USA
cMaterials Science Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
dLuxembourg Institute of Science and Technology, Luxembourg
eDepartment of Materials Science and Engineering, University of California, Berkeley, CA 94720, USA
fMolecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: kapersson@lbl.gov
First published on 11th January 2022
Abstract
Machine learning (ML) methods have great potential to transform chemical discovery by accelerating the exploration of chemical space and drawing scientific insights from data. However, modern chemical reaction ML models, such as those based on graph neural networks (GNNs), must be trained on a large amount of labelled data in order to avoid overfitting the data and thus possessing low accuracy and transferability. In this work, we propose a strategy to leverage unlabelled data to learn accurate ML models for small labelled chemical reaction data. We focus on an old and prominent problem—classifying reactions into distinct families—and build a GNN model for this task. We first pretrain the model on unlabelled reaction data using unsupervised contrastive learning and then fine-tune it on a small number of labelled reactions. The contrastive pretraining learns by making the representations of two augmented versions of a reaction similar to each other but distinct from other reactions. We propose chemically consistent reaction augmentation methods that protect the reaction center and find they are the key for the model to extract relevant information from unlabelled data to aid the reaction classification task. The transfer learned model outperforms a supervised model trained from scratch by a large margin. Further, it consistently performs better than models based on traditional rule-driven reaction fingerprints, which have long been the default choice for small datasets, as well as those based on reaction fingerprints derived from masked language modelling. In addition to reaction classification, the effectiveness of the strategy is tested on regression datasets; the learned GNN-based reaction fingerprints can also be used to navigate the chemical reaction space, which we demonstrate by querying for similar reactions. The strategy can be readily applied to other predictive reaction problems to uncover the power of unlabelled data for learning better models with a limited supply of labels.
1. Introduction
Machine learning methods, especially deep learning, have significantly expanded a chemist's toolbox, enabling the construction of quantitatively predictive models directly from data without explicitly designing rule-based models using chemical insights and intuitions. They have recently been successfully applied to address challenging chemical reaction problems, ranging from the prediction of reaction and activation energies,1–5 reaction products,6,7 and reaction conditions,8,9 as well as designing synthesis routes10,11 to name a few. A key ingredient underlying these successes is that modern machine learning methods excel in extracting the patterns in data from sufficient, labelled training examples.12 It has been shown that the performance of these chemical machine learning models can be systematically improved with the increase of training examples.1,13 Despite various recent efforts to generate large labelled reaction datasets that are suitable for modern machine learning,3,14–17 they are typically sparse and still small considering the size of the chemical reaction space.18 Many chemical reaction datasets, especially experimental ones, are rather limited, consisting of only thousands or even hundreds of labelled examples.19,20 For such small datasets, the machine learning models can easily become overfitted, resulting in low accuracy and transferability. Therefore, it would be of interest to seek new approaches to train the models using only a small number of reliable, labelled reactions while still retaining the accuracy.When the number of labelled reactions is small compared with the complexity of the machine learning model required to perform the task, it helps to seek some other source of information to initialize the feature detectors in the model and then to fine-tune these feature detectors using the limited supply of labels.21 In transfer learning, the source of information is another related supervised learning task that has an abundant number of labelled data. The model transfers beneficial information from the related task to aid its decision-making on the task with limited labels, resulting in improved performance. For example, transfer learning has enabled the molecular transformer to predict reaction outcomes with a small labelled dataset.22,23 Transfer learning, however, still requires a large labelled dataset to train the related task, which often is not readily available. Actually, it is possible to initialize the feature detectors using reactions without any labels at all. Although without explicit labels, unlabelled reactions contain extra information that can be leveraged to learn a better model and they are much easier to obtain. For example, the publicly available USPTO dataset14 contains ∼3 million reactions, the commercial Reaxys database24 and the CAS database25 have ∼56 millions and ∼156 millions records of reactions, respectively. In this work, we present a generic unsupervised learning strategy to distill information from unlabelled chemical reactions. For the purpose of demonstration, we focus on the problem of classifying reactions into distinct families.
Reaction family classification has great value for chemists. It facilitates the communication of complex concepts like how a reaction happens in terms of atomic rearrangement and helps to efficiently navigate the chemical reaction space by systematic indexing of reactions in books and databases.26–28 Many iconic rules for reactivity prediction require reactions to be in the same family,29 such as the Bell–Evans–Polanyi principle for estimating activation energy from reaction energy30,31 and the Woodward–Hoffmann rules for predicting reaction outcomes of pericyclic transformations.32
Given the importance, there is a long tradition in classifying reactions into families, and the techniques can be broadly grouped into two categories: rule-driven and data-driven methods.26,27 Rule-driven methods are based on a library of elaborate expert-written rules, and thus reactions without a preconceived rule cannot be classified. To overcome such limitations, data-driven methods first convert a reaction to its fingerprint (typically a numerical vector) and then apply machine learning algorithms to generate reaction families by analyzing the fingerprints of a set of reactions.33,34 Traditionally, reaction fingerprints are constructed from manually crafted molecule descriptors, such as the atom-pairs35 and extended-connectivity36 molecule descriptors. Such traditional reaction fingerprints with only a few tunable parameters have long been used as the default choice for learning reaction properties on small datasets. More recently, a new class of reaction fingerprints that are learned directly from data have emerged. Schwaller et al.28,37,38 used the transformer39 natural language processing model to learn fingerprints from reaction SMILES string.40 Wei et al.41 developed the first learnable graph neural network (GNN) reaction fingerprints based on GNN molecule descriptors.42,43 The GNN reaction fingerprints are flexible to adapt themselves to unseen reactions and have achieved satisfying results in a number of applications, such as the prediction of reaction energy and activation energy.1,3 However, as many other modern machine learning methods, they need a large number of labelled reactions to train.
We present a GNN-based model to classify reactions and propose a strategy to train the model using only a small number of labelled reactions. The strategy can be categorized as a transfer learning technique discussed above: we first pretrain the model on a large number of unlabelled reactions and then fine-tune it using a small number of labelled reactions. The pretraining is based on recent advances in contrastive self-supervised learning in computer vision,44–46 where representations of unlabelled images are learned by contrasting different views of them. In contrast, our GNN model extracts generic concepts of reactions by contrasting augmented versions of unlabelled reactions. The core idea behind this is straightforward: if we modify a reaction, for example, by removing an atom away from the reaction center, oftentimes we would still get the “same” reaction in terms of which class it belongs to. Taking advantage of this “an augmented reaction resembles itself” idea, we pretrain the model by requiring the fingerprints of various augmentations of a reaction be as similar to each other as possible. (This pretraining is unsupervised since no labels are used).
The pretrain-fine-tuned model outperforms supervised GNN models trained from scratch and traditional fingerprint-based models by a large margin for small datasets. For example, using only 8 labelled reactions per class in the Schneider33 training set, it achieves an F1 score of 0.86, while the supervised model and the traditional fingerprints-based model get an F1 score of 0.64 and 0.63, respectively. Even without fine-tuning, the reaction representation (RxnRep) fingerprint derived from our model still performs better than traditional rule-driven reaction fingerprints and more recent masked-language reaction fingerprints. We explored various reaction augmentation methods and found that appropriate reaction augmentation is the key to the success of the contrastive pretraining. Selecting a reaction center based on altered bonds and then augmenting the reaction beyond a subgraph around the reaction center turns out to be a simple yet robust augmentation method. To elucidate how the contrastive pretraining helps to learn a better model, we analyzed the high-dimensional learned reaction fingerprints by projecting them into a two-dimensional space and found that the pretraining itself can already push the fingerprints of reactions in the same class close to each other, forming clear clusters. The learned model can be repurposed for other chemical applications, either as the starting point for other supervised tasks or being directly used in unsupervised tasks, which we demonstrate via the query for similar reactions.
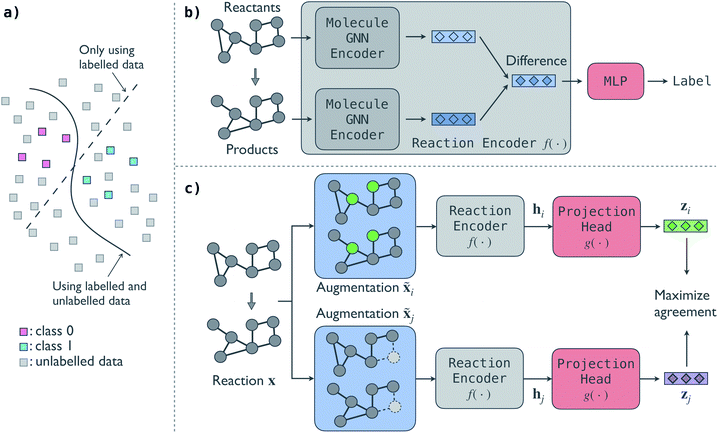
2. Contrastive self-supervised model
An illustrative overview of the contrastive self-supervised learning approach to train GNN models for reaction classification is presented in Fig. 1. As introduced in Section 1, the overall idea is to leverage the information in unlabelled reactions to help the model make better decisions, as schematically shown in Fig. 1a. In this section, we first introduce the base predictive GNN model for reaction classification and then discuss the proposed contrastive approach to distill information from unlabelled reactions. In-depth description of individual model architecture is given in Section S1 of the ESI.†The predictive GNN model is based on our previous BonDNet model1 for the prediction of bond dissociation energy. In the model (Fig. 1b), each reactant and product molecule in a reaction is represented as a graph with atoms as nodes and bonds as edges. The molecular graphs are attributed: each node is associated with a feature vector describing the atom (e.g. atom type) and similarly each edge has a feature vector describing the bond (e.g. whether a bond is in a ring). In addition, a global feature vector is introduced to incorporate molecule-level information (e.g. the molecular weight). Taking the attributed molecular graphs of a reaction as the input x, a molecule GNN encoder iteratively updates the atom, bond, and global features to obtain better representations of the molecules using a message-passing scheme.47 We emphasize that a reaction can have multiple reactants and products, and each reactant and product molecule is processed separately by the molecule GNN encoder. Unlike traditional molecule descriptors that generate a fixed-size vector for each molecule, our model keeps individual atom, bond, and global features during the message passing, and then directly aggregates them to form a reaction representation. To achieve this, in the last molecule GNN encoder layer, we take the difference of the two feature vectors of each atom between the products and reactants, and then use an attention-based pooling to convert the set of difference feature vectors into a single vector h, which we call the fingerprint of the reaction. Finally, we map the reaction fingerprint to the reaction class label using a multilayer perceptron (MLP). In essence, the predictive model has two parts: (a) a GNN reaction encoder f(·) that takes the molecular graphs of a reaction x as input and generates a vector fingerprint h for the reaction, h = f(x), and (b) an MLP that decodes the reaction fingerprint h to the reaction class label, y = MLP(h).
One can train the predictive GNN model using a fully labelled dataset by minimizing a loss function, e.g. the cross-entropy loss function. However, this supervised training approach that trains a model from scratch generally needs a large number of labelled reactions. For small labelled datasets, we propose a contrastive self-supervised learning approach to pretrain the GNN reaction encoder f(·) to leverage the information in unlabelled reactions. The contrastive model (Fig. 1c) consists of four parts.
• A reaction augmentation module that modifies the input molecular graphs of a reaction. Two augmentations are selected from a pool of augmentation methods and applied to the input reaction x, resulting in two augmented reactions, ![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif) i and
i and ![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif) j. We consider five reaction augmentation methods: mask atom features, drop atoms, mask bond features, drop bonds, and take molecular subgraphs. They are further discussed in Section 3.1.
j. We consider five reaction augmentation methods: mask atom features, drop atoms, mask bond features, drop bonds, and take molecular subgraphs. They are further discussed in Section 3.1.
• A reaction encoder that converts a reaction to its vector fingerprint. The reaction encoder f(·) is the same as that used in the predictive model, into which the knowledge in the unlabelled reactions will be injected. Two fingerprints hi = f(![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif) i) and hi = f(
i) and hi = f(![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif) j) are obtained via the reaction encoder, one for each augmented reaction.
j) are obtained via the reaction encoder, one for each augmented reaction.
• A projection head g(·) that maps a reaction fingerprint to its final vector representation, with which we get zi = g(hi) and zj = g(hj). An MLP is used as the projection head.
• A contrastive loss that maximizes the agreement between the two final representations zi and zj of a reaction, but distinguishes them from the final representations of other reactions. At each training step, we randomly sample a minibatch of N reactions. After the above three steps, we obtain 2N vectors z1, z2, …, z2N, where z2n−1 and z2n denote the two final vector representations of reaction n (n = 1, 2, …, N). From the 2N final representations, we construct a loss function:
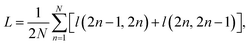 | (1) |
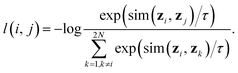 | (2) |
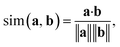 | (3) |
The supervision is fully provided by the reactions themselves via the augmentations, and thus no labels are needed in training the contrastive model. A model trained via this contrastive self-supervised approach would distill generic information of the reactions. Fine-tuned using some labels, the model can then be applied to perform specific tasks. To do this, we only keep the trained reaction encoder f(·) and discard the other parts. We then replace the reaction encoder in the predictive model by the pretrained one from the contrastive model. Finally, we train the predictive model by minimizing the cross-entropy loss function on the labelled data as discussed above.
Going forward, we will employ the following naming conventions for the models: a supervised model refers to a predictive model trained from scratch on labelled data; a pretrained model is trained via the contrastive self-supervised approach without using any label; and a fine-tuned model is first pretrained using the contrastive self-supervised approach and then fine-tuned with labels.
3. Results
3.1 Reaction augmentation strategy
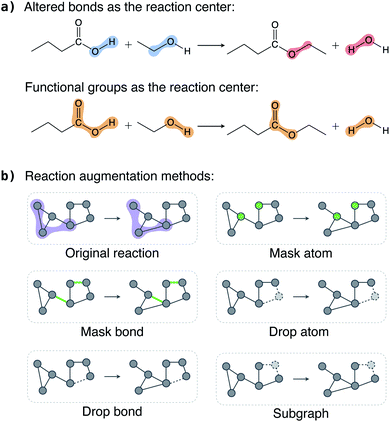
In this section, we discuss the key considerations and strategies in augmenting reactions and show that appropriate chemically consistent augmentation is the key to the success of the contrastive model.Each reaction has multiple reactant and product molecules; we can augment each molecule individually using existing molecular graph augmentation methods,48–50 but this naive approach is far from optimal. Instead, we add two restrictions on what can be augmented. First, atoms (bonds) in the reaction center should be kept intact, that is, we can only select atoms (bonds) outside the reaction center to modify. This restriction is motivated by the assumption that atoms (bonds) in the reaction center are significant in defining a reaction, and, in general, atoms (bonds) far away from the reaction center are less important. This is particularly true for the reaction classification problem studied in this work. Second, if an atom (bond) in the reactants is selected for augmentation, the same atom (bond) in the products should also be selected, and vice versa. Atoms always have a one-to-one correspondence between the reactants and products, but bonds do not. For example, a broken bond only exists in the reactants but not in the products. Therefore, we only select bonds that exist in both the reactants and products for augmentation.
To define a reaction center, we explore three modes (Fig. 2a): altered bonds, functional groups, and none. Given a reaction and the atom mapping between the reactants and products, we can identify the broken and formed bonds. The altered bonds center mode regards the broken and formed bonds together with the atoms that they connect to as the reaction center. In reality, a reaction typically occurs between functional groups. For example, a carboxylic acid group reacts with an alcohol to form an ester in the esterification reaction shown in Fig. 2a. This motivates us to use the reacting functional groups as another reaction center mode. To determine the functional group in a molecule that reacts in a reaction, we loop over a list of predefined functional groups and inspect whether it is associated with the altered bonds. (A detailed description of the process is given in Section 5 and an algorithm is given as Algorithm 1 in the ESI†). Finally, the “none” mode means no atoms and bonds are fixed as reaction center and thus all are available for augmentation.
Once the reaction center is determined, we keep it intact and randomly select a portion of atoms (bonds) outside it for augmentation. We explored five augmentation methods, and they are schematically illustrated in Fig. 2b.
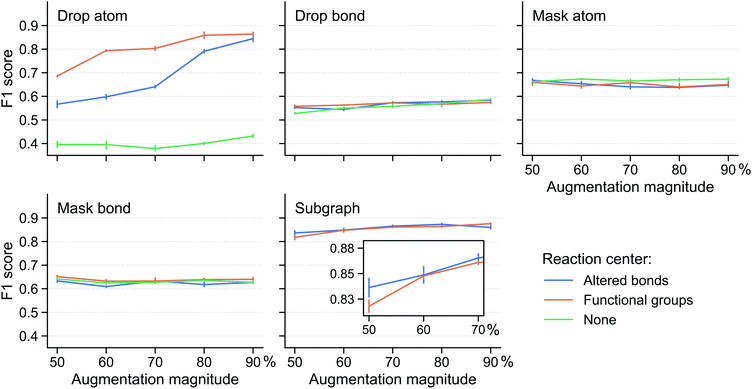
Fig. 3 shows the performance of the fine-tuned model for various reaction center modes and augmentation methods at different augmentation magnitude (i.e. the percentage of augmented atoms/bonds). The results are obtained using the Schneider dataset33 (see Section 5) with 8 labelled reactions per class. Mask atom and mask bond are found to be ineffective augmentation methods. Their classification F1 scores are around that of the supervised model (0.64) and change very little with reaction center mode and augmentation magnitude. This shows the importance of the input atom/bond features: changing them will misguide the contrastive pretraining, making it unable to distill any useful information to aid the classification task. Drop bond performs even worse, with F1 scores lower than the supervised model, suggesting that the reaction class families depend on bonds outside the reaction center and removing these bonds greatly affect the model (similar observation discussed below on drop atom and subgraph).
In contrast, drop atom and subgraph are effective augmentation methods which can improve the performance of the fine-tuned model compared with the supervised model. Two observations from the results are made; first, the reaction center mode makes a substantial difference. For drop atom, the “none” reaction center mode impacts the model performance negatively. It gets an F1 score of ∼0.40, significantly below that of the supervised model. This is because any atom can be dropped in the “none” mode and dropping atoms in the reaction center drastically changes the nature of the reaction. For drop atom, the functional groups center mode achieves a higher score than the altered bonds center mode across a range of augmentation magnitudes. This beneficial effect, however, disappears and the two center modes are on par with each other when using the subgraph augmentation method. We speculate that this distinction originates from the protection of the reaction center. For drop atom, the functional groups center mode (compared with the altered bonds center mode) can identify more relevant atoms and bonds that correlate with the reaction class and keep them from being disrupted. In the case of the subgraph augmentation, the protection is effective irrespective of how the reaction center is determined because atoms far away from the center are removed first. Second, stronger augmentation leads to better performance. This is apparent from the drop atom case where the scores of both the altered bonds and functional groups center modes increase with the augmentation magnitude. For the subgraph augmentation method, this is more clear from the inset.
Additional results for models trained using 16 labelled reactions per class are given in Fig. S2 in the ESI,† which provide further support for the conclusions discussed above. In addition, the same augmentation method is applied to both augmentations i and j of a reaction in the above discussion. We further sought to identify whether a combination of different augmentation methods can benefit the contrastive pretraining and found that as long as one of the two augmentations is drop atom or subgraph, the model performs well and no further benefit is obtained (Fig. S3 in the ESI†).
In summary, we find that the subgraph-based method provides robust augmentation regardless of the reaction center mode and augmentation magnitude. Opting for simplicity, we select the altered bonds reaction center mode in the below discussions, instead of the functional groups center mode.
3.2 Model performance on small datasets
Using the subgraph augmentation method with the altered bonds reaction center mode and an augmentation magnitude of 0.8, we next investigate the effects of the contrastive pretraining on small datasets. The pretraining can improve model performance on both classification and regression problems; we focus on classification here and discuss regression in Section S3.5 of the ESI.† We curated three reaction classification datasets, namely, the Schneider, TPL100, and Grambow datasets. For each dataset, instead of using the entire training set, we intentionally draw 4, 8, …, 128 labelled reactions per class from the training set to simulate the small data regime and train the models on these small datasets. More information of the three datasets and how the models are trained are given in Section 5.Performance of the models trained on these small datasets are shown in Fig. 4. For each dataset, contrastive pretraining significantly improves the classification F1 score. For example, with 8 labelled reactions per class in the Schneider training set, the supervised model only gets a score of 0.64; in contrast, with the help of the contrastive pretraining, the fine-tuned model achieves a score of 0.86, an increase of 34%. An analysis of the classification error (Fig. S4 in the ESI†) shows that the fine-tuned model can correctly identify most reaction classes and that the remaining error is mainly from the misclassification of reactions that are very similar to each other, such as “methyl esterification” and “Fischer–Speier esterification” reactions. As expected, the performance gap gradually closes when more reactions are added to the training set; the two models perform almost the same with 128 reactions per class. This trend is also observed for the TPL100 and Grambow datasets. A difference worth noting is that the performance gap closes more slowly for the Grambow dataset. The Grambow dataset only has five classes (as a comparison, TPL100 has 100 classes), and thus although the number of training data per class increases, the total number of training reactions does not vary much and it is still small. In this very small data regime, the fine-tuned model always performs better than the supervised model.
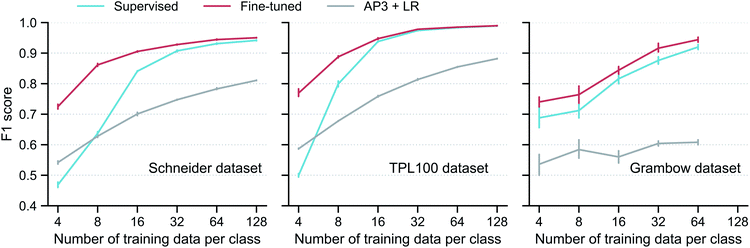 | ||
Fig. 4 Model performance on reaction classification. Classification F1 score versus training set size for the supervised and fine-tuned GNN models, as well as a logistic regression (LR) model on the traditional AP3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 fingerprint (AP3 + LR). The vertical bar denotes the uncertainty, obtained as the standard deviation from five different runs, each with a different resampling of the training data. No result at 128 is given for the Grambow dataset since its smallest reaction class has fewer than 128 reactions. 33 fingerprint (AP3 + LR). The vertical bar denotes the uncertainty, obtained as the standard deviation from five different runs, each with a different resampling of the training data. No result at 128 is given for the Grambow dataset since its smallest reaction class has fewer than 128 reactions. | ||
Fig. 4 also includes the results of a model using traditional reaction fingerprint as proposed in ref. 33: AP3 + LR (logistic regression on the AP3 fingerprints (atom pairs with a maximum path length of three35)). This model is inferior to both the supervised and fine-tuned GNN-based models, except for extremely small Schneider and TPL100 training sets with 4 reactions per class.
As discussed in Section 2, the predictive model consists of two parts: a GNN reaction encoder and an MLP decoder. For the results shown in Fig. 4, model parameters in both the encoder and the decoder are optimized. However, after pretraining, it is possible to keep the encoder fixed (i.e. not allow its parameters to change) and use it as a featurizer to convert a reaction to its fingerprint. We call such reaction fingerprint obtained from our pretrained GNN encoder the RxnRep (reaction representation) fingerprint. Table 1 lists the F1 score obtained using an MLP decoder on the fixed RxnRep fingerprint, together with results obtained using the AP333 fingerprint, as well as the RXNFP28 and DRFP51 fingerprints based on masked language modelling on SMILES.40 Even without optimizing the parameters in the GNN reaction encoder, our RxnRep fingerprint still performs better than the other fingerprints. Similar behavior is observed for the TPL100 and Grambow datasets (Section S3.3 of the ESI†).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 is a fingerprint based on expert rules; RXNFP28 and DRFP51 are fingerprints based on masked language modelling. The employed classification model is either a logistic regression (LR) algorithm or a multilayer perceptron (MLP). Values outside and inside the parentheses are the mean and standard deviation, respectively, of the scores from five runs, each with a different resampling of the training data
33 is a fingerprint based on expert rules; RXNFP28 and DRFP51 are fingerprints based on masked language modelling. The employed classification model is either a logistic regression (LR) algorithm or a multilayer perceptron (MLP). Values outside and inside the parentheses are the mean and standard deviation, respectively, of the scores from five runs, each with a different resampling of the training data
| Training data size (reactions per class) | AP3 + LR | AP3 + MLP | RxnRep + MLP | RXNFP + MLP | DRFP + MLP |
|---|---|---|---|---|---|
| 4 | 0.541 (0.008) | 0.518 (0.004) | 0.441 (0.010) | 0.322 (0.012) | 0.100 (0.005) |
| 8 | 0.628 (0.005) | 0.620 (0.004) | 0.634 (0.003) | 0.394 (0.013) | 0.129 (0.004) |
| 16 | 0.701 (0.011) | 0.703 (0.006) | 0.767 (0.003) | 0.471 (0.010) | 0.199 (0.008) |
| 32 | 0.747 (0.002) | 0.761 (0.002) | 0.831 (0.002) | 0.531 (0.006) | 0.266 (0.007) |
| 64 | 0.782 (0.004) | 0.799 (0.004) | 0.875 (0.003) | 0.575 (0.005) | 0.338 (0.006) |
| 128 | 0.811 (0.002) | 0.828 (0.004) | 0.900 (0.002) | 0.618 (0.004) | 0.398 (0.002) |
Finally, we note that the above results are obtained using the gated graph convolutional network (GatedGCN)52 as the molecule encoder. To check the general applicability of the contrastive pretraining approach, we tested on two other widely used GNNs, the graph isomorphism network (GIN)53 and graph attention network (GAT).54 The results confirm that the contrastive pretraining can indeed help to learn better models for small reaction datasets regardless of the used GNN molecule encoder (Section S3.4 in the ESI†).
3.3 Analysis of reaction fingerprints
The above discussion shows that the contrastive pretraining can significantly improve model performance on small reaction datasets. Next, we examine how pretraining helps to learn better models. To this end, we embed the learned high-dimensional reaction fingerprint vectors into a two-dimensional space and analyze the patterns in the embedding space.TMAP55 embeddings for reactions in the Schneider test set are presented in Fig. 5 (see Section 5 for a description of TMAP). The pretrained model uses the same reaction augmentations as in Section 3.2; the supervised and fine-tuned models are trained on 8 labelled reactions per class. The 46 reaction classes in the Schneider dataset are derived from 8 super classes based on the RXNO ontology,56 and the reactions in the plot are colored according to the super class labels. The supervised model is able to single out some reaction classes such as oxidation (brown) and functional group interconversion reactions (pink). However, supervised by a limited supply of labels, it struggles to clearly distinguish other reactions classes. For example, heteroatom alkylation and arylation (blue), acylation and related processes (yellow), and C–C bond formation (green) are intermixed with each other. Not surprisingly, the pretrained model without using any labels cannot distinguish between all reaction classes either, but it is encouraging to see that the pretrained model can already separate some reactions from the rest, such as deprotection (red) and reduction (purple) reactions. Fine-tuned using a small number of labels, the model becomes capable of distinguishing all reactions. The most intriguing observation is related to the heteroatom alkylation and arylation (blue), acylation and related processes (yellow), and C–C bond formation (green) reactions, which the supervised model struggles with. When only pretrained, the three seem to be highly intermixed, and thus one might guess that the pretraining would not help in learning a better model. However, after fine-tuning, the boundaries between them become more clear compared with the supervised model, although a small number of blue and yellow dots are still intermixed, which correspond to “methyl esterification” and “Fischer–Speier esterification” reactions that are very similar to each other as discussed in Section 3.2. This suggests, although not explicitly, that the pretraining indeed provides important channels for the fine-tuned model to take advantage of, e.g. transforming the model parameters into a space easier to learn.
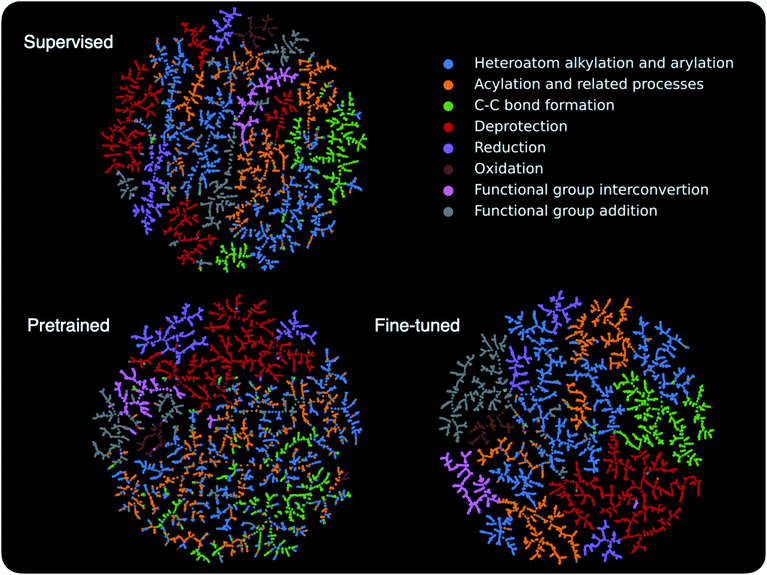 | ||
| Fig. 5 Embedding of the reaction fingerprints in a two-dimensional space. Each dot in the plot represents a reaction and is colored according to its super family label. The graph layout is generated by TMAP,55 and, in general, similar reaction fingerprints are embedded closer to each other. | ||
In essence, the contrastive pretraining by itself can already separate some reaction classes from others, and, for the intermixed reactions, it makes the task easier for later fine-tuning. The fine-tuning takes advantage of the structural information in the unlabelled reactions, which is distilled and injected into the model via the contrastive pretraining.
3.4 Searching for similar reactions
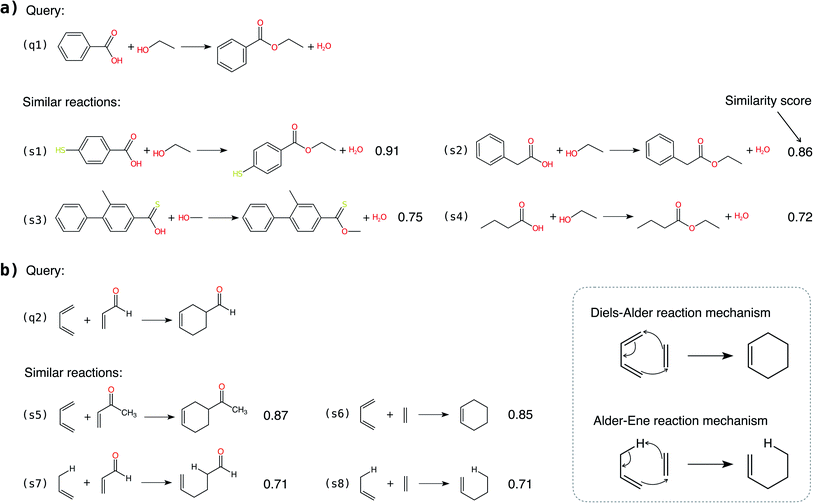
In addition to classifying reactions, the model can be repurposed for other use cases. For example, the learned reaction encoder can be readily used as a featurizer to turn a reaction into its vector fingerprint, replacing traditional rule-driven ones derived from molecule descriptors (e.g. atom pairs35). The reaction fingerprints can then be applied to other supervised machine learning tasks for reactions, such as the prediction of reaction conditions and reaction yields. Here, we focus on an unsupervised task—searching for similar reactions, which plays an important role in many chemical applications such as information retrieval in large reaction databases and synthesis route planning.Given a query reaction, we compute its fingerprint h and then search for similar training set reactions in the fingerprint space using the k-nearest-neighbor algorithm with the cosine similarity as defined in eqn (3). We consider two scenarios: querying for one reaction whose class is in the training data and for another reaction whose class is not in the training data. For the former case, we query for a Fischer–Speider esterification reaction that generates an ester from an alcohol and a carboxylic acid. As the training data contains such reactions, it is not too surprising that the first %7E200 retrieved reactions are all of the same type as the query reaction. Nevertheless, this means that the model is effectively able to learn the notion of functional groups that take part in a reaction, although such information is never disclosed to the model. (The model does know the reaction center of a reaction via the altered bonds, but not the functional groups). Four representative retrieved reactions are shown in Fig. 6a (more in Fig. S8 in the ESI†). Retrieved reactions (S1), (S2), and (S4)† have decreasing similarity scores to the query reaction q1, suggesting that the model not only recognizes the functional groups in the reaction center, but also attends to structures away from the center. Reaction (S3),† in which the ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in the carboxylic acid group is replaced by a
O bond in the carboxylic acid group is replaced by a ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S bond, further confirms the model's assigned importance of structure away from the reaction center since it has a higher similarity score than reaction S4.†
S bond, further confirms the model's assigned importance of structure away from the reaction center since it has a higher similarity score than reaction S4.†
As a second more challenging scenario, we query for a Diels–Alder reaction whose class is not in the training data. For demonstration, we compiled a new set of Diels–Alder and Alder–Ene reactions to search, and four representatives are plotted in Fig. 6b. The Diels–Alder reactions (S5) and (S6)† have similarity scores of ∼0.86, much higher than that of the most similar reaction retrieved from the original training data (0.64). More importantly, the Alder–Ene reactions S7 and S8† also exhibit higher similarity scores compared to the query reaction. The task is more challenging than it seems in Fig. 6 because hydrogens are not explicitly modeled in the input graphs to our model. (Due to the large number of hydrogens in the molecules, including them greatly increases the size of the graphs and thus the computational burden). In fact, Diels–Alder and Alder–Ene reactions have very similar reaction mechanisms: they are both 6-electron pericyclic reactions. The underlying driving force is the formation of new σ-bonds, which are energetically more stable than the reactant π-bonds. It is unlikely that our model has parametrized such delicate rules, given that the inputs are simple 2D molecular graphs. Nevertheless, it is encouraging that the reaction encoder can generate meaningful reaction fingerprints for reaction classes that the encoder are never exposed to for learning. Furthermore, it assigns high similarity scores for reactions that exhibit very similar reaction mechanisms. Hence, the methodology presented here may be useful for discovering or designing novel chemical reactions, as many “new” reactions share similarities with or are variations on mechanisms of known reactions.
The two scenarios demonstrate that the reaction encoder can generate meaningful reaction fingerprints for querying similar reactions, respecting both the functional groups in the reaction center and features away from the center without knowing the functional groups a priori. The results indicate capabilities beyond previous reaction query systems that depend on matching predefined reaction templates defined by functional groups. Furthermore, we note that the reaction encoder can be applied to reaction classes and mechanisms that are very different from any provided in the training data, although care should be taken to not extrapolate inappropriately to avoid unbounded uncertainty.57
4. Conclusions
We have designed a machine learning model based on graph neural networks (GNNs) for reaction classification and proposed a contrastive approach to pretrain the model using only unlabelled data. The contrastive approach trains a model via self-supervision by pulling different augmented versions of a reaction together and pushing them away from other reactions. We have found that a chemically consistent reaction augmentation strategy that protects the reaction center is the key to the success of the contrastive approach. Selecting reaction centers based on the broken and formed bonds in a reaction and then augmenting the reaction by dropping atoms beyond a subgraph around the reaction center is found to be a robust augmentation strategy. GNN models pretrained using this augmentation strategy and then fine-tuned on a small number of labelled reactions significantly outperform both supervised models trained from scratch and models based on reaction fingerprints derived from expert rules or masked language modelling.By analyzing the learned GNN reaction fingerprints, we found that the pretraining by itself can already help to separate some reaction families from others; leveraging a small number of exact labels, the pretrain-fine-tuning approach learns an even better model. The learned models can be repurposed for other applications, which is demonstrated by searching for similar reactions in the fingerprint space. This demonstration also shows that the learned reaction fingerprints understand both the functional groups in the reaction center and chemical/structural features away from the center, and it has certain transferability to reactions not in the training data. We expect that the reaction fingerprints can also be used as the starting point for transfer learning other reaction properties from small datasets, such as predicting reaction conditions and reaction yields. Our graph-based approach does not consider stereochemistry and requires all reactions to be balanced; however, these limitations can be overcome by incorporating techniques developed in, e.g. ref. 58 and 59, respectively.
Overall, we have demonstrated a simple yet powerful approach to pretrain machine learning models for chemical reaction data without requiring any label information. We believe such chemically consistent pretraining approaches constitute a key component to the future success of applying modern machine learning methods to solve challenging chemical problems, e.g. guiding experiments where it is extremely time-consuming or expensive to obtain a large number of labelled data.
5. Methods
5.1 Data
We have curated three reaction datasets, namely, the Schneider, TPL100, and Grambow datasets. The Schneider and TPL100 datasets are derived from the Schneider 50k dataset33 and the 1k TPL dataset,28 respectively, both of which are descendants of the USPTO dataset of patent reactions.14 After further cleaning (add missing atom map numbers and remove reactions whose elements are not balanced between the reactants and products), 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 reactions with 46 classes remain in the Schneider dataset. Reactions in this dataset are labelled according to the RSC RXNO ontology.56 The 1k TPL dataset has 1000 reaction classes, obtained by selecting the 1000 most frequent template labels from a template extraction workflow.28 This dataset is extremely imbalanced. After further cleaning (the same as for the Schneider dataset), the most frequent 100 reaction classes, each with 850 reactions, are selected to form the TPL100 dataset. The Grambow dataset is derived from a dataset of reaction and activation energies by Grambow and coworkers.3,60 We generate the class labels by matching the reactions to the reaction mechanism generator (RMG) templates.61 Only a very small portion of reactions have an RMG template and thus a small dataset of 1602 reactions with 5 reaction classes is obtained.
800 reactions with 46 classes remain in the Schneider dataset. Reactions in this dataset are labelled according to the RSC RXNO ontology.56 The 1k TPL dataset has 1000 reaction classes, obtained by selecting the 1000 most frequent template labels from a template extraction workflow.28 This dataset is extremely imbalanced. After further cleaning (the same as for the Schneider dataset), the most frequent 100 reaction classes, each with 850 reactions, are selected to form the TPL100 dataset. The Grambow dataset is derived from a dataset of reaction and activation energies by Grambow and coworkers.3,60 We generate the class labels by matching the reactions to the reaction mechanism generator (RMG) templates.61 Only a very small portion of reactions have an RMG template and thus a small dataset of 1602 reactions with 5 reaction classes is obtained.
For each dataset, the contrastive pretraining uses all data, ignoring the class labels. For the supervised training and fine-tuning, a dataset is randomly split into the training, validation, and test subsets with a ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. To simulate the case of small datasets, we intentionally do not use the full training set, but randomly draw 4, 8, …, 128 reactions per class from the training set to form small subsets. We optimize the model parameters using the training subsets, select hyperparameters based on model performance on the validation set, and report results on the test set. We emphasize that the hyperparameter search is only conducted for the supervised model to ensure their best performance. For the pretrained and fine-tuned models, the same hyperparameters as their supervised counterparts are adopted, except for one hyperparameter—temperature τ in the loss function of eqn (2), which is determined via the performance of the fine-tuned model. We find that a value of 0.1 is robust for different datasets and thus adopt it for all experiments. The optimal model hyperparameters are obtained via grid search and are given in Tables S2 and S3 in the ESI.†
1. To simulate the case of small datasets, we intentionally do not use the full training set, but randomly draw 4, 8, …, 128 reactions per class from the training set to form small subsets. We optimize the model parameters using the training subsets, select hyperparameters based on model performance on the validation set, and report results on the test set. We emphasize that the hyperparameter search is only conducted for the supervised model to ensure their best performance. For the pretrained and fine-tuned models, the same hyperparameters as their supervised counterparts are adopted, except for one hyperparameter—temperature τ in the loss function of eqn (2), which is determined via the performance of the fine-tuned model. We find that a value of 0.1 is robust for different datasets and thus adopt it for all experiments. The optimal model hyperparameters are obtained via grid search and are given in Tables S2 and S3 in the ESI.†
5.2 Model training
The inputs to the models are attributed molecular graphs with atom, bond, and global features. Following our previous work,1 we opt for simple features that can be generated with RDKit,62 and a summary of the selected features is given in Table S1 in the ESI.† In addition to the attributed molecular graphs, the model also needs atom mapping between the reactants and products to accomplish two tasks: computing the difference features in the reaction encoder and selecting the same atoms (bonds) in the reactants and products for augmentation. The three datasets used in this work all come with atom mapping. For a dataset where atom mapping is not readily available, it can be obtained via integer linear programming63 and even data-driven approaches.38 We refer to ref. 64 for a benchmark of many existing open-source and commercial atom mapping tools.The models are implemented using DGL65 with a PyTorch66 backend. We train all models using the Adam optimizer67 with an initial learning rate of 10−3 and a cosine learning rate scheduler to dampen the learning rate to 10−6 towards the end of the training. For the supervised and fine-tuned models, we train for a maximum of 200 epochs with a minibatch size of 100 (64 for the Grambow dataset) by minimizing the cross-entropy loss function. For the contrastive self-supervised model, we train for 100 epochs with a larger minibatch size of 1000 (large batch size improves performance of the contrastive model44) by minimizing the loss function in eqn (1). A total number of 100 epochs is enough for the contrastive model since the loss does not further decrease after ∼60 epochs (an example loss versus epoch curve is given in Fig. S1 in the ESI†).
For models using fixed reaction fingerprints, the AP333 fingerprint is calculated using RDKit;62 the RXNFP28 and DRFP51 fingerprints are obtained using codes associated with the papers that introduce them. We use scikit-learn68 to train the logistic regression algorithm on the AP3 fingerprint and use PyTorch to train MLPs on all the fingerprints (including our RxnRep fingerprint).
5.3 Functional group determination
To determine the functional group in a molecule that participates in a reaction, we loop over a list of predefined functional groups and check whether a functional group is in the molecule by SMARTS matching69 as implemented in RDKit.62 If a functional group is in the molecule and it also contains atoms in the broken or formed bonds, it is reserved as a candidate. Among the candidates, the one with the most number of atoms is selected as the functional group for the molecule (see Algorithm 1 in the ESI†). For example, in the reaction shown in Fig. 2a, there are two candidate functional groups for the butyric acid, –OH and –COOH, both of which contain atoms in the broken oxygen–hydrogen bond. The –COOH group is selected because it has more atoms. The DayLight example SMARTS70 are employed as the predefined functional groups.5.4 TMAP embedding
We embed the high-dimensional reaction fingerprints into a two-dimensional space using TMAP.55 TMAP first builds a k-nearest-neighbor graph using a similarity measure of the high-dimensional reaction fingerprints. (We use the k-nearest-neighbor algorithm implemented in scikit-learn68 and the cosine similarity defined in eqn (3)) .Based on the k-nearest-neighbor graph, TMAP then calculates a minimum spanning tree and finally generates a layout for the resulting minimum spanning tree.Data availability
The code is released as an open-source repository at https://github.com/mjwen/rxnrep. The Schneider, TPL100, and Grambow datasets are provided along with the repository. The original Schneider 50k, 1k TPL, and Grambow datasets are described in ref. 28, 33 and 60, respectively, and can be obtained therein.Author contributions
Conceptualization, methodology, data curation, and writing–original draft: M. W.; formal analysis and investigation: M. W., S. M. B, and X. X.; writing–review & editing: M. W., S. M. B, X. X., S. D., and K. A. P.; funding acquisition: K. A. P.; supervision: K. A. P.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The method development was collaboratively supported by the Joint Center for Energy Storage Research, an Energy Innovation Hub funded by the US Department of Energy, Office of Science, Basic Energy Sciences as well as by the Silicon Consortium Project (SCP) directed by Brian Cunningham under the Assistant Secretary for Energy Efficiency and Renewable Energy, Office of Vehicle Technologies of the U.S. Department of Energy, Contract No. DE-AC02-05CH11231. Computational resources were provided by the Department of Energy's Office of Energy Efficiency and Renewable Energy (located at the National Renewable Energy Laboratory). This research also used the Lawrencium computational cluster resource provided by the IT Division at the Lawrence Berkeley National Laboratory (Supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231).Notes and references
- M. Wen, S. M. Blau, E. W. C. Spotte-Smith, S. Dwaraknath and K. A. Persson, Chem. Sci., 2021, 12, 1858–1868 RSC
.
- X. Xie, E. W. C. Spotte-Smith, M. Wen, H. D. Patel, S. M. Blau and K. A. Persson, J. Am. Chem. Soc., 2021, 143, 13245–13258 CrossRef PubMed
.
- C. A. Grambow, L. Pattanaik and W. H. Green, J. Phys. Chem. Lett., 2020, 11, 2992–2997 CrossRef CAS PubMed
.
- P. Friederich, G. dos Passos Gomes, R. De Bin, A. Aspuru-Guzik and D. Balcells, Chem. Sci., 2020, 11, 4584–4601 RSC
.
- G. dos Passos Gomes, R. Pollice and A. Aspuru-Guzik, Trends Chem., 2021, 3, 96–110 CrossRef CAS
.
- C. W. Coley, R. Barzilay, T. S. Jaakkola, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2017, 3, 434–443 CrossRef CAS PubMed
.
- P. Schwaller, T. Gaudin, D. Lányi, C. Bekas and T. Laino, Chem. Sci., 2018, 9, 6091–6098 RSC
.
- H. Gao, T. J. Struble, C. W. Coley, Y. Wang, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2018, 4, 1465–1476 CrossRef CAS PubMed
.
- M. R. Maser, A. Y. Cui, S. Ryou, T. J. DeLano, Y. Yue and S. E. Reisman, J. Chem. Inf. Model., 2021, 61, 156–166 CrossRef CAS PubMed
.
- C. W. Coley, L. Rogers, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2017, 3, 1237–1245 CrossRef CAS PubMed
.
- M. H. S. Segler and M. P. Waller, Chem.–Eur J., 2017, 23, 5966–5971 CrossRef CAS PubMed
.
- Y. Zhang and C. Ling, npj Comput. Mater., 2018, 4, 1–8 CrossRef
.
- O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, Nat. Rev. Chem., 2020, 4, 347–358 CrossRef
.
- D. Lowe, Chemical reactions from US patents (1976–Sep 2016), https://doi.org/10.6084/m9.figshare.5104873.v1, accessed 2021-06-30.
- G. F. von Rudorff, S. N. Heinen, M. Bragato and O. A. von Lilienfeld, Machine Learning: Science and Technology, 2020, 1, 045026 Search PubMed
.
- E. W. C. Spotte-Smith, S. Blau, X. Xie, H. Patel, M. Wen, B. Wood, S. Dwaraknath and K. Persson, Sci. Data, 2021, 8, 203 CrossRef CAS PubMed
.
- S. M. Kearnes, M. R. Maser, M. Wleklinski, A. Kast, A. G. Doyle, S. D. Dreher, J. M. Hawkins, K. F. Jensen and C. W. Coley, J. Am. Chem. Soc., 2021, 143, 18820–18826 CrossRef CAS PubMed
.
- S. Stocker, G. Csányi, K. Reuter and J. T. Margraf, Nat. Commun., 2020, 11, 1–11 Search PubMed
.
- R. Roszak, W. Beker, K. Molga and B. A. Grzybowski, J. Am. Chem. Soc., 2019, 141, 17142–17149 CrossRef CAS PubMed
.
- S. Gallarati, R. Fabregat, R. Laplaza, S. Bhattacharjee, M. D. Wodrich and C. Corminboeuf, Chem. Sci., 2021, 12, 6879–6889 RSC
.
- Y. Bengio, Y. Lecun and G. Hinton, Commun. ACM, 2021, 64, 58–65 CrossRef
.
- G. Pesciullesi, P. Schwaller, T. Laino and J.-L. Reymond, Nat. Commun., 2020, 11, 1–8 Search PubMed
.
- Y. Zhang, L. Wang, X. Wang, C. Zhang, J. Ge, J. Tang, A. Su and H. Duan, Org. Chem. Front., 2021, 8, 1415–1423 RSC
.
- Reaxys chemical database, https://www.reaxys.com, accessed 2021-06-30 Search PubMed.
- CAS reaction collection, https://www.cas.org/cas-data/cas-reactions, accessed 2021-06-30 Search PubMed.
- H. Kraut, J. Eiblmaier, G. Grethe, P. Löw, H. Matuszczyk and H. Saller, J. Chem. Inf. Model., 2013, 53, 2884–2895 CrossRef CAS PubMed
.
- W. A. Warr, Mol. Inf., 2014, 33, 469–476 CrossRef CAS PubMed
.
- P. Schwaller, D. Probst, A. C. Vaucher, V. H. Nair, D. Kreutter, T. Laino and J.-L. Reymond, Nat. Mach. Intell., 2021, 3, 144–152 CrossRef
.
- T. Stuyver and C. W. Coley, 2021, arXiv preprint arXiv:2107.10402.
- R. P. Bell, Proc. Roy. Soc. Lond. Math. Phys. Sci., 1936, 154, 414–429 Search PubMed
.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1936, 32, 1333 RSC
.
- R. B. Woodward and R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 395–397 CrossRef CAS
.
- N. Schneider, D. M. Lowe, R. A. Sayle and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 39–53 CrossRef CAS PubMed
.
- G. M. Ghiandoni, M. J. Bodkin, B. Chen, D. Hristozov, J. E. Wallace, J. Webster and V. J. Gillet, J. Chem. Inf. Model., 2019, 59, 4167–4187 CrossRef CAS PubMed
.
- R. E. Carhart, D. H. Smith and R. Venkataraghavan, J. Chem. Inf. Comput. Sci., 1985, 25, 64–73 CrossRef CAS
.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed
.
- D. Kreutter, P. Schwaller and J.-L. Reymond, Chem. Sci., 2021, 12(25), 8648–8659 RSC
.
- P. Schwaller, B. Hoover, J.-L. Reymond, H. Strobelt and T. Laino, Sci. Adv., 2021, 7, eabe4166 CrossRef PubMed
.
- J. Devlin, M.-W. Chang, K. Lee and K. Toutanova, 2018, arXiv preprint arXiv:1810.04805.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS
.
- J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, ACS Cent. Sci., 2016, 2, 725–732 CrossRef CAS PubMed
.
- D. Duvenaud, D. Maclaurin, J. Aguilera-Iparraguirre, R. Gómez-Bombarelli, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, 2015, arXiv preprint arXiv:1509.09292.
- S. Kearnes, K. McCloskey, M. Berndl, V. Pande and P. Riley, J. Comput.-Aided Mol. Des., 2016, 30, 595–608 CrossRef CAS PubMed
.
-
T. Chen, S. Kornblith, M. Norouzi and G. Hinton, International conference on machine learning, 2020, pp. 1597–1607 Search PubMed
.
-
K. He, H. Fan, Y. Wu, S. Xie and R. B. Girshick, 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020, pp. 9726–9735 Search PubMed
.
- M. Caron, I. Misra, J. Mairal, P. Goyal, P. Bojanowski and A. Joulin, 2020, arXiv preprint arXiv:2006.09882.
-
J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International conference on machine learning, 2017, pp. 1263–1272 Search PubMed
.
- Y. You, T. Chen, Y. Sui, T. Chen, Z. Wang and Y. Shen, Adv. Neural Inf. Process. Syst. 10, 2020, 33, 5812–5823 Search PubMed
.
- Y. Fang, H. Yang, X. Zhuang, X. Shao, X. Fan and H. Chen, 2021, arXiv preprint arXiv:2103.13047.
- Y. Wang, J. Wang, Z. Cao and A. B. Farimani, 2021, arXiv preprint arXiv:2102.10056.
- D. Probst, P. Schwaller and J.-L. Reymond, ChemRxiv, 2021 Search PubMed
.
- X. Bresson and T. Laurent, 2017, arXiv preprint arXiv:1711.07553.
- K. Xu, W. Hu, J. Leskovec and S. Jegelka, 2018, arXiv preprint arXiv:1810.00826.
- P. Veličković, G. Cucurull, A. Casanova, A. Romero, P. Lio and Y. Bengio, 2017, arXiv preprint arXiv:1710.10903.
- D. Probst and J.-L. Reymond, J. Cheminf., 2020, 12, 1–13 Search PubMed
.
- RXNO Reaction Ontology, Royal Society of Chemistry, http://www.rsc.org/ontologies/RXNO/index.asp, accessed 2021-06-30 Search PubMed.
- M. Wen and E. B. Tadmor, npj Comput. Mater., 2020, 6, 124 CrossRef
.
- K. Adams, L. Pattanaik and C. W. Coley, 2021, arXiv preprint arXiv:2110.04383.
- E. Heid and W. H. Green, J. Chem. Inf. Model., 2021 Search PubMed
.
- C. A. Grambow, L. Pattanaik and W. H. Green, Sci. Data, 2020, 7, 1–8 CrossRef PubMed
.
- M. Liu, A. Grinberg Dana, M. S. Johnson, M. J. Goldman, A. Jocher, A. M. Payne, C. A. Grambow, K. Han, N. W. Yee and E. J. Mazeau, et al., J. Chem. Inf. Model., 2021, 61(6), 2686–2696 CrossRef CAS PubMed
.
- RDKit, Open-source cheminformatics, http://www.rdkit.org, accessed 2021-06-30 Search PubMed.
- E. L. First, C. E. Gounaris and C. A. Floudas, J. Chem. Inf. Model., 2012, 52, 84–92 CrossRef CAS PubMed
.
- A. Lin, N. Dyubankova, T. I. Madzhidov, R. I. Nugmanov, J. Verhoeven, T. R. Gimadiev, V. A. Afonina, Z. Ibragimova, A. Rakhimbekova and P. Sidorov,
et al.
, Mol. Inform., 2021, 2100138 CrossRef PubMed
.
-
M. Wang, L. Yu, D. Zheng, Q. Gan, Y. Gai, Z. Ye, M. Li, J. Zhou, Q. Huang, C. Ma, Z. Huang, Q. Guo, H. Zhang, H. Lin, J. Zhao, J. Li, A. J. Smola and Z. Zhang, ICLR Workshop on Representation Learning on Graphs and Manifolds, 2019 Search PubMed
.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein and L. Antiga,
et al.
, Adv. Neural Inf. Process. Syst., 2019, 8026–8037 Search PubMed
.
- D. P. Kingma and J. Ba, 2014, arXiv preprint arXiv:1412.6980.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed
.
- SMARTS – A Language for Describing Molecular Patterns, https://www.daylight.com/dayhtml/doc/theory/theory.smarts.html, accessed 2021-06-30 Search PubMed.
- SMARTS Examples, https://www.daylight.com/dayhtml_tutorials/languages/smarts/smarts_examples.html, accessed 2021-06-30 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: In-depth description of the models and model training, as well as extra results. See DOI: 10.1039/d1sc06515g |
| This journal is © The Royal Society of Chemistry 2022 |