X-ray scattering as an effective tool for characterizing liquid metal composite morphology†
Erin R.
Crater‡
 ac,
Ravi
Tutika‡
ac,
Ravi
Tutika‡
 bc,
Robert B.
Moore
bc,
Robert B.
Moore
 ac and
Michael D.
Bartlett
ac and
Michael D.
Bartlett
 *bc
*bc
aDepartment of Chemistry, Virginia Tech, Blacksburg, VA 24061, USA
bDepartment of Mechanical Engineering, Soft Materials and Structures Lab, Virginia Tech, Blacksburg, VA 24061, USA. E-mail: mbartlett@vt.edu
cMacromolecules Innovation Institute (MII), Virginia Tech, Blacksburg, VA 24061, USA
First published on 30th September 2022
Abstract
Quantitative analysis of particle size and size distribution is crucial in establishing structure–property relationships of composite materials. An emerging soft composite architecture involves dispersing droplets of liquid metal throughout an elastomer, enabling synergistic properties of metals and soft polymers. The structure of these materials is typically characterized through real-space microscopy and image analysis; however, these techniques rely on magnified images that may not represent the global-averaged size and distribution of the droplets. In this study, we utilize ultra-small angle X-ray scattering (USAXS) as a reciprocal-space characterization technique that yields global-averaged dimensions of eutectic gallium indium (EGaIn) alloy soft composites. The Unified fit and Monte Carlo scattering methods are applied to determine the particle size and size distributions of the liquid metal droplets in the composites and are shown to be in excellent agreement with results from real-space image analysis. Additionally, all methods indicate that the droplets are getting larger as they are introduced into composites, suggesting that the droplets are agglomerating or possibly coalescing during dispersion. This work demonstrates the viability of X-ray scattering to elucidate structural information about liquid metal droplets for material development for applications in soft robotics, soft electronics, and multifunctional materials.
1 Introduction
Soft, stretchable materials with unique combinations of thermal and electrical functionalities have the potential to play a pivotal role in diverse fields ranging from soft robotics to deformable electronics.1–3 These fields have seen tremendous growth in materials research and development in the past decade. In particular, soft, conformal material systems based on low melting point metal alloys have garnered attention as solid–liquid composite systems. These metals include room temperature liquids such as gallium, eutectic gallium indium (EGaIn) and Galinstan (GaInSn), as well as Field's metal that melts at 62 °C.4–7 The gallium-based liquid metal alloys are attractive due to their low toxicity and viscosity, high thermal and electrical conductivity, and a surface oxide which rapidly forms a nanometer thick shell on droplets.8 Liquid metal materials and their composites have enabled unprecedented combinations of high thermal conductivity,9–11 electrical conductivity,12 and self-healing abilities in soft elastomers.13,14 To increase their adaptation in industry and to promote further development at the academic level, methods to tune the material properties and expand characterization techniques to elucidate the governing morphological features are being explored.Soft composite systems have traditionally utilized rigid phase inclusions to enhance the functionality of the polymer matrix, including solid metal, ceramic, or carbon-based fillers. However, these rigid inclusions often result in undesirable changes to the bulk mechanical behavior, such as reduced extensibility and increased stiffness, owing to the interfacial incompatibilities and the compliance mismatch that arises from the different mechanical properties of the rigid filler and the soft matrix.15–17 These tradeoffs in mechanical and functional properties are common features of rigid phase inclusion-based polymer composites. Composites with liquid phase fillers can overcome this compliance mismatch for high stretchability and multifunctionality that is generally uncommon in polymer composites. As such, liquid filler composites are promising in applications of soft robotics, soft electronics, and reconfigurable matter that are pushing towards unconventional combinations of functional properties with soft and highly deformable mechanical responses. To this end, liquid metal-based soft composites have been developed, where the liquid metal droplets are dispersed in an elastomer matrix. In the composites, the droplets are dispersed in the liquid polymer phase through mixing or sonication and rapidly form an oxide shell during processing, which can help aid in dispersion without the need for surfactants or emulsifying agents.18–20 The composites are then cured, resulting in a solid elastomer phase which encapsulates the dispersed liquid metal droplets. With liquid phase inclusions, the composite architecture must be designed to achieve desirable properties. For example, in liquid metal-based soft composites, a number of droplet features can affect the ultimate material behavior, namely the droplet shape, size, loading, and size distribution.21–23 Therefore, characterization of droplet dimensions is critical to the design and development of soft composite materials.
In conventional composites, solid filler particle dimensions are often prescribed prior to composite fabrication; however, in liquid filler composites, liquid inclusions can change size and shape during material processing.24 Thus, in order to determine liquid droplet structures, post-fabrication analysis is required. Present techniques utilize imaging, either through optical or electron microscopy, and often image analysis to determine number-averaged size distributions of the inclusions.25–29 While these procedures are widely accepted, they are time-intensive and are only capable of analyzing a limited number of inclusions that are visible within a particular field of view. A technique for determining bulk, volume-averaged size distributions is currently lacking. Thus, an alternative droplet characterization technique that can be effectively applied to reliably analyze the composite morphology is essential.
As an alternative to microscopy analysis of composite materials, X-ray scattering has been extensively used to characterize the shape, size, and interfaces of fillers in a wide variety of matrix materials.30,31 Due to the reciprocal relationship between dimension and scattering angle, wide angle X-ray scattering (WAXS) provides structural information on the atomic scale (<1 nm), small angle X-ray scattering (SAXS) characterizes structures on the order of 1–100 nm, and ultra-small angle X-ray scattering (USAXS) characterizes structures up to several microns in size. Thus, by measuring scattered X-rays over a broad angular range, information spanning several decades of length scales can be acquired. Most reports of X-ray scattering of composites consist of solid particles embedded in a solid matrix.32–34 In contrast, examples of scattering by liquid metal (LM) fillers are sparse. Wide angle X-ray diffraction has been used to probe the composition of multi-phase LM materials,17,35,36 while SAXS has been used to confirm the presence of Ga particles in GaInSn37 and to study orientation effects in an LM-embedded fiber.38 A systematic morphological study of LM composites using X-ray scattering, particularly at length scales greater than 100 nm, is absent.
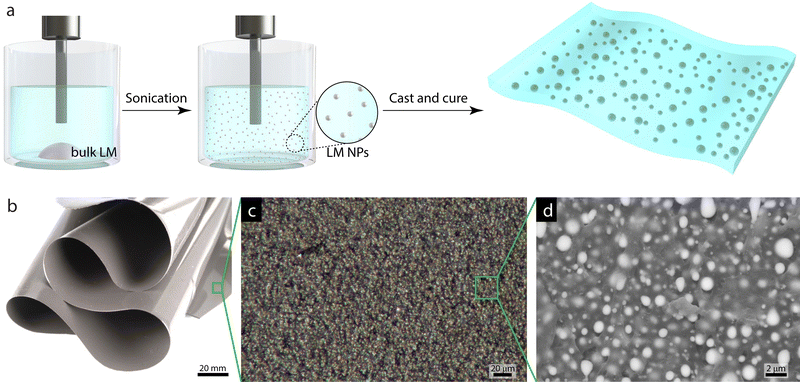
In this study, we report a systematic investigation of liquid metal soft composites using microscopy and X-ray scattering techniques. The purpose of this research was to demonstrate that X-ray scattering can be used as a complementary characterization tool to provide information about the droplet sizes and size distributions in liquid filler polymer composites. To study the effects of filler loading, soft composites were prepared with nanodroplets (∼300 nm) of EGaIn LM dispersed as a filler in a poly(dimethylsiloxane) (PDMS) elastomer matrix at different volume loadings (ϕ = 0.1% to ϕ = 20% LM) (Fig. 1(a) and (b)). The local, real-space morphologies of the composites were analyzed using optical and scanning electron microscopy (SEM) (Fig. 1(c) and (d)) and compared to the global morphologies of the composites from analysis of USAXS. Through this work, X-ray scattering is shown to be a facile route to obtaining global-averaged droplet size distributions and informing how materials processing can influence the droplet sizes. One outcome of this analysis is that as LM droplets prepared in solution are dispersed into elastomeric composites, we find increasing droplet sizes, suggesting that the droplets are agglomerating or possibly coalescing in the composites. Given the myriad of materials based on liquid metal, the broader impact of this work is to accelerate the development of soft, functional composites through the establishment of structure–property-processing relationships in liquid metal-based materials.
2 Methods
2.1 LM droplet and composite fabrication
Bulk LM was prepared by mixing Ga![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) In at a 3
In at a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio by mass, which forms the eutectic alloy EGaIn. LM droplets were prepared by sonicating ∼200 mg of bulk LM in 5 mL toluene solvent using a QSonica Q700 tip sonicator for 80 min at an amplitude of 30% (Fig. 1(a)). The LM–polymer composites were fabricated by dispersing the LM droplets in a two-component silicone elastomer (Dow Corning Sylgard 184). Initially, the silicone prepolymer was prepared by combining parts A (base) and B (curing agent) at a 10
1 ratio by mass, which forms the eutectic alloy EGaIn. LM droplets were prepared by sonicating ∼200 mg of bulk LM in 5 mL toluene solvent using a QSonica Q700 tip sonicator for 80 min at an amplitude of 30% (Fig. 1(a)). The LM–polymer composites were fabricated by dispersing the LM droplets in a two-component silicone elastomer (Dow Corning Sylgard 184). Initially, the silicone prepolymer was prepared by combining parts A (base) and B (curing agent) at a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio by mass in a planetary centrifugal mixer (FlackTek Speedmixer). The toluene was decanted from the droplet dispersion prior to adding the droplets to the prepolymer mixture. For higher LM loadings (ϕ = 10, 20%), multiple batches of sonicated droplets were combined to achieve the desired mass and then toluene was decanted. The prepolymer/LM droplet mixture was mixed again for ca. 20 min under vacuum to create an emulsion and to remove any residual toluene. The final mass of the mixture was measured and compared to the amount of LM droplets and prepolymer added to ensure complete toluene removal before casting. The final mixture was cast on a glass slide with a Universal applicator (ZUA 2000; Zehntner Testing Instruments), creating a composite film approximately 70 μm thick. The films were cured in a convection oven at 80 °C for 12 hours. All the fabrication procedures were carried out at ambient conditions.
1 ratio by mass in a planetary centrifugal mixer (FlackTek Speedmixer). The toluene was decanted from the droplet dispersion prior to adding the droplets to the prepolymer mixture. For higher LM loadings (ϕ = 10, 20%), multiple batches of sonicated droplets were combined to achieve the desired mass and then toluene was decanted. The prepolymer/LM droplet mixture was mixed again for ca. 20 min under vacuum to create an emulsion and to remove any residual toluene. The final mass of the mixture was measured and compared to the amount of LM droplets and prepolymer added to ensure complete toluene removal before casting. The final mixture was cast on a glass slide with a Universal applicator (ZUA 2000; Zehntner Testing Instruments), creating a composite film approximately 70 μm thick. The films were cured in a convection oven at 80 °C for 12 hours. All the fabrication procedures were carried out at ambient conditions.
2.2 Optical microscopy
The optical micrograph of the composite film was obtained using a Zeiss Axio Zoom v16 stereo microscope.2.3 Scanning electron microscopy characterization
To characterize the droplets prior to loading them into the PDMS matrix, a sample of the pristine droplets was prepared. The LM droplet sample was prepared by pipetting the LM droplet/toluene dispersion onto an adhesive carbon tape attached to an SEM standard pin stub and leaving overnight at room temperature to allow for toluene evaporation. To prepare the composite films for SEM analysis, a 500 μm layer of PDMS was first cast on a glass slide using the ZUA 2000 Universal applicator and cured at 80 °C for 2 hours. Next, the cured composite film was placed on the PDMS layer and then a second 500 μm layer of PDMS was cast on top and cured at 80 °C for another 2 hours. This procedure to sandwich the 70 μm composite film with thicker PDMS layers was performed to facilitate easy handling of the film during the subsequent steps. The sandwiched composite film was frozen in liquid nitrogen to crystallize the LM droplets and a razor blade was used to cut the sandwiched sample, exposing the interior of the LM composite. The sample cross-section was then attached to an adhesive carbon tape on the SEM standard pin stub and sputter coated with a Pt–Pd layer of ∼10 nm thickness prior to SEM analysis. The micrographs were obtained on a FEI Quanta 600 FEG-SEM in back-scattered electron (BSE) mode at a spot size of 4 and an accelerating voltage of 20 kV. The BSE mode was chosen as this provides enhanced contrast between the matrix and the droplets and allows for a higher penetration depth into the sample compared to the secondary electron mode (Fig. S1, ESI†). The droplet sizes in the SEM micrographs were analyzed using Fiji image analysis software. Details about the method used to analyze these images are discussed in Section 3.1.2.4 X-Ray scattering characterization
The LM droplets were prepared for X-ray scattering analysis by pipetting the LM droplet emulsion in toluene onto a polyimide substrate and allowing the toluene to evaporate at room temperature overnight. The LM droplet/polyimide sample was then mounted onto a solid sample plate for analysis. The composites were analyzed by mounting the as-prepared LM composite films onto a solid sample plate.Ultra-small-angle X-ray scattering (USAXS) measurements were conducted at beam line 9-ID-C at the Advanced Photon Source at Argonne National Laboratory (Lemont, Illinois).39,40 The USAXS/SAXS instrument was configured with an X-ray energy of 21 keV (λ = 0.5895 Å), an X-ray photon flux of ≈5 × 1012 mm−2 s−1, and a combined q range of 1 × 10−3 nm−1 to 1 nm−1 (q = 4π/λ sin(θ), where q is the scattering vector, λ is the wavelength and θ is 1/2 of the scattering angle). The Irena program was used to reduce the 2D USAXS detector profiles into 1D datasets (intensity vs. scattering vector, q) and to remove the effects of collimation-dependent instrumental smearing to generate desmeared USAXS scattering profiles.41 The observed scattering features of the desmeared USAXS profiles were analyzed using the Unified fit by Beaucage,42 and the maximum entropy size distribution method43 described in the Irena tool suite.41 The open-source McSAS software package developed by Breßler and coworkers was used to obtain Monte Carlo droplet size distributions from the desmeared USAXS data.44 Wide angle X-ray scattering experiments were performed to confirm the presence of the amorphous composite components using a Xenocs Xeuss 3.0 SAXS/WAXS, equipped with a GeniX 3D Cu HFVLF microfocus X-ray source with a wavelength of 0.154 nm (Cu Kα) (Fig. S2, ESI†). The sample-to-detector distance was 55 mm for WAXS, and the q-range was calibrated using a lanthanum hexaboride standard. The 2D WAXS patterns were obtained using a Dectris EIGER 4M detector and reduced into 1D intensity vs. q profiles using XSACT software. The scattering length densities (SLD) of PDMS and EGaIn were calculated using the NIST Scattering Length Density Calculator.
3 Results and discussion
3.1 SEM image analysis
Analysis of the SEM micrographs of the pristine LM droplets and the LM composites was performed to characterize the real-space morphology and to determine the droplet dimensions. The general method sequence is shown in Fig. 2 with the SEM micrographs for LM droplets in Fig. 2(a) and ϕ = 20% LM composite in Fig. 2(b). Using image analysis (Fiji software), the SEM images were first adjusted for brightness and contrast and converted into a binary format (Fig. 2(c) and (d)). The bright regions indicate LM droplets and the dark regions represent background or PDMS for the pristine droplets or composites, respectively. Next, the connected particles were separated, requiring careful observation of the pre- and post-processed images to ensure correct boundaries. The resulting isolated bright regions were considered individual droplets, and their areas were calculated by generating the best fit ellipse for the respective area. The ellipse fits are overlaid on the original micrograph as green outlines and represent the particles well (Fig. 2(e) and (f)), the green outline overlays for remaining LM composite SEM images are shown in Fig. S3 (ESI†). In each image, the major and minor axes of the fit ellipses were obtained with the droplet size represented by the major axis. The size distributions are shown as the frequency % droplets analyzed vs. major diameter (D), with representative examples of the LM droplets and ϕ = 20% LM composite shown in Fig. 2(g) and (h). A log-normal fit was performed on the plotted size distribution histograms, providing the mean diameter and standard deviation ranging from 344 ± 168 nm for the pristine LM droplets to 795 ± 330 nm for the ϕ = 20% LM composite. These results indicate that the initial measured LM droplet size of 300 nm increases to approximately 800 nm as the droplets are incorporated as a filler into the PDMS elastomer matrix. To determine why the droplets are larger in the composites compared to the precursor droplet dispersion, an experiment was conducted to determine when during the fabrication procedure the droplets increase in size. This was done by comparing the sizes of the pristine, sonicated droplets to the droplets in a 20% LM composite that used the same batch of LM droplets. The initial droplet diameter after sonication in toluene was 302 ± 202 nm and increased to 468 ± 306 nm upon shear-mixing in PDMS in a Flacktek speedmixer at 800 rpm for 15 min (SEM image analysis presented in Fig. S4, ESI†). Thus, the shear forces of mixing the LM droplets into the uncured matrix are likely responsible for the droplet size increase, by either aggregation or coalescence of smaller particles.3.2 X-ray scattering curves
Based on the size scale of the particles determined from SEM analysis and as noted in the introduction, it was hypothesized that these materials would display size-dependent scattering features from USAXS/SAXS. The morphological characterization of the LM droplets and composites over a wide range of length scales was performed using USAXS/WAXS. Desmeared USAXS profiles (intensity vs. scattering vector, q) of the LM droplets and composites at various LM loadings (ϕ = 0.1, 1, 2, 10, 20%) are shown in Fig. 3(a). This data compares the effects of droplet processing and filler loading on the X-ray scattering features of these materials. The unfilled PDMS matrix is not shown for comparison because the featureless weak scattering in the USAXS region is essentially identical to the background. Given the high contrast in electron density between EGaIn (SLD = 4.5 × 10−5 Å−2) and PDMS (SLD = 8.8 × 10−6 Å−2), the pristine LM droplets and composites show intense scattering, indicating structure on the nanometer to micron length scale (Fig. 3(a)).Because the scattering intensity depends not only on the form factor (size and shape) of the scattering entities, but also on the structure factor (spatial distribution of particles), it is important to identify the concentration regimes where the structure factor becomes significant.45 Concentration effects were studied by using the method described by McGlasson,45 and the concentration series was plotted as I/ϕ vs. q (Fig. 3(b)). The curves superimpose at intermediate q (0.01 nm−1 < q < 0.1 nm−1), consistent with composites from the same base structure (EGaIn droplets). However, the scattering curves of the ϕ = 10 and 20% LM composites show significantly reduced scattering intensity at low q (0.001 nm−1 < q < 0.003 nm−1) due to overlap of droplet/aggregate features consistent with a semidilute regime.45 As will be discussed later, due to the presence of interdroplet interactions in all of the composites, it is likely that the dilute regime is below ϕ = 0.1%, so all samples reside in the semidilute regime. In order to quantify characteristic dimensions from these data, the scattering profiles were quantitatively analyzed using a modified Unified fit approach and a Monte Carlo model.
3.3 Unified fit analysis
The Unified fit approach has been used extensively to quantitatively analyze scattering profiles from heterogeneous systems having hierarchical structure.42,46,47 In this model, the knee-like features (e.g., the slope change occurring around q = 0.01 nm−1 in the LM droplets profile, Fig. 3(a)) are interpreted as corresponding to the Guinier regime, defined by eqn (1) as: | (3.1) |
| I(q) = I0 + Bq−P | (3.2) |
The Unified fit approach by Beaucage combines contributions from Guinier and Porod regimes into a single level, i, consisting of a knee and a power law regime in the Unified equation (eqn (3)):42,50
 | (3.3) |
 .48 Therefore, the diameter of the corresponding spherical radius for the ϕ = 2% composite was determined as 570 ± 5 nm. While this size is larger than the mean size determined from image analysis (422 ± 200 nm), it is well known that analysis of the Guinier region tends to overestimate the mean particle size in polydisperse systems, as large particles dominate the scattering volume.51,52 The level 1 power law exponent P1 for the LM droplets was 4, suggesting a smooth gallium oxide interface at the surface of the spherical LM droplets.48 A smooth droplet surface is consistent with the SEM images of the droplets (Fig. 2). The parameters obtained from analysis on the samples are tabulated in Table 1 and the additional fits can be found in Fig. S5 (ESI†).
.48 Therefore, the diameter of the corresponding spherical radius for the ϕ = 2% composite was determined as 570 ± 5 nm. While this size is larger than the mean size determined from image analysis (422 ± 200 nm), it is well known that analysis of the Guinier region tends to overestimate the mean particle size in polydisperse systems, as large particles dominate the scattering volume.51,52 The level 1 power law exponent P1 for the LM droplets was 4, suggesting a smooth gallium oxide interface at the surface of the spherical LM droplets.48 A smooth droplet surface is consistent with the SEM images of the droplets (Fig. 2). The parameters obtained from analysis on the samples are tabulated in Table 1 and the additional fits can be found in Fig. S5 (ESI†).
 | ||
| Fig. 4 Two-level Unified fit of ϕ = 2% LM composite. Structural level 1 represents scattering from the primary droplets, and structural level 2 represents scattering from the mass-fractal LM aggregates. The fit parameters can be found in Table 1. | ||
| Composite | Level 1 Unified fit – primary particle | Level 2 Unified fit – mass fractal aggregate | |||||||
|---|---|---|---|---|---|---|---|---|---|
| G 1 × 106 (cm−1) | R g,1 (nm) | D 1 (nm) | B 1 × 10−6 (cm−1 Å −P1) | P 1 | G2 × 106 (cm−1) | R g,2 (nm) | B 2 (cm−1 Å −P2) | P 2 | |
| LM droplets | 2.0 ± 0.05 | 140 ± 2 | 360 ± 5 | 6.6 ± 0.01 | 4 | — | — | 1.3 ± 0.5 | 2.0 ± 0.01 |
| 0.1% LM | 1.5 ± 0.2 | 210 ± 7 | 540 ± 20 | 0.81 ± 0.004 | 4 | — | — | 0.030 ± 0.01 | 2.4 ± 0.04 |
| 1.0% LM | 20 ± 2 | 210 ± 5 | 540 ± 13 | 9.6 ± 0.05 | 4 | 2.5 ± 0.1 | 1500 ± 60 | 0.023 ± 0.01 | 2.8 ± 0.04 |
| 2.0% LM | 36 ± 1 | 220 ± 2 | 570 ± 5 | 18 ± 0.03 | 4 | 3.9 ± 0.1 | 1200 ± 10 | 0.28 ± 0.08 | 2.5 ± 0.03 |
At lower q (0.001 nm−1 < q < 0.007 nm−1), structural level 2 consists of a Guinier and power law region arising from scattering from larger aggregates of primary droplets (Fig. 4). The level 2 power law exponent, P2, which ranges from 2.4 to 2.8 in the ϕ = 0.1, 1, and 2% composites, is consistent with mass fractal aggregates comprised of mass-fractal particles arranged in a self-similar fashion.49 The level 2 Guinier region was used to determine the radius of gyration of the mass-fractal aggregates as Rg ≈ 1.2 μm. This aggregate size is in good agreement with the aggregates observed via SEM (Fig. 4 inset). Additionally, the degree of aggregation (the number of primary droplets per aggregate) was calculated from the fit parameters according to previously reported methods53,54 as approximately 100 droplets per aggregate. This is consistent with the number of droplets observed in the aggregates via SEM analysis and will be the focus of future studies related to the aggregation of droplets in LM composites.
The ϕ = 1% composite also displays a second Guinier and power law region at low q arising from scattering from the mass fractal aggregates (Fig. 3(b)). The approximate size of the aggregates, Rg,2, is 1.5 μm. This is again consistent with the SEM images that display aggregates of primary droplets approximately 1–2 μm in size (Fig. 8(b)). Although the ϕ = 0.1% LM composite displays a second level of power law scattering (Fig. 3(a)), a second Guinier region corresponding to the mass fractal aggregates is not observed. A reasonable explanation for the absence of this feature despite the presence of aggregates in the SEM images (Fig. 8(b)) is that the ϕ = 0.1% composite is just entering the semidilute regime, where only a small fraction of particles exist as aggregates with minimal contribution in the USAXS region.
| S(q) = 1/(1 + p × θ(q,η)) | (3.4) |
θ(q,η) = 3[sin(qη) − qη![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(qη)]/(qη)3 cos(qη)]/(qη)3 | (3.5) |
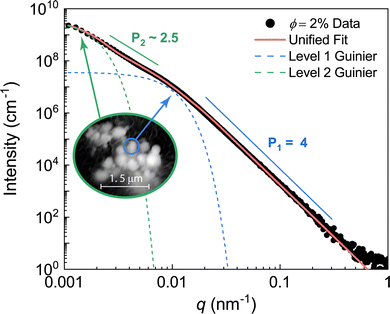
The scattering data of the ϕ = 10% and 20% LM composites were modelled using the Unified/Born–Green approach due to the distinct peak/knee observed near q = 0.005 nm−1 (Fig. 3(b)). An example fit to the ϕ = 20% data is shown in Fig. 5. The Guinier region was used to quantify the size of the primary droplets as D = 1.1 ± 0.2 μm. Additionally, the correlation length shown as the interdroplet distance in Fig. 5 inset was determined as 940 ± 20 nm. The Unified parameters for the ϕ = 10 and 20% composites are tabulated in Table 2. The packing factor, which ranges from 0 for uncorrelated systems to 5.92 for closely packed spheres,42 was determined as p = 0.62 ± 0.06 and 0.98 ± 0.09 for the ϕ = 10 and 20% composites, respectively. The slight increase in packing factor with increasing volume fraction is expected, and the relatively low packing factors are consistent with semidilute compositions.
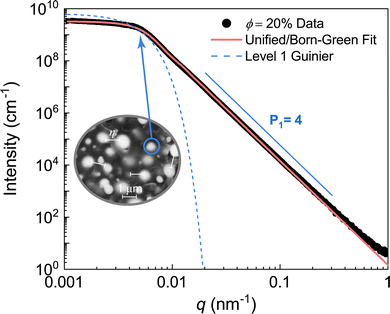 | ||
| Fig. 5 Unified fit of ϕ = 20% LM composite. The single structural level represents scattering from the primary droplets. The correlation length calculated from the Unified/Born–Green equation is on the order of 1 μm. The fit parameters can be found in Table 2. | ||
| Composite | Level 1 Unified/Born–Green – primary particle | ||||||
|---|---|---|---|---|---|---|---|
| G 1 × 109 (cm−1) | R g,1 (nm) | D 1 (nm) | B 1 × 10−4 (cm−1 Å−P1) | P 1 | η | Packing factor, p | |
| 10% LM | 6.5 ± 0.2 | 580 ± 10 | 1500 ± 30 | 0.57 ± 0.001 | 4 | 1500 ± 30 | 0.62 ± 0.06 |
| 20% LM | 6.5 ± 0.3 | 430 ± 8 | 1100 ± 20 | 1.4 ± 0.003 | 4 | 940 ± 20 | 0.98 ± 0.09 |
3.4 Particle size distribution methods
In addition to the mean particle size, the particle size distribution has been shown to impact the bulk properties of nanocomposites,56 and the presence of both large and small droplets is apparent in the SEM images (Fig. 2). To elucidate the distribution of droplet sizes present in the composites from the X-ray scattering profiles, several scattering models were applied and compared.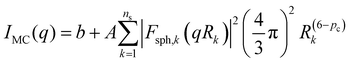 | (3.6) |
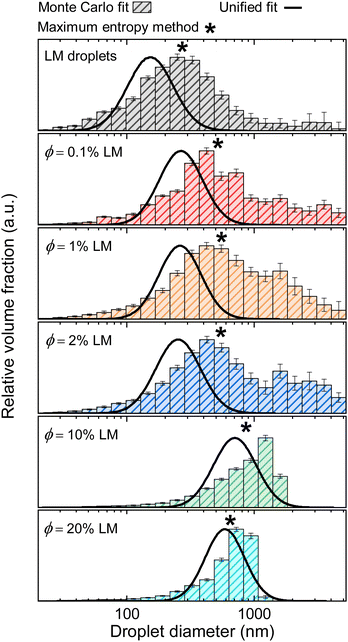
The volume-weighted MC droplet size distributions for the LM droplets and composites are shown in Fig. 6. For the LM droplets and the composites, the histograms reveal a broad distribution of droplet sizes. For the ϕ = 1 and 2% composites, an additional population of larger features appears, which is related to the intensity upturn at low q (Fig. 3). The histograms for the ϕ = 10 and 20% LM composites reveal an asymmetric distribution with a limiting size of D ≈ 1500 nm. The primary droplet diameter from the Monte Carlo method was chosen as the mode of the histograms (i.e., the most prevalent droplet size corresponding to the height of the histogram distribution) and is shown in Fig. 7. In agreement with the Unified size distribution, the MC method also reveals that the droplet sizes increase as the volume fraction of the filler is increased. The slight weighting of the Monte Carlo distributions towards larger droplet sizes can be attributed to the fact that the Unified method models a single level of the scattering profile, whereas the MC method modelled the whole scattering profile. The MC model fits are shown in Fig. S6 (ESI†). The maximum entropy method, another robust method for determining arbitrary size distributions of dilute scatterers,43,63,64 was also used to determine the droplet size distribution (Fig. S7 and S8, ESI†) and the median droplet size is denoted by an asterisk (*) in Fig. 6. Again, the maximum entropy method reveals reasonable agreement between the particle size distribution methods.
3.5 Comparison of SEM and X-ray scattering methods
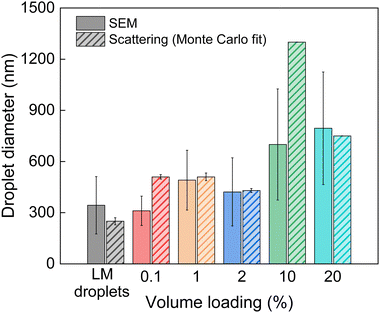
The droplet sizes obtained from the Monte Carlo method are compared to the sizes obtained from SEM image analysis in Fig. 7. This analysis of the prevalent droplet sizes demonstrates strong agreement between the different characterization methods.A comparison of the particle size distributions obtained from SEM image analysis and the Monte Carlo analysis of the scattering data is visualized in Fig. 8(a), where the size distributions from both SEM and Monte Carlo scattering analyses are plotted together, alongside representative SEM images for the corresponding specimen (Fig. 8(b)). One notable observation is that the results from the Monte Carlo analysis show the presence of scatterers larger than the individual droplets observed in SEM analysis. This observation can be attributed to the mass fractal aggregates that form through agglomeration of primary droplets. Again, this is seen in the SEM images of the low volume loading composites (ϕ = 0.1, 1, and 2%) that show distinct agglomeration (Fig. 8(b)). From the comparison in Fig. 6 and 7, it is clear that X-ray scattering is capable of detecting the structures of LM composites across many length scales and revealing size distributions that would require many SEM images to elucidate. While the structure-free Monte Carlo method is typically applied for dilute systems, it showed excellent agreement with the Unified model and maximum entropy size distribution methods. The small discrepancies between SEM image analysis and X-ray scattering techniques can be understood by microscopy being a surface technique, providing only a local two-dimensional description of the morphology, whereas scattering is a bulk measurement technique providing more information as it relates to the bulk of the sample.
4 Conclusions
This work details the characterization of LM composite morphologies through a combination of scanning electron microscopy and X-ray scattering. Results from USAXS were interpreted using the Unified and Unified/Born–Green approaches to characterize the droplet dimensions, the mass-fractal aggregates, and the interdroplet interactions. The Unified, Monte Carlo, and maximum entropy particle size distribution methods were used to characterize the primary droplet and aggregate size distributions and revealed the presence of droplets spanning many length scales in size. The results from each method clearly reveal that the LM droplet sizes in the composites are slightly larger compared to the pristine droplets, which suggests that smaller droplets are agglomerating and possibly coalescing to form larger droplets or clusters during the fabrication process. Future studies with varying mixing conditions and higher volume loading composites could provide more insight on coalescing mechanisms. For additional future studies, we will use this X-ray scattering method to systematically study the effects of a variety of important processing parameters such as mixing protocols, solvent choice, and interfacial compatibility on the dimensions of liquid metal composites.The high electron density of EGaIn and other liquid metals, relative to the polymer matrix, positions X-ray scattering to be a sensitive and effective tool to study the morphology of a variety of nano-structured LM-containing systems. For example, X-ray scattering can be utilized to study the shape and size transformation of LM droplets in solutions,65 and soft robots.66 This method will be particularly useful in light of recent advancements of techniques to carefully control the size and distribution of the droplets in the 1–100 nm size range.67 We anticipate the USAXS/SAXS/WAXS technique,68,69 in combination with the scattering models presented here, will be attractive methods to non-destructively characterize global-averaged size distributions and polydispersity in many of these widely studied and utilized materials.
Author contributions
E. R. C., R. T., R. B. M., and M. D. B. designed research; E. R. C. and R. T. performed research; E. R. C., R. T., R. B. M, and M. D. B. analyzed data; E. R. C., R. T., R. B. M, and M. D. B. wrote and revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. D. B. and R. T. acknowledge support from NSF (No. CMMI-2054409) and DARPA YFA (D18AP00041). Purchase of the Xenocs Xeuss 3.0 SAXS/WAXS instrument used to obtain results included in this publication was supported by the National Science Foundation under the award DMR MRI 2018258. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. The authors acknowledge support from the Institute for Critical Technology and Applied Science (ICTAS) at Virginia Tech. This work was performed in part at the Nanoscale Characterization and Fabrication Laboratory, which is supported by the Virginia Tech National Center for Earth and Environmental Nanotechnology Infrastructure (NanoEarth), a member of the National Nanotechnology Coordinated Infrastructure (NNCI), supported by NSF (ECCS 1542100 and ECCS 2025151). The authors would like to thank Dr Jan Ilavsky and acknowledge the use of beamline 9ID-C for all USAXS/SAXS experiments. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.References
- J. A. Rogers, T. Someya and Y. Huang, Science, 2010, 327, 1603–1607 CrossRef CAS PubMed
.
- C. J. Thrasher, Z. J. Farrell, N. J. Morris, C. L. Willey and C. E. Tabor, Adv. Mater., 2019, 31, 1903864 CrossRef CAS
.
- M. Wehner, R. L. Truby, D. J. Fitzgerald, B. Mosadegh, G. M. Whitesides, J. A. Lewis and R. J. Wood, Nature, 2016, 536, 451–455 CrossRef CAS PubMed
.
- R. W. Style, R. Tutika, J. Y. Kim and M. D. Bartlett, Adv. Funct. Mater., 2021, 31, 2005804 CrossRef CAS
.
- I. D. Tevis, L. B. Newcomb and M. Thuo, Langmuir, 2014, 30, 14308–14313 CrossRef CAS PubMed
.
- D. Hwang, E. J. Barron III, A. T. Haque and M. D. Bartlett, Sci. Robot., 2022, 7, eabg2171 CrossRef PubMed
.
- S. Sharifi, A. Mohammadi Nasab, P.-E. Chen, Y. Liao, Y. Jiao and W. Shan, Adv. Eng. Mater., 2022, 2101533 CrossRef CAS
.
- M. D. Dickey, R. C. Chiechi, R. J. Larsen, E. A. Weiss, D. A. Weitz and G. M. Whitesides, Adv. Funct. Mater., 2008, 18, 1097–1104 CrossRef CAS
.
- S. H. Jeong, S. Chen, J. Huo, E. K. Gamstedt, J. Liu, S.-L. Zhang, Z.-B. Zhang, K. Hjort and Z. Wu, Sci. Rep., 2015, 5, 18257 CrossRef CAS PubMed
.
- M. I. Ralphs, N. Kemme, P. B. Vartak, E. Joseph, S. Tipnis, S. Turnage, K. N. Solanki, R. Y. Wang and K. Rykaczewski, ACS Appl. Mater. Interfaces, 2018, 10, 2083–2092 CrossRef CAS
.
- A. T. Haque, R. Tutika, R. L. Byrum and M. D. Bartlett, Adv. Funct. Mater., 2020, 30, 2000832 CrossRef CAS
.
- T. V. Neumann, E. G. Facchine, B. Leonardo, S. Khan and M. D. Dickey, Soft Matter, 2020, 16, 6608–6618 RSC
.
- E. J. Markvicka, M. D. Bartlett, X. Huang and C. Majidi, Nat. Mater., 2018, 17, 618–624 CrossRef CAS PubMed
.
- R. Tutika, A. T. Haque and M. D. Bartlett, Commun. Mater., 2021, 2, 1–8 CrossRef
.
- P.-A. Toulemonde, J. Diani, P. Gilormini, N. Desgardin and R. Neviere, J. Mater. Sci., 2017, 52, 878–888 CrossRef CAS
.
- R. J. Young, M. Liu, I. A. Kinloch, S. Li, X. Zhao, C. Vallés and D. G. Papageorgiou, Compos. Sci. Technol., 2018, 154, 110–116 CrossRef CAS
.
- R. Tutika, S. H. Zhou, R. E. Napolitano and M. D. Bartlett, Adv. Funct. Mater., 2018, 28, 1804336 CrossRef
.
- T. A. Pozarycki, D. Hwang, E. J. Barron III, B. T. Wilcox, R. Tutika and M. D. Bartlett, Small, 2022, 2203700 CrossRef
.
- E. J. Krings, H. Zhang, S. Sarin, J. E. Shield, S. Ryu and E. J. Markvicka, Small, 2021, 17, 2104762 CrossRef CAS
.
- A. T. Haque, R. Tutika, M. Gao, A. Martinez, J. Mills, J. A. Clement, J. Gao, M. Tabrizi, M. R. Shankar, Q. Pei and M. D. Bartlett, Multifunct. Mater., 2020, 3, 044001 CrossRef CAS
.
- A. Mohammadi Nasab, T. L. Buckner, B. Yang and R. Kramer-Bottiglio, Adv. Mater. Technol., 2021, 2100920 Search PubMed
.
- R. Tutika, S. Kmiec, A. T. Haque, S. W. Martin and M. D. Bartlett, ACS Appl. Mater. Interfaces, 2019, 11, 17873–17883 CrossRef CAS PubMed
.
- C. Pan, E. J. Markvicka, M. H. Malakooti, J. Yan, L. Hu, K. Matyjaszewski and C. Majidi, Adv. Mater., 2019, 31, 1900663 CrossRef PubMed
.
- A. Haake, R. Tutika, G. M. Schloer, M. D. Bartlett and E. J. Markvicka, Adv. Mater., 2022, 2200182 CrossRef CAS PubMed
.
- T. R. Lear, S.-H. Hyun, J. W. Boley, E. L. White, D. H. Thompson and R. K. Kramer, Extreme Mech. Lett., 2017, 13, 126–134 CrossRef
.
- A. Hajalilou, A. F. Silva, P. A. Lopes, E. Parvini, C. Majidi and M. Tavakoli, Adv. Mater. Interfaces, 2022, 2101913 CrossRef CAS
.
- F. Krisnadi, L. L. Nguyen, J. Ma, M. R. Kulkarni, N. Mathews and M. D. Dickey, Adv. Mater., 2020, 32, 2001642 CrossRef CAS
.
- Y. Han, L.-E. Simonsen and M. H. Malakooti, Adv. Energy Mater., 2022, 12, 2201413 CrossRef CAS
.
- M. H. Malakooti, M. R. Bockstaller, K. Matyjaszewski and C. Majidi, Nanoscale Adv., 2020, 2, 2668–2677 RSC
.
- A.-C. Genix and J. Oberdisse, Curr. Opin. Colloid Interface Sci., 2015, 20, 293–303 CrossRef CAS
.
- P. Fratzl, J. Appl. Crystallogr., 2003, 36, 397–404 CrossRef CAS
.
- M. Takenaka, Polym. J., 2013, 45, 10–19 CrossRef CAS
.
- N. S. Hmeidat, R. C. Pack, S. J. Talley, R. B. Moore and B. G. Compton, Addit. Manuf., 2020, 34, 101385 CAS
.
- G. D. Barber, B. H. Calhoun and R. B. Moore, Polymer, 2005, 46, 6706–6714 CrossRef CAS
.
- J. Tang, X. Zhao, J. Li, R. Guo, Y. Zhou and J. Liu, ACS Appl. Mater. Interfaces, 2017, 9, 35977–35987 CrossRef CAS
.
- Z.-F. Gao, L.-L. Zheng, W.-L. Fu, L. Zhang, J.-Z. Li and P. Chen, Nanomaterials, 2022, 12, 1177 CrossRef CAS PubMed
.
- I. A. de Castro, A. F. Chrimes, A. Zavabeti, K. J. Berean, B. J. Carey, J. Zhuang, Y. Du, S. X. Dou, K. Suzuki, R. A. Shanks, R. Nixon-Luke, G. Bryant, K. Khoshmanesh, K. Kalantar-zadeh and T. Daeneke, Nano Lett., 2017, 17, 7831–7838 CrossRef PubMed
.
- L. Zheng, M. Zhu, B. Wu, Z. Li, S. Sun and P. Wu, Sci. Adv., 2021, 7, eabg4041 CrossRef CAS PubMed
.
- J. Ilavsky, F. Zhang, R. N. Andrews, I. Kuzmenko, P. R. Jemian, L. E. Levine and A. J. Allen, J. Appl. Crystallogr., 2018, 51, 867–882 CrossRef CAS PubMed
.
- J. Ilavsky, F. Zhang, A. Allen, L. Levine, P. Jemian and G. Long, Metall. Mater. Trans. A, 2013, 44, 68–76 CrossRef CAS
.
- J. Ilavsky and P. R. Jemian, J. Appl. Crystallogr., 2009, 42, 347–353 CrossRef CAS
.
- G. Beaucage, J. Appl. Crystallogr., 1995, 28, 717–728 CrossRef CAS
.
- J. Potton, G. Daniell and B. Rainford, J. Appl. Crystallogr., 1988, 21, 891–897 CrossRef
.
- I. Breßler, B. R. Pauw and A. F. Thünemann, J. Appl. Crystallogr., 2015, 48, 962–969 CrossRef PubMed
.
- A. McGlasson, K. Rishi, G. Beaucage, M. Chauby, V. Kuppa, J. Ilavsky and M. Rackaitis, Macromolecules, 2020, 53, 2235–2248 CrossRef CAS
.
- S. J. Talley, S. L. Vivod, B. A. Nguyen, M. A. B. Meador, A. Radulescu and R. B. Moore, ACS Appl. Mater. Interfaces, 2019, 11, 31508–31519 CrossRef CAS PubMed
.
- A. Mulderig, G. Beaucage, K. Vogtt, H. Jiang and V. Kuppa, J. Aerosol Sci., 2017, 109, 28–37 CrossRef CAS
.
-
R.-J. Roe
et al.
, Methods of X-ray and neutron scattering in polymer science, Oxford University Press on Demand, 2000 Search PubMed
.
- G. Beaucage, J. Appl. Crystallogr., 1996, 29, 134–146 CrossRef CAS
.
- G. Beaucage and D. W. Schaefer, J. Non-Cryst. Solids, 1994, 172, 797–805 CrossRef
.
- A. Hasmy, R. Vacher and R. Jullien, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(2), 1305–1308 CrossRef CAS
.
- T. P. Rieker, S. Misono and F. Ehrburger-Dolle, Langmuir, 1999, 15, 914–917 CrossRef CAS
.
- G. Beaucage, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70(3), 031401 CrossRef CAS PubMed
.
- G. Beaucage, Biophys. J., 2008, 95, 503–509 CrossRef CAS PubMed
.
- G. Beaucage, T. Ulibarri, E. Black and D. Schaefer, ACS Symp. Ser., 1995, 97–111 CrossRef CAS
.
- J. J. Burgos-Marmol and A. Patti, Polymer, 2017, 113, 92–104 CrossRef CAS
.
- G. Beaucage, H. K. Kammler and S. E. Pratsinis, J. Appl. Crystallogr., 2004, 37, 523–535 CrossRef CAS
.
- J. S. Pedersen, J. Appl. Crystallogr., 1994, 27, 595–608 CrossRef
.
- B. R. Pauw, J. S. Pedersen, S. Tardif, M. Takata and B. B. Iversen, J. Appl. Crystallogr., 2013, 46, 365–371 CrossRef CAS PubMed
.
- B. R. Pauw, C. Kästner and A. F. Thünemann, J. Appl. Crystallogr., 2017, 50, 1280–1288 CrossRef CAS PubMed
.
- Y. Yang, S. Liao, Z. Luo, R. Qi, N. Mac Fhionnlaoich, F. Stellacci and S. Guldin, Nanoscale, 2020, 12, 12007–12013 RSC
.
- J. Maes, N. Castro, K. De Nolf, W. Walravens, B. Abécassis and Z. Hens, Chem. Mater., 2018, 30, 3952–3962 CrossRef CAS
.
- P. Jemian, J. Weertman, G. Long and R. Spal, Acta Metall. Mater., 1991, 39, 2477–2487 CrossRef CAS
.
- J. Skilling and R. Bryan, Mon. Not. R. Astron. Soc., 1984, 211, 111 CrossRef
.
- Y. Lin, Y. Liu, J. Genzer and M. D. Dickey, Chem. Sci., 2017, 8, 3832–3837 RSC
.
- X. Wang, R. Guo and J. Liu, Adv. Mater. Technol., 2019, 4, 1800549 Search PubMed
.
- F. Yu, J. Xu, H. Li, Z. Wang, L. Sun, T. Deng, P. Tao and Q. Liang, Prog. Nat. Sci.: Mater. Int., 2018, 28, 28–33 CrossRef CAS
.
- G. R. Mitchell and A. Odajima, Polym. J., 1984, 16, 351–357 CrossRef CAS
.
- Q. Yu, F. M. Guo, X. D. Wang, K. Stahl, Y. Ren, Q. P. Cao, D. X. Zhang and J. Z. Jiang, J. Mol. Liq., 2019, 293, 111464 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00796g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |