Revisiting ultrasmall phosphine-stabilized rhodium-doped gold clusters AunRh (n = 5, 6, 7, 8): geometric, electronic, and vibrational properties†
Jenica Marie L.
Madridejos
 ab,
Jason F.
Alvino
ab,
Jason F.
Alvino
 a,
Yunpeng
Lu
a,
Yunpeng
Lu
 b,
Vladimir B.
Golovko
b,
Vladimir B.
Golovko
 c and
Gregory F.
Metha
c and
Gregory F.
Metha
 *a
*a
aDepartment of Chemistry, The University of Adelaide, South Australia 5005, Australia. E-mail: greg.metha@adelaide.edu.au
bSchool of Chemistry, Chemical Engineering and Biotechnology, Nanyang Technological University, Singapore 639798, Singapore
cThe MacDiarmid Institute for Advanced Materials and Nanotechnology, Department of Chemistry, University of Canterbury, Christchurch, 8140, New Zealand
First published on 24th January 2024
Abstract
Incorporation of other transition metals in Au nanoclusters has been thriving recently due to its effect on their electronic and photophysical properties. Here, the ultrasmall phosphine-stabilized Rh-doped gold clusters AunRh (n = 5, 6, 7, 8), with metal core structures represented as fragments of a rhodium-centered icosahedron, are considered. The geometric and electronic properties of these nanoclusters are revisited and analyzed using density functional theory (DFT). Moreover, infrared spectra are simulated to identify the effects of Rh doping on the clusters through vibrational properties. Peaks are assigned to breathing-like normal modes for all AuRh clusters except for Au8Rh, likely due to the presence of bound Cl ligands. Unlike their pure gold core counterparts, the % motions of both Au and Rh atoms are lower in the mixed metal clusters, suggesting more restrained metal cores by rhodium, which could result in other novel physical and chemical properties not hitherto discovered.
1 Introduction
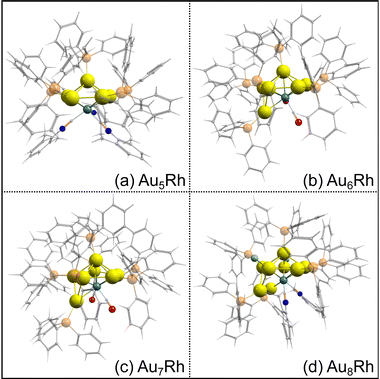
Ligand-stabilized atomically-precise metal nanoclusters have generated tremendous interest over the recent years because of their distinct physicochemical properties and potential applications.1 A large number of structurally determined nanoclusters with defined elemental compositions have been prepared in the past decade, with various ligands used for stabilization. In ultrasmall gold nanoparticles, there has been an increasing interest in the understanding of transition bimetallic clusters. Doping a different transition metal atom into a metal cluster dramatically changes the electronic properties and catalytic behaviour of the host cluster.2–5 There have been extensive theoretical and experimental studies on noble metal clusters such as Au and Ag, most especially due to their distinctive chemical properties. In early work on gas phase cationic AunXm+ clusters (X = Cu, Al, Y, and In), the cluster geometries and electronic shell were shown to depend on the nature of dopant atoms.6 Heinebrodt et al. described the binding patterns of Au with Al, In, and Cs, wherein charge transfer takes place between Au and In while ionic interaction prevails between Au and Cs.7 Additionally, anionic binary AunM− clusters (M = Pd, Ni, Zn, Cu, and Mg) were explored by Koyasu et al. using anion photoelectron spectroscopy.8 Density functional theory (DFT) studies of neutral bimetallic gold clusters have also been reported for Ni, Pd and Pt,9 Fe,10 Ag and Cu,11 Ti,12 Sc,13 and Rh.14 Buendia et al. reported the experimental and theoretical photoelectron (PES) and IR spectra of neutral and anionic non-ligated AunRhm (n = 1–7 and m = 1–2) clusters in vacuum.15 Additionally, mechanistic insight into the catalyzed hydrogenation reaction revealed that the activation barrier of monorhodium-doped gold clusters is reduced compared to pure gold clusters.3 Notably, transition metal-doped gold clusters have been comprehensively studied due to their synergistic effects on catalysis.1,16 Tsukuda and co-workers reported the use of Pd- and Rh-doped Au34 superatom for hydrogenation catalysis wherein Rh-doped Au:PVP cluster proved to be superior.4,5 Recently, doping metals onto Au13 nanoclusters has been observed to enhance quantum yield with an increased HOMO–LUMO gap and was reported to act as more efficient and stable photocatalysts.17Decades ago, Bott et al. reported a series of ultrasmall gold-rhodium clusters AunRh clusters (n = 5–8) with triphenylphosphine groups as their main ligands: [Au5Rh(PPh3)5(C9H9N)3]2+, [Au6Rh(PPh3)6(CO)2]+, [Au7Rh(PPh3)7(CO)2]2+, and [Au8Cl2(PPh3)6Rh(C9H9N)2]+ (hereafter referred to as Au5Rh, Au6Rh, Au7Rh, and Au8Rh, respectively).18 Their gold-rhodium cores were all found to be structurally represented as fragments of the rhodium-centered icosahedron in Fig. 1. Based on the structures of the AunRh core alone, the lower-numbered gold-rhodium clusters could be obtained from the sequential removal of Au(PPh3) moieties of the Au8Rh cluster. In this study, we analyze the geometric and electronic structures of this series of AunRh clusters using density functional theory based on their experimental crystal structures.
 | ||
| Fig. 1 The structural relationship among the AuRh clusters synthesized by Bott et al.18 The idealized metal core geometries are shown as fragments of a centered icosahedron with rhodium atom (turquoise) at the center. | ||
Takano et al. have reported the importance of core rigidification by the ligands in the effective photoluminescence of Ru-doped Au12 clusters.19 Metal core motion and ligand suppression can be analyzed using infrared spectroscopy by detecting the vibrational modes of key functional groups. Several studies have reported the IR spectra of ligand-stabilized gold clusters,20–23 but we are not aware of any involving the AunRh clusters. This present work extends our previous far-IR and computational studies of atomically precise gold-based clusters20,21 and ruthenium-based clusters24 to ligand-protected bimetallic AunRh clusters (n = 5–8) focused on low frequency vibrational modes (λ = 50–450 cm−1).
2 Computational details
Geometry optimization and harmonic vibrational frequency calculations (including force constant, k) of the fully-ligated Au5Rh, Au6Rh Au7Rh, and Au8Rh clusters were performed using M06 density functional25 with all atoms treated with the LANL2DZ basis set and related effective core potentials (ECP)26 using the Gaussian 09 suite of programs.27 This level of theory has been used for similar metal cluster systems previously, and has shown good agreement to experimental far IR spectra.20,24 Initial geometries of Au5Rh (CSD Refcode KOFTOO), Au7Rh (CSD Refcode KOFVAC), Au8Rh (CSD Refcode JAPWOM) were taken from previously reported X-ray crystal structures of the synthesized clusters deposited in the Cambridge Crystallographic Database.28 The initial structure of Au6Rh was based on the description of Bott et al. wherein one AuPPh3 unit in an equatorial position of Au7Rh is removed.18 Counter ions were removed, with the appropriate number of electrons removed from the calculations to balance the charge and no symmetry constraints were used in the calculations. After optimization, a frequency calculation was performed to confirm that the optimized geometry is a true minimum without any imaginary frequencies. To obtain the simulated IR spectra, all peaks were convoluted with a Gaussian line shape function with 8 cm−1 full width at half-maximum (FWHM). The Cartesian coordinates of the optimized structures for these four clusters are also provided in the ESI.†3 Results and discussion
3.1 Geometric parameters and ligand binding energies
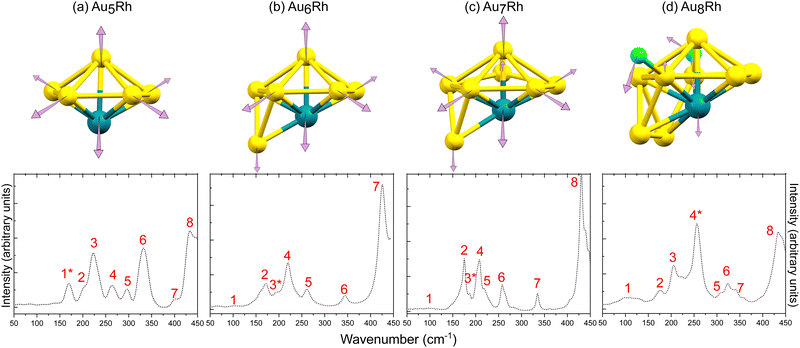
The optimized structures of the AunRh clusters are shown in Fig. 2. Both Au6Rh and Au7Rh have 2 carbonyl ligands attached to the Rh atom while Au5Rh and Au8Rh have 3 and 2 isocyanide-based xylyl ligands attached on their central Rh atom, respectively. The Au8Rh also has additional Cl atoms attached to two Au atoms. For all AunRh clusters in this study, the ligands attached to the Rh atom are known to be easily removed. Moreover, the PPh3 ligands attached on the Au atoms also require lower temperature to be removed than their thiolate counterparts.29 The DFT-optimized structures have longer bond lengths when compared to the crystal structures because the experimental geometries are tightly-packed in condensed phase rather than in “gas-phase” of the calculations. Even so, a close match between the optimized geometries and experimental crystal structures is observed for the gold-rhodium clusters (Fig. S1, ESI†).To calculate the binding energies of the ligands in Table 1, we use the following equation:
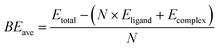 | (1) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ligands of Rh atom have similar average binding energies to PPh3.
O ligands of Rh atom have similar average binding energies to PPh3.
| Cluster | BEave of Rh-bound ligands | BEave of PPh3 |
|---|---|---|
| Au5Rh | 51.2 (xylyl) | 56.9 |
| Au6Rh | 51.3 (CO) | 43.6 |
| Au7Rh | 49.7 (CO) | 59.1 |
| Au8Rh | 56.8 (xylyl) | 48.5 |
3.2 Electronic structure
The AunRh clusters offer a specific perspective into the contribution of Rh to the electronic structure. Tsukuda and co-workers summarized the effect of doping on the spherical superatoms of gold clusters using the jellium model.36 When dopants are more electronegative (such as Pt, Pd, and Rh) than gold, the superatomic orbitals are destabilized due to reductions of the effective positive charge of the core, resulting in an upshift to their energy levels. This is only observed when icosahedral Au cores are considered. However, the AunRh clusters presented here are fragments of a centered icosahedron, Au13, as shown in Fig. 1. Therefore, we can also consider z-axis compression based on the closed-shell electron count of Hakkinen's superatom concept (SAC) equation.37 If Rh is considered as another Au atom, we expect the following electron count for the AunRh clusters: 4e (Au5Rh) and 6e (Au6Rh, Au7Rh, Au8Rh). Thus, the Au5Rh cluster is expected to adopt a prolate shape with z-axis expansion while the others have an oblate shape with z-axis compression. This in turn results in an orbital with 1pz character for the Au5Rh HOMO and 1px and 1py character for the LUMO and LUMO+1, respectively. On the other hand, 6e clusters should exhibit 1px and 1py characteristics for HOMO and HOMO–1, and 1pz and 1d character for the LUMO and LUMO+1 orbitals.The topological plots of the frontier molecular orbitals (FMO) of the AunRh clusters are shown in Fig. 3. All FMO plots reveal that the HOMO−1, HOMO, LUMO, and LUMO+1 are mainly localized on the AuRh core (Tables S1 and S2, ESI†). The contribution of Rh in the HOMO of Au5Rh is significantly higher than the other clusters, with approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Au and Rh contributions to the orbital based on the results of three different partition methods. Interestingly, the shapes of the frontier MOs of Au5Rh deviate from the expected trend based on SAC electron count and z-axis expansion discussed above. The HOMO−1, HOMO, and LUMO all have 1p characteristics while the LUMO+1 displays 1d character in Au5Rh, similar to Au6Rh and Au7Rh. This suggests an effect from the heteroatom on the electronic properties of the Au5Rh cluster, wherein the Rh contribution on the HOMO is evident by the presence of its δ orbitals. The Au8Rh cluster has similar FMO characteristics as the butterfly structure of [Au9(PPh3)8]3+,38 wherein the LUMO has 1d character while the LUMO+1 has 1p character, evidently similar to the previous MO calculations presented by Mingos and co-workers.39 Both the structures of Au8Rh and the butterfly isomer of Au9 are toroidal rather than spherical in shape such as in the case of the crown isomer of Au9 and Au8Pd.38–40 This difference in the bonding pattern causes the 1pz orbital to be higher in energy, making it unavailable for skeletal bonding and subsequently deviating from the expected MO trend based on electron count. Additionally, the contribution of δ orbitals from Rh stabilizes the LUMO+1 (1pz) orbital of Au8Rh. The trend of the HOMO–LUMO energy gaps of the AuRh clusters is also consistent with the colors of the synthesized crystals. The Au7Rh and Au8Rh clusters both have a relatively low calculated energy gap of ∼3.20 eV and both exhibit a red color. On the other hand, Au6Rh has an orange-like color while Au5Rh has a distinct yellow color, and with both having larger HOMO–LUMO energy gaps calculated to be 3.42 and 3.82 eV, respectively.
1 ratio of Au and Rh contributions to the orbital based on the results of three different partition methods. Interestingly, the shapes of the frontier MOs of Au5Rh deviate from the expected trend based on SAC electron count and z-axis expansion discussed above. The HOMO−1, HOMO, and LUMO all have 1p characteristics while the LUMO+1 displays 1d character in Au5Rh, similar to Au6Rh and Au7Rh. This suggests an effect from the heteroatom on the electronic properties of the Au5Rh cluster, wherein the Rh contribution on the HOMO is evident by the presence of its δ orbitals. The Au8Rh cluster has similar FMO characteristics as the butterfly structure of [Au9(PPh3)8]3+,38 wherein the LUMO has 1d character while the LUMO+1 has 1p character, evidently similar to the previous MO calculations presented by Mingos and co-workers.39 Both the structures of Au8Rh and the butterfly isomer of Au9 are toroidal rather than spherical in shape such as in the case of the crown isomer of Au9 and Au8Pd.38–40 This difference in the bonding pattern causes the 1pz orbital to be higher in energy, making it unavailable for skeletal bonding and subsequently deviating from the expected MO trend based on electron count. Additionally, the contribution of δ orbitals from Rh stabilizes the LUMO+1 (1pz) orbital of Au8Rh. The trend of the HOMO–LUMO energy gaps of the AuRh clusters is also consistent with the colors of the synthesized crystals. The Au7Rh and Au8Rh clusters both have a relatively low calculated energy gap of ∼3.20 eV and both exhibit a red color. On the other hand, Au6Rh has an orange-like color while Au5Rh has a distinct yellow color, and with both having larger HOMO–LUMO energy gaps calculated to be 3.42 and 3.82 eV, respectively.
 | ||
| Fig. 3 The plots of frontier molecular orbital (HOMO−1, HOMO, LUMO, LUMO+1) of Au5Rh, Au6Rh, Au7Rh, and Au8Rh clusters as calculated by M06/LANL2DZ with an isosurface value of 0.02 a.u. | ||
3.3 Far IR spectroscopy
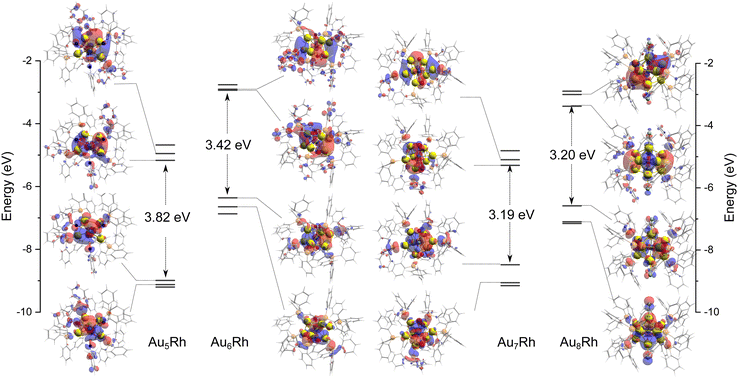
The DFT-simulated far IR spectra of the four AunRh clusters are presented in Fig. 4. A summary of the peak assignments for each cluster is shown in Tables S3 to S6, ESI.† The normal coordinate motions that involve significant motion of Au, Rh, P, and Cl (for Au8Rh) are identified and shown as percentages of total non-mass-weighted atomic motion. The simulated spectra were scaled from the DFT-calculated numbers by a functional-independent correction factor (eqn (2)) used previously for low-frequency vibrations.41![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) corr = 22 cm−1 + corr = 22 cm−1 + ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) calc × 0.94 calc × 0.94 | (2) |
 | ||
| Fig. 4 Calculated normal mode displacements associated with the cluster core vibrations for (a) Au5Rh at 164.3 cm−1, (b) Au6Rh at 182.5 cm−1, (c) Au7Rh at 175.4 cm−1, and (d) Au8Rh at 246.7 cm−1. The simulated (bottom) far-IR spectra of the AunRh clusters are also shown and numbered based on their peak assignments in the ESI.† The IR peaks denoted with asterisks are those assigned to the calculated normal mode displacements presented. | ||
Generally, all four clusters exhibit large peaks between 430–450 cm−1 which were previously assigned to distortion of the triphenylphosphine ligands (PPh3), while peaks <250 cm−1 are transitions involving the Au core distortions.20,24
The % Au motions of Au5Rh are significantly lower than previously found for Au6; 14–16% Au motion in the previous study20 but only 1.2% Au and 0.3% Rh motion in Au5Rh. The vibrations arising from the xylyl ligands appear from 220 cm−1 onwards and the Rh–C wagging and twisting motions are assigned to the large peaks at 300 and 330 cm−1, respectively. The normal modes of vibration due to PPh3 ligands are visible at 260 and 430 cm−1 as has been previously reported.20
4 Conclusion
We report the geometric, electronic, and vibrational properties of ultrasmall bimetallic gold-rhodium nanoclusters AunRh (n = 5, 6, 7, and 8). The average ligand binding energies are calculated to be ∼50 kcal mol−1, which is low enough to be removed at calcination temperatures of 150–200 °C. The calculated electronic properties indicate a stabilization effect of the Rh atom in the Au5Rh and Au8Rh clusters. Additionally, the calculated HOMO–LUMO energy gap trend corresponds to the observed colors of the respective crystals. The metal core transitions are significantly affected by the presence of the Rh atom which inhibits the motion of Au atoms as observed in the simulated IR spectra. Likewise, all clusters display the symmetric breathing mode of the AuRh core except for Au8Rh due to the presence of Cl ligands.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. M. L. M. acknowledges previous financial support from Adelaide Scholarship International (ASI), Future Fuels Cooperative Research Center (FFCRC), and the Ministry of Education, Singapore, under its Academic Research Fund Tier 1 RG83/20. Supercomputing resources at the University of Adelaide and Nanyang Technological University were provided by the Phoenix and Gekko HPC services, respectively.Notes and references
-
(a) H. Qian, M. Zhu, Z. Wu and R. Jin, Acc. Chem. Res., 2012, 45, 1470–1479 Search PubMed
; (b) G. Li and R. Jin, Acc. Chem. Res., 2013, 46, 1749–1758 Search PubMed
; (c) S. Yamazoe, K. Koyasu and T. Tsukuda, Acc. Chem. Res., 2014, 47, 816–824 Search PubMed
; (d) R. Jin, C. Zeng, M. Zhou and Y. Chen, Chem. Rev., 2016, 116, 10346–10413 Search PubMed
; (e) I. Chakraborty and T. Pradeep, Chem. Rev., 2017, 117, 8208–8271 CrossRef CAS PubMed
; (f) Z. Lei, X.-K. Wan, S.-F. Yuan, Z.-J. Guan and Q.-M. Wang, Acc. Chem. Res., 2018, 51, 2465–2474 CrossRef CAS PubMed
; (g) R. R. Nasaruddin, T. Chen, N. Yan and J. Xie, Coord. Chem. Rev., 2018, 368, 60–79 CrossRef CAS
; (h) Y. Du, H. Sheng, D. Astruc and M. Zhu, Chem. Rev., 2020, 120, 526–622 CrossRef CAS PubMed
; (i) R. H. Adnan, J. M. L. Madridejos, A. S. Alotabi, G. F. Metha and G. G. Andersson, Adv. Sci., 2022, 9, 2105692 CrossRef CAS PubMed
.
-
(a) R. Jin and K. Nobusada, Nano Res., 2014, 7, 285–300 CrossRef CAS
; (b) Y. Negishi, W. Kurashige, Y. Niihori, T. Iwasa and K. Nobusada, Phys. Chem. Chem. Phys., 2010, 12, 6219 RSC
; (c) S. Wang, Y. Song, S. Jin, X. Liu, J. Zhang, Y. Pei, X. Meng, M. Chen, P. Li and M. Zhu, J. Am. Chem. Soc., 2015, 137, 4018–4021 CrossRef CAS PubMed
; (d) L. Liao, S. Zhou, Y. Dai, L. Liu, C. Yao, C. Fu, J. Yang and Z. Wu, J. Am. Chem. Soc., 2015, 137, 9511–9514 CrossRef CAS PubMed
; (e) M. Zhou, H. Qian, M. Y. Sfeir, K. Nobusada and R. Jin, Nanoscale, 2016, 8, 7163–7171 RSC
; (f) S. Takano, H. Hirai, S. Muramatsu and T. Tsukuda, J. Am. Chem. Soc., 2018, 140, 8380–8383 CrossRef CAS PubMed
.
- T. Sengupta, J. S. Chung and S. G. Kang, Nanoscale, 2020, 12, 5125–5138 RSC
.
- S. Hayashi, R. Ishida, S. Hasegawa, S. Yamazoe and T. Tsukuda, Top. Catal., 2018, 61, 136–141 CrossRef CAS
.
- S. Hasegawa, S. Takano, S. Yamazoe and T. Tsukuda, Chem. Commun., 2018, 54, 5915–5918 RSC
.
- W. Bouwen, F. Vanhoutte, F. Despa, S. Bouckaert, S. Neukermans, L. Theil Kuhn, H. Weidele, P. Lievens and R. E. Silverans, Chem. Phys. Lett., 1999, 314, 227–233 CrossRef CAS
.
- M. Heinebrodt, N. Malinowski, F. Tast, W. Branz, I. M. L. Billas and T. P. Martin, J. Chem. Phys., 1999, 110, 9915–9921 CrossRef CAS
.
- K. Koyasu, Y. Naono, M. Akutsu, M. Mitsui and A. Nakajima, Chem. Phys. Lett., 2006, 422, 62–66 CrossRef CAS
.
- D. W. Yuan, Y. Wang and Z. Zeng, J. Chem. Phys., 2005, 122, 114310 CrossRef CAS PubMed
.
- D. Die, X.-Y. Kuang, J.-J. Guo and B.-X. Zheng, J. Mol. Struct. THEOCHEM, 2009, 902, 54–58 CrossRef
.
- Y. Xu, C. Xu, T. Zhou and C. Cheng, J. Mol. Struct. THEOCHEM, 2009, 893, 88–92 CrossRef CAS
.
- M.-X. Chen and X. H. Yan, J. Chem. Phys., 2008, 128, 174305 CrossRef PubMed
.
- G.-x. Ge, H.-x. Yan and Q. Jing, Chin. J. Chem. Phys, 2010, 23, 416–424 CrossRef CAS
.
- J.-X. Yang, C.-F. Wei and J.-J. Guo, Phys. B Condens. Matter, 2010, 405, 4892–4896 CrossRef CAS
.
- F. Buendía, M. R. Beltrán, X. Zhang, G. Liu, A. Buytendyk and K. Bowen, Phys. Chem. Chem. Phys., 2015, 17, 28219–28227 RSC
.
-
(a) N. Toshima and T. Yonezawa, New J. Chem., 1998, 22, 1179–1201 RSC
; (b) T. Balcha, J. R. Strobl, C. Fowler, P. Dash and R. W. J. Scott, ACS Catal., 2011, 1, 425–436 CrossRef CAS
; (c) R. N. Dhital, C. Kamonsatikul, E. Somsook, K. Bobuatong, M. Ehara, S. Karanjit and H. Sakurai, J. Am. Chem. Soc., 2012, 134, 20250–20253 CrossRef CAS PubMed
; (d) H. Zhang, T. Watanabe, M. Okumura, M. Haruta and N. Toshima, Nat. Mater., 2012, 11, 49–52 CrossRef PubMed
.
- H. Hirai, S. Takano, T. Nakashima, T. Iwasa, T. Taketsugu and T. Tsukuda, Angew. Chem., Int. Ed., 2022, 61, e202207290 CrossRef CAS PubMed
.
- S. G. Bott, H. Fleischer, M. Leach, D. M. P. Mingos, H. Powell, D. J. Watkin and M. J. Watson, J. Chem. Soc., Dalton Trans., 1991, 2569–2578 RSC
.
- S. Takano, H. Hirai, T. Nakashima, T. Iwasa, T. Taketsugu and T. Tsukuda, J. Am. Chem. Soc., 2021, 143, 10560–10564 CrossRef CAS PubMed
.
- J. F. Alvino, T. Bennett, D. Anderson, B. Donoeva, D. Ovoshchnikov, R. H. Adnan, D. Appadoo, V. Golovko, G. Andersson and G. F. Metha, RSC Adv., 2013, 3, 22140 RSC
.
- T. Bennett, A. J. Falcinella, R. J. White, R. H. Adnan, V. Golovko, G. G. Andersson and G. F. Metha, RSC Adv., 2015, 5, 74499–74505 RSC
.
-
(a) M. J. Hostetler, J. J. Stokes and R. W. Murray, Langmuir, 1996, 12, 3604–3612 CrossRef CAS
; (b) J. Petroski, M. Chou and C. Creutz, J. Organomet. Chem., 2009, 694, 1138–1143 CrossRef CAS
; (c) A. Tlahuice-Flores, Prog. Nat. Sci.: Mater. Int., 2016, 26, 510–515 CrossRef CAS
; (d) A. Tlahuice-Flores, Mol. Simul., 2013, 39, 428–431 CrossRef CAS
; (e) A. Wing-Bocanegra and A. Tlahuice-Flores, Phys. Chem. Chem. Phys., 2019, 21, 23855–23864 RSC
.
- A. Tlahuice-Flores, R. L. Whetten and M. Jose-Yacaman, J. Phys. Chem. C, 2013, 117, 12191–12198 CrossRef CAS
.
- T. Bennett, R. H. Adnan, J. F. Alvino, V. Golovko, G. G. Andersson and G. F. Metha, Inorg. Chem., 2014, 53, 4340–4349 CrossRef CAS PubMed
.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed
.
-
H. Dunning and P. J. Hay, in Gaussian Basis Sets for Molecular Calculations, ed. H. F. Schaefer, Springer US, Boston, MA, 1977, pp. 1–27 Search PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, 2016 Search PubMed
.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388 CrossRef PubMed
.
- J. Kilmartin, R. Sarip, R. Grau-Crespo, D. Di Tommaso, G. Hogarth, C. Prestipino and G. Sankar, ACS Catal., 2012, 2, 957–963 CrossRef CAS
.
- O. D. Haeberlen and N. Roesch, J. Phys. Chem., 1993, 97, 4970–4973 CrossRef CAS
.
- V. Q. Vuong, J. M. L. Madridejos, B. Aradi, B. G. Sumpter, G. F. Metha and S. Irle, Chem. Sci., 2020, 11, 13113–13128 RSC
.
- A. O. Borissova, A. A. Korlyukov, M. Y. Antipin and K. A. Lyssenko, J. Phys. Chem. A, 2008, 112, 11519–11522 CrossRef CAS PubMed
.
- P. Schwerdtfeger, H. L. Hermann and H. Schmidbaur, Inorg. Chem., 2003, 42, 1334–1342 CrossRef CAS PubMed
.
- D. P. Anderson, R. H. Adnan, J. F. Alvino, O. Shipper, B. Donoeva, J.-Y. Ruzicka, H. Al Qahtani, H. H. Harris, B. Cowie, J. B. Aitken, V. B. Golovko, G. F. Metha and G. G. Andersson, Phys. Chem. Chem. Phys., 2013, 15, 14806 RSC
.
- D. P. Anderson, R. H. Adnan, J. F. Alvino, O. Shipper, B. Donoeva, J.-Y. Ruzicka, H. Al Qahtani, H. H. Harris, B. Cowie, J. B. Aitken, V. B. Golovko, G. F. Metha and G. G. Andersson, Phys. Chem. Chem. Phys., 2013, 15, 14806 RSC
.
- T. Omoda, S. Takano and T. Tsukuda, Small, 2021, 17, 2001439 CrossRef CAS PubMed
.
- M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Grönbeck and H. Häkkinen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157–9162 CrossRef CAS PubMed
.
- S. Yamazoe, S. Matsuo, S. Muramatsu, S. Takano, K. Nitta and T. Tsukuda, Inorg. Chem., 2017, 56, 8319–8325 CrossRef CAS PubMed
.
- S. G. Bott, D. M. P. Mingos and M. J. Watson, J. Chem. Soc., Chem. Commun., 1989, 1192–1193 RSC
.
-
(a) J. M. L. Madridejos, T. Harada, A. J. Falcinella, T. D. Small, V. B. Golovko, G. G. Andersson, G. F. Metha and T. W. Kee, J. Phys. Chem. C, 2021, 125, 2033–2044 CrossRef CAS
; (b) S. Muramatsu, Y. Nakahigashi, T. Omoda, S. Takano, T. Tsukuda and Y. Inokuchi, J. Phys. Chem. Lett., 2023, 14, 5641–5647 CrossRef CAS PubMed
.
- L. Lin, P. Claes, P. Gruene, G. Meijer, A. Fielicke, M. T. Nguyen and P. Lievens, Chem. Phys. Chem., 2010, 11, 1932–1943 CrossRef CAS PubMed
.
-
(a) H. E. Sauceda, D. Mongin, P. Maioli, A. Crut, M. Pellarin, N. Del Fatti, F. Vallée and I. L. Garzón, J. Phys. Chem. C, 2012, 116, 25147–25156 CrossRef CAS
; (b) B. Lan and D. Y. Sun, Phys. Rev. B, 2021, 103, 1–8 Search PubMed
.
-
(a) J. F. Parker, J.-P. Choi, W. Wang and R. W. Murray, J. Phys. Chem. C, 2008, 112, 13976–13981 CrossRef CAS
; (b) B. Varnholt, P. Oulevey, S. Luber, C. Kumara, A. Dass and T. Bürgi, J. Phys. Chem. C, 2014, 118, 9604–9611 CrossRef CAS
.
- Q. Martinet, A. Berthelot, A. Girard, B. Donoeva, C. Comby-Zerbino, E. Romeo, F. Bertorelle, M. van der Linden, N. Tarrat, N. Combe and J. Margueritat, J. Phys. Chem. C, 2020, 124, 19324–19332 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05976f |
| This journal is © the Owner Societies 2024 |