Open Access Article
Open Access ArticleA methodology for estimating indoor sources contributing to PM2.5†
Shiva
Nourani
 ab,
Ana María
Villalobos
ab,
Ana María
Villalobos
 a and
Héctor
Jorquera
a and
Héctor
Jorquera
 *ab
*ab
aDepartamento de Ingeniería Química y Bioprocesos, Pontificia Universidad Católica de Chile, Avda. Vicuña Mackenna 4860, Santiago 7820436, Chile. E-mail: jorquera@uc.cl
bCenter for Sustainable Urban Development (CEDEUS), Los Navegantes 1963, Providencia, Santiago 7520246, Chile
First published on 1st November 2024
Abstract
Quantifying source contributions to indoor PM2.5 levels by indoor PM2.5 sources has been limited by the costs associated with chemical speciation analyses of indoor PM2.5 samples. Here, we propose a new methodology to estimate this contribution. We applied FUzzy SpatioTemporal Apportionment (FUSTA) to a database of indoor and outdoor PM2.5 concentrations in school classrooms plus surface meteorological data to determine the main spatiotemporal patterns (STPs) of PM2.5. We found four dominant STPs in outdoor PM2.5, and we denoted them as regional, overnight mix, traffic, and secondary PM2.5. For indoor PM2.5, we found the same four outdoor STPs plus another STP with a distinctive temporal evolution characteristic of indoor-generated PM2.5. Concentration peaks were evident for this indoor STP due to children's activities and classroom housekeeping, and there were minimum contributions on sundays when schools were closed. The average indoor-generated estimated contribution to PM2.5 was 5.7 μg m−3, which contributed to 17% of the total PM2.5, and if we consider only school hours, the respective figures are 8.1 μg m−3 and 22%. A cluster-wise indoor–outdoor PM2.5 regression was applied to estimate STP-specific infiltration factors (Finf) per school. The median and interquartile range (IQR) values for Finf are 0.83 [0.7–0.89], 0.76 [0.68–0.84], 0.72 [0.64–0.81], and 0.7 [0.62–0.9], for overnight mix, secondary, traffic, and regional sources, respectively. This cost-effective methodology can identify the indoor-generated contributions to indoor PM2.5, including their temporal variability.
Environmental significanceThis methodology can be used to estimate the contribution of indoor PM sources to indoor PM2.5 concentrations. Estimated indoor-generated PM2.5 contributions provide insights into the dynamics of these indoor sources and how much they contribute to overall indoor PM2.5 exposure. This estimation does not require the use of chemical speciation data. Only continuous measurements of indoor and outdoor PM2.5 and local meteorological information are needed. The processing of input data and results is simple, and the required computational routines are available in the R open software. Thus, this methodology can be straightforwardly applied to any study of indoor air quality that has measured the above parameters. |
1 Introduction
Different environmental factors can affect the health, growth, and development of children. Good indoor air quality is necessary for children's health and well-being, and is a priority for the public.1 Among indoor pollutants, fine particulate matter (PM) with an aerodynamic diameter below 2.5 μm (PM2.5) can be detrimental to health.2 Different health problems in children have been associated with exposure to indoor PM2.5, including negative effects on the respiratory3 and immune4 systems, and impairment of cognitive development.5 This exposure may also increase the risks of health impairments later in life, including cardiovascular diseases or cancer.6,7People spend most of their time indoors. Low-cost sensors enable estimation of the effects of total exposure of indoor and outdoor pollutants upon human health.8,9 A quantitative metric for characterizing the outdoor–indoor relationship is the infiltration factor (Finf)10,11 Recently, the proliferation of affordable PM2.5 sensors has allowed researchers to increase the number of indoor sites sampled, as compared to more expensive equipment for measuring indoor PM2.5.12 It has been shown that it is useful and reliable to use low-cost sensors to understand the impacts of outdoor air pollution on the indoor environment.13
A quantitative source apportionment of PM2.5 is key for selecting measures to control PM2.5.14 Outdoor PM2.5 source apportionment is carried out using air quality models (AQMs) and receptor models (RMs). Both models are widely used to design effective strategies to reduce harmful air.15 However, AQMs include several sources of uncertainty, such as meteorology, emission inventories, and parametrization of atmospheric physical and chemical processes. RMs require the chemical speciation of outdoor or indoor PM2.5 samples, and because these analyses are expensive, they have been applied mostly in developed16 and in short-term campaigns. Zhao et al.17 applied a receptor model for 24 h integrated filter samples during 7 days in four seasons in New York City. They found four external sources (motor vehicle emission, soil, secondary sulfate, and secondary nitrate) and four internal sources (environmental tobacco smoke and its mixture, personal care/activity, Cu-factor mixed with indoor soil, and cooking). In another study, Zwoździak et al.18 found twenty elements indoors and outdoors by X-ray fluorescence analyses of measurements taken during weekends (24 h samples) or 8 h (teaching hours, 08:00 am–4:00 pm) and 16 h (4:00 pm–08:00 am) measurements obtained during workdays, for one week per month from December 2009 to October 2010 in just one public school. According to this analysis, the main sources were non-crustal sources and combustion sources.
Since the 1970s, clustering techniques have been applied in atmospheric science, first on climate and meteorological data, and later in air pollution studies. The k-means technique has been extensively used in air pollution research during the last four,19 but it has not been applied to indoor air pollution, nor used for source identification estimates. Furthermore, the hard or traditional clustering approaches such as k-means and k-medoids may be too rigid for actual management.20 These hard-clustering algorithms create crisp partitions of the original data set so that each observation belongs to only one cluster. However, actual ambient pollutant concentrations are a sum of contributions from different sources (traffic, residential, industrial) at any given time, and therefore, they cannot be analyzed from that hard clustering standpoint.21
The novelty of the approach pursued here (named FUzzy SpatioTemporal Apportionment (FUSTA)) is its capacity to identify sources of gaseous industrial emissions.21 FUSTA achieves source identification using the ‘meteorological fingerprints’ associated with each source. When this fuzzy clustering algorithm is applied to a set of ambient concentrations, and surface meteorology is measured at a given monitoring site, the outcome is a finite set of spatiotemporal patterns (STPs) of air pollution. Each STP is associated with one major air pollution source (traffic, residential, industrial) or a mixture of sources through a specific set of values of meteorological variables—a distinctive meteorological fingerprint. Jorquera et al.21 have shown that the STPs resolved by FUSTA are similar to those generated by applying an AQM to the major SO2 sources in an industrial zone. FUSTA uses available ambient information, and it has the flexibility to include intermittent sources and outliers through the noisy cluster concept. This fuzzy clustering technique has not been applied to indoor air pollution thus far, and therefore, this study is the very first application of this technique, specifically in classroom environments.
FUSTA is a cost-effective approach as compared with a receptor modeling application because it uses available ambient low-cost sensors for measuring PM2.5 and open-access R libraries to obtain quantitative results (see Section 2.3 below for details). Nonetheless, there are some limitations to the use of low-cost sensors.
Our present aim is to analyze the indoor and outdoor PM2.5 concentrations in schools using the FUSTA algorithm (see Section 2.3 below) to identify the major (single or mixed) sources contributing to outdoor (and indoor) PM2.5, and estimate their associated infiltration factors. Furthermore, we will extract the indoor-generated PM2.5 source contribution because it has no outdoor counterpart. Next, we present the methodology, results, discussion, and conclusions for this novel approach.
2 Methodology
2.1. Locations and monitoring periods
Thirty schools were selected for this study, namely, S1 to S30, located in Santiago, Chile (30.5°S, 70.7°W). At each school, measurements were conducted in one outdoor location near to the main school entrance and two locations inside the school in two classrooms (‘far’ and ‘near’ classrooms with respect to the street), to assess the spatial variability in indoor PM2.5. These classrooms were next to other classrooms and hallways, but they were not near indoor sources such as the cafeteria or chemistry laboratories, for instance. We had 15 low-cost sensors available, and therefore, at most, 5 schools were being measured at the same time. Continuous monitoring was carried out for PM2.5 concentrations, temperature, and relative humidity (RH) for three weeks at each school. The sampling campaigns were conducted from May 5th to December 15th, 2022, that is, during the austral fall, winter, and spring seasons. Some data sets were excluded due to a loss of internet connection in specific sensor measurements in S4, S21, S22, S26, S27, S28 and due to changes in protocols for downloading and reporting PM2.5 concentration data (S23, S24, S25, S29, and S30). Therefore, in total, complete data were obtained for 19 schools.Table S1† includes the type of schools sampled (kindergarten, elementary, or high school), and Fig. S1† shows the locations of the schools and the ambient environmental monitoring stations. Due to the COVID-19 pandemic, all windows and doors were open all the time, and children were present during the sampling and going about their regular activities, such as studying and playing. Schools S1 to S3 were sampled in autumn, S5 to S16 in winter, and S17 to S20 in spring. The entire protocol for contacting schools and carrying out measurements was approved by the Ethics in Research Committee at the Pontificia Universidad Católica de Chile.
2.2. Data collection and instrumentation
Outdoor and indoor PM2.5 concentrations were measured with low-cost sensors (PurpleAir Inc., UT, USA). PurpleAir sensors are low-cost air quality monitors that use laser particle counters to estimate PM concentrations, including PM2.5. The algorithm that we chose was the CF_ATM algorithm. There are limitations to the accuracy and precision of these low-cost sensors, and normally, there is 50–55% overestimation in their measurement22,23 when concentrations are low, although their performance improves at higher concentrations.22,23 Therefore, they were tested before the campaigns to confirm that they record comparable measurements. To do this, they were placed in a laboratory room for a couple of days, and then their measurements were plotted to detect any potential bias. All sensors were factory-calibrated before the start of the measurement campaign. The monitoring station of the Chilean Air Quality Monitoring Network (SINCA in Spanish, https://sinca.mma.gob.cl/) nearest to each school was selected for comparison of outdoor PM2.5 measurements, and hourly average surface meteorological data for wind speed and direction, air temperature, and pressure were collected from these stations as well. Real-time monitoring (with a 2 min logging interval) was conducted in 2 classrooms (one far from the street and another near the street), and one outdoor sensor was placed on each school.2.3. Data processing and analysis
First, the PM2.5 data sampled by the PurpleAir low-cost sensors (CF_ATM algorithm) were hourly averaged. Then for each school, the processed data were merged with hourly meteorological data obtained from the nearest air quality monitoring station. Data analysis was then performed on the merged dataset using the statistical computing software R, with the assistance of the Openair package for air pollution analysis.24The hourly data (PM2.5 and meteorology) from all schools were merged into three databases: school outdoor, far, and near classrooms. In the first data processing step, the PM2.5 concentrations were log-transformed to obtain near normal distributions. Then, the wind speed and direction were transformed to Cartesian wind components (u,v) in a manner similar to that of Openair's bivariate polar plots.25 In FUSTA methodology, outliers are not removed, but missing values are removed from the database. Finally, all variables are standardized before being processed with the following fuzzy clustering algorithm:20
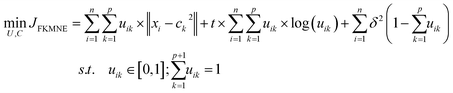 | (1) |
The fclust package available in R software26 was used to perform a fuzzy clustering algorithm for the above three data sets. We used routine FKM.ent.noise with the default t and d parameters in eqn (1), as in previous work with outdoor SO2 and PM2.5.21,27 After the matrix U of fuzzy clustering membership {uik} was obtained from solving the above eqn (1), the PM2.5 concentrations can be written as:
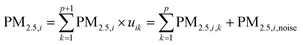 | (2) |
2.4. PM2.5 source identification for indoor and outdoor clusters
The major fuzzy clusters (or STPs) contributing to PM2.5 concentrations may be identified by examining their spatiotemporal variability. For instance, traffic sources will peak near the morning/evening rush hour and decrease over weekends, residential sources will peak overnight in the cold seasons (fall and winter), and regional PM2.5 values will peak in the afternoon when wind speeds are the highest. However, because we do not have access to simultaneous information such as chemical speciation data, these classifications should be regarded as tentative. Nonetheless, this labeling does not affect the estimation of the indoor-generated PM2.5 contributions, as we describe below. In addition, bivariate polar plots25 provide the spatial distribution of these STP contributions to PM2.5 concentrations as well, adding additional pieces of information. Thus, by comparing indoor clusters with outdoor ones, it is possible to pair them according to their STP features. Furthermore, the indoor-generated sources are identified as indoor clusters that have no outdoor counterparts.Once the major sources (single or mixed) contributing to outdoor and indoor PM2.5 were identified, we applied a linear regression for each pair of clusters to estimate the respective source-specific infiltration factor:
| (Cin)i = Finf·(Cout)i + eii = 1, 2,…, p; | (3) |
3 Results and discussion
3.1. Accuracy of the low-cost sensors for measuring PM2.5 concentration
The performance of the low-cost PM sensors was characterized under realistic conditions, and therefore, it was evaluated with major axis regression using the package lmodel2 in R between the outdoor PM2.5 measured and the corresponding PM2.5 values from the closest ambient monitoring station. The coefficient of determination value based on the hourly average was used to determine the agreement between the reference and the sensor. As shown in Table S1,† the R2 values were greater than 0.6 for 79% of the 19 schools (median R2 = 0.7, IQR: [0.6, 0.7]). The lower R2 values (0.37 to 0.57) for some schools can be ascribed to the distance between those schools and the nearest ambient monitoring station and to uncertainties in the low-cost sensors as well. For instance, ESI Fig. S1b† shows several schools that are closer to a regulatory monitoring station, and as the distance to the monitoring station increases, the R2 values decrease. This is a limitation in the present results.The average PM2.5 ratio of the outdoor PurpleAir sensor to the closest SINCA station varied between 0.9 and 1.7 (median = 1.4, IQ range: [1.3, 1.5]) (Table S1†). These high ratios suggest that the CF_ATM algorithm from the PurpleAir sensors overestimated the PM2.5 values by an average of 37% in this study, which is in agreement with studies that have reported overestimation by these sensors.22,23 This figure could be regarded as an upper bound because it is possible that a higher outdoor PM2.5 in schools is also explained by their proximity to main roads, as compared to the regulatory urban background monitors.29,30 Thus, the results showed acceptable correlations between the low-cost sensors and the reference monitors (Table S1†). Fig. S2† shows an example for schools S12 and S15 on a daily average basis, where the outdoor sensor measured values and trends similar to those measured by the reference station. These results were obtained at most of the other schools as well.
3.2. Spatiotemporal patterns for outdoor and indoor PM2.5
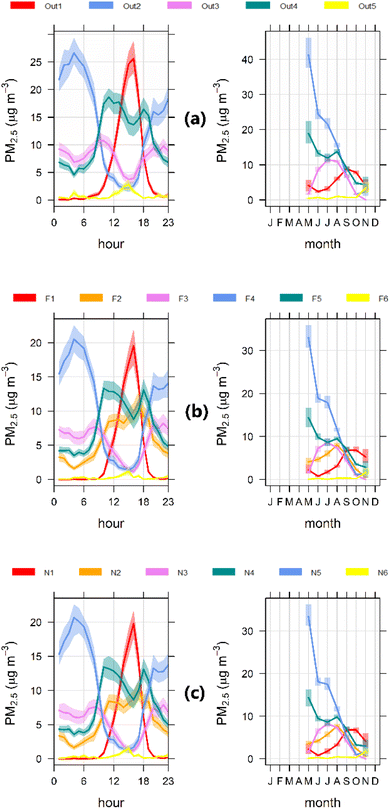
We applied fuzzy clustering to the outdoor and indoor PM2.5 and meteorology databases for different cluster numbers (p) to determine interpretable solutions using the criteria explained in Section 2.4. As a result, a five-cluster solution (4 regular clusters + 1 noise cluster) for outdoor and a six-cluster solution (5 regular clusters + 1 noise cluster) for indoor environments (far and near classrooms) were found to be adequate. Fig. 1 presents a time variability plot for all PM2.5 clusters resolved by fuzzy clustering for (a) outdoor, (b) far, and (c) near classrooms.It is clear in Fig. 1 that the STPs (fuzzy clusters) for the far and near classrooms are similar to the ones resolved for the outdoor PM2.5 data, but they have an extra cluster that has no outdoor counterpart, and this corresponds to the indoor-generated PM2.5. ESI Fig. S3† shows these three results when they are projected along the (u,v) components of wind velocity. The size of the symbols is scaled with the respective membership values {uik}, and therefore, there are small membership values for the points more distant to the clusters' centroids.
One group of similar STPs can be seen in the clusters Out2, F4, and N5 for outdoor, far, and near classrooms, respectively (henceforth, we shall use this notation to refer to FUSTA results). These STPs are identified as an overnight mixed source with the highest contributions during the evening and night (left panels of Fig. 1 – diurnal variation) and (austral) during the fall and winter seasons (right panels of Fig. 1 – seasonal variation), which correspond to the months of May through August in the southern hemisphere. This source corresponds to a mixture of direct PM2.5 emissions from residential heating, which peak during the fall and winter seasons, and aged emissions recirculate in Santiago because of mountain-valley overnight winds. The diurnal profile of the source of this overnight mix is similar to the diurnal profile of biomass burning oxidized aerosols (BBOA) measured in Santiago by Carbone et al.,31 suggesting that this contribution is dominated by residential heating sources.
Another set of similar clusters corresponds to Out4, F5, and N4 in outdoor, far, and near classrooms, respectively. The contributions of these clusters are two peaks in the early afternoon (12 pm) and late afternoon (6 pm), and they are higher in the fall and winter seasons. Thus, we identified this source as secondary aerosols that are formed in Santiago's atmosphere, originating from local sources such as traffic. Aerosol Chemical Speciation Monitor (ACSM) measurements in Santiago31 have clearly shown that ammonium nitrate and oxidized organic aerosols (OOA) peak at approximately noon, remain high in the afternoon, and decrease overnight, and therefore, their STP is similar to the three above-mentioned clusters.
The concentrations of clusters Out3, F3, and N3 peak during the morning and evening rush hour, with a clear peak in the winter season. This time variability is similar to that measured in Santiago for black carbon and hydrocarbon-like organic aerosol (HOA) by Carbone et al.31 Hence, we identified this source as originating from traffic.
The contributions from clusters Out1, F1, and N1 peak in the early afternoon, and this increase is followed by a decrease in contributions later in the evening; these contributions increase in spring. This behavior is related to anabatic winds that transport pollution toward the east side of the city.32 We identified this as a regional source, and because it also includes secondary aerosols generated en route to the measurement sites, it is a mix of sources.
The noise clusters include those contributions that could not be included in other clusters, and they can be seen in Out5, F6, and N6 in outdoor, far, and near classrooms, respectively. The similarities in indoor and outdoor time variabilities suggest that the intermittent sources are derived from the same outdoor sources.
F2 and N2 are indoor clusters that are not found in outdoor sources. As Fig. 1 shows, their values are higher during schools' activity hours, increase from May to August, and then decrease to lower values during the warm season (see Section 3.3 below for further comments).
Fig. 1b and c shows little difference between clusters in near and far classrooms, and the temporal variability for all STPs is the same, suggesting little indoor PM2.5 variability across the schools' indoor environments. This may be explained by the lack of significant outdoor PM2.5 sources within school boundaries. Fig. S4† shows that the indoor average concentrations did not significantly change according to school sample type.
3.3. Comparison between indoor and outdoor clusters
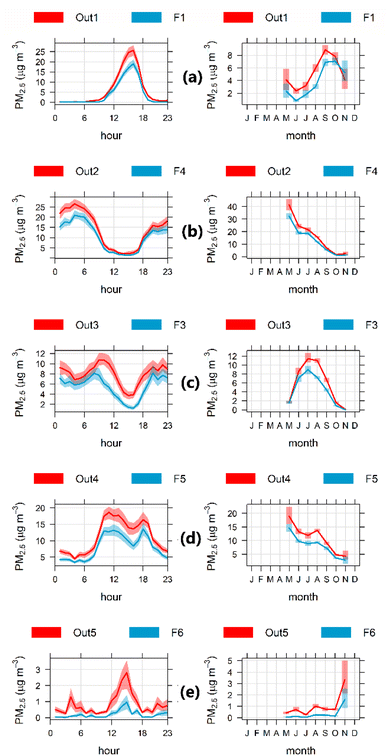
We used the results of the previous section to pair indoor and outdoor clusters according to their spatiotemporal variations. The time variabilities of each outdoor cluster contribution paired with far and near classroom counterparts are shown in Fig. 2 and S5,† respectively. In these figures, the excellent agreement between each pair of indoor and outdoor STPs is evident, and the outdoor concentrations are higher than the indoor ones, as expected for each outdoor source penetrating into the classrooms. Furthermore, Fig. S6 and S7† provide cluster comparisons using polar plots, and show satisfactory agreement between clusters generated by the same sources.Fig. 2(a) (clusters Out1-F1) and S5(a) (clusters Out1-N1) show the contributions that peak in the early afternoon and in the spring season, originating from regional sources of PM2.5; these clusters are also depicted in panel (a) in Fig. S6 and S7.† The correlation coefficients are R2 = 0.79 for Out1-N1 and R2 = 0.74 for Out1-F1. The next matching pair of clusters is Out2-F4 (R2 = 0.82) and Out2-N5 (R2 = 0.83), which can be seen in Fig. 2(b), S5(b),† and panel (b) in Fig. S6 and S7.† The highest PM2.5 contributions occur during the fall and winter seasons, and originate from overnight mixed sources (and low temperatures; see Fig. S7†), as explained in Section 3.2.
Fig. 2(c) shows the matching of outdoor cluster (Out3) with the far cluster (F3) that is derived from the traffic source (R2 = 0.69). The analogous paired cluster is the outdoor cluster (Out3) and cluster (N3) in Fig. S5(c)† (R2 = 0.69). Both figures show contributions, with an outdoor peak during the morning and afternoon rush hours and in the winter season. The associated polar plots are shown in panel (c), Fig. S6 and S7.† Next, Fig. 2(d) and S5(d)† show the secondary aerosol sources; the respective polar plots are shown in panel (d) in Fig. S6 and S7.† The timing of these peaks agrees with organic and inorganic secondary PM2.5 peaks measured at a central site in Santiago by Carbone et al.31 The correlation coefficients are R2 = 0.78 for Out4-N4 and R2 = 0.75 for Out4-F5. Finally, Fig. 2(e) and S5(e)† show the matching of noise clusters between indoor and outdoor PM2.5 (Out5-F6 and Out5-N6 with R2 equal to 0.58 and 0.67, respectively).
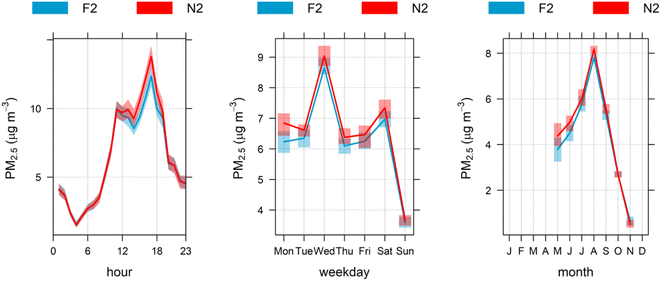
Fig. 3 shows the indoor-generated clusters N2 and F2 for near and far classrooms, respectively. These peak between 12 to 6 pm and during the winter season, and the contributions are produced mainly during school hours from children's activities and classroom cleaning.33 It should be noted that there is a distinctive drop in this source on Sundays when schools are closed (on Saturdays, housekeeping activities occur at schools, and some schools carry out extra activities as well). Considering that pandemic conditions forced all schools to keep classrooms' windows and doors open, the air exchange rate in those classrooms would depend on environmental conditions, primarily wind speed and the indoor–outdoor temperature difference. Minimum wind speed and ambient temperature is prevalent in the winter season, with a maximum in the spring season, and fall season values are in-between. This seasonality explains why indoor-generated concentrations increased from May to August and then decreased to a minimum in spring, as presented above in Section 2.3.
3.4. Quantifying Finf for different sources
Fig. S8† shows the infiltration factors for different clusters in (a) near and (b) far classrooms and for all major sources resolved by FUSTA: regional, overnight mix, traffic, and secondary aerosol contributions. Overall, the Finf values vary in agreement with literature results. For instance, in the review by Chen et al.,34Finf values were reported ranging from 0.3 to 0.82. Although there are a few estimates of Finf above 1.0 in Fig. S8,† which may be ascribed to error propagation resulting from uncertainties in low-cost sensor measurements, they correspond to only a small fraction of results.There is a significantly higher Finf in spring for regional and secondary source contributions: p-value = 0 and 0.02, respectively (Fig. S9†). As mentioned in Section 3.3 above, higher wind speeds in the spring season, especially in the afternoon when these two source contributions peak, favor increased air exchange rates, which in turn increase Finf values. However, for traffic contributions, PM2.5 infiltration did not show a seasonal effect. For the overnight mix sources, the lack of seasonality was expected because the windows and doors of all classrooms were closed.
3.5. Source identification results
Fig. 4 shows the average source identification estimates for outdoor and indoor PM2.5, including all schools. On average, the indoor PM2.5 contributions from outdoor and indoor-generated particles are 31%, 24%, 17%, 16%, 12%, and 1% for the overnight mix, secondary aerosols, indoor-generated, traffic, regional, and intermittent (noise) sources, respectively.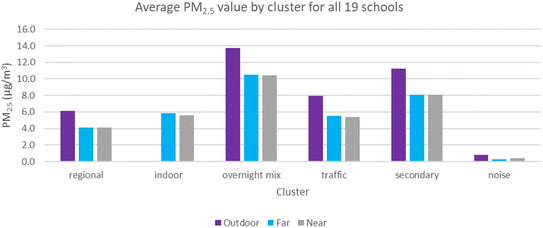 | ||
| Fig. 4 Average concentration of PM2.5 for different clusters (regional, indoor, overnight mix source, traffic, secondary aerosols, and noise clusters) for all schools (μg m−3). | ||
Fig. S10† shows the PM2.5 contributions for each cluster at each school for (a) outdoor, (b) far, and (c) near classrooms. The seasonality of the data is clear, with higher concentrations in fall and winter, and lower concentrations in spring. This seasonality is explained by meteorological factors (higher mixing heights and wind speeds in spring) and local emissions from residential heating that increase in fall and winter. The higher ambient PM2.5 concentrations in the fall are explained by rainfall amounts that are lower than those measured during winter (during which the peak of precipitation occurs); a higher frequency of rainfall in winter reduces the residence time of PM2.5 in the city's basin.
Regarding the spatial variability of the indoor PM2.5 for each school (for all clusters), there was no significant difference between near and far classrooms (p-value = 0.98); the overall PM2.5 concentrations for near and far classrooms were 34 and 34.3 μg m−3, respectively. This is ascribed to a lack of relevant outdoor PM2.5 sources within each school.
Fig. S11† shows an average PM2.5 source contribution according to cold (autumn–winter) and warm (spring) seasons for all clusters. The cold season contributions are higher for all clusters except for regional sources, which are higher in spring, when wind speed increases. From both figures, seasonality drives outdoor, and thus indoor PM2.5 concentrations, as discussed above.
3.6. Limitations of the present work
We acknowledge that there are limitations involved in the present work. The use of low-cost sensors requires confirming that these PM2.5 measurements agree with reference instruments. We compared the data from each outdoor sensor with the data from the closest regulatory monitoring site, and the overall results are acceptable (Table S1†), yet there are some cases where the correlation was lower than 0.6, and therefore, uncertainties may have been higher at some specific schools. Also, low-cost sensors tend to overestimate PM2.5 concentrations. Hence, uncertainties may propagate throughout the new proposed methodology. This propagated effect is evident in estimates of infiltration factor (Finf) above 1 (Fig. S8†). Thus, we recommend a data quality assurance/quality control step to minimize uncertainty in the outcomes of FUSTA. This would entail comparisons of the low-cost sensors against a reference monitor, for instance. In the present work, all brand new sensors were compared before the campaign to ensure a lack of sensor bias. Because low-cost sensors require a steady Wi-Fi connection, it is important to consider backup power units to avoid missing data.Another limitation has been the short-term (three week) measurements collected at each school, due to the limited resources available. The obtainment of long-term records would allow a separate analysis for each school with FUSTA, and this would more accurately capture the variability of PM2.5 between schools as well.
Because the FUSTA methodology only uses meteorological information to identify sources, sometimes only a mixture of sources is identified. For example, in this work, an overnight mix of sources was resolved. This source is a mix of residential heating sources and sources included in the overnight mountain-valley wind recirculation in Santiago, such as aged traffic emissions and secondary PM2.5. To improve the source attribution, a parallel chemical speciation campaign could be performed, and the receptor modeling results could be compared with those STPs found with FUSTA. Another method could be to apply air quality modeling to outdoor emissions and compare these results with the STPs resolved with FUSTA.
4 Conclusions
In this work, we have proposed a new methodology to identify the contribution of indoor PM sources to indoor PM2.5 concentrations. This is a cost-effective methodology that uses indoor and outdoor measurements of PM2.5 and meteorology that are analyzed with a fuzzy clustering method (FUSTA) using R open software. This method uses the meteorological fingerprint associated with each major PM2.5 source (single or mixed) to identify them, for outdoor and indoor environments. One key assumption is that the contribution of indoor PM2.5 is distinct from indoor PM2.5 generation and is unlike the outdoor sources that penetrate indoors.We applied this new methodology to a set of PM2.5 measurements obtained with low-cost sensors in classrooms from 19 schools in Santiago, Chile. We found four major outdoor sources contributing to outdoor PM2.5: regional, overnight mix, traffic, and secondary aerosols. For indoor PM2.5, the methodology identified an indoor-generated source that exhibits a diurnal and weekly trend based on children's and cleaning activities in the classroom. The seasonality of this indoor source contribution (higher in winter, lower in spring) is controlled by the environment (wind speed and temperature) through the classroom air exchange rate (higher in spring, lower in winter). For the four identified outdoor PM2.5 sources, infiltration factors were estimated for each outdoor–indoor source pair. Most of these estimated values agreed with literature values.
The average concentrations of outdoor and indoor PM2.5 during school hours are 14.8 and 10.6 μg m−3 for secondary, 12.3 and 8.7 μg m−3 for regional, 8.1 and 4.4 μg m−3 for traffic, and 5.5 and 4 μg m−3 for overnight mix sources, respectively. The average indoor-generated contribution is 8.1 μg m−3. Therefore, the indoor PM2.5 contributions are 29%, 24%, 22%, 12%, 11%, and 1% for the secondary, regional, indoor-generated, traffic, overnight mix, and intermittent (noise) sources, respectively.
One limitation of the present results originates from the use of low-cost sensors to measure PM2.5. The uncertainty of these PM2.5 sensors was determined by comparing the outdoor school measurements with the closest regulatory PM2.5 monitor. Although most of these comparisons were acceptable (R2 above 0.6), uncertainties at some schools were higher. This was indirectly diagnosed by a few estimated infiltration factors above 1, which shows how the uncertainty in this type of sensor propagates through the methodology. Another limitation was the sample size: because of limited resources, each school was measured for only three weeks. Hence, the analyses carried out herein were for the combined set of 19 schools, with complete data sets. Because FUSTA uses local meteorology to identify PM2.5 sources, sometimes only a mixture of sources may be identified, and therefore, the results need to be assessed with caution.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Shiva Nourani: field campaigns, data analysis, data curation, visualization, writing – original draft. Ana María Villalobos: campaign logistics, data analysis, writing – editing. Héctor Jorquera: conceptualization, formal analysis, writing – final draft and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research was financially supported by the Becas de Doctorado Nacional doctoral scholarship program, grant ANID-PFCHA/2020-21200430, and by grant ANID-FONDAP 1523A0004. Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02).References
- WHO, WHO global air quality guidelines: particulate matter (PM2.5 and PM10), ozone, nitrogen dioxide, sulfur dioxide and carbon monoxide, 2021, [cited 2024 Aug 2], Available from: https://www.who.int/publications/i/item/9789240034228.
- A. Mainka and E. Zajusz-Zubek, Indoor air quality in urban and rural preschools in upper Silesia, Poland: Particulate matter and carbon dioxide, Int. J. Environ. Res. Public Health, 2015, 12(7), 7697–7711 CrossRef CAS PubMed
.
- J. C. Rufo, I. Annesi-Maesano, P. Carreiro-Martins, A. Moreira, A. C. Sousa and M. R. Pastorinho,
et al., Issue 2 – “Update on adverse respiratory effects of indoor air pollution” Part 1: Indoor air pollution and respiratory diseases: A general update and a Portuguese perspective, Pulmonology, 2024, 30(4), 378–389 CrossRef CAS PubMed
.
- G. S. Leonardi, D. Houthuijs, P. A. Steerenberg, T. Fletcher, B. Armstrong and T. Antova,
et al., Immune Biomarkers In Relation To Exposure To Particulate Matter: A Cross-Sectional Survey in 17 Cities of Central Europe, Inhalation Toxicol., 2000, 12(sup4), 1–14 CrossRef CAS
.
- J. Sunyer, E. Suades-González, R. García-Esteban, I. Rivas, J. Pujol and M. Alvarez-Pedrerol,
et al., Traffic-related Air Pollution and Attention in Primary School Children, Epidemiology, 2017, 28(2), 181–189 CrossRef PubMed
.
- W. Nazar and M. Niedoszytko, Air Pollution in Poland: A 2022 Narrative Review with Focus on Respiratory Diseases, Int. J. Environ. Res. Public Health, 2022, 19(2), 895 CrossRef CAS PubMed
.
- E. Błaszczyk, W. Rogula-Kozłowska, K. Klejnowski, I. Fulara and D. Mielżyńska-Švach, Polycyclic aromatic hydrocarbons bound to outdoor and indoor airborne particles (PM2.5) and their mutagenicity and carcinogenicity in Silesian kindergartens, Poland, Air Qual., Atmos. Health, 2017, 10(3), 389–400, DOI:10.1007/s11869-016-0457-5
.
- J. Drzymalla and A. Henne, Use of low-cost PM-sensors to determine the infiltration of outdoor particles into indoor environments, 2019, available from: http://creativecommons.org/licenses/by/4.0/.
- H. Shen, W. Hou, Y. Zhu, S. Zheng, S. Ainiwaer and G. Shen,
et al., Temporal and spatial variation of PM2.5 in indoor air monitored by low-cost sensors, Sci. Total Environ., 2021, 770 Search PubMed
.
- H. Jorquera, F. Barraza, J. Heyer, G. Valdivia, L. N. Schiappacasse and L. D. Montoya, Indoor PM2.5 in an urban zone with heavy wood smoke pollution: The case of Temuco, Chile, Environ. Pollut., 2018, 236, 477–487 CrossRef CAS PubMed
.
- F. Barraza, H. Jorquera, G. Valdivia and L. D. Montoya, Indoor PM2.5 in Santiago, Chile, spring 2012: Source apportionment and outdoor contributions, Atmos. Environ., 2014, 94, 692–700 CrossRef CAS
.
- J. Bi, N. Carmona, M. N. Blanco, A. J. Gassett, E. Seto and A. A. Szpiro,
et al., Publicly available low-cost sensor measurements for PM2.5 exposure modeling: Guidance for monitor deployment and data selection, Environ. Int., 2022, 158 Search PubMed
.
- P. D. M. Nguyen, N. Martinussen, G. Mallach, G. Ebrahimi, K. Jones and N. Zimmerman,
et al., Using low-cost sensors to assess fine particulate matter infiltration (Pm2.5) during a wildfire smoke episode at a large inpatient healthcare facility, Int. J. Environ. Res. Public Health, 2021, 18(18), 9811 CrossRef CAS PubMed
.
- B. Xu, H. Xu, H. Zhao, J. Gao, D. Liang and Y. Li,
et al., Source apportionment of fine particulate matter at a megacity in China, using an improved regularization supervised PMF model, Sci. Total Environ., 2023, 879, 163198 CrossRef CAS PubMed
.
- EPA, Support Center for Regulatory Atmospheric Modeling (SCRAM), Air Quality Models, 2024, [cited 2024 Oct 12], Available from: https://www.epa.gov/scram/air-quality-models.
- P. K. Hopke, Q. Dai, L. Li and Y. Feng, Global review of recent source apportionments for airborne particulate matter, Sci. Total Environ., 2020, 740 Search PubMed
.
- W. Zhao, P. K. Hopke, E. W. Gelfand and N. Rabinovitch, Use of an expanded receptor model for personal exposure analysis in schoolchildren with asthma, Atmos. Environ., 2007, 41(19), 4084–4096 CrossRef CAS
.
- A. Zwoździak, I. Sówka, B. Krupińska, J. Zwoździak and A. Nych, Infiltration or indoor sources as determinants of the elemental composition of particulate matter inside a school in Wrocław, Poland?, Build. Environ., 2013, 66, 173–180 CrossRef
.
- P. Govender and V. Sivakumar, Application of k-means and hierarchical clustering techniques for analysis of air pollution: A review (1980–2019), Atmos. Pollut. Res., 2020, 11(1), 40–56 CrossRef CAS
.
- M. B. Ferraro and P. Giordani, A toolbox for fuzzy clustering using the R programming language, Fuzzy Sets Syst., 2015, 279, 1–16 CrossRef
.
- H. Jorquera and A. M. Villalobos, A new methodology for source apportionment of gaseous industrial emissions, J. Hazard. Mater., 2023, 443(Part B), 130335 CrossRef CAS PubMed
.
- L. Wallace, J. Bi, W. R. Ott, J. Sarnat and Y. Liu, Calibration of low-cost PurpleAir outdoor monitors using an improved method of calculating PM2.5, Atmos. Environ., 2021, 256, 118432 CrossRef CAS
.
- D. L. Robinson, N. Goodman and S. Vardoulakis, Five Years of Accurate PM2.5 Measurements Demonstrate the Value of Low-Cost PurpleAir Monitors in Areas Affected by Woodsmoke, Int. J. Environ. Res. Public Health, 2023, 20(23), 7127 CrossRef CAS PubMed
.
- D. C. Carslaw and K. Ropkins, Openair – An r package for air quality data analysis, Environ. Model. Softw., 2012, 27–28, 52–61 CrossRef
.
- I. Uria-Tellaetxe and D. C. Carslaw, Conditional bivariate probability function for source identification, Environ. Model. Softw., 2014, 59, 1–9 CrossRef
.
- M. B. Ferraro, P. Giordani and A. Serafini, fclust: An R Package for Fuzzy Clustering, The R Journal, 2019, 1–18 Search PubMed
.
- J. Rodríguez, A. M. Villalobos, J. Castro-Molinare and H. Jorquera, Local and NON-LOCAL source apportionment of black carbon and combustion generated PM2.5, Environ. Pollut., 2024, 1, 346 Search PubMed
.
- J. Rodríguez, M. Á. García, I. A. Pérez and H. Jorquera, Saharan dust contributions to high hourly PM10 concentrations at a background station in Southwestern Europe, Stoch. Environ. Res. Risk Assess., 2023, 37(10), 3779–3795 CrossRef
.
- O. G. Rose, D. Bousiotis, C. Rathbone and F. D. Pope, Investigating Indoor Air Pollution Sources and Student’s Exposure Within School Classrooms: Using a Low-Cost Sensor and Source Apportionment Approach, Indoor Air, 2024, 2024(1), 5544298 CrossRef CAS
.
- V. N. Matthaios, I. Holland, C. M. Kang, J. E. Hart, M. Hauptman and J. M. Wolfson,
et al., The effects of urban green space and road proximity to indoor traffic-related PM2.5, NO2, and BC exposure in inner-city schools, J. Exposure Sci. Environ. Epidemiol., 2024, 34, 745–752 CrossRef CAS PubMed
.
- S. Carbone, S. Saarikoski, A. Frey, F. Reyes, P. Reyes and M. Castillo,
et al., Chemical characterization of submicron Aerosol particles in Santiago de Chile, Aerosol Air Qual. Res., 2013, 13(2), 462–473 CrossRef CAS
.
- E. Gramsch, A. Muñoz, J. Langner, L. Morales, C. Soto and P. Pérez,
et al., Black carbon transport between Santiago de Chile and glaciers in the Andes Mountains, Atmos. Environ., 2020, 232, 117546 CrossRef CAS
.
- B. Pradhan, R. Jayaratne, H. Thompson and L. Morawska, An application of low-cost sensors to monitor children’s exposure to air pollution at five schools in Queensland, Australia, Atmos. Environ., 2024, 325, 120424 CrossRef CAS
.
- C. Chen and B. Zhao, Review of relationship between indoor and outdoor particles: I/O ratio, infiltration factor and penetration factor, Atmos. Environ., 2011, 45(2), 275–288 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4em00538d |
| This journal is © The Royal Society of Chemistry 2024 |