Open Access Article
Open Access ArticleDelocalisation enables efficient charge generation in organic photovoltaics, even with little to no energetic offset†
Daniel
Balzer
 and
Ivan
Kassal
and
Ivan
Kassal
 *
*
School of Chemistry, University of Sydney Nano Institute, University of Sydney, NSW 2006, Australia. E-mail: ivan.kassal@sydney.edu.au
First published on 8th February 2024
Abstract
Organic photovoltaics (OPVs) are promising candidates for solar-energy conversion, with device efficiencies continuing to increase. However, the precise mechanism of how charges separate in OPVs is not well understood because low dielectric constants produce a strong attraction between the charges, which they must overcome to separate. Separation has been thought to require energetic offsets at donor–acceptor interfaces, but recent materials have enabled efficient charge generation with small offsets, or with none at all in neat materials. Here, we extend delocalised kinetic Monte Carlo (dKMC) to develop a three-dimensional model of charge generation that includes disorder, delocalisation, and polaron formation in every step from photoexcitation to charge separation. Our simulations show that delocalisation dramatically increases charge-generation efficiency, partly by enabling excitons to dissociate in the bulk. Therefore, charge generation can be efficient even in devices with little to no energetic offset, including neat materials. Our findings demonstrate that the underlying quantum-mechanical effect that improves the charge-separation kinetics is faster and longer-distance hops between delocalised states, mediated by hybridised states of exciton and charge-transfer character.
In organic photovoltaics (OPVs), understanding how charges overcome their large Coulomb attraction to separate efficiently has remained elusive.1–3 Due to the low dielectric constants in organic semiconductors (εr ≈ 3–4), photoexcitation produces tightly bound excitons. To overcome the large exciton-binding energies and enable charges to separate, OPVs are made by blending donor and acceptor materials to form a heterojunction. At the donor–acceptor interface, the offset between the energy levels of the two materials produces a driving force to dissociate the exciton, resulting in one of the charges moving across the interface to form a slightly separated charge-transfer (CT) state. Nevertheless, charges in a CT state are still coulombically bound to each other with a strength more than an order of magnitude larger than the available thermal energy, an obstacle they must overcome to separate. The efficiency of the separation process is the internal quantum efficiency (IQE), the proportion of excitons that generate separated charges. The near-unity IQE in some OPVs has been attributed to delocalisation, with several groups observing efficient and fast separation of delocalised charges.4–9 The delocalisation enhancement has been attributed to a reduced electron–hole binding energy when the charges in a CT state delocalise and their separation increases. However, charge separation is a multi-step process, and when disorder and entropy are considered, the free-energy barrier to separation disappears10 and actually increases when delocalisation is included,11 indicating that delocalisation enhancements must come from non-equilibrium kinetic effects, rather than solely energetic ones.11,12 Therefore, a full kinetic model is required for studying the effects of delocalisation on charge separation. Significant progress has been made towards this goal, with many kinetic models including delocalisation and finding improved efficiencies.13–24 However, the computational difficulty of tracking the correlated motion of two quantum-mechanically delocalised charges limits these simulations to small systems or reduced dimensionality. Recently, we overcame this challenge to produce three-dimensional simulations of charge separation, finding that delocalisation enhancements to CT-separation efficiency are indeed a kinetic effect, with improved IQE even though delocalisation increases the binding energy.25
Recent developments have further challenged conventional assumptions about the mechanism of charge generation. In particular, non-fullerene acceptors (NFAs) have produced efficient OPV devices26–28 without the large energetic offsets thought to be required for exciton dissociation.3,29,30 Explaining this observation is an outstanding theoretical challenge,3 with one hypothesis being that low offsets enable the formation of hybridised states with the character of both excitons and separated charges.31–34 Furthermore, experimental evidence suggests that delocalised and partially separated intermediate states form within NFA phases before reaching an interface,27,35–40 suggesting separation may not proceed through the typical pathway involving interfacial CT states. An even greater theoretical challenge is explaining the detection of free carriers in devices made of neat materials, where there is no interfacial energetic offset, including Y6.41–43
Here, we show that delocalisation can enable efficient charge generation in OPVs with little or no energetic offset. To do so, we extend our delocalised kinetic Monte Carlo (dKMC) algorithm—which has already been used to show that delocalisation improves charge and exciton transport44,45 and the separation of charges from a CT state25—to consider the full charge generation process, from excitons to separated charges. dKMC includes all of the essential ingredients: disorder, delocalisation, and polaron formation. We find that delocalisation produces large charge-generation improvements, especially in systems with little to no energetic offset, helping to explain the efficient low-offset and homojunction devices. The mechanism of the improved exciton dissociation is a kinetic, quantum effect: delocalised hops of greater speed and distance, mediated by hybridised states, allow separation to out-compete recombination. Overall, our findings support both of the hypotheses above, that delocalisation enables excitons to fully or partially separate in the bulk of one phase and that charge generation involves hybridisation of exciton and weakly bound states.
I. Methods
We begin by describing the dKMC model of charge generation. The details of the underlying quantum master equation, the approximations, and the full algorithm are in Secs. S1–S5 of the ESI.†A. Model
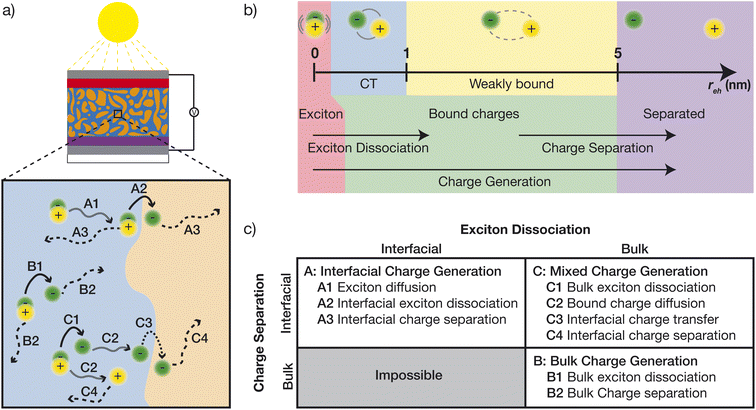
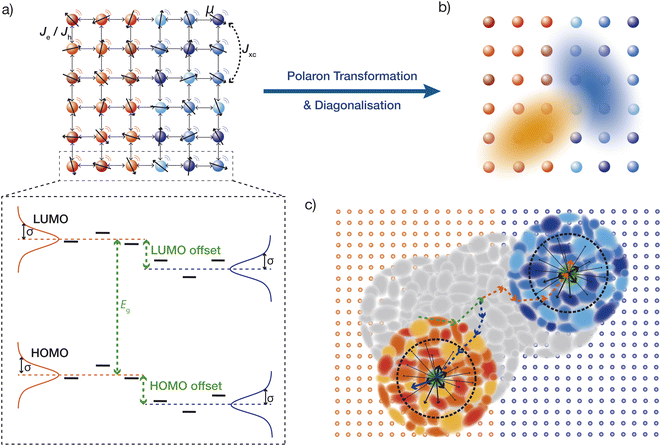
We model an OPV heterojunction using a tight-binding model on a cubic lattice with lattice spacing a and Nd sites (molecules or parts of molecules), where N is the number of sites along each of d dimensions. The left Nd/2 sites represent the donor and the rest the acceptor (Fig. 2a). Every site is assigned a randomly oriented transition dipole moment μn with constant magnitude μ as well as HOMO and LUMO energies for a hole or an electron occupying that site, respectively.Energetic disorder is modelled by drawing site energies from Gaussian distributions 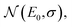 centred on E0 and with standard deviation σ measuring the disorder.46 There are four distributions (Fig. 2): the donor HOMO energy centred at 0, the donor LUMO centred at Eg, the acceptor HOMO centred at −EHOMOoffset, and the acceptor LUMO centred at Eg − ELUMOoffset.
centred on E0 and with standard deviation σ measuring the disorder.46 There are four distributions (Fig. 2): the donor HOMO energy centred at 0, the donor LUMO centred at Eg, the acceptor HOMO centred at −EHOMOoffset, and the acceptor LUMO centred at Eg − ELUMOoffset.
The energies drawn from these four distributions must be correlated to ensure that the exciton disorder is smaller than the electronic disorder. For uncorrelated LUMO and HOMO energies with disorders σLUMO and σHOMO and a constant exciton-binding energy Eb, the disorder in the exciton energy Exc = ELUMO − EHOMO − Eb would be 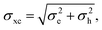 which is larger than either electronic disorder. However, σxc should be less than σe and σh because local electrostatic variations shift HOMO and LUMO energies in the same direction (Fig. 2a). Therefore, we correlate the HOMO and LUMO energies to achieve a correlation ρ = Cov(ELUMO,EHOMO)/σHOMOσLUMO, which gives σ2xc = σ2LUMO + σ2HOMO − 2Cov(ELUMO,EHOMO). Assuming for simplicity that σ = σLUMO = σHOMO leads to ρ = 1 − σ2xc/2σ2, meaning that σxc can be chosen independently of σ. The correlated energies for the donor are drawn from the bivariate normal distribution
which is larger than either electronic disorder. However, σxc should be less than σe and σh because local electrostatic variations shift HOMO and LUMO energies in the same direction (Fig. 2a). Therefore, we correlate the HOMO and LUMO energies to achieve a correlation ρ = Cov(ELUMO,EHOMO)/σHOMOσLUMO, which gives σ2xc = σ2LUMO + σ2HOMO − 2Cov(ELUMO,EHOMO). Assuming for simplicity that σ = σLUMO = σHOMO leads to ρ = 1 − σ2xc/2σ2, meaning that σxc can be chosen independently of σ. The correlated energies for the donor are drawn from the bivariate normal distribution
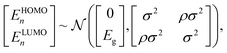 | (1) |
while those for the acceptor are drawn in the same way, but shifted by [−EHOMOoffset,−ELUMOoffset]. Throughout this work, we assume σ = 150 meV and σxc = 30 meV, corresponding to ρ = 0.98.
As exciton dissociation is a two-particle problem, the Hilbert space is spanned by site-pairs |m,n〉, which describe an electron on site m and a hole on site n. In this basis, the system is described by the Hamiltonian
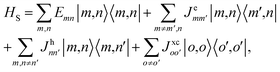 | (2) |
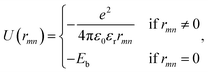 | (3) |
Eqn (2) shows that site-pair |m,n〉 is coupled to other site-pairs |m′,n′〉 in three cases. First, if only the electron is moving (n = n′), the two site-pairs are coupled by the electron coupling 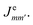 Second, if only the hole is moving (m = m′), they are coupled by the hole coupling
Second, if only the hole is moving (m = m′), they are coupled by the hole coupling 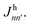 We assume constant, nearest–neighbour Je and Jh, but this assumption could easily be relaxed to allow for disordered or non-nearest–neighbour couplings. Third, if both site-pairs represent excitons (m = n = o and m′ = n′ = o'), they are coupled by the long-range dipole–dipole coupling
We assume constant, nearest–neighbour Je and Jh, but this assumption could easily be relaxed to allow for disordered or non-nearest–neighbour couplings. Third, if both site-pairs represent excitons (m = n = o and m′ = n′ = o'), they are coupled by the long-range dipole–dipole coupling 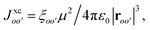 where the distance vector between o and o′ is roo′ and the orientation factor is
where the distance vector between o and o′ is roo′ and the orientation factor is 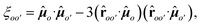 with hats indicating unit vectors.
with hats indicating unit vectors.
The environment is modelled as an independent bath of harmonic oscillators on each site,47,48
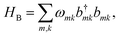 | (4) |
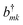 and bmk.
and bmk.
The interaction between the system and the environment is modelled as a linear coupling of each site to each of its bath modes, with separate coupling strengths for electrons gemk, holes, and excitons gxcok,
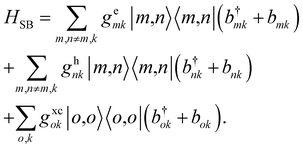 | (5) |
Crucial to OPVs is the formation of polarons, quasi-particles consisting of charges or excitons dressed by the induced distortion in the environment.49,50 Polarons are incorporated using the polaron transformation51
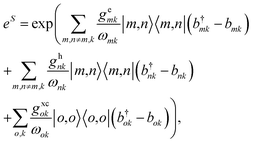 | (6) |
which displaces bath modes and transforms the entire Hamiltonian (H = HS + HB + HSB) into the polaron-transformed version, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) = eSHe−S =
= eSHe−S = ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) S +
S + ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) B +
B + ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) SB, given in Sec. S1 of the ESI.†
SB, given in Sec. S1 of the ESI.†
B. Polaron states
The polaron states are the eigenstates of the polaron-transformed system Hamiltonian![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) S and represent the simultaneous state of the delocalised electron and hole in the polaron frame (Fig. 2b).
S and represent the simultaneous state of the delocalised electron and hole in the polaron frame (Fig. 2b).
The polaron transformation leads to spatially smaller states, which are computationally more manageable. This occurs because the transformation decreases the electronic couplings, reducing eigenstate delocalisation.52 We quantify the delocalisation of a polaron state |ν〉 using the inverse participation ratio (IPR)
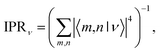 | (7) |
a measure of how many site-pairs |m,n〉 the polaron state is spread across. The extent of delocalisation is determined by the parameters in the model: electronic couplings and transition dipole moments increase IPRs, while disorder and system-bath coupling decrease them.
We classify the polaron states into categories based on their overlaps with the different types of site-pairs shown in Fig. 1b: exciton site-pairs, bound site-pairs (which are either CT site-pairs or weakly bound site-pairs), and separated site-pairs. Every polaron has an overlap with each of these types of site-pairs; for example, the exciton character of polaron |ν〉 is ∑o|〈o,o|ν〉|2 and its separated-charge character is ∑m,n|〈m,n|ν〉|2, where the sum goes over site-pairs |m,n〉 in which the electron–hole separation exceeds rsep = 5 nm. We classify the polaron states by which type of site-pair they overlap with the most. For example, exciton states have most of their population on exciton site-pairs. In addition, a state is hybridised if it has more than 25% of its population on both exciton and non-exciton site-pairs.
Fig. 3 shows the polaron states found by diagonalising a representative ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) S. At small electron–hole separations, the Coulomb attraction is largest, reducing the energy of the states. For small couplings (Fig. 3a), each state is approximately a site-pair, meaning they are localised close to the lattice. However, for higher couplings (Fig. 3b), the states become delocalised and are no longer centred close to the lattice. Furthermore, a significant number of hybridised states only forms in the higher-couplings case. The IPRs of the states as a function of energy are included in Sec. S7 of the ESI.†
S. At small electron–hole separations, the Coulomb attraction is largest, reducing the energy of the states. For small couplings (Fig. 3a), each state is approximately a site-pair, meaning they are localised close to the lattice. However, for higher couplings (Fig. 3b), the states become delocalised and are no longer centred close to the lattice. Furthermore, a significant number of hybridised states only forms in the higher-couplings case. The IPRs of the states as a function of energy are included in Sec. S7 of the ESI.†
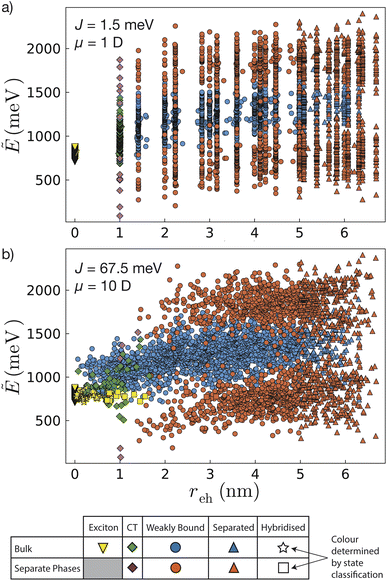 | ||
Fig. 3 Delocalised polaron states. Energy Ẽ and electron–hole separation reh of polaron states of a representative ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) S for (a) small couplings and dipole moments (J = 1.5 meV, μ = 1 D) and (b) large ones (J = 67.5 meV, μ = 10 D). States are classified based on which type of site-pair they overlap with the most and whether the electron and the hole in those site-pairs are predominantly in the bulk (same phase) or in separate phases. The two bands of separate-phase states correspond to whether the electron is in the donor and the hole in the acceptor or vice versa. For small couplings, the states are localised to about one site-pair centred on the lattice, with no hybridised states forming. When the couplings are larger, states become delocalised, are no longer centred on the lattice, and can be hybridised, with both exciton and non-exciton character. All results are in 2D for ELUMOoffset = EHOMOoffset = 500 meV, and the other simulation parameters are in Sec. S6 of the ESI.† S for (a) small couplings and dipole moments (J = 1.5 meV, μ = 1 D) and (b) large ones (J = 67.5 meV, μ = 10 D). States are classified based on which type of site-pair they overlap with the most and whether the electron and the hole in those site-pairs are predominantly in the bulk (same phase) or in separate phases. The two bands of separate-phase states correspond to whether the electron is in the donor and the hole in the acceptor or vice versa. For small couplings, the states are localised to about one site-pair centred on the lattice, with no hybridised states forming. When the couplings are larger, states become delocalised, are no longer centred on the lattice, and can be hybridised, with both exciton and non-exciton character. All results are in 2D for ELUMOoffset = EHOMOoffset = 500 meV, and the other simulation parameters are in Sec. S6 of the ESI.† | ||
C. dKMC dynamics
dKMC propagates the dynamics through hops among the partially delocalised polaron states (Fig. 2c). The polaron transformation allows a perturbative treatment of the dynamics by moving most of the system-bath interaction into the polaron itself. As a result, the polaron interacts relatively weakly with its environment and this remaining coupling can often be treated perturbatively.51 Treating the perturbation to second order leads to the secular polaron-transformed Redfield master equation (sPTRE)53 for transition rates between polaron states, as described in Sec. S2 of the ESI.† dKMC is a kinetic Monte Carlo procedure that tracks (and subsequently averages over) individual trajectories through the polaron states using sPTRE rates, in a similar way to how standard KMC uses Marcus or Miller-Abrahams rates to track classical trajectories across sites. The details are given in Secs. S3–S5 of the ESI.†![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) S that describes a neighbourhood of the selected excitation location that is large enough to contain the states the initial exciton is likely to hop to (Fig. 2c). The size of the neighbourhood is calibrated to ensure accuracy as described previously45 and in Sec. S3 of the ESI.† Finally, the initial exciton state is chosen at random among exciton states centred within 1 nm of the excitation location, and in proportion to their oscillator strengths, which describe the probability that they would be excited by light.
S that describes a neighbourhood of the selected excitation location that is large enough to contain the states the initial exciton is likely to hop to (Fig. 2c). The size of the neighbourhood is calibrated to ensure accuracy as described previously45 and in Sec. S3 of the ESI.† Finally, the initial exciton state is chosen at random among exciton states centred within 1 nm of the excitation location, and in proportion to their oscillator strengths, which describe the probability that they would be excited by light.
At each step, the polaron state can also recombine due to its overlap with exciton site-pairs or CT site-pairs. The expressions for these rates are given in Sec. S4 of the ESI,† and take the form of constant recombination rates modified by the square of amplitudes on site-pairs that can recombine, as in previous work.25,54,55
As in KMC, one hopping destination (including recombination) is chosen probabilistically in proportion to the size of the corresponding rates. The current state and the elapsed time are updated, before diagonalising a new subset of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) S, centred on the new state.
S, centred on the new state.
The complete algorithm above is repeated for ntraj trajectories and on niters realisations of disorder. These numbers determine the uncertainty of the calculations and, in our calculations, are chosen so that the standard error of the mean in IQE calculations is never more than 2 percentage points (the values are listed in Sec. S6 of the ESI).† Finally, the IQE is calculated as the proportion of trajectories that separate.
D. Pathways of delocalised charge generation
As a framework for analysing our results, we describe the three pathways for charge generation, illustrated in Fig. 1. Charge generation is the full conversion of excitons into separated charges, and can be divided into two steps (Fig. 1b). Exciton dissociation, involves an exciton dissociating into a bound state, either a CT state or a weakly bound state. After that, charge separation is the separation of a bound state into separated charges.Both steps—exciton dissociation and charge separation—can occur using the interface or entirely in the bulk of a single phase. The combinations of these possibilities lead to the three charge-generation pathways in Fig. 1a. Interfacial charge generation (pathway A) is the conventional pathway involving interfacial exciton dissociation and interfacial charge separation, i.e., the exciton dissociates at the interface and the charges then separate in the different phases. In bulk charge generation (pathway B), both the exciton dissociation and the charge separation occur in the same phase. Finally, mixed charge generation (pathway C) involves bulk exciton dissociation followed by interfacial charge separation. A combination involving interfacial exciton dissociation and bulk charge separation is not possible because interfacial exciton dissociation yields charges on different sides of the interface, whose separation cannot occur in the bulk of one phase.
II. Results and discussion
A. Delocalisation increases the IQE
To determine the effect of delocalisation on charge generation, we compare the IQE predicted by dKMC (which includes delocalisation) to that predicted by standard KMC (which does not include it). KMC results are calculated for localised charges hopping between sites using a Marcus-theory rate,56 which is the localised limit of charge transport reproduced by dKMC in the correct regime (e.g., weak inter-site coupling or strong system-bath coupling). Fig. 4a and b shows the two IQEs as a function of the electronic coupling J and the transition dipole moment μ; these parameters independently increase the delocalisation of charges and excitons (other parameters being fixed), allowing the effect of charge and exciton delocalisation to be independently assessed. At small J and μ, the IQEs predicted by dKMC and KMC agree, as expected in the limit of localised states. As J and μ increase, the IQE predicted by dKMC increases compared to classical KMC, demonstrating that both charge and exciton delocalisation improve charge generation. Over our parameter ranges, we see up to a 5× enhancement in 2D, and as much as 3× in 3D, despite the more modest J and μ.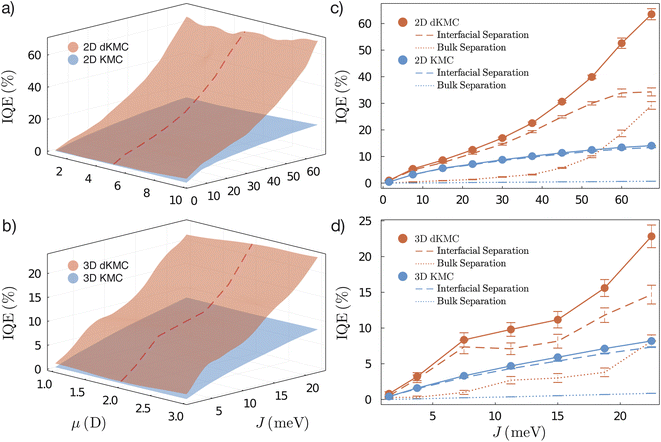 | ||
| Fig. 4 Delocalisation enhances charge generation. (a and b) IQE of charge generation predicted by KMC (blue) and dKMC (orange) as a function of electronic coupling J and transition dipole moment μ in (a) 2D and (b) 3D. As J and μ increase, and the charges and excitons become more delocalised, the IQE predicted by dKMC increases compared to KMC, showing that both charge and exciton delocalisation improve charge generation, increasing the IQE by up to 5× in 2D, and 3× in 3D. (c and d) For a slice of the 2D and 3D results, indicated by the red dashed line in (a and b), the IQE is split into additive contributions due to trajectories where charges separate across the interface (pathways A and C) and trajectories where they separate entirely in one phase (pathway B). In both 2D and 3D, delocalisation both helps charges separate across the interface and enables them to separate in the bulk, without the assistance of interfacial energetic offsets. We set ELUMOoffset = EHOMOoffset = 500 meV and the other simulation parameters are in Sec. S6 of the ESI.† The error bars are the standard errors of the mean (see text for details). | ||
The surfaces in Fig. 4, as well as our other results, are not perfectly monotonic due to the stochastic nature of the simulations, which require averaging over ntraj trajectories on each of niters realisations of disorder. Error bars in figures provide the standard errors of the mean in each case, and could be reduced by increasing ntraj and niters. With the current choices of ntraj and niters, the standard errors of the mean in IQE calculations were less than 2 percentage points.
B. Delocalisation enables charge generation without energetic offsets
Delocalisation enhances the IQE both by enhancing charge generation involving the interface and by enabling charge generation in the bulk of a single phase. In Fig. 4c and d, we split the IQE into contributions due to interfacial charge separation—trajectories that separate across the interface, so that the electron and hole are on opposite sides (pathways A and C)—from those due to bulk charge separation—trajectories that separate completely in one phase, with the electron and hole on the same side of the interface (pathway B). As J increases and the charges become more delocalised, dKMC predicts an enhancement in the number of trajectories separating across the interface compared to KMC (up to 3× in 2D and 2× in 3D for our parameter choices), demonstrating that both charge and exciton delocalisation are beneficial at improving interfacial charge separation. However, Fig. 4c and d reveals that delocalisation also enables charges to separate in the bulk of one phase via pathway B, i.e., without the assistance of an interfacial energetic offset. In both 2D and 3D, KMC predicts a negligible bulk-separation IQE, as expected for localised charges, which struggle to overcome the exciton binding energy without the interfacial energetic offset providing a driving force. However, as J increases and the states become delocalised, dKMC shows that excitons are able to separate efficiently within a single material, especially in 3D. Compared to KMC, there is an enhancement of up to 47× in 2D and already 12× in 3D for the smaller J and μ. Therefore a large proportion of delocalised charge generation occurs in the bulk without the assistance of an interfacial offset.Indeed, delocalisation enables efficient charge generation even in a single phase (a homojunction), without energetic offset to assist in separation. Fig. 5 shows the IQE for a homojunction, with KMC again unable to predict efficient separation at any J and μ. However, when the states are delocalised, at high J and μ, dKMC predicts considerable IQEs, with enhancements of 48× in 2D, and already 11× in 3D for modest J and μ. This demonstration that delocalisation can enable charge generation in a homojunction could explain observations of charge generation in neat Y6.35,41,43
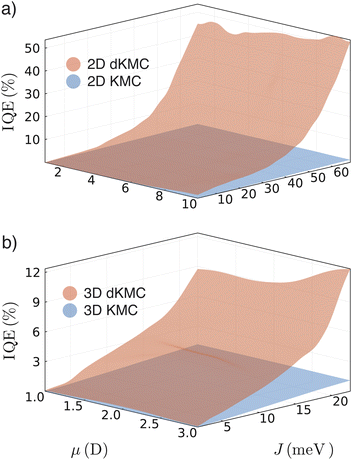 | ||
| Fig. 5 Delocalisation enables charge generation without energetic offsets. IQE of charge generation in a homojunction (no interfacial energetic offset) predicted by KMC (blue) and dKMC (orange) as a function of the electronic coupling J and transition dipole moment μ in (a) 2D (b) and 3D. Both charge and exciton delocalisation improve the efficiency, especially in 3D. Simulation parameters are in Sec. S6 of the ESI,† except that ELUMOoffset = EHOMOoffset = 0. | ||
C. Energetic offsets are still beneficial for delocalised charge generation
Of course, interfacial energetic offsets are beneficial even with delocalisation because they can still drive interfacial charge separation. Fig. 6 shows heterojunction IQEs for varying LUMO offset, finding that for KMC to predict significant charge generation, a large offset is required. By contrast, dKMC predicts charge generation at all offsets, including small ones and even zero (as in the homojunctions above), a finding that could help explain efficient low-offset NFA devices.3,29,30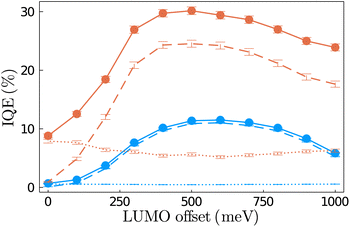 | ||
| Fig. 6 Interfacial energetic offsets remain beneficial with delocalisation. IQE predicted by KMC (blue dots) and dKMC (orange dots) in 2D. Dashed lines are the contributions to the IQE from trajectories where charges separate across the interface (pathways A and C) and dotted lines are contributions from trajectories that separate in the bulk (pathway B). With KMC, large energetic offsets are required to see significant charge generation. By contrast, with dKMC, delocalisation enables charge generation in the bulk without interfacial energetic offsets. However, even though the interface is not required, it still improves interfacial charge generation by providing a driving force to dissociate excitons and by further separating states that have dissociated in the bulk but not fully separated. We set J = 45 meV, μ = 5 D, EHOMOoffset = 500 meV, and the other simulation parameters are in Sec. S6 of the ESI.† The error bars are the standard errors of the mean (see text for details). | ||
However, Fig. 6 also shows that driving forces are still helpful for delocalised charge generation by improving separation across the interface. This improvement arises for two reasons.
First, as in conventional theories, an energetic offset helps dissociate excitons that would otherwise recombine in the bulk. Our results share another feature of classical theories based on Marcus theory, the inverted regime at very high offsets, where the transition is so far energetically downhill that the charge-transfer rates across the interface decrease.
The second benefit of the offset, which is not seen in conventional theories, is enabling mixed charge generation (pathway C in Fig. 1). Mixed charge generation occurs when an exciton dissociates in the bulk to a bound state without fully separating, and the bound state then uses an interface for the charges to separate completely. Our finding that delocalisation enables mixed charge generation supports the hypothesis of delocalised, partially separated intermediate states forming in single domains before they reach the interface.27,35–40
D. Mechanism of delocalisation enhancements
Microscopically, the enhancements above arise because delocalisation enables longer and faster hops, which can bypass CT states and involve hybridised states instead. To see this, we note that delocalisation can improve overall charge generation by enhancing either the exciton-dissociation or the charge-separation steps in Fig. 1b. Previously, we described that delocalisation benefits charge separation by increasing the overlaps between states to kinetically assist charges in overcoming their Coulomb attraction.25 And once separated, delocalised charges are more easily extracted because the longer and faster hops increase their mobilities.44 Having extended dKMC to include excitons, we can now show that delocalisation benefits exciton dissociation in the same way, by accelerating long-distance hopping.To understand the delocalisation enhancement of exciton dissociation, we study the exciton–dissociation event, the last hop in each trajectory out of an exciton state and into a non-exciton one. To do so, we identify trajectories where charges have separated, find the hop where the state character changed from predominantly exciton to non-exciton, and then analyse the two states immediately before and after the hop. In the following analysis, we study both types of exciton–dissociation events—at the interface and in the bulk—together, as the mechanism by which delocalisation improves them is the same (see Sec. S8 of the ESI).†
Delocalised charges hop further out of an exciton during dissociation (Fig. 7a) and they do so faster (Fig. 7b). Fig. 7a shows that when charges are localised, or when classical KMC is used, the separation after leaving an exciton state is 1 lattice spacing, as expected for charges forming a tightly bound CT state. For dKMC, as the states become more delocalised with increasing couplings, the charges can hop further out of the exciton state, causing reh to exceed 1 lattice spacing. The ability to hop further provides the additional benefit of more possible hopping destinations, which can be important in disordered materials and when dissociating an exciton in systems with little or no energetic offset. The larger overlaps between delocalised states also increase the speed of individual hops, allowing for faster hopping out of the exciton state (Fig. 7b).
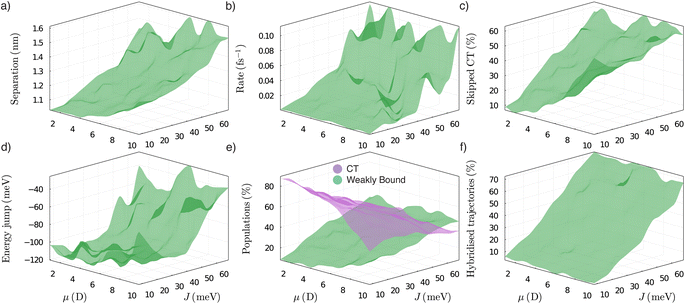 | ||
| Fig. 7 The mechanism of delocalisation enhancement of exciton dissociation. Delocalisation enables charges to hop further and faster out of an exciton, allowing them to skip CT states and use hybridised states. (a) As delocalisation increases with electronic coupling J and transition dipole moment μ, charges hop further out of the exciton. Shown is the mean electron–hole separation in the first state following exciton dissociation. (b) Excitons dissociate faster with delocalised states, as shown by the rate of the exciton dissociation event. (c) Because of longer-range hopping, the fraction of separated trajectories that skip CT states increases with the couplings. (d) By skipping CT states, trajectories that are more delocalised can avoid large downhill hops, meaning they are less likely to become trapped in low-energy CT states. Shown is the average energy lost during the exciton dissociation event. (e) As couplings increase, and states become more delocalised, the character of the first bound state following exciton dissociation changes from CT state to weakly bound state. Shown are the mean populations of this state on CT and weakly bound site-pairs. (f) With stronger couplings, exciton dissociation is more likely to involve a hybridised state. Shown is the fraction of separated trajectories where exciton dissociation involves a state with more than 25% of both exciton and non-exciton character. All results are in 2D for ELUMOoffset = EHOMOoffset = 500 meV, and the other simulation parameters are in Sec. S6 of the ESI.† | ||
The longer hopping distance means that charges departing exciton states can often skip CT states, as shown by the proportion of separating trajectories that skip CT states in Fig. 7c. Because CT states tend to be tightly bound, skipping them means that a trajectory can avoid deeply downhill hops, which risk trapping it in a low-energy CT state. As shown in Fig. 7d, the average energy lost upon hopping out of an exciton is indeed less for more delocalised states.
The enhancements above are facilitated by strong couplings, which also change the character of the states involved. As the delocalised charges hop further, the first separated state has less CT character and more weakly bound character, as shown in Fig. 7e. Indeed, the strong couplings cause the formation of hybridised states, whose prevalence increases for more delocalised states (Fig. 7f). This result supports the hypothesis that hybridisation is involved in delocalised charge separation.31–34
E. Outlook
Our results are the first three-dimensional simulations of charge generation that include disorder, delocalisation, and polaron formation. They are possible because dKMC reduces the computational cost of sPTRE by as much as 54 orders of magnitude (see Sec. S3 of the ESI).†dKMC is a general method, and our concrete parameter choices could easily be altered. For example, we assumed isotropic couplings Je and Jh for concreteness, but they could be made anisotropic to simulate, say, stronger couplings along polymer chains. Similarly, site energies could be arranged to simulate morphologies other than the bilayer.
However, three-dimensional dKMC remains limited by its computational complexity to moderate couplings and transition dipole moments (see Fig. 4 and 5). Future work may extend these calculations using further simplifications to dKMC, such as jKMC.57
Furthermore, dKMC is limited by approximations in the underlying sPTRE, which could be relaxed if necessary, albeit at increased computational expense. For example, sPTRE is accurate in the regimes studied here,53,58 but can become inaccurate for systems weakly coupled to slow baths.58 To treat such systems, the full polaron transformation could be replaced with a variational version.59,60 The secular approximation ignores coherences, which is ordinarily valid because sunlight does not induce coherences61–68 and even if they were induced otherwise, they would not survive on charge-transport timescales. However, if required, coherences could be tracked at additional computational expense by not making the secular approximation and tracking the entire density matrix. Finally, sPTRE uses a local system-bath coupling, as is relevant for disordered molecular systems,48 but to treat organic crystals, non-local system-bath couplings may need to be included to describe the fluctuations of electronic couplings.69–71
We expect that using dKMC in multiscale simulations could enable a full device model that incorporates delocalisation. This would involve parameterising dKMC using atomistic simulations, such as molecular mechanics followed by electronic-structure calculations. The results of dKMC could then parameterise drift-diffusion models for computing device properties. We also expect that dKMC can be extended to model other fundamental processes in organic devices, such as singlet fission, which is theoretically similar to charge generation.
III. Conclusion
Extending dKMC to the full charge-separation process, from excitons to separated charges, explains observations of efficient charge separation in disordered OPVs, especially those with little to no energetic offset. dKMC reveals that delocalisation produces large IQEs compared to those predicted by classical KMC. Delocalisation does so by enabling separated charges to be generated in the bulk and by enabling charges to hop faster and further out of an exciton during dissociation, mediated by hybridised states. Together with past dKMC studies, our results show that delocalisation accelerates all the fundamental processes in organic electronics—charge transport,44 exciton diffusion,45 charge separation,25 and exciton dissociation (this work)—in essentially the same way, by allowing polaron states to hop further and faster. We anticipate that this new mechanistic understanding of charge generation in OPVs will explain the performance of efficient low-offset heterojunctions and neat devices and help design more efficient future ones.Data availability
All data needed to evaluate the conclusions in the paper are present in the paper.Author contributions
D. B. developed the theory, carried out the calculations, analyzed the data, and wrote the manuscript. Both authors conceived the project idea and edited the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We were supported by a Westpac Scholars Trust Future Leaders Scholarship, the Australian Research Council (DP220103584), the Australian Government Research Training Program, and by computational resources from the National Computational Infrastructure (Gadi) and the University of Sydney Informatics Hub (Artemis).References
- T. M. Clarke and J. R. Durrant, Charge photogeneration in organic solar cells, Chem. Rev., 2010, 110, 6736 CrossRef CAS PubMed.
- S. Few, J. M. Frost and J. Nelson, Models of charge pair generation in organic solar cells, Phys. Chem. Chem. Phys., 2015, 17, 2311 RSC.
- J. Hou, O. Inganäs, R. H. Friend and F. Gao, Organic solar cells based on non-fullerene acceptors, Nat. Mater., 2018, 17, 119 CrossRef CAS PubMed.
- A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, The role of driving energy and delocalized states for charge separation in organic semiconductors, Science, 2012, 335, 1340 CrossRef CAS PubMed.
- A. E. Jailaubekov, A. P. Willard, J. R. Tritsch, W.-L. Chan, N. Sai, R. Gearba, L. G. Kaake, K. J. Williams, K. Leung, P. J. Rossky and X.-Y. Zhu, Hot charge-transfer excitons set the time limit for charge separation at donor/acceptor interfaces in organic photovoltaics, Nat. Mater., 2013, 12, 66 CrossRef CAS PubMed.
- G. Grancini, M. Maiuri, D. Fazzi, A. Petrozza, H.-J. Egelhaaf, D. Brida, G. Cerullo and G. Lanzani, Hot exciton dissociation in polymer solar cells, Nat. Mater., 2013, 12, 29 CrossRef CAS PubMed.
- S. Gélinas, A. Rao, A. Kumar, S. L. Smith, A. W. Chin, J. Clark, T. S. van der Poll, G. C. Bazan and R. H. Friend, Ultrafast long-range charge separation in organic semiconductor photovoltaic diodes, Science, 2014, 343, 512 CrossRef PubMed.
- S. M. Falke, C. A. Rozzi, D. Brida, M. Maiuri, M. Amato, E. Sommer, A. De Sio, A. Rubio, G. Cerullo, E. Molinari and C. Lienau, Coherent ultrafast charge transfer in an organic photovoltaic blend, Science, 2014, 344, 1001 CrossRef CAS PubMed.
- Y. Tamai, Y. Fan, V. O. Kim, K. Ziabrev, A. Rao, S. Barlow, S. R. Marder, R. H. Friend and S. M. Menke, Ultrafast long-range charge separation in nonfullerene organic solar cells, ACS Nano, 2017, 11, 12473 CrossRef CAS PubMed.
- S. N. Hood and I. Kassal, Entropy and disorder enable charge separation in organic solar cells, J. Phys. Chem. Lett., 2016, 7, 4495 CrossRef CAS PubMed.
- A. Gluchowski, K. L. Gray, S. N. Hood and I. Kassal, Increases in the charge separation barrier in organic solar cells due to delocalization, J. Phys. Chem. Lett., 2018, 9, 1359 CrossRef CAS PubMed.
- L. Shi, C. K. Lee and A. P. Willard, The enhancement of interfacial exciton dissociation by energetic disorder is a nonequilibrium effect, ACS Cent. Sci., 2017, 3, 1262 CrossRef CAS PubMed.
- H. Tamura and I. Burghardt, Ultrafast charge separation in organic photovoltaics enhanced by charge delocalization and vibronicly hot exciton dissociation, J. Am. Chem. Soc., 2013, 135, 16364 CrossRef CAS PubMed.
- E. R. Bittner and C. Silva, Noise-induced quantum coherence drives photo-carrier generation dynamics at polymeric semiconductor heterojunctions, Nat. Commun., 2014, 5, 3119 CrossRef PubMed.
- Z. Sun and S. Stafström, Dynamics of charge separation at an organic donor-acceptor interface, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 115420 CrossRef.
- S. L. Smith and A. W. Chin, Ultrafast charge separation and nongeminate electron–hole recombination in organic photovoltaics, Phys. Chem. Chem. Phys., 2014, 16, 20305 RSC.
- S. L. Smith and A. W. Chin, Phonon-assisted ultrafast charge separation in the pcbm band structure, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 201302 CrossRef.
- V. Abramavicius, V. Pranculis, A. Melianas, O. Inganäs, V. Gulbinas and D. Abramavicius, Role of coherence and delocalization in photo-induced electron transfer at organic interfaces, Sci. Rep., 2016, 6, 32914 CrossRef CAS PubMed.
- G. D'Avino, L. Muccioli, Y. Olivier and D. Beljonne, Charge separation and recombination at polymer–fullerene heterojunctions: Delocalization and hybridization effects, J. Phys. Chem. Lett., 2016, 7, 536 CrossRef PubMed.
- V. Janković and N. Vukmirović, Origin of space-separated charges in photoexcited organic heterojunctions on ultrafast time scales, Phys. Rev. B, 2017, 95, 075308 CrossRef.
- V. Janković and N. Vukmirović, Combination of charge delocalization and disorder enables efficient charge separation at photoexcited organic bilayers, J. Phys. Chem. C, 2018, 122, 10343 CrossRef.
- Y. Yan, L. Song and Q. Shi, Understanding the free energy barrier and multiple timescale dynamics of charge separation in organic photovoltaic cells, J. Chem. Phys., 2018, 148, 84109 CrossRef PubMed.
- V. Janković and N. Vukmirović, Energy-temporal pathways of free-charge formation at organic bilayers: Competition of delocalization, disorder, and polaronic effects, J. Phys. Chem. C, 2020, 124, 4378 CrossRef.
- W.-T. Peng, D. Brey, S. Giannini, D. Dell'Angelo, I. Burghardt and J. Blumberger, Exciton dissociation in a model organic interface: Excitonic state-based surface hopping versus multiconfigurational time-dependent hartree, J. Phys. Chem. Lett., 2022, 13, 7105 CrossRef CAS PubMed.
- D. Balzer and I. Kassal, Even a little delocalization produces large kinetic enhancements of charge-separation efficiency in organic photovoltaics, Sci. Adv., 2022, 8, eabl9692 CrossRef CAS PubMed.
- C. Li, J. Zhou, J. Song, J. Xu, H. Zhang, X. Zhang, J. Guo, L. Zhu, D. Wei, G. Han, J. Min, Y. Zhang, Z. Xie, Y. Yi, H. Yan, F. Gao, F. Liu and Y. Sun, Non-fullerene acceptors with branched side chains and improved molecular packing to exceed 18% efficiency in organic solar cells, Nat. Energy, 2021, 6, 605 CrossRef CAS.
- L. Zhu, J. Zhang, Y. Guo, C. Yang, Y. Yi and Z. Wei, Small exciton binding energies enabling direct charge photogeneration towards low-driving-force organic solar cells, Angew. Chem., Int. Ed., 2021, 60, 15348 CrossRef CAS PubMed.
- Z. Zheng, J. Wang, P. Bi, J. Ren, Y. Wang, Y. Yang, X. Liu, S. Zhang and J. Hou, Tandem organic solar cell with 20.2% efficiency, Joule, 2022, 6, 171 CrossRef CAS.
- H. Bin, L. Gao, Z.-G. Zhang, Y. Yang, Y. Zhang, C. Zhang, S. Chen, L. Xue, C. Yang, M. Xiao and Y. Li, 11.4% Efficiency non-fullerene polymer solar cells with trialkylsilyl substituted 2d-conjugated polymer as donor, Nat. Commun., 2016, 7, 13651 CrossRef CAS PubMed.
- L. Perdigón-Toro, H. Zhang, A. Markina, J. Yuan, S. M. Hosseini, C. M. Wolff, G. Zuo, M. Stolterfoht, Y. Zou, F. Gao, D. Andrienko, S. Shoaee and D. Neher, Barrierless free charge generation in the high-performance PM6:Y6 bulk heterojunction non-fullerene solar cell, Adv. Mater., 2020, 32, 1906763 CrossRef PubMed.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X.-K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J.-L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Design rules for minimizing voltage losses in high-efficiency organic solar cells, Nat. Mater., 2018, 17, 703 CrossRef CAS PubMed.
- F. D. Eisner, M. Azzouzi, Z. Fei, X. Hou, T. D. Anthopoulos, T. J. S. Dennis, M. Heeney and J. Nelson, Hybridization of local exciton and charge-transfer states reduces nonradiative voltage losses in organic solar cells, J. Am. Chem. Soc., 2019, 141, 6362 CrossRef CAS PubMed.
- V. Coropceanu, X.-K. Chen, T. Wang, Z. Zheng and J.-L. Brédas, Charge-transfer electronic states inorganic solar cells, Nat. Rev. Mater., 2019, 4, 689 CrossRef.
- D. Qian, S. M. Pratik, Q. Liu, Y. Dong, R. Zhang, J. Yu, N. Gasparini, J. Wu, T. Zhang, V. Coropceanu, X. Guo, M. Zhang, J.-L. Bredas, F. Gao and J. R. Durrant, Correlating the hybridization of local-exciton and charge-transfer states with charge generation in organic solar cells, Adv. Energy Mater., 2023, 2301026 CrossRef CAS.
- R. Wang, C. Zhang, Q. Li, Z. Zhang, X. Wang and M. Xiao, Charge separation from an intra-moiety intermediate state in the high-performance PM6:Y6 organic photovoltaic blend, J. Am. Chem. Soc., 2020, 142, 12751 CrossRef CAS PubMed.
- Z. Tu, G. Han and Y. Yi, Barrier-free charge separation enabled by electronic polarization in high-efficiency non-fullerene organic solar cells, J. Phys. Chem. Lett., 2020, 11, 2585 CrossRef CAS PubMed.
- G. Zhang, X.-K. Chen, J. Xiao, P. C. Y. Chow, M. Ren, G. Kupgan, X. Jiao, C. C. S. Chan, X. Du, R. Xia, Z. Chen, J. Yuan, Y. Zhang, S. Zhang, Y. Liu, Y. Zou, H. Yan, K. S. Wong, V. Coropceanu, N. Li, C. J. Brabec, J.-L. Bredas, H.-L. Yip and Y. Cao, Delocalization of exciton and electron wavefunction in non-fullerene acceptor molecules enables efficient organic solar cells, Nat. Commun., 2020, 11, 3943 CrossRef CAS PubMed.
- O. P. Dimitriev, Dynamics of excitons in conjugated molecules and organic semiconductor systems, Chem. Rev., 2022, 122, 8487 CrossRef CAS PubMed.
- Q. Li, R. Wang and C. Zhang, The dynamics of delocalized excitations in organic solar cells with nonfullerene acceptors, J. Phys. Chem. Lett., 2023, 14, 3031 CrossRef CAS PubMed.
- Q. Li, R. Wang, T. Yu, X. Wang, Z.-G. Zhang, Y. Zhang, M. Xiao and C. Zhang, Long-range charge separation enabled by intramoiety delocalized excitations in copolymer donors in organic photovoltaic blends, J. Phys. Chem. Lett., 2023, 14, 7498 CrossRef CAS PubMed.
- M. B. Price, P. A. Hume, A. Ilina, I. Wagner, R. R. Tamming, K. E. Thorn, W. Jiao, A. Goldingay, P. J. Conaghan, G. Lakhwani, N. J. L. K. Davis, Y. Wang, P. Xue, H. Lu, K. Chen, X. Zhan and J. M. Hodgkiss, Free charge photogeneration in a single component high photovoltaic efficiency organic semiconductor, Nat. Commun., 2022, 13, 2827 CrossRef CAS PubMed.
- Z. Zhang, L. Li, C. Xu, P. Jin, M. Huang, Y. Li, H. Wang, Y. Yi, C. Zhang, Y. Yang, W. Xu and Y. Lin, Single photovoltaic material solar cells with enhanced exciton dissociation and extended electron diffusion, Cell Rep. Phys. Sci., 2022, 3, 100895 CrossRef CAS.
- E. Sağlamkaya, A. Musiienko, M. S. Shadabroo, B. Sun, S. Chandrabose, O. Shargaieva, G. Lo Gerfo, M. N. F. van Hulst and S. Shoaee, What is special about Y6; the working mechanism of neat Y6 organic solar cells, Mater. Horiz., 2023, 10, 1825 RSC.
- D. Balzer, T. J. A. M. Smolders, D. Blyth, S. N. Hood and I. Kassal, Delocalised kinetic Monte Carlo for simulating delocalisation-enhanced charge and exciton transport in disordered materials, Chem. Sci., 2021, 12, 2276 RSC.
- D. Balzer and I. Kassal, Mechanism of delocalization-enhanced exciton transport in disordered organic semiconductors, J. Phys. Chem. Lett., 2023, 14, 2155 CrossRef CAS PubMed.
- H. Bässler, Charge transport in disordered organic photoconductors a Monte Carlo simulation study, Phys. Status Solidi B, 1993, 175, 15 CrossRef.
- A. Köhler and H. Bässler, Electronic processes in organic semiconductors: an introduction, Wiley, 2015 Search PubMed.
- V. May and O. Kühn, Charge and energy transfer dynamics in molecular systems, Wiley-VCH, 3rd edn, 2011 Search PubMed.
- H. Fröhlich, Electrons in lattice fields, Adv. Phys., 1954, 3, 325 CrossRef.
- T. Holstein, Studies of polaron motion: Part i. The molecular-crystal model, Ann. Phys., 1959, 8, 325 CAS.
- M. Grover and R. Silbey, Exciton migration in molecular crystals, J. Chem. Phys., 1971, 54, 4843 CrossRef CAS.
- B. Rice, A. A. Y. Guilbert, J. M. Frost and J. Nelson, Polaron states in fullerene adducts modeled by coarse-grained molecular dynamics and tight binding, J. Phys. Chem. Lett., 2018, 9, 6616 CrossRef CAS PubMed.
- C. K. Lee, J. Moix and J. Cao, Coherent quantum transport in disordered systems: A unified polaron treatment of hopping and band-like transport, J. Chem. Phys., 2015, 142, 164103 CrossRef PubMed.
- R. Tempelaar, L. J. A. Koster, R. W. A. Havenith, J. Knoester and T. L. C. Jansen, Charge recombination suppressed by destructive quantum interference in heterojunction materials, J. Phys. Chem. Lett., 2016, 7, 198 CrossRef CAS PubMed.
- N. B. Taylor and I. Kassal, Generalised Marcus theory for multi-molecular delocalised charge transfer, Chem. Sci., 2018, 9, 2942 RSC.
- R. A. Marcus, On the theory of oxidation-reduction reactions involving electron transfer. I, J. Chem. Phys., 1956, 24, 966 CrossRef CAS.
- J. T. Willson, W. Liu, D. Balzer and I. Kassal, Jumping kinetic Monte Carlo: Fast and accurate simulations of partially delocalized charge transport in organic semiconductors, J. Phys. Chem. Lett., 2023, 14, 3757 CrossRef CAS PubMed.
- C. K. Lee, J. Moix and J. Cao, Accuracy of second order perturbation theory in the polaron and variational polaron frames, J. Chem. Phys., 2012, 136, 204120 CrossRef PubMed.
- F. A. Pollock, D. P. McCutcheon, B. W. Lovett, E. M. Gauger and A. Nazir, A multi-site variational master equation approach to dissipative energy transfer, New J. Phys., 2013, 15, 075018 CrossRef.
- S. J. Jang, Partially polaron-transformed quantum master equation for exciton and charge transport dynamics, J. Chem. Phys., 2022, 157, 104107 CrossRef CAS PubMed.
- X. Jiang and P. Brumer, Creation and dynamics of molecular states prepared with coherent vs partially coherent pulsed light, J. Chem. Phys., 1991, 94, 5833 CrossRef CAS.
- T. Mančal and L. Valkunas, Exciton dynamics in photosynthetic complexes: Excitation by coherent and incoherent light, New J. Phys., 2010, 12, 065044 CrossRef.
- P. Brumer and M. Shapiro, Molecular response in one-photon absorption via natural thermal light vs. pulsed laser excitation, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19575 CrossRef CAS PubMed.
- I. Kassal, J. Yuen-Zhou and S. Rahimi-Keshari, Does coherence enhance transport in photosynthesis?, J. Phys. Chem. Lett., 2013, 4, 362 CrossRef CAS PubMed.
- P. Brumer, Shedding (incoherent) light on quantum effects in light-induced biological processes, J. Phys. Chem. Lett., 2018, 9, 2946 CrossRef CAS PubMed.
- S. Tomasi, S. Baghbanzadeh, S. Rahimi-Keshari and I. Kassal, Coherent and controllable enhancement of light-harvesting efficiency, Phys. Rev. A, 2019, 100, 043411 CrossRef CAS.
- S. Tomasi and I. Kassal, Classification of coherent enhancements of light-harvesting processes, J. Phys. Chem. Lett., 2020, 11, 2348 CrossRef CAS PubMed.
- S. Tomasi, D. M. Rouse, E. M. Gauger, B. W. Lovett and I. Kassal, Environmentally improved coherent light harvesting, J. Phys. Chem. Lett., 2021, 12, 6143 CrossRef CAS PubMed.
- A. Troisi and G. Orlandi, Dynamics of the intermolecular transfer integral in crystalline organic semiconductors, J. Phys. Chem. A, 2006, 110, 4065 CrossRef CAS PubMed.
- A. Troisi and G. Orlandi, Charge-transport regime of crystalline organic semiconductors: Diffusion limited by thermal off-diagonal electronic disorder, Phys. Rev. Lett., 2006, 96, 086601 CrossRef PubMed.
- J. Aragó and A. Troisi, Regimes of exciton transport in molecular crystals in the presence of dynamic disorder, Adv. Funct. Mater., 2016, 26, 2316 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc05409h |
| This journal is © The Royal Society of Chemistry 2024 |