Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Retro-Cope elimination of cyclic alkynes: reactivity trends and rational design of next-generation bioorthogonal reagents†
Steven E.
Beutick‡
 ab,
Song
Yu‡
ab,
Song
Yu‡
 a,
Laura
Orian
a,
Laura
Orian
 b,
F. Matthias
Bickelhaupt
b,
F. Matthias
Bickelhaupt
 acd and
Trevor A.
Hamlin
acd and
Trevor A.
Hamlin
 *a
*a
aDepartment of Chemistry and Pharmaceutical Sciences, Amsterdam Institute of Molecular and Life Sciences (AIMMS), Vrije Universiteit Amsterdam, De Boelelaan 1108, Amsterdam, 1081 HZ, The Netherlands. E-mail: t.a.hamlin@vu.nl
bDipartimento di Scienze Chimiche, Università degli Studi di Padova, Via Marzolo 1, Padova, 35129, Italy
cInstitute of Molecules and Materials, Radboud University, Heyendaalseweg 135, Nijmegen, 6525 AJ, The Netherlands
dDepartment of Chemical Sciences, University of Johannesburg, Auckland Park, Johannesburg 2006, South Africa
First published on 27th August 2024
Abstract
The retro-Cope elimination reaction between dimethylhydroxylamine (DMHA) and various cyclic alkynes has been quantum chemically explored using DFT at ZORA-BP86/TZ2P. The purpose of this study is to understand the role of the following three unique activation modes on the overall reactivity, that is (i) additional cycloalkyne predistortion via fused cycles, (ii) exocyclic heteroatom substitution on the cycloalkyne, and (iii) endocyclic heteroatom substitution on the cycloalkyne. Trends in reactivity are analyzed and explained by using the activation strain model (ASM) of chemical reactivity. Based on our newly formulated design principles, we constructed a priori a suite of novel bioorthogonal reagents that are highly reactive towards the retro-Cope elimination reaction with DMHA. Our findings offer valuable insights into the design principles for highly reactive bioorthogonal reagents in chemical synthesis.
Introduction
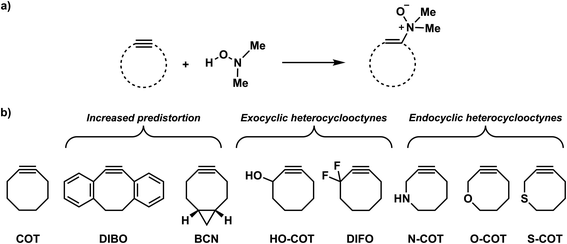
Bioorthogonal chemistry has emerged as a powerful tool for studying and manipulating biological systems.1 Bioorthogonal reactions are biocompatible and robust, go with fast reaction rate constants, and do not interfere or react with the native biological environment. Bioorthogonal reagents that meet these requirements enable the probing of biological processes by labeling and imaging target molecules, both in vitro and in vivo.2 Common biorthogonal reactions are the tetrazine-based inverse electron demand Diels–Alder (IED-DA),3 traceless Staudinger ligation reactions,4 and 1,3-dipolar cycloadditions5 such as copper(I)-catalyzed azide–alkyne cycloaddition (CuAAC). Bertozzi and co-workers developed the strain-promoted azide–alkyne cycloaddition reaction (SPAAC) as a selective biorthogonal chemical reaction.6 The field continues to flourish with the development of several novel bioorthogonal reactions, including strain-promoted alkyne-nitrone cycloadditions (SPANC),7 isonitrile-based [4 + 1] cycloadditions,8 and photoactivated tetrazole ligations.9Recently, Kang et al. presented the retro-Cope elimination reaction (hydroamination of cyclic cyclooctyne) between functionalized (cyclic) alkynes and N,N-dialkylhydroxylamines as a novel bioorthogonal reaction (Scheme 1a).10 The calculated Gibbs free energy activation barrier at M06-2X/6-311G(2d,p)//M06-2X/6-31G(d,p) for the parent cyclooctyne was determined to be 18.9 kcal mol−1, which is adequate for the reaction to proceed at room temperature. Experimentally, the retro-Cope elimination reaction between the non-substituted cyclooctyne (COT) and hydroxylamine in CD3CN at room temperature shows second-order rate constants of 3.25 × 10−2 M−1 s−1, an order of magnitude higher than the strain-promoted azide–alkyne cycloaddition (SPAAC) reaction with benzyl azide.10a,11 Notably, the retro-Cope elimination reaction is highly regioselective when the COT is substituted with electronegative heteroatoms at the propargylic position. Furthermore, Kang et al. showcased the retro-Cope elimination reaction in an in vitro study and demonstrated mutual orthogonality in conjunction with the inverse electron demand Diels Alder (IED-DA) reaction between tetrazine and strained alkenes.10a,12 In doing so, they nicely underscored the potential of this reaction to be applied in mutually orthogonal bioorthogonal chemistry.
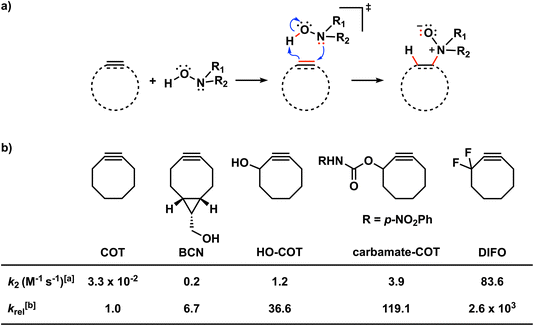 | ||
Scheme 1 (a) The retro-Cope elimination reactions between cyclic alkynes or alkenes and hydroxylamines. (b) Effects of modifying cyclic octynes on the reactivity in the retro-Cope elimination reaction with diethylhydroxylamine.10aa The second-order rate constants were determined for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of the reactants in CD3CN at room temperature using NMR spectroscopy.1b The relative second-order rate constants (krel) were calculated relative to the parent cyclooctyne, COT (krel = k/kCOT). 1 ratio of the reactants in CD3CN at room temperature using NMR spectroscopy.1b The relative second-order rate constants (krel) were calculated relative to the parent cyclooctyne, COT (krel = k/kCOT). | ||
Decorated cyclooctynes have emerged as functional bioorthogonal reagents in 1,3-dipolar cycloadditions.5e,13 Similarly, these cyclic alkynes show high reactivity and selectivity towards the retro-Cope elimination reaction.10a Kim and co-workers10a reported only a minor reactivity enhancement after the introduction of additional strain by three-membered ring fusion in bicyclo[6.1.0]nonyne (BCN), in contrast to a drastic two-order magnitude increase in the second-order rate constants observed for the SPAAC reaction reported by Dommerholt et al.14 The authors described further enhanced reactivity upon adding electronegative substituents on the exocyclic propargylic position, achieving up to three orders of magnitude increase in the second-order rate constants (Scheme 2). Using the distortion/interaction model, Kang et al. show that the predistortion gives rise to the lowering of the activation barrier for the strained cyclooctyne relative to its linear counterpart.15,16a Interestingly, upon the addition of electronegative substituents on the propargylic position, they found that the lowering of the activation barrier was not caused by a less favorable interaction term but, rather, driven by the lowering of the strain energy for both fragments. They further attribute this to a shift of the transition state towards the reactants in accordance with the Hammond postulate.
We have computationally investigated the concerted retro-Cope elimination reaction between dimethylhydroxylamine (DMHA) and cyclic alkynes at ZORA-BP86/TZ2P (Scheme 2). Three sets of cyclooctynes were studied. The first set includes cyclic alkynes with increased predistortion due to the introduction of cyclic functionality (DIBO and BCN). The second and third sets consist of cycloalkynes modified at the exocyclic (HO-COT and DIFO) and endocyclic (N-COT, O-COT, and S-COT) propargylic position, respectively. The anti-pathways (dimethyl groups and propargylic substituent on opposite sides) and the syn-pathways (dimethyl groups and propargylic substituent on the same side) were investigated. To gain insight into the physical factors that control the reactivity, the activation strain model (ASM)16 of reactivity in conjunction with the matching energy decomposition analysis (EDA) and quantitative Kohn–Sham molecular orbital (KS-MO)17 theory analysis. Based on our found rational design principles, we constructed a priori a suite of novel bioorthogonal reagents that are highly reactive towards the retro-Cope elimination reaction with DMHA.
Computational methods
Computational details
All calculations were performed with the AMS2021 program (an example input file is provided in the ESI†).18 After a conformational search using Grimme's CREST 2.12 (ref. 19) using default settings in the gas phase, all geometries and energies were computed using the generalized gradient approximation (GGA) functional BP86,20 and the MOs were expanded using a large uncontracted set of Slater-type orbitals (STO): TZ2P.21 Our benchmarks22a,b and numerous DFT studies22c–g support the use of this method to compute trends in reactivity for similar reactions. The trends in reactivity remain the same in implicit solvent (COSMO(acetonitrile)-BP86/TZ2P//BP86/TZ2P). Additionally, the trends were successfully reproduced with dispersion corrections (BP86-D3(BJ)/TZ2P//BP86/TZ2P), and at M06-2X/TZ2P//BP86/TZ2P, and DLPNO-CCSD(T)/def2-QZVPP//BP86/TZ2P (Table S3†). The zeroth order approximation (ZORA) accounted for the scalar relativistic effects.23 The accuracies of the fit scheme (Zlm fit)24a and the integration grid (Becke grid)24b were set to VERYGOOD. The convergence criteria for the SCF and geometry optimization procedures were set to 10−5 hartree. Frequency calculations were performed to characterize the nature of stationary points where local minima had real frequencies while transition structures had a single imaginary frequency. The steepest descent path from the TS was calculated using the intrinsic reaction coordinate (IRC) method,25 which follows the transition vector (the vibrational normal mode associated with the reaction and with a negative force constant) from the transition structure toward the reactants and product and was analyzed with the aid of the PyFrag 2019.26 All structures were visualized using CYLview.27Activation strain model and energy decomposition analysis
Quantitative analyses of the activation barriers associated with the studied reactions were obtained using the activation strain model (ASM) of reactivity.16 The PES, that is, ΔE(ζ), was decomposed into the strain energy, ΔEstrain(ζ), and interaction energy, ΔEint(ζ) [eqn (1)]. All energy terms were projected onto the length of the forming C⋯H bond, which undergoes a well-defined change during the reaction. Other reaction coordinates, such as the length of the C⋯N bond or C⋯C stretch, were shown to provide the same general conclusions.28| ΔE(ζ) = ΔEstrain(ζ) + ΔEint(ζ) | (1) |
The ΔEstrain(ζ) is associated with the rigidity and the structural deformation of the reactants from their equilibrium structure to the geometry they adopt at the coordinate of ζ during the reaction. The ΔEint(ζ) is related to the electronic structure of the reactants and their spatial orientation and represents the mutual interactions between the deformed reactants.
To obtain a deeper insight into the physical mechanism behind ΔEint(ζ), we employed our canonical energy decomposition analysis (EDA),17 which decomposes the ΔEint between the deformed reactants, within the framework of Kohn–Sham MO theory, into three physically meaningful terms [eqn (2)].
| ΔEint(ζ) = ΔVelstat(ζ) + ΔEPauli(ζ) + ΔEoi(ζ) | (2) |
The electrostatic interaction, ΔVelstat(ζ), corresponds to the classical electrostatic interaction between the unperturbed charge distributions of the deformed reactants. The Pauli repulsion, ΔEPauli(ζ), comprises the Pauli-repulsive orbital interactions between closed-shell orbitals. The term ΔEoi(ζ) represents the stabilizing orbital interactions, such as charge transfer, namely, the interactions between the occupied orbitals of one reactant and the unoccupied orbitals of the other reactant, and polarization, that is, the occupied–unoccupied orbital mixing within one reactant due to the presence of the other reactant.
Voronoi deformation density analysis
The electron density distribution is analyzed using the Voronoi deformation density (VDD) method29 for computing atomic charges. The VDD atomic charge on atom A (QVDDA) is computed as the (numerical) integral of the deformation density in the volume of the Voronoi cell of atom A (eqn (3)). The Voronoi cell of atom A is defined as the compartment of space bounded by the bond midplanes on and perpendicular to all bond axes between nucleus A and its neighboring nuclei.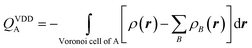 | (3) |
Here, ρ(r) is the electron density of the molecule, and 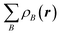 is the superposition of atomic densities ρB of a fictitious promolecule without chemical interactions that is associated with the situation in which all atoms are neutral. The interpretation of the VDD charge QVDDA is rather straightforward and transparent: instead of measuring the amount of charge associated with a particular atom A, QVDDA directly monitors how much charge flows, due to chemical interactions, out of (QVDDA > 0) or into (QVDDA < 0) the Voronoi cell of atom A.
is the superposition of atomic densities ρB of a fictitious promolecule without chemical interactions that is associated with the situation in which all atoms are neutral. The interpretation of the VDD charge QVDDA is rather straightforward and transparent: instead of measuring the amount of charge associated with a particular atom A, QVDDA directly monitors how much charge flows, due to chemical interactions, out of (QVDDA > 0) or into (QVDDA < 0) the Voronoi cell of atom A.
Results and discussion
Cyclic alkynes
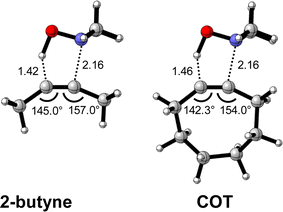
First, we discuss the effect of the bending of the alkyne, or alkyne predistortion, on the retro-Cope elimination reactivity by comparison of the linear 2-butyne and cyclooctyne (COT). The computed electronic activation energies (ΔE‡) and reaction energies (ΔErxn) associated with the retro-Cope elimination reaction between these reactants and dimethylhydroxylamine (DMHA) are provided in Table 1. The electronic activation barrier is significantly lowered from 15.8 kcal mol−1 to 4.6 kcal mol−1 (Table 1) going from 2-butyne to COT.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a
| 2-Butyne | COT | |
|---|---|---|
| a Computed at ZORA-BP86/TZ2P. b Δr is the difference in length between the forming C⋯N and C⋯H bonds at the transition state. c The relative second-order rate constants (krel) were calculated relative to the COT (k/kCOT). | ||
| Δrb | 0.74 | 0.70 |
| ΔERC | −3.0 | −3.0 |
| ΔE‡ | 15.8 | 4.6 |
| ΔErxn | −6.9 | −14.4 |
| ΔG‡ | 26.7 | 15.8 |
| k rel | 1.2 × 10−8 | 1.0 |
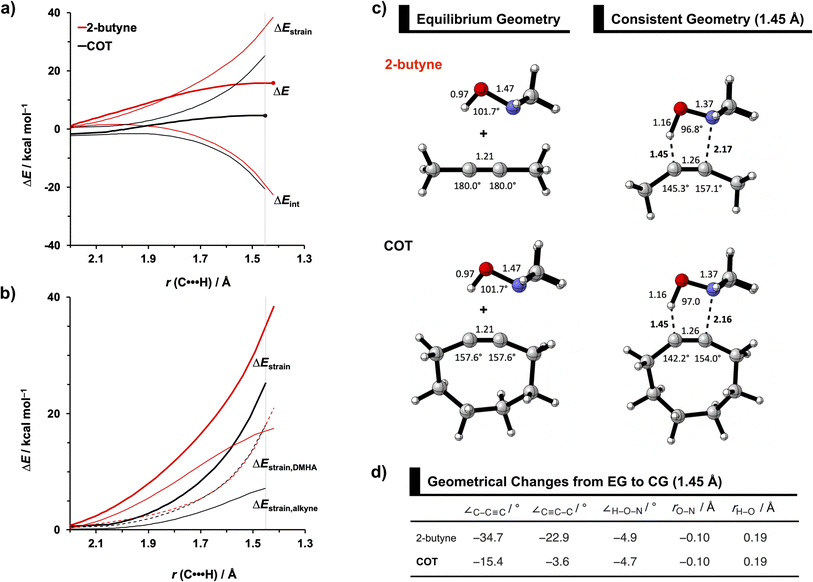
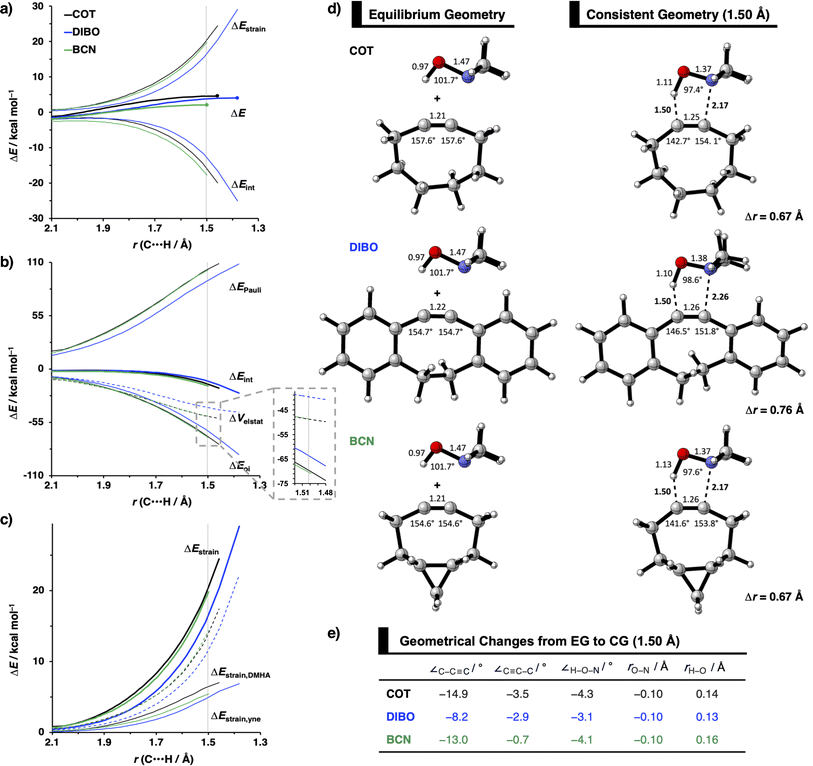
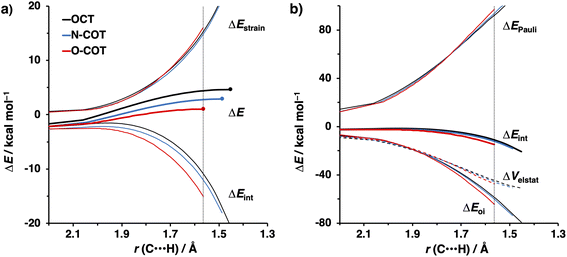
To identify the physical factors leading to the enhanced retro-Cope elimination reactivity of the strained alkynes relative to the linear 2-butyne, the activation strain model (ASM) of reactivity is applied (Fig. 1a). We find that predistortion of the alkyne in COT serves to enhance retro-Cope elimination reactivity via (1) reducing the activation strain and (2) enhancing the overall interaction energy via more stabilizing orbital interactions. Kim et al. also observed a notable reduction in the activation strain of the retro-Cope elimination reaction with COT.10 Relative to its linear counterpart, the strain in COT is reduced by approximately 10 kcal mol−1 at a consistent geometry, where the lengths of the C⋯H bond are 1.45 Å, and the slope of the strain in the alkyne fragment is smaller along the reaction coordinate. By partitioning the strain energy in terms of the two fragments (Fig. 1b), we confirm that the strain is lowered for the COT fragment, due to the alkyne predistortion in the COT reagent. To understand the origin of this effect, further analysis of both equilibrium geometry and consistent geometry (Fig. 1c and d) reveals that the reaction of predistorted alkyne, COT, simply requires less bending of the alkyne to react with DMHA.
In addition, we show how predistortion of COT also acts to enhance the stabilizing interaction energy with DMHA (Fig. 1a). Using our EDA, we could pinpoint the enhanced interaction energy originates from significantly more stabilizing orbital interactions (Fig. S3b†). The predistortion of the alkyne results in a stabilization of the LUMO and a slight destabilization of the HOMO.30 The lowering of the LUMO, is caused by the in-phase mixing of the σ* and π* orbitals, resulting in a smaller π*-LUMOCOT and HOMODMHA energy gap.
Cyclic alkynes with additional predistortion
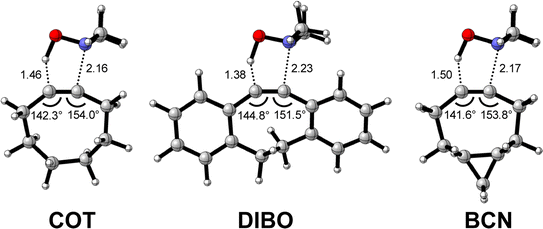
Next, we compare the reactivity of our parent COT with two popular bioorthogonal cyclic alkynes reagents in 1,3-dipolar cycloaddition reactions5 dibenzocyclooctyne (DIBO)31 and bicyclononyne (BCN)14 that feature additional alkyne predistortion (∠C–C–C) from the presence of fused carbocycles (154.7° and 154.5° relative to 157.6° for COT in the optimized reactants (Fig. S1†)). The computed electronic activation energies (ΔE‡) and reaction energies (ΔErxn) associated with the retro-Cope elimination reaction between these reactants and dimethylhydroxylamine (DMHA) are shown in Table 2. Our calculations show that the activation barrier for the retro-Cope elimination reaction with DMHA decreases from 4.6 to 4.1 to 2.1 kcal mol−1, as going from COT to DIBO to BCN.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a
| COT | DIBO | BCN | |
|---|---|---|---|
| a Computed at ZORA-BP86/TZ2P. b Δr is the difference in length between the forming C⋯N and C⋯H bonds at the transition state. c The relative second-order rate constants (krel) were calculated relative to COT (k/kCOT). | |||
| Δrb | 0.70 | 0.85 | 0.67 |
| ΔERC | −3.0 | −2.7 | −3.1 |
| ΔE‡ | 4.6 | 4.1 | 2.1 |
| ΔErxn | −14.4 | −9.4 | −12.7 |
| ΔG‡ | 15.8 | 15.6 | 13.9 |
| k rel | 1.0 | 1.5 | 27.0 |
The physical factors leading to the enhanced retro-Cope elimination reactivity of DIBO and BCN compared to COT are next analyzed using the ASM. In Fig. 2b, the ASM diagram shows that the retro-Cope elimination reaction of DIBO benefits from significantly less destabilizing strain energy (ΔEstrain), as compared to COT. The retro-Cope elimination reaction of BCN with DMHA also benefits from less destabilizing strain but is paralleled by a more stabilizing interaction energy (ΔEint), as compared to COT (Fig. 2b). Decomposition of the strain energies reveals that DIBO benefits a reduced strain in both the DIBO and DMHA fragments, whereas the reduced strain for BCN at consistent geometry originates solely from the BCN fragment (Fig. 2d). Our structural analyses at the equilibrium geometry show that DIBO and BCN both have a more predistorted backbone than the parent COT (157.6°) in the equilibrium geometry, with internal C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C alkyne bond angles of 154.7° and 154.6°, respectively. This predistortion results in a structurally less distorted alkyne fragment at consistent geometry (Fig. 2d), and, consequently, reduced activation strain. For DIBO, the lowering of the activation strain is more pronounced because also the O⋯H bond breaking distance and compression of the H–O–N angle are less progressed, which causes the strain of the DMHA fragment to be shifted to the right (Fig. 2a). As will be explained in more detail later on, this can be traced back to a more slanted reaction path, that is, the C⋯N bond is formed later than the C⋯H bond for DIBO (Δr = 0.76 Å, where Δr is the difference in length between the C⋯N and C⋯H bonds at the consistent geometry) than for COT (Δr = 0.67 Å).
C alkyne bond angles of 154.7° and 154.6°, respectively. This predistortion results in a structurally less distorted alkyne fragment at consistent geometry (Fig. 2d), and, consequently, reduced activation strain. For DIBO, the lowering of the activation strain is more pronounced because also the O⋯H bond breaking distance and compression of the H–O–N angle are less progressed, which causes the strain of the DMHA fragment to be shifted to the right (Fig. 2a). As will be explained in more detail later on, this can be traced back to a more slanted reaction path, that is, the C⋯N bond is formed later than the C⋯H bond for DIBO (Δr = 0.76 Å, where Δr is the difference in length between the C⋯N and C⋯H bonds at the consistent geometry) than for COT (Δr = 0.67 Å).
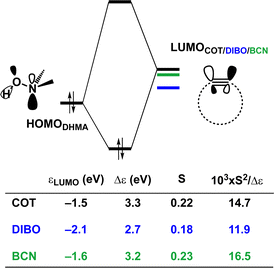
Hamlin and coworkers have shown that, in addition to the reduction of the destabilizing strain, a more stabilizing interaction energy is at the root of the enhanced reactivity in 1,3-dipolar cycloaddition between azides and strained alkynes (SPAAC).30 Energy decomposition analyses in conjunction with KS-MO analyses illustrated that the bending of alkynes has a profound effect on the frontier molecular orbitals (FMOs), i.e., the LUMO 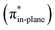 is stabilized and the HOMO (πin-plane) is slightly destabilized because of mixing with the adjacent σ*- and σ-orbitals, respectively. Thus, a more bent alkyne has a lower LUMOalkyne, giving rise to a smaller HOMODMHA–LUMOCOT gap. Therefore, the reaction of BCN, which has a 3.0° smaller internal C–C
is stabilized and the HOMO (πin-plane) is slightly destabilized because of mixing with the adjacent σ*- and σ-orbitals, respectively. Thus, a more bent alkyne has a lower LUMOalkyne, giving rise to a smaller HOMODMHA–LUMOCOT gap. Therefore, the reaction of BCN, which has a 3.0° smaller internal C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C angle at equilibrium geometry, goes with a smaller initial HOMODMHA–LUMOBCN gap than the reaction of COT (Fig. 3). It must be noted that, with the exception of DIBO, the
C angle at equilibrium geometry, goes with a smaller initial HOMODMHA–LUMOBCN gap than the reaction of COT (Fig. 3). It must be noted that, with the exception of DIBO, the 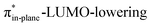 along the reaction coordinate (the slope), relative to the energy at equilibrium geometry, is approximately equal (Fig. S4d†). As for BCN the Δr remains equal, this leads to a larger S2/Δε term, i.e., the more favorable HOMODMHA–LUMOBCN interaction and, consequently, more stabilizing orbital interactions associated with the retro-Cope elimination reaction between BCN and DMHA.
along the reaction coordinate (the slope), relative to the energy at equilibrium geometry, is approximately equal (Fig. S4d†). As for BCN the Δr remains equal, this leads to a larger S2/Δε term, i.e., the more favorable HOMODMHA–LUMOBCN interaction and, consequently, more stabilizing orbital interactions associated with the retro-Cope elimination reaction between BCN and DMHA.
Despite DIBO having a lower 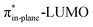 energy than COT, the overall orbital interactions for the DIBO reaction are less stabilizing (Fig. 3). This can be rationalized by the reduced HOMODMHA–LUMODIBO orbital overlap brought about by the C⋯N bond formation distance in the reaction of DIBO (Δr = 0.76 Å) lagging substantially behind that of COT (Δr = 0.67 Å). This geometric effect also brings about considerably less destabilizing Pauli repulsion. At a double consistent geometry (Table S4†), where Δr is equal to that of COT at consistent geometry (Δr = 0.67 Å), the Pauli repulsion exceeds the more stabilizing orbital and electrostatic interaction. This is due to the overlap of various filled in-plane orbitals of the DMHA fragment overlapping with the HOMO−4, HOMO−2 and, HOMO−1 of DIBO (Fig. S7†). It is the buildup of this Pauli repulsion that is effectively absorbed into the reaction path causing the more slanted reaction path (higher Δr). As a result, the Pauli repulsion is lowered, and, concomitantly, the orbital overlaps between the two fragments are reduced, also decreasing the HOMODMHA–LUMODIBO overlap. Similar to the retro-Cope elimination reaction with linear alkynes with added steric bulk,28 the Pauli lowering effect originates in more (not less) steric repulsion introduced by the fused aryls in DIBO.
energy than COT, the overall orbital interactions for the DIBO reaction are less stabilizing (Fig. 3). This can be rationalized by the reduced HOMODMHA–LUMODIBO orbital overlap brought about by the C⋯N bond formation distance in the reaction of DIBO (Δr = 0.76 Å) lagging substantially behind that of COT (Δr = 0.67 Å). This geometric effect also brings about considerably less destabilizing Pauli repulsion. At a double consistent geometry (Table S4†), where Δr is equal to that of COT at consistent geometry (Δr = 0.67 Å), the Pauli repulsion exceeds the more stabilizing orbital and electrostatic interaction. This is due to the overlap of various filled in-plane orbitals of the DMHA fragment overlapping with the HOMO−4, HOMO−2 and, HOMO−1 of DIBO (Fig. S7†). It is the buildup of this Pauli repulsion that is effectively absorbed into the reaction path causing the more slanted reaction path (higher Δr). As a result, the Pauli repulsion is lowered, and, concomitantly, the orbital overlaps between the two fragments are reduced, also decreasing the HOMODMHA–LUMODIBO overlap. Similar to the retro-Cope elimination reaction with linear alkynes with added steric bulk,28 the Pauli lowering effect originates in more (not less) steric repulsion introduced by the fused aryls in DIBO.
We observe that the additional repulsive interaction occurs between the various in-plane orbitals of DMHA and the HOMO−1, HOMO−2, and HOMO−4 orbitals in DIBO. In contrast, the literature attributes this repulsive effect to “flagpole” hydrogens.6d,32 At double consistent geometry, the occupied–occupied orbital overlaps that actually increase are not in the vicinity of the “flagpole” hydrogen atoms. Instead, the three orbitals are combinations of the πin-plane-HOMO of COT and the π-HOMOs of the benzene substituents. The πin-plane-HOMO of COT is allowed to mix with the π-system benzene substituents due to the twisted nature of DIBO (Fig. S7†).
Thus, although the introduction of fused benzenes causes a substantially smaller HOMODMHA–LUMODIBO gap (Fig. 3), the more stabilizing orbital interaction are hampered by lowered HOMODMHA–LUMODIBO overlaps, due to the C⋯N bond forming distance in DIBO lagging behind that of COT. The greater C⋯N bond forming distance can be traced back to the increased two-center four-electron Pauli repulsion, which is absorbed into the geometry of the reaction system by forcing it into a slanted reaction path. As a result, the overlap between the filled FMOs decreases, ultimately reducing Pauli repulsion, which outweighs the concurrent decrease in stabilizing orbital and electrostatic interactions. The smaller HOMODMHA–LUMODIBO gap in DIBO, together with the introduction of additional HOMO–LUMO interactions, limit the destabilization by the additional in-plane steric bulk between the two fragments.
Considering that orbital interactions play a key role in the enhanced reactivity of DIBO and BCN compared to COT, we performed an additional analysis on the key π*-LUMOin-plane that engages with the π-HOMODHMA. We sought to determine the factors that lead to the observed lowering of the π*-LUMOin-plane orbital energies of DIBO and BCN relative to COT. To do so, we constrained COT in the equilibrium geometries of the respective substituted cyclic alkynes and reported the π-HOMOin-plane and π*-LUMOin-plane orbital energies in Fig. S4c.† The root of the π*-LUMOin-plane-lowering in the equilibrium geometry was further analyzed by decomposing the change in orbital energy, ΔεMO, into substituent, Δεsub, and bending, Δεdeform, contributions, which were defined as (Fig. S4a and b†):
| ΔεMO = ΔεMO,predist + ΔεMO,sub | (4) |
| ΔεMO,predist = εMO(COTconstrained) − εMO (COTeq) | (5) |
| ΔεMO,sub = εMO (sub) − εMO (COTconstrained) | (6) |
At the equilibrium geometry, the π*-LUMOin-plane-lowering of BCN is primarily caused by the additional bending of the alkyne enforced by the fused cyclopropane (0.14 eV (79%)) and only lowered by 0.04 eV (21%) because of the addition of the fused cyclopropane to the deformed cyclooctyne. In contrast, the π*-LUMOin-plane-lowering in DIBO primarily finds its origin in substituent effects instead of the additional bending of the alkyne. In equilibrium geometry, DIBO is stabilized by the bending of the alkyne enforced by the more rigid cyclic backbone by only 0.24 eV (23%), whereas the substitution by the dibenzo-substituents accounts for a stabilization of 0.78 eV (77%).
Additionally, the π*-LUMOin-plane orbital energies along the reaction coordinate associated with the retro-Cope elimination reaction are shown in Fig. S4d.† The orbital energy profiles of the π*-LUMOin-plane orbitals look alike with similar steepness along the reaction coordinate and differ primarily in the π*-LUMOin-plane orbital energy in the equilibrium geometry. DIBO stands out in that the steepness is lower, i.e., the rigid DIBO is less affected by deformation of the alkyne along the reaction coordinate. This is likely due to the smaller angle deformation needed for consistent geometry (Fig. 2a), resulting from the more slanted reaction path (larger Δr).
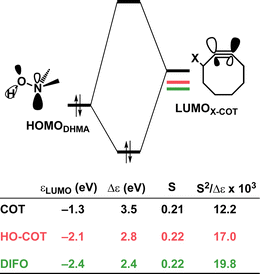
Effect of exocyclic propargylic substitution
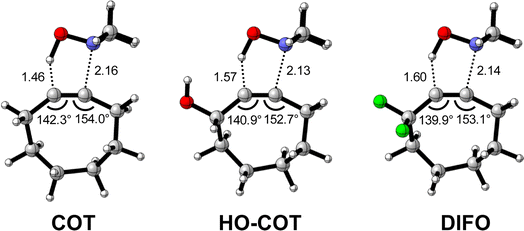
Next, we discuss the modulation of COT at the exocyclic propargylic position. We studied the effect of appending a hydroxy group (HO-COT) and difluoro group (DIFO) at the exocyclic propargylic position of COT. Cyclooctynes activated by exocyclic propargylic substitution prefer the anti-Markovnikov adduct (anti-pathway) over the Markovnikov adduct (syn-pathway) in the retro-Cope elimination reaction with DMHA (Tables S1 and S2†), as such, we focus on the retro-Cope elimination reaction along the anti-pathways. The relative electronic energies for the reactant complex (ΔERC), activation barriers (ΔE‡), and the reaction energies (ΔErxn) for cyclooctynes substituted on the exocyclic propargylic position towards the retro-Cope elimination reaction along the anti-pathway are shown in Table 3. Replacing the exocyclic propargylic hydrogen with the more electronegative HO-COT and DIFO lowers the activation barrier from 4.6 to 2.3 and 0.2 kcal mol−1, respectively.| COT | HO-COT | DIFO | |
|---|---|---|---|
| a Computed at ZORA-BP86/TZ2P. b Δr is the difference in length between the forming C⋯N and C⋯H bonds at the transition state. c The relative second-order rate constants (krel) were calculated relative to the parent propyne (k/kCOT). Only the anti-pathway was considered. | |||
| Δrb | 0.70 | 0.56 | 0.54 |
| ΔERC | −3.0 | −4.9 | −2.1 |
| ΔE‡ | 4.6 | 2.3 | 0.2 |
| ΔErxn | −14.4 | −15.3 | −15.9 |
| ΔG‡ | 15.8 | 14.6 | 13.0 |
| k rel | 1.0 | 8.7 | 1.3 × 102 |
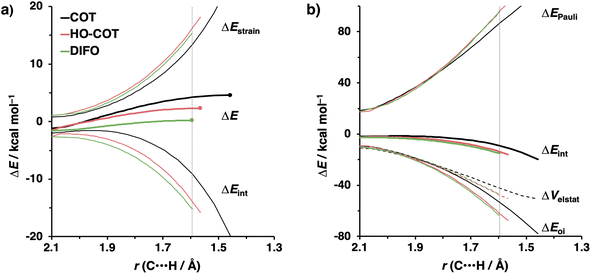
Kang et al. suggested that the reaction does not benefit from a more stabilizing interaction energy upon the addition of electronegative substituents but, rather, from a decrease in strain energy.10a Our analysis at the transition states also furnishes the same insight. However, performing our activation strain and energy decomposition analyses along the full reaction coordinate provides us with a more comprehensive picture of the factors dictating the reactivity.22a In Fig. 4a, the ASM diagram reveals that, at consistent geometry, the activation strain follows a trend opposite to the activation barriers. This would indicate, at odds with Kang et al.10a that the strain is not responsible for observed rate enhancements, but instead it is the progressively more stabilizing interaction energy going from COT to HO-COT to DIFO that is key for the enhanced reactivity. Because the HO-COT and DIFO benefit from more stabilizing interaction energy, the transition states shift to an early point on the reaction coordinate towards the reactants. This, in turn, causes the reactants to be less structurally deformed in their respective TSs.
Our energy decomposition analyses (EDA) (Fig. 4b) show that the more stabilizing ΔEint term associated with the retro-Cope elimination reactions of HO-COT and DIFO arises from a more stabilizing ΔEoi, reinforced by a smaller contribution from the ΔVelstat. The reverse trend in ΔEPauli to that of ΔEint shows that ΔEPauli is not responsible for the more stabilizing interaction energy.
To determine the origin of the enhanced orbital interactions, we quantified all donor–acceptor orbital interactions associated with the retro-Cope elimination reaction of COT, HO-COT, and DIFO at consistent geometry where C⋯H bond forming distance is 1.60 Å and confirmed the HOMODMHA–LUMOX-COT interaction as the most important contributor (Fig. S8†). Further KS-MO analyses reveal that the enhanced orbital interactions of HO-COT and DIFO compared to COT originate in their lowered LUMOs and a slightly more efficient orbital overlap. Especially the former brings about a larger orbital interaction term (∝S2/Δε term) as the energy gap reduces from 3.5 to 2.8 to 2.4 eV going from COT to HO-COT to DIFO (Fig. 5). The origin of the π*-LUMOin-plane-lowering in the equilibrium geometry was further analyzed by decomposing the change in orbital energy into, Δεπ*-LUMO, into substituent, Δεsub, and bending, Δεbend, contributions. We confirmed that the LUMO-lowering effect principally stems from the substituent effect and not the deformation of the alkyne (Fig. S4c†).
Effect of endocyclic propargylic substitution
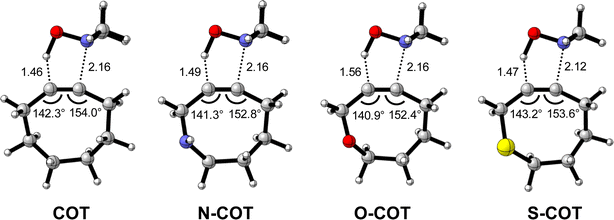
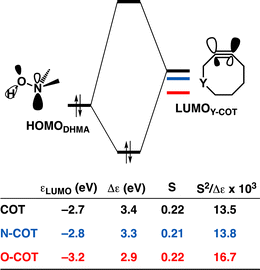
Lastly, we analyzed the reactivity of a group of endocyclic heterocyclooctynes (Y-COT) toward the retro-Cope elimination reaction with DMHA. We substitute the endocyclic propargylic carbon with the nitrogen (N-COT), oxygen (O-COT), and sulfur (S-COT). Analogous to the cyclooctynes activated by exocyclic propargylic substitution (Tables S1 and S2†), we find that the cyclooctynes activated by endocyclic propargylic substitution prefer the anti-Markovnikov adduct (anti-pathway) over the Markovnikov adduct (syn-pathway) in the retro-Cope elimination reaction with DMHA (Tables S1 and S2†). Therefore, we center our analysis on the retro-Cope elimination reaction along the anti-pathways. Table 4 presents the relative electronic energies for the reactant complex (ΔERC), activation barriers (ΔE‡), and the reaction energies (ΔErxn) for Y-COT cyclooctynes towards the retro-Cope elimination reaction along the anti-pathway. Replacing the endocyclic propargylic carbon COT with the more electronegative N-COT and O-COT lowers the activation barrier from 4.6 kcal mol−1 to 2.9 and 1.1 kcal mol−1, respectively. Incorporation of a sulfur heteroatom (S-COT) at the endocyclic propargylic position raises the activation barrier to 5.9 kcal mol−1.| COT | N-COT | O-COT | S-COT | |
|---|---|---|---|---|
| a Computed at ZORA-BP86/TZ2P. b Δr is the difference in length between the forming C⋯N and C⋯H bonds at the transition state. c The relative second-order rate constants (krel) were calculated relative to COT (k/kCOT). Only the anti-pathway was considered. | ||||
| Δrb | 0.70 | 0.67 | 0.59 | 0.66 |
| ΔERC | −3.0 | −2.9 | −2.7 | −2.7 |
| ΔE‡ | 4.6 | 2.9 | 1.0 | 5.8 |
| ΔErxn | −14.4 | −15.8 | −19.5 | −13.4 |
| ΔG‡ | 15.8 | 14.3 | 13.1 | 17.0 |
| k rel | 1.0 | 13.7 | 95.3 | 0.1 |
To gain a quantitative understanding of the physical factors that are at the root of the trends in reactivity, we again turned to ASM. In Fig. 6a, the activation strain diagram highlights that the reduction in activation barrier height from COT to N-COT to O-COT cyclooctyne is driven by an increasingly stabilizing ΔEint term. Despite observing a more favorable interaction energy for the S-COT cyclooctyne at consistent geometry, this is offset by the considerable increase in activation strain (Fig. S9†). The larger atomic radius of the sulfur relative to oxygen allows the alkyne to be less bent i.e., less predistorted, and consequently, a greater structural deformation of the Δ∠(C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) is necessary at consistent geometry (Table S6†). Consequently, the reduced reactivity of S-COT towards the retro-Cope elimination reaction is attributed to the higher activation strain.
C) is necessary at consistent geometry (Table S6†). Consequently, the reduced reactivity of S-COT towards the retro-Cope elimination reaction is attributed to the higher activation strain.
Our canonical EDA analyses (Fig. 6b) reveal that the more stabilizing ΔEoi is responsible for the progressively more stabilizing ΔEint term associated with the retro-Cope elimination reaction going from COT to N-COT to O-COT. The differences in the ΔVelstat curves are minimal, whereas the ΔEPauli shows a reverse trend to that of ΔEint and is, thus, not responsible for the more stabilizing interaction energy.
As the more stabilizing orbital interactions were identified as a key factor that dictated the enhanced reactivity of Y-COT, we screened all orbital donor–acceptor interactions associated with the retro-Cope elimination reactions of COT, N-COT, and O-COT at consistent geometry where the length of the forming C⋯H bond is 1.56 Å (Fig. S10†). The HOMODMHA–LUMOY-COT interaction was confirmed as the most important contributor. The KS-MO analyses at the consistent geometries reveal that it is the consistent lowering of the π*-LUMOalkyne of the Y-COT cyclooctyne that causes the more favorable orbital interactions between HOMODMHA and LUMOY-COT (Fig. 7). Because of the lowering of the 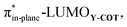 the HOMODMHA–LUMOY-COT energy gap is reduced from Δε = 2.6 to 2.4 to 2.1 eV. The orbital overlap is minimally affected by substitution on the endocyclic propargylic position. As the changes in orbital overlaps remain limited, we can conclude that the enhanced orbital interactions of N-COT and O-COT in retro-Cope elimination reactions can directly be ascribed to the LUMOY-COT-lowering effect of the endocyclic propargylic substitution, which causes the smaller HOMODMHA–LUMOY-COT energy gaps.
the HOMODMHA–LUMOY-COT energy gap is reduced from Δε = 2.6 to 2.4 to 2.1 eV. The orbital overlap is minimally affected by substitution on the endocyclic propargylic position. As the changes in orbital overlaps remain limited, we can conclude that the enhanced orbital interactions of N-COT and O-COT in retro-Cope elimination reactions can directly be ascribed to the LUMOY-COT-lowering effect of the endocyclic propargylic substitution, which causes the smaller HOMODMHA–LUMOY-COT energy gaps.
Next-generation bioorthogonal reagents
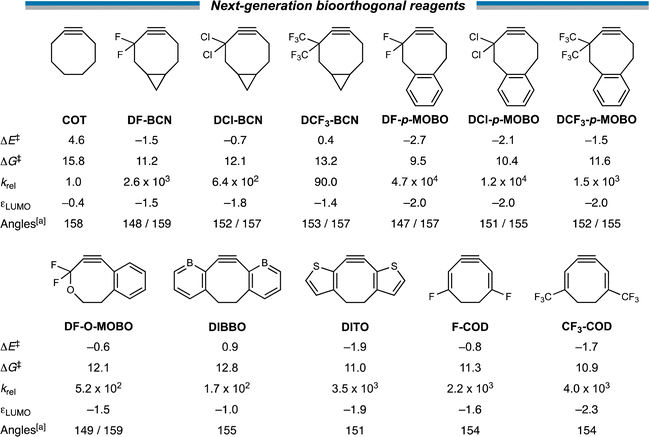
Next, with our new design principles in hand, we sought to generate a suite of novel reagents that exhibit enhanced retro-Cope reactivity relative to current state-of-the-art reagents. Firstly, we propose the judicious combination of rigid cyclic substituents in tandem with both endo- and exocyclic heteroatoms. Based on this, we present 3,3-difluoro-BCN (DF-BCN) and a cyclooctyne annulated with single aryl substituent combined with difluoro and oxide substituents on the exo- and endocyclic propargylic position, respectively (DF-O-MOBO). Based on our computations, we predict a that the reactivity is further enhanced (relative to COT) by ΔΔE‡ = 6.1 and 5.2 with krel values of 2.6 × 103 and 5.2 × 102, respectively. Fusion of aryl groups on the carbons 5 and 6 of the cyclooctyne with difluoro-substituents on the exocyclic propargylic position (DF-p-MOBO) furnished a reagent with a remarkable krel value of 4.7 × 104.32b Additionally, substitution by chloro (DCl-BCN, DF-p-MOBO) and trifluoromethyl (DCF3-BCN, DCF3-p-MOBO) substituents enhanced the krel values up to four orders of magnitude.Additionally, we propose modulations of the DIBO to employ the strong LUMO-lowering effect that is observed in DIBO. By replacing the two aryl rings by borabenzenes (DIBBO) and thiophenes (DITO) the reactivity was enhanced (relative to COT) by ΔΔE‡ = −3.7 and −6.5 kcal mol−1 with krel values of 1.7 × 102 and 3.5 × 103, respectively. Lastly, we added strongly electron withdrawing groups i.e., fluoro (F-COD) and trifluoromethyl (CF3-COD) substituents on a cycloocta-1,5-dien-3-yne (COD), significantly lowering the πin-plane-LUMO, without adding additional bulk in the vicinity of the triple bond. This resulted krel values of 2.2 × 103 and 4.0 × 103, respectively (Scheme 3).
Conclusions
Our theoretical study reveals that the retro-Cope elimination reaction between dimethylhydroxylamine (DMHA) and cyclic alkynes can be accelerated by judicious functionalization of the alkyne. We explored three distinct activation modes, (i) additional predistortion of the alkyne by fused cycles and decorating the cycloalkyne with (ii) exocyclic heteroatom substituents, and (iii) endocyclic heteroatom substitution on the cycloalkyne. Our design principles and judicious combination of these activation modes were used to rationally design a suite of novel bioorthogonal reagents that feature second-order rate constants that outperform all other current reagents in these retro-Cope elimination reactions.Our activation strain and Kohn–Sham molecular orbital analyses identified the enhanced retro-Cope elimination reactivity upon predistortion of the alkyne (linear to cyclic) arises from a reduction in activation strain and a strengthening of stabilizing orbital interactions. Predistortion of the alkyne via cyclization induces a stabilization of the propyne π*-LUMOalkyne, which results in a smaller, more favorable HOMODMHA–LUMOalkyne gap and thus more stabilizing inverse electron demand (IED) orbital interactions. Appending the COT with fused cycles imparts additional predistortion of the alkyne, leading to even less activation strain and even more stabilizing IED orbital interactions. Decorating COT with exo- and endocyclic heteroatom substituents also stabilizes the π*-LUMOalkyne, and consequently further enhances the stabilizing IED orbital interactions.
A secondary effect is observed in the case of DIBO, a dibenzo-annulated cyclooctyne, which exhibits a more pronounced decrease in the activation strain that occurs at the consistent geometry, that is, a consistent point along the reaction coordinate (r(C⋯H)), relative to BCN (bicyclononyne). This can be related to the more slanted reaction path, where the formation of the C⋯N bond lags behind that of the C⋯H bond because of the following: Due to the twisted nature of DIBO, the πin-plane-HOMO of COT mixes in with the π-system of the benzene substituents, heightening the steric Pauli repulsion. The strong repulsive interaction is absorbed by adapting the reaction system to a more slanted reaction path. As a consequence, the overlaps are reduced, thereby lowering both the repulsive Pauli repulsion and the favorable orbital interactions. Notably, because of this more slanted reaction path, both reactants are less distorted at consistent geometry, causing a more pronounced decrease in the activation strain.
Our rational design principles allowed us to construct a priori a suite of novel bioorthogonal reagents that are highly reactive towards the retro-Cope elimination reaction with DMHA. Based on the judicious substitution of the parent COT, our novel reagents exhibit reactivities that are two to four orders of magnitude greater than COT.
Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
TAH conceived the project. SEB and SY carried out the quantum chemical computations and bonding analyses. SEB, SY, and TAH drafted the manuscript. All authors discussed the results and reviewed the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the Netherlands Organization for Scientific Research (NWO) and the Fondazione Cassa di Risparmio di Padova e Rovigo (CARIPARO). This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative.References
- (a) H. C. Hang, C. Yu, D. L. Kato and C. R. Bertozzi, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14846–14851 CrossRef CAS PubMed; (b) E. M. Sletten and C. R. Bertozzi, Angew. Chem., Int. Ed., 2009, 48, 6974–6998 CrossRef CAS PubMed; (c) E. M. Sletten and C. R. Bertozzi, Acc. Chem. Res., 2011, 44, 666–676 CrossRef CAS PubMed; (d) C. R. Bertozzi, Acc. Chem. Res., 2011, 44, 651–653 CrossRef CAS PubMed.
- (a) J. M. Baskin, J. A. Prescher, S. T. Laughlin, N. J. Agard, P. V. Chang, I. A. Miller, A. Lo, J. A. Codelli and C. R. Bertozzi, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16793–16797 CrossRef CAS PubMed; (b) S. T. Laughlin, J. M. Baskin, S. L. Amacher and C. R. Bertozzi, Science, 2008, 320, 664–667 CrossRef CAS PubMed; (c) P. Agarwal, B. J. Beahm, P. Shieh and C. R. Bertozzi, Angew. Chem., Int. Ed., 2015, 54, 11504–11510 CrossRef CAS PubMed; (d) N. K. Devaraj, R. Weissleder and S. A. Hilderbrand, Bioconjugate Chem., 2008, 19, 2297–2299 CrossRef CAS PubMed; (e) R. Rossin, P. R. Verkerk, S. M. van den Bosch, R. C. Vulders, I. Verel, J. Lub and M. S. Robillard, Angew. Chem., Int. Ed., 2010, 49, 3375–3378 CrossRef CAS PubMed; (f) J. Yang, J. Seckute, C. M. Cole and N. K. Devaraj, Angew. Chem., Int. Ed., 2012, 51, 7476–7479 CrossRef CAS PubMed.
- (a) M. L. Blackman, M. Royzen and J. M. Fox, J. Am. Chem. Soc., 2008, 130, 13518–13519 CrossRef CAS PubMed; (b) N. K. Devaraj, R. Weissleder and S. A. Hildebrand, Bioconjugate Chem., 2008, 19, 2297–2299 CrossRef CAS PubMed; (c) D. M. Patterson, L. A. Nazarova, B. Xie, D. N. Kamber and J. A. Prescher, J. Am. Chem. Soc., 2012, 134, 18638–18643 CrossRef CAS PubMed; (d) D. Svatunek, M. Wilkovitsch, L. Hartmann, K. N. Houk and H. Mikula, J. Am. Chem. Soc., 2022, 144, 8171–8177 CrossRef CAS PubMed; (e) D. Svatunek, K. Chojnacki, T. Deb, H. Eckvahl, K. N. Houk and R. M. Franzini, Org. Lett., 2023, 25, 6340–6345 CrossRef CAS PubMed; (f) D. Svatunek, Top. Curr. Chem., 2024, 382, 17 CrossRef CAS PubMed.
- (a) E. Saxon and C. R. Bertozzi, Science, 2000, 287, 2007–2010 CrossRef CAS PubMed; (b) L. Shah, S. T. Laughlin and I. S. Carrico, J. Am. Chem. Soc., 2016, 138, 5186–5189 CrossRef CAS PubMed; (c) C. I. Schilling, N. Jung, M. Biskup, U. Schepers and S. Bräse, Chem. Soc. Rev., 2011, 40, 4840–4871 RSC.
- (a) R. Huisgen, Proc. Chem. Soc., London, 1961, 357–369 Search PubMed; (b) R. Huisgen, Angew. Chem., Int. Ed. Engl., 1963, 2, 565–598 CrossRef; (c) R. Huisgen, Angew. Chem., Int. Ed. Engl., 1963, 2, 633–645 CrossRef; (d) M. Breugst and H.-U. Reissig, Angew. Chem., Int. Ed., 2020, 59, 12293–12307 CrossRef CAS PubMed; (e) S. E. Beutick, P. Vermeeren and T. A. Hamlin, Chem.–Asian J., 2022, 17, e202200553 CrossRef CAS PubMed.
- (a) N. J. Agard, J. A. Prescher and C. R. Bertozzi, J. Am. Chem. Soc., 2004, 126, 15046–15047 CrossRef CAS PubMed; (b) J. C. Jewett and C. R. Bertozzi, Chem. Soc. Rev., 2010, 39, 1272–1279 RSC; (c) L. Liang and D. Astruc, Coord. Chem. Rev., 2011, 255, 2933–2945 CrossRef CAS; (d) D. Svatunek, N. Houszka, T. A. Hamlin, F. M. Bickelhaupt and H. Mikula, Chem.–Eur. J., 2019, 25, 754–758 CrossRef CAS PubMed.
- X. Ning, R. P. Temming, J. Dommerholt, J. Guo, D. B. Ania, M. F. Debets, M. A. Wolfert, G.-J. Boons and F. L. van Delft, Angew. Chem., Int. Ed., 2010, 49, 3065–3068 CrossRef CAS PubMed.
- (a) H. Stöckmann, A. A. Neves, S. Stairs, K. M. Brindle and F. J. Leeper, Org. Biomol. Chem., 2011, 9, 7303–7305 RSC; (b) Y. A. Wainman, A. A. Neves, S. Stairs, H. Stöckmann, H. Ireland-Zecchini, K. M. Brindle and F. J. Leeper, Org. Biomol. Chem., 2013, 11, 7297–7300 RSC; (c) J. Tu, D. Svatunek, S. Parvez, H. J. Eckvahl, M. Xu, R. T. Peterson, K. N. Houk and R. M. Franzini, Chem. Sci., 2020, 11, 169–179 RSC.
- (a) Y. Wang, W. J. Hu, W. Song, R. K. V. Lim and Q. Lin, Org. Lett., 2008, 10, 3725–3728 CrossRef CAS PubMed; (b) R. K. V. Lim and Q. Lin, Acc. Chem. Res., 2011, 44, 828–839 CrossRef CAS PubMed.
- (a) D. Kang and J. Kim, J. Am. Chem. Soc., 2021, 143, 5616–5621 CrossRef CAS PubMed; (b) D. Kang, S. T. Cheung and J. Kim, Angew. Chem., Int. Ed., 2021, 60, 16947–16952 CrossRef CAS PubMed; (c) D. Kang, S. T. Cheung, A. Wong-Rolle and J. Kim, ACS Cent. Sci., 2021, 7, 631–640 CrossRef CAS PubMed; (d) D. Kang, S. Lee and J. Kim, Chem, 2022, 8, 2260–2277 CrossRef CAS PubMed.
- N. J. Agard, J. A. Prescher, C. R. A. Bertozzi and C. R. A, J. Am. Chem. Soc., 2004, 126, 15046–150476 CrossRef CAS PubMed.
- (a) R. A. Carboni and R. V. Lindsey, J. Am. Chem. Soc., 1959, 81, 4342–4346 CrossRef CAS; (b) F. Thalhammer, U. Wallfahrer and J. Sauer, Tetrahedron Lett., 1990, 31, 6851–6854 CrossRef CAS; (c) M. L. Blackman, M. Royzen and J. M. Fox, J. Am. Chem. Soc., 2008, 130, 13518–13519 CrossRef CAS PubMed; (d) N. K. Devaraj, R. Weissleder and S. A. Hildebrand, Bioconjugate Chem., 2008, 19, 2297–2299 CrossRef CAS PubMed; (e) F. Liu, Y. Liang and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 11483–11493 CrossRef CAS PubMed.
- (a) B. Gold, G. B. Dudley and I. V. Alabugin, J. Am. Chem. Soc., 2013, 135, 1558–1569 CrossRef CAS PubMed; (b) E. G. Burke, B. Gold, T. T. Hoang, R. T. Raines and J. M. Schomaker, J. Am. Chem. Soc., 2017, 139, 8029–8037 CrossRef CAS PubMed; (c) E. Das, M. A. M. Feliciano, P. Yamanushkin, X. Lin and B. Gold, Org. Biomol. Chem., 2023, 21, 8857–8862 RSC.
- (a) J. Dommerholt, S. Schmidt, R. Temming, L. J. A. Hendriks, F. P. J. T. Rutjes, J. C. M. van Hest, D. J. Lefeber, P. Friedl, F. L. van Delft, Angew. Chem., Int. Ed., 2010, 49, 9422–9425Angew. Chem., 2010, 122, 9612–9615 Search PubMed; (b) D. Svatunek, A. Murnauer, Z. Tan, K. N. Houk and K. Lang, Chem. Sci., 2024, 15, 2229–2235 RSC.
- D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198 CrossRef CAS PubMed.
- (a) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed; (b) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649–667 CrossRef CAS PubMed; (c) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967 RSC; (d) P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Chem. Commun., 2021, 57, 5880–5896 RSC.
- (a) F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley, Hoboken, 2000, pp. 1–86 Search PubMed; (b) T. A. Hamlin, P. Vermeeren, C. Fonseca Guerra and F. M. Bickelhaupt, in Complementary Bonding Analysis, ed. S. Grabowsky, De Gruyter, Berlin, 2021, pp. 199–212 Search PubMed.
- (a) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS; (b) C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed; (c) AMS 2021, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- (a) T. A. Hamlin, D. Svatunek, S. Yu, L. Ridder, I. Infante, L. Visscher and F. M. Bickelhaupt, Eur. J. Org Chem., 2019, 378–386 CrossRef CAS; (b) P. Vermeeren, M. Dalla Tiezza, M. E. Wolf, M. E. Lahm, W. D. Allen, H. F. Schaefer III, T. A. Hamlin and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2022, 24, 18028–18042 RSC; (c) P. Vermeeren, T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2020, 59, 6201–6206 CrossRef CAS PubMed; (d) S. Yu, P. Vermeeren, K. van Dommelen, F. M. Bickelhaupt and T. A. Hamlin, Chem.–Eur. J., 2020, 26, 11529–11539 CrossRef CAS PubMed; (e) S. Yu, P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Chem.–Eur. J., 2021, 27, 5683–5693 CrossRef CAS PubMed; (f) S. Yu, F. M. Bickelhaupt and T. A. Hamlin, ChemistryOpen, 2021, 10, 784–789 CrossRef CAS PubMed; (g) E. H. Tiekink, P. Vermeeren, F. M. Bickelhaupt and T. A. Hamlin, Eur. J. Org Chem., 2021, 5275–5283 CrossRef CAS.
- (a) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS; (b) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS.
- (a) M. Franchini, P. H. T. Philipsen, E. van Lenthe and L. Visscher, J. Chem. Theory Comput., 2014, 10, 1994–2004 CrossRef CAS PubMed; (b) M. Franchini, P. H. T. Philipsen and L. Visscher, J. Comput. Chem., 2013, 34, 1819–1827 CrossRef CAS PubMed.
- (a) L. Deng, T. Ziegler and L. Fan, J. Chem. Phys., 1993, 99, 3823–3835 CrossRef CAS; (b) L. Deng and T. Ziegler, Int. J. Quantum Chem., 1994, 52, 731–765 CrossRef CAS.
- (a) W.-J. van Zeist, C. Fonseca Guerra and F. M. Bickelhaupt, J. Comput. Chem., 2008, 29, 312–315 CrossRef CAS PubMed; (b) X. Sun, T. M. Soini, J. Poater, T. A. Hamlin and F. M. Bickelhaupt, J. Comput. Chem., 2019, 40, 2227–2233 CrossRef CAS PubMed; (c) X. Sun, T. Soini, L. P. Wolters, W.-J. van Zeist, C. Fonseca Guerra, T. A. Hamlin and F. M. Bickelhaupt, PyFrag 2019, Vrije Universiteit, Amsterdam, The Netherlands Search PubMed.
- C. Y. Legault, CYLview, 1.0b, Université de Sherbrooke, Sherbrooke, QC, Canada, 2009, http://www.cylview.org Search PubMed.
- S. E. Beutick, S. Yu, L. Orian, F. M. Bickelhaupt and T. A. Hamlin, ChemistryEurope, 2024, 2, e202300072 CrossRef.
- C. Fonseca Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189–210 CrossRef PubMed.
- T. A. Hamlin, B. J. Levandowski, A. K. Narsaria, K. N. Houk and F. M. Bickelhaupt, Chem.–Eur. J., 2019, 25, 6342–6348 CrossRef CAS PubMed.
- X. Ning, J. Guo, M. A. Wolfert and G.-J. Boons, Angew. Chem., Int. Ed., 2008, 47, 2253–2255 CrossRef CAS PubMed.
- (a) C. G. Gordon, J. L. Mackey, J. C. Jewett, E. M. Sletten, K. N. Houk and C. R. Bertozzi, J. Am. Chem. Soc., 2012, 134, 9199–9208 CrossRef CAS PubMed; (b) K. Chenoweth, D. Chenoweth and W. A. Goddard III, Org. Biomol. Chem., 2009, 7, 5255–5258 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc04211e |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |