Open Access Article
Open Access ArticleComplex relaxation of trapped spin-states in spin crossover materials†
Nadeem
Natt
 and
Benjamin J.
Powell
and
Benjamin J.
Powell
 *
*
School of Mathematics and Physics, The University of Queensland, Brisbane, Queensland 4072, Australia. E-mail: powell@physics.uq.edu.au
First published on 2nd October 2024
Abstract
A diverse range of relaxation dynamics of trapped spin-states are observed in spin crossover (SCO) materials, including exponential, sigmoidal, stretched exponential, multi-step, and mixed kinetics. We reproduce and explain this full range of relaxation behaviours using a semi-empirical, semi-classical model that combines crystal field theory with elastic inter-molecular interactions. We show that frustrated intermolecular interactions, which are responsible for multistep thermal transitions, also lead to multiple energetically competitive ordered phases, even in systems that contain only one crystallographically distinct SCO site. This rugged free energy landscape leads to dynamic disorder and thence the complex dynamics widely observed in SCO materials. Similar mechanisms are vital for understanding dynamics of more complex materials from proteins to quantum materials.
1 Introduction
Coordination complexes of transition metals can have either low spin (LS) or high spin (HS) ground states.1 In spin crossover (SCO) compounds2 switching between these states can be driven by external stimuli, such as temperature, light, pressure, magnetic field, X-rays, and even nuclear decay.3 Temperature-induced SCO ranges from smooth crossovers to hysteric phase transitions, with single- and multi-step transitions observed.2 Both crystallographically distinct SCO sites4 and frustrated elastic interactions5,6 have been identified as mechanisms driving multistep transitions.SCO materials exhibit a wide range of dynamic behaviours as they relax to the ground state after light induced spin-state trapping (LIESST),3,7–17 thermal-quenching induced excited spin-state trapping (TIESST),18–20 nuclear-decay induced excited spin-state trapping (NIESST),21 and hard X-ray induced excited spin-state trapping (HAXIESST).22 This relaxation has been studied with two complementary experimental approaches. (1) In the isothermal kinetics approach, a sample is trapped in the HS state at a fixed temperature and evolution of the properties of the sample are monitored over time. (2) In thermally accelerated relaxation studies, the low-temperature trapped sample is slowly warmed while its properties are recorded.
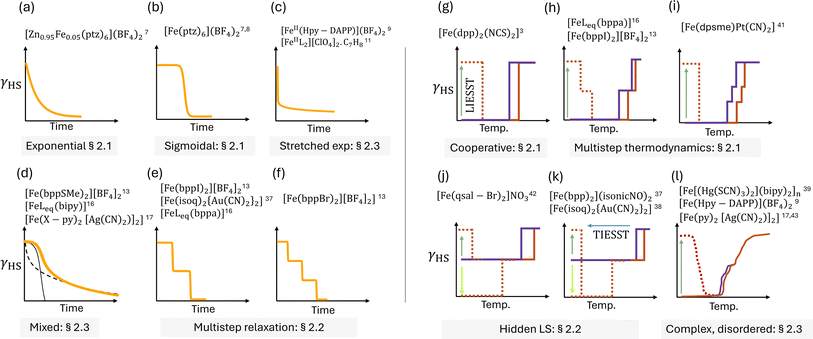
Relaxation from metastable spin-states in SCO materials shows a wide range of dynamics, as summarised in Fig. 1. In solution, isothermal relaxation of an excited state is typically simple exponential,7Fig. 1a. This implies that the interactions between molecules do not strongly influence the decay of the excited state. Sigmoidal decay, Fig. 1b, is common in the solid state SCO.8 This shows that cooperativity – due to elastic interactions between molecules – accelerates the relaxation. In the mean-field approximation, cooperative kinetics are described8 by
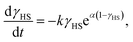 | (1) |
Moreover, a wide variety of highly complex kinetics is also observed in SCO materials.7–17,23 Slow relaxation – e.g., stretched exponential, Fig. 1c – is found in some materials,9–11 while others exhibit a change of relaxation regime with temperature12 or kinetics that are not consistent with simple rate models,13–15Fig. 1d. In some experiments, phenomenological descriptions of spin-crossover relaxation could only be obtained by mixing multiple decay functions to fit the observed decay.12,16,17 These complex kinetics are observed in materials exhibiting both single-step11 and multi-step9,23 thermodynamic transitions.
It is important to note that complex kinetics are observed in SCO materials composed of a single species and those containing multiple species.17 In materials containing multiple distinct SCO sites, different intramolecular potential barriers for the trapped state to the ground state may give rise to multiple decay rates and non-linear kinetics. On the other hand, materials containing only one SCO species have uniform intramolecular physics and the observation of complex kinetics in these materials indicates a subtle role of collective effects beyond the mean-field that have not previously received a proper explanation.
Frustrated elastic interactions can drive spontaneous symmetry-breaking, intermediate spin-states having lower symmetry, in thermal SCO.5,6,24 A great deal of effort has gone into developing theories to explain these thermal changes, including Ising-like models,25–27 electro-elastic models,5,6,27–29 and phenomenological elastic interaction models.30–35 However, there has been far less theoretical work describing the dynamics of relaxation from trapped spin states.
Kinetic experiments suggest that spontaneous symmetry-breaking also manifests in the relaxations of trapped spin-states in SCO materials.13,16,36–38 Two-step, Fig. 1e, and multistep, Fig. 1f, relaxations from photo-induced HS states have been observed in several spin-crossover materials,13,16,37 accompanied by lower symmetry intermediate states. Often a fast first step and a slower second step are observed, with each exhibiting different decay forms,13,16,37,38e.g., the isothermal relaxation of the trapped HS state in [Fe(bppI)2][BF4]2 is two-step: the first step decays exponentially but the second step decays sigmoidally.13 Therefore, a systematic investigation of how elastic frustration leads to multistep kinetics and stabilises kinetically trapped symmetry-breaking intermediates is important for understanding the role of elastic frustration in SCO kinetics.
A wide range or behaviours are also observed in thermally accelerated relaxation experiments, Fig. 1g–l. Most commonly,3 one observes single step transitions in both thermal cycling and on warming the trapped HS state, Fig. 1g. In several experiments, intermediate plateaus have also been observed during thermally accelerated relaxation.13,16,18,37,39,40 This indicates a relatively stable kinetically trapped intermediate phase.18,39 Two-step thermal transitions can lead to two-step relaxation after LIESST,13,16Fig. 1h, but are sometime accompanied by one-step relaxation from the trapped excited state,41Fig. 1i. Incomplete SCO is also observed in several materials,37,38,42Fig. 1j and k, whereby on thermal cycling an (often symmetry breaking) intermediate mixed phase is reached at low temperatures. Often the HS phase can be reached by LIESST and the LS phase can be reached by reverse-LIESST. Interestingly, in some cases thermally accelerated relaxation from the trapped HS phase returns the system to the mixed phase,42Fig. 1j; but in others the trapped HS phase relaxes to the LS phase,37,38Fig. 1k. Finally, some systems display two9,17,43 or more39 indistinct steps with disordered in the intermediate phases, Fig. 1l. This is accompanied by complex thermally accelerated relaxation curves.
Theoretically, the mechanisms of complex relaxations are not described by single-molecule theory7 or the mean-field consideration of cooperativity.8 The theory of thermal SCO has highlighted the significance of elastic cooperation and frustration,5,6 particularly for the emergence of symmetry-breaking intermediate spin-states. Beyond mean-field theory, the excited state dynamics of interacting spin-crossover molecules have been studied within Ising-like and electro-elastic models widely using kinetic Monte Carlo.44–47 This work highlighted the significance of short-range antiferroelastic interactions in driving two-step kinetics.47 However, explaining the emergence of the vast range of dynamic behaviours of metastable states in the solid-state requires a theory beyond the phenomenological parameters and dynamics of Ising-like models. To comprehensively understand the fascinating body of SCO kinetic experiments requires a tractable model that captures both the single-molecular physics and collective effects.
1.1 Semi-empirical, semi-classical model
Here we present molecular dynamics simulations of trapped phases using a recently developed semi-empirical, semi-classical theory of spin-crossover material,48 summarised in Fig. 2. The two-body elastic interactions between neighbours (n = 1, 2, or 3) are modelled as springs with force constants κn, as depicted in Fig. 2b. Additionally, a three-body angular interaction with force constant κθ is included. Elastic frustration arises in spin crossover materials if all interactions cannot be minimised simultaneously, this leads to some force constants κn being negative6,29 (see Fig. S1†). We will refer to a κn > 0, which favours both molecules connected by the spring having the same spin state,6,29 as ferroelastic and a κn < 0, which favours the two molecules connected by the spring having different spin states,6,29 as antiferroelastic.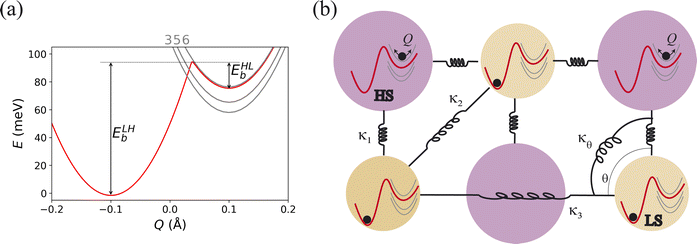 | ||
| Fig. 2 Schematic of the model. (a) Each molecule is described by potential energy surfaces, Vν(Q), derived from crystal field theory. Spin–orbit coupling is included perturbatively, allowing the intermediate spin term to be integrated out. This results in a double well (red), and fourteen pure HS levels (grey; degeneracies as labelled). The barriers EHLb and ELHb that regulate the single molecular kinetics are labelled. Only the breathing mode, Q, is considered explicitly, with the other molecular vibrations included only by their entropic contributions. (b) Molecules form a square lattice with elastic intermolecular interactions, κn, defined in eqn (S1–S3).† | ||
We simulate a 30 × 30 square lattice in the constant temperature, constant pressure ensemble. To simulate the dynamics, we initialise the simulation in an excited state, e.g., an all-HS state at 10 K, and let the ensemble evolve. For thermal SCO, we initialise in an all-HS state at high temperatures and cool down to 10 K. More detailed discussion of the model, the parameter values and computational details is provided in Table 1 and the ESI.†
| Fig. | Kinetic behaviour | Intermediate | Dq/B | κ 1 [eV Å−2] | κ 2/κ1 | κ 3/κ1 | κ θ /κ1 |
|---|---|---|---|---|---|---|---|
| 3a | Mean-field cooperative | None | 2.039 | 0.86 | 0.2 | 0 | 0 |
| 4 | Two-step isothermal kinetics | Stripe | 2.039 | 0.86 | 0.6 | −0.15 | 0 |
| 4b | Two-step thermally activated kinetics | Stripe | 2.039 | 0.86 | 0.5 | −0.25 | 0 |
| S2 | Two-step thermally activated kinetics | Chequerboard | 2.039 | 0.86 | 0.15 | −0.25 | 0 |
| S3 | Three-step isothermal relaxation | γ 1/3, γ2/3 | 2.0459 | 1.55 | −0.21 | 0.1 | 0.56 |
| 5 | Hidden metastability, three step thermally activated relaxation | γ 1/3, γ2/3 | 2.0459 | 1.55 | −0.33 | 0.11 | 0.56 |
| 6 | Mixed single-step kinetics | Dynamic disorder | 2.039 | 0.86 | 0.2 | −0.15 | 0 |
| 7 | Complex multi-step kinetics | Dynamic disorder | 2.039 | 0.86 | 0.23 | −0.25 | 0 |
Note that we choose to simulate a 2D lattice for reasons of computational expediency. It is known that, because elastic interactions are long-ranged, SCO is in the mean-field universality class.31 This implies that the change from 2D to 3D will cause minor quantitative changes, but not qualitative changes.49,50 Most importantly the Hohenberg–Mermin–Wagner theorem51,52 does not apply, so long-range order is allowed in 2D systems at non-zero temperatures (as is confirmed by the results below). We choose to simulate 2D lattices as this allows our molecular dynamics simulations to run in a reasonable time frame and reduces the number of free parameters in the model. We expect simulations in 3D to show the same qualitative behaviours as we report here in 2D. Our goal below is therefore to identify and discuss the general qualitative behaviours that should be expected in SCO materials. Where we compare to experimental results we will limit our comparisons to this qualitative level. We do not aim to provide detailed modelling of any particular material and leave such comparisons for future work.
A key difference from phenomenological model previously used to study the dynamics of relaxation in SCO materials is that the model used here is derived from a quantum chemical description of a single molecule;48 crystal field theory is used here, but this could straightforwardly be extended to a higher level of theory. Our simulations naturally reproduce the observed complex relaxation behaviours and elucidate their controlling factors, particularly the role of frustration. We show that the frustrated elastic interactions control the stability of intermediate trapped phases in SCO. Furthermore, we show that the emergence of dynamic disorder due to spin-state frustration drives complex kinetics of spin-crossover materials and discuss the generality of this mechanism in other systems.
2 Results and discussion
We begin by demonstrating that our model reproduces common experimental results described by previous theories. We then show that the model describes multistep relaxation, which extends previous work describing multistep thermal spin crossover. Finally, we show that the same competing frustrated interactions can drive complex kinetic behaviours in single- and multi-step transitions. Thus, a single model derived from the simplest microscopic picture of a coordination complex can describe the full gamut of relaxation behaviours observed in SCO materials to date, Fig. 1.2.1 Mean-field-like kinetics
When all the interactions are ferroelastic (κn > 0 for all neighbours n) there is no frustration. In this regime we find that both the quasi-equilibrium behaviours and the relaxation dynamics are described by well-understood theories.7,8 The relaxation of the trapped HS state is captured by mean-field theory (eqn (1)).The LS and HS states have different magnetic susceptibilities, χ, at a temperature, T: χT ≃ 0 in the LS state, whereas χT ≃ 3 cm3 K mol−1 for the HS state.2 Thus, a sigmoidal time dependence of χT signals mean-field-like relaxation from the HS phase to the LS phase (Fig. 3a). Weaker interactions, Fig. 3b, reduce cooperativity and hence the degree of self-acceleration, α. For vanishingly small intermolecular interactions α → 1 and the excited spin-state decay regains the simple exponential form characteristic of a single molecule.
 | ||
| Fig. 3 Mean-field-like isothermal relaxation from the trapped HS state in an unfrustrated system. (a) The sigmoidal model (eqn (1)) fits the calculations well at all temperatures for unfrustrated interactions (e.g., the typical parameters listed in Tables 1 and S1,† shown here). The rate constant, k, and the self-acceleration parameter, α, are defined in eqn (1) and are given in the figure. (b) Lower interaction strengths, here κ2 = 0.06κ1 (versus κ2 = 0.2κ1 in (a), see also Table 1), decreases the cooperativity, which reduces k and α. The difference in χT at t = 0 for different temperatures is due to the temperature dependence of χT in the HS state, which is a consequence of the zero-field splitting of the HS states by spin–orbit coupling. | ||
In strongly cooperative unfrustrated systems we find a single step, first order transition in thermal sweeps, while thermally accelerated relaxation displays a single inflexion point in χT, Fig. S1,† which defines TLIESST. As cooperativity is reduced, the hysteresis width decreases and, eventually, vanishes when the transition is replaced by a crossover. The thermally activated relaxation of trapped HS states shows a concomitant reduction in TLIESST (Fig. S1†).
All of these behaviours are well understood on the basis of mean field theory. However, this description breaks down if the system is frustrated, below we show that this can lead to qualitatively different relaxation behaviours.
2.2 Weakly frustrated kinetics: multi-step relaxation
In this section we demonstrate that weak elastic frustration can drive isothermal relaxations in two or more well-defined steps. Importantly, we show this in a model with a single SCO species – demonstrating that multiple SCO sites are not required for multistep relaxation. For example, weak frustration due to antiferroelastic third nearest neighbour interactions (κ3 < 0) leads to two-step relaxation of the trapped HS state, Fig. 4a. Both steps are sigmoidal. The intermediate plateau has short range stripe order with approximately half of the SCO centres in the HS state, Fig. 4b.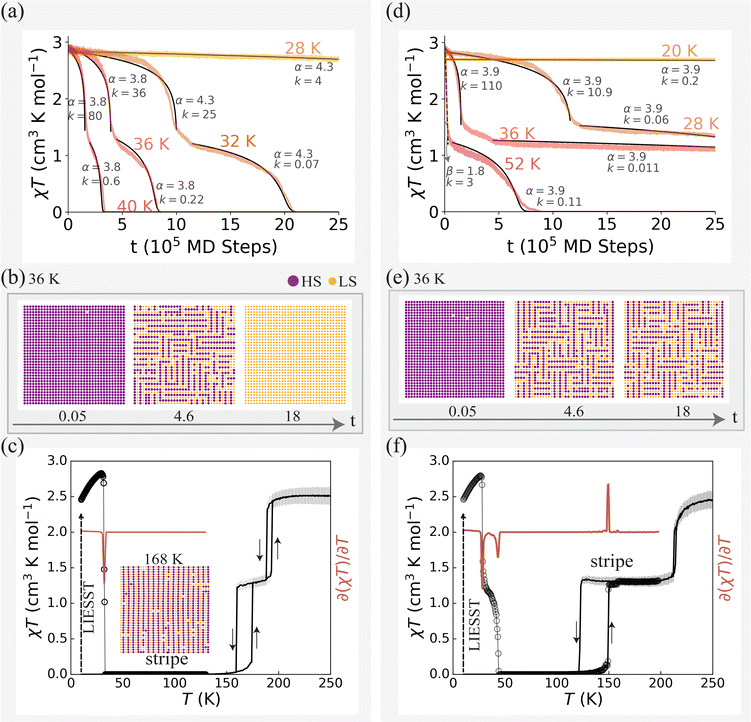 | ||
| Fig. 4 Weak elastic frustration drives two-step relaxation kinetics and two-step thermal transitions. (a and d) Two-step isothermal decay from the trapped HS state. (a) The metastable phase in the intermediate plateau has short-range stripe order. At all temperatures, good sigmoidal fits can be found for both steps (solid lines; eqn (1), parameters given in the figure). (d) Increased frustration stabilises the stripe phase. At 28 K, the decay is sigmoidal in both steps. At 52 K, the first relaxation step becomes compressed exponential, e−ktβ, where β is the compressing exponent, (dashed line, with parameters as marked), but the second step remains sigmoidal. This change occurs at ca. 46 K. (b and e) Corresponding evolution of spin-state configurations at 36 K. (c and f) Thermally accelerated relaxation of the trapped HS state (black circles) and SCO under thermal cycling (black lines). (c) Thermally accelerated relaxation following LIESST shows a single step characterised by a dip in ∂(χT)/∂T at TLIESST = 32 K (red line). Thermal SCO has an intermediate symmetry breaking phase with long-range stripe order (inset). (f) The increased stability of the intermediate stripe phase (due to increased frustration) leads to two well-defined steps in the relaxation after LIESST, characterised by two dips in ∂(χT)/∂T at T(1)LIESST = 28 K and T(2)LIESST = 44 K, and increases the range of temperatures at which the intermediate phase is stable under thermal cycling. (a–c) κ2 = 0.6κ1 and κ3 = −0.15κ1. (d–f) κ2 = 0.5κ1 and κ3 = −0.2κ1. All other parameters as in Tables 1 and S1.† | ||
For this weakly frustrated system, thermal cycling shows a two-step transition with long-range stripe order in the intermediate plateau, Fig. 4c. The long-range order of the intermediate plateau spontaneously breaks the symmetry of crystal, doubling the unit cell length in one direction. However, as the kinetically trapped stripe state is short-lived thermally accelerated relaxation skips the intermediate plateau, yielding a single-step relaxation of the trapped HS state with TLIESST = 32 K, Fig. 4c. Note that the isothermal kinetics still occurs in two well-defined steps for all temperatures below T1/2 (the temperature where γHS = 1/2 in thermal equilibrium), which includes a significant temperature range above TLIESST, Fig. 4a. However, as the kinetically trapped stripe state is short-lived thermally accelerated relaxation does not reveal the intermediate plateau, Fig. 4c. This emphasises a well-known limitation of the thermally accelerated relaxation, which is strongly dependent on the heating rate used in the experiment.
A moderate increase in the frustration (making κ3 more negative) results in a longer lived intermediate state, Fig. 4d. At low temperatures, the HS → stripe decay remains sigmoidal (e.g., the 28 K data); but at higher temperatures, it becomes fast and takes a compressed-exponential form (e.g., the 52 K data). Nevertheless, the stripe → LS decay remains slow and sigmoidal in both temperature regimes. Similar two-step isothermal relaxations with a fast, exponential-like first step and a slower, sigmoidal second step have been observed in several materials,13,16,37 the layered (quasi-2D) framework [Fe(isoq)2{Au(CN)2}2] also shows a stripe intermediate plateau.37
Increased frustration leads to two-step thermally accelerated relaxation, Fig. 4f, with short-range stripe order in the intermediate plateau. Two negative peaks in the derivative indicate two temperatures, T(1)LIESST = 28 K and T(2)LIESST = 44 K, Experimentally, two-step thermally accelerated relaxation has been observed in several spin-crossover materials.16,37,39,40
Two-step relaxation with chequerboard order in the intermediate plateau is found when κ2 is lowered, Fig. S2.† However, the change in the intermediate order does not lead to significant changes in the relaxation dynamics. A layered FeII–ReV cyanido-bridged framework36 exhibits two step thermodynamic transition and thermally accelerated relaxation involving a chequerboard intermediate.
The frustration is further enhanced if the nearest and next nearest neighbour interactions compete, for example, for antiferroelastic κ2. This can lead to three-step relaxation processes, as shown in Fig. 5, where the relaxation proceeds via two intermediate states. Again, longer-lived intermediate metastable states can also appear during the thermally activated relaxation after LIESST. We are not aware of any experiment yet reporting three-step thermally assisted decay of a trapped HS state.
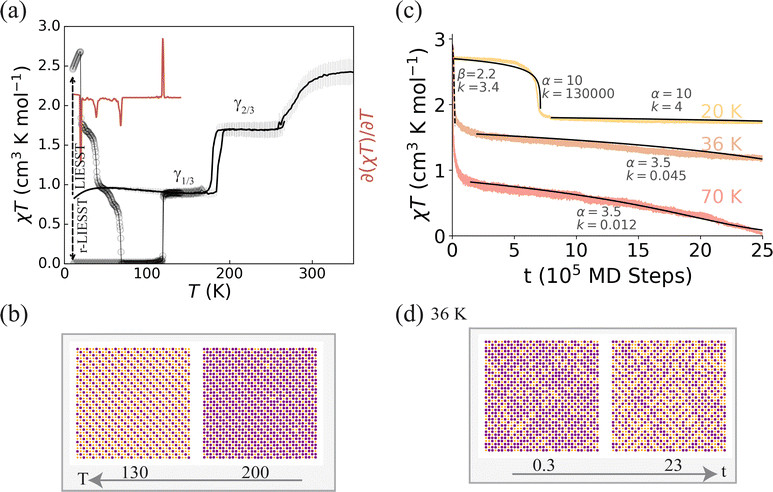 | ||
| Fig. 5 Three-step thermally accelerated relaxation and two-step incomplete thermal transitions in a highly frustrated system. (a) Thermally accelerated relaxation of the low-temperature trapped HS state proceeds via two intermediate plateaus (black circles). This leads to three negative peaks in ∂(χT)/∂T (red line) at T(1)LIESST = 22 K, T(2)LIESST = 40 K and T(3)LIESST = 82 K. Thermal SCO (black lines) shows as incomplete two-step transition with long-range ordered phases in the intermediate plateau (γ2/3) and low-temperature phase (γ1/3). The LS phase is accessible via reverse-LIESST at 10 K, and relaxes to the γ1/3 phase at Tr-LIESST = 120 K, yielding a peak in ∂(χT)/∂T. (b) Typical spin-state configurations of the γ1/3 (at 130 K) and γ2/3 (at 200 K) phases on cooling from high temperature. (c) Calculated isothermal relaxations of the trapped HS state at various temperatures show that intermediate steps are stable for long times. This is clearly responsible for the multistep thermally accelerated relaxation. Fits to sigmoidal (solid lines, eqn (1)) or compressed exponential (dashed line, e−ktβ) are shown, with the parameters marked in the figure. (d) The spin-state configurations during relaxation at 36 K show significant disorder, unlike the orderly configurations observed during thermal crossover (b). This suggests that at low temperatures the LS phase is thermodynamically stable and the dynamic disorder following thermally accelerated relaxation prevents the system from becoming kinetically trapped in the γ1/3 phase, as it does on thermal cycling. Here the ligand-field strength (see ESI†) is Dq/B = 2.0459, κ1 = 1.55 eV Å−2, κ2 = −0.33κ1, κ3 = 0.11κ1, and κθ = 0.56κ1 and the rest of the parameter values used for both of these cases are listed in Tables 1 and S1.† | ||
The corresponding thermal SCO, Fig. 5a, is an incomplete two-step transition, with a low-temperature phase, γ1/3, with HS fraction 1/3, and an intermediate spin-state phase, γ2/3, with HS fraction 2/3. Both of these phases have lower symmetry than the high-temperature HS state. At low temperatures, reverse-LIESST, γ1/3 → LS, allows access to a hidden LS phase. Interesting the LS phase is also reached after thermally accelerated relaxation following LIESST, TIESST, etc. Similar behaviour has been observed in several layered SCO materials.37,42
To understand why the systems reaches the LS state after LIESST, but not on thermal cycling, it is important to recognise the differences in the spin-state configurations in the plateaus with a HS fraction γHS = 1/3. On thermal cycling the γ1/3 phase has true long-range order (Fig. 5b). On thermal accelerated relaxation after LIESST we find a highly disordered state in the γHS = 1/3 plateau, with only short-range order. Importantly, this disorder varies in both space and time – that is, the disorder is dynamic. Our results indicate that the barrier between the long-range ordered γ1/3 phase (Fig. 5b) and the LS phase is too large to be overcome in the relevant temperature range (≤100 K). However, the barrier between the disordered γHS = 1/3 state (Fig. 5d) and the LS phase is small enough to be overcome at T(3)LIESST = 82 K. Thus, the dynamics of the disorder allows the system escape kinetic traps and access states that would otherwise be inaccessible. This may be an important general lesson for understand other dynamically disorder systems. It is interesting to compare this with, for example, the functional advantage dynamic disorder is believed to provide proteins with in binding to specific substrates.53
On lowering the frustration (e.g., making κ2 less negative), the intermediate metastable states become less stable, erasing the intermediate plateaus in the thermally activated relations after LIESST and allowing direct access to the LS phase on thermal cycling, Fig. S3.†
2.3 Complex kinetics: dynamic disorder from competing orders
In highly frustrated systems we find significantly altered kinetic processes as well as multistep relaxation. We observe that multiple intermediate ordered states are energetically competitive, indicating that the free energy landscape is rugged. Furthermore, we observe that dynamic spin-state disorder, due to this ruggedness, causes complex relaxation kinetics, Fig. 6 and 7.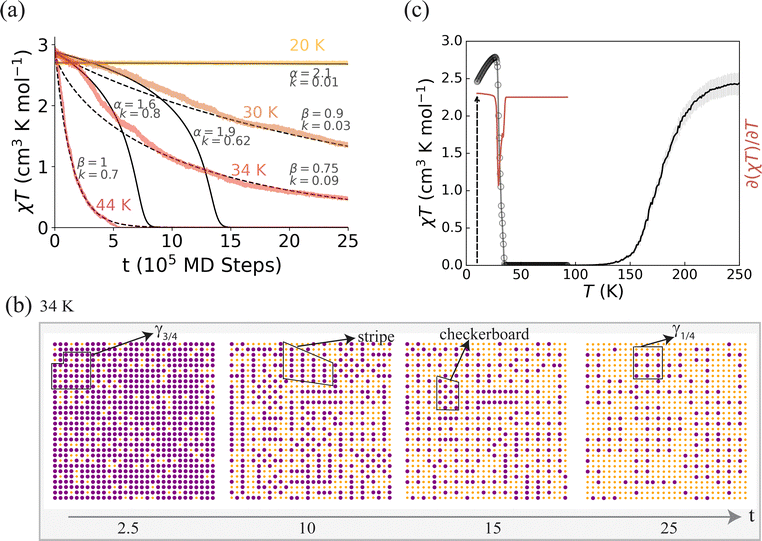 | ||
| Fig. 6 Complex isothermal relaxation from a rugged free energy landscape and dynamical disorder due to competing phases in a model with a single SCO species. (a) Isothermal relaxation slows as it proceeds. At short times and low temperatures the relaxation is sigmoidal (eqn (1); solid line; parameters as marked); at long times and high temperatures the relaxation follows a stretched exponential form (ektβ, β < 1; dashed line; parameters as marked). (b) The spin-state evolution at 34 K shows microdomains domains of competing chequerboard, stripe, γ1/4 and γ3/4 phases. (c) For these parameters, thermal SCO and thermally activated relaxation are both single-step processes. Here κ3 = −0.15κ1, with the rest of the parameters as listed in Tables 1 and S1.† | ||
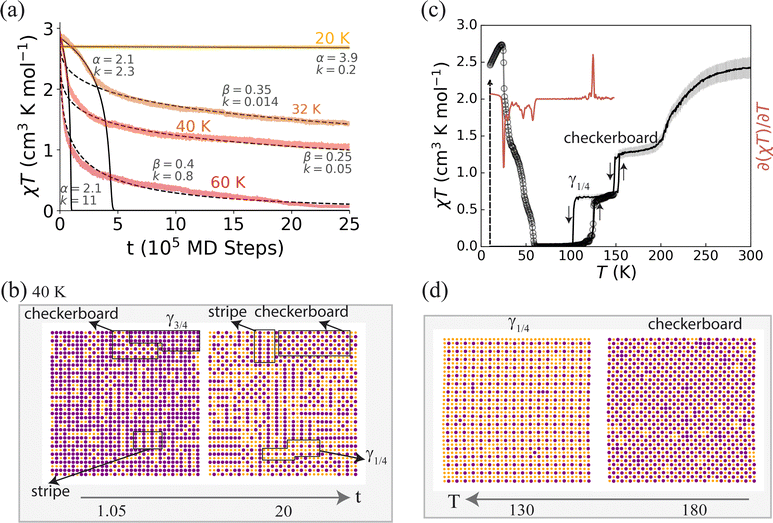 | ||
| Fig. 7 A rugged free energy landscape leading to complex isothermal relaxation, multistep thermally assisted relaxation, and multistep the thermal SCO. (a) Isothermal relaxation is sigmoidal at short times and low temperatures (eqn (1); solid line; parameters marked) but becomes stretched exponential (ektβ, β < 1; dashed line; parameters marked) at long times and high temperatures. (b) Snapshots of the spin-state distributions during the isothermal relaxation at 40 K show competing domains of stripe, chequerboard, γ1/4 and γ3/4 spin-state orders. (c) The thermally accelerated decay of the trapped HS state is extremely complicated, ∂(χT)/∂T shows several well defined negative peaks and multiple subtle dips. Thermal SCO proceeds via two long-range ordered intermediate phases, γ1/4 and chequerboard. (d) Typical snapshots at the SCO steps on cooling from high temperatures. Here κ2 = 0.23κ1 and κ3 = −0.2κ1, the other parameters are as given in Tables 1 and S1.† | ||
Intermediate orders compete in broad parameter ranges of the semi-empirical, semi-classical model; even when the thermally accelerated decay and thermal spin-crossover are both single-step, as shown in Fig. 6. We find that in these parameter ranges the calculated χT cannot be fit by standard phenomenological rate models, Fig. 6a. At intermediate temperatures (ca. 30–40 K), no single simple relaxation form fits the isothermal relaxation data well.
A common behaviour (seen, for example, in the 34 K data in Fig. 6) is that χT initially relaxes sigmoidally, but at longer times the relaxation slows and can be fit to a stretched exponential function, e−ktβ with β < 1. Experimentally, such ‘mixed relaxations’ have been observed in several SCO materials.9,13,16,17 For example, [Fe(bppSMe)2][BF4]2 exhibits behaviour similar to the calculations presented in Fig. 6: single step SCO, a single negative peak in ∂(χT)/∂T, and mixed isothermal kinetics with stretched tails.13 We observe complex relaxation dynamics with temperature dependent regime changes for many other parameter regimes with a wide range of intermediate incipient orders.
It has been speculated that such complex kinetics require materials with multiple crystallographically distinct SCO centers.12,13,16,47 However, our result shows that mixed relaxation can occur with only one spin-crossover species, consistent with experiment.17 Snapshots of spin-state distributions during the relaxation reveal small areas of four metastable spin-state orders: stripe, chequerboard, γ1/4 and γ3/4, Fig. 6b. None of these phases stabilises into long-range order or lives for long times. However, the competition between these incipient orders leads to a dynamic spin-state disorder, resulting in a complex relaxation process, where the trapped spin-state initially decays rapidly, but later decay is frustrated by the need to disentangle the competing orders, dramatically slowing the decay to γHS = 0.
For even more highly frustrated systems the free energy landscape is even more rugged. This leads to more complicated dynamics because the competing intermediate states are stable on longer timescales. An example with four incompatible incipient spin-state orders with multiple steps is shown in Fig. 7. In comparison to the single step case, Fig. 6a, the more stable dynamic disorder induces stretched exponential relaxation at high temperatures, e.g., the 60 K data in Fig. 7a. Such high temperature stretched relaxation is often observed in SCO materials.9,17
To further characterise the dynamic disorder, we have calculated the static structure factor, which can be measured via X-ray diffraction. Fig. S4† shows the static structure factor averaged over time and five different runs, for the 40 K isothermal relaxation presented in Fig. 7a. In addition to the Bragg peak centred at (0,0), additional peaks in the structure factor show that nano-domains of multiple spin-state orders simultaneously appear during the kinetics. Moreover, peak splitting due to the different unit cell lengths in different spin-state orders is also observed, Fig S4b.† Since the spin-states have only short range order, the intensity of the additional peaks is low compared to the Bragg peaks. This suggests that a careful analysis of experimental X-ray diffuse scatter could be used to detect dynamic disorder in SCO materials exhibiting complex relaxations.
Signatures of competing orders are also be found in thermal SCO and thermally accelerated relaxation, Fig. 7c. Competing orders lead to poorly defined steps in thermally accelerated decay, highly reminiscent of the behaviours of 2D coordination polymers [Fe[(Hg(SCN)3)2](4,40– bipy)2]n and Fe(py)2[Ag(CN)2]2.17,39,43 Here the corresponding thermal SCO, Fig. 7c, has two well defined intermediate steps: at γHS = 1/2 and 1/4 with chequerboard and γ1/4 states respectively. The chequerboard phase has significantly more disorder than we found in the weakly frustrated cases discussed above. This is highly reminiscent of Fe(py)2[Ag(CN)2]2, which exhibits an incomplete two-step thermal SCO with a disordered phase at the intermediate plateau and complex isothermal HS → LS relaxations with stretched form at later times during the decay.17,43
3 Conclusion
We have used a semi-empirical, semi-classical theory to understand and characterise the dynamics of frustrated, dynamically disordered SCO materials beyond standard phenomenological approaches. It is important that this model describes intramolecular processes and intramolecular elastic interactions on an equal footing. Both play key roles in the dynamics of SCO materials: the potential barriers in single molecules, Fig. 2, sets the basic timescales for dynamic processes, while intermolecular elastic interactions stabilise the intermediate phases, which can lead to dynamics that are slow on the basic molecular timescale.This theory has enabled us to explain the emergence of a range of isothermal relaxation behaviours of the trapped states including sigmoidal, stretched, compressed exponential, and mixed relaxation, Fig. 1 and Table 1. These occur because elastic interactions introduce (metastable) ordered phases that can act as kinetic traps, greatly complicating the relaxation dynamics. We emphasise that we have not constructed detailed models of specific materials. Nevertheless, our model qualitatively reproduces the wide range of complex dynamics observed in SCO materials. An important task for future extensions of our work will be to construct detailed models of specific SCO materials and show that these reproduce the behaviours seen experimentally in those materials.
We have also shown that dynamical disorder allows the system to escape kinetic traps. This explains why SCO materials that show incomplete transitions often relax to the LS phase after LIESST. TIESST, etc. The thermal intermediate plateau is long-range ordered and therefore significantly more stable than the dynamically disordered intermediate plateau reached on thermally accelerated relaxation following LIESST. This parallels the selective advantages provided to proteins by dynamic disorder.
In elastically frustrated SCO materials, multiple competing incipient orders give rise to rugged free energy landscapes. This ruggedness results in dynamically disordered spin-state configurations and hence explains the changes in relaxation regime with temperature seen experimentally in SCO materials.12 For example, the, frequently observed, quantitative and qualitative slowing of the relaxation at long times can be understood as the system becomes stuck in these metastable states. The rugged free energy landscapes are also responsible for multistep isothermal decay, multistep thermally activated relaxation, and multistep thermal SCO. For the latter two of these it is crucial to recall that the relative stability of different many-body states changes with temperature.
Previously, complex relaxation kinetics have often been attributed to non-uniform SCO species or sample impurities.12,13,16 However, we find the full range of kinetic behaviours observed experimentally in a model with only one species of SCO complexes and no impurities or imperfections.
Chemically, SCO materials are highly tunable. This positions SCO materials as outstanding model systems to study complex dynamics. This is potential is significantly enhanced by the relatively simple theory, presented here, explaining the experiments. In the future, these materials may help to establish a universal understanding of these concepts in broader contexts, from biomolecular dynamics to quantum materials. In particular, the current approach of integrating out the local quantum effects, to give a classical Marcus-Hush like PES, while retaining interactions between subunits on longer length scales could be a useful first step for understanding the complex dynamics due to frustration and dynamic disorder in a wide range of materials.
Many porous SCO frameworks have been synthesised.41,54 These frameworks allow the absorption of a range of guest molecules, which can significantly alter the physics of SCO.54–56 Therefore, it is interesting to speculate whether dynamic disorder due to competing ordered states in such frameworks could enable behaviours analogous to fuzzy (adaptable) binding in proteins.
Data availability
Data available on reasonable request.Author contributions
M. Nadeem: conceptualisation, model, method, code, simulations, analysis and writing – original draft. Ben J. Powell: conceptualisation, model, method, funding acquisition, project administration, supervision, writing – review and editing.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
It is a pleasure to acknowledge helpful conversations with Cameron Kepert, Ross McKenzie, Suzanne Neville, and Shuang Yaun. This work was supported by the ARC through projects DP200100305 and DP230100139.References
- S. Sugano, Y. Tanabe and H. Kamimura, Multiplets of transition-metal ions in crystals, Academic Press, 1970 Search PubMed.
- P. Gütlich and H. A. Goodwin, in Spin crossover—an overall perspective, ed. P. Gütlich and H. Goodwin, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 1–47 Search PubMed.
- G. Chastanet, M. Lorenc, R. Bertoni and C. Desplanches, Compt. Rendus Chem., 2018, 21, 1075–1094 CAS.
- G. Azzolina, R. Bertoni and E. Collet, J. Appl. Phys., 2021, 129, 085106 CrossRef CAS.
- M. Paez-Espejo, M. Sy and K. Boukheddaden, J. Am. Chem. Soc., 2016, 138, 3202–3210 CrossRef CAS.
- J. Cruddas and B. J. Powell, Inorg. Chem. Front., 2020, 7, 4424–4437 RSC.
- A. Hauser, Coord. Chem. Rev., 1991, 111, 275–290 CrossRef CAS.
- A. Hauser, J. Jeftić, H. Romstedt, R. Hinek and H. Spiering, Coord. Chem. Rev., 1999, 190–192, 471–491 CrossRef CAS.
- M. Buron-Le Cointe, N. Ould Moussa, E. Trzop, A. Moréac, G. Molnar, L. Toupet, A. Bousseksou, J. F. Létard and G. S. Matouzenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 214106 CrossRef.
- C. Enachescu, J. Linares, F. Varret, K. Boukheddaden, E. Codjovi, S. G. Salunke and R. Mukherjee, Inorg. Chem., 2004, 43, 4880–4888 CrossRef CAS PubMed.
- V. Mishra, R. Mukherjee, J. Linares, C. Balde, C. Desplanches, J.-F. Létard, E. Collet, L. Toupet, M. Castro and F. Varret, Inorg. Chem., 2008, 47, 7577–7587 CrossRef CAS PubMed.
- G. Chastanet, N. F. Sciortino, S. M. Neville and C. J. Kepert, Eur. J. Inorg. Chem., 2018, 2018, 314–319 CrossRef CAS.
- L. J. Kershaw Cook, H. J. Shepherd, T. P. Comyn, C. Baldé, O. Cespedes, G. Chastanet and M. A. Halcrow, Chem.–Eur. J., 2015, 21, 4805–4816 CrossRef CAS PubMed.
- V. A. Money, C. Carbonera, J. Elhaïk, M. A. Halcrow, J. A. Howard and J.-F. Létard, Chem.–Eur. J., 2007, 13, 5503–5514 CrossRef CAS PubMed.
- C. Enachescu, J. Linares, E. Codjovi, K. Boukheddaden and F. Varret, J. Optoelectron. Adv. Mater., 2003, 5, 261–266 CAS.
- C. Baldé, W. Bauer, E. Kaps, S. Neville, C. Desplanches, G. Chastanet, B. Weber and J. F. Létard, Eur. J. Inorg. Chem., 2013, 2013, 2744–2750 CrossRef.
- J. A. Rodríguez-Velamazán, C. Carbonera, M. Castro, E. Palacios, T. Kitazawa, J.-F. Létard and R. Burriel, Chem.–Eur. J., 2010, 16, 8785–8796 CrossRef.
- K. D. Murnaghan, C. Carbonera, L. Toupet, M. Griffin, M. M. Dîrtu, C. Desplanches, Y. Garcia, E. Collet, J.-F. Létard and G. G. Morgan, Chem.–Eur. J., 2014, 20, 5613–5618 CrossRef CAS PubMed.
- Y. Garcia, V. Ksenofontov, S. Mentior, M. M. Dîrtu, C. Gieck, A. Bhatthacharjee and P. Gütlich, Chem.–Eur. J., 2008, 14, 3745–3758 CrossRef CAS PubMed.
- G. A. Craig, J. Sánchez Costa, O. Roubeau, S. J. Teat and G. Aromí, Chem.–Eur. J., 2011, 17, 3120–3127 CrossRef CAS.
- A. Hauser, in Light-Induced Spin Crossover and the High-Spin → Low-Spin Relaxation, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 155–198 Search PubMed.
- G. Vankó, F. Renz, G. Molnár, T. Neisius and S. Kárpáti, Angew. Chem., Int. Ed., 2007, 46, 5306–5309 CrossRef.
- G. Chastanet, N. F. Sciortino, S. M. Neville and C. J. Kepert, Eur. J. Inorg. Chem., 2018, 2018, 314–319 CrossRef CAS.
- C. Shi, X.-B. Han and W. Zhang, Coord. Chem. Rev., 2019, 378, 561–576 CrossRef CAS.
- J. Wajnflasz and R. Pick, J. Phys. Colloq., 1971, 32, C1 CrossRef.
- A. Bousseksou, F. Varret and J. Nasser, J. Phys., 1993, 3, 1463–1473 CAS.
- A.-I. Popa, L. Stoleriu and C. Enachescu, J. Appl. Phys., 2021, 129, 131101 CrossRef CAS.
- Y. Konishi, H. Tokoro, M. Nishino and S. Miyashita, Phys. Rev. Lett., 2008, 100, 067206 CrossRef.
- J. Cruddas and B. Powell, J. Am. Chem. Soc., 2019, 141, 19790–19799 CrossRef CAS.
- M. Nishino, K. Boukheddaden, Y. Konishi and S. Miyashita, Phys. Rev. Lett., 2007, 98, 247203 CrossRef PubMed.
- S. Miyashita, Y. Konishi, M. Nishino, H. Tokoro and P. A. Rikvold, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 014105 CrossRef.
- K. Boukheddaden, M. Nishino and S. Miyashita, Phys. Rev. Lett., 2008, 100, 177206 CrossRef PubMed.
- M. Nishino, K. Boukheddaden and S. Miyashita, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 012409 CrossRef.
- M. Nishino, C. Enachescu, S. Miyashita, K. Boukheddaden and F. m. c. Varret, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 020409 CrossRef.
- M. Nishino, Y. Singh, K. Boukheddaden and S. Miyashita, J. Appl. Phys., 2021, 130, 141102 CrossRef CAS.
- S. Chorazy, T. Charytanowicz, D. Pinkowicz, J. Wang, K. Nakabayashi, S. Klimke, F. Renz, S.-i. Ohkoshi and B. Sieklucka, Angew. Chem., Int. Ed., 2020, 59, 15741–15749 CrossRef CAS PubMed.
- Y.-C. Chen, Y. Meng, Y.-J. Dong, X.-W. Song, G.-Z. Huang, C.-L. Zhang, Z.-P. Ni, J. Navařík, O. Malina, R. Zbořil and M.-L. Tong, Chem. Sci., 2020, 11, 3281–3289 RSC.
- V. Jornet-Mollá, C. Giménez-Saiz, L. Canadillas-Delgado, D. S. Yufit, J. A. Howard and F. M. Romero, Chem. Sci., 2021, 12, 1038–1053 RSC.
- C. Mariette, E. Trzop, S. Zerdane, P. Fertey, D. Zhang, F. J. Valverde-Munoz, J.-A. Real and E. Collet, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 660–668 CrossRef CAS PubMed.
- M. Seredyuk, K. Znovjyak, F. J. Valverde-Muñoz, M. C. Muñoz, V. M. Amirkhanov, I. O. Fritsky and J. A. Real, Inorg. Chem., 2023, 62, 9044–9053 CrossRef CAS.
- N. F. Sciortino, K. R. Scherl-Gruenwald, G. Chastanet, G. J. Halder, K. W. Chapman, J.-F. Létard and C. J. Kepert, Angew. Chem., Int. Ed., 2012, 51, 9944 CrossRef CAS.
- R. Díaz-Torres, G. Chastanet, E. Collet, E. Trzop, P. Harding and D. J. Harding, Chem. Sci., 2023, 14, 7185–7191 RSC.
- J. A. Rodríguez-Velamazán, M. Castro, E. Palacios, R. Burriel, T. Kitazawa and T. Kawasaki, J. Phys. Chem. B, 2007, 111, 1256–1261 CrossRef PubMed.
- B. Hôo, K. Boukheddaden and F. Varret, Eur. Phys. J. B, 2000, 17, 449–457 CrossRef.
- K. Boukheddaden, J. Linares, E. Codjovi, F. Varret, V. Niel and J. Real, J. Appl. Phys., 2003, 93, 7103–7105 CrossRef CAS.
- M. Nishino, K. Boukheddaden, S. Miyashita and F. Varret, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 224402 CrossRef.
- S. Mouri, K. Tanaka, S. Bonhommeau, N. O. Moussa, G. Molnár and A. Bousseksou, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 174308 CrossRef.
- M. Nadeem, J. Cruddas, G. Ruzzi and B. J. Powell, J. Am. Chem. Soc., 2022, 144, 9138–9148 CrossRef CAS PubMed.
- M. Plischke and B. Bergersen, Equilibrium Statistical Physics, World Scientific, 2006 Search PubMed.
- P. Chaikin and T. Lubensky, Principles of Condensed Matter Physics, Cambridge University Press, 2000 Search PubMed.
- P. C. Hohenberg, Phys. Rev., 1967, 158, 383–386 CrossRef CAS.
- N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133–1136 CrossRef CAS.
- S. Gianni, M. I. Freiberger, P. Jemth, D. U. Ferreiro, P. G. Wolynes and M. Fuxreiter, Acc. Chem. Res., 2021, 54, 1251–1259 CrossRef CAS PubMed.
- Z.-P. Ni, J.-L. Liu, M. N. Hoque, W. Liu, J.-Y. Li, Y.-C. Chen and M.-L. Tong, Coord. Chem. Rev., 2017, 335, 28–43 CrossRef CAS.
- M. Ahmed, K. A. Zenere, N. F. Sciortino, K. S. A. Arachchige, G. F. Turner, J. Cruddas, C. Hua, J. R. Price, J. K. Clegg, F. J. Valverde-Muñoz, J. A. Real, G. Chastanet, S. A. Moggach, C. J. Kepert, B. J. Powell and S. M. Neville, Inorg. Chem., 2022, 61, 6641–6649 CrossRef CAS PubMed.
- M. Ahmed, K. S. A. Arachchige, Z. Xie, J. R. Price, J. Cruddas, J. K. Clegg, B. J. Powell, C. J. Kepert and S. M. Neville, Inorg. Chem., 2022, 61, 11667–11674 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of molecular dynamics calculations and additional data. See DOI: https://doi.org/10.1039/d4sc04225e |
| This journal is © The Royal Society of Chemistry 2024 |