Stress amplification and relaxation imaging around cracks in nanocomposite gels using ultrasound elastography†
H.
Le Blay
 ab,
T.
Deffieux
ab,
T.
Deffieux
 b,
L.
Laiarinandrasana
b,
L.
Laiarinandrasana
 c,
M.
Tanter
c,
M.
Tanter
 *b and
A.
Marcellan
*b and
A.
Marcellan
 *ad
*ad
aLaboratoire de Sciences et Ingénierie de la Matière Molle, ESPCI Paris, Université PSL, Sorbonne Université, CNRS, F-75005 Paris, France
bInstitute Physics for Medicine Paris, Inserm U1273, ESPCI Paris, Université PSL CNRS UMR8631, Paris, France
cCentre des Matériaux, Mines Paris, PSL University, CNRS UMR 7633, F-91003 Evry Cedex, France
dInstitut Universitaire de France,
First published on 25th October 2024
Abstract
The quantification and modeling of gel fracture under large strain and dissipative conditions is still an open issue. In this study, a novel method for investigating the mechanical behavior of gels under highly deformed states, specifically in the vicinity of the crack tip, was developed to gain insights into fracture processes. Shear wave elastography, originally developed for the biomedical community, is employed as a powerful tool to quantitatively map the local elasticity of model gels. Here, the local stress is experimentally measured from the shear wave velocity according to nonlinear acoustoelasticity theory. The stress concentration observed at the crack tip in elastic gels is validated using classical finite element methods. Subsequently, the mechanisms of network rearrangements in viscoelastic gels (with silica nanoparticles) are analyzed both spatially and temporally. These gels consist of 90 wt% water and are synthesized with sticky nanoparticles to introduce exchangeable sacrificial bonds that facilitate stress relaxation. The nanoparticles efficiently provide stress relaxation around the crack tip, mitigating a stress singularity. The amplitude of stress relaxation was measured quantitatively and appears to be higher closer to the crack. This paper showcases the feasibility and potential of a new experimental approach that enables non-invasive and dynamic mapping of gel fracture mechanics.
Introduction
Nature largely inspired humans in the field of polymer gel engineering. Primitive forms of living matter, such as jellyfish or sea cucumber, have been able to produce essentially water-based tissues, i.e., gels, which possess large compliance under low deformation, together with high strength and robustness under large strains.1 From a materials science perspective and within a global context of preservation of resources, these features are intriguing and attractive.2–4Synthetic hydrogels have emerged and recent advances have opened tracks for the rational and efficient design of high performance gels as synthetic load-bearing polymers.5–7 Beyond the personal care field, gels are now being subjected to more demanding mechanical loading (in the bulk or at interfaces) for the design of stretchable electronics,8,9 soft robotics or flexible prosthetics,10 mechanically responsive tissue engineering,11 or drug delivery.12 In this way, the sacrificial bond concept inspired by bone fracture13 paved the way for the prolific designs of strikingly tough gels or gel assemblies by accounting for their large water via the introduction of contrasting structure or properties5,14–16 at length scales larger or at the same order of magnitude as the polymer network mesh size (ξ ∼ 1–100 nm). It seems clear that damage and fracture propagation in soft matter involve a complex multi-scale coupling,17 from molecular scale failure processes,18–20 to mesoscale energy dissipation,21 and to larger-scale geometrical effects.22 Yet, non-linear large strain behavior in addition to viscoelastic effects provides a comprehensive picture of the non-linear mechanisms operating at the crack-tip challenging and the definition of a predictive fracture criterion even more complex. Are the reinforcement and repair mechanisms that are supposed to work in the undeformed state identical to those that operate under extreme deformation conditions, for instance, at the crack tip? In which characteristic volume ahead of the crack do the dissipative mechanisms take place? In contrast, synthetic gel design and characterization often primarily considers only its behavior at rest or at small strains. Yet, by definition, soft matter operates under a highly deformed state where non-linearities are expected to prevail. Under these conditions, it is of large deformations, in particular that effective reinforcement architectures and dynamics need to be devised.
Several noteworthy methods have been recently investigated to identify physical processes that arise in gels: focusing around a crack tip by using particle tracking on polyacrylamide gels,23 photoelasticity on slide-ring gels,24 finite element method (FEM) simulations coupled to a camera to record fracture events in triblock copolymer elastic gels25 and physically cross-linked viscoelastic PVA gels;26 or FEM coupled to digital image correlation (DIC) in PEG/PEGMA elastic gels.27 It appears that results differ since Liu and colleagues24 found good agreement with linear elastic fracture mechanics (LEFM) theory (i.e., the stress at the crack tip decreases as σ ∼ z−1/2, where z is the distance ahead of the crack tip) on both elastic and viscoelastic gels while all other authors mentioned have found that LEFM underestimates the stress at the crack tip. Here, the works of Geubelle and Knauss28 and Knowles and Sternberg29,30 dealing with the theoretical development for estimating the asymptotic stress singularity near the crack tip for elastomeric materials are considered.
All these methods rely on the quantitative measure of the local strain and its amplification at the vicinity of the crack, but often it is rather difficult to make a comprehensive link with macromolecular mechanisms or network architectures. Recently, new progress in chemistry have enabled the incorporation of mechanophores in polymer networks31,32 to observe and define a damage zone in which bonds are broken. However, this method, dedicated to dried gels, requires complex chemistries and does not yet allow a local stress level description.
Here, we propose to develop a new tool dedicated to the fracture study of both elastic and viscoelastic gels that can provide a real-time stress mapping – through a sample thickness – based on an ultrasound imaging technique.33 The stress field measurement is not so straightforward, especially near a crack. Unlike standard elastography, which maps the elastic modulus of tissues at rest, our concept relies on mapping the local stress state throughout the thickness of the sample.
Silica nanoparticle (NP) hybrid gels were used as model systems. The synthesis34 and the structure were extensively studied by our group and appeared to be simple and robust.35,36 Thus, dispersion of the silica NP in the gel matrix is perfectly controlled. Polymer adsorption onto NP surfaces involves constant adsorption/desorption traffic of polymer segments which allows stresses to be relaxed on a large scale by local rearrangement of the network.15 The nature of interactions has been recently investigated experimentally.37 We have demonstrated that polymer adsorption onto silica NP surfaces proceeds by hydrogen bonding between polymer carbonyl groups and silanol groups from silica NP surfaces. Adsorption efficiency and dynamics can be tuned by the surface chemistry of NPs (with parameters such as pH and ionic strength) and an appropriate balance of polymer–solvent interactions that favors adsorption. These dissipative mechanisms induced by polymer rearrangements at the silica surface can be exploited to generate robust gel adhesion38,39 or even for initiating crack pinning.40
So far, fracture energies of hybrid gels have been estimated and appeared to correlate with the content of NPs.36,37 Typically, gel fracture ranges from 10 J m−2 to 500 J m−2 for gels without NPs and 20 vol% silica NPs, respectively. Yet, a comprehensive picture of local fracture mechanisms, those at the crack tip, was still lacking. While silica NPs (30 nm-diameter) serve as multi-functional macro-crosslinks, a sort of platform for topological network rearrangements, the question remains as to how the strain–stress fields at the crack tip are affected by NPs (i.e., a decreased distance between exchangeable crosslinks). Is the magnitude of network rearrangements impacted by NPs and can we identify a size of the process zone, i.e. the high-stress region ahead of the crack tip where nonlinear behavior may occur?
A preliminary study41 confirmed the reliability of using ultrasound elastography for a quantitative assessment of a modulus (kPa) at rest for a series of synthetic gels, including viscoelastic NP gels. By developing ultrasound imaging elastography in the non-linear regime with a focus on fracture processes, the main benefit of this work is to obtain, non-invasively, a map of the stress state (kPa) near the crack tip in the bulk of the specimen (not at the gel surface).
After a brief description of the synthesis procedure, the elastography principle, and the several experimental setups developed, we present our experimental investigations of gels subjected to large deformations, whose mechanical behavior will be probed through polarized shear waves. Focusing on purely elastic gels (without NPs) first, the acoustoelasticity (AE) theory will allow us to explore and identify experimentally the material's nonlinear coefficients by coupling an in situ macroscopic stress measurement with an ultrasound elastography technique. The crack tip stress fields will be measured by elastography and the results will be discussed in the light of finite element calculations. Then, we will expand the approach to get a spatio-temporal mapping of the local stress near the tip of an opening crack for NP gels with varied NP contents, i.e., 0.5% and 10% vol NPs.
Materials/methods
Hydrogel synthesis
N,N-dimethylacrylamide (DMA, 99%), potassium peroxodisulfate (KPS), N,N,N′,N′-tetramethylethylenediamine (TEMED), N,N′-methylenebis-(acrylamide) (MBA) and silica nanoparticles (Ludox TM-50, 50 wt% suspension and pH = 9) were obtained from Sigma Aldrich and used as received. The nanoparticles are spherical in shape with a radius of R ∼ 14 nm. Agar was used to enhance the echogenicity of the gel and was provided by VWR chemicals.The gels were prepared following the protocol detailed elsewhere.37 Hydrogels were prepared at 25 °C by free-radical polymerization (under nitrogen conditions) of DMA and MBA in an aqueous suspension of silica nanoparticles using KPS and TEMED as redox initiators. For all syntheses, gel matrix hydration was well-controlled (i.e., 88 wt%), and the (DMA)/(KPS) and (DMA)/(TEMED) molar ratios were fixed at 100. The cross-linking density was also held constant using a cross-linker/monomer molar ratio (MBA/DMA) of 0.1 mol%. The synthesis of NP gels was shown to be simple, robust, and reproducible as already shown in the literature.15,34
To obtain sufficient ultrasonic speckle41,42 within the hydrogels, the 1 wt% agar powder was added right before molding the gel, and mixed with the preparation for few seconds, making sure that the mechanical properties were neither affected nor changed (see Fig. S1, ESI†).
To avoid any change in hydrogel compositions, induced by swelling or drying, samples were then stored in paraffin oil.
Ultrasound shear wave elastography
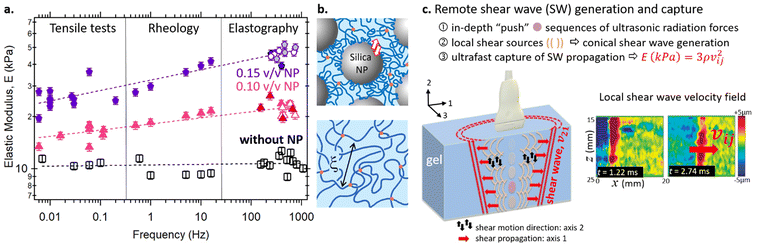
An ultrafast ultrasound scanner (Aixplorer; Supersonic Imagine, Aix-en-Provence, France) coupled with a linear piezoelectric transducer array (SuperLinear 10-2; Supersonic Imagine, Aix-en-Provence, France) was used in shear wave elastography mode. A remote palpation, based on the acoustic radiation force of focused ultrasonic beams – called “pushing beams” –, generated transient tissue displacements at focus and consequently created shear wave within the gel, as illustrated in Fig. 1. The ultrasonic frequency for each pushing beam was set at 6.4 MHz, similarly to the ultrasonic frequency for ultrafast plane wave imaging. The push duration was established at 300 μs and the event duration was established at 350 μs. The plane waves for ultrafast imaging were sent with three different flat angles [−2°, 0°, and 2°]. The maximum framerate obtained was around 5000 Hz (∼4648 Hz). With a temporal resolution of tens of milliseconds, the spatial resolution of the ultrasonic images was 200 μm. The size of the shear source was related to the size of the ultrasonic focal spot (by the radiation force). The size of the focal spot was related to the wavelength λUS (depending on the push frequency used), and the aperture ratio f/D was set to 1. The width of the focal spot was about λUS f/D = 0.2 mm in the imaging plane. The ultrasound (US) beam was focused at three focal points z = 5, 10, and 15 mm, creating an approximative Mach cone of about 10 mm in length. The ultrafast imaging sequence enabled tracking of the transient propagation of the shear wave in the gel. Then, the local speed of the shear wave was locally estimated and linked to the local shear modulus. It should be noted that the propagating shear wave generates very low displacements and this propagation occurs in the linear regime. The shear wave frequency cannot be chosen by the operator because it indirectly depends on the medium of absorption and density and it is limited by the push frequency and push duration.43 Therefore, the push frequency and push duration were changed to tune the shear wave frequency (from 2 to 10 MHz and 100 to 300 ms, respectively). The shear wave frequency was deduced using a Fourier transform of the signal.Rheology
A specific set of alumina plates were designed in the context of this study. Linear viscoelasticity was studied using a strain-controlled rheometer (Rheometrics RFSII, TA Instruments, Guyancourt, France) in a parallel-plate geometry with a 25 mm diameter. The gels were deformed by 3% within the linear viscoelastic range, as determined using a frequency of 1 Hz. Specific alumina plates were used to apply a stabilized normal force of 0.5 N (i.e., a normal stress of around 1 kPa). The frequency range investigated was comprised between 0.1 rad s−1 and 100 rad s−1. The sample thickness was fixed at 2 mm. The tensile modulus was calculated from the shear storage μ′ and the shear loss modulus μ′′, assuming incompressibility: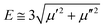 .
.
Coupling with conventional large strain mechanical testing
Tests were performed using a tensile testing machine (model 5565, Instron, Elancourt, France) equipped with a 10 N or 100 N load cell (with a relative uncertainty of 0.16%, in the range of 0 to 0.1 N) respectively, for tension and compression. Set-ups were designed to ensure the coupling between the tensile machine with the US imaging technique. So, experiments involved US elastography probing – with micrometer perturbations – of the gel stretched under large deformations applied using the tensile machine. The apparent Young's modulus was calculated in the linear regime of the stress–strain curve (up to 5% strain).In both compression and tensile tests, we calculated the true stress, σ∞, also called the Cauchy stress, which is the applied load F, divided by the actual cross-sectional area S (the changing area with time, with S0, being the initial area) of the specimen at that load, as:
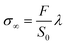 | (1) |
Finite element method
Finite element simulations were carried out so as to assess the true stress field at the local scale ahead of the crack tip using Z-set software (https://www.zset-software.com/).44- A nearly incompressible model, noted as the Rivlin model, using hybrid elements, with a strain energy function:
| W = C10(I1 − 3) + C01(I2 − 3) | (2) |
- A “compressible” model, called Mooney, using regular elements (not hybrid) where an isostatic deformation energy was added so as to take the compressibility into account. The strain energy density is given by:
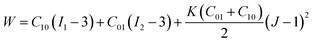 | (3) |
Results
Bridge between conventional mechanical testing and ultrasound elastography at rest
In our initial experiment, we conducted a comparative analysis of Young's modulus at rest or under small perturbation using conventional mechanical tools (tensile testing and rheology) and ultrasound imaging through shear wave elastography (Fig. 1). To ensure accurate measurements, an ultrasound gel was applied between the probe and the sample to eliminate air interference. It is important to note that in shear wave elastography, the shear wave frequency cannot be directly selected as it is indirectly influenced by factors such as push duration, focal spot, medium absorption, density, and stiffness.43 However, the frequency can be extracted from the Fourier transform of the signal.Ultrasound elastography has been initially developed as a medical imaging modality that maps the elastic properties and stiffness of soft tissues.33 Basically, two types of mechanical waves propagate in a medium: the compression wave (P wave) and the shear wave (S wave). Conventional ultrasound echography is based on the P wave while elastography is based on the S wave. Ultrasound elastography is a subtle combination of these two mechanical waves. As shown in Fig. 1 right, shear waves can be generated within the medium using an acoustic radiation force (Bercoff, Tanter et al. 2004). First, an ultrasound beam (P wave) is focused at different depths (focal points) in the medium for several hundreds of milliseconds. This part is called the “push” generation and induces a remote force that varies with the acoustic intensity and the time duration of the push. In this study, we will focus on the induced shear (S wave) on which elastography is based. The radiation force induces a local stress which induces a micrometric displacement along the acoustic beam. When the beam is stopped, the medium comes back to its original position, creating shear waves that propagate transversally. The combination of these shear waves created at different depths interfere constructively as a larger conical shear wave (similarly to a Mach Cone). The cone appears as two planar shear wave fronts propagating in opposite directions. Just after generating the shear waves, the probe switches to ultrafast imaging mode using ultrasound plane waves (P waves) to image the shear wave propagation in real-time (∼5000 frames per second) to determine the shear wave velocity. By using the time-of-flight method described by Tanter,45 the shear wave speed, vij (ij is the phase and propagation directions, respectively), can be extracted. At rest or for small perturbations, the medium is isotropic, and the shear wave carries important information since its velocity is closely linked to the shear modulus of the medium. Indeed, the product of the medium density times the square of the shear wave velocity gives rise to a parameter with the dimension of a stress (kPa) being:
| ρvij2 = μ | (4) |
Through the assumption of a quasi-incompressible gel, it is possible to retrieve Young's modulus, which is equal to E ≅ 3μ ≅ 3ρv2, where the local density ρ is considered to be constant (ρ ∼ 1000 kg m−3 due to the high-water content).
At rest, the gel is isotropic considering the negligible effect of gravity already studied in the literature.46 Consequently, we obtain a nearly equivalent Young's modulus for different probe configurations (Fig. S4, ESI†). For the elastic gel, the mean Young's modulus from the stress–strain curve was found to be E = 11.0 ± 0.5 kPa. From rheology and shear wave elastography, the modulus was estimated assuming nearly incompressible behavior. The mean values are in line with E = 9.3 ± 0.2 kPa for rheology and 10.4 ± 0.7 kPa for US elastography. Thus, we observe strong agreement in Young's modulus values between these techniques for the elastic gel. It is important to note that the presence of agar in the gel does not impact the mechanical results but enhances the echogenicity of the gel (see Fig. S1, ESI†). As the volume fraction of nanoparticles (NPs) increases, a significant increase in initial stiffness is observed, accompanied by pronounced frequency dependence. The elastic gel (without NPs) exhibits no change in Young's modulus at higher frequencies, indicating a lack of frequency-dependence compared to the nanocomposite gels, where E increases in a power-law manner as the frequency increases (see Table 1).
| E ≅ E0.006Hzfp | E 0.006Hz | p |
|---|---|---|
| Elastic gel (without NPs) (n = 20) | 10.5 ± 0.3 kPa | 0.003 ± 0.006 |
| Viscoelastic gels | ||
| 0.10 v/v NPs (n = 10) | 18.1 ± 0.4 kPa | 0.035 ± 0.004 |
| 0.15 v/v NPs (n = 10) | 32.4 ± 0.7 kPa | 0.060 ± 0.004 |
Elastic gel behavior under stress (nonlinear regime)
The shear wave velocity is dependent on mechanical loading (see Fig. S3, ESI†) and additional terms are required when the mechanical behavior becomes nonlinear46–49 (see Theoretical background50,51 in the ESI†). When a stress is applied to the material, the shear wave velocity is changed according to the AE theory which is based on nearly incompressibility of the material. As the shear wave is polarized, we need to add the index ij for the shear and propagation directions, respectively. Under compression stress, we now get three different equations: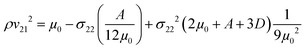 | (5) |
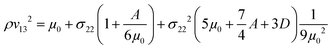 | (6) |
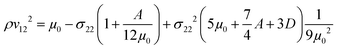 | (7) |
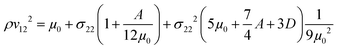 | (8) |
As shown in Fig. 2, various experimental configurations (N = 3 in compression and N = 1 in tension modes) under static stress were investigated (more configurations are shown with a polar plot in Fig. S4, ESI†). These coupled experiments offer simultaneous measures of the shear wave speed inside the gel by elastography and the macroscopic force and displacement by tensile/compression tests. To the best of our knowledge, this is the first time that measurements with US elastography have been coupled with the stress assessment by the in situ mechanical measurement. Indeed, the Cauchy stress is usually calculated with linear elasticity via Hooke's law, from the measure of the strain46,52–54 or deduced from the strain maps.55 Here, from these experimental configurations, the shear wave velocity was recorded for a wide range of applied stress and nonlinear acoustoelasticity (AE) equations (eqn (5)–(8)) enabled the identification of the nonlinear coefficients A and D. The shear modulus, μ0, was fixed according to the measurements carried out at rest. As shown in Fig. 2, qualitatively, experimental shear wave velocities are in good agreement with AE equations and the obtained fitted A and D values are of the same order of magnitude for the 4 experimental configurations (see Table S1, ESI†). It should be noted that, due to geometrical constraints in compression, the tensile configuration allows probing of the drastically larger deformation range (until rupture), thereby providing the more accurate identification of A and D parameters (where these coefficients are of great importance in large deformations) (see Fig. 3).
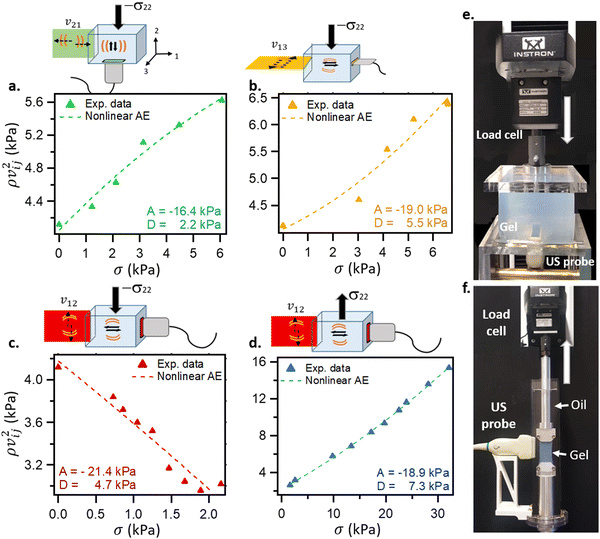 | ||
| Fig. 2 Elastic gels (without NPs) under stress: coupling macroscopic (standard compression/traction tests) and ultrasound elastography mechanical measurements. (a)–(d) The experimental data from ultrasound elastography, ρvij2, are plotted versus the measured Cauchy stress (obtained from the load cell) for 4 configurations. Nonlinear acoustoelastic (AE) coefficients, A and D, are determined from eqn (5)–(8). (e) Compression tests were carried out up to 30% compression (except for (c) where the maximum possible strain was 15% due to the probe configuration) while (f) is for tensile test until gel failure, typically 400%. | ||
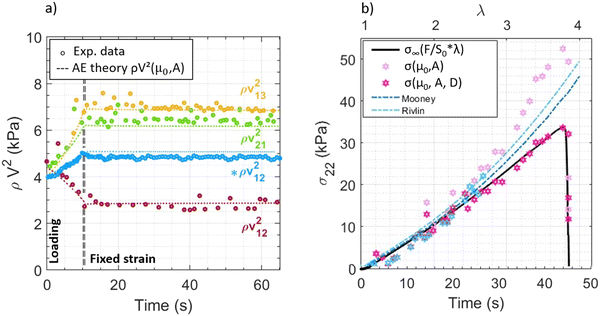 | ||
| Fig. 3 Calibration of the large strain behavior of elastic gels (without NPs) with ultrasound elastography experiments. (a) Compression test: fixed 30% strain for 55 seconds. The AE theory is verified experimentally for four different configurations (3 in compression mode and 1 in tension mode, in blue, represented by *). (b) Tensile test until fracture. The Cauchy (infinite) stress is recorded from the conventional mechanical testing machine (black), while the σ22 value obtained from the shear wave velocity is determined following the AE theory up to the third and fourth order, respectively. The A and D coefficients of Fig. 2 were used. The simulated stress from FEM calculations is shown (in blue) with the two models used, Rivlin and Mooney. These curves were plotted using the C10 material parameter obtained from the notched gel. Here, the compressible assumption is closer to the AE theory. | ||
As reported in Fig. 2, the mean A value from the compression test is really close to that of the tensile test: A = −18.9 kPa (the mean of the three configurations) and A = −18.9 kPa, respectively. For the D coefficient, it differs from 7.3 kPa for a tensile test with an experimental range of stress from 30 kPa to 4.1 kPa for the compression test with an experimental range of up to 6 kPa. Since the coefficient D concerns the 4th order of nonlinear elasticity, meaning larger deformation, D identification under tension seems more robust. Therefore, for the rest of the study, the coefficients A = 18.9 kPa and D = 7.3 kPa will be used.
Experiments are conducted in real-time, as illustrated in Fig. 3. First, in Fig. 3a, tests consist of a monotonic loading (compression and/or tension) up to a strain of about 0.30 (i.e., a λ value of either 0.7 or 1.3) followed by a holding step at the fixed strain level. The experimental parameter, ρvij2 (kPa), is displayed for various ultrasound probe positions. As expected from nonlinear AE theory, the shear wave velocity is sensitive to the stress state. Indeed, v12 increases in tension and decreases in compression. Under fixed strain conditions, shear wave velocities remain constant since the stress relaxation is almost negligible, as expected from gels without NPs (see Fig. S1, ESI†). From the identified A and D values obtained under static conditions (Fig. 2 and Table S1, ESI†) and the Cauchy stress value recorded (from the load cell of mechanical testing machine), the parameter, ρvij2, was retrieved with eqn (5)–(8). Fig. 3a shows rather good agreement between calculated and measured ρvij2 (kPa) even with D = 0, for relatively small strains (λ < 1.3).
Finally, a tensile test until the fracture experiment was performed, where important nonlinear effects are expected. In Fig. 3b, we convert the shear wave velocity (kPa) into stress (kPa). The experimental stress is obtained from the mechanical testing machine and from ultrasound elastography, which depends on the shear wave velocity that propagates in real time inside the gels during the tensile test and on the identified elastic constants. Moreover, the stresses from the Mooney and Rivlin models used for FEM are also plotted in Fig. 3b. It should be noted that the material parameters have been optimized by using the load versus the opening displacement curve on pre-cracked gels.
As shown in Fig. 3, a new approach to quantify, non-invasively, the stress state in deformed gels from the shear wave velocity is demonstrated. Compared to the Cauchy stress, measured by the force applied on the sample divided by its area surface, the measured stress from AE fits well. This stress only depends on the shear wave velocity propagating into the bulk material and the material constants, μ0, A and D, the 2nd, 3rd and 4th order of incompressible elasticity, respectively.
AE theory developed for the third order as well as the Mooney/Rivlin models is not sufficient to fit the experimental data at large strains, since Fig. 3b shows a deviation of the fitting data for λ values above 2.8. Nonlinearity processes become too important at high deformations; thus, further development of the fourth order of the strain energy density function is needed. In large deformations, the parameter D becomes important and allows the last part of the curve to be properly fitted. The same methodology can be applied to viscoelastic gels, i.e., with NPs (see Fig. S5, ESI†).
These experiments show the feasibility of obtaining the macroscopic stress imposed on a gel using AE theory and at large strain. The calibration of σ22 stress was obtained satisfactorily under a homogeneous stress field, i.e., using simple geometries. The next step consists of mapping the local stress state in complex geometries.
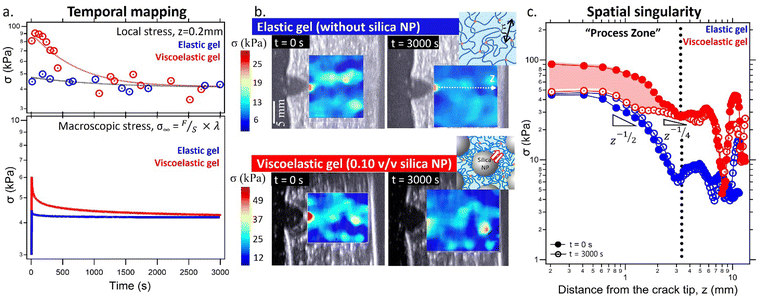
Evolution of the local stress field at the vicinity of the crack tip in elastic gels
As shown in Fig. 4, in this section, pre-notched specimens were investigated. For the sake of simplicity, the first elastic gels (without NPs) will be studied. The load vs. the crack opening displacement (COD) curve was analyzed to provide insights into the framework of a global approach in fracture mechanics (Fig. S5, ESI†). Ultrasound images were used to visualize the crack opening at different COD values. The experimental setup involved a gel specimen with a crack depth ratio of a/W = 0.5, where a refers to the crack length (10 mm) and W denotes the specimen width (22 mm). The force versus the COD relationship exhibited a linear trend, except for the last diverging point at COD = 9.5 mm. | ||
| Fig. 4 Experimental local stress state: the stress field at the vicinity of the crack tip on elastic gels (without NPs). (a) A scheme of the single edge notched gel at a certain strain λ. The stress field will be extracted on the crack plane, in the sample midplane as the local stress σ22versus z, the distance from the crack tip. The notch opens and the COD (crack opening displacement) can be extracted as a function of the force F imposed. The imaging plane is represented in blue. A video of the opening of the notch is available in supplementary data (Video S1, ESI†). (b) Force as a function of the COD. Experimental data and simulations are represented. The opening of the crack is shown for different COD in ultrasound images. For this first result, we present a gel with a crack depth ratio of a/W = 0.5, corresponding to a = 10 mm and W = 22 mm. Except for the last diverging point at COD = 9.5 mm, the evolution of the force vs. COD is linear. (c) The local stress field ahead of the crack tip, along z-axis, where a/W = 0.5. (d) An experimental map obtained using an ultrasound scanner (shear wave velocity) compared to the two FEM models (Cauchy stress) for the COD = 8.3 mm (penultimate point in the force–COD) curve. | ||
During the test, the crack opening progressively increased, resulting in morphological changes in the crack mouth. Consequently, the shear wave speed exhibited non-uniform behavior, with an increase in the shear wave velocity observed at the crack tip, as highlighted on the elastic map in Fig. 4a and Video S1 (ESI†). Elastography enabled the spatial mapping of the ultrasound shear wave velocity at regular intervals of 200 μm along the z-axis, extending from the crack tip to the width's end. By employing calculations based on the AE theory, a stress field map was generated along the z-axis. The presence of a red spot at the crack tip was investigated and confirmed to be unrelated to artifacts arising from the gel/oil interface. Notably, this red spot was absent at the rest state “crack-tip mimicking” shape (see Fig. S6, ESI†). Thus, the observed stress amplification is obtained directly from the local increase in the shear wave velocity in the vicinity of the crack.
Consequently, this region of interest was selected for further investigation. The stress field surrounding the crack tip lips appeared relatively homogeneous compared to the crack tip itself (refer to Fig. S6, ESI†).
To better assess the stress concentration ahead of the crack tip, a comparison was made between the experimental local stress σ22 values obtained from ultrasound elastography and numerical simulations using the finite element method (FEM). The spatial variation of stress along the z-axis for a COD of 8.3 mm is plotted in Fig. 4c. It was observed that the stress levels measured through the ultrasound elastography technique were approximately three times higher than those obtained from the FEM simulations. These results indicate the need to establish a scale factor for stress levels between the two methodologies. However, the stress gradients obtained from both methods exhibited good agreement, with a close approximation to z−1/2. It should be noted that, above for z > 5–6 mm, stress measurements are not accurate because “pushing” ultrasonic beams are not able to generate shear waves beyond this depth. These stress variations are not significant but clearly do not affect the results for z < 5–6 mm.
Fig. 4d allows the comparison between the deformed image at the same COD for experimental and FE simulations using the nearly incompressible (Rivlin) model and compressible (Mooney) model. Although both models were in good agreement with the crack mouth shape, it was observed that the transverse contraction (negative strain) was more pronounced for the Rivlin model than for the Mooney model. This can be attributed to “Poisson's ratio effects” for which the transverse strain is half of the longitudinal one for isochoric (incompressible) deformation (ν = 0.5). For the compressible model, the Poisson ratio is lower than 0.5, therefore so is the transverse strain. It can be seen in Fig. 4d that the deformed remaining ligament is closer to the experiment for the Mooney model than for the Rivlin model. Therefore, the stress level is more “relaxed” for the Mooney model in comparison with the Rivlin model.
Both temporal and spatial mapping around the crack tip in gels without NPs (elastic) and in the presence of NPs (viscoelastic)
The same procedure was applied to calibrate the shear wave velocity with σ22 local stress for viscoelastic gels (see Fig. S5 and S7, ESI†). Time and spatial evolutions of the stress at the crack tip were compared for an elastic gel and a viscoelastic gel (10 vol% silica NP) with a crack opening ratio of a/W = 0.2 for both gels (Fig. 5).As expected, for an elastic gel, no dissipation occurred at the crack tip macroscopically. It has also been verified that this stress far from the tip is close to the Cauchy stress measured by the macroscopic tensile test (around 4 kPa). We notice a huge stress amplification at the crack tip (z = 0.2 mm). The local stress at the crack tip is one order of magnitude higher. The gradient depends strongly on the type of gel (elastic or viscoelastic) and the gel geometry, especially the crack depth ratio a/W. For a/W = 0.2 (Fig. 5) and a/W = 0.5 (Fig. 4), the stress decreases as σ ∝ z−1/2.
Concerning the viscoelastic gel, as shown in Fig. 5a, NPs enable higher local stresses to be achieved than in gels without NPs. Local stress is increased by 2-fold initially for t = 0. Interestingly, at a long timescale, both elastic and viscoelastic responses converge. There is a full screening of NPs and only covalent crosslinks govern the stress level. Thus, the stress concentration was erased with time (also visible on the ultrasound images Fig. 5b). The stress gradient is displayed in Fig. 5c for t = 0 and t = 30 min. As expected, for the elastic gel, no change is observed over time. Our experimental results suggest a stress decay z−1/2 for both elastic and viscoelastic gels (for t = 0). Results are somewhat reminiscent of the LEFM theory and favor the idea of a singularity for z → 0. Experimentally, due to spatial resolution, the first experimental points can be obtained (200 μm) from the crack tip. The presence of NPs does not alter the shape of the stress field at t = 0. Local stresses are doubled over the entire experimental z-range. However, over time, NPs enable stress relaxation by topological rearrangements of the polymer network through adsorption/desorption. This leads to a mechanism of shielding that mitigates the stress amplification to a slope near to σ ∝ z−1/4 (Fig. 5c). The method enables visualization of a process zone (few mm) around the crack tip where large and quantified stress relaxation processes operate. A 3D plot (x, z, t) combines spatial and temporal mappings in Fig. S8, ESI.†
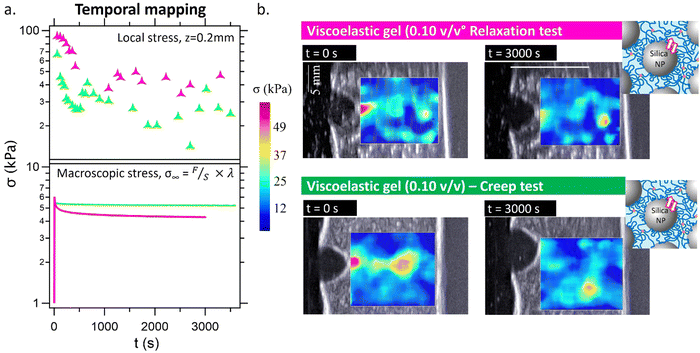
Role of NPs in creep vs. relaxation recovery processes at the crack tip
The stress field in the previous section was obtained at a fixed COD, i.e., under stress relaxation conditions. Here, the opposite experiment has been done, and by fixing the macroscopic force, the same maximum value reached during the relaxation test (∼0.9 N, corresponding to a Cauchy stress of ∼6 kPa) (Fig. 6). This allows a focus on the local relaxation at the crack tip while suppressing macroscopic relaxation.During the creep experiment, the displacement was automatically adjusted by the test stand to maintain a constant force, counteracting the macroscopic relaxation processes. As a result, the elongation parameter, λ, slightly increased (visible in the ultrasound images, where the crack opening displacement is greater compared to the relaxation test). It should be noted that, in these experiments, the total length of the gel (L0) differed between the relaxation test (42 mm) and the creep test (52 mm). This discrepancy makes the direct comparison between the two results challenging. However, it is evident that the local stress around the crack tip experienced relaxation, even though the macroscopic or Cauchy stress remained unchanged during the creep experiment. This observation demonstrates the feasibility of studying local relaxation, which is independent of the macroscopic relaxation. The relative variation in stress can be found in Fig. S8, ESI.† During the creep test, the macroscopic relaxation was minimal and not significant (approximately 5% decrease in the initial macroscopic stress value, compared to a 30% decrease in the relaxation test). In contrast, the local relaxation in the creep test was pronounced as in the relaxation test, with a decrease of 50–60% in the initial local stress at the crack tip.
Discussion
In this study, ultrasound shear wave elastography was explored, revealing the potential of this technique to study the mechanical and fracture behaviors of our model gels. This method allows us to study mechanisms at an intermediate scale by evaluating stress fields at crack tips with a spatial resolution of 10–100 micrometers, thereby helping to bridge the gap in understanding between mechanisms at the molecular and macroscopic scales. As expected, an excellent correlation in Young's modulus between our approach and conventional mechanical methods (tension/compression and rheology) was obtained at rest or under small perturbation conditions. Additionally, ultrasound shear wave elastography expands the experimental frequency range. Thus, both elastic and viscoelastic gels were measured across a frequency range of 0.06 Hz to nearly 1000 Hz.Beyond the linear regime, under large deformations, shear wave propagation in the medium becomes more complex and the method requires calibration of higher-order elastic constants in order to be quantitative. Nonlinear AE elasticity was explored experimentally for the first time by coupling standard tension/compression testing with ultrasound elastography. Therefore, by measuring the applied Cauchy stress and the shear wave velocity, the four test configurations studied converge on robust values for A and D. The stress was then quantified through the travelling shear wave cone in the material. In un-notched samples, the stress field can be assumed homogeneous and the shear wave velocity was observed indeed to be almost constant within the gel.
In notched gels, the shear wave velocity was no longer homogeneous due to the geometrical singularity. A net increase of the ultrasound shear wave velocity was observed at the crack tip, as it is expected from linear elastic fracture mechanics. Instead of considering the shear wave velocity cone traveling through the gel, it is possible to examine this shear wave pixel by pixel with a resolution of 200 μm, which we referred in the paper as the local shear wave velocity, σ22. While the shear wave cone velocity was closely linked to the Cauchy stress applied, the local shear wave velocity could provide insight into the local stress as predicted by the AE theory. Consequently, the AE theory enabled us to study the nonlinear material response at large strains, such as during a tensile test until fracture or around the crack tip. Being non-invasive, the method enables extraction of the stress filed in different planes of the specimen. In our study, we focused primarily on the local opening stress σ22 in the vicinity of the crack tip. A spatial and temporal analysis was performed. As expected for elastic gels, no macroscopic or local dissipation effects were observed. A stress amplification was present at t = 0 and at t = 3000 s. Spatially, LEFM theory predicts stress singularities at the crack tip, characterized by σ ∝ z−1/2, where z is the distance ahead of the crack tip. The theory is confirmed with Fig. 4 and 5 while the stress fields appear to be well verified close to the crack tip, beyond 10 mm from the crack, strong instabilities in the propagation velocity were systematically observed. The main reason for these measurement artifacts can be explained by the way the shear waves were generated. Indeed, for these experiments, we induced “pushing” beams at depths limited to z = 5 mm to 15 mm. The resulting shear waves then propagate transversely to the depth direction. As we did not “push” at higher depths, we do not induce a shear wave propagation beyond 15 mm. Thus, the measured values of the shear wave speed below this depth are not accurate, as very limited shear energy is propagating in these deep regions. In order to properly image beyond 15 mm, we should have generated push beams below this depth. Using this linear piezoelectric probe, we think that this could be possible to generate and image shear waves up to 30 mm depth (corresponding to the elevation focus of the probe) as long as the system is programmed to induce radiation force “pushing” beams up to this depth.
In the case of viscoelastic gels filled with silica NPs, significant relaxation processes were observed locally around the crack tip during both relaxation and creep tests. The creep experiment specifically allowed for the examination of local relaxation processes without the occurrence of macroscopic relaxation. Once again, the linear elastic fracture mechanics (LEFM) theory was verified near the crack tip at t = 0 s with σ22 ∝ z−1/2. At t = 3000 s, due to extensive stress relaxation processes over a distance around 3 mm from the crack tip, the stress amplification becomes less significant so that σ22 ∝ z−1/4. Note that this 3 mm-distance is rather large compared to current observations in double network elastomers ∼10–100 μm using mechanochemistry32 or even in double network gels ∼500 μm by mechanoradical polymerization.56 Yet, this order of magnitude seems consistent with a fracto-cohesive length,21 where Gc is the fracture energy and W is the work of extension; considering previous works, we obtain around 1.5 mm for viscoelastic gels.37 This change in the stress field prevented the hydrogel from undergoing fracture, by reducing significantly the stress in the vicinity of the crack. The stress relaxation is directly linked to the presence of silica nanoparticles, which facilitate the long-range rearrangement of the polymer network by desorption/adsorption of the polymer strands onto the silica particles. The NP surface provides a platform for exchangeable sacrificial bonds. The hydrogen bonding between the polymer and silica nanoparticles and its dynamics play a crucial role in inducing these relaxation processes. Interestingly, the ultrasound elastography is also able to capture the field of stress relaxation. The amount of information collected is substantial. Thus, stress relaxation dynamics appears to be accelerated at the crack tip (see Fig. S9, ESI†). A systematic in-depth study of crack-tip relaxation dynamics would be worthwhile.
where Gc is the fracture energy and W is the work of extension; considering previous works, we obtain around 1.5 mm for viscoelastic gels.37 This change in the stress field prevented the hydrogel from undergoing fracture, by reducing significantly the stress in the vicinity of the crack. The stress relaxation is directly linked to the presence of silica nanoparticles, which facilitate the long-range rearrangement of the polymer network by desorption/adsorption of the polymer strands onto the silica particles. The NP surface provides a platform for exchangeable sacrificial bonds. The hydrogen bonding between the polymer and silica nanoparticles and its dynamics play a crucial role in inducing these relaxation processes. Interestingly, the ultrasound elastography is also able to capture the field of stress relaxation. The amount of information collected is substantial. Thus, stress relaxation dynamics appears to be accelerated at the crack tip (see Fig. S9, ESI†). A systematic in-depth study of crack-tip relaxation dynamics would be worthwhile.
Ultrasound elastography offers relevant perspectives for studying the mechanics of gels or more generally soft matter fracture. In our study, we use the commercially available ultrafast ultrasound coupled with a linear piezoelectric transducer array for the shear wave elastography mode. These devices were developed initially for medical diagnosis dedicated to soft tissues, typically tissues below E ∼ 300 kPa. In this regime, the velocity of the shear wave is typically of 1–10 m s−1. Our gels are typically in this range of moduli and stresses, and the experimental set-up is particularly well-suited. But ultrasound elastography can also be applied to other soft matter systems. For highly stiff gels or elastomers with μ ∼ MPa, the shear wave velocity increases to 10–100 m s−1 and the tracking of the shear wave comes more difficult. The sensor should be modified to be able to follow this shear wave velocity. This could be achieved for instance by increasing the length of the transducer array. The frame rate should also be increased typically from 2000 fps to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fps. This is possible but it limits the imaging depth to 2 cm. In such cases, it is possible to track typical shear wave speed up to 20 m s−1 corresponding to E ∼ 1.2 MPa. This was already evaluated for muscle stiffness imaging in humans with stiffness values reaching these high stiffness values during contraction.33 Nevertheless, beyond 1 MPa, it becomes very difficult to track the transient propagation of the shear wave that travels too fast in the medium. Another limitation consists of the imaging depth. For the generation of the radiation force, the ultrasonic beam is focused at increasing depths in the medium. As the conventional 1D linear ultrasonic probe contains geometrical lens in the elevation direction (perpendicular to the imaging plane) in order to enforce the ultrasonic waves to propagate only within the imaging plane, it becomes difficult to push at depths deeper than the elevation focus of this geometrical focus (in our case 30 mm for the L10-2 linear probe). As shear waves cannot be easily generated at higher depths, it becomes impossible to image stiffness deeper than the elevation focus of the probe.
000 fps. This is possible but it limits the imaging depth to 2 cm. In such cases, it is possible to track typical shear wave speed up to 20 m s−1 corresponding to E ∼ 1.2 MPa. This was already evaluated for muscle stiffness imaging in humans with stiffness values reaching these high stiffness values during contraction.33 Nevertheless, beyond 1 MPa, it becomes very difficult to track the transient propagation of the shear wave that travels too fast in the medium. Another limitation consists of the imaging depth. For the generation of the radiation force, the ultrasonic beam is focused at increasing depths in the medium. As the conventional 1D linear ultrasonic probe contains geometrical lens in the elevation direction (perpendicular to the imaging plane) in order to enforce the ultrasonic waves to propagate only within the imaging plane, it becomes difficult to push at depths deeper than the elevation focus of this geometrical focus (in our case 30 mm for the L10-2 linear probe). As shear waves cannot be easily generated at higher depths, it becomes impossible to image stiffness deeper than the elevation focus of the probe.
Furthermore, the ultrafast imaging ability of ultrasound scanners to capture transient events opens the possibility of studying dynamic fracture propagation up to 1000 frames per s. It would be particularly interesting to examine the fracture propagation and define a damage area. The role of network topology and the effect of viscoelasticity in defining a characteristic size of the “process” or “damage” zone could be explored. We could better understand the physical processes that occur during the crack burst, which would improve our understanding of how energy is released from the gel. Initial observations of randomly distributed spontaneous sources of shear waves during fracture were made possible thanks to this high ultrasonic frame rate and highlight the interest of this technology to gain new insights into the field of soft matter fracture (see Video S2, ESI†).
Conclusions
This work proposes to consider a new soft matter tool for local nonlinear mechanical mapping of gel fracture. The main advantages of the method are (1) quantification of local stresses in real time and under large deformations, e.g., at a crack tip, with a resolution of a few microns; (2) non-invasiveness, allowing for simultaneous mapping at different thicknesses of the specimen, at the core or near the surface; and (3) the ability to perform high-frequency imaging (up to 1000 images per s). To our knowledge, this paper reports the first measurements of a two-dimensional crack-tip through-thickness stress field.Experimentally, we were able to identify a process zone – in the first 3 mm – around the crack tip where significant quantified stress relaxation processes operate. Initially, at t = 0, the presence of NPs does not seem to affect the stress field, except that local stresses are multiplied by 2 over the entire space compared to gels without NPs. Over time, however, the stress amplification is efficiently mitigated by the NPs. There is no marked difference in stress relaxation processes both locally and macroscopically, apart from greater rearrangement dynamics at the crack tip.
Finally, the method opens up promising prospects for the study of dynamic fracture.
Author contributions
AM conceptualized the project and obtained the funding. HLB made the experiments. HLB prepared the figures and wrote the initial draft. HLB, TD, LL, MT and AM analyzed the data, wrote the manuscript and reviewed the manuscript. TD and MT ensured the supervision of the US elastography part, LL the finite element modelling and AM the gel fracture.Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its ESI.† The data that support the findings of this study are available from the corresponding author, AM, upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully thank the international program “UPtoPARIS” which fund this work. This project has received funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 754387. Ludovic Olanier, Jean-Claude Mancer, and Guylaine Ducouret from the SIMM lab are warmly thanked for their technical help in setting up the devices. Shelby Hutchens, invited Prof. at the SIMM lab, is thanked for her read-through and correction of English.References
- X. Z. Wang, H. L. Wang and H. R. Brown, Soft Matter, 2011, 7, 211–219 RSC
.
- M. J. Webber, E. A. Appel, E. W. Meijer and R. Langer, Nat. Mater., 2016, 15, 13–26 CrossRef CAS PubMed
.
- B. R. Freedman and D. J. Mooney, Adv. Mater., 2019, 31, 1806695 CrossRef PubMed
.
- W. Huang, D. Restrepo, J. Y. Jung, F. Y. Su, Z. Q. Liu, R. O. Ritchie, J. McKittrick, P. Zavattieri and D. Kisailus, Adv. Mater., 2019, 31, 1901561 CrossRef CAS PubMed
.
- J. P. Gong, Y. Katsuyama, T. Kurokawa and Y. Osada, Adv. Mater., 2003, 15, 1155–1158 CrossRef CAS
.
- T. Matsuda, R. Kawakami, R. Namba, T. Nakajima and J. P. Gong, Science, 2019, 363, 504 CrossRef CAS PubMed
.
- J. Y. Sun, X. H. Zhao, W. R. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. G. Suo, Nature, 2012, 489, 133–136 CrossRef CAS PubMed
.
- S. Bauer, S. Bauer-Gogonea, I. Graz, M. Kaltenbrunner, C. Keplinger and R. Schwodiauer, Adv. Mater., 2014, 26, 149–162 CrossRef CAS PubMed
.
- X. Pu, M. Liu, X. Chen, J. Sun, C. Du, Y. Zhang, J. Zhai, W. Hu and Z. L. Wang, Sci. Adv., 2017, 3, e1700015 CrossRef PubMed
.
- H. Yuk, B. Lu and X. Zhao, Chem. Soc. Rev., 2019, 48, 1642–1667 RSC
.
- M. Gupta, B. R. Sarangi, J. Deschamps, Y. Nematbakhsh, A. Callan-Jones, F. Margadant, R.-M. Mège, C. T. Lim, R. Voituriez and B. Ladoux, Nat. Commun., 2015, 6, 7525 CrossRef CAS PubMed
.
- D. Gupta, A. Gangwar, K. Jyoti, V. Jyothi, R. K. Sodhi, N. K. Mehra, S. B. Singh and J. Madan, Colloids Surf., B, 2020, 194, 111171 CrossRef CAS PubMed
.
- P. Hansma, G. Fantner, J. Kindt, P. Thurner, G. Schitter, P. Turner, S. Udwin and M. Finch, J. Musculoskeletal Neuronal Interact., 2005, 5, 313–315 CAS
.
- K. Haraguchi, T. Takehisa and S. Fan, Macromolecules, 2002, 35, 10162–10171 CrossRef CAS
.
- S. Rose, A. Dizeux, T. Narita, D. Hourdet and A. Marcellan, Macromolecules, 2013, 46, 4095–4104 CrossRef CAS
.
- Q. Wang, J. L. Mynar, M. Yoshida, E. Lee, M. Lee, K. Okuro, K. Kinbara and T. Aida, Nature, 2010, 463, 339–343 CrossRef CAS PubMed
.
- R. Long, C.-Y. Hui, J. P. Gong and E. Bouchbinder, Annu. Rev. Condens. Matter Phys., 2021, 12, 71–94 CrossRef
.
- G. J. Lake and A. G. Thomas, Proc. R. Soc. London, Ser. A, 1967, A300, 108–119 Search PubMed
.
- G. E. Fantner, T. Hassenkam, J. H. Kindt, J. C. Weaver, H. Birkedal, L. Pechenik, J. A. Cutroni, G. A. Cidade, G. D. Stucky, D.
E. Morse and P. K. Hansma, Nat. Mater., 2005, 4, 612–616 CrossRef CAS PubMed
.
- G. E. Fantner, E. Oroudjev, G. Schitter, L. S. Golde, P. Thurner, M. M. Finch, P. Turner, T. Gutsmann, D. E. Morse, H. Hansma and P. K. Hansma, Biophys. J., 2006, 90, 1411–1418 CrossRef CAS PubMed
.
- C. Costantino and C. Matteo, Rep. Prog. Phys., 2016, 79, 046601 CrossRef PubMed
.
- C. Y. Hui, A. Jagota, S. J. Bennison and J. D. Londono, Proc. R. Soc. London, Ser. A, 2003, 459, 1489–1516 CrossRef
.
- A. Livne, E. Bouchbinder and J. Fineberg, Phys. Rev. Lett., 2008, 101, 264301 CrossRef PubMed
.
- C. Liu, K. Mayumi, K. Hayashi, L. Jiang, H. Yokoyama and K. Ito, J. Electrochem. Soc., 2019, 166, B3143–B3147 CrossRef CAS
.
- M. E. Seitz, D. Martina, T. Baumberger, V. R. Krishnan, C.-Y. Hui and K. R. Shull, Soft Matter, 2009, 5, 447–456 RSC
.
- J. Guo, M. Liu, A. T. Zehnder, J. Zhao, T. Narita, C. Creton and C.-Y. Hui, J. Mech. Phys. Solids, 2018, 120, 79–95 CrossRef CAS
.
- J. Zhang, Y. An, K. Yazzie, N. Chawla and H. Jiang, Soft Matter, 2012, 8, 8107–8112 RSC
.
- P. H. Geubelle and W. G. Knauss, J. Elasticity, 1994, 35, 61–98 CrossRef
.
- J. K. Knowles and E. Sternberg, J. Elasticity, 1973, 3, 67–107 CrossRef
.
- J. K. Knowles and E. Sternberg, J. Elasticity, 1974, 4, 201–233 CrossRef
.
- E. Ducrot, Y. Chen, M. Bulters, R. P. Sijbesma and C. Creton, Science, 2014, 344, 186–189 CrossRef CAS PubMed
.
- J. Slootman, V. Waltz, C. J. Yeh, C. Baumann, R. Gostl, J. Comtet and C. Creton, Phys. Rev. X, 2020, 10, 041045 CAS
.
- J. L. Gennisson, T. Deffieux, M. Fink and M. Tanter, Diagn. Interv. Imaging, 2013, 94, 487–495 CrossRef PubMed
.
- L. Carlsson, S. Rose, D. Hourdet and A. Marcellan, Soft Matter, 2010, 6, 3619–3631 RSC
.
- S. Rose, A. Marcellan, T. Narita, F. Boue, F. Cousin and D. Hourdet, Soft Matter, 2015, 11, 5905–5917 RSC
.
- A.-C. Le Gulluche, G. Ducouret, L. Olanier, A. Brûlet, O. Sanseau, P. Sotta and A. Marcellan, Macromolecules, 2023, 56, 8344–8358 CrossRef CAS
.
- A.-C. Le Gulluche, N. Pantoustier, A. Brûlet, O. Sanseau, P. Sotta and A. Marcellan, Macromolecules, 2023, 56, 8024–8038 CrossRef CAS
.
- S. Rose, A. Prevoteau, P. Elziere, D. Hourdet, A. Marcellan and L. Leibler, Nature, 2014, 505, 382–385 CrossRef CAS PubMed
.
- A. Meddahi-Pelle, A. Legrand, A. Marcellan, L. Louedec, D. Letourneur and L. Leibler, Angew. Chem., Int. Ed., 2014, 53, 6369–6373 CrossRef CAS PubMed
.
- O. Ronsin, I. Naassaoui, A. Marcellan and T. Baumberger, Phys. Rev. Lett., 2019, 123, 158002 CrossRef CAS PubMed
.
- J.-L. Gennisson, A. Marcellan, A. Dizeux and M. Tanter, IEEE Trans. Ultrason. Eng., 2014, 61, 946–954 Search PubMed
.
- S. Casciaro, F. Conversano, A. Ragusa, M. Ada Malvindi, R. Franchini, A. Greco, T. Pellegrino and G. Gigli, Invest. Radiol., 2010, 45, 715–724 CrossRef PubMed
.
- A. P. Sarvazyan, O. V. Rudenko, S. D. Swanson, J. B. Fowlkes and S. Y. Emelianov, Ultrasound Med. Biol., 1998, 24, 1419–1435 CrossRef CAS PubMed
.
- J. Besson and R. Foerch, Comput. Methods Appl. Mech. Eng., 1997, 142, 165–187 CrossRef
.
- M. Tanter, J. Bercoff, A. Athanasiou, T. Deffieux, J.-L. Gennisson, G. Montaldo, M. Muller, A. Tardivon and M. Fink, Ultrasound Med. Biol., 2008, 34, 1373–1386 CrossRef PubMed
.
- J.-L. Gennisson, M. Rénier, S. Catheline, C. Barrière, J. Bercoff, M. Tanter and M. Fink, J. Acoust. Soc. Am., 2007, 122, 3211–3219 CrossRef PubMed
.
- M. F. Hamilton, Y. A. Ilinskii and E. A. Zabolotskaya, J. Acoust. Soc. Am., 2004, 116, 41–44 CrossRef
.
- M. Destrade and R. W. Ogden, J. Acoust. Soc. Am., 2010, 128, 3334–3343 CrossRef PubMed
.
-
L. D. Landau and E. M. Lifshits, Theory of Elasticity, Pergamon Press, 1959 Search PubMed
.
- S. Catheline, J.-L. Gennisson and M. Fink, J. Acoust. Soc. Am., 2003, 114, 3087–3091 CrossRef CAS PubMed
.
- E. A. Zabolotskaya, M. F. Hamilton, Y. A. Ilinskii and G. D. Meegan, J. Acoust. Soc. Am., 2004, 116, 2807–2813 CrossRef
.
- H. Latorre-Ossa, J. L. Gennisson, E. D. Brosses and M. Tanter, IEEE Trans. Ultrason. Eng., 2012, 59, 833–839 Search PubMed
.
- M. E. Fernández-Sánchez, S. Barbier, J. Whitehead, G. Béalle, A. Michel, H. Latorre-Ossa, C. Rey, L. Fouassier, A. Claperon, L. Brullé, E. Girard, N. Servant, T. Rio-Frio, H. Marie, S. Lesieur, C. Housset, J.-L. Gennisson, M. Tanter, C. Ménager, S. Fre, S. Robine and E. Farge, Nature, 2015, 523, 92–95 CrossRef PubMed
.
- S. Aristizabal, C. A. Carrascal, I. Z. Nenadic, J. F. Greenleaf and M. W. Urban, IEEE Trans. Ultrason. Eng., 2018, 65, 188–200 Search PubMed
.
- S. Goswami, R. Ahmed, M. M. Doyley and S. A. McAleavey, IEEE Trans. Ultrason. Eng., 2019, 66, 1292–1303 Search PubMed
.
- T. Matsuda, R. Kawakami, T. Nakajima and J. P. Gong, Macromolecules, 2020, 53, 8787–8795 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00909f |
| This journal is © The Royal Society of Chemistry 2024 |