Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A dynamical system approach to relaxation in glass-forming liquids†
Jack F.
Douglas
 *a,
Qi-Lu
Yuan
*a,
Qi-Lu
Yuan
 bc,
Jiarui
Zhang
d,
Hao
Zhang
bc,
Jiarui
Zhang
d,
Hao
Zhang
 *d and
Wen-Sheng
Xu
*d and
Wen-Sheng
Xu
 *bc
*bc
aMaterials Science and Engineering Division, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, USA. E-mail: jack.douglas@nist.gov
bState Key Laboratory of Polymer Physics and Chemistry, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Changchun 130022, P. R. China. E-mail: wsxu@ciac.ac.cn
cSchool of Applied Chemistry and Engineering, University of Science and Technology of China, Hefei 230026, P. R. China
dDepartment of Chemical and Materials Engineering, University of Alberta, Edmonton, Alberta T6G 1H9, Canada. E-mail: hao7@ualberta.ca
First published on 8th November 2024
Abstract
The “classical” thermodynamic and statistical mechanical theories of Gibbs and Boltzmann are both predicated on axiomatic assumptions whose applicability is hard to ascertain. Theoretical objections and an increasing number of observed deviations from these theories have led to sustained efforts to develop an improved mathematical and physical foundation for them, and the search for appropriate extensions that are generally applicable to condensed materials at low temperatures (T) and high material densities where the assumptions of these theories start to become particularly questionable. These theoretical efforts have largely focused on minimal models of condensed material systems, such as the Fermi–Ulam–Pasta–Tsingou model, and other simplified models of condensed materials that are amenable to numerical and analytic treatments and that can serve to illuminate essential features of relaxation processes in condensed materials under conditions approaching integrable dynamics where clear departures from classical thermodynamics and dynamics can be generally expected. These studies indicate an apparently general multi-step relaxation process, corresponding to an initial “fast” relaxation process (termed the fast β-relaxation in the context of cooled liquids), followed by a longer “equipartition time”, namely, the α-relaxation time τα in the context of cooled liquids. This relaxation timescale can be enormously longer than the fast β-relaxation time τβ so that τα is the primary parameter governing the rate at which the material comes into equilibrium, and thus is a natural focus of theoretical attention. Since the dynamics of these simplified dynamical systems, originally intended as simplified models of real crystalline materials exhibiting anharmonic interactions, greatly resemble the observed relaxation dynamics of both heated crystals and cooled liquids, we adapt this dynamical system approach to the practical matter of estimating relaxation times in both cooled liquids and crystals at elevated temperatures, which we identify as weakly non-integrable dynamical systems.
1 Introduction
Statistical mechanics aims to explain the macroscopic thermodynamic and dynamic properties of materials in terms of the molecular dynamics of the molecules comprising them, on the basis of an appropriate description of the interactions between the molecules and equations describing their subsequent evolution in time. In addtion to the striking successes of this approach in understanding the properties of gases by Clausius,1,2 Maxwell,3 and Jeans,4 and in extensions of this atomistic “kinetic theory” to describe interacting gas molecules based on the Enskog theory,5–7 this approach has been applied to perfectly ordered crystalline materials,8–10 in which a high degree of structural order simplifies the theoretical treatment. These theoretical works represent triumphs of the mechanical view of material properties that were crowned by Boltzmann's entropy equation. This relation provides a fundamental linkage between the entropy of materials, defined in terms of formal thermodynamic theory, and the entropy, defined in terms of the microscopic evolution of the molecular components described in terms of Newtonian dynamics, thereby establishing a fundamental bridge between the macroscopic and molecular scale descriptions of matter.11 Lebowitz12,13 has summarized the subtle nature of Boltzmann's reasoning and the implications of this “bridge relation”11 for understanding the widespread applicability of statistical mechanical theory to materials. It should be appreciated, nonetheless, that Boltzmann's entropy equation was formulated as a hypothesis. Moreover, there is no corresponding general bridge relation linking the dynamic properties of condensed materials to their molecular dynamics, although there has been a lot of theoretical and phenomenological groping at this problem,14,15 and the present work represents another attempt in this direction.The grand vision of Boltzmann of a general statistical mechanical description of matter, based on first principles molecular mechanics, has sometimes run into difficulties when attempts were made to apply this mathematical formalism to condensed materials rather than dilute gases. Specfiically, the problem of reconciling the reversible nature of the classical equations of motion describing the molecular dynamics of Hamiltonian (constant energy) dynamical systems and the evidently irreversible nature of the evolution of macroscopic material systems was noted soon after Boltzmann formulated his entropy equation. Specifically, Zermelo harshly criticized Boltzmann's work based on the reasoning that the inherent reversibility of Hamiltonian dynamics under time reversal meant that an “equilibrium material state”, as defined by Boltzmann, could not possibly exist so that statistical mechanics was just nonsense. (See the works of Mazur and Montroll16 and McQuarrie,17 and the biography of Boltzmann of Broda,18 respectively, for a discussion of scientific and personal aspects of this controversy.) Lebowitz12,13 argued how the “probabilistic” aspect of his Boltzmann's theory resolves this “paradox”, based on the astronomical number of microstates of the equilibrium dynamical system associated with the entropy of the material system. However, one can reasonably wonder whether or not Boltzmann's approach applies to the thermodynamics and dynamics of “complex” condensed materials, such as liquids, at low temperatures (T) where the strong interaction between the particles gives rise to a progressive drop in the fluid configurational entropy of the material upon cooling. We may also wonder about heated crystals in which the configurational entropy progressively increases somewhat from a vanishing value at zero temperature. The existence of ergodicity even in dilute gases has recently been seriously disputed,19 so there appears to be no end of controversy in this field, even in the “simple” case of gases.
Questions about the validity of Boltzmann's entropy equation and the associated technical matter of “ergodicity”, which underlies the mathematical machinery relating time and spatial averages on which statistical mechanics is based, came to fore in one of the earliest molecular dynamics (MD) simulations of a condensed material by Fermi, Ulam, Pasta, and Tsingou (FUPT).20,21 This initial study by FUPT was based on a “toy model” of a crystal described as a one-dimensional chain of anharmonic oscillators, where periodic boundary conditions were introduced to simplify the simulations. At the time, it was apparently anticipated from prior results of Poincare and Fermi22 that any anharmonicity in the interparticle interaction, no matter how small, should be sufficient to destroy the integrability (periodicity of the dynamics) of this many-body Hamiltonian system so that the system once perturbed should just quickly relax to an equilibrium state based on the physical intuition derived from Boltzmann's entropy equation. We refer the reader unfamiliar with the concept of integrable dynamical systems to Wikipedia for much useful background information about such systems and their central role in fields on non-linear dynamics. For a more indepth discussion of integrability, along with historical aspects of the FUPT problem, see the review by Ford.23
The inherently periodic nature of the dynamics of integrable dynamical systems implies that the relaxation time is formally infinite for such systems so that the emergence of chaotic dynamics, relaxation, and diffusion arise in material systems from the combined action of thermal energy and anharmonicity in intermolecular interactions. We emphasize that while integrable systems have periodic solutions, the anharmonic interactions lead to a new class of periodic modes, “breathers” or “intrinsically localized modes”,24–29 that are distinct in their characteristics from the periodic modes of a lattice of atoms derived from an assumed harmonic potential, i.e., phonons.30 Moreover, the interaction between these anharmonic modes can dominate the relaxation process of weakly non-integrable dynamical systems, a phenomenon that can make relaxation times astronomical in magnitude when the interaction between these modes is strong and short-ranged in nature.30–32 (The range of interaction is normally discussed in the technical literature in terms of the “range of interaction in action space” where the action variables are the conserved variables of the integrable dynamical system to which the anharmonic modes correspond;30,33 our discussion of these interactions is more informal in the present work.) By tuning the energy per particle, it is possible to increase the range of the anharmonic mode interactions so that the relaxation process becomes simpler and the relaxation time becomes relatively fast, a situation that we discuss below. Danieli et al.30 provide a lucid discussion of integrability and weak integrability of Hamiltonian dynamical systems in the context of the Klein-Gordon chain model and Mithun et al.33 provide a detailed discussion of the dynamics of weakly non-integrable Josephson Junction chains, in the important case in which the non-linear modes exhibit strong short-ranged interactions that make the relaxation times extremely long in relation to the initial fast relaxation process (discussed extensively below). Mithun et al.33 characterize this dramatic slowing down of the dynamics in this model material as corresponding to a “dynamical glass” state and they further suggest that this behavior is a “generic property of a large class of dynamical systems, where ergodization timescales depend sensitively on control parameters.” Goldfriend and Kurchan34 further discuss this type of “quasi-integrable” dynamical system and its practical significance. Importantly, ergodicity on an infinite averaging timescale is not broken in such materials, but the fact that relaxation times can become astronomically large means that one often encounters the practical situation in which the system cannot explore its phase space on any reasonable timescale so that effective non-ergodic behavior is observed when the averaging timescale is shorter than the relaxation time. The appearance of ergodicity is then determined by how long the system is observed.
This type of transition in ergodicity is then a natural consequence of the slowing down of dynamics upon approaching a state of integrable dynamics. We hypothesize that this mechanism fundamentally of slowing down of material dynamics underlies glass formation in all materials, and that our model of the dynamics of glassy materials developed below is based on this basic hypothesis. With regard to the FUPT model, the exactly solvable Toda lattice,35,36 which describes a chain of anharmonic oscillators with an exponential interaction between nearest-neighbor atoms similar to a Morse-potential,37 is the specific integrable dynamical system corresponding to the FUPT model.34,38,39 Much of what is rigorously known about the FUPT model after many years of investigation is an outgrowth of this discovery, and we discuss some of these results below. As a final general comment, we note that the transition from an ergodic state with varying degrees of non-integrability to a non-ergodic integrable state is not equivalent to the loss of ergodicity associated with becoming trapped in some limited region of phase space because of high potential or free energy barriers so that time and spatial averages are not equivalent. We are rather interested in modeling the weakly chaotic dynamics that generically arises upon approaching the limit of integrability as a model of relaxation in cooled liquids and heated crystals. We next return to a discussion of the FUPT model.
The original exploratory simulations of FUPT for the particular model parameters chosen, indicated that a relaxation to equilibrium simply did not occur, but rather the system evolved in a “strange” quasi-periodic way. Uhlenbeck quoted Fermi as saying that these were surprising results at the time, “providing intimations that the prevalent beliefs of the universality of mixing and thermalization in non-linear systems may not always be justified”. (See Carati et al.22 and Ford23 for a discussion of Uhlenbeck's personal commentary about his interactions with Fermi and other interesting and scientific historical aspects of the FUPT problem.) Seemingly, the rug had been pulled out of the foundation of statistical mechanics and the FUPT model has been the subject of intensive studies ever since to understand what was going on in these pioneering simulations.40,41 The resulting analytic work stimulated by these “numerical experiments” was highly fruitful in stimulating developments in mathematical physics, leading to the rediscovery of solitons37,42–45 to describe the highly directed motion seen in these simulations, and the occurrence of spontaneous non-linear excitations in the lattice that derive exclusively from the anharmonicity of interparticle interactions, “intrinsically localized modes” or “breathers”,24–26,46–49 these dynamical structures being increasingly recognized as playing a crucial role in the dynamics of condensed materials.
There are many excellent reviews describing the many attempts to understand the FUPT model, perhaps the simplest model of a condensed material exhibiting non-linear intermolecular interactions exhibited by real materials and we do not discuss these findings in the present work, except for noting some relevant results relating to the description of relaxation in these materials, which we think have general relevance in glass-forming (GF) materials by extension. We next summarize some basic features in the dynamics of GF liquids and heated crystals that merit this comparison with the dynamics of the extensively studied FUPT model and which raise some questions of a dynamical system nature.
Relaxation in liquids, as typically measured by the self-intermediate scattering function50,51 (a dynamical extension of the static structure factor) at the conventional scale of the interparticle separation, generally undergoes a single relaxation process at elevated temperatures in condensed liquids, but a new slow relaxation mode arises rather universally upon cooling in molecular liquids or increasing density in hard-sphere liquids. These relaxation processes are normally termed the fast β- and α-relaxation processes, respectively, and the α-relaxation process is the principal object of simulation studies of structural relaxation in GF liquids and many neutron scattering studies of the dynamics of cooled liquids. The relaxation time τβ of the fast β-relaxation process is typically on the order of a ps in molecular fluids generally, both polymeric and non-polymeric, while the relaxation time τα ranges from a ps to a timescale on the order of a minute near the material's glass transition so that τα evidently varies over an enormous range as T is varied in cooled molecular fluids or as the particle concentration is increased in particle suspensions. Cooled liquids also generically exhibit “dynamic heterogeneity” in the form of dynamic clusters of molecules with high and low mobility and clusters in which particles exhibit highly correlated motion, and much effort has recently been made in understanding how this heterogeneity relates to observable properties, such as the macroscopic transport properties of the material.52–54 It is noted that the observation of a relatively “fast” relaxation process, after which the system settles into a metastable state persisting for long times, and this plateau in autocorrelation functions describing the relaxation process is followed by a decay of the transient metastable state after an “ergodicity time” or “relaxation time” beyond which the autocorrelation function decays to zero. This is a generic phenomenon in “weakly ergodic” Hamiltonian dynamical systems, so we may expect to see “glassy dynamics” in diverse physical contexts beyond glassy materials, ranging from the dynamics of planetary systems to Josephson junction in superconducting grains.33,34,55,56 Our main point here is that the physical scope of a dynamical system approach to relaxation in Hamiltonian dynamical systems extends far beyond just GF liquids, although these materials are our primary interest.
Dynamic heterogeneity is another general phenomenon in diverse weakly ergodic dynamical systems, including GF liquids,57,58 but we do not dwell on this aspect of the problem of understanding the dynamics of GF liquids in the present paper. Rather, we are primarily concerned with how the fast dynamics of the relaxation process of fluids might encode information about their long-time relaxation and molecular diffusion process occurring on a vastly different timescale upon approaching the glass transition temperature. We mention at the outset that some outstanding theoretical results have been obtained between measures of the “chaoticity” of the dynamics (i.e., maximum Lyapunov exponents λmax and the Kolmogorov–Sinai entropy hKS, the sum of the positive Lyapunov exponents) and the diffusion coefficient in the Lorentz gas model, a toy model of a hard-sphere gas in an array of fixed obstructions.59–61 We take this type of relation as suggesting the possibility of a general bridge between the “degree of chaoticity” of dynamical systems, as reflected in the fast dynamics, and long-time dynamical transport properties defined in terms of integrals of autocorrelation functions and on long timescales comparable to τα. Since there is no obvious way to measure λmax and hKS in either simulation or experiment, we must consider alternative physical quantities to get a theoretical “handle” on this possible relation between the fast dynamics and long-time structural relaxation. Previous analyses of relaxation in the FUPT model offer a possible framework for approaching this general problem, which we next develop into a model that makes predictions of τα in terms of experimental measures of the fast dynamics of the dynamical system that are presumably related to λmax and hKS. At the outset, we note that the FUPT model also exhibits a transition from a single relaxation mode to two relaxation modes upon cooling where the relaxation time of the slow mode analogous to the α-relaxation process of GF liquids becomes astronomically large at low T and where the fast relaxation time is nearly T invariant, as in GF liquids62 (see Fig. S1 of ref. 63). It is now appreciated that the apparent non-ergodic behavior observed by FUPT is just the consequence of this relaxation time being much longer than the simulation times,40 and recent simulations have confirmed that this is the case for the conditions under which the FUPT simulations were performed. Notably, this model exhibits a rapid approach to equilibrium by simply raising the temperature.
The work of Krylov64–66 initiated a new way of thinking about ergodicity that subsequently profoundly influenced modern studies of the nature of “equilibrium” states and relaxation in materials. He argued that the original conception of ergodicity was fraught with logical inner contradictions that explained the many paradoxes arising in attempts at developing ergodic theory and emphasized the consequential slow progress in developing any theoretical framework having any practical significance for predicting whether any given material might be ergodic or not. He then simply rejected the ergodic hypothesis and decided that the only reasonable way to proceed forward was to focus on the decay of correlations in dynamical systems as being the necessary objects fundamental to understanding the foundations of statistical mechanics and thermodynamics. Prigogine and coworkers67–70 amplified on Krylov's view that thermodynamics and dynamics should be fundamentally understood in terms of the chaoticity of the underlying molecular dynamics rather than just being probabilistic consequences of an assumed vast number of configurational states of material systems, as advocated by other scientists even to the present day.11,71
At any rate, after Krylov's highly influential work, there was a shift from studies aimed at understanding the conditions under which the ergodicity of material systems should hold, which so far has not been answered by either simulation or analytic theory, to a consideration of the relaxation processes governing the approach to an equilibrium state at long times.22 The relaxation function times have the advantage of being measurable properties, rendering the whole enterprise less academic in nature. Krylov's initial work showed the applicability of this way of thinking for dilute gases of hard spheres, but modern theoretical studies of dynamical systems focus on building up the theory of thermodynamics in a bottom-up way from the molecular dynamics rather than from top-down theoretical postulates. This philosophy directly addresses Einstein's strong critique of Boltzmann's formal probabilistic formulation of statistical mechanics in a top-down fashion (see a discussion of Einstein's views of Boltzmann's statistical mechanics by Cohen72). The simple takeaway message from the Einstein and Cohen commentaries is that a proper statistical dynamic theory should be grounded in molecular dynamics rather than in terms of postulates based on probability theory.
The many studies of the FUPT model, and the closely related one dimensional Ising model and non-linear spring models of the duplex DNA,24,73,74 have provided a general framework for understanding the emergence of multistage relaxation involved in a relatively fast and subsequent slow relaxation processes, although these features of the FUPT model are still under active investigation.75,76 The chaotic dynamics of the FUPT and related “chain models” have also been investigated exhaustively.27,77 These models serve as a kind of analog of the hydrogen atom or hydrogen molecule models in quantum theory, in the sense that these simple models share many of the features of more complex many-body dynamical systems and lend themselves to some degree to analytic treatment and comprehensive numerical studies.
The basic picture that has emerged from the studies of FUPT from a dynamical system perspective is that the degree of chaoticity of the dynamics of the FUPT model, as measured by hKS, progressively increases with the specific energy εs (and thus temperature), defined as the total energy of the system divided by the number of particles in the system (sometimes inaccurately referred to as energy density). The system energy is the only conserved property of Hamiltonian dynamical systems on an infinite timescale when the system is non-integrable, so this is the natural parameter to characterize the state of the dynamical system. Interestingly, although this property is easy to calculate in MD simulations, it is rarely reported in the simulations of either cooled liquids or heated crystals. Many studies have shown that in the FUPT model and simplified crystal models involving more realistic Lennard-Jones (LJ) interactions, there are at least two “critical” values of εs upon heating the material (raising εs).40,78–85 There is an initial stochastic threshold (ST) εs1 beyond which chaotic behavior is clearly exhibited (characterized by a positive hKS), followed by a strong stochastic threshold (SST) εs2 at elevated temperatures, at which the system evolution becomes strongly chaotic.77,81,83,85 This situation corresponds to the well-known case of a dilute hard-sphere gas studied by Boltzmann (see the papers by Lebowitz12,13 for an accessible discussion) and Krylov.64–66 Although the finiteness of the ST energy in the thermodynamic limit generally depends on the type of anharmonic potential,40 we suspect that this critical energy in effect exists for any realistic interparticle potential. Further research on this question is required,22 along with the matter of what sort of generalized statistical mechanics and other implications might apply at conditions lower than the ST value.84,86–90 The SST seems to persist robustly in the thermodynamic limit for this class of many-body Hamiltonian systems,40 and we strongly suspect that the existence of transition values of εs is universal, and that this quantity also explains the transition from a regime of relaxation in which there is a single “fast” relaxation mode at elevated temperatures to a multi-step relaxation below an onset temperature TA, which we hypothesize corresponds exactly to the SST critical energy condition mentioned above. It has recently been appreciated that the plateau in the relaxation function of the FUPT and related models represents a metastable state,91,92 whose long lifetime can be traced to the presence of persistent non-linear excitations mentioned above.25,27,28,93 The T range above TA corresponds to the specific energy range in which simple stochastic Langevin models94–97 of material dynamics may become suitable, but even in this T range, the existence of collective motion necessary for particle motion in the condensed state leads to memory effects that can invalidate this type of probabilistic formulation of material dynamics. A great accomplishment of kinetic theories over the last century was the overcoming of the difficulties of accounting for this type of many-body effect on fluid transport properties.98
Another outgrowth of many years of largely fruitless mathematical studies aimed at determining conditions sufficient to establish the existence of ergodicity in many-body dynamical systems (see Saito et al.99 for a review of these early dynamical system theories as well as their accomplishments and limitations) was a shift to the problem of estimating non-perturbative bounds on the time required to reach equilibrium. In particular, Nekhoroshev100 derived some highly influential bounds in association with relatively simple anharmonic Hamiltonian dynamical systems, which suggested a quantitative mathematical mechanism for the rapid increase of the relaxation time governing the return to equilibrium when the system transitions from being “chaotic” to “regular” (λmax = hKS = 0) in its dynamics. This bound has been interpreted thereafter for more complex dynamical systems to imply that the relaxation time τe needed to achieve equilibration should scale as,101,102
τe ∼ τe,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(1/Kδ) exp(1/Kδ) | (1) |
τe ∼ τe,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(εs,o/εs)δ] exp[(εs,o/εs)δ] | (2) |
In a particularly influential work, Pettini and Landofi104 found that eqn (2) described their observations on both the FUPT and related one-dimensional field theoretic models to a good approximation when τe,0, εs,o, and δ are taken to be adjustable parameters, and they also observed that λmax scaled empirically as a power of εs, although the power-law exponent changed for εs values above and below the STT value; see also the paper of Livi et al.77 Many subsequent studies have made favorable comparisons of this kind106 so that the relaxation time estimate in eqn (2) has emerged as being a plausible general expression for “equilibration time” τe on the specific energy εs in the range in which the molecular dynamics is “weakly chaotic”, i.e., corresponding to the specific energy εs (temperature) range between the ST and SST energy values. This is exactly the range of physical interest in GF liquids.
In the next section, we consider the applicability of eqn (2) to model relaxation in metallic and polymeric GF liquids in the T range below TA, but above the temperature To at which the structural relaxation time τα is observed to extrapolate to infinity and the material becomes effectively or strictly non-ergodic. In addition to estimating εs for these model materials for the first time in such a context, we relate this quantity to a readily measurable “fast dynamics” property (corresponding to a timescale of an initial β-relaxation time τβ on the order of a ps in condensed molecular and atomic materials) to enable a more direct test of this dynamical systems-inspired model of relaxation to experiment. Importantly, this relation might be expected to apply to any non-integrable Hamiltonian many-body dynamical system below the strong stochastic threshold specific energy at which the dynamics becomes fully chaotic so that the last vestiges of regular motion characteristic of integrable dynamics are lost. Thus, potential applications extend far beyond just GF materials, anharmonic heated crystalline materials, thermally reversible gels, etc. We indeed find evidence of a broad applicability of our general estimate of τα in terms of fast dynamics properties of the material, providing some insight into the linkage between dynamical properties measured on vastly different timescales. We suspect that this relation might provide the bridge between the microscopic dynamics and the material macro-dynamics mentioned above.
In recent years, advances in the analytic theory of relaxation in the FUPT model56,91,107–109 have provided a solid theoretical foundation for understanding the success of eqn (2) in comparison to simulation observations (technically for a finite number of particles in the model), and the physical nature of the multi-step relaxation process occurring in the FUPT model, and by extension many material systems if relaxation in this system is “generic” for many-body Hamiltonian systems as many believe. The breakthrough in modeling relaxation in this model56,91,107–109 came from the recognition that the integrable model corresponding to the FUPT in the low εs limit does not correspond to a lattice of atoms having harmonic interactions, but rather to a Toda lattice.110 The dynamics of this non-linear lattice model is also analytically solvable and its dynamics has been shown to be integrable,111,112 providing the theoretical foundation for rigorous mathematical advances in the description of the dynamics of the FUPT model based on an analytic theory. For example, the intuitive hypothesis that εs should be taken as the fundamental measure of “non-integrability” implicit in eqn (2) has been fundamentally justified91,109 and estimates of the relaxation time and thermodynamic properties have been made through systematic analytic calculations and simulations based on this non-linear dynamics perspective. In addition to theoretically justifying the functional form of the relaxation time for the FUPT model in eqn (2), this general advance provided a clear picture of the physical origin of the multi-step relaxation in this model material. In particular, the first stage of the fast relaxation process corresponds to the thermal excitation of low-frequency non-linear modes associated with the Toda lattice, which persist by virtue of their mutual interactions, explaining the long plateau in the relaxation process after the fast relaxation process. Ultimately, these collective excitations decay by virtue of the gradual excitation of higher frequency modes that cause slow energy transfer to these modes, causing the ultimate decay of the initially excited non-linear modes so that the system approaches the “equilibrium state” originally anticipated by FUPT. However, this relaxation timescale can be astronomical in size if εs is small as FUPT originally chose this parameter in their pioneering study so that they observed dynamical behavior associated with the weakly perturbed Toda lattice,110 which naturally explains how solitons come into the theoretical picture of the FUPT model. In short, these new theoretical developments have provided a firm foundation for understanding essential aspects of relaxation in condensed materials at low temperatures and the origin of the long relaxation times of “glassy” systems, as we shall see below. This theoretical work has not resolved the situation with relaxation in the FUPT model in the thermodynamic limit when the number of particles approaches infinity, but there has been some effort at deriving a stability time condition of the form of eqn (2), starting from the non-linear continuum wave equation formulation of the FUPT model, which inspired the earlier Zabusky-Kruskal soliton theory105,106, and from a direct formulation of the dynamics of model anharmonic lattices in the thermodynamic limit having an infinite number of atoms.113 We mention a more recent work advocating the FUPT model as a model system for understanding the dynamics of GF liquids,114 but this work offered limited testable predictions for the relaxation times of GF liquids and heated crystalline materials.
In a previous work,115 we argued for the applicability of eqn (2) as a generic model of structural relaxation in GF liquids and heated crystals for understanding both the temperature dependence of relaxation of the entire material and local variations in the interfacial regions of these materials. Here, we take the opportunity to validate and expand on these ideas.
To accomplish our task of developing a testable model of the dynamical properties of condensed materials based on a dynamical system perspective, we first establish a direct link between the specific energy εs (energy per particle) of a material, the fundamental parameter in the dynamical system approach to a measurable property of condensed materials, and the mean squared displacement of the molecules on the timescale of the relaxation time τβ of the fast β-relaxation process, 〈u2〉. This relationship, in conjunction with a proposed general relationship between τα and εs, allows us to estimate τα in terms of 〈u2〉, and we test the validity of this highly general relationship in polymeric and metallic GF liquids and a model crystalline material (UO2) where the model appears to be highly promising and general as we had hoped. We also show in the particular case of a LJ fluid of small system size of 34 atoms that 〈u2〉 is strongly correlated with the maximum Lyapunov exponent λmax, suggesting that this quantity can be taken as a measure of material “chaoticity”, in addition to the previous observations indicating that 〈u2〉 can also be interpreted as a practical measure of liquid relative mobility and relative material stiffness in the glass state. We conclude that the dynamical system approach to relaxation appears to provide a powerful framework for understanding general patterns of relaxation observed in many real materials that do not conform to classical theories.
2 Model and simulation details
2.1 Model metallic glass-forming materials
The details of our model metallic GF materials, as well as crystalline counterparts and superionic crystalline UO2, can be found in our previous papers,54,115–117 so our description is brief here. The interatomic interaction in all our metallic glass systems was described using semi-empirical potentials. In particular, the embedded atom method (EAM) potentials were employed to describe the interaction in Cu–Zr, Ni–Nb, and Pd–Si metallic glass systems,118–121 where the potentials were optimized to reproduce the static structure factor and other equilibrium and dynamic properties of the alloys, and a Mishin form of the EAM potential122 was used to describe the interatomic interaction for crystalline copper. For UO2, a many-body empirical potential of the Cooper–Rushton–Grimes (CRG) type,123 which combines the pairwise effects, including a long-range electrostatic interaction and a short-range effective interatomic pair interaction, and many-body effects based on the EAM, was employed. All our MD simulations employed the large-scale atomic/molecular massively parallel simulator (LAMMPS), which was developed at Sandia National Laboratories.124,125 The simulation timestep used for all simulations of this study was 1 femtosecond. The Parrinello–Rahman algorithm126 was applied to maintain constant pressure, the Nosé–Hoover thermostat was employed to control temperature, and Nosé–Hoover-style non-Hamiltonian equations of motion were used to perform the time integration during the simulation.127,128A bulk metallic GF alloy was formed by first heating a crystalline alloy above melting, then keeping the system at the elevated temperature for 5 ns to allow relaxation to ensure the formation of a structurally homogeneous GF liquid, and finally, cooling down to 300 K with a cooling rate of 100 K ns−1. During the entire procedure, an NPT ensemble was employed with zero pressure and periodic boundary conditions. The Cu64Zr36 thin film metallic glasses with thicknesses of 60 Å, 50 Å, 40 Å, 30 Å, 20 Å, 15 Å, and 10 Å were formed by cutting them from the bulk box and adding two 30 Å thick vacuum layers on both sides of the thin films. The Cu64Zr36 nanoparticles with 60 Å, 50 Å, 40 Å, 30 Å, and 20 Å diameters were also cut from the bulk alloy and vacuum layers were added on all sides with large vacuum layers (at least 30 Å) to ensure that atoms are not interacting with their own image when using periodic boundary conditions.
For crystalline thin film counterparts, simulation cells of single crystal Cu with approximately 6.4 nm in all three directions were created so that the X-axis is perpendicular to the desired surface (100), (110), and (111) planes. After relaxation at 300 K, two 30 Å vacuum layers are added on both sides along X-axis. In addition, crystalline Cu nanoparticles with diameters of 60 Å, 50 Å, 40 Å, 30 Å, and 20 Å were cut from a perfect Cu crystal and vacuum layers were added on all directions. All simulations on metallic materials were performed in three spatial dimensions and the same situation applies to polymeric and other material systems described below.
In all of the simulations considered in the present section, isothermal heating was performed under constant particle number, constant volume, and constant temperature conditions (i.e., in the NVT ensemble) for an extended time to ensure that the system reached near equilibrium to probe kinetic processes that cannot be observed under continuous heating conditions.
2.2 Model glass-forming polymer melts
Our study of GF polymer melts is based on the same generic, coarse-grained model utilized in our previous paper,129 so our description is brief here. This model describes the basic characteristics of polymers by representing the chains in terms of a certain number of connected statistical segments or beads. To maintain chain connectivity, neighboring beads along a chain are bonded to each other through the finitely extensible nonlinear elastic (FENE) potential,130,131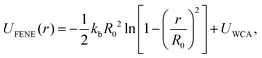 | (3) |
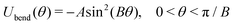 | (4) |
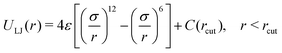 | (5) |
We perform simulations under different constant P conditions for a polymer melt with the chain length of M = 20. The total number of beads is N = 8000 or 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for A = 0ε or 6ε. We describe all quantities and results in standard reduced LJ units. Specifically, length, time, temperature, and pressure are, respectively, given in units of σ, τref, ε/kB, and ε/σ3, where
000 for A = 0ε or 6ε. We describe all quantities and results in standard reduced LJ units. Specifically, length, time, temperature, and pressure are, respectively, given in units of σ, τref, ε/kB, and ε/σ3, where 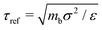 with mb being the bead mass. MD simulations are carried out under periodic boundary conditions utilizing the LAMMPS package, where the pressure P and temperature T are maintained by a Nosé–Hoover barostat and thermostat and a time step of Δt = 0.005τref is used to integrate the equations of motion. Properties are calculated in the NVT ensemble after the melt is further equilibrated for a period typically over 10 to 100 times longer than the structural relaxation time τα at the given P and T.
with mb being the bead mass. MD simulations are carried out under periodic boundary conditions utilizing the LAMMPS package, where the pressure P and temperature T are maintained by a Nosé–Hoover barostat and thermostat and a time step of Δt = 0.005τref is used to integrate the equations of motion. Properties are calculated in the NVT ensemble after the melt is further equilibrated for a period typically over 10 to 100 times longer than the structural relaxation time τα at the given P and T.
2.3 Kob–Andersen binary Lennard-Jones mixture model
The binary model of Kob and Andersen was first formulated as a cartoon model of real Ni80P20 metallic glass,134,135 and this model has emerged as a “canonical” model of atomic and small molecule GF liquids. This model liquid is composed of two particle species A and B having an equal mass m that interact through a truncated-and-shifted LJ potential (eqn (5)). We report results in reduced units, with units of length, energy, and time scales being σ = σAA, ε/kB = εAA/kB, and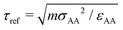 , respectively. The system contains 4000 LJ particles (NA
, respectively. The system contains 4000 LJ particles (NA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NB = 4
NB = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) with parameters εAB/εAA = 1.5, εBB/εAA = 0.5, σAB/σAA = 0.8, and σBB/σAA = 0.88.
1) with parameters εAB/εAA = 1.5, εBB/εAA = 0.5, σAB/σAA = 0.8, and σBB/σAA = 0.88.
We perform simulations under both constant volume (V) and constant pressure (P) conditions using the LAMMPS package with periodic boundary conditions. In all simulations, a time step of Δt = 0.002τref or 0.005τref is used to integrate the equations of motion. For both constant V and P conditions, we initially prepare equilibrated systems at relatively high temperatures and then quench them to the target temperatures to generate the initial configurations for each temperature. For constant V conditions, simulations are performed over a range of fixed number densities (ρ = N/V = 1.2σ−3 to 2.0σ−3) in the NVT ensemble, where T is maintained by the Nosé–Hoover thermostat. For constant P conditions, our results are obtained along an isobaric path over a range of pressures (P = 0ε/σ3 to 400ε/σ3) by employing the procedure described below. At the first stage, the simulations are performed for a given T and P in the NPT ensemble, where the temperature and pressure are maintained by the Nosé–Hoover barostat and thermostat. These NPT simulations then allow for the determination of the desired density at the given T and P. For both constant V and P conditions, properties are calculated at the target density in the NVT ensemble, following an equilibration procedure that typically lasts for a period 10 to 100 times longer than the structural relaxation time τα.
2.4 One-component Lennard-Jones liquid
We also perform MD simulations for a simple LJ liquid to better understand the liquid dynamics in the high-temperature regime. In line with the work of Sastry,136 our simulations are conducted at a reduced density of ρ = 1.0σ−3 for a system of 32 particles interacting via the truncated-and-shifted LJ potential (eqn (5)). The temperature is varied from T = 6.80ε/kB to 2.54ε/kB. As for polymer melts, the quantities and results of the LJ liquid are also expressed in standard reduced LJ units. MD simulations are conducted using the LAMMPS package, with periodic boundary conditions applied. A time step of Δt = 0.002τref or 0.001τref is used to integrate the equations of motion. Our study for LJ liquids starts by preparing an equilibrated melt system at a constant temperature of T = 7.0ε/kB within the NVT ensemble, where the temperature is maintained by the Nosé–Hoover thermostat. Subsequently, we perform a quenching process on the equilibrated melt to generate the initial configurations for each temperature under scrutiny. Before properties of interest are calculated from the simulation particle trajectories, the configurations are further equilibrated for a period typically over 10 to 100 times longer than τα in the NVT ensemble.3 Specific energy for model glass-forming liquids and the localization model
Based on computational results obtained for the model systems in the previous section, we calculate the specific energy of model metallic and polymeric GF liquids over a large T range. Relaxation in these materials has been extensively investigated in past works,54,115–117 so we refer the reader to these previous works, where both thermodynamic and dynamic properties of these materials are discussed.Since a previous work has taken εs to be a measure of the perturbation from the integrable dynamics achieved at low temperatures where the particles are localized in a non-ergodic state, we consider some measure of the material property which directly quantifies the anharmonicity of intermolecular interactions. In particular, the mean squared displacement 〈u2〉 of a particle localized in a harmonic potential is well known to increase proportionally with the thermal energy kBT so that the deviation of the ratio 〈u2〉/kBT from a constant value provides a readily accessible measure of deviations from the low-temperature harmonic state. Accordingly, we plot the specific energy εs of our fluids as a function of 〈u2〉/kBT in Fig. 1, and we find, as expected, that εs varies linearly with 〈u2〉/kBT for both our metallic GF liquids at fixed pressure and model flexible and semi-flexible polymer melts having variable pressure. We have previously shown that 〈u2〉 extrapolates to zero at the characteristic temperature To at which the relaxation time τα diverges when the data are extrapolated in all these fluids so that the intercept in each case corresponds to εs(To)/c, where c is a material constant dependent on the fluid type. This finding motivates the consideration of the relationship between the long-time relaxation time τα and our surrogate for the specific energy 〈u2〉,
τα = τA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(uA2/〈u2〉)δ − 1] exp[(uA2/〈u2〉)δ − 1] | (6) |
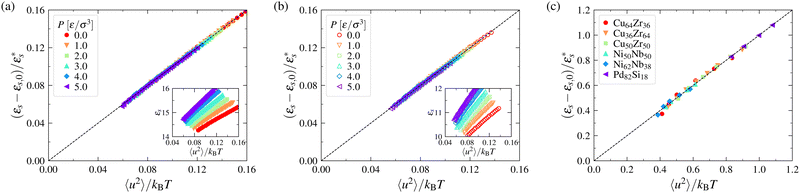 | ||
Fig. 1 Relation between the specific energy εs and the Debye–Waller parameter normalized by the temperature, 〈u2〉/kBT, for polymer melts and metallic glasses over a range of T. Panels (a) and (b) correspond to the results for flexible and semi-flexible polymer melts over a range of pressures P, respectively. The insets show εsversus 〈u2〉/kBT. Panel (c) corresponds to the results for a series of metallic glasses at P = 0 MPa, where 〈u2〉 is given in units of σ2. The parameters εs,0 and 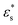 in constructing these plots are summarized in Section S1 of the ESI.† in constructing these plots are summarized in Section S1 of the ESI.† | ||
As described in greater depth in previous papers,54,115–117 we first performed a quantitative test of the LM without any free parameters in Cu–Zr metallic glasses with five representative compositions, i.e., Cu68Zr32, Cu64Zr36, Cu58Zr42, Cu50Zr50, and Cu36Zr64, over a wide range of temperatures.137 We found that the LM could describe all our simulation data for Cu–Zr metallic GF liquids by relating the α -structural relaxation time τα to the Debye–Waller parameter 〈u2〉, a property determined on a ps timescale. The LM was also confirmed in superionic crystalline UO2.11 Later, we examined the validation of the LM for Cu64Zr36 metallic glass thin films and crystalline Cu thin films having different orientations. Unsurprisingly, 〈u2〉 in these model amorphous and crystalline materials can be extended to predict the local interfacial dynamics of model amorphous and crystalline thin films through the LM.115 More recently, we found that the LM for the dynamics of condensed materials can account quantitatively for the temperature dependence of the structural relaxation time in the interfacial regions of both Cu64Zr36 metallic glass and Cu crystalline nanoparticles.117
It is evident that the variables on the x-axis of Fig. 1 are not dimensionless and the physical significance of the unexpected kBT factor in these figures requires comment. We may gain insight into this factor by considering the physical significance of the reduced specific energy with regard to our simulated GF liquids. This quantity measures the extent to which the dynamical system deviates from integrability so that this quantity is a practical measure of the degree of “chaoticity” of the dynamical system. Below, we discuss the relation between this quantity and a more conventional chaoticity measure, the maximum Lyapunov exponent λmax in a smaller-sized dynamical system (liquid) than considered in Fig. 1, which allows for explicit calculations of λmax as a function of T.
The natural measure of ergodicity in fluids is 1 minus the “non-ergodicity parameter” fs,q, defined by the plateau in the self-intermediate scattering function Fs(q,t) at a length scale q,
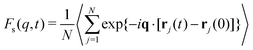 | (7) |
Explicit simulations for both metallic and polymer GF liquids have previously shown that fs,q* is a near-universal function of the dimensionless variable (q*)2〈u2〉,62,129 as illustrated in Section B of the ESI,† and we generally expect any ergodicity measure to be a function of the dimensionless variable (q*)2〈u2〉. Consistency of the data showing our “chaoticity parameter” εs under constant pressure conditions depends robustly on 〈u2〉/kBT in Fig. 1 would then seem to imply that qp2 should scale as qp2 ∼ 1/kBT under constant pressure conditions. We next check this interpretation of the 〈u2〉/kBT scaling through explicit calculations for the same polymer melt simulations.
Fig. 2 indicates that qp2 indeed scales as 1/kBT to a good approximation for both the flexible and semi-flexible model polymer melts considered in Fig. 1 under constant P conditions. The unexpected factor kBT in the 〈u2〉 − εs relation then simply reflects the thermal expansion of the material, as noted above. We frankly admit that it took us a long time to figure out where the kBT factor was coming from. The parameters a and b in Fig. 2 are P dependent and the values of these parameters are summarized in Section S1 of the ESI.† As a further check on the origin of the kBT factor, we note that essentially no change in qp2 with T is expected to occur under constant volume conditions, and below, we show explicitly that the specific energy of a LJ fluid under constant volume conditions scales linearly with 〈u2〉 without the factor 1/kBT, consistent with the average interparticle distance parameter qp2 being nearly constant under constant density conditions. We further establish this point, in Section S1 of the ESI,† where it is directly shown that qp2 is insensitive to T in the single component LJ fluid under constant density conditions.
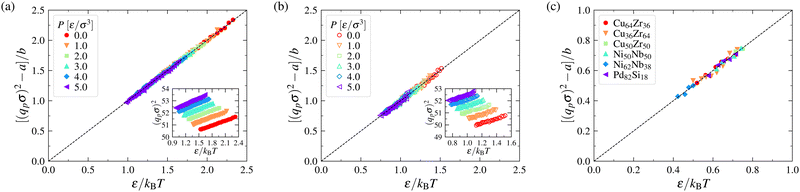 | ||
| Fig. 2 Relations between the mean squared interparticle spacing qp2 and the inverse temperature ε/kBT for polymer melts and metallic glasses over a range of T. Panels (a) and (b) correspond to the results for flexible and semi-flexible polymer melts over a range of pressures P, respectively. Panel (c) corresponds to the results for a series of metallic glasses at P = 0 MPa. The parameters a and b in constructing these plots are summarized in Section S1 of the ESI.† | ||
4 Application of localization model to relaxation and diffusion in condensed materials
4.1 Test of the localization model for a range of metallic glass materials
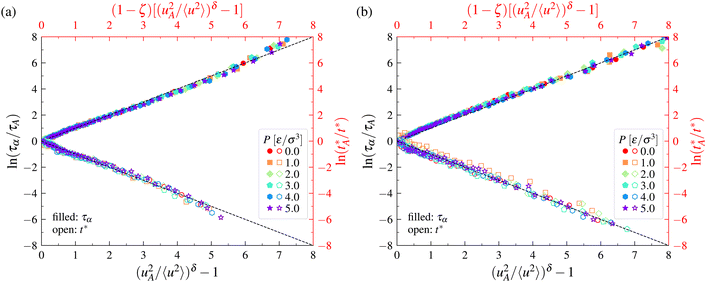
To test the LM in metallic GF liquids, we first estimated the α-relaxation time τα from Fs(q,t).137Fs(q,t) normally exhibits a “stretched exponential” variation in GF liquids, i.e., Fs(q,t) ∼ exp[−(t/τα)βs], where the exponent βs varies with T. The onset temperature TA of glass formation was estimated from the condition that 〈u2〉 becomes about 9 times its value at Tg. Fig. 3 shows that the LM relation for τα (eqn (6)) holds to a good approximation in Cu–Zr metallic glasses covering the full range of temperatures and alloy compositions investigated in our simulations. As noted earlier, the exponent is taken to be δ = 3/2 here. Using the empirical fractional Stokes–Einstein (FSE) relation, we can link diffusion coefficients to τα, in the form of the scaling D/T ∼ (1/τα)1−ζ, where ζ is the “decoupling exponent”. We note that a fundamental understanding of the exponent ζ is one of the outstanding problems in GF liquids, and we have investigated this quantity in numerous GF liquids.129,140,141 It is anticipated that ζ should have an interpretation in terms of a dynamical system theory or from the theory of liquids, but its interpretation has proven highly elusive up to the present. In Fig. 3, we show our estimates of the self-diffusion coefficient of individual elements Di/T, normalized by its values Di,A at TA for the alloys, versus (1 − ζi)[(uA2/〈u2〉)3/2 − 1], the predicted variation based on the LM. In all cases considered, the LM holds to a remarkable approximation. The values of the exponents ζi linking relaxation times to diffusion times are tabulated in a previous publication.137 We note that there are no free parameters in the comparison of the relaxation time data in the metallic glass with the LM, which seems remarkable to us.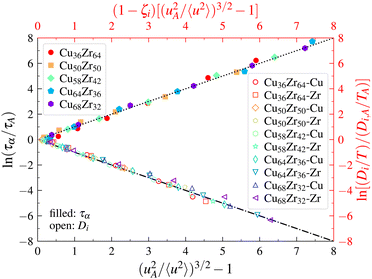 | ||
| Fig. 3 Localization model description of relaxation time and diffusion data for a range of Cu–Zr bulk metallic glasses. A description of the original simulations is given by Douglas et al.137 | ||
It is also noted that Hu and Tanaka142 found that the LM with δ taken to be adjustable rather than 3/2 as in Fig. 3, applied very well to relaxation time data for a model two-dimensional GF liquid originally developed as a model of a metallic GF liquid. This observation accords with observations on other GF materials.143–147 The exponent δ would appear to exhibit some non-universality whose origin is not yet understood. We also note that Horstman and Vogel148 have shown that the LM describes relaxation time data for a range of water models over a large T range, where δ was fixed at 3/2 as in the metallic glass simulation data in Fig. 3, but where the onset temperature variable uA2 was phenomenologically varied.
4.2 Test of the localization model for a superionic crystalline material
We next apply the LM prediction of a relationship between the α-structural relaxation time τα and oxygen ion diffusion coefficient DO and 〈u2〉 for a model superionic material, crystalline UO2 under superionic conditions at high T where such crystals exhibit remarkably high mobility.149–155 The important difference between this system and the Cu–Zr metallic GF liquids described in the previous section is that no decoupling arises in this and apparently other crystalline materials156 so that we have the further simplifying relationship, DO/kBT ∼ 1/〈u2〉. Fig. 4 shows that in addition to τα, the diffusivity of the oxygen atoms DO also obeys the predicted LM relationship to a remarkable approximation with no free parameters,| DO/T = (DO,A/TA)exp[(uA2/〈u2〉)3/2 − 1] | (8) |
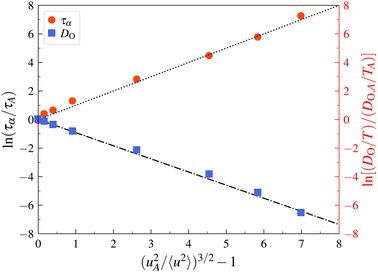 | ||
| Fig. 4 Localization model description of relaxation time and diffusion data for superionic UO2. A description of the original simulations is given by Zhang et al.116 | ||
4.3 Test of the localization model for thin film and nanoparticle materials
The magnitude of 〈u2〉 is evidently larger near free boundaries where atomic motions are less constrained. It is thus interesting to inquire whether or not the LM can be applied to make predictions of the mobility and relaxation time in the interfacial dynamics of both GF and crystalline materials. The question is then whether or not the LM applies locally within a material at equilibrium. We again draw upon previous simulations of the interfacial dynamics of Cu64Zr36 model metallic glass and crystalline (Cu) free-standing films115 (see Fig. 5) and nanoparticles117 (see Fig. 6), where the details of the simulations and the definition of the interfacial region are described in ref. 115 and 117. In the case of free-standing thin films, Cu64Zr36 model metallic glass with thicknesses of 60 Å, 50 Å, 40 Å, 30 Å, 20 Å, 15 Å, and 10 Å and a 60 Å thin film simple crystal Cu with (100), (110), and (111) surfaces were considered. We also defined the interfacial region width in the model metallic glass thin film by the points at which 〈u2〉 deviates by 5% from its bulk-like value deep within the film and the outermost point of the film surface. In the case of nanoparticles, Cu64Zr36 model metallic glasses and crystalline Cu with diameters of 60 Å, 50 Å, 40 Å, 30 Å, and 20 Å were considered. The definition of the interfacial region width for nanoparticles is the same as that used in thin film studies. Remarkably, we find in Fig. 5 and 6 that the LM applies to the interfacial dynamics of both thin films and nanoparticles, where the model applies both to GF and crystalline materials, so that the model appears to apply rather broadly to the metallic materials that we have investigated so far. In addition, the model appears to apply to the dynamics of the entire material and the local dynamics of the interfacial region.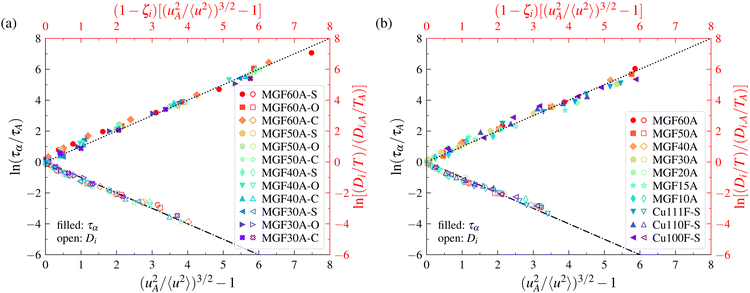 | ||
| Fig. 5 Localization model description of relaxation time and diffusion data for metallic glass and crystalline thin films. Panel (a) corresponds to the results for Cu64Zr36 metallic glass thin films. Panel (b) corresponds to the results for Cu64Zr36 metallic glass and crystalline thin films. For the definition of the figure legend, Cu64Zr36 metallic glass films with a thickness of 60 Å are labelled as MGF60A, a crystalline copper film with (110) surface is labelled as Cu110F, etc. In addition, MGF60A-O, MGF60A-S, and MGF60A-C correspond, respectively, to the overall, two interfacial regions, and core of the MGF60A thin film.115 | ||
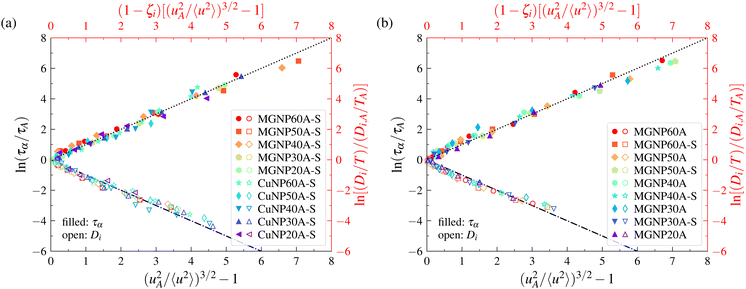 | ||
| Fig. 6 Localization model description of relaxation time and diffusion data for metallic glass and crystalline nanoparticles. Panel (a) corresponds to the results for the interfacial regions of Cu64Zr36 metallic glass and Cu crystalline nanoparticles. Panel (b) corresponds to the results for the interfacial regions of Cu64Zr36 metallic glass nanoparticles and the overall systems. For the definition of the figure legend, the Cu64Zr36 metallic glass nanoparticle with a diameter of 60 Å is labelled as MGNP60A and the crystalline Cu nanoparticle with a diameter of 60 Å is labelled as CuNP60A. The interfacial layer of MGNP60A is labelled as MGNP60A-S and the interfacial layer of CuNP60A as CuNP60A-S, etc.117 | ||
4.4 Test of the localization model for model polymeric materials
The LM relation between τα and 〈u2〉 in eqn (6) was first observed empirically in the case of model polymer fluids,157 so it should not be surprising that the LM has proven to robustly describe relaxation in this class of materials, including supported polymer films and polymer nanocomposites, where the polymer surface interaction strength is moreover varied.138 Small deviations of δ from 3/2 were reported in the present work, however, for the polymer models studied and between the polymer films and nanocomposites. A recent work of polymer nanocomposites having a wide range of nanoparticle sizes and a large range of T158 has indicated a δ value consistent with the value observed originally in neat polymers,157δ = 3/2, when the onset value uA2 was taken to be an adjustable parameter, indicating that some of the uncertainty can be associated with the uncertainty in estimates of the onset temperature TA. Recent simulation observations on coarse-grained thermoset materials with variable cross-linking and cohesive energy density145,146 have also shown the apparent applicability of the LM under all conditions simulated for these materials, although the apparent value of δ was reported to be different from 3/2. Simmons and coworkers159 made some studies of model GF liquids and found δ values different than 3/2, where this result was rationalized in terms of the variable shape of the geometrical domains swept out by particles in the condensed state. Given the apparent coupling between the uA2 and δ parameters in the fitting of some material systems, we view the estimation of δ as being somewhat uncertain. Further work aimed at calculating uA2 should help resolve this uncertainty. In a recent exhaustive investigation of Kob–Andersen model, we have shown that the time at which 〈u2〉 is defined can influence the magnitude of δ.141In the present work, we revisit the relation between τα and 〈u2〉 for a wide range of coarse-grained polymer models having variable chain stiffness and P so that the test of the LM is distinct from previous studies focused on flexible polymer melts in the bulk and polymer thin films and nanocomposites.138 In small molecule liquids, the molecular diffusion correlates strongly with the peak time t* of the non-Gaussian parameter, which describes the effective lifetime of the mobile clusters in ordinary GF liquids, D/kBT ∼ 1/t*.52,141,160,161 and since this time is also well-defined in polymer melts,52,129,146,162,163 we add this to our comparison to the LM in the case of polymers so that we can also compare to the simulations of metallic materials described above. Our comparison of the LM model to the simulation data of coarse-grained polymer melts in Fig. 7 again leads to a remarkable reduction of all the simulation data, as in the case of metallic materials. It should be noted that the value of δ in Fig. 7 is taken to be an adjustable parameter and is generally somewhat different from 3/2, a point that has been discussed previously.158
5 Power-law relaxation in the metastable state: Some speculation about the origin of stretched exponential relaxation from a dynamical system perspective
There are also interesting implications of the metastable nature of the material following the fast β-relaxation process on the functional form of relaxation function. Particle displacements in this regime occur in an intermittent fashion described by a power-law distribution,164 a phenomenon associated with string-like jump events, which also arises in the one-dimensional anharmonic oscillator chain models.27,28 These jump events are also associated with colored noise in the energy fluctuations of the particles and the occurrence of quake-like particle displacement events that are highly reminiscent of the phenomenology of earthquakes,165,166 a phenomenology observed earlier in non-linear excitations in non-linear chain models.29 This phenomenology was first seen by the authors in simulations of the interfacial dynamics of Ni165,166 and Cu167 nanoparticles, but it has since been observed in the interfacial dynamics of bulk Ni,168 the interfacial dynamics of ice,169 and the internal dynamics of the protein ubiquitin.170 It is our general impression that this intermittent displacement is a universal property of glassy materials, and this idea was central to a theory of glass formation introduced some time ago by Odagaki.171Now, if we take the event process giving rise to the decay of the metastable state established after the ps induction time, τβ is taken to be described by a fractal time event process occurring at average time-dependent rate R(t) ∼ t−β, which accounts for Odagaki's power-law distribution in the jumping time distribution (a power-law in the rate at which the system decays from a metastable plateau state in the FUPT model has been observed to be the case in the FUPT model76), then we have a situation in which the time of the dynamical system evolves according to a fractal time clock. An exponential relaxation process, characterized by a relaxation function exp[(−t/τB)] and a bare relaxation time τB in the strongly chaotic regime above TA, then changes to exp[(−t/τc)1−β], where the effective relaxation time becomes “renormalized” as, τc ∼ (τβ)1/(1−β), on account of the temporal intermittency. (This scenario is apparently consistent with the phenomenological “Coupling Model” of Ngai and coworkers,172 where a decorrelation time on the order of a ps is also emphasized.173) The breather excitations that are apparently responsible for the intermittency of particle displacements evidently exert a qualitative influence on the decay of the metastable plateau in the autocorrelation function describing relaxation in the weakly ergodic dynamics regime174,175 of relevance to the dynamics of GF liquids. We note that stretched exponential dynamics is observed in the thermalized FUPT model when the system is quenched to a low temperature,176 a procedure that allows for the direct observation of the breathers governing this relaxation process. A stretched exponential relaxation at a fixed temperature has also been observed in the autocorrelation function describing particle displacements in the closely related Peyrard–Bishop non-linear spring model introduced to model base-pair opening fluctuations in duplex DNA.177 In Section S2 of the ESI,† we provide an additional discussion on the universal multistep decay of relaxation in GF liquids based on our simulation results, along with the relation between 〈u2〉 and the non-ergodicity parameter fs,q*. We note that if the material was in a true equilibrium state in which the event process occurs in such a power-law fashion, the relaxation function for a Hamiltonian dynamical system at equilibrium would then be described by a Mittag-Leffler function, which exhibits a long-time power-law rather than a stretched exponential decay.178,179 The stretched exponential decay then carries the signature of the decay of a metastable state, although this is not the sole mechanism that can lead to this type of relaxation.178,179
We may also understand the rather distinct nature of relaxation processes within the metastable plateau regime, which can persist essentially forever in the “glass state” at low εs (or low temperature). The Johari–Goldstein (JG) relaxation process of GF liquids occurs in this plateau regime and involves intermittent jump-like displacements having a power-law distribution. The dynamics in the plateau region can be viewed as being in a quasi-equilibrium state or “quasi-state”91,108 rather than a decaying unstable state, and we may then reasonably apply the theory of relaxation of Hamiltonian dynamical systems under equilibrium conditions180,181 to understand the nature of the JG relaxation process.182 If we take the event process governing the relaxation process to be an intermittent renewal process described by a Levy stable distribution governing the jump displacement distribution,178,179,183 at least asymptotically, then this formalism predicts that the relaxation function ψ(t) becomes a Mittag-Leffler function, which exhibits a long-time power-law decay rather than a stretched exponential decay.178,179 (This type of power-law decay is evident in the FUPT model; see Fig. 2 in ref. 76.) Under conditions in which the quasi-state persists for extremely long times so that the system is either truly or effectively non-ergodic so that striking deviations from Boltzmann–Gibbs thermodynamics can arise,184–188 which has been effectively modeled phenomenologically by the generalized thermodynamic theory of Tsallis and coworkers.189,190 Under these low energy conditions, ergodicity in the strict Boltzmann–Gibbs sense no longer exists,84 but a generalized “non-extensive thermodynamics” appropriate for weakly mixing dynamical systems can arise from a change in the geometry of the phase space trajectories,191,192 so we may talk about new types of “equilibrium states” that retain many of the conventional properties of thermodynamics, but not others.190 Deviations from Boltzmann–Gibbs thermodynamics also arise in gases and harmonic systems when the number of particles is finite193,194 or by the presence of long-range interactions.184–187,195–198 Subtle issues arise regarding the validity of thermodynamics in connection with taking the thermodynamic limit. Finally, we mention that the long-time power-law decay relaxation in Hamiltonian dynamical systems is consistent with the Tsallis thermodynamics,199 and this observation that the ultimate decay of autocorrelation functions to vanishing small values does not ensure the existence of equilibrium in the sense of Boltzmann and Gibbs.
The JG relaxation is widely observed to exhibit the Mittag-Leffler form (or equivalently the Cole–Cole form in the frequency domain) and this form of relaxation arises in diverse types of condensed materials.178,200,201 Since the JG process occurs in the plateau regime, it is a fundamental precursor of the α-relaxation process associated with the decay of the metastable state. Ngai and coworkers172 have plausibly argued that the “bare” relaxation time τB noted above can be exactly identified with the relaxation time τJG of the JG relaxation process so that the α-relaxation and JG β-relaxation times are linked by a power-law relation, τα ∼ (τJG)1/(1−β). This “decoupling” relation is supported by a large body of evidence based on an astoundingly large range of condensed materials. There is then the prospect of understanding the rather universal occurrence of power-law and stretched exponential relaxation in condensed materials178,179,200,201 in different stages of the hierarchical relaxation process in condensed materials under weakly chaotic conditions based on a dynamical system theoretical framework.
6 Dynamical system interpretation of the Debye–Waller parameter 〈u2〉
The interpretation of the LM relation between the relaxation time τα and the Debye–Waller parameter 〈u2〉, and the fundamental origin of the extremely long relaxation times of GF liquids at low T, as being a generalized Nekhroshev relation suggests a completely new perspective for physically interpreting 〈u2〉. Evidently, 〈u2〉 can qualitatively be interpreted as a measure of the “chaoticity” of the dynamics so that some relation to the maximum Lyapunov exponent λmax of the dynamical system, the standard chaoticity measure of dynamical systems, may be anticipated. Interestingly, many authors have previously come to the same conclusion based on different arguments. In particular, authors taking a dynamical system approach to the “melting” of small atomic clusters suggested that λmax should vary similarly to 〈u2〉, thereby providing a new way of interpreting the phenomenological Lindemann criterion of melting based on 〈u2〉 becoming a critical fraction of the average interparticle distance.202–205 Thereafter, the potential utility of λmax for estimating the onset of mobility in glassy clusters was suggested by Nayak et al.206 and λmax has been noted to exhibit “kinks” in its temperature variation in association with phase transitions, such as those observed in the planar Heisenberg model207 and the incipient collapse of polymer chains.208 These results, and other results of this kind, have greatly stimulated an ongoing effort to describe various aspects of phase transitions based on a dynamical system perspective.209 These advances have also stimulated new methods for estimating and interpreting the Lyapunov exponents.136,210The correspondence between λmax and 〈u2〉 explored previously in the context of the dynamical properties of clusters was only qualitative and, hence, it is of some interest to examine how these quantities might be quantitatively related in liquids, the type of dynamical system that most interests us. Despite continual improvements in methodology, the calculation of λmax(T) for a fluid containing a large number of particles over a large T range remains a difficult task. Fortunately, calculations of this kind have been performed for a small LJ system136 and we compare these results to calculations of 〈u2〉 for the same model having the same size and under the same thermodynamic conditions. We take calculations of λmax(T) for a LJ liquid over a wide range of T by Sastry136 to be suitable for the present purpose of exploring the quantitative relation between λmax and 〈u2〉 for a model, albeit only composed of 32 atoms and at constant density to facilitate the estimation of λmax.
We next make some general observations from the data shown in Fig. 8. Firstly, 〈u2〉 is a linear function of the specific energy εs, normalized by the LJ well-depth parameter ε to an excellent approximation. Moreover, λmax varies approximately linearly with 〈u2〉, and the inset to this figure indicates that 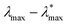 scales as (εs/ε)δ, where the empirical constants are δ = 0.68 and
scales as (εs/ε)δ, where the empirical constants are δ = 0.68 and 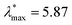 . This scaling is quite understandable since exact calculations for λmax as a function of εs, based on random matrix theory,211 should exactly equal 2/3 in the regime of fully developed chaos. This scaling has been observed and discussed at length in previous studies of model dynamic systems.104,208
. This scaling is quite understandable since exact calculations for λmax as a function of εs, based on random matrix theory,211 should exactly equal 2/3 in the regime of fully developed chaos. This scaling has been observed and discussed at length in previous studies of model dynamic systems.104,208
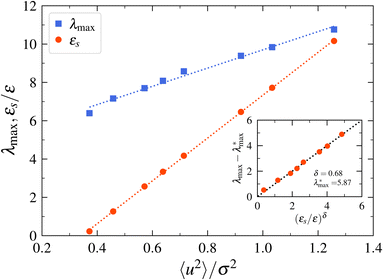 | ||
| Fig. 8 Relation between the maximum Lyapunov exponent λmax, the specific energy εs, and the Debye–Waller parameter 〈u2〉 for a model Lennard-Jones liquid. The main figure shows λmax and εs as a function of 〈u2〉. The inset depicts the relation between λmax and εs. The estimates of λmax for this fluid are taken from the paper of Sastry136 and the values of εs and 〈u2〉 are calculated for the same fluid under the same conditions as Sastry, as described in Section 2.4. | ||
We further notice that the scaling just mentioned implies, λmax ∼ 〈u2〉3/2 so that the recognized “degree of chaoticity” of a dynamical system, λmax, directly scales like the “dynamic free volume”, 〈u2〉3/2. From the discussion above, we may also interpret 〈u2〉3/2 as a “chaoticity parameter”, in addition to its interpretation as a mobility and rigidity parameter.90,145,146,212–215 This interesting correspondence between λmax and 〈u2〉3/2 can be rationalized qualitatively a posteriori by previous observations by Cleary216 based on a “toy” low dimensional dynamical system, where it was noted that there was a direct correlation between the magnitude of λmax and the phase space volume of the chaotic regions inferred from the surfaces of section and that the local chaoticity of a weakly chaotic dynamical system could be understood qualitatively based on this geometric perspective. Apparently, these estimates are finite time estimates of λmax217 since the long time λmax, divided by the number of particles in the system, is an intensive property of the entire dynamical system.218 This quantity corresponds to an average over the entire phase space available to the dynamical system. We may interpret 〈u2〉3/2 as the volume in which the local chaotic motion of the molecules in real space and we may view local variations of 〈u2〉3/2, which can be readily visualized in MD simulations,90,129,145,146,167,215,219 as corresponding to regions of the material in which the local chaoticity varies.
The dynamics of fluids becomes relatively simple in the strongly chaotic regime above the SST where memory efforts are relatively weak, as in gases. This is the regime in which stochastic theories such as Langevin models94,95 and the Kramers activated transport96,97 theory of relaxation and reaction in liquids can be expected to apply to a good approximation. To establish this point, we show the self-intermediate scattering function Fs(q,t) in Fig. 9 for the model LJ system discussed in Fig. 8 under the same strongly chaotic conditions, but still in the condensed liquid regime. We see that the long lime relaxation is well approximated by an exponential relaxation, consistent with the expectations of a strongly chaotic dynamical system, while Fs(q,t) is dominated by Gaussian relaxation at short times. This short-time limiting behavior applies to all equilibrium condensed materials because at times shorter than the average collision time, all particles in such materials exhibit inertially dominated dynamics similar to that of a dilute gas.51,220 Further, the relaxation time of the inertial relaxation process correlates strongly with the inverse of λmax, the “Lyapunov time”, τLyapunov ~ 1/λmax,33,34,221 as in the case of relaxation in gases.222 (An approximate inverse scaling between the relaxation time and λmax is also anticipated to be a general behavior in weakly non-integrable dynamical systems,31 in which particles have “soft”, i.e., long-range mean-field-like interactions that enhance the rate of decay of metastable states.) The relaxation time of the long-time relaxation is well approximated by an Arrhenius T dependence, consistent with the expectations of transition state theory and its Langevin dynamics models.94–97 This high T stochastic dynamics regime can be expected to correspond also to the T regime in which the Gibbs–Boltzmann thermodynamics safely applies and provides a natural reference point for cooled liquids where overt non-ergodic behavior begins to emerge. As noted above, we identify the condition of strongly chaotic dynamics with the characteristic temperature TA in GF liquids, where an ideal stochastic dynamics applies. It is noted that popular Langevin models of the dynamics of liquids neglect persistent correlations arising from the emergence of hydrodynamic interactions and the propagation of these interactions by vorticity diffusion even in the high T fluid regime. This phenomenon can be incorporated into an extended Langevin model description of liquid dynamics and leads to “memory effects” that cause the velocity autocorrelation function to decay as a power-law rather than as an exponential.98 These memory effects are often simply neglected in the modeling of the dynamics of condensed materials, leading to some “surprise” when Gaussian particle displacement as in the classical Brownian motion theory is not normally observed experimentally.223–225 Nonetheless, the observations in Fig. 9 indicate that the neglect of memory effects can yield a reasonable approximate description of the liquids, at least in the high T regime where the liquid dynamics is highly chaotic and stochastic theory becomes a reasonable approximation. This type of modeling cannot be expected to be a reasonable approximation T below TA, however.
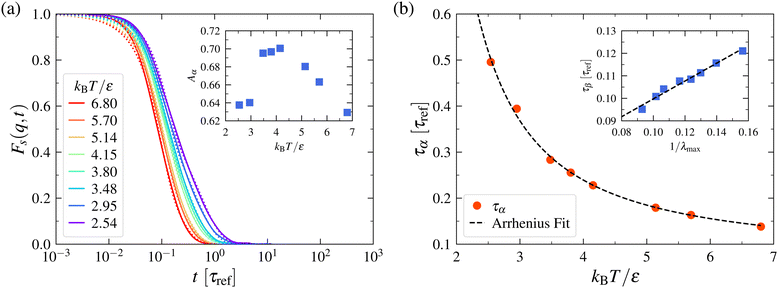 | ||
Fig. 9 (a) Self-intermediate scattering function Fs(q,t) for a range of T for the same model LJ fluid as indicated in Fig. 8 in the strongly chaotic high T fluid regime. Here, q = q* ≈ 7.0σ−1 is determined by the principal peak position of the static structure factor, a measure of the interparticle distance in the condensed state. Dashed lines indicate the relation, Fs(q,t) = (1 − Aα)exp[−(t/τβ)2] + Aα![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(t/τα)], where Aα, τβ, and τα are fitting parameters. The inset shows the amplitude Aα of the exponential relaxation as a function of T. The long time relaxation is approximated by an exponential relaxation, as expected for a strongly chaotic dynamic system, but Fs(q,t) is dominated by Gaussian relaxation at times shorter than the average collision time. The decay associated with chaotic motion occurs after a fast β-relaxation time τβ, which is a decorrelation time for the fast inertial dynamics, which scales inversely with λmax, while the long-time exponential relaxation time of the corresponding to the α-relaxation of GF liquids exhibits an Arrhenius T dependence, as expected from the Kramers theory.96,97 In cooled liquids, the exponents βf and βα for the Gaussian and exponential relaxation processes, respectively, become “stretched”, i.e., reduced in magnitude in comparison to their limiting values of 2 and 1 in the high T strongly stochastic regime.63 exp[−(t/τα)], where Aα, τβ, and τα are fitting parameters. The inset shows the amplitude Aα of the exponential relaxation as a function of T. The long time relaxation is approximated by an exponential relaxation, as expected for a strongly chaotic dynamic system, but Fs(q,t) is dominated by Gaussian relaxation at times shorter than the average collision time. The decay associated with chaotic motion occurs after a fast β-relaxation time τβ, which is a decorrelation time for the fast inertial dynamics, which scales inversely with λmax, while the long-time exponential relaxation time of the corresponding to the α-relaxation of GF liquids exhibits an Arrhenius T dependence, as expected from the Kramers theory.96,97 In cooled liquids, the exponents βf and βα for the Gaussian and exponential relaxation processes, respectively, become “stretched”, i.e., reduced in magnitude in comparison to their limiting values of 2 and 1 in the high T strongly stochastic regime.63 | ||
7 Conclusions
The long saga of trying to grip on the conditions over which statistical mechanical theories and stochastic models of liquid dynamics are applicable has led to a new appreciation of the complex non-linear dynamics in many-body dynamical systems under constant energy and equilibrium conditions where Hamiltonian dynamics may be taken as a reasonable model of real material systems. Progress in the study of prototypical model dynamical systems of this kind, such as the FUPT model, has led to a new appreciation of the role of non-linear excitations in understanding the timescale required for “equipartition of energy” in these systems that were sought in the pioneering studies of the FUPT model initiated over 80 years ago. The apparently generic nature of the relaxation process in other many-body dynamical systems that have been studied, and the observed similarity of the phenomenology of these idealized material models, have emboldened us to attempt to apply the same dynamical system framework to the description of relaxation in GF liquids. To achieve this extension, we had to find a readily measurable property of liquids and solids that is directly related to the fundamental “non-integrability” of dynamical system theory, the specific energy εs. After showing that this quantity is strongly correlated with the mean squared displacement of the particles in the condensed state at the readily measurable fast β-relaxation time τβ, 〈u2〉, we translate the well-known Nekhoroshev-type estimate of the relaxation time τα in terms of εs to an expression expressed in terms of the convenient liquid state variable 〈u2〉. Subsequent tests of this model to simulation data on polymeric and metallic GF liquids and the anharmonic superionic crystalline material UO2 indicated that this dynamical system estimate of 〈u2〉 is remarkably predictive and of general application to rather diverse materials. We take these observations as highly encouraging of the possible general validity of this type of dynamical system-based estimate of the relaxation time to diverse material systems. The model form of relaxation time that we find through our dynamical system analysis happens to conform to a phenomenological model already employed to model GF liquids, the Localization Model,137,138,143 so the present work provides a rationalization of the success of this model in disordered materials.We admit that our tests of the relaxation model are limited to metallic crystalline and glass-forming materials and coarse-grained polymeric glass-forming materials and that it is not clear if our formalism can be applied to describe relaxation in more complex materials. For example, we might consider applying the model to entangled polymer chains, given that molecular localization at larger scales of the chain (e.g., at the scale of a “tube”) can be made in a well-defined way.226 The idea of this extension is that the dynamical system might have a hierarchy of metastable states, and a succession of relaxation processes describing the relaxation of these states at larger length and time scales. Indeed, stress and dielectric relaxation measurements on polymer materials often exhibit multiple step-like decays corresponding to a succession of relaxation processes over a range of time and length scales so that this type of extension seems plausible. Benettin et al.102 have also argued that the Nekhoroshev-type estimate of relaxation times should depend on different relaxation modes within complex molecules, which is perhaps related to the observation that relaxation on the scale of chain segments of polymers is often reported to have a greatly different temperature dependence than relaxation on the scale of the chains, which is of importance in determining the viscosity and rate of molecular diffusion of polymer melts.227–232 We plan to consider the applicability of our model to more complex fluids having a hierarchy of “caging” scales in the future. Finally, we mention that successful coarse-grained models of polymer dynamics at elevated temperatures, such as the Rouse and reptation models, rely on phenomenological “friction coefficients” describing the glassy dynamics predominating the segmental scale dynamics, so even a limited description of the polymer segmental and normal model dynamics could be extremely useful in modeling the large-scale properties of polymer melts and solutions.
To gain a better understanding of the physical meaning of 〈u2〉 in relation to more conventional measures of the chaoticity of dynamical systems, we showed that this quantity is highly correlated with the maximum Lyapunov exponent of the dynamical system using a small Lennard-Jones simulation as the basis of this comparison. Evidently, 〈u2〉 can be understood as being a measure the inherent chaoticity of the molecular dynamics that has the advantage of often being readily measurable both in simulation and measurement. 〈u2〉 has the further advantage that it can be estimated locally in the material to make a map of local fluctuations in chaoticity and corresponding mobility.90,145,146,212,215 This feature is especially valuable in estimating local variations of relaxation times near the boundaries of materials in thin films, the interfacial region of nanoparticles, and in the interfacial regions of hydration in proteins and the interfacial region of polymer nanocomposites, to name a few applications. In the future, it would be interesting to explore if this measure of the rate of relaxation and mobility can be used to explore dynamical processes under non-equilibrium conditions in which 〈u2〉 evolves in time. The dynamical system approach to relaxation and estimating transport properties of condensed materials offers a new and practical approach for modeling the dynamics of weakly chaotic dynamical systems, for which simple stochastic models of dynamics simply do not apply. This approach also provides insight into the non-linear molecular dynamics-based mechanisms underlying relaxation, which ultimately dictate the achievement of conditions under which equilibrium thermodynamics apply.
As a final comment, we note the existence of fragmentary experimental and computational evidence indicating deviations from the predictions of Gibbs–Boltzmann equilibrium thermodynamics in glass-forming liquids for temperatures below the onset temperature TA, where the mean squared displacement of particles becomes overtly non-Gaussian and where relaxation and diffusion both start to deviate significantly from the Arrhenius behavior predicted by classical transition state theory. This is exactly the temperature range in which the Localization Model is applicable. Fischer233 and Torquato and coworkers234,235 have independently indicated, based both on experimental observations on diverse glass-forming liquids and simulated glass-forming liquids, respectively, that the general thermodynamic sum rule relating the structure factor S(q) at low q to the isothermal compressibility, thermal energy kBT and the material density ρ is violated at temperatures below TA. Taken at face value, these claims would imply that many experimental and theoretical studies that were previously assumed to be at “equilibrium” in the sense of Gibbs–Boltzmann are actually in some sort of metastable state instead. While such claims should not be accepted uncritically, the observations on which these conclusions were based certainly deserve further consideration because of the large potential implications for understanding the fundamental origin of the complex dynamics of glass-forming liquids in terms of generalized thermodynamics and corresponding dynamics appropriate for “weakly ergodic” systems.
Data availability
The data used to generate the figures in this manuscript are available at Open Science Framework at https://osf.io/arz6k/.Conflicts of interest
There are no conflicts to declare.Acknowledgements
W.-S. X. acknowledges the support from the National Natural Science Foundation of China (No. 22222307 and 21973089). J. R. Z. and H. Z. gratefully acknowledge the support of the Natural Sciences and Engineering Research Council of Canada under the Discovery Grant Program (RGPIN-2022-03661) and China Scholarship Council (No. 202006440033). This research used resources of the Network and Computing Center at Changchun Institute of Applied Chemistry, Chinese Academy of Sciences.References
- R. Clausius, London, Edinburgh Dublin Philos. Mag. J. Sci., 1857, 14, 108–127 CrossRef.
- R. Clausius, London, Edinburgh Dublin Philos. Mag. J. Sci., 1859, 17, 81–91 CrossRef.
- J. Maxwell, Philos. Trans. R. Soc. London, 1867, 157, 49–88 CrossRef.
- J. Jeans, An Introduction to the Kinetic Theory of Gases, Cambridge University Press, Cambridge Cambridgeshire, 2009, p. 311 Search PubMed.
- B. J. Alder, D. M. Gass and T. E. Wainwright, J. Chem. Phys., 1970, 53, 3813 CrossRef CAS.
- S. Chapman and T. Cowling, The Mathematical Theory of Nonuniform Gases, Cambridge University Press, London, 1939 Search PubMed.
- J. O. Hirschfelder, Molecular Theory of Gases and Liquids, Wiley, New York, 1954, p. 1219 Search PubMed.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon Press, Oxford, 1954, p. xii, 420 p Search PubMed.
- G. Venkataraman, L. A. Feldkamp and V. C. Sahni, Dynamics of Perfect Crystals, MIT Press, Cambridge, 1975, p. xv, 517 p Search PubMed.
- E. Kiely, R. Zwane, R. Fox, A. M. Reilly and S. Guerin, CrystEngComm, 2021, 23, 5697–5710 RSC.
- C. Sergio, R. Lamberto and V. Angelo, Commun. Theor. Phys., 2014, 62, 469–475 CrossRef.
- J. L. Lebowitz, Phys. A, 1993, 194, 1–27 CrossRef.
- J. L. Lebowitz, Phys. Today, 1993, 46, 32–38 CrossRef.
- X. Xu, J. F. Douglas and W.-S. Xu, Macromolecules, 2022, 55, 8699–8722 CrossRef CAS.
- J. F. Douglas and W.-S. Xu, Macromolecules, 2021, 54, 3247–3269 CrossRef CAS.
- P. Mazur and E. Montroll, J. Math. Phys., 1960, 1, 70–84 CrossRef.
- D. A. McQuarrie, Statistical Mechanics, Harper and Row, New York, 1976 Search PubMed.
- E. Broda, Ludwig Boltzmann: Man, Physicist, Philosopher, Ox Bow Press, 1983 Search PubMed.
- B. Gaveau and L. S. Schulman, Eur. Phys. J.: Spec. Top., 2015, 224, 891–904 Search PubMed.
- E. Fermi, J. Pasta and S. Ulam, E. Fermi: Note e Memorie (Collected Papers), Accademia Nazionale dei Lincei, Roma, and The University of Chicago Press, Chicago, 1965, vol. II, pp. 977–988 Search PubMed.
- E. Fermi, P. Pasta, S. Ulam and M. Tsingou, Studies of the Nonlinear Problems, Los Alamos National Laboratory, Los Alamos, New Mexico (United States) Report, 1955 Search PubMed.
- A. Carati, L. Galgani and A. Giorgilli, Chaos, 2005, 15, 015105 CrossRef CAS PubMed.
- J. Ford, Phys. Rep., 1992, 213, 271–310 CrossRef.
- M. Peyrard and J. Farago, Phys. A, 2000, 288, 199–217 CrossRef CAS.
- T. Cretegny, T. Dauxois, S. Ruffo and A. Torcini, Phys. D, 1998, 121, 109–126 CrossRef.
- D. K. Campbell, S. Flach and Y. S. Kivshar, Phys. Today, 2004, 57, 43–49 CrossRef CAS.
- S. Flach and G. Mutschke, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5018–5024 CrossRef PubMed.
- S. Flach and J. Siewert, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 14910–14922 CrossRef PubMed.
- M. Jenssen and W. Ebeling, Phys. D, 2000, 141, 117–132 CrossRef.
- C. Danieli, T. Mithun, Y. Kati, D. K. Campbell and S. Flach, Phys. Rev. E, 2019, 100, 032217 CrossRef CAS PubMed.
- T. Mithun, C. Danieli, M. V. Fistul, B. L. Altshuler and S. Flach, Phys. Rev. E, 2021, 104, 014218 CrossRef CAS PubMed.
- C. Danieli, D. K. Campbell and S. Flach, Phys. Rev. E, 2017, 95, 060202 CrossRef CAS PubMed.
- T. Mithun, C. Danieli, Y. Kati and S. Flach, Phys. Rev. Lett., 2019, 122, 054102 CrossRef CAS PubMed.
- T. Goldfriend and J. Kurchan, Phys. Rev. E, 2019, 99, 022146 CrossRef CAS PubMed.
- M. Toda, J. Phys. Soc. Jpn., 1967, 22, 431–436 CrossRef CAS.
- M. Toda, J. Phys. Soc. Jpn., 1967, 23, 501–506 CrossRef CAS.
- W. E. Ferguson, H. Flaschka and D. W. McLaughlin, J. Comput. Phys., 1982, 45, 157–209 CrossRef.
- T. Goldfriend, J. Stat. Phys., 2023, 190, 70 CrossRef.
- K. A. Reiss and D. K. Campbell, Entropy, 2023, 25, 300 CrossRef PubMed.
- M. Pettini, L. Casetti, M. Cerruti-Sola, R. Franzosi and E. G. D. Cohen, Chaos, 2005, 15, 015106 CrossRef PubMed.
- G. P. Berman and F. M. Izrailev, Chaos, 2005, 15, 015104 CrossRef CAS PubMed.
- N. J. Zabusky and M. D. Kruskal, Phys. Rev. Lett., 1965, 15, 240 CrossRef.
- N. J. Zabusky, Chaos, 2005, 15, 015102 CrossRef PubMed.
- Y. Hong, C. Kwak and C. Yang, Arch. Ration. Mech. Anal., 2021, 240, 1091–1145 CrossRef.
- A. Ponno, Europhys. Lett., 2003, 64, 606 CrossRef CAS.
- A. J. Sievers and S. Takeno, Phys. Rev. Lett., 1988, 61, 970–973 CrossRef CAS PubMed.
- S. Flach, K. Kladko and C. R. Willis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 2293–2303 CrossRef PubMed.
- G. P. Tsironis and S. Aubry, Phys. Rev. Lett., 1996, 77, 5225–5228 CrossRef CAS PubMed.
- R. Dusi, G. Viliani and M. Wagner, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 9809–9818 CrossRef CAS PubMed.
- L. Van Hove, Phys. Rev., 1954, 95, 249–262 CrossRef CAS.
- G. H. Vineyard, Phys. Rev., 1958, 110, 999–1010 CrossRef CAS.
- F. W. Starr, J. F. Douglas and S. Sastry, J. Chem. Phys., 2013, 138, 12A541 CrossRef PubMed.
- H. Zhang, C. Zhong, J. F. Douglas, X. D. Wang, Q. P. Cao, D. X. Zhang and J. Z. Jiang, J. Chem. Phys., 2015, 142, 164506 CrossRef PubMed.
- X. Y. Wang, W.-S. Xu, H. Zhang and J. F. Douglas, J. Chem. Phys., 2019, 151, 184503 CrossRef PubMed.
- Z. Zhang, C. Tang and P. Tong, Phys. Rev. E, 2016, 93, 022216 CrossRef PubMed.
- G. Benettin, H. Christodoulidi and A. Ponno, J. Stat. Phys., 2013, 152, 195–212 CrossRef.
- L. Berthier and G. Biroli, Rev. Mod. Phys., 2011, 83, 587–645 CrossRef CAS.
- W.-S. Xu, J. F. Douglas and Z.-Y. Sun, Macromolecules, 2021, 54, 3001–3033 CrossRef CAS.
- P. Gaspard and G. Nicolis, Phys. Rev. Lett., 1990, 65, 1693–1696 CrossRef PubMed.
- J. R. Dorfman and P. Gaspard, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 28–35 CrossRef CAS PubMed.
- P. Gaspard, Phys. A, 2006, 369, 201–246 CrossRef.
- B. A. P. Betancourt, F. W. Starr and J. F. Douglas, J. Chem. Phys., 2018, 148, 104508 CrossRef PubMed.
- A. Giuntoli, F. Puosi, D. Leporini, F. W. Starr and J. F. Douglas, Sci. Adv., 2020, 6, eaaz0777 CrossRef PubMed.
- N. S. Krylov, Works on the Foundations of Statistical Physics, Princeton University Press, Princeton, N.J., 1979, pp. xxviii, 283 p Search PubMed.
- N. Krylov, Nature, 1944, 153, 709–710 CrossRef CAS.
- M. Berry, A. Eades, D. Field, T. Poston, G. Reece, J. Ziman and J. Charap, Nature, 1980, 285, 186 CrossRef.
- I. Prigogine and I. Stengers, Order out of Chaos: Man's New Dialogue with Nature, Bantam Books, New York, 1984 Search PubMed.
- B. Misra, I. Prigogine and M. Courbage, Phys. A, 1979, 98, 1–26 CrossRef.
- B. Misra, I. Prigogine and M. Courbage, Proc. Natl. Acad. Sci. U. S. A., 1979, 76, 3607–3611 CrossRef CAS PubMed.
- B. Misra, Proc. Natl. Acad. Sci. U. S. A., 1978, 75, 1627–1631 CrossRef CAS PubMed.
- I. Aleksandr and A. Khinchin, Mathematical Foundations of Statistical Mechanics, Courier Corporation, 1949 Search PubMed.
- E. G. D. Cohen, Phys. A, 2002, 305, 19–26 CrossRef.
- M. Peyrard and A. R. Bishop, Phys. Rev. Lett., 1989, 62, 2755–2758 CrossRef CAS PubMed.
- T. Dauxois, M. Peyrard and A. R. Bishop, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 684–695 CrossRef CAS PubMed.
- H. J. Matsuyama and T. Konishi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022917 CrossRef PubMed.
- C. Danieli, D. K. Campbell and S. Flach, Phys. Rev. E, 2017, 95, 060202(R) CrossRef PubMed.
- R. Livi, A. Politi and S. Ruffo, J. Phys. A: Math. Gen., 1986, 19, 2033–2040 CrossRef.
- P. Bocchieri, A. Scotti, B. Bearzi and A. Loinger, Phys. Rev. A: At., Mol., Opt. Phys., 1970, 2, 2013 CrossRef.
- M. C. Carotta, C. Ferrario, G. L. Vecchio and L. Galgani, Phys. Rev. A: At., Mol., Opt. Phys., 1978, 17, 786–794 CrossRef.
- G. Benettin, G. L. Vecchio and A. Tenenbaum, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 1709–1719 CrossRef.
- R. Livi, M. Pettini, S. Ruffo and A. Vulpiani, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 2740–2742 CrossRef PubMed.
- M. Pettini and M. Cerrutisola, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 975–987 CrossRef PubMed.
- M. Pettini, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 828–850 CrossRef PubMed.
- R. Simonazzi and A. Tenenbaum, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 964–967 CrossRef CAS PubMed.
- M. Cerruti-Sola, M. Pettini and E. G. D. Cohen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 6078–6081 CrossRef CAS PubMed.
- L. Galgani and A. Scott, Phys. Rev. Lett., 1972, 28, 1173 CrossRef.
- L. Galgani and G. Benettin, Lett. Al Nuovo Cimento 1971-1985, 1982, 35, 93–96 Search PubMed.
- A. Carati and L. Galgani, Phys. A, 2000, 280, 106–114 CrossRef.
- A. Carati and L. Galgani, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 4791–4794 CrossRef CAS PubMed.
- X. Wang, H. Zhang and J. F. Douglas, J. Chem. Phys., 2021, 155, 204504 CrossRef CAS PubMed.
- D. Bambusi and A. Ponno, Commun. Math. Phys., 2006, 264, 539–561 CrossRef.
- G. Benettin, A. Carati, L. Galgani and A. Giorgilli, The Fermi-Pasta-Ulam Problem: A Status Report, Springer Berlin Heidelberg, Berlin, Heidelberg, 2008, pp. 151–189 Search PubMed.
- M. Peyrard, Acta Phys. Pol., B, 1994, 25, 955–992 CAS.
- G. E. Uhlenbeck and L. S. Ornstein, Phys. Rev., 1930, 36, 823–841 CrossRef CAS.
- S. Chandrasekhar, Rev. Mod. Phys., 1943, 15, 1–89 CrossRef.
- H. A. Kramers, Physica, 1940, 7, 284–304 CrossRef CAS.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- E. G. D. Cohen, Phys. A, 1993, 194, 229–257 CrossRef CAS.
- N. Saito, N. Ooyama, Y. Aizawa and H. Hirooka, Suppl. Prog. Theor. Phys., 1970, 45, 209–230 CrossRef.
- N. N. Nekhoroshev, Funct. Anal. Appl., 1971, 5, 338–339 CrossRef.
- K. Kaneko and T. Konishi, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 40, 6130–6133 CrossRef PubMed.
- G. Benettin, L. Galgani and A. Giorgilli, Nature, 1984, 311, 444–446 CrossRef CAS.
- S. Flach, K. Kladko and R. S. MacKay, Phys. Rev. Lett., 1997, 78, 1207–1210 CrossRef CAS.
- M. Pettini and M. Landolfi, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 768–783 CrossRef PubMed.
- D. Bambusi and N. N. Nekhoroshev, Phys. D, 1998, 122, 73–104 CrossRef.
- L. Berchialla, A. Giorgilli and S. Paleari, Phys. Lett. A, 2004, 321, 167–172 CrossRef CAS.
- G. Benettin and A. Ponno, J. Stat. Phys., 2011, 144, 793–812 CrossRef.
- A. Ponno, H. Christodoulidi, Ch Skokos and S. Flach, Chaos, 2011, 21, 043127 CrossRef CAS PubMed.
- G. Benettin, S. Pasquali and A. Ponno, J. Stat. Phys., 2018, 171, 521–542 CrossRef.
- M. Toda, Theory of Nonlinear Lattices, Springer, Berlin, Heidelberg, 1989, p. 225 Search PubMed.
- H. Flaschka, Phys. Rev. B: Solid State, 1974, 9, 1924–1925 CrossRef.
- M. Hénon, Phys. Rev. B: Solid State, 1974, 9, 1921–1923 CrossRef.
- G. Benettin, J. Fröhlich and A. Giorgilli, Commun. Math. Phys., 1988, 119, 95–108 CrossRef.
- A. Carati, A. Maiocchi, L. Galgani and G. Amati, Math. Phys. Anal. Geom., 2015, 18, 31 CrossRef.
- G. Mahmud, H. Zhang and J. F. Douglas, J. Chem. Phys., 2020, 153, 124508 CrossRef CAS PubMed.
- H. Zhang, X. Y. Wang and J. F. Douglas, J. Chem. Phys., 2019, 151, 071101 CrossRef PubMed.
- G. Mahmud, H. Zhang and J. F. Douglas, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 33 CrossRef CAS PubMed.
- M. I. Mendelev, M. J. Kramer, R. T. Ott, D. J. Sordelet, D. Yagodin and P. Popel, Philos. Mag., 2009, 89, 967–987 CrossRef CAS.
- Y. Zhang, R. Ashcraft, M. I. Mendelev, C. Z. Wang and K. F. Kelton, J. Chem. Phys., 2016, 145, 204505 CrossRef CAS PubMed.
- EAM Potentials: https://sites.google.com/site/eampotentials/Home/PdSi.
- S. M. Foiles, M. I. Baskes and M. S. Daw, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7983–7991 CrossRef CAS PubMed.
- Y. Mishin, M. J. Mehl, D. A. Papaconstantopoulos, A. F. Voter and J. D. Kress, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 224106 CrossRef.
- M. J. Qin, M. W. D. Cooper, E. Y. Kuo, M. J. D. Rushton, R. W. Grimes, G. R. Lumpkin and S. C. Middleburgh, J. Phys.: Condens. Matter, 2014, 26, 495401 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- Lammps Web Page: https://www.lammps.org, The present work utilized the version released on 12/12/2018.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- X. Xu, J. F. Douglas and W.-S. Xu, Macromolecules, 2023, 56, 4929–4951 CrossRef CAS.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- G. S. Grest and K. Kremer, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3628–3631 CrossRef CAS PubMed.
- H.-P. Hsu and K. Kremer, J. Chem. Phys., 2019, 150, 091101 CrossRef PubMed.
- W.-S. Xu, J. F. Douglas and X. Xu, Macromolecules, 2020, 53, 4796–4809 CrossRef CAS.
- W. Kob and H. C. Andersen, Phys. Rev. Lett., 1994, 73, 1376–1379 CrossRef CAS PubMed.
- W. Kob and H. C. Andersen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4626–4641 CrossRef CAS PubMed.
- S. Sastry, Phys. Rev. Lett., 1996, 76, 3738–3741 CrossRef CAS PubMed.
- J. F. Douglas, B. A. Pazmino Betancourt, X. Tong and H. Zhang, J. Stat. Mech.: Theory Exp., 2016, 2016, 054048 CrossRef.
- B. A. P. Betancourt, P. Z. Hanakata, F. W. Starr and J. F. Douglas, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2966–2971 CrossRef PubMed.
- C. De Michele, E. Del Gado and D. Leporini, Soft Matter, 2011, 7, 4025–4031 RSC.
- Z. Yang, X. Xu, J. F. Douglas and W.-S. Xu, J. Chem. Phys., 2024, 160, 044503 CrossRef CAS PubMed.
- Q.-L. Yuan, X. Xu, J. F. Douglas and W.-S. Xu, J. Phys. Chem. B, 2024, 128, 9889–9904 CrossRef CAS PubMed.
- Y.-C. Hu and H. Tanaka, Nat. Phys., 2022, 18, 669–677 Search PubMed.
- D. S. Simmons, M. T. Cicerone, Q. Zhong, M. Tyagi and J. F. Douglas, Soft Matter, 2012, 8, 11455–11461 RSC.
- J.-H. Hung, T. K. Patra, V. Meenakshisundaram, J. H. Mangalara and D. S. Simmons, Soft Matter, 2019, 15, 1223–1242 RSC.
- X. Zheng, Y. Guo, J. F. Douglas and W. Xia, J. Chem. Phys., 2022, 157, 064901 CrossRef CAS PubMed.
- X. Zheng, Y. Guo, J. F. Douglas and W. Xia, Macromolecules, 2022, 55, 9990–10004 CrossRef CAS.
- X. Zheng, W. Nie, Y. Guo, J. F. Douglas and W. Xia, Macromolecules, 2023, 56, 7636–7650 CrossRef CAS.
- R. Horstmann and M. Vogel, J. Chem. Phys., 2017, 147, 034505 CrossRef CAS PubMed.
- W. Luo, B. Johansson, O. Eriksson, S. Arapan, P. Souvatzis, M. I. Katsnelson and R. Ahuja, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9962–9964 CrossRef CAS PubMed.
- A. B. Belonoshko, T. Lukinov, J. Fu, J. Zhao, S. Davis and S. I. Simak, Nat. Geosci., 2017, 10, 312–316 CrossRef CAS.
- L. Vočadlo, D. Alfè, M. J. Gillan, I. G. Wood, J. P. Brodholt and G. D. Price, Nature, 2003, 424, 536–539 CrossRef PubMed.
- E. Schwegler, M. Sharma, F. Gygi and G. Galli, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 14779–14783 CrossRef CAS PubMed.
- M. Millot, S. Hamel, J. R. Rygg, P. M. Celliers, G. W. Collins, F. Coppari, D. E. Fratanduono, R. Jeanloz, D. C. Swift and J. H. Eggert, Nat. Phys., 2018, 14, 297–302 Search PubMed.
- C. Cavazzoni, G. L. Chiarotti, S. Scandolo, E. Tosatti, M. Bernasconi and M. Parrinello, Science, 1999, 283, 44–46 CrossRef CAS PubMed.
- J. Sun, B. K. Clark, S. Torquato and R. Car, Nat. Commun., 2015, 6, 8156 CrossRef CAS PubMed.
- H. Zhang, M. Khalkhali, Q. Liu and J. F. Douglas, J. Chem. Phys., 2013, 138, 12A538 CrossRef PubMed.
- F. W. Starr, S. Sastry, J. F. Douglas and S. C. Glotzer, Phys. Rev. Lett., 2002, 89, 125501 CrossRef PubMed.
- T. Q. McKenzie-Smith, J. F. Douglas and F. W. Starr, Phys. Rev. Lett., 2021, 127, 277802 CrossRef CAS PubMed.
- J. H. Mangalara and D. S. Simmons, ACS Macro Lett., 2015, 4, 1134–1138 CrossRef CAS PubMed.
- M. Adhikari, S. Karmakar and S. Sastry, J. Phys. Chem. B, 2021, 125, 10232–10239 CrossRef CAS PubMed.
- P. Das and S. Sastry, J. Non-Cryst. Solids: X, 2022, 14, 100098 CAS.
- W.-S. Xu, J. F. Douglas and K. F. Freed, Macromolecules, 2016, 49, 8355–8370 CrossRef CAS.
- W.-S. Xu, J. F. Douglas and K. F. Freed, Macromolecules, 2017, 50, 2585–2598 CrossRef CAS.
- H. Zhang, X. Wang, H. B. Yu and J. F. Douglas, J. Chem. Phys., 2021, 154, 084505 CrossRef CAS PubMed.
- H. Zhang and J. F. Douglas, Soft Matter, 2013, 9, 1254–1265 RSC.
- H. Zhang and J. F. Douglas, Soft Matter, 2013, 9, 1266–1280 RSC.
- G. Mahmud, H. Zhang and J. F. Douglas, J. Chem. Phys., 2022, 157, 114505 CrossRef CAS PubMed.
- H. Zhang, Y. Yang and J. F. Douglas, J. Chem. Phys., 2015, 142, 084704 CrossRef PubMed.
- X. Y. Wang, X. H. Tong, H. Zhang and J. F. Douglas, J. Chem. Phys., 2017, 147, 194508 CrossRef PubMed.
- E. J. Haddadian, H. Zhang, K. F. Freed and J. F. Douglas, Sci. Rep., 2017, 7, 41671 CrossRef CAS PubMed.
- T. Odagaki, Phys. Rev. Lett., 1995, 75, 3701–3704 CrossRef CAS PubMed.
- K. L. Ngai, J. Phys.: Condens. Matter, 2000, 12, 6437–6451 CrossRef CAS.
- K. L. Ngai, S. Capaccioli, M. Paluch and L. Wang, Philos. Mag., 2020, 100, 2596–2613 CrossRef CAS.
- G. Bel and E. Barkai, Phys. Rev. Lett., 2005, 94, 240602 CrossRef.
- A. Rebenshtok and E. Barkai, Phys. Rev. Lett., 2007, 99, 210601 CrossRef CAS PubMed.
- A. Bikaki, N. K. Voulgarakis, S. Aubry and G. P. Tsironis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 1234–1237 CrossRef CAS.
- G. Kalosakas, K. O. Rasmussen and A. R. Bishop, Chem. Phys. Lett., 2006, 432, 291–295 CrossRef CAS.
- J. F. Douglas, J. Phys.: Condens. Matter, 1999, 11, A329–A340 CrossRef CAS.
- J. F. Douglas and J. B. Hubbard, Macromolecules, 1991, 24, 3163–3177 CrossRef CAS.
- B. J. Berne, J. P. Boon and S. A. Rice, J. Chem. Phys., 1966, 45, 1086–1096 CrossRef CAS.
- R. Zwanzig, Theoretical Physics, Interscience, New York, 1961, vol. 3 Search PubMed.
- H. Zhang, X. Y. Wang, H. B. Yu and J. F. Douglas, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 56 CrossRef CAS PubMed.
- X. J. Wang, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 8407–8417 CrossRef PubMed.
- C. Anteneodo and C. Tsallis, Phys. Rev. Lett., 1998, 80, 5313–5316 CrossRef CAS.
- R. Salazar and R. Toral, Phys. Rev. Lett., 1999, 83, 4233–4236 CrossRef CAS.
- V. Latora, A. Rapisarda and C. Tsallis, Phys. A, 2002, 305, 129–136 CrossRef.
- B. J. C. Cabral and C. Tsallis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 065101 CrossRef PubMed.
- T. Mithun, Y. Kati, C. Danieli and S. Flach, Phys. Rev. Lett., 2018, 120, 184101 CrossRef CAS PubMed.
- C. Tsallis, E. P. Borges and F. Baldovin, Phys. A, 2002, 305, 1–18 CrossRef CAS.
- C. Tsallis, Phys. D, 2004, 193, 3–34 CrossRef.
- A. Carati, Phys. A, 2005, 348, 110–120 CrossRef.
- A. Carati, Phys. A, 2008, 387, 1491–1503 CrossRef.
- J. A. S. Lima and R. Silva, Phys. Lett. A, 2005, 338, 272–276 CrossRef CAS.
- E. M. Titulaer, Physica, 1973, 70, 257–275 CrossRef.
- M. Antoni, H. Hinrichsen and S. Ruffo, Chaos, Solitons Fractals, 2002, 13, 393–399 CrossRef.
- S. S. Apostolov, Z. A. Mayzelis, O. V. Usatenko and V. A. Yampol'skii, J. Phys. A: Math. Theor., 2009, 42, 095004 CrossRef.
- T. M. Rocha Filho, M. A. Amato, A. E. Santana, A. Figueiredo and J. R. Steiner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 032116 CrossRef CAS PubMed.
- F. Miceli, M. Baldovin and A. Vulpiani, Phys. Rev. E, 2019, 99, 042152 CrossRef CAS PubMed.
- F. Brouers and O. Sotolongo-Costa, Phys. A, 2005, 356, 359–374 CrossRef.
- A. K. Jonscher, Nature, 1977, 267, 673–679 CrossRef CAS.
- K. L. Ngai, A. K. Jonscher and C. T. White, Nature, 1979, 277, 185–189 CrossRef CAS.
- S. K. Nayak, R. Ramaswamy and C. Chakravarty, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 3376–3380 CrossRef CAS PubMed.
- S. K. Nayak, Mol. Phys., 1996, 89, 809–817 CAS.
- V. Mehra, S. K. Nayak and R. Ramaswamy, Pramana, 1997, 48, 603–615 CrossRef CAS.
- F. Calvo and P. Labastie, J. Phys. Chem. B, 1998, 102, 2051–2059 CrossRef CAS.
- S. K. Nayak, P. Jena, K. D. Ball and R. S. Berry, J. Chem. Phys., 1998, 108, 234–239 CrossRef CAS.
- P. Butera and G. Caravati, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 962–964 CrossRef PubMed.
- A. Mossa, M. Pettini and C. Clementi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 041805 CrossRef PubMed.
- M. Das and J. R. Green, Nat. Commun., 2019, 10, 2155 CrossRef PubMed.
- L. Caiani, L. Casetti, C. Clementi and M. Pettini, Phys. Rev. Lett., 1997, 79, 4361–4364 CrossRef CAS.
- G. Parisi and A. Vulpiani, J. Phys. A: Math. Gen., 1986, 19, L425 CrossRef.
- F. Puosi and D. Leporini, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 87 CrossRef CAS PubMed.
- F. Puosi and D. Leporini, J. Chem. Phys., 2012, 136, 041104 CrossRef CAS PubMed.
- S. Saw and P. Harrowell, Phys. Rev. Lett., 2016, 116, 137801 CrossRef PubMed.
- R. A. Riggleman, J. F. Douglas and J. J. de Pablo, Soft Matter, 2010, 6, 292–304 RSC.
- P. W. Cleary, J. Math. Phys., 1989, 30, 689–695 CrossRef.
- C. Amitrano and R. S. Berry, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 3158–3173 CrossRef CAS PubMed.
- M. Das, A. B. Costa and J. R. Green, Phys. Rev. E, 2017, 95, 022102 CrossRef PubMed.
- A. Alesadi and W. J. Xia, Macromolecules, 2020, 53, 2754–2763 CrossRef CAS.
- P. Allegrini, J. F. Douglas and S. C. Glotzer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 5714–5724 CrossRef CAS PubMed.
- Y. Liu and D. He, Phys. Rev. E, 2021, 103, L040203 CrossRef CAS PubMed.
- C. Dellago and H. A. Posch, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, R9–R12 CrossRef CAS.
- B. Wang, J. Kuo, S. C. Bae and S. Granick, Nat. Mater., 2012, 11, 481–485 CrossRef CAS PubMed.
- B. Wang, S. M. Anthony, S. C. Bae and S. Granick, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15160–15164 CrossRef CAS PubMed.
- F. Rusciano, R. Pastore and F. Greco, Phys. Rev. Lett., 2022, 128, 168001 CrossRef CAS PubMed.
- V. Sorichetti, A. Ninarello, J. Ruiz-Franco, V. Hugouvieux, E. Zaccarelli, C. Micheletti, W. Kob and L. Rovigatti, J. Chem. Phys., 2023, 158, 074905 CrossRef CAS PubMed.
- Y. Ding and A. P. Sokolov, Macromolecules, 2006, 39, 3322–3326 CrossRef CAS.
- D. J. Plazek, J. Phys. Chem., 1965, 69, 3480–3487 CrossRef CAS.
- D. J. Plazek and V. M. O'Rourke, J. Polym. Sci., Part A-2, 1971, 9, 209–243 CrossRef CAS.
- D. J. Plazek, Polym. J., 1980, 12, 43–53 CrossRef CAS.
- D. J. Plazek, J. Polym. Sci., Polym. Phys., 1982, 20, 729–742 CrossRef CAS.
- D. J. Plazek, I.-C. Chay, K. L. Ngai and C. M. Roland, Macromolecules, 1995, 28, 6432–6436 CrossRef CAS.
- E. W. Fischer, Phys. A, 1993, 201, 183–206 CrossRef CAS.
- É. Marcotte, F. H. Stillinger and S. Torquato, J. Chem. Phys., 2013, 138, 12A508 CrossRef PubMed.
- T. E. Gartner, S. Torquato, R. Car and P. G. Debenedetti, Nat. Commun., 2021, 12, 3398 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The fit parameters related to the specific energy and mean squared interparticle spacing and the relation between the non-ergodicity and Debye–Waller parameters. See DOI: https://doi.org/10.1039/d4sm00976b |
| This journal is © The Royal Society of Chemistry 2024 |