Mapping deformation dynamics to composition of topologically-active DNA blends

Abstract

Blends of circular and linear polymers have fascinated researchers for decades, and the role of topology on their stress response and dynamics remains fervently debated. While linear polymers adopt larger coil sizes and form stronger, more pervasive entanglements than their circular counterparts, threading of circular polymers by linear chains can introduce persistent constraints that dramatically decrease mobility, leading to emergent rheological properties in blends. However, the complex interplay between topology-dependent polymer overlap and threading propensity, along with the large amounts of material required to sample many compositions, has limited the ability to experimentally map stress response to composition with high resolution. Moreover, the role of supercoiling on the response of circular-linear blends remains poorly understood. Here, we leverage in situ enzymatic topological conversion to map the deformation dynamics of DNA blends with over 70 fractions of linear, ring and supercoiled molecules that span the phase space of possible topological compositions. We use OpTiDDM (optical tweezers integrating differential dynamic microscopy) to map strain-induced deformation dynamics to composition, revealing that strain-coupling, quantified by superdiffusive dynamics that are aligned with the strain, is maximized for blends with comparable fractions of ring and linear polymers. Increasing the supercoiled fraction dramatically reduces strain-coupling, while converting rings to linear chains offers more modest coupling reduction. We demonstrate that these results are a direct consequence of the interplay between increasing polymer overlap and decreasing threading probability as circular molecules are converted to linear chains, with a careful balance achieved for blends with ample ring fractions but devoid of supercoiled molecules.

---

Introduction

Blends of polymers of different topologies are widely used in industry to improve performance metrics such as miscibility and strength-to-weight ratios,^1–7 and are leveraged by many biological systems, such as the cell cytoplasm, to enable key mechanical processes.^8–13 The advantage of blends over single constituent systems is their expanded breadth of relaxation modes and timescales, as well as intrinsic length scales, allowing for broader dynamic range and enhanced tunability. Cells harness these features to perform numerous distinct processes that occur over decades of spatiotemporal scales.^14–17 Biology takes this advantageous design one step further by utilizing enzymes to alter the topologies and lengths of biopolymers, such as DNA, to enable a diversity of mechanical processes and state transitions that are dictated by the varying intra- and inter-polymer interactions.^18–22 At the same time, many industrial processes performed on blends may intentionally or unintentionally shear, break or otherwise alter the topologies comprising polymers.^23–27 Understanding how the time-varying alteration of blend composition alters the response dynamics of the polymers subject to stresses and strains, remains poorly understood.

Moreover, previous studies have shown that polymeric blends and composites exhibit scale-dependent mechanical properties and dynamics, with the bulk rheological response not directly mapping to the microscale relaxation dynamics;^28–33 as well as signatures of dynamic heterogeneities and glassiness.^34–37 For example, previous particle-tracking microrheology studies showed that the viscosity of solutions of overlapping circular double-stranded DNA steadily increased as the polymers were enzymatically linearized (i.e., both strands were cleaved at a single location).²⁰ This effect was shown to arise from increased polymer overlap due to the size of the random coil of a linear chain being substantially larger than that of a circular (ring or supercoiled) polymer of equal length. Namely, as the solution composition became a blend of increasing linear fraction, the degree of overlap and entanglements increased, restricting the polymer motion and increasing local viscosity. The rheological response at the bulk scale was shown to be highly distinct from the microscale, with the viscoelastic moduli exhibiting sharp transitions from fluid-like to elastic-like states, rather than steady increase,³⁷ which was shown to arise from cooperative clustering of entangled linear chains.³⁵ This cooperative clustering of the ‘slow’ population in the blend also gave rise to an unexpected decrease in ensemble-averaged DNA mobility as they were enzymatically fragmented into shorter constructs.²⁸

The scale-dependent dynamics of ring-linear blends are further complicated by the ability of ring polymers to become threaded by neighboring linear chains and, to a lesser extent, ring and supercoiled chains.^{1,5,31,35,36,38–41} In both solutions and melts, threading drastically slows the motion of the rings by essentially pinning them in place until the penetrating linear chains can diffuse out of the ring center and release their constraint. At high enough polymer concentrations and lengths, threading dominates the rheological and dynamical fingerprint of ring-linear blends, leading to an emergent increase in the elastic plateau modulus, viscosity, and relaxation timescales compared to their pure linear and ring counterparts over a range of blend compositions.^{29,36,38–40,42–44} Threading has also been suggested to lead ring-linear blends to exhibit more pronounced entropic stretching and shear-thinning in response to strain, increased heterogeneities in transport modes, slower diffusion, and more pronounced subdiffusion compared to pure solutions of linear or ring polymers.^{36,38–40,42,45,46} However, the exact dependence of these effects on the blend composition (i.e., the fraction of each topology) is a topic of debate due to the difficulty in preparing enough different blend compositions to comprehensively map the effect of composition onto dynamics. Moreover, while some of these emergent properties have been observed in both solutions and melts, such as increased viscosity and extended relaxation times,^40,46,47 other features, such as an extended rubbery regime,^29,48 have only been reported in solutions. These challenges are further complicated by the inherent scale-dependence and heterogeneity of these properties, rendering results from different measurement techniques that probe different scales difficult to couple.

Here, we leverage the enzymatic topological conversion of concentrated solutions of DNA to map the deformation dynamics of DNA solutions with dozens of fractions of linear, ring and supercoiled molecules that span the phase space of possible compositions. We use OpTiDDM (Optical Tweezers integrating Differential Dynamic Microscopy) to measure the polymer dynamics induced by local strains imposed by optically trapped probes; and elucidate how both the alignment of the DNA motion with the imposed strain, as well as the DNA transport properties, depend on composition and distance from the local strain. To determine the deformation dynamics with high resolution in composition and across a range of spatiotemporal scales, we perform measurements during the active cleaving of DNA by enzymes at multiple stoichiometries, to measure dynamics of blends with over 70 different compositions that range from purely circular, with ∼65% rings and ∼35% supercoiled, to purely linear chains of the same length.

Results

Design of topologically-active DNA solutions to span the composition space of blends of ring, supercoiled and linear polymers

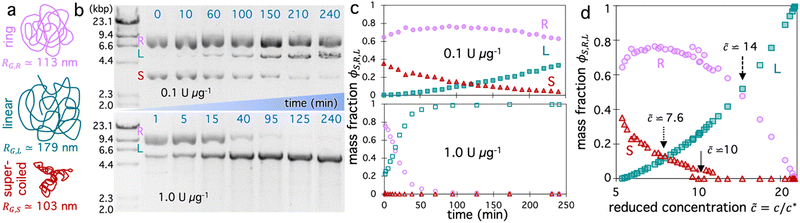
We aimed to design a system in which we could perform dozens of measurements over time that each capture a unique topological composition of a single sample, and could span the full range of possible blend compositions. To this end, we start with a solution of 5.9 kbp DNA (Fig. 1a) that comprises ∼65% relaxed circular (ring) and ∼35% supercoiled molecules at a total concentration of c = 6 mg mL⁻¹, corresponding to ∼5.3× above the overlap concentration of c* ≃ 1.14 mg mL⁻¹ for this specific topological composition (see Methods).^28,49

Fig. 1 Mapping the composition space of topological DNA blends. (a) Cartoon of different topologies of 5.9 kbp DNA comprising blends – ring (R), linear (L), and supercoiled (S) –color-coded and ordered as they appear in (b) and with their radius of gyration R_G listed. (b) Images of gel electrophoresis of blends of ∼65% ring and ∼35% supercoiled DNA with total mass concentration c = 6 mg mL⁻¹ undergoing linearization by BamHI at a BamHI:DNA stoichiometry of 0.1 U μg⁻¹ (top) or 1 U μg⁻¹ (bottom). Far-left lane is λ-HindIII molecular weight marker with the size of linear DNA corresponding to each band listed. Each subsequent lane shows the topological state of the DNA blend at a distinct time-point during linearization, listed in mins above the corresponding lane. Each band corresponds to a distinct topology (R, L, S) as labeled to the right of the marker, and the relative intensity of each band indicates its relative mass fraction ϕ_S,R,L = c_S,R,L/c. (c) Mass fraction of ring (purple circles), supercoiled (dark red triangles), and linear (teal squares) DNA as functions of digestion time, determined via gel electrophoresis band intensity analysis for 0.1 U μg⁻¹ (top, filled symbols) and 1 U μg⁻¹ (bottom, open symbols). (d) Data shown in (c), with both stoichiometries plotted together as a function of the reduced concentration c̃ = c/c*, which provides a measure of the degree of coil overlap for each unique blend composition defined by (ϕ_R, ϕ_S, ϕ_L). Arrows indicate key topological transitions with their c̃ values listed: linear fraction surpasses supercoiled fraction (dotted), supercoiled chains are eliminated (double solid), and linear fraction becomes the largest topological fraction (dashed).

To vary the blend composition, we introduce a single-site restriction endonuclease, BamHI, that cuts both strands of the DNA in a single location to convert both supercoiled and ring constructs to linear form (Fig. 1a and b).^49,50 By using a low stoichiometry of enzyme to DNA we allow digestion kinetics to be slow on the timescale of a single 50-s OpTiDDM measurement, so that the solution can be considered to be in quasi-steady-state,²⁰ and so a high composition resolution can be achieved (Fig. 1b and c). However, to capture the full range of blend compositions, i.e., allowing the enzyme to fully digest (linearize) all of the DNA, we need digestion kinetics to be fast enough to complete digestion before potentially deleterious photobleaching effects or enzymatic star activity occur (after ∼6 hours). Due to the exponential Michaelis–Menten digestion kinetics,²⁰ achieving complete digestion in a limited amount of time requires that the digestion rate is prohibitively high at early times to resolve closely spaced compositions and maintain the quasi-steady-state assumption (Fig. 1b). However, reducing the initial digestion rate to achieve this resolution prohibits reaching complete digestion in the limited time window. Therefore, to achieve these upper and lower bounds on kinetics, we perform measurements with two different stoichiometries that differ by 10-fold, 0.1 U μg⁻¹ and 1 U μg⁻¹. With these two stoichiometries, we are able to accurately capture the full range of compositions from initial to saturating (all linear) conditions while ensuring the quasi-steady-state assumption is valid over each 50-s experiment (Fig. 1a and b).

Fig. 1b shows the fraction of each topology over the course of 4 hours for each stoichiometry, determined from gel electrophoresis band intensity analysis (see Methods), showing thorough sampling of the full composition range. Because the radius of gyration of the DNA molecules are topology-dependent, with values of R_G,S ≃ 103 nm, R_G,R ≃ 113 nm, and R_G,L ≃ 179 nm for supercoiled, ring and linear topologies,^50–52 the coil overlap concentration c* = (3/4π)(M/N_A)R_G⁻³ varies in time as the fraction of each topology, ϕ_S,R,L = c_S,R,L/c, changes. Specifically, c* decreases as ring and supercoiled constructs are converted to linear topology, according to the expression c* = (3/4π)(M/N_A)/(ϕ_LR_G,L³ + ϕ_RR_G,R³ + ϕ_SR_G,S³),^20,41 such that the reduced concentration, c̃ = c/c*, which quantifies the degree of overlap, increases (Fig. 1c).

We expect the initial primarily circular blends (ϕ_L ≃ 0, c̃ ≃ 5) to be overlapping but not entangled due to the reduced concentration being below the nominal entanglement concentration c̃_e ≃ 6 (Fig. 1c).^20,53 Several studies have also suggested that circular polymers display weaker and less persistent intermolecular interactions compared to canonical linear chain entanglements.^35,54–56 Conversely, for the completely digested system, with c̃ ≃ 23, we expect the DNA to be classically entangled and their dynamics governed by entanglement tube confinement.^20,57 We focus our discussion in the following sections on the compositions that lie between these bounds, for which the dynamics are still poorly understood and expected to be much richer.

Strain-induced DNA dynamics display complex dependence on degree of coil overlap

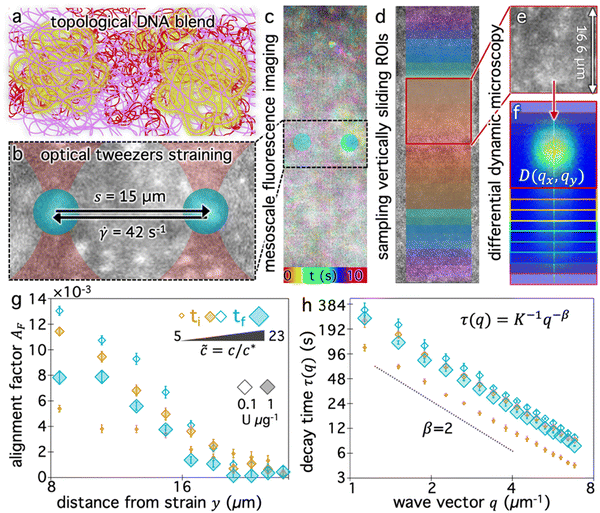
We now seek to determine how the blend composition impacts the ability of the surrounding molecules to couple their motion to a local strain, and how this coupling decays with distance from the strain. We use OpTiDDM⁴⁵ to cyclically sweep an optically trapped probe through the DNA solution and simultaneously image fluorescent-labeled DNA molecules in the solution in a field-of-view (FOV) that encompasses the horizontally aligned strain path (Fig. 2a and b) and extends 35 μm vertically above and below the strain path (Fig. 2c). We fix the strain distance (s = 15 μm) and rate ([small gamma, Greek, dot above] = 42 s⁻¹) to be large compared to the intrinsic lengthscales and timescales of the system and match previously used parameters that maximize the coupling in similar systems.^28,45 Specifically, the strain rate corresponds to Weissenberg numbers of Wi ≈ 11 and Wi ≈ 176 and Deborah numbers of De ≈ 0.8 and De ≈ 12.6 for c̃ ≃ 5 and c̃ ≃ 23, respectively (see Methods). We are thus well within the nonlinear regime and probing the viscoelastic response of the polymers. We expect the flow field induced by the probe to be primarily shear-dominated,^58,59 but also exhibit signatures of extensional flow.^42,60

Fig. 2 Spatially and temporally resolving the deformation dynamics of topologically-varying DNA blends using OpTiDDM. (a) Cartoon of initial blend of ∼65% ring (purple) and ∼35% supercoiled (dark red) DNA with a small fraction of labeled DNA indicated by yellow glow. (b) Cartoon of optical tweezers straining of DNA blends doped with fluorescent-labeled molecules (white features) to visualize deformation dynamics. A focused laser beam (red) moves an optically-trapped microsphere probe (blue) of radius r = 2.25 μm back and forth at a constant rate [small gamma, Greek, dot above] = 42 s⁻¹ over a strain distance s = 15 μm through the blend for a total time of 50 s per measurement, with a 3 s cessation period between each sweep. (c) During each strain, time-series of labeled molecules are collected within a 72 μm × 16.6 μm field-of-view, centered vertically on the strain path and enveloping the strain horizontally, as shown. The temporal color map shows the DNA motion during 3 consecutive sweeps (∼10 s) with colors corresponding to different times relative to the beginning of the first sweep. (d) The FOV is divided into 20 ROIs (translucent squares) of size (16.6 μm)² centered horizontally with the strain path and centered vertically at 10 ±distances from the strain path. Increasing ±y values follow a rainbow scale from y₀ = 8 μm (red) to y_f = 27 μm (magenta). (e) and (f) DDM analysis of individual ROIs (e) provides 2D image structure functions D(q_x, q_y) for each distance y. (g) and (h) OpTiDDM measurements are performed every ∼1–10 minutes from the beginning (t_i ⋍ 5 min, orange) to end of the digestion period (t_f = 240 min) for stoichiometries (U μg⁻¹) of 0.1 (open symbols) and 1 (translucent filled symbols). The symbol sizes denote the relative reduced concentrations c̃ at the beginning and end of each stoichiometric digestion period (see legend). (g) The alignment factor A_F, which quantifies the preferential alignment of DNA motion along the strain path, is determined by assessing the anisotropy of D(q_x, q_y) for a given distance y, and generally decreases with increasing y values. (h) The decay time τ(q), determined by azimuthal averaging and fitting of D(q_x, q_y, Δt), quantifies the type and rate of motion. τ(q) typically follows power-law scaling τ(q) = K⁻¹q^−β. Dashed line denotes β = 2 which is indicative of normal diffusive motion.

Fig. 2c qualitatively depicts the strain-induced deformation field for the starting composition (Fig. 2a), showing more pronounced motion near the strain and reduced motion further from the strain. We note that the signal-to-noise is low and single molecules are not easily resolved. This effect is a consequence of including a relatively high fraction of labeled molecules in solution to ensure ample statistics within small spatially resolved region-of-interests (ROIs), and is one of our motivations for using differential dynamic microscopy (DDM), rather than, e.g., particle-tracking or particle-image-velocimetry, to quantify DNA dynamics.

Specifically, we divide the FOV into (16 μm)² ROIs centered at 20 vertical positions from y₀ = 8 μm to y_f = 27 μm (Fig. 2d), and perform DDM on each ROI (Fig. 2e–h). As described in Methods, DDM converts a time-series into stacks of image differences which encode information about how correlated two images separated by a given lag time Δt are, which can be analyzed to extract dynamics.^16,61–63 In practice, DDM transforms image differences to Fourier space to compute image structure functions 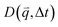(Fig. 2e and f) that quantify correlations in density fluctuations at a given spatial frequency, or wave vector 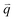, as a function of Δt (Fig. 2f). As described in the following sections, from 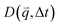we determine the (1) extent to which the direction of DNA motion aligns with the strain direction, which we quantify by the alignment factor A_F(y, c̃) (Fig. 2g), and (2) type and rate of DNA motion, which we quantify by analyzing the q-dependent DDM decay time τ(q, y, c̃) (Fig. 2h). Fig. 2g and h shows these metrics measured near the beginning and end of each stoichiometric digestion (0.1 and 1 U μg⁻¹), demonstrating that composition generally has a significant effect on the dynamics. We also observe that both metrics display a similar non-monotonic dependence on c̃, with the strongest alignment and longest decay time occurring at intermediate c̃ values. In the absence of topological conversion, one may expect these metrics to increase monotonically with c̃, insofar as stronger connectivity and increased steric hindrances are expected to slow motion (increasing τ) and enhance affine response to strain (increasing A_F). We investigate the functional form of these non-monotonic dependences and their underlying mechanisms in the remaining sections. We choose to characterize composition primarily by c̃ rather than the mass fraction of linearized molecules ϕ_L because c̃ accounts for the fraction of all three topologies in a single quantity. Conversely, a single ϕ_L value could correspond to multiple compositions with varying relative fractions of ring and supercoiled molecules, which we expect to have a marked effect on dynamics due to their differing sizes and propensities for threading.^28,64

Strain alignment and propagation are maximized at intermediate reduced concentrations

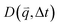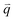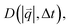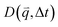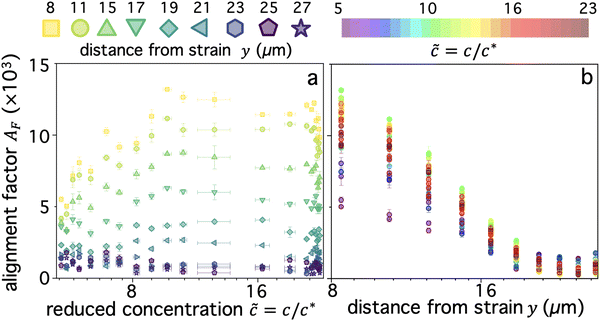
For isotropic motion, such as Brownian motion, is radially symmetric, and taking the azimuthal average over provides a 1D image structure function, that can be fit to models to determine the type and rate of motion.^16,62 However, for motion that has a preferred direction, is anisotropic, with higher correlations being weighted more heavily along the director axis,⁴⁵ a feature that we leverage to quantify the degree of alignment. Specifically, we compute the alignment factor A_F of the image structure function relative to the q_x-axis by computing weighted azimuthal integrals of D(q_x, q_y, Δt), i.e., integrals over θ where θ = tan⁻¹(q_y/q_x): 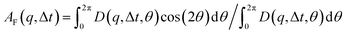(see Methods, Fig. 2g).^65,66A_F increases from 0 (for purely isotropic motion) as motion becomes more aligned along the strain direction (x-axis).⁴⁵ We find that A_F decays with increasing distance from the strain y for all compositions, as expected (Fig. 3a). However, the degree of alignment closest to the strain (y₀ = 8 μm), and the extent to which alignment persists as y increases, displays a non-monotonic dependence on composition (Fig. 2g and 3).

Fig. 3 Strain alignment of DNA motion decays with increasing distance from the strain and displays non-monotonic dependence on reduced concentration. (a) Alignment factor A_F as a function reduced concentration c̃ measured at 10 vertical distances from the strain, ranging from y₀ = 8 μm (yellow squares) to y_f = 27 μm (purple stars), as indicated in the legend. Vertical and horizontal error bars are standard error across replicates and consecutive measurements, respectively (see Methods), and data points are means across both. (b) Data shown in (a), plotted as a function of y for each sampled blend composition, characterized by a different c̃ denoted by a different color. The rainbow colorscale shows the range of sampled c̃ values from c̃_i ≈ 5 to c̃_f ≈ 23, with increasing values shown as progressively warmer tones. Data points and error bars represent the mean and standard error across replicates.

As shown in Fig. 3a, A_F(y₀) initially increases as c̃ increases from the initial value of c̃_i ≃ 5.4 until c̃ ≃ 10 where A_F reaches a maximum. As c̃ increases further, the alignment factor becomes largely independent of composition, with A_F values remaining substantially higher than that for c̃_i. This behavior persists until the highest c̃ values (c̃ ≳ 22), in which the solutions comprise nearly all linear chains (Fig. 1d), at which point we see a subsequent drop in A_F. This general non-monotonic dependence of c̃ on A_F holds for increasing y values until y ≃ 17 μm, at which point A_F becomes increasingly insensitive to composition, and is essentially statistically insignificant for y > 20 μm.

This effect can also be seen clearly in Fig. 3b which shows A_F as a function of y for different blend compositions, denoted by the rainbow colorscale. For y < 20 μm, the non-monotonic c̃ dependence is shown by the maximum and minimum values being green (c̃ ≃ 10) and purple (c̃_i ≈ 5) while the red tones that denote c̃ ≳ 17 reside between these extrema. Two other features that are apparent are: the decrease in composition dependence for y > 20 μm, seen as a much smaller spread in the data compared to y < 20 μm; and the enhanced y dependence for c̃ ≃ 10 compared to higher or lower values, with A_F dropping by a factor of ∼15 as y increases, versus ∼5 and ∼10 for c̃_i ≈ 5 and c̃_f ≈ 23.

These results suggest that interactions between linear and circular molecules, which are absent for c̃_i and c̃_f (Fig. 1d) provide more effective mechanisms for coupling to the strain compared to linear–linear and circular–circular interactions. As described in the Introduction, numerous previous studies have shown strong evidence of threading of rings by linear chains, which dramatically slows relaxation processes and enhances shear-thinning and viscosity. These features align with the enhanced stretching of threaded rings, as compared to entangled linear or ring polymers, reported by several studies.^5,40,45,60 Likewise, we can understand the increased strain alignment at intermediate c̃ values as arising from threaded rings being maximally stretched along the strain direction due to the rigid constraints imposed by the threading chains that strongly resist strain-induced flow. In other words, as the ring is pulled along the strain path, the constraints (threadings) pull against the strain, thereby entropically stretching the threaded ring in the strain direction. A similar effect can occur for entangled linear polymers that are constrained by entanglements from neighboring chains. However, these constraints are expected to be less persistent than threadings, relaxing via reptation versus constraint release, rendering the entropic stretching weaker. We note that due to the nonlinear nature of the straining, we expect convective constraint release (CCR) to play a role in the dynamics for all entangled systems, regardless of the degree of threading.^48,57 CCR, which reduces the local entanglement density, likely counteracts the propensity for chains to stretch along the strain direction, thereby dampening the strain-coupling we observe.

Collectively, this topological dependence on stretching is a plausible mechanism for the initial strong increase in alignment as c̃ increases from c̃_i ≃ 5.4 to c̃_max ≃ 10, followed by a modest decrease and greater spread as c̃ increases further to c̃_f ≃ 23. Namely, as the degree of overlap increases and supercoiled molecules are replaced with linear chains (Fig. 1d), the entanglement density increases substantially and threading events become more pervasive. However, further increases in the degree of overlap (beyond c̃_max ≃ 10), a result of rings being converted to linear chains, come at the cost of threading events, so serve to weaken alignment. It is important to note that if increased alignment was primarily a result of increased overlap/entanglement density, then A_F should increase monotonically with c̃. Instead, the non-monotonic dependence on c̃ is direct evidence of topological effects dictating the strength of strain coupling. This conjecture is further supported by the larger drop in alignment that only occurs at the very highest c̃ values (c̃ ≳ 22) where the solutions comprise nearly all linear chains (Fig. 1d and 3a).

Finally, we note that the region of composition space in which the degree of alignment is maximized is that in which the fraction of linear chains ϕ_L surpasses that of supercoiled molecules ϕ_S (Fig. 1d, c̃ > 7.6) but remains lower than the fraction of rings ϕ_R (c̃ < 14). We also note that the maximally aligned composition (c̃_max ≃ 10) occurs at the point at which supercoiled molecules are completely eliminated, at which point we expect that all molecules (rings and linear chains) likely participate in threading events.

Strain-induced superdiffusivity is facilitated by rings and maximized for ring-linear blends

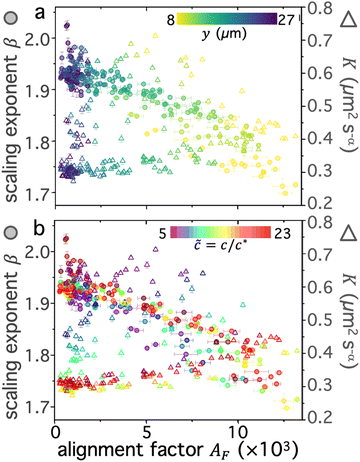
The data shown in Fig. 3 suggests that the strain induces athermal directed motion of the DNA, which is maximized at an intermediate overlap of c̃_max ≃ 10 and significant for distances out to y ≈ 20 μm. To shed light on the nature of this athermal motion and the extent to which the strain dynamics can fingerprint onto the DNA, we turn to analyzing the q-dependent decay time τ(q), as described above and in Methods (Fig. 2h). τ(q) typically displays power-law dependence on wave vector q, τ(q) = K⁻¹q^−β, where β = 2, 1 < β < 2 and β = 1 denote diffusive, superdiffusive and ballistic dynamics, respectively.^16,45,67 The larger τ(q) is for a given q, the slower the dynamics, which is quantified by the generalized transport coefficient K. Higher K values generally indicate faster motion; and for purely diffusive or ballistic motion, K respectively equates to the diffusion coefficient or speed.

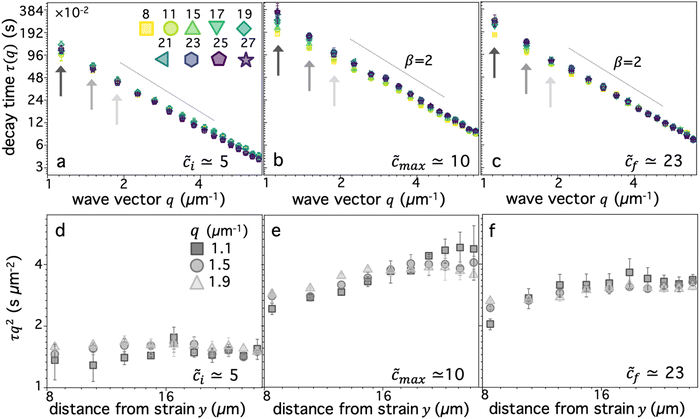
We first examine dynamics closest to the strain (y₀ = 8 μm), where we observe the most pronounced alignment (Fig. 4a and b). We find that τ(q) curves for all compositions obey power-law scaling that approximately aligns with diffusive behavior (β = 2). However, the magnitude of τ(q) is generally highest for c̃ ≈ 10–12 and lowest for c̃_i ≈ 5, following a similar non-monotonic trend as A_F. These features can be seen more clearly by examining the functional form of τq², which is a horizontal line for β = 2 and adopts increasingly positive slopes as β decreases to more superdiffusive exponents (Fig. 4b). The relative rate of motion can also be approximated as the inverse of τq². All compositions appear to display modest superdiffusivity over at least some region of q space, which appears to be most extreme for intermediate compositions. The mobility also markedly slows as c̃ increases from its initial value to c̃_max ≃ 10.

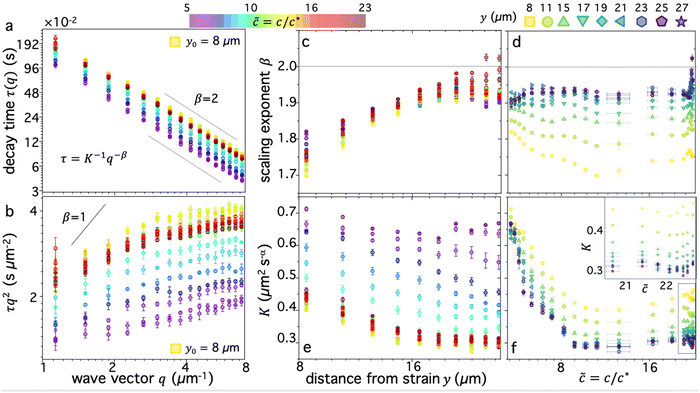Fig. 4 Digestion of supercoiled DNA enhances strain-coupled superdiffusivity while slowing transport. (a) DDM decay time τ(q) versus wave vector q, evaluated at y₀ = 8 μm, for varying blend compositions, characterized by c̃, represented as cool to warm colors for c̃_i ≃ 5 (purple) to c̃_f ≃ 23 (dark red). Green and yellow data points which are extremal for nearly all q values, correspond to c̃ ≈ 10. Dashed scaling bars denote diffusive (β = 2) scaling exponents associated with the expected power-law relation τ(q) = K⁻¹q^−β. (b) Data shown in (a) plotted as τq²versus q, which is independent of q for diffusive motion (β = 2) and displays an increasingly positive slope as motion becomes more superdiffusive, bounded above by ballistic scaling β = 1 (solid line). (c) and (d) Scaling exponent β versus (c) distance y and (d) blend composition c̃, determined from fitting τ(q) for each blend composition and distance to τ(q) = K⁻¹q^−β. Dashed horizontal line denotes diffusive scaling and data that falls below is superdiffusive. (e) and (f) Transport coefficient K versus (e) distance y and (f) blend composition c̃, determined from the same fits used for (c) and (d). K values are in units of μm² s^−α, where α = 2/β. Inset in (f) is zoom-in of high c̃ data enclosed in the main plot, showing increase in K when all circular DNA is digested (highest c̃). Note that lower scaling exponents β (more superdiffusive) generally correlate nonintuitively with lower transport coefficients K (slower motion). Colors, symbols and error bars are as in Fig. 3.

To quantitatively examine these features and determine the extent to which they persist for molecules that are increasingly farther from the strain, we fit the data for each composition and distance to τ(q) = K⁻¹q^−β and evaluate β and K as functions of y (Fig. 4c–f). We observe that for all compositions, β increases with increasing distance y, extending from superdiffusive values as low as β ≈ 1.7 at y₀ to diffusive scaling at the largest distance. Insofar as superdiffusivity can be taken as an indicator of strain-coupling, which adds a component of directed ballistic motion to the otherwise thermal diffusive motion of the DNA, this result is intuitive and corroborates our alignment factor analysis (Fig. 3). Moreover, β values display a similar non-monotonic dependence on composition, with c̃ ≈ 10 exhibiting the most pronounced superdiffusivity for nearly all y values, while c̃_i and c̃_f blends have higher (less superdiffusive) β values. Also mirroring the alignment factor analysis, we observe a significant uptick in β near c̃_f, where we expect blends to be nearly devoid of rings. This non-trivial composition dependence can also be seen clearly by examining β versus c̃ for the different distances (Fig. 4d), which display global minima at c̃_max ≈ 10 for distances out to y ≈ 20 μm, a feature that is most pronounced closest to the strain.

Perhaps less intuitive is the larger effect of composition on β at both small and large distances compared to intermediate y values, which can be seen by the larger spread in the data at the left and right edges (low and high y) of Fig. 4c compared to the middle values. Examination of Fig. 4d reveals that this large spread is due to distinct trends for close versus far distances. Namely, at small y values, the spread is due to the large decrease in β values as c̃ increases to ∼10, while for large distances this spread is from a larger increase in β values at the very highest c̃ values compared to the other distances. The spread in values extends to β > 2, indicative of subdiffusive motion, which has been reported for entangled linear DNA.⁴⁵ This finding suggests that even a small number of rings in the blend may be sufficient to enhance strain coupling, in accord with recent observations that a small fraction of rings in synthetic ring-linear blends substantially increases the melt viscosity.⁴⁶

To shed further light on these results, we also examine the dependence of transport coefficients K on c̃ and y (Fig. 4e and f). We observe similar non-monotonic dependence on c̃ as for the scaling exponents (Fig. 4c and d) and alignment factor (Fig. 3), with K decreasing substantially from c̃_i to c̃_max followed by a modest increase as c̃ increases to c̃_f (Fig. 4e and f). Also consistent with the trends of the other metrics, K generally decreases with increasing distance from the strain, and this decrease is more pronounced for higher c̃ values. Finally, at the highest c̃ values (c̃ > 21), we observe a more substantial uptick in K values, similar to the trends observed for β and A_F.

While the general trends are consistent across metrics, the relationship between K and β appears complex and perhaps counter to expectations. One may expect that increased superdiffusivity, manifested as lower β values (within the range 2 ≥ β ≥ 1), should result in generally faster motion, described by a higher transport coefficient K. This relation is indeed what we observe for the y dependence: β increases and K decreases with increasing y values (Fig. 4c and e). This dependence suggests that it is the strain-coupling that primarily dictates the expected inverse relationship, with molecules closer to the strain being more strongly stretched along the strain path, resulting in faster and more directed motion. This strain-coupling decays as we move further from the strain site. Conversely, the coupled dependence of K and β on c̃ displays an opposite trend, whereby increasing β values correlate with increasing K values. In other words, as motion becomes ostensibly more superdiffusive (strain-coupled) it actually appears to be slower, i.e., the rate of motion is smaller. This effect can be seen in Fig. 4c and e, where c̃ ≈ 10 blends have the lowest values of both β (Fig. 4c) and K (Fig. 4e) among the different compositions; and in Fig. 4d and f which shows that both values generally decrease from c̃_i to c̃_max, followed by a modest increase.

We conjecture that this positive correlation between β and K arises from the slowing of quiescent thermal relaxation modes due to threading events that likewise enhance strain-coupling. Stronger constraints lead to stronger strain-coupling, captured by increased alignment and superdiffusivity. However, they also more strongly suppress thermal motion, which contributes to the transport coefficient in a non-trivial way. When constraints are weaker and/or threading is limited, we expect faster thermal transport (higher K) but less strain-induced motion (higher β, lower A_F). Thus, for low c̃ we expect K and β to be generally high and to display the weakest dependence on y, as we see in Fig. 4c–e.

To quantitatively verify this effect, we estimate the diffusion coefficients for the lowest and highest concentration cases as the transport coefficients at the largest y distance, where β values are near 2 (diffusive) and we expect little effect of the strain on dynamics. The values for c̃ ≈ 5 and c̃ ≈ 23 blends are K ≃ 0.65 μm² s⁻¹ and K ≃ 0.3 μm² s⁻¹, respectively. Closest to the strain, these transport coefficients increase to K ≃ 0.7 μm² s^−1.1 and K ≃ 0.45 μm² s^−1.2. The ∼50% increase in K for c̃ ≈ 23 is significantly higher than the ∼8% increase for c̃ ≈ 5. We can therefore conclude that the correlated decrease in K and β for high c̃ compared to low c̃ blends is a result of, respectively, suppressed diffusion and increased strain-coupling.

Moreover, the speed of the moving probe is v = 45 μm s⁻¹ and the strain distance is s = 15 μm, so the resulting Peclet numbers are Pe ≈ vs/D ≈ 10³. As such, if the polymers were completely coupled to the strain, then thermal motion would indeed be negligible. However, the extent to which the polymers couple to the strain depends on the degree to which the polymers are sterically constrained (e.g., entangled, threaded) and the extent to which CCR reduces the density of constraints. For less entangled blends, the coupling is weaker, so thermal motion contributes more to the dynamics on the timescale of the strain.

Transport deviates more strongly from diffusive behavior at larger lengthscales and for blends without supercoiled molecules

In the previous section, we approximated all τ(q) curves as obeying a simple power-law with a single q-independent scaling exponent β. However, closer inspection of τ(q) for varying distances reveals deviations from a single scaling law at small q values (q < 2 μm⁻¹), which are more pronounced closer to the strain (Fig. 5a–c). This weaker scaling, indicative of more pronounced superdiffusivity, suggests that strain-coupling is more pronounced for larger lengthscale dynamics, i.e., at scales λ = 2πq⁻¹ > 3 μm. This effect may indicate the necessity for many molecules to be sterically interacting, via entanglements/constraints, for dynamics to effectively couple to the strain, which we expect to only occur at scales several times larger than the polymer coil sizes, .⁵⁷

Fig. 5 Transport displays increased distance dependence at larger lengthscales which is maximized at intermediate reduced concentration. (a)–(c) DDM decay time τ(q) versus wave vector q for varying distances y (listed in μm in legend in (a)), evaluated for blend compositions of (a) c̃_i ≃ 5, (b) c̃_max ≃ 10, and (c) c̃_f ≃ 23. (d)–(f) Data indicated by grey arrows in (a)–(c) plotted as τq²versus y, according to the legend shown in (d). All blends display modest increase in τq² values (slower transport) with increasing distance, with the most pronounced and weakest slowing observed for c̃_max ≃ 10 (e) and c̃_i ≃ 5 (d), respectively. These trends are coupled with, respectively, the overall slowest and fastest transport (highest and lowest τq² values).

We also find that the deviation towards enhanced superdiffusivity is most pronounced for c̃_max ≃ 10 (Fig. 5b) and weakest for c̃_i ≃ 5 (Fig. 5a). This result is coupled with the slowest and fastest transport, respectively, which can be seen by examining τq² for the three smallest q values (Fig. 5d–f), where lower/higher values indicate faster/slower transport. These data also clearly show that the maximally strain-coupled composition (c̃_max ≃ 10) is also the one with the largest dependence of mobility on distance from the strain site. Namely, τq² displays the largest increase with increasing y, signifying the strongest strain-coupling; and this dependence is strongest for the smallest q value. This result corroborates the physical picture that strain-coupling is a many-polymer phenomena that requires numerous constraints and interactions to effectively propagate stress.

Entropic stretching and superdiffusive dynamics are linked effects that drive coupling of DNA dynamics to the strain

The results described in the previous sections suggest a direct linkage between alignment and superdiffusivity, which are both reporters of strain-coupling, while transport coefficients are sensitive to both strain-induced directed motion and quiescent thermal fluctuations. Moreover, the non-monotonic dependence of these metrics on blend composition demonstrates that DNA blends with comparable ring and linear topologies and devoid of supercoiled constructs, occurring at reduced concentrations of c̃ ≈ 10–12, exhibit emergent strain-coupling due to pervasive threading events. The dynamics of blends with lower c̃ values, which have non-zero fractions of supercoiled constructs, are highly sensitive to variations in c̃, with metrics substantially increasing (A_F) or decreasing (β, K) with increasing c̃. Because supercoiled molecules are not expected to participate in threading events,^20,28,64 this result corroborates the importance of threading in strain-coupling. The sensitivity is likely amplified by the increasing overlap as smaller supercoiled molecules are replaced with larger linear ones, increasing the entanglement density.

For concentrations above c̃ ≃ 10, the dependence on c̃ is much weaker due to competing effects of increasing overlap and entanglements and reducing threading probability. The latter appears to dominate the strain-coupling, resulting in metrics generally decreasing (A_F) or increasing (β, K) for c̃ > 10. Again, highlighting the importance of threading, we observe a greater change in all metrics (A_F, β, K) for c̃ ≳ 22 blends, which have immeasurably low ring content, compared to 10 ≲ c̃ < 22 blends that maintain a measurable fraction of rings. To summarize and more closely examine the correlations between the different metrics and their dependence on blend composition and distance, we evaluate pairings of scaling exponents and transport coefficients with their corresponding alignment factor for all distances (Fig. 6a) and compositions (Fig. 6b).

Fig. 6 Superdiffusivity is strongly coupled to alignment while the rate of transport is maximized at intermediate alignment values. Scaling exponents β (left axis, translucent circles) and transport coefficients K (right axis, open triangles) plotted as functions of alignment factor A_F for all blend compositions and vertical distances. Data points are colorized by (a) vertical distance y or (b) blend composition c̃ according to the corresponding colorscales.

As shown in Fig. 6a, the scaling exponent and alignment factor are generally inversely correlated for all distances, with the highest β and lowest A_F values occurring at the largest distance y_f = 27 μm and the lowest/highest β/A_F occurring at y₀ = 8 μm. This relation is consistent with the results discussed above. Conversely, K does not appear to be strongly correlated with alignment, but rather exhibits a large spread in values with the highest ones occurring at intermediate alignment.

To understand these results, we examine the dependence of c̃ on correlations between these metrics (Fig. 6b). We find that the large spread in K values at intermediate alignment factors (Fig. 6a) appears to be a signature of low c̃ blends (blue and purple triangles) that are weakly constrained and exhibit the weakest strain-coupling. These compositions likewise generally display higher (less subdiffusive) scaling exponents compared to higher c̃ blends. This behavior is distinct from that for blends with c̃ ≳ 10, in which the transport coefficients generally increase and scaling exponents β decrease with increasing alignment. Additionally, we note that while all c̃ ≳ 10 blends display similar correlations of metrics, c̃_max ≈ 10 blends have lower values of β and K values than for blends with c̃ ≳ 15 across the full range of measured alignment factors. Finally, we find that the large cluster of data points that exhibit diffusive (β ≈ 2), isotropic (A_F ≈ 0) motion, which occurs at the largest y values (Fig. 6a), are predominantly from the highest c̃ blends (dark red tones), which are comprised of primarily linear chains. This effect further corroborates our interpretation that the presence of rings, at even a very small fraction, substantially enhance long-range stress propagation and entropic stretching, in line with bulk rheology observations of even low fractions of rings enhancing viscosity of ring-linear blends.⁴⁶

Conclusions

Topological polymer blends exhibit fascinating emergent properties that continue to be a topic of great interest and debate. The roles that threading of circular polymers by linear chains and other neighboring rings,^{34,36,38,43,44,60} and steric entanglements between and among circular and linear polymers,^31,46,54,68 play in the emergent properties remain poorly understand. The extent to which supercoiling alters these roles has also been scarcely studied.^41,64,69 Here, we shed important new light on these open questions by measuring the spatially resolved mechanical response of circular-linear DNA blends with high compositional resolution. We leverage time-controlled enzymatic linearization of circular and supercoiled DNA to resolve over 70 different topological compositions, which we delineate by a unique single quantity, the reduced concentration c̃, that captures the relative fractions of all three topologies: ring, supercoiled and linear.

We visualize the dynamics of DNA comprising blends in response to local strains, and quantify the extent to which the strain fingerprints onto the DNA dynamics. We identify this coupling as deviations from isotropic Brownian motion, which manifest in our analysis as alignment of DNA motion along the strain path, superdiffusivity, and substantial dependence of metrics on the distance from the strain path. We observe robust non-monotonic dependences of all strain-coupling metrics on blend composition, which show extrema at c̃ ≈ 10, which comprises ϕ_R ≈ 68%, ϕ_L ≈ 32%, and ϕ_S ≈ 0. We rationalize this emergent behavior as arising from increased constraints imposed by threadings that facilitate entropic stretching of circular polymers along the strain path.^5,43,60,70 Our findings reveal intriguing new information regarding the optimization of topological blend composition for specific performance metrics; and have important implications in the design of materials that can couple efficiently to manufacturing processes via ample stretching and distribution of imposed stresses.

Methods

DNA preparation

We prepare solutions of double-stranded circular DNA of length 5.9 kbp (1.97 μm, N = 19.6) via replication of pYES2 plasmid constructs in Escherichia coli, alkaline lysis, and purification, following well-established protocols described previously.⁴⁹ Following purification, we resuspend the DNA in nanopure deionized water and concentrate the solution using vacuum rotary evaporation to achieve a mass concentration of c ≃ 12 mg mL⁻¹. Immediately following replication, the solution comprises purely supercoiled molecules (ϕ_S ≃ 1), but the subsequent purification process introduces nicks into a fraction of the supercoiled constructs, which allow the supercoils to unwind, resulting in relaxed circular (ring) topology. As such, the resulting DNA solution is a topological blend of ∼65% relaxed circular (ring) (ϕ_R ≃ 0.65), ∼35% supercoiled (ϕ_S ≃ 0.35), and ∼0% linear (ϕ_L ≃ 0) molecules (Fig. 1b and c). We quantify c and topological mass fraction ϕ_R,S,Lvia gel electrophoresis and band intensity analysis using Life Technologies E-Gel Imager and Gel Quant Express software.²⁰

For all measurements, we dilute the stock DNA solution to c ≃ 6 mg mL⁻¹ to match concentrations used in previous works^20,28,45 and achieve sufficient degree of polymer coil overlap (Fig. 1d). To determine the degree of overlap we compute the coil overlap concentration by modifying the expression for the overlap concentration for monodisperse polymer solutions, c* = (3/4π)(M/N_A)R_G⁻³ where M is the DNA molecular weight, to account for the different coil sizes of the different topologies: c* = (3/4π)(M/N_A)/(ϕ_LR_G,L³ + ϕ_RR_G,R³ + ϕ_SR_G,S³).^20,41 Using previously reported radius of gyration values of R_G,S ≃ 103 nm, R_G,R ≃ 113 nm and R_G,L ≃ 179 nm for ring, supercoiled and linear topologies (Fig. 1a),^20,50,52 we determine an initial overlap concentration of 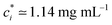. The initial reduced concentration 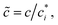which provides a measure of the degree of polymer overlap, is c̃_i ≈ 5.3.

At this initial concentration, we do not expect the DNA to be entangled, since it is below the nominal entanglement concentration c̃_i ≈ 6.^20,53 The longest relaxation timescale in this semidilute unentangled regime is the Rouse time, which we compute to be τ_R ≈ 2NR_G²/πD₀ ≈ 261 ms, where N = 19.6 and D₀ ≃ 1.53 μm² s⁻¹ is the tracer diffusion coefficient.^50,57 At the highest concentration of c̃_i ≈ 23, in which the polymers are well entangled, the longest relaxation timescale is the disengagement time, which we compute to be τ_D ≈ 3Zτ_R ≈ 4.2 s, where Z ≃ (c/c_e)^5/4 ≃ 5 is the entanglement density.^57,71

To image the blends during measurements, we fluorescent-label a small batch of the purified DNA with covalent dye MFP488 (MirusBio) that has excitation/emission peaks at 501/523 nm. We use the manufacturer-supplied Label IT Labeling Kit and corresponding protocols to label molecules at a dye to basepair ratio of 1:5.

Restriction endonuclease

We use the high-fidelity restriction endonuclease BamHI (New England BioLabs) to linearize circular DNA in solution. BamHI cleaves circular pYES2 constructs at a single recognition site, converting each ring and supercoiled molecule to linear topology. To ensure that we can achieve sufficient sampling across the entire composition space (from purely circular to purely linear), we perform measurements with two different BamHI:DNA stoichiometries: 0.1 U μg⁻¹ and 1 U μg⁻¹ (Fig. 1b and c).

Gel electrophoresis

To characterize the topological state of DNA solutions during linearization of circular DNA via BamHI, we use direct current agarose gel electrophoresis to separate the different topologies. Specifically, we prepare 40 μL samples of c ≃ 6 mg mL⁻¹ DNA, 0.1% Tween, and either 0.1 U μg⁻¹ or 1 U μg⁻¹ BamHI, suspended in CutSmart Buffer (0.5 M potassium acetate, 0.2 M Tris–acetate, 0.1 M magnesium acetate; New England BioLabs), We incubate the samples at RT for 240 min, during which we remove a 1 μL aliquot from each reaction in regular intervals and quench the aliquot with TE buffer (100 mM Tris–HCl (pH 8), 1 mM EDTA) and gel loading dye. We load 50 ng of DNA from each ‘kinetic aliquot’ onto a 1% agarose gel prepared with TAE (Tris–acetate–EDTA) buffer.^20,37 We run the gel at 5 V cm⁻¹ for 2.5 hours, allowing for separation of the DNA into distinct bands corresponding to ring, supercoiled, and linear topologies (Fig. 1b). To quantify the fraction of each topology at each interval, we perform standard band intensity analysis as described above,²⁰ using intensity as a proxy for mass to determine the relative DNA mass in each band of a given lane.

Sample preparation

For all optical tweezers experiments, we prepare samples as described above, and add 10 μg mL⁻¹ of MFP488-labeled DNA and a trace amount of polystyrene beads of radius r = 2.25 μm (Polysciences, Inc.) (Fig. 2a and b). We coat beads with AlexaFluor594-BSA (ThermoFisher) to prevent DNA adsorption and allow for fluorescence imaging with different excitation/emission spectra than for DNA. Labeling beads and DNA tracers with spectrally distinct fluorophores ensures that the beads do not contribute to the DNA signal used in DDM analysis. To mitigate photobleaching, we add an oxygen-scavenging system comprising 45 μg mL⁻¹ glucose, 43 μg mL⁻¹ glucose oxidase, 7 μg mL⁻¹ catalase, and 5 μg mL⁻¹ β-mercaptoethanol.

We mix the solution by pipetting up and down with a wide-bore pipet tip, and add BamHI last, marking the time at which it is added as t = 0. The buffer conditions and temperature (20 °C) provide good solvent conditions for the DNA.^71–75 We construct sample chambers, measuring 20 × 3 × 0.1 mm³, using a microscope glass slide and coverslip, both coated with BSA to prevent DNA adsorption, and separated by two layers of double-sided tape. We introduce DNA samples into chambers via capillary action, using a wide-bore pipette tip, after which we seal chambers with epoxy.

OpTiDDM instrumentation and measurements

We use a custom-built optical trap formed from a 1064 nm Nd:YAG fiber laser (Manlight) focused with a 60× 1.4 NA objective (Olympus) and integrated into an Olympus IX71 epifluorescence microscope, as described previously.^58,59 To image the MPF488-labeled DNA and AlexaFluor594-labeled microspheres in the samples we use 490/525 nm and 530/575 nm excitation/emission filter cubes and an ORCA-Flash 4.0 LT+ CMOS camera (Hamamatsu). To impose a local strain in the sample, we use a piezoelectric actuator mirror (PI USA) to move the trap relative to the sample chamber while keeping the 554 × 128 square-pixel (16.6 μm × 72 μm) field-of-view (FOV) that we use for DDM analysis fixed and centered at the resting trap position.⁴⁵

As shown in Fig. 2b, the microrheological strain program we apply consists of repeatedly sweeping the trapped bead back and forth horizontally (along the x-axis) at constant speed through a strain distance s = 15 μm. We pause between each 15 μm sweep for a fixed cessation time of 3 s to allow the polymers to relax. We perform all measurements at a speed of v = 40 μm s⁻¹, which equates to a strain rate of [small gamma, Greek, dot above] = 42 s⁻¹via the relation 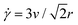.^45,76 We chose this speed based on our previous work that showed that this rate allowed for the most pronounced strain coupling in comparable DNA solutions.⁴⁵ For reference, the corresponding Weissenberg numbers for the initial and final concentrations (c̃_i ≈ 5, c̃_i ≈ 23) are Wi ≈ [small gamma, Greek, dot above]τ_R ≈ 11 and Wi ≈ [small gamma, Greek, dot above]τ_D ≈ 176. Considering that the time for the probe to complete one 15 μm strain is t_p = 0.33 s, the corresponding Deborah numbers for these two extremal concentrations are De = τ_R/t_p ≈ 0.8 and De = τ_D/t_p ≈ 12.6. Therefore, we expect to be in the nonlinear regime and to be probing the viscoelastic response of the polymers.

We perform each oscillatory strain measurement for 50 s, during which we capture a time-series of images of the labeled DNA in the sample at 60 fps (Fig. 2b–e). We perform measurements every ∼1–10 min, depending on the digestion rate, for 4 hours, resulting in >80 measurements that are each performed with a new particle in a new location in the sample chamber, separated by >200 μm from the previous location. All data shown is the average across at least two replicates and three consecutive measurements. Vertical and horizontal error bars are standard error from averaging across replicates and consecutive measurements, respectively.

Differential dynamic microscopy (DDM)

As previously described in detail,⁴⁵ to determine how the strain-induced DNA dynamics depend on the orthogonal distance y from the strain path, we divide the 554 × 128 square-pixel FOV into 128 × 128 square-pixel (16.6 μm)² ROIs, centered horizontally at the midpoint of the s = 15 μm strain path and shifted along the ±y direction in 16-pixel increments, with the bottom edge of the first ROI at y = 0 (and its center at y₀ = 8 μm) and the farthest ROI centered at y_f = 27 μm. We analyze 10 ROIs in each of the +y and −y directions and average the ± data for each y, as they exhibit expectedly statistically indistinguishable dynamics.

We use custom-written scripts (Python) to perform DDM analysis, which takes two-dimensional Fourier transforms of differences between images, separated by a range of lag times Δt, to quantify how the correlation of density fluctuations decays with Δt.⁶⁷ We quantify this correlation as a function of the 2D wave vector q⃑ = (q_x, q_y) via the image structure function D(q⃑, Δt) (Fig. 2e and f).

To determine the extent to which the DNA dynamics are preferentially aligned along the strain path (x-axis) (Fig. 2 and 3), we compute an alignment factor A_F with respect to the strain path (x-axis) by computing weighted azimuthal integrals of D(q_x, q_y, Δt), i.e., integrals over θ where θ = tan⁻¹(q_y/q_x): 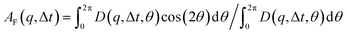(Fig. 2g).^65,66 Here, θ is defined relative to the x-axis such that isotropic and completely x-aligned dynamics correspond to A_F = 0 and A_F = A(q)/(A(q) + 2B(q)), respectively, where A(q) and B(q) are amplitude and background terms that we determine from DDM analysis, as described below. Larger A_F values indicate more alignment. To obtain a single A_F value for each distance y, we average over Δt = 0.17–1 s and q = 1–7 μm⁻¹, where there is no statistically significant dependence of A_F on these parameters.

To determine the type and rate of motion of the DNA, we radially average each D(q⃑, Δt) (Fig. 2f) to get a 1D image structure function that can be described by D(q, Δt) = A(q)[1 − f(q, Δt)] + B(q), where f(q, Δt) is the intermediate scattering function (ISF). We model the ISF as a stretched exponential: f(q, Δt) = e^{−(Δt/τ(q))δ} where τ(q) is the decay time and δ the stretching exponent.

By evaluating the functional form of τ(q) determined from fitting the ISF, we analyze the extent to which τ(q) can be described by power-law scaling τ(q) ∼ q^−β where the scaling exponent β describes the type of motion (Fig. 2h, 4 and 5). Specifically, β = 2 and β = 1 are indicative of diffusive and ballistic motion, respectively, and 1 < β < 2 indicates superdiffusion.^16,77,78

Author contributions

RMRA conceived the project, guided the experiments, interpreted the data, wrote the manuscript and prepared figures. KRP performed the experiments, analyzed and interpreted the data, and prepared figures. RJM developed analysis software and helped guide experiments and analysis and write the manuscript.

Data availability

All data shown in the manuscript is provided in ESI.† Raw data from which the presented data was determined will be made available upon reasonable request to the corresponding author.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This research was funded by grants from the Air Force Office of Scientific Research (AFOSR-FA9550-17-1-0249, AFOSR-FA9550-21-1-0361) and National Science Foundation (DMREF DMR 2119663) awarded to RMRA, and National Institutes of Health (R15GM123420, 2R15GM123420-02) awarded to RJM and RMRA.

References

1. G. S. Grest, T. Ge, S. J. Plimpton, M. Rubinstein and T. C. O’Connor, Entropic Mixing of Ring/Linear Polymer Blends, ACS Polym. Au, 2023, 3(2), 209–216,  DOI:10.1021/acspolymersau.2c00050.
2. Y. Kobayashi, Y. Doi, S. S. Abdul Rahman, E. Kim, T.-H. Kim, A. Takano and Y. Matsushita, SANS Study of Ring Topology Effects on the Miscibility of Polymer Blends, Macromolecules, 2018, 51(5), 1885–1893,  DOI:10.1021/acs.macromol.7b02359.
3. Z. Bartczak and A. Galeski, Mechanical Properties of Polymer Blends, in Polymer Blends Handbook, ed. L. A. Utracki and C. A. Wilkie, Springer Netherlands, Dordrecht, 2014, pp. 1203–1297 DOI:10.1007/978-94-007-6064-6_13.
4. S. H. Goh, Miscible Polymer Blends, in Polymer Blends Handbook, ed. L. A. Utracki and C. A. Wilkie, Springer Netherlands, Dordrecht, 2014, pp. 1915–2151 DOI:10.1007/978-94-007-6064-6_24.
5. T. C. O’Connor, T. Ge and G. S. Grest, Composite Entanglement Topology and Extensional Rheology of Symmetric Ring-Linear Polymer Blends, J. Rheol., 2022, 66(1), 49–65,  DOI:10.1122/8.0000319.
6. E. Lattuada, T. Pietrangeli and F. Sciortino, Interpenetrating Gels in Binary Suspensions of DNA Nanostars, J. Chem. Phys., 2022, 157(13), 135101,  DOI:10.1063/5.0117047.
7. S. Thomas, D. Durand, C. Chassenieux and P. Jyotishkumar, Handbook of Biopolymer-Based Materials: From Blends and Composites to Gels and Complex Networks, John Wiley & Sons, 2013.
8. S. Banerjee, M. L. Gardel and U. S. Schwarz, The Actin Cytoskeleton as an Active Adaptive Material, Annu. Rev. Condens. Matter Phys., 2020, 11(1), 421–439,  DOI:10.1146/annurev-conmatphys-031218-013231.
9. M. Drechsler, F. Giavazzi, R. Cerbino and I. M. Palacios, Active Diffusion and Advection in the Drosophila Ooplasm Result from the Interplay of the Actin and Microtubule Cytoskeletons, bioRxiv, 2017, 7, 098590,  DOI:10.1101/098590.
10. D. A. Fletcher and R. D. Mullins, Cell Mechanics and the Cytoskeleton, Nature, 2010, 463(7280), 485–492,  DOI:10.1038/nature08908.
11. O. Wintner, N. Hirsch-Attas, M. Schlossberg, F. Brofman, R. Friedman, M. Kupervaser, D. Kitsberg and A. Buxboim, A Unified Linear Viscoelastic Model of the Cell Nucleus Defines the Mechanical Contributions of Lamins and Chromatin, Adv. Sci., 2020, 7(8), 1901222,  DOI:10.1002/advs.201901222.
12. F. Erdel, M. Baum and K. Rippe, The Viscoelastic Properties of Chromatin and the Nucleoplasm Revealed by Scale-Dependent Protein Mobility, J. Phys.: Condens. Matter, 2015, 27(6), 064115,  DOI:10.1088/0953-8984/27/6/064115.
13. C.-H. Yu, S. Redemann, H.-Y. Wu, R. Kiewisz, T. Y. Yoo, W. Conway, R. Farhadifar, T. Müller-Reichert and D. Needleman, Central-Spindle Microtubules Are Strongly Coupled to Chromosomes during Both Anaphase A and Anaphase B, Mol. Biol. Cell, 2019, 30(19), 2503–2514,  DOI:10.1091/mbc.E19-01-0074.
14. W. Alt and M. Dembo, Cytoplasm Dynamics and Cell Motion: Two-Phase Flow Models, Math. Biosci., 1999, 156(1), 207–228,  DOI:10.1016/S0025-5564(98)10067-6.
15. E. H. Barriga and R. Mayor, Adjustable Viscoelasticity Allows for Efficient Collective Cell Migration, Semin. Cell Dev. Biol., 2019, 93, 55–68,  DOI:10.1016/j.semcdb.2018.05.027.
16. R. Cerbino and P. Cicuta, Perspective: Differential Dynamic Microscopy Extracts Multi-Scale Activity in Complex Fluids and Biological Systems, J. Chem. Phys., 2017, 147(11), 110901,  DOI:10.1063/1.5001027.
17. B. Alberts, Molecular Biology of the Cell, Garland, 2004.
18. Y. S. Kim, B. Kundukad, A. Allahverdi, L. Nordensköld, P. S. Doyle and J. R. C. van der Maarel, Gelation of the Genome by Topoisomerase II Targeting Anticancer Agents, Soft Matter, 2013, 9(5), 1656–1663,  10.1039/C2SM27229F.
19. M. Jinek, K. Chylinski, I. Fonfara, M. Hauer, J. A. Doudna and E. Charpentier, A Programmable Dual-RNA–Guided DNA Endonuclease in Adaptive Bacterial Immunity, Science, 2012, 337(6096), 816–821,  DOI:10.1126/science.1225829.
20. D. Michieletto, P. Neill, S. Weir, D. Evans, N. Crist, V. A. Martinez and R. M. Robertson-Anderson, Topological Digestion Drives Time-Varying Rheology of Entangled DNA Fluids, Nat. Commun., 2022, 13(1), 4389,  DOI:10.1038/s41467-022-31828-w.
21. A. Pingoud, G. G. Wilson and W. Wende, Type II Restriction Endonucleases—a Historical Perspective and More, Nucleic Acids Res., 2014, 42(12), 7489–7527,  DOI:10.1093/nar/gku447.
22. O. A. Saleh, B. Jeon and T. Liedl, Enzymatic Degradation of Liquid Droplets of DNA Is Modulated near the Phase Boundary, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(28), 16160–16166,  DOI:10.1073/pnas.2001654117.
23. L.-Y. Zhou, J. Fu and Y. He, A Review of 3D Printing Technologies for Soft Polymer Materials, Adv. Funct. Mater., 2020, 30(28), 2000187,  DOI:10.1002/adfm.202000187.
24. D. Kokkinis, F. Bouville and A. R. Studart, 3D Printing of Materials with Tunable Failure via Bioinspired Mechanical Gradients, Adv. Mater., 2018, 30(19), 1705808,  DOI:10.1002/adma.201705808.
25. T. G. Mezger, The Rheology Handbook, Vincentz Network, 2006.
26. C. L. C. Chan, J. M. Taylor and E. C. Davidson, Design of Soft Matter for Additive Processing, Nat. Synth., 2022, 1(8), 592–600,  DOI:10.1038/s44160-022-00115-3.
27. F. M. Haque and S. M. Grayson, The Synthesis, Properties and Potential Applications of Cyclic Polymers, Nat. Chem., 2020, 12(5), 433–444,  DOI:10.1038/s41557-020-0440-5.
28. P. Neill, N. Crist, R. McGorty and R. Robertson-Anderson, Enzymatic Cleaving of Entangled DNA Rings Drives Scale-Dependent Rheological Trajectories, Soft Matter, 2024, 20(12), 2750–2766,  10.1039/D3SM01641B.
29. D. Kong, S. Banik, M. J. San Francisco, M. Lee, R. M. Robertson Anderson, C. M. Schroeder and G. B. McKenna, Rheology of Entangled Solutions of Ring–Linear DNA Blends, Macromolecules, 2022, 55(4), 1205–1217,  DOI:10.1021/acs.macromol.1c01672.
30. G. B. McKenna, D. Chen, S. C. H. Mangalara, D. Kong and S. Banik, Some Open Challenges in Polymer Physics, Polym. Eng. Sci., 2022, 62(5), 1325–1355,  DOI:10.1002/pen.25938.
31. M. A. Ubertini, J. Smrek and A. Rosa, Entanglement Length Scale Separates Threading from Branching of Unknotted and Non-Concatenated Ring Polymers in Melts, Macromolecules, 2022, 55(23), 10723–10736,  DOI:10.1021/acs.macromol.2c01264.
32. W. J. Weigand, A. Messmore, J. Tu, A. Morales-Sanz, D. L. Blair, D. D. Deheyn, J. S. Urbach and R. M. Robertson-Anderson, Active Microrheology Determines Scale-Dependent Material Properties of Chaetopterus Mucus, PLoS One, 2017, 12(5), e0176732,  DOI:10.1371/journal.pone.0176732.
33. J. Roovers and P. M. Toporowski, Microheterogeneity in Miscible Blends of 1,2-Polybutadiene and 1,4-Polyisoprene, Macromolecules, 1992, 25(13), 3454–3461,  DOI:10.1021/ma00039a023.
34. D. Michieletto, N. Nahali and A. Rosa, Glassiness and Heterogeneous Dynamics in Dense Solutions of Ring Polymers, Phys. Rev. Lett., 2017, 119(19), 197801,  DOI:10.1103/PhysRevLett.119.197801.
35. D. Michieletto and T. Sakaue, Dynamical Entanglement and Cooperative Dynamics in Entangled Solutions of Ring and Linear Polymers, ACS Macro Lett., 2021, 10(1), 129–134,  DOI:10.1021/acsmacrolett.0c00551.
36. Y. Zhou, C. D. Young, M. Lee, S. Banik, D. Kong, G. B. McKenna, R. M. Robertson-Anderson, C. E. Sing and C. M. Schroeder, Dynamics and Rheology of Ring-Linear Blend Semidilute Solutions in Extensional Flow: Single Molecule Experiments, J. Rheol., 2021, 65(4), 729–744,  DOI:10.1122/8.0000219.
37. J. Marfai, R. J. McGorty and R. M. Robertson-Anderson, Cooperative Rheological State-Switching of Enzymatically-Driven Composites of Circular DNA And Dextran, Adv. Mater., 2023, 35(46), 2305824,  DOI:10.1002/adma.202305824.
38. J. Smrek, K. Kremer and A. Rosa, Threading of Unconcatenated Ring Polymers at High Concentrations: Double-Folded vs Time-Equilibrated Structures, ACS Macro Lett., 2019, 8(2), 155–160,  DOI:10.1021/acsmacrolett.8b00828.
39. D. G. Tsalikis and V. G. Mavrantzas, Size and Diffusivity of Polymer Rings in Linear Polymer Matrices: The Key Role of Threading Events, Macromolecules, 2020, 53(3), 803–820,  DOI:10.1021/acs.macromol.9b02099.
40. D. Parisi, M. Kaliva, S. Costanzo, Q. Huang, P. J. Lutz, J. Ahn, T. Chang, M. Rubinstein and D. Vlassopoulos, Nonlinear Rheometry of Entangled Polymeric Rings and Ring-Linear Blends, J. Rheol., 2021, 65(4), 695–711,  DOI:10.1122/8.0000186.
41. R. Peddireddy K., M. Lee, Y. Zhou, S. Adalbert, S. Anderson, M. Schroeder C. and M. Robertson-Anderson, R., Unexpected Entanglement Dynamics in Semidilute Blends of Supercoiled and Ring DNA, Soft Matter, 2020, 16(1), 152–161,  10.1039/C9SM01767D.
42. K. R. Peddireddy, M. Lee, C. M. Schroeder and R. M. Robertson-Anderson, Viscoelastic Properties of Ring-Linear DNA Blends Exhibit Nonmonotonic Dependence on Blend Composition, Phys. Rev. Res., 2020, 2(2), 023213,  DOI:10.1103/PhysRevResearch.2.023213.
43. K. R. Peddireddy, R. Clairmont and R. M. Robertson-Anderson, Polymer Threadings and Rigidity Dictate the Viscoelasticity of Entangled Ring-Linear Blends and Their Composites with Rigid Rod Microtubules, J. Rheol., 2023, 67(1), 125–138,  DOI:10.1122/8.0000529.
44. A. F. Katsarou, A. J. Tsamopoulos, D. G. Tsalikis and V. G. Mavrantzas, Dynamic Heterogeneity in Ring-Linear Polymer Blends, Polymers, 2020, 12(4), 752,  DOI:10.3390/polym12040752.
45. K. R. Peddireddy, R. Clairmont, P. Neill, R. McGorty and R. M. Robertson-Anderson, Optical-Tweezers-Integrating-Differential-Dynamic-Microscopy Maps the Spatiotemporal Propagation of Nonlinear Strains in Polymer Blends and Composites, Nat. Commun., 2022, 13(1), 5180,  DOI:10.1038/s41467-022-32876-y.
46. D. Parisi, J. Ahn, T. Chang, D. Vlassopoulos and M. Rubinstein, Stress Relaxation in Symmetric Ring-Linear Polymer Blends at Low Ring Fractions, Macromolecules, 2020, 53(5), 1685–1693,  DOI:10.1021/acs.macromol.9b02536.
47. J. D. Halverson, G. S. Grest, A. Y. Grosberg and K. Kremer, Rheology of Ring Polymer Melts: From Linear Contaminants to Ring-Linear Blends, Phys. Rev. Lett., 2012, 108(3), 038301,  DOI:10.1103/PhysRevLett.108.038301.
48. P. Khanal, K. R. Peddireddy, J. Marfai, R. McGorty and R. M. Robertson-Anderson, DNA Topology Dictates Emergent Bulk Elasticity and Hindered Macromolecular Diffusion in DNA-Dextran Composites, J. Rheol., 2022, 66(4), 699–715,  DOI:10.1122/8.0000447.
49. S. Laib, R. M. Robertson and D. E. Smith, Preparation and Characterization of a Set of Linear DNA Molecules for Polymer Physics and Rheology Studies, Macromolecules, 2006, 39(12), 4115–4119,  DOI:10.1021/ma0601464.
50. R. M. Robertson, S. Laib and D. E. Smith, Diffusion of Isolated DNA Molecules: Dependence on Length and Topology, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(19), 7310–7314,  DOI:10.1073/pnas.0601903103.
51. D. E. Smith, T. T. Perkins and S. Chu, Dynamical Scaling of DNA Diffusion Coefficients, Macromolecules, 1996, 29(4), 1372–1373,  DOI:10.1021/ma951455p.
52. D. R. Latulippe and A. L. Zydney, Radius of Gyration of Plasmid DNA Isoforms from Static Light Scattering, Biotechnol. Bioeng., 2010, 107(1), 134–142,  DOI:10.1002/bit.22787.
53. R. M. Robertson and D. E. Smith, Self-Diffusion of Entangled Linear and Circular DNA Molecules: Dependence on Length and Concentration, Macromolecules, 2007, 40(9), 3373–3377.
54. T. Ge, S. Panyukov and M. Rubinstein, Self-Similar Conformations and Dynamics in Entangled Melts and Solutions of Nonconcatenated Ring Polymers, Macromolecules, 2016, 49(2), 708–722,  DOI:10.1021/acs.macromol.5b02319.
55. R. M. Robertson and D. E. Smith, Direct Measurement of the Confining Forces Imposed on a Single Molecule in a Concentrated Solution of Circular Polymers, Macromolecules, 2007, 40(24), 8737–8741,  DOI:10.1021/ma071440e.
56. A. Y. Grosberg, Annealed Lattice Animal Model and Flory Theory for the Melt of Non-Concatenated Rings: Towards the Physics of Crumpling, Soft Matter, 2013, 10(4), 560–565,  10.1039/C3SM52805G.
57. M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, 1988.
58. C. D. Chapman and R. M. Robertson-Anderson, Nonlinear Microrheology Reveals Entanglement-Driven Molecular-Level Viscoelasticity of Concentrated DNA, Phys. Rev. Lett., 2014, 113(9), 098303,  DOI:10.1103/PhysRevLett.113.098303.
59. R. M. Robertson-Anderson, Optical Tweezers Microrheology: From the Basics to Advanced Techniques and Applications, ACS Macro Lett., 2018, 7(8), 968–975,  DOI:10.1021/acsmacrolett.8b00498.
60. Q. Huang, J. Ahn, D. Parisi, T. Chang, O. Hassager, S. Panyukov, M. Rubinstein and D. Vlassopoulos, Unexpected Stretching of Entangled Ring Macromolecules, Phys. Rev. Lett., 2019, 122(20), 208001,  DOI:10.1103/PhysRevLett.122.208001.
61. R. Cerbino, F. Giavazzi and M. E. Helgeson, Differential Dynamic Microscopy for the Characterization of Polymer Systems, J. Polym. Sci., 2022, 60(7), 1079–1089,  DOI:10.1002/pol.20210217.
62. R. Cerbino and V. Trappe, Differential Dynamic Microscopy: Probing Wave Vector Dependent Dynamics with a Microscope, Phys. Rev. Lett., 2008, 100(18), 188102,  DOI:10.1103/PhysRevLett.100.188102.
63. D. M. Wulstein, K. E. Regan, R. M. Robertson-Anderson and R. McGorty, Light-Sheet Microscopy with Digital Fourier Analysis Measures Transport Properties over Large Field-of-View, Opt. Express, 2016, 24(18), 20881–20894,  DOI:10.1364/OE.24.020881.
64. J. Smrek, J. Garamella, R. Robertson-Anderson and D. Michieletto, Topological Tuning of DNA Mobility in Entangled Solutions of Supercoiled Plasmids, Sci. Adv., 2021, 7(20), eabf9260,  DOI:10.1126/sciadv.abf9260.
65. L. M. Walker and N. J. Wagner, SANS Analysis of the Molecular Order in Poly(γ-Benzyl l-Glutamate)/Deuterated Dimethylformamide (PBLG/d-DMF) under Shear and during Relaxation, Macromolecules, 1996, 29(6), 2298–2301,  DOI:10.1021/ma951127p.
66. Z. Varga and J. W. Swan, Large Scale Anisotropies in Sheared Colloidal Gels, J. Rheol., 2018, 62(2), 405–418,  DOI:10.1122/1.5003364.
67. H. N. Verwei, G. Lee, G. Leech, I. I. Petitjean, G. H. Koenderink, R. M. Robertson-Anderson and R. J. McGorty, Quantifying Cytoskeleton Dynamics Using Differential Dynamic Microscopy, JoVE, 2022, 184, e63931,  DOI:10.3791/63931.
68. J. Wang and T. Ge, Crazing Reveals an Entanglement Network in Glassy Ring Polymers, Macromolecules, 2021, 54(16), 7500–7511,  DOI:10.1021/acs.macromol.1c01080.
69. B. A. Krajina and A. J. Spakowitz, Large-Scale Conformational Transitions in Supercoiled DNA Revealed by Coarse-Grained Simulation, Biophys. J., 2016, 111(7), 1339–1349,  DOI:10.1016/j.bpj.2016.07.045.
70. T. C. O’Connor, T. Ge, M. Rubinstein and G. S. Grest, Topological Linking Drives Anomalous Thickening of Ring Polymers in Weak Extensional Flows, Phys. Rev. Lett., 2020, 124(2), 027801,  DOI:10.1103/PhysRevLett.124.027801.
71. S. Banik, D. Kong, M. J. San Francisco and G. B. McKenna, Monodisperse Lambda DNA as a Model to Conventional Polymers: A Concentration-Dependent Scaling of the Rheological Properties, Macromolecules, 2021, 54(18), 8632–8654,  DOI:10.1021/acs.macromol.0c02537.
72. D. Michieletto, P. Neill, S. Weir, D. Evans, N. Crist, V. A. Martinez and R. M. Robertson-Anderson, Topological Digestion Drives Time-Varying Rheology of Entangled DNA Fluids, Nat. Commun., 2022, 13(1), 4389,  DOI:10.1038/s41467-022-31828-w.
73. R. M. Robertson, S. Laib and D. E. Smith, Diffusion of Isolated DNA Molecules: Dependence on Length and Topology, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(19), 7310–7314,  DOI:10.1073/pnas.0601903103.
74. S. Pan, D. At Nguyen, T. Sridhar, P. Sunthar and J. Ravi Prakash, Universal Solvent Quality Crossover of the Zero Shear Rate Viscosity of Semidilute DNA Solutions, J. Rheol., 2014, 58(2), 339–368,  DOI:10.1122/1.4861072.
75. J. R. Prakash, Universal Dynamics of Dilute and Semidilute Solutions of Flexible Linear Polymers, Curr. Opin. Colloid Interface Sci., 2019, 43, 63–79,  DOI:10.1016/j.cocis.2019.03.001.
76. T. M. Squires and T. G. Mason, Fluid Mechanics of Microrheology, Annu. Rev. Fluid Mech., 2010, 42(1), 413–438,  DOI:10.1146/annurev-fluid-121108-145608.
77. Y. Gao, J. Kim and M. E. Helgeson, Microdynamics and Arrest of Coarsening during Spinodal Decomposition in Thermoreversible Colloidal Gels, Soft Matter, 2015, 11(32), 6360–6370,  10.1039/C5SM00851D.
78. D. Germain, M. Leocmach and T. Gibaud, Differential Dynamic Microscopy to Characterize Brownian Motion and Bacteria Motility, Am. J. Phys., 2016, 84(3), 202–210,  DOI:10.1119/1.4939516.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01065e

---