Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fluorinated 2D conjugated porous organic polymer films with modular structural topology for controlled molecular sieving†
Jessica
Gayle‡
a,
Rifan
Hardian‡
 b,
Galio
Guo
a,
Xu
Wang
c,
Muhammad M.
Rahman
b,
Galio
Guo
a,
Xu
Wang
c,
Muhammad M.
Rahman
 a,
Rafael
Verduzco
a,
Rafael
Verduzco
 ad,
Robert
Vajtai
ad,
Robert
Vajtai
 a,
Pulickel
Ajayan
*a,
Soumyabrata
Roy
*a and
Gyorgy
Szekely
a,
Pulickel
Ajayan
*a,
Soumyabrata
Roy
*a and
Gyorgy
Szekely
 *be
*be
aDepartment of Materials Science and NanoEngineering, Rice University, Houston, Texas 77005, USA
bAdvanced Membranes and Porous Materials Center, Physical Science and Engineering Division, King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Saudi Arabia Web: http://www.SzekelyGroup.com
cShared Equipment Authority, Rice University, Houston, Texas, USA
dDepartment of Chemical and Biomolecular Engineering, Rice University, Houston, Texas 77005, USA
eChemical Engineering Program, Physical Science and Engineering Division (PSE), King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia
First published on 31st July 2024
Abstract
Two-dimensional conjugated porous organic polymers (2D CPOPs) exhibit excellent structural tunability and stability in organic solvents, making them suitable for controlled nanofiltration applications. We report the fabrication of free-standing, flexible films of adaptable thickness and surface areas through a facile drop-cast approach using four novel fluorinated imine-linked 2D CPOPs. The resulting structures exhibit various pore sizes (2.6–3.2 nm), structural topologies (homopore and heteropore topologies), and skeletal backbone functionalities (with and without fluorine). The films comprise tightly packed layered sheets, which are easily exfoliated into nanometer-thick sheets with large lateral domains. The properties of the films, such as hydrophobicity, flexibility, hardness, porosity, thermal stability, morphology, and anisotropic properties of the films are evaluated. The films exhibit controlled nanofiltration performance that can be tuned by tailoring the pore architectures in terms of pore size, pore functionality, and structural topology. Particularly for the heteropore structure, the larger pores control the molecular weight cutoff (MWCO) while allowing the solvent molecules to pass through, whereas the smaller pores only act as channels for solvent transport. We report the experimental and theoretical observations of these structures, providing new insights into the fundamental understanding of molecular transportation through materials with multiple pore sizes.
Introduction
Two-dimensional conjugated porous organic polymers (2D CPOPs) are covalently linked, carbon-bonded structures with permanent intrinsic porosity. These materials are polymerized from an assembly of rigid functional building blocks in-plane to form layered structures.1 The skeletal frameworks comprise large aromatic units and strong carbon bonds, making them insoluble and significantly challenging to process into large, defect-free, free-standing films, hindering their translation into performance-driven applications.1,2 Owing to their structural regularity, high aromaticity, and strong carbon bonds that offer tunable performance properties along with high chemical stability and robust mechanical properties, 2D CPOPs have garnered great interest in membrane separation applications, such as organic solvent nanofiltration (OSN).3–6 OSN is a membrane-based separation technique that enables the separation of solutes from either polar or nonpolar organic solvents. Unlike the conventional thermal separation techniques, OSN offers an energy-efficient alternative,7,8 and thus it has been widely applied in various industries, including the pharmaceutical, fine chemical, petrochemical, food, and textile industries.One of the most promising strategies to adjust the performance of 2D CPOPs involves changing their skeletal structures using adjustable pore sizes, topologies, and functional groups.9 Incorporating hydrogen-bonding pendant groups such as methoxy, hydroxyl, or fluorine can modulate the microstructural properties of the films by enhancing interplanar interactions, sheet stacking, and planarity.10–12 Adjusting the surface properties of these materials, through the incorporation of hydrophilic oxygen or hydrophobic fluorine groups, has shown great potential in controlling the wettability of films for membrane separation applications.13–16 In addition to conventional homopore 2D structures characterized by a single pore size, heteropore structures constructed by assembling materials with different pore sizes have emerged as novel 2D materials.17–20 However, the applicability and fundamentals of molecular transport through such heteropore structures are not well explored.
The majority of synthesis strategies for 2D CPOPs report the use of solvothermal methods producing insoluble powders that are difficult to be readily processed into workable films.21–23 Furthermore, fabrication of freestanding films using pure crystalline porous analogs often suffers from inherent defects arising from crystalline.24 While some polymerization strategies for CPOPs such as vapor deposition, dip-coating, electrodeposition, have been explored to produce films, these methods often produce films that require the support of a substrate.25–27 Some strategies have been introduced to fabricate free-standing films. However, facile control of the thickness and area of the films is a major problem that restricts scalability. For instance, the Langmuir–Blodgett method to transfer the film from the liquid surface onto the substrate often needs to be repeated many times to construct a robust membrane, and it faces difficulty in direct control of the thickness.28–31
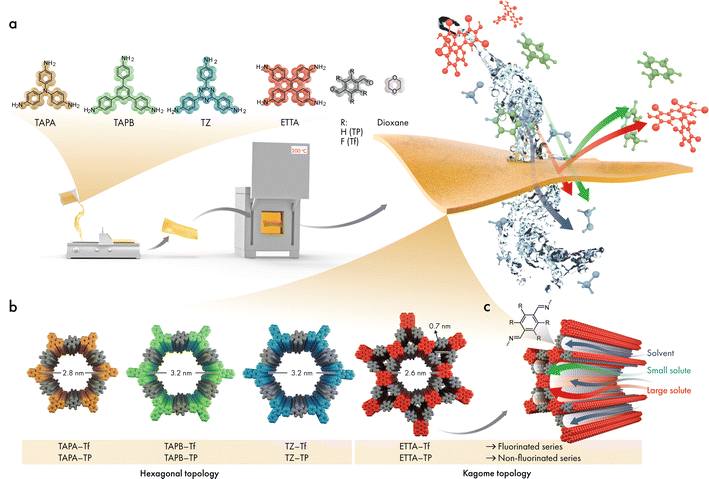
Herein, four 2D CPOP structures comprising single and dual porosities with and without fluorine functionalization were synthesized using a facile drop-cast technique (Fig. 1). The pore sizes of the 2D CPOP films were estimated from the proposed crystalline structure counterparts, by carefully taking into consideration three pore sizes of a single structure due to possible linker rotation around the connector axis. We examined the role of fluorination in the formation of the 2D layers and the subsequent stacking of sheets, and compared the changes in microstructure, stability, and hydrophobicity with those of nonfluorinated analogs. Furthermore, the effects of pore size, functionality, and structural topology (single and dual porosities) were investigated for OSN applications. The nanofiltration performance was investigated both experimentally and theoretically to reveal a fundamental understanding of the transport model, particularly through the dual-pore structure.
Results and discussion
Synthesis and properties of the 2D CPOP films
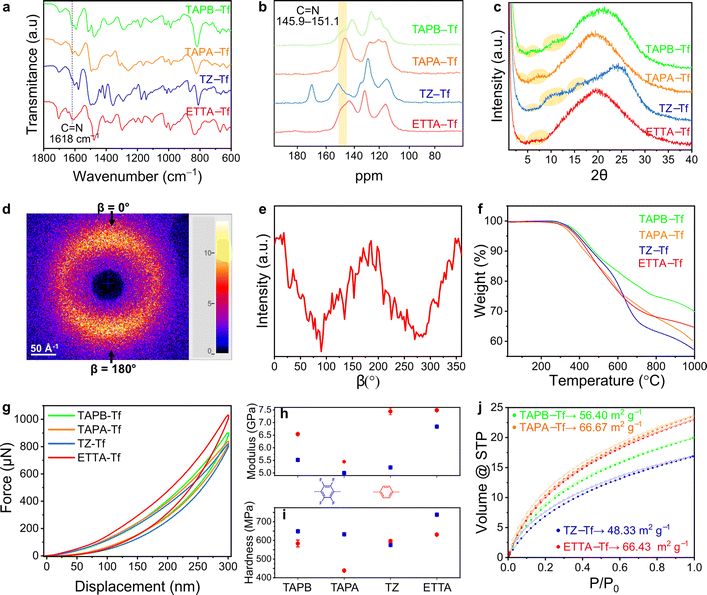
The skeletal frameworks of the 2D CPOPs were predesigned to form two distinct pore topologies. A homopore configuration containing hexagonal pores was constructed from the rigid aromatic building blocks with three functional sites that could polymerize, forming an imine bond. The Kagome configuration with dual porosities (comprising the assembly of hexagonal and trigonal pores) was controlled by selecting rigid aromatic building blocks with four functional sites. Three 2D CPOPs with hexagonal pore structures having theoretical pore sizes between 2.8 and 3.2 nm were synthesized by polymerizing tri-functionalized 4,4′,4′′-triaminotriphenylamine (TAPA), 1,3,5-tris(4-aminophenyl)benzene (TAPB), or 5,5′,5′′-((1,3,5-triazine-2,4,6-tryl)trianiline) (TZ) with 2,3,5,6-tetrafluoroterephthalaldehyde (Tf), a di-functionalized building block enriched with four fluorine groups to form TAPA–Tf, TAPB–Tf, and TZ–Tf, respectively (Fig. 1). One Kagome topology was predesigned with pore apertures of 0.7 and 2.6 nm by polymerizing tetra-functionalized 4′4′,4′′,4′′′-(ethene-1,1,2,2-tetrayl)tetraaniline (ETTA) with -di-functionalized Tf to form ETTA–Tf. Further information detailing the synthesis procedure is provided in ESI (Fig. S1–S4†). Nonfluorinated 2D CPOPs were synthesized through a similar method, where Tf was replaced with an unfluorinated building block, namely, terephthalaldehyde (TP), to form TAPB–TP, TAPA–TP, TZ–TP, and ETTA–TP. Although the precursors used to fabricate the 2D CPOPs are the same with those for COF synthesis, applying different synthesis method resulting in different products. The 2D CPOP films are amorphous 2D layered materials (lacking long-range order) in contrast to crystalline COFs with well-defined, in-plane periodic pore structures. The synthesis method of 2D CPOPs yields the disordered kinetic product resulting from the brief solvent evaporation step.The successful Schiff base polymerization of TAPB–Tf, TAPA–Tf, TZ–Tf, and ETTA–Tf films was confirmed by the attenuation of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching (1698 cm−1) and appearance of C
O stretching (1698 cm−1) and appearance of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretching vibration peak at 1610–1619 cm−1 in the corresponding Fourier transformed infrared (FTIR) spectra (Fig. 2a and S5–S8†). To further investigate whether annealing can alter imine bond conversion, the intermediate films were heated at 200 °C, 225 °C, and 250 °C under vacuum for 12 h. As shown in the FTIR spectra (Fig. S9–S12†), annealing TAPA–Tf, TZ–Tf, and ETTA–Tf films at 200 °C resulted in improved relative intensity of imine (C
N stretching vibration peak at 1610–1619 cm−1 in the corresponding Fourier transformed infrared (FTIR) spectra (Fig. 2a and S5–S8†). To further investigate whether annealing can alter imine bond conversion, the intermediate films were heated at 200 °C, 225 °C, and 250 °C under vacuum for 12 h. As shown in the FTIR spectra (Fig. S9–S12†), annealing TAPA–Tf, TZ–Tf, and ETTA–Tf films at 200 °C resulted in improved relative intensity of imine (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) stretch relative to C
N) stretch relative to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, while increasing the annealing temperature to 225 °C did not show any further change. Meanwhile, annealing at 250 °C showed a decrease in relative intensity of imine to C
O, while increasing the annealing temperature to 225 °C did not show any further change. Meanwhile, annealing at 250 °C showed a decrease in relative intensity of imine to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch for ETTA–Tf and TZ–Tf films, which can be attributed to thermal instability and imine bond decomposition. TAPB–Tf did not undergo any changes at any of the annealing temperatures. Based on these observations, all films were annealed at 200 °C to obtain the optimal fabrication.
O stretch for ETTA–Tf and TZ–Tf films, which can be attributed to thermal instability and imine bond decomposition. TAPB–Tf did not undergo any changes at any of the annealing temperatures. Based on these observations, all films were annealed at 200 °C to obtain the optimal fabrication.
Solid-state 13C nuclear magnetic resonance (ss-13CNMR) was performed to further corroborate the polymerization of building blocks through imine bond formation. Both cross-polarized and nonquaternary suppression experiments were performed to identify the nonquaternary carbon within the imine linkage. In nonquaternary suppression experiments, all films showed immediate decay of the peaks at 147.8, 145.9, 151.1, and 147.8 ppm, indicating the presence of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N peak (Fig. 2b and S13–S16†). The ss-13CNMR cross-polarized spectra also closely matched the spectra for structurally similar crystalline powder counterparts, further supporting the proposed chemical structures.32
N peak (Fig. 2b and S13–S16†). The ss-13CNMR cross-polarized spectra also closely matched the spectra for structurally similar crystalline powder counterparts, further supporting the proposed chemical structures.32
All films were predominantly amorphous and devoid of long-range order, as indicated by the broad powder X-ray diffraction (PXRD) peaks centered around 2θ = 18.95°–24.05° (Fig. 2c and S17–S20†). These broad peaks correspond to a broad distribution of interlayer spacing resulting from the disordered stacking of 2D polymeric sheets.33 Similar broadening behavior has been widely reported in the case of graphite or other 2D polymers, where in-plane defects and disorder originated from the oxygen functional group at the edges of the sheets, disrupt the ordered stacking of individual layers.34–36
The addition of fluorine groups favored perfluoroarene–arene interactions, thereby reducing the parallel stacking displacement between sheets,37,38 as reflected in the high angles diffraction peaks. The smaller d-spacing in the fluorinated 2D CPOPs indicates a tighter interplanar packing of 2D sheets than in the nonfluorinated structures.39 The broad peaks at high angles corresponding to the (001) plane centered at 2θ = 20.91°, 20.64°, 24.05°, and 20.05° for fluorinated TAPB–Tf, TAPA–Tf, TZ–Tf, and ETTA–Tf, correspond to d-spacing values of 0.42, 0.43, 0.37, and 0.44 nm, respectively. These d-spacing values were slightly smaller than those of nonfluorinated structures with peaks centered around 2θ = 19.3°, 19.15°, 19.55°, and 18.95°, corresponding to d-spacing values of 0.46, 0.46, 0.45, and 0.47 nm, respectively.40
At low angle, diffraction peaks correspond to the inner nanosheets structure. Fluorination slightly enhanced the broad peaks at low angle compared to their non-fluorinated counterparts, indicating increased crystallinity.40 This crystallinity enhancement can be attributed to enhanced π–π interactions between the sheets promoted by fluorine groups. A similar observation was reported in a previous study where the increased fluorination of the COF structure led to an enhancement in the crystallinity and porosity, as a direct result of the fluorine-driven self-complementary π electronic forces that maximized the stacking energy and reduced the unit cell size.41 The PXRD spectra of fluorinated films show the presence of broad peaks at low angle centered around 3.74°, 3.75°, 4.1°, and 3.79° for (100) plane and 6.02°, 5.82°, 6.12°, and 6.35° for (110) planes; these peaks correspond to the longer-range periodicity of the structures within the films (Fig. S17–S20†). The (100) reflection of the TAPB–Tf, TAPA–Tf, TZ–Tf, and ETTA–Tf films corresponded to d-spacings of 2.36, 2.36, 2.05, and 2.33 nm, respectively. These spacings were lower than the expected values for (100) facet for the predicted hexagonal lattice of the skeletal pore structures, indicating a structure that was less ordered than crystalline covalent organic frameworks (COFs).32,42,43
To further investigate the interplanar sheet stacking and ordering throughout the thickness of fluorinated and nonfluorinated films, we performed 2D wide-angle X-ray scattering (WAXS) analysis of the film cross-section, which aligned normal to the beam (Fig. S21†). The WAXS patterns of fluorinated and nonfluorinated films showed broad, extended X-ray scattering with increased poles of intensity toward β = 0° and 180°, thereby supporting the formation of a 2D layered structure (Fig. 2d, e, and S22–S25†). Notably, the fluorinated films displayed larger extended diffraction (and therefore had a smaller d-spacing) than the nonfluorinated films. These results corroborated the PXRD observations that the fluorination of 2D CPOPs leads to increased ordering within the polymers through better stacking alignment. Similar trend has also been shown in other 2D COF materials where the incorporation of fluorine-rich building blocks lead to improved stacking and more ordered interlayer spacing of sheets.10 Thermogravimetric analysis (TGA) revealed that all fluorinated films are thermally stable up to ∼290 °C (Fig. 2f). However, early degradation could occur at a lower temperature. As shown by FTIR analysis (Fig. S9–S12†), annealing the films at 250 °C started to show indication of decreased relative intensity of imine. Therefore, we annealed the films at the temperature 200 °C to ensure the absence of imine bond degradation. TAPA–Tf film underwent the highest thermal degradation because it contains the triphenylamine node in the place of the tetraphenylethylene, 1,3,5-triphenylbenzene, or 2,4,6-triphenyl-1,3,5-triazine nodes and because the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds are thermally more robust than C–N bonds.44,45 Expectedly, TAPB–Tf film exhibited the highest thermal stability among the fluorinated films, resulting from thermally robust 1,3,5-triphenylbenzene node.46 All the fluorinated structures were thermally stable up to ∼300 °C, although a slightly lower thermal stability was observed compared to their nonfluorinated counterparts. This is because functionalization increases the steric repulsion, causing interlayer disruptions in the 2D polymer sheets, which makes the layer stacking becomes more disordered. A disordered layer stacking might cause some parts become closer to each other and the other parts become far away from each other. Nevertheless, according to the WAXS results (Fig. S22–S25†), which show smaller d-spacing between nanosheets in fluorinated samples, indicate that the interlayer disruption was dominated by the shortening of the interlayer distance between the nanosheets in fluorinated films. A similar phenomenon was reported for hexagonal 2D structures functionalized with methyl, ethyl, or bromine groups.47
N bonds are thermally more robust than C–N bonds.44,45 Expectedly, TAPB–Tf film exhibited the highest thermal stability among the fluorinated films, resulting from thermally robust 1,3,5-triphenylbenzene node.46 All the fluorinated structures were thermally stable up to ∼300 °C, although a slightly lower thermal stability was observed compared to their nonfluorinated counterparts. This is because functionalization increases the steric repulsion, causing interlayer disruptions in the 2D polymer sheets, which makes the layer stacking becomes more disordered. A disordered layer stacking might cause some parts become closer to each other and the other parts become far away from each other. Nevertheless, according to the WAXS results (Fig. S22–S25†), which show smaller d-spacing between nanosheets in fluorinated samples, indicate that the interlayer disruption was dominated by the shortening of the interlayer distance between the nanosheets in fluorinated films. A similar phenomenon was reported for hexagonal 2D structures functionalized with methyl, ethyl, or bromine groups.47
The nanomechanical properties of porous aromatic framework films depend on the connectivity and dimensionality of the structure.48,49 The reduced compressive modulus and hardness of the materials were evaluated using the nanoindentation method at five different depths and in five distinct regions of the sample. The reduced compressive modulus and hardness values of all films remained relatively stable at a penetration depth of 10% of the thickness (Fig. S30–S32, Tables S1 and S2†), which is consistent with the results of other studies on depth-displacement in thin films.50,51 The loading–unloading curves showed that all fluorinated films are highly elastic, as proven by the complete return of the hysteresis (Fig. 2g). This elastic response is attributed to the strong carbon-bonded porous frameworks within these structures that allow temporary deformation into the open voids, forgoing irreversible bond breakage.52,53 Among the fluorinated films, the ETTA–Tf film had the highest compressive modulus (6.84 GPa) and could withstand the largest load of 1031 μN at the same depth of penetration as other fluorinated films. The compressive modulus of TAPA–Tf, TAPB–Tf, and TZ–Tf films were 5.01, 5.52, and 5.22 GPa, respectively (Fig. S32†). Since the elastic modulus is a bulk property highly dependent on the chemical composition and chemical bonds, the differences in the compressive modulus are likely caused by the differences in the skeletal structures of these materials.54 The ETTA–Tf film contains rigid benzene rings and carbon double bonds, whereas the TZ–Tf and TAPA–Tf films contain triazine and triphenylamine nodes. The average hardness values of TAPA–Tf, TAPB–Tf, and ETTA–Tf films were 633 MPa, 649 MPa, and 738 MPa, respectively (Fig. S32†). Among these films, the TZ–Tf film exhibited the lowest hardness (575 MPa), which could be attributed to the changes in the local surface properties of the film.54
The fluorinated films showed a higher elastic recovery and reduced compressive modulus than the nonfluorinated ones. This can be explained by the higher porosity and accessible void space within these structure, making them less stiff and capable of deforming under a given load (Fig. 2h).55 The fluorinated polymers can withstand a larger loading force under the same penetration depth of 10% film thickness, leading to higher hardness values (Fig. 2i). This characteristic can be due to the reduction of local defects resulting from better interplanar sheet stacking upon fluorination.52
A comparison of the nanomechanical properties of these 2D CPOPs with other reported membrane used in separation applications is tabulated in Table S3.† The compressive modulus and hardness of the 2D CPOP films were substantially higher than those of 1D polymer membranes of similar thickness such, as Nafion 117, Nylon, poly(vinyl alcohol), or polyvinylidene fluoride, as a result of the strong covalent bonds and aromatic rings in these structures that lead to an increase in stiffness and local hardness properties.39,56–58 Although 1D polyaromatic polymers such as polyethersulfone and polyaramid have good mechanical properties, they were still lower than both the nonfluorinated and fluorinated films reported here. Furthermore, the 2D CPOPs synthesized in this work are considerably less dense than 1D polymers, giving them a significantly higher stiffness and hardness. Notably, despite lacking long-range order or crystallinity, the elastic modulus and hardness values of these films are comparable to many crystalline imidazole-linked zeolite framework materials.53 However, comparison of these materials with other 2D COFs remains challenging as there are only few reports on investigating the nanomechanical properties of COFs membranes through nanoindentation.52,59
The surface areas of the films were evaluated from the adsorption isotherms obtained using CO2 at 273 K because of the enhanced diffusion of this molecule into narrow pore apertures at relatively higher temperatures due to its smaller kinetic diameter compared to N2.60,61 Further, N2 may not be as suitable for BET surface area analysis of thin films with low surface areas (due to higher vapor pressure and sublimation capacity of N2).62 The surface areas of TAPB–Tf, TAPA–Tf, TZ–Tf, and ETTA–Tf were 56.40, 66.67, 48.33, and 66.43 m2 g−1, respectively. These surface areas were higher than those of nonfluorinated TAPB–TP, TAPA–TP, TZ–TP, and ETTA–TP films, which were 33.43, 40.45, 29.49, and 50.58 m2 g−1, respectively (Fig. 2j).55 All films showed facile CO2 desorption, as indicated by the absence of hysteresis between the adsorption–desorption isotherms. Using NLDFT on N2 adsorption measurements obtained at 77 K, pore width distributions were found to be centered around 3.03, 2.77, 3.03, and 2.70 nm for TAPB–Tf, TAPA–Tf, TZ–Tf, and ETTA–Tf films, respectively (Fig. S33 and S34†). These centered pore distributions suggest the formation of closed porous frameworks over hyperbranched structures, which aligned with previously reported pore distributions for structurally similar porous polymers.32,63,64
Morphology, anisotropy, and exfoliation of the films
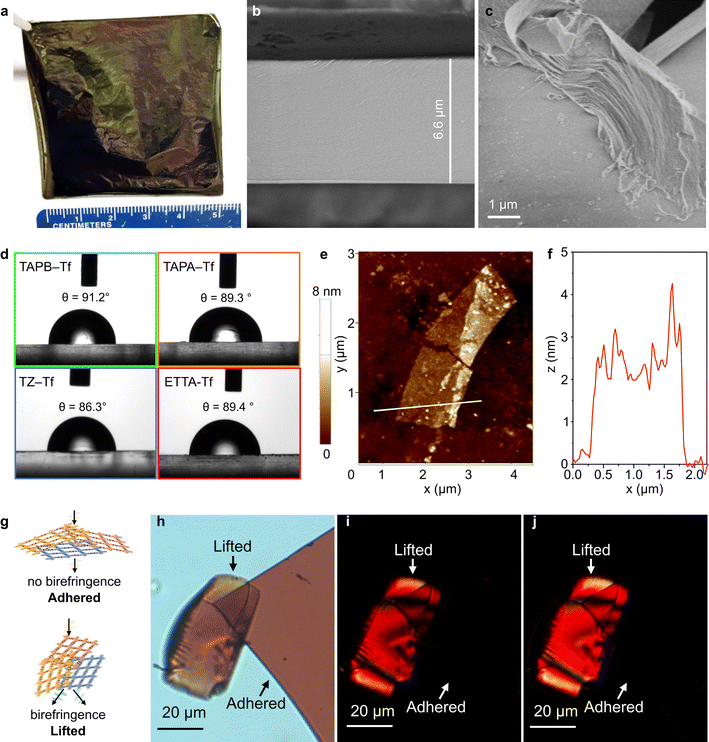
The drop-casting technique produced films with tunable areas and thicknesses. The combination of short fabrication time and adjustable membrane size offered both simplicity and scalability. Flexible free-standing films with large areas (5 cm × 5 cm) were produced by scaling up the precursor solution and maintaining the solution concentration (Fig. 3a). Film thickness could be adjusted by controlling the concentration of the precursors (Fig. 3b and S35–S38†). The bulk films comprised thin layered structures, as shown by the scanning electron microscopy (SEM) images (Fig. 3c and S39†) at the broken film edges. All bulk films showed smooth surface topologies and continuous cross-sections (Figs. S39 and S40†). The absence of large voids on the surface benefits selective diffusion driven by the physicochemical and nanostructural properties of each film.65–69Film wettability was investigated by using the water contact angle measurement using sessile drop method. All the fluorinated films were generally hydrophobic, with water contact angle values in the range of 86°–91° (Fig. 3d). This hydrophobicity can be explained by the presence of aromatic benzene rings and the incorporation of fluorine groups in the structures. In comparison, nonfluorinated analogs are more hydrophilic with lower water contact angle values (75–89°).55 The ability to tune the hydrophobicity of these structures is beneficial for tailoring the nanofiltration performance in polar and nonpolar solvents.
Exfoliating the bulk films into nanosheets (NSs) provided a better understanding of the interesting 2D-anisotropic optical properties. The 2D layered sheets constructed of a strong in-plane carbon bonds were assembled into bulk structures via non-covalent interactions (weak interplanar van der Waals interactions between the 2D sheets). This allowed the films to be exfoliated into NSs (with thicknesses ranging between 0.6–6 nm) of large domains using a top-down mechanochemical exfoliation approach (Fig. 3e and S41–S44†).70 The fluorinated NSs were deposited onto silicon substrates for thickness measurement using atomic force microscopy (AFM). Although NSs are only ∼2 nm thick, they have large lateral domains because of the anisotropic bonding (in-plane vs. the vertical z direction) (Fig. 3e). For instance, an exfoliated ETTA–Tf NS with a lateral dimension of ∼4 μm exhibited a thickness of ∼2.5 nm (Fig. 3f). Meanwhile, TZ–Tf nanosheets with smaller domains (∼300 nm) were observed to be as thin as 0.6 nm (Fig. S43†), which is about two stacked monolayers.32 Polarizing optical microscopy (POM) was performed on fluorinated film NSs to further explore the optical properties and 2D anisotropic structure. The films were placed on glass substrates and the transmission mode of the microscope was used; the films were exposed to cross-polarized light. The fluorinated films exhibited in-plane isotropy and did not show birefringence when adhered flat to the glass. Meanwhile, the films that were angled and lifted-up displayed out-of-plane anisotropy, resulting in the presence of birefringence (Fig. 3g, h and S45–S47†). When the cross-polarized light was rotated by 45°, similar birefringence phenomenon was observed for both adhered and lifted films. The rotation of light caused different areas of the film pieces to be illuminated and to undergo a color change, which indicated the angle-dependent polarization induced by a change in light resonance. This birefringence can be explained by the disordered stacking of sheets along the z-axis and isotropic behavior along x–y axes (Fig. 3g and h).71,72 This disordered stacking of sheets results in a unique birefringence behavior that has seldom been reported for 2D COF constituents. Recently, highly anisotropic birefringence within 2D metastructure COFs was reported; although these structures were huge, they exhibited limited tunability of birefringence.73
Effects of structural architectures on nanofiltration performance
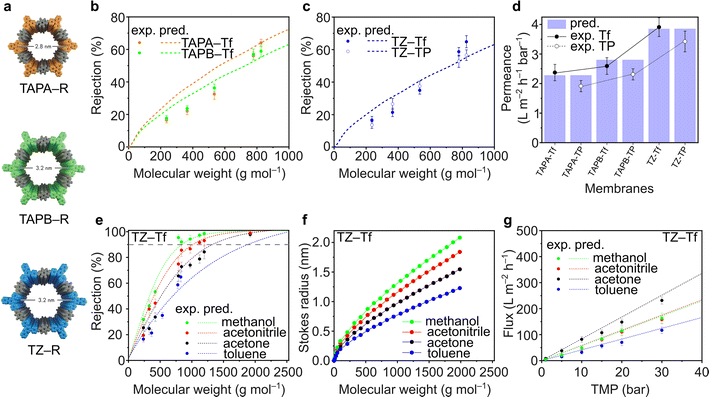
Fluorinated and nonfluorinated 2D CPOP films exhibited high chemical stability toward organic solvents. The TGA and FTIR spectra of the films before and after soaking in acetone, methanol, and hexane for 30 days did not show any notable changes, indicating that the films retain their structure (Fig. S48–S59†). The nanofiltration performance of TAPA–Tf, TAPB–Tf, and TZ–Tf films was investigated by comparing the experimental rejection curves with the theoretically predicted rejection curves. The predictive rejection curves were developed using the pore flow model (details in ESI†) by considering the pore size and the geometrical dimensions of the structures (Fig. 4a), and assuming a laminar solution flux through the cylindrical pore channels perpendicular to the plane of the membrane. Details on the theoretical prediction of nanofiltration is provided in the ESI (Section 3.1†). The rejection of the molecules by the membranes are mostly affected by the pore size of the membrane. Whereas the solvent permeance through the membranes is affected by the pore size, membrane thickness, applied pressure, porosity, and solvent viscosity in confined space. The predicted rejection curve of the TAPA–Tf film was slightly higher than that of the TAPB–Tf because the later has larger pore size (Fig. 4b). Their experimental rejection values are within the predicted rejection curves. The effect of the fluorinated structure on solute rejection is shown in Fig. 4c. Compared to the TZ–Tf film, the TZ–TP film exhibited slightly higher rejection towards nonpolar solute molecules (such as isodrine and hexaphenylbenzene). This indicates that the nonpolar characteristics of TZ–Tf attracted nonpolar solutes, providing better wetting degrees, and facilitating faster flow through the pores of the fluorinated membrane. These observations agree with the results of previous studies.74–76The toluene permeance through the films was experimentally measured and theoretically predicted (Fig. 4d). Toluene is particularly interesting because it is a non-polar solvent that are widely used in various applications, such as in paints, cosmetics, lacquers, adhesives, textiles, and rubber industries. TAPA–Tf, which had the smallest pore size and was relatively thin (5.7 μm), exhibited a low solvent permeance (2.37 ± 0.28 L m−2 h−1 bar−1). The effect of film thickness on the toluene permeance was demonstrated by comparing TAPB–Tf and TZ–TF films. Although both films have identical pore sizes (3.2 nm), the thinner TZ–Tf film (5.2 μm) had a higher toluene permeance (3.91 ± 0.32 L m−2 h−1 bar−1) than the thicker TAPB–Tf film (6.6 μm; 2.59 ± 0.28 L m−2 h−1 bar−1). Thicker membrane possesses longer path for the molecular transport and increases the resistant between the solvent and pore walls which reduces the permeance. All the experimental toluene permeance values matched well with their predictive values. The permeances of toluene (a nonpolar solvent) through the fluorinated structures were higher compared to its permeances through the nonfluorinated structures; thus, confirming the nonpolar–nonpolar interaction that results in better wetting degrees and facilitates faster flow, hence higher permeances.
The rejection curves of TZ–Tf in various organic solvents are provided in Fig. 4e. Depending on the solvent used, the molecular weight cutoff (MWCO) values of TZ–Tf increased in the following order: methanol (841 g mol−1) < acetonitrile (1024 g mol−1) < acetone (1342 g mol−1) < toluene (1884 g mol−1). The interactions between solvents and solutes affect the mobility of the solutes by influencing the effective solute molecular size (i.e., Stokes radius) via solvation.77 Changes in the Stokes radius of the solutes in different solvents resulted in a noticeable rejection curve. As per the theoretical calculation correlating the Wilke–Chang solute diffusivity in different solvents (eqn (S11)) with the Stokes radius (eqn (S12)) in the ESI,† the solute molecular sizes decrease in the following order: methanol > acetonitrile > acetone > toluene (Fig. 4f). Therefore, the rejection in methanol is higher than that in other studied solvents.
The pure solvent fluxes through TZ–Tf were evaluated against various transmembrane pressures (TMPs) (Fig. 4g). Acetone exhibited the highest flux among the solvents because it has the lowest viscosity (viscosity = 0.30 (acetone), 0.37 (acetonitrile), 0.55 (methanol), and 0.59 (toluene) mPa s). Thus, the solvent resistance against the pore walls is minimized and the solvent flux is maximized in acetone. There is no apparent correlation between solvent flux and other solvent properties, such as molecular diameter, polarity, and molar volume (Fig. S62†). However, the solvent fluxes demonstrated a linear correlation with pressure, indicating the mechanical stability of membranes under high pressures and the absence of concentration polarization that can reduce the permeance. The experimental fluxes were in good agreement with the theoretically predicted values. The nanofiltration performance comparison with other relevant membranes were tabulated in Table S14.†
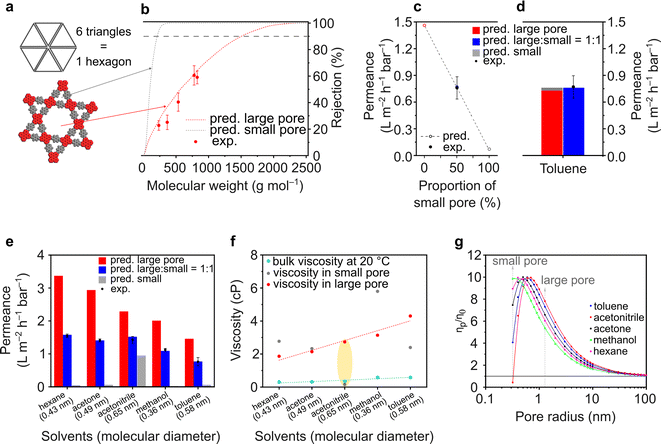
The ETTA–Tf film is particularly interesting because of the expected dual porosity in the structure. A small pore size of 0.7 nm is governed by a triangular geometry, while a large pore size of 2.6 nm is governed by a hexagonal geometry (Fig. 5a). To the best of our knowledge, this is the first report on the examination of nanofiltration using dual porosities via both experimental and theoretical approaches. In a conventional scenario, where isoporosity (only one pore size) is assumed, the pore flow model to predict solvent permeance and solute rejection can be directly applied, as done for TAPA–Tf, TAPB–Tf, and TZ–Tf films (Fig. 4). The details of the calculation methodology for isoporous structure have been previously demonstrated in several publications,3,4,78 and it is presented in the ESI (Section 3.1†). In a particular case in which the structure possesses dual porosity (e.g., ETTA–Tf), a modified pore flow predictive model was applied considering the ratio of the large and small pores.
For the heterostructure ETTA–Tf film, although the rejection curves can be theoretically calculated for both small and large pores, in reality, only the larger pores will govern the rejection because both small and large molecules can pass through the larger pores, which will determine the molecular weight cutoff (MWCO). Moreover, the triangular pore (0.7 nm) is too small for solute molecules to pass through. Therefore, the experimental rejection values only exhibited a single rejection curve, which coincided with the predictive rejection curve of the large pore (Fig. 5b).
The pore flow model enabled the prediction of the solvent (toluene) permeance in various pore assemblance scenarios (Fig. 5c). If the structure was constructed only by assembling large hexagonal pores, the toluene permeance exhibited the highest predicted value at 1.46 L m−2 h−1 bar−1. Whereas, if the structure was assembled only with the smaller triangular pores, the solvent permeance exhibited the lowest predicted value at 0.07 L m−2 h−1 bar−1. Depending on the proportion of the small triangular and large hexagonal pores forming the structure, the predicted solvent permeance values fall between completely hexagonal and completely triangular pore configurations. Interestingly, the experimental toluene permeance exhibited a value of 0.76 ± 0.13 L m−2 h−1 bar−1, which matched very well with the predicted permeance value (0.77 L m−2 h−1 bar−1) when the structure comprised small and large pores in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Indeed, as shown in Fig. 5a, the ETTA–Tf structure is governed by six units of small triangular pores and one unit of large hexagonal pore. The total area of the six units of small triangular pores is equal to that of one unit of the large hexagonal pore. Thus, the ETTA–Tf structure contains small triangular and large hexagonal pore sizes in equal proportions. The geometrical ratio in the structure is not linearly translated into permeance value. The solvent permeance is affected by: (1) pore area (accessible area for molecular transport), (2) porosity (ratio between accessible and inaccessible area), and (3) solvent viscosity in confined space. In the particular case of toluene, the pore area, porosity, and solvent viscosity in hexagonal pores are higher than those in triangular pores by ∼17 times, ∼2.5 times, and ∼1.2 times. Unconventionally, the combination of toluene molecular size and smaller triangular pore size resulted in the viscosity value which is higher than the viscosity in the larger hexagonal pore size. Considering all these parameters, theoretically, the smaller triangular pores in the heterostructure ETTA allowed for the permeance of 0.03 L m−2 h−1 bar−1. Meanwhile, the larger hexagonal pores allowed for the permeance of 0.73 L m−2 h−1 bar−1, which is 24 times higher than that in triangular pores, or in other words, governing 96% of the permeance (Fig. 5d).
1 ratio. Indeed, as shown in Fig. 5a, the ETTA–Tf structure is governed by six units of small triangular pores and one unit of large hexagonal pore. The total area of the six units of small triangular pores is equal to that of one unit of the large hexagonal pore. Thus, the ETTA–Tf structure contains small triangular and large hexagonal pore sizes in equal proportions. The geometrical ratio in the structure is not linearly translated into permeance value. The solvent permeance is affected by: (1) pore area (accessible area for molecular transport), (2) porosity (ratio between accessible and inaccessible area), and (3) solvent viscosity in confined space. In the particular case of toluene, the pore area, porosity, and solvent viscosity in hexagonal pores are higher than those in triangular pores by ∼17 times, ∼2.5 times, and ∼1.2 times. Unconventionally, the combination of toluene molecular size and smaller triangular pore size resulted in the viscosity value which is higher than the viscosity in the larger hexagonal pore size. Considering all these parameters, theoretically, the smaller triangular pores in the heterostructure ETTA allowed for the permeance of 0.03 L m−2 h−1 bar−1. Meanwhile, the larger hexagonal pores allowed for the permeance of 0.73 L m−2 h−1 bar−1, which is 24 times higher than that in triangular pores, or in other words, governing 96% of the permeance (Fig. 5d).
The effect of dual porosities on the permeances of various solvents is shown in Fig. 5e. Interestingly, all the tested solvents exhibited similar trends where the experimentally measured permeance matched the predicted value well in the case of structures comprising small and large pores in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. These findings validate the robustness of our developed theoretical model. As expected, the predicted solvent permeance through large pores decreases as the viscosity of the solvents in these pores increases (Fig. 5e and f). However, the predicted solvent permeance through the small pores exhibited anomalies; among the solvents, acetonitrile had the highest permeance through the small pores though its molecule size is the largest (0.65 nm). These anomalies were also reflected in the viscosity plots (Fig. 5f and g), where the viscosity of acetonitrile is lower than its bulk viscosity. These anomalies arise because the pore flow model (used to calculate the permeance and effective viscosity) only considered physical parameters, such as pore size, solvent viscosity, and solvent diameter, but did not take into account the molecular interaction (such as between pore walls and solvent molecules). The pore flow model was successfully used to predict the permeance through both large and small pores. Importantly, the viscosity must be critically evaluated because of its anomalies in the confined space. It is worth noting that the viscosity of a fluid in a confined space differs from its bulk viscosity.79,80 According to the theoretical calculation on the viscosity inside a confined space (eqn (S24)†), when the pore size is larger than the size of the molecules (as in the case of methanol, hexane, acetone, and toluene), the viscosity initially increases dramatically until it reaches a critical value after which it started decreasing to approach its bulk viscosity value (Fig. 5g). This is because when the pore size is very small, the interactions between the pore wall and solvent molecules become significant, and the diffusing molecules undergo more frequent reflections at the wall, thereby reducing the diffusivity.79,81 The nanofiltration investigation of the heteropore film provided new insights into the fundamental understanding of molecular transportation through materials with multiple pore sizes.
1 ratio. These findings validate the robustness of our developed theoretical model. As expected, the predicted solvent permeance through large pores decreases as the viscosity of the solvents in these pores increases (Fig. 5e and f). However, the predicted solvent permeance through the small pores exhibited anomalies; among the solvents, acetonitrile had the highest permeance through the small pores though its molecule size is the largest (0.65 nm). These anomalies were also reflected in the viscosity plots (Fig. 5f and g), where the viscosity of acetonitrile is lower than its bulk viscosity. These anomalies arise because the pore flow model (used to calculate the permeance and effective viscosity) only considered physical parameters, such as pore size, solvent viscosity, and solvent diameter, but did not take into account the molecular interaction (such as between pore walls and solvent molecules). The pore flow model was successfully used to predict the permeance through both large and small pores. Importantly, the viscosity must be critically evaluated because of its anomalies in the confined space. It is worth noting that the viscosity of a fluid in a confined space differs from its bulk viscosity.79,80 According to the theoretical calculation on the viscosity inside a confined space (eqn (S24)†), when the pore size is larger than the size of the molecules (as in the case of methanol, hexane, acetone, and toluene), the viscosity initially increases dramatically until it reaches a critical value after which it started decreasing to approach its bulk viscosity value (Fig. 5g). This is because when the pore size is very small, the interactions between the pore wall and solvent molecules become significant, and the diffusing molecules undergo more frequent reflections at the wall, thereby reducing the diffusivity.79,81 The nanofiltration investigation of the heteropore film provided new insights into the fundamental understanding of molecular transportation through materials with multiple pore sizes.
Conclusions
In summary, four fluorinated imine-linked 2D CPOPs were synthesized using a facile drop-cast approach that produced free-standing, flexible films of adaptable thickness and surface areas. The distinct building blocks of each polymer enabled the construction of different 2D CPOPs with various pore sizes (between 2.6 and 3.2 nm) and skeletal backbone functionalities. The fabricated films comprised tightly packed layered sheets and could easily be exfoliated into nanometer-thick sheets of large domains. Fluorinated 2D CPOP films exhibited increased hydrophobicity, higher flexibility, and greater hardness than their nonfluorinated counterparts while still possessing superior nanomechanical properties. The films exhibited mechanical stability under high pressure (up to 30 bar) during the nanofiltration experiment. The nanofiltration performance was successfully controlled by tuning the pore size and functionality of the 2D CPOPs. Particularly, the ratio of large and small pores in heteropore 2D CPOP structures is essential for regulating its nanofiltration performance. The larger pores control the molecular weight cutoff (MWCO) while allowing the solvent molecules to pass through, whereas the smaller pores only act as channels for solvent transport.Experimental section
Film synthesis
Fluorinated films were synthesized through condensation reactions between bi-functional aldehyde monomer Tf with either tri-(TAPB, TAPA, TZ) or tetra-functionalized (ETTA) amine monomers. To form TAPB–Tf, TAPA–Tf, and TZ–Tf films, 0.0317 mmol of TAPB, TAPA, or TZ was dissolved with 0.0476 mmol Tf in 1.5 mL of dioxane to form a dilute precursor solution. The dispersity of the particles in the solution was analyzed using Tyndall test by illuminating laser through the precursor solution. An observable scattered light was clearly visible along the path of the beam, indicating that the solution is colloidal, containing the particles with the size in between 1–1000 nm. A continuous beam line through the solution indicating that the particles are well dispersed. For ETTA–Tf film, the same method was modified to adjust for proper molar ratios using 0.0264 mmol ETTA and 0.0528 mmol for Tf. Synthesis of nonfluorinated films (–TP) followed the previously reported method.40 More synthetic details are mentioned in the ESI.†Nanofiltration experiment
A nanofiltration experiment was performed using a crossflow membrane unit (Fig. S63†) at various TMPs of 1–40 bar, a feed flow rate of 3 L h−1, and a crossflow volume rate of 100 L h−1 in toluene at room temperature. Toluene was selected as the solvent in this filtration experiment because it is one of the most commonly used solvents in OSN. In addition, we also provided a set of filtration results under different solvents, such as acetone, acetonitrile, and methanol. Crossflow experiments were conducted with multiple membrane samples to ensure reproducibility and to ensure that the permeate and retentate were recycled for long-term experiments to warrant a constant feed concentration. The permeate (Vpermeate) was collected, and the collection period (t) was recorded after reaching a steady state. The flux of the studied organic solvents was calculated using eqn (1) for an effective membrane area of 10 cm2. The solutes used for nanofiltration experiments are listed in Table S9 in the ESI.† Samples from the feed and permeate were collected and analyzed by high-performance liquid chromatography to calculate the rejection of the prepared membranes using the concentration of the solute in feed (Cf) and permeate (Cp), as shown in eqn (2). Nine solutes in the feed stream with different molecular weights were tested to determine the MWCO for the membranes. The reported results are the average values of at least two independently prepared membranes.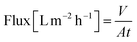 | (1) |
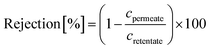 | (2) |
Data availability
Data supporting the findings of this study have been included as part of the ESI† and additional data are available from the corresponding authors upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
SR and PMA would like to acknowledge U.S. Air Force Office of Scientific Research and Clarkson Aerospace Corp. under Award FA9550-21-1-0460 for funding support. Special acknowledgment to Rice University's Shared Equipment Authority (SEA) for providing resources for SS-13C-NMR studies. RH and GS acknowledge the financial support from the King Abdullah University of Science and Technology (KAUST). The Table of Content illustration and Fig. 1 were created by Ana Bigio, a scientific illustrator at KAUST.References
- J.-S. M. Lee and A. I. Cooper, Chem. Rev., 2020, 120, 2171–2214 CrossRef CAS PubMed.
- D. Rodríguez-San-Miguel and F. Zamora, Chem. Soc. Rev., 2019, 48, 4375–4386 RSC.
- R. Hardian, K. A. Miller, L. Cseri, S. Roy, J. M. Gayle, R. Vajtai, P. M. Ajayan and G. Szekely, Chem. Eng. J., 2023, 452, 139457 CrossRef CAS.
- K. Miller, J. M. Gayle, S. Roy, M. H. Abdellah, R. Hardian, L. Cseri, P. G. Demingos, H. R. Nadella, F. Lee, M. Tripathi, S. Gupta, G. Guo, S. Bhattacharyya, X. Wang, A. B. Dalton, A. Garg, C. V. Singh, R. Vajtai, G. Szekely and P. Ajayan, Small, 2024, 2401269 CrossRef PubMed.
- B. Liang, H. Wang, X. Shi, B. Shen, X. He, Z. A. Ghazi, N. A. Khan, H. Sin, A. M. Khattak, L. Li and Z. Tang, Nat. Chem., 2018, 10, 961–967 CrossRef CAS PubMed.
- C. Wang, C. Li, E. R. C. Rutledge, S. Che, J. Lee, A. J. Kalin, C. Zhang, H.-C. Zhou, Z.-H. Guo and L. Fang, J. Mater. Chem. A, 2020, 8, 15891–15899 RSC.
- R. P. Lively and D. S. Sholl, Nat. Mater., 2017, 16, 276–279 CrossRef CAS PubMed.
- M. Galizia and K. P. Bye, Front. Chem., 2018, 6, 511 CrossRef PubMed.
- Z. Wang, S. Zhang, Y. Chen, Z. Zhang and S. Ma, Chem. Soc. Rev., 2020, 49, 708–735 RSC.
- S. B. Alahakoon, G. T. McCandless, A. A. K. Karunathilake, C. M. Thompson and R. A. Smaldone, Chem.–Eur. J., 2017, 23, 4255–4259 CrossRef CAS PubMed.
- C. Kang, Z. Zhang, A. K. Usadi, D. C. Calabro, L. S. Baugh, K. Yu, Y. Wang and D. Zhao, J. Am. Chem. Soc., 2022, 144, 3192–3199 CrossRef CAS PubMed.
- L. Zhang, S.-L. Wang, G.-H. Zhang, N. Shen, H. Chen, G. Tao, G.-H. Tao, F. Yong, J. Fu, Q.-H. Zhu and L. He, Cell Rep. Phys. Sci., 2022, 101114 CrossRef CAS.
- N. Han, Z. Zhang, H. Gao, Y. Qian, L. Tan, C. Yang, H. Zhang, Z. Cui, W. Li and X. Zhang, ACS Appl. Mater. Interfaces, 2020, 12, 2926–2934 CrossRef CAS PubMed.
- S. Mukherjee, Z. Zeng, M. M. Shirolkar, P. Samanta, A. K. Chaudhari, J.-C. Tan and S. K. Ghosh, Chem.–Eur. J., 2018, 24, 11771–11778 CrossRef CAS PubMed.
- Z. Liu, Q. Su, P. Ju, X. Li, G. Li, Q. Wu and B. Yang, Chem. Commun., 2020, 56, 766–769 RSC.
- Z. Li, S. Das, T. Sekine, H. Mabuchi, R. Kaneko, J. Sakai, T. Irie, E. Kamio, T. Yoshioka, J. Suo, Q. Fang, T. Kawawaki, H. Matsuyama and Y. Negishi, ACS Appl. Nano Mater., 2022, 5, 17632–17639 CrossRef CAS.
- R.-R. Liang, S.-Y. Jiang, R.-H. A and X. Zhao, Chem. Soc. Rev., 2020, 49, 3920–3951 RSC.
- R.-R. Liang and X. Zhao, Org. Chem. Front., 2018, 5, 3341–3356 RSC.
- S.-Y. Jiang, Z.-B. Zhou, S.-X. Gan, Y. Lu, C. Liu, Q.-Y. Qi, J. Yao and X. Zhao, Nat. Commun., 2024, 15, 698 CrossRef CAS PubMed.
- Y. Tian, S.-Q. Xu, R.-R. Liang, C. Qian, G.-F. Jiang and X. Zhao, CrystEngComm, 2017, 19, 4877–4881 RSC.
- X. Liu, Y. Xu and D. Jiang, J. Am. Chem. Soc., 2012, 134, 8738–8741 CrossRef CAS PubMed.
- X. Li, Q. Gao, J. Wang, Y. Chen, Z.-H. Chen, H.-S. Xu, W. Tang, K. Leng, G.-H. Ning, J. Wu, Q.-H. Xu, S. Y. Quek, Y. Lu and K. P. Loh, Nat. Commun., 2018, 9, 2335 CrossRef PubMed.
- Y. Tian, S.-Q. Xu, C. Qian, Z.-F. Pang, G.-F. Jiang and X. Zhao, Chem. Commun., 2016, 52, 11704–11707 RSC.
- J. Gong, R.-B. Lin and B. Chen, Chem, 2018, 4, 2269–2271 CAS.
- H. Fan, A. Mundstock, J. Gu, H. Meng and J. Caro, J. Mater. Chem. A, 2018, 6, 16849–16853 RSC.
- M. Liu, Y. Liu, J. Dong, Y. Bai, W. Gao, S. Shang, X. Wang, J. Kuang, C. Du, Y. Zou, J. Chen and Y. Liu, Nat. Commun., 2022, 13, 1411 CrossRef CAS PubMed.
- Z. Liu, Y. Yin, M. Eginligil, L. Wang, J. Liu and W. Huang, Polym. Chem., 2021, 12, 807–821 RSC.
- J. Liu, G. Han, D. Zhao, K. Lu, J. Gao and T.-S. Chung, Sci. Adv., 2020, 6, eabb1110 CrossRef CAS PubMed.
- M. Matsumoto, L. Valentino, G. M. Stiehl, H. B. Balch, A. R. Corcos, F. Wang, D. C. Ralph, B. J. Mariñas and W. R. Dichtel, Chem, 2018, 4, 308–317 CAS.
- F. Yu, W. Liu, B. Li, D. Tian, J.-L. Zuo and Q. Zhang, Angew. Chem., Int. Ed., 2019, 58, 16101–16104 CrossRef CAS PubMed.
- Y. Li, Q. Wu, X. Guo, M. Zhang, B. Chen, G. Wei, X. Li, X. Li, S. Li and L. Ma, Nat. Commun., 2020, 11, 599 CrossRef CAS PubMed.
- Q. Liao, C. Ke, X. Huang, G. Zhang, Q. Zhang, Z. Zhang, Y. Zhang, Y. Liu, F. Ning and K. Xi, J. Mater. Chem. A, 2019, 7, 18959–18970 RSC.
- Y. Jiang, L. Cao, X. Hu, Z. Ren, C. Zhang and C. Wang, Inorg. Chem., 2018, 57, 15123–15132 CrossRef CAS PubMed.
- F. T. Johra, J.-W. Lee and W.-G. Jung, J. Ind. Eng. Chem., 2014, 20, 2883–2887 CrossRef CAS.
- B. Gupta, N. Kumar, K. Panda, V. Kanan, S. Joshi and I. Visoly-Fisher, Sci. Rep., 2017, 7, 45030 CrossRef CAS PubMed.
- J. Park, J. Sharma, C. J. Jafta, L. He, H. M. Meyer, J. Li, J. K. Keum, N. A. Nguyen and G. Polizos, Batteries, 2022, 8, 12 CrossRef CAS.
- R. Xu, W. B. Schweizer and H. Frauenrath, J. Am. Chem. Soc., 2008, 130, 11437–11445 CrossRef CAS PubMed.
- E. Elacqua, K. B. Manning, D. S. Lye, S. K. Pomarico, F. Morgia and M. Weck, J. Am. Chem. Soc., 2017, 139, 12240–12250 CrossRef CAS PubMed.
- K. A. Miller, L. B. Alemany, S. Roy, Q. Yan, P. G. Demingos, C. V. Singh, S. Alahakoon, E. Egap, E. L. Thomas and P. M. Ajayan, ACS Appl. Mater. Interfaces, 2022, 14, 1861–1873 CrossRef CAS PubMed.
- J. Gayle, S. Roy, S. Gupta, S. Hassan, A. Rao, P. G. Demingos, K. Miller, G. Guo, X. Wang, A. Garg, C. V. Singh, R. Vajtai, J. T. Robinson and P. M. Ajayan, ACS Appl. Mater. Interfaces, 2024, 16, 2726–2739 CrossRef CAS PubMed.
- X. Chen, M. Addicoat, S. Irle, A. Nagai and D. Jiang, J. Am. Chem. Soc., 2013, 135, 546–549 CrossRef CAS PubMed.
- G. Jiang, W. Zou, Z. Ou, L. Zhang, W. Zhang, X. Wang, H. Song, Z. Cui, Z. Liang and L. Du, Angew. Chem., Int. Ed., 2022, 61, e202208086 CrossRef CAS PubMed.
- D.-G. Wang, N. Li, Y. Hu, S. Wan, M. Song, G. Yu, Y. Jin, W. Wei, K. Han, G.-C. Kuang and W. Zhang, ACS Appl. Mater. Interfaces, 2018, 10, 42233–42240 CrossRef CAS PubMed.
- D. Sheehan, A. P. Bentz and J. C. Petropoulos, J. Appl. Polym. Sci., 1962, 6, 47–56 CrossRef CAS.
- N. Z. Tomić, in Compatibilization of Polymer Blends, ed. A. R. Ajitha and S. Thomas, Elsevier, 2020, pp. 489–510 Search PubMed.
- I. B. Johns, E. A. McElhill and J. O. Smith, J. Chem. Eng. Data, 1962, 7, 277–281 CrossRef CAS.
- A. M. Evans, M. R. Ryder, W. Ji, M. J. Strauss, A. R. Corcos, E. Vitaku, N. C. Flanders, R. P. Bisbey and W. R. Dichtel, Faraday Discuss., 2021, 225, 226–240 RSC.
- J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080 RSC.
- J. C. Tan, J. D. Furman and A. K. Cheetham, J. Am. Chem. Soc., 2009, 131, 14252–14254 CrossRef CAS PubMed.
- Z. Wei, G. Zhang, H. Chen, J. Luo, R. Liu and S. Guo, J. Mater. Res., 2009, 24, 801–815 CrossRef CAS.
- Development of Semi-empirical Formulation for Extracting Materials Properties from Nanoindentation Measurements, https://ocul-gue.primo.exlibrisgroup.com, accessed November 12, 2022 Search PubMed.
- S. Mohata, K. Dey, S. Bhunia, N. Thomas, E. B. Gowd, T. G. Ajithkumar, C. M. Reddy and R. Banerjee, J. Am. Chem. Soc., 2022, 144, 400–409 CrossRef CAS PubMed.
- J. C. Tan, T. D. Bennett and A. K. Cheetham, Proc. Natl. Acad. Sci. USA, 2010, 107, 9938–9943 CrossRef CAS PubMed.
- A. C. Pinho and A. P. Piedade, ACS Appl. Mater. Interfaces, 2013, 5, 8187–8194 CrossRef CAS PubMed.
- J. Gayle, S. Roy, S. Gupta, S. Hassan, A. Rao, P. G. Demingos, K. Miller, G. Guo, X. Wang, A. Garg, C. V. Singh, R. Vajtai, J. T. Robinson and P. M. Ajayan, ACS Appl. Mater. Interfaces, 2024, 16, 2726–2739 CrossRef CAS PubMed.
- R. Xia, H. Zhou, Z. Zhang, R. Wu and W.-P. Wu, Polym. Eng. Sci., 2018, 58, 2071–2077 CrossRef CAS.
- Y. Zhu, H. Wang, J. Zhu, L. Chang and L. Ye, Appl. Surf. Sci., 2015, 349, 27–34 CrossRef CAS.
- T. Roopa, H. N. Murthy, D. Harish, A. Jain and G. Angadi, Polym. Polym. Compos., 2021, 29, 198–206 CAS.
- K. Dey, S. Bhunia, H. S. Sasmal, C. M. Reddy and R. Banerjee, J. Am. Chem. Soc., 2021, 143, 955–963 CrossRef CAS PubMed.
- A. Mukhtar, N. Mellon, S. Saqib, S.-P. Lee and M. A. Bustam, SN Appl. Sci., 2020, 2, 1232 CrossRef CAS.
- J. Garrido, A. Linares-Solano, J. M. Martin-Martinez, M. Molina-Sabio, F. Rodriguez-Reinoso and R. Torregrosa, Langmuir, 1987, 3, 76–81 CrossRef CAS.
- R. Haul, Ber. Bunsenges. Phys. Chem., 1982, 86, 957 CrossRef.
- P. Zhang, K. Wu, J. Guo and C. Wang, ACS Macro Lett., 2014, 3, 1139–1144 CrossRef CAS PubMed.
- R. Chen, T. Hu, W. Zhang, C. He and Y. Li, Microporous Mesoporous Mater., 2021, 312, 110739 CrossRef CAS.
- X. Wang, B. Shi, H. Yang, J. Guan, X. Liang, C. Fan, X. You, Y. Wang, Z. Zhang, H. Wu, T. Cheng, R. Zhang and Z. Jiang, Nat. Commun., 2022, 13, 1020 CrossRef CAS PubMed.
- S. Sorribas, P. Gorgojo, C. Téllez, J. Coronas and A. G. Livingston, J. Am. Chem. Soc., 2013, 135, 15201–15208 CrossRef CAS PubMed.
- X. Li, Y. Wang, X. Lu and C. Xiao, J. Membr. Sci., 2008, 320, 477–482 CrossRef CAS.
- J. H. Kim, Y. Choi, J. Kang, J. Y. Kim, J. H. Bae, O. Kwon and D. W. Kim, Carbon, 2022, 191, 563–570 CrossRef CAS.
- F. Wang, Z. Zhang, I. Shakir, C. Yu and Y. Xu, Adv. Sci., 2022, 9, 2103814 CrossRef CAS PubMed.
- J. Li, X. Jing, Q. Li, S. Li, X. Gao, X. Feng and B. Wang, Chem. Soc. Rev., 2020, 49, 3565–3604 RSC.
- L. G. Trung, S. Subedi, A. K. Rella, V. Kumar and S.-W. Kang, Liq. Cryst., 2021, 1–11 Search PubMed.
- H. Yang, H. Jussila, A. Autere, H.-P. Komsa, G. Ye, X. Chen, T. Hasan and Z. Sun, ACS Photonics, 2017, 4, 3023–3030 CrossRef CAS.
- S. Wang, Y. Yang, H. Zhang, Z. Zhang, C. Zhang, X. Huang, D. Kozawa, P. Liu, B.-G. Li and W.-J. Wang, J. Am. Chem. Soc., 2021, 143, 5003–5010 CrossRef CAS PubMed.
- R. Hardian, A. Ghaffar, C. Shi, E. Y.-X. Chen and G. Szekely, J. Membr. Sci. Let., 2024, 4, 100067 CrossRef.
- A. Miao, M. Wei, F. Xu and Y. Wang, J. Membr. Sci., 2020, 604, 118087 CrossRef CAS.
- Q. Xu, Y. Yang, X. Wang, Z. Wang, W. Jin, J. Huang and Y. Wang, J. Membr. Sci., 2012, 415–416, 435–443 CrossRef CAS.
- C. Ji, S. Xue, C.-W. Lin, W. H. Mak, B. T. McVerry, C. L. Turner, M. Anderson, J. C. Molas, Z. Xu and R. B. Kaner, ACS Appl. Mater. Interfaces, 2020, 12, 30796–30804 CrossRef CAS PubMed.
- L. Cseri, R. Hardian, S. Anan, H. Vovusha, U. Schwingenschlögl, P. M. Budd, K. Sada, K. Kokado and G. Szekely, J. Mater. Chem. A, 2021, 9, 23793–23801 RSC.
- S. Álvarez-Quintana, F. J. Carmona, L. Palacio, A. Hernández and P. Prádanos, Microporous Mesoporous Mater., 2020, 303, 110289 CrossRef.
- S. K. Bhatia, M. R. Bonilla and D. Nicholson, Phys. Chem. Chem. Phys., 2011, 13, 15350–15383 RSC.
- S. K. Bhatia and D. Nicholson, J. Chem. Phys., 2007, 127, 124701 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Detailed methodology, synthesis, characterizations, and nanofiltration studies. See DOI: https://doi.org/10.1039/d4ta04342a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |