Open Access Article
Open Access ArticleCO2 adsorption in natural deep eutectic solvents: insights from quantum mechanics and molecular dynamics†
Chengxu
Zhu
 ab,
Hannah
Wood
ab,
Hannah
Wood
 c,
Paola
Carbone
c,
Paola
Carbone
 c,
Carmine
D’Agostino
c,
Carmine
D’Agostino
 *bd and
Sam P.
de Visser
*bd and
Sam P.
de Visser
 *ab
*ab
aManchester Institute of Biotechnology, The University of Manchester, 131 Princess Street, Manchester M1 7DN, UK. E-mail: sam.devisser@manchester.ac.uk
bDepartment of Chemical Engineering, The University of Manchester, Oxford Road, Manchester M13 9PL, UK
cDepartment of Chemistry, The University of Manchester, Oxford Road, Manchester M13 9PL, UK
dDipartimento di Ingegneria Civile, Chimica, Ambientale e dei Materiali (DICAM), Alma Mater Studiorum – Università di Bologna, Via Terracini, 28, 40131, Bologna, Italy
First published on 6th January 2025
Abstract
CO2 capture is an important process for mitigating CO2 emissions in the atmosphere. Recently, ionic liquids have been identified as possible systems for CO2 capture processes. Major drawbacks of such systems are mostly in the high cost of synthesis of such liquids and poor biodegradability. Natural deep eutectic solvents, a class of eutectic solvents using materials of natural origin, have been developed, which compared to ionic liquids are low-cost and more environmentally benign. However, very little is known on the details at a molecular level that govern the CO2 adsorption in these systems and what the limits are of the adsorption features. Elucidating such aspects would represent a step forward in the design and implementation of such promising systems in mitigating CO2 emissions. Herein, we report a computational study on the mechanisms and characteristics of CO2 adsorption in natural deep eutectic solvents containing arginine/glycerol mixtures. We establish details of the hydrogen bonding effects that drive the carbon dioxide capture in systems composed of L-arginine and glycerol using molecular dynamics and quantum mechanics simulations. Our findings indicate that, although both arginine and glycerol contain multiple atoms capable of acting as hydrogen bond donors and hydrogen bond acceptors, L-arginine primarily functions as the hydrogen bond acceptor while glycerol serves as the hydrogen bond donor in most interactions. Furthermore, both compounds contribute hydrogen bond donors that participate in CO2 binding. This study provides valuable insights into the behaviour of CO2 adsorption in natural deep eutectic solvents and enhances our understanding from the perspective of hydrogen bonding interactions.
Introduction
Carbon dioxide (CO2) emissions from excessive combustion of fossil fuels are a significant contributor to the adverse climate change. Scientific research, therefore, is pushing the boundaries on either CO2 utilization or CO2 capture.1 The utilization of CO2 is challenging due to its strong and inert C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds. Consequently, CO2 capture and storage plays a crucial role in mitigating the total emissions. In recent years, ionic liquids (ILs) have emerged as promising adsorbents of CO2 due to their unique properties, such as high stability, non-flammability, and very low vapor pressure.2 The ILs offer the potential for customization with over 1018 possible combinations, allowing the design of specific ILs for targeted CO2 capture.3 However, the synthesis of ILs involves complex chemical reactions and purification steps that increase their cost dramatically. Additionally, some ILs are toxic and poorly biodegradable, and their high viscosity often limits large-scale applications.4 To address these drawbacks, deep eutectic solvents (DES) have garnered attention as novel environmentally benign alternatives for CO2 capture.5 DES share many characteristics with ILs, such as very low vapor pressure and tunable performance.6 Moreover, DES offer significant advantages over ILs, including low cost, renewability, low toxicity, reduced environmental impact, and efficient solvent recovery.7 DES are formed by mixing a hydrogen bond donor with a hydrogen bond acceptor in specific molar ratios, resulting in a substantial decrease in the melting or solidification temperature due to intermolecular hydrogen bonds.8 These attractive properties have led to extensive research on DES in various fields, including CO2 capture.9
O bonds. Consequently, CO2 capture and storage plays a crucial role in mitigating the total emissions. In recent years, ionic liquids (ILs) have emerged as promising adsorbents of CO2 due to their unique properties, such as high stability, non-flammability, and very low vapor pressure.2 The ILs offer the potential for customization with over 1018 possible combinations, allowing the design of specific ILs for targeted CO2 capture.3 However, the synthesis of ILs involves complex chemical reactions and purification steps that increase their cost dramatically. Additionally, some ILs are toxic and poorly biodegradable, and their high viscosity often limits large-scale applications.4 To address these drawbacks, deep eutectic solvents (DES) have garnered attention as novel environmentally benign alternatives for CO2 capture.5 DES share many characteristics with ILs, such as very low vapor pressure and tunable performance.6 Moreover, DES offer significant advantages over ILs, including low cost, renewability, low toxicity, reduced environmental impact, and efficient solvent recovery.7 DES are formed by mixing a hydrogen bond donor with a hydrogen bond acceptor in specific molar ratios, resulting in a substantial decrease in the melting or solidification temperature due to intermolecular hydrogen bonds.8 These attractive properties have led to extensive research on DES in various fields, including CO2 capture.9
DES like ILs can be classified as physical or chemical adsorbers for CO2 capture. Most conventional DES capture CO2 through physical adsorption, while functionalized DES, such as those based on strong bases, capture CO2 chemically.10 In a 2011 report, Choi et al.11 introduced natural low eutectic solvents (NaDES) as a new type of green DES. NaDES are synthesized by heating environmentally friendly natural materials like primary metabolites, carboxylic acids, amino acids, choline chloride, sugars, and urea without further purification. These solvents are produced with 100% atom economy and exhibit lower sensitivity to impurities compared to ILs, making them highly suitable for CO2 capture.12 In particular, NaDES were shown to adsorb CO2 better in alkaline environments, lead to viscosity changes and have more volatility than ionic liquids.13,14
The greatest potential of DES and NADES lies in their application as designer solvents. By adjusting the type of hydrogen bond acceptor and hydrogen bond donor and their molar ratios, it is possible to design solvents with specific properties. The hydrogen bonding network between the components largely determines the behavior of a given mixture, influencing properties such as surface tension, melting point, and viscosity.15 The type and molar ratio of hydrogen bond acceptor and hydrogen bond donor in DES and NaDES also affect their CO2 uptake capacity.16
NaDES based on L-arginine (L-Arg) and glycerol (Gly) can be used for CO2 capture.17 The multiple atoms in arginine and glycerol that act as both hydrogen bond acceptor and hydrogen bond donor create a complex hydrogen bonding network within NaDES. CO2 capture through hydrogen bonding implies sequential binding of CO2 to multiple hydrogen bond donor atoms in L-arginine and glycerol. Currently, no systematic study has investigated the hydrogen bonding in L-arginine/glycerol mixtures and their adsorption ability of CO2, and little is known on the role of the different species in the NaDES in the CO2 adsorption mechanism. Therefore, this study aims to explore the mechanism of hydrogen bonding affecting CO2 uptake in NaDES using molecular dynamics and quantum mechanics simulations. The work provides new insights into hydrogen bonding mechanisms in NaDES and their ability to adsorb CO2 efficiently. Furthermore, the calculations offer theoretical guidance for developing more efficient CO2 capture technologies.
Methodology
Model set-up
The starting structures were generated using Packmol (version 18.104).18 model A is a cubic box of 3 × 3 × 3 nm dimensions containing one L-arginine molecule in the centre of the box surrounded by 200 glycerol molecules randomly placed (designated 1A200G box). In addition, different molar ratios of arginine versus glycerol ranging from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to 1
3 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 with models in a box of 5 × 5 × 5 nm size were explored (model B). The model B structures were used to verify the accuracy of the force field parameters and charges used, and from the results the simulated density values of the NaDESs were determined and compared with the experimental values (shown in Table S1, ESI†). A final model (model C) is a chemical system with three equal-size compartments that is symmetric around the z-axis with a liquid phase in the middle and two gas-phase regions on each side, designated the interfacial system, with overall size 5 × 5 × 15 nm.
9 with models in a box of 5 × 5 × 5 nm size were explored (model B). The model B structures were used to verify the accuracy of the force field parameters and charges used, and from the results the simulated density values of the NaDESs were determined and compared with the experimental values (shown in Table S1, ESI†). A final model (model C) is a chemical system with three equal-size compartments that is symmetric around the z-axis with a liquid phase in the middle and two gas-phase regions on each side, designated the interfacial system, with overall size 5 × 5 × 15 nm.
Molecular dynamics simulations
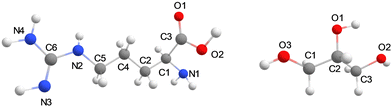
The general protocol of the set-up of our MD simulations follows previously reported and validated methods.19 The molecular structures of glycerol, L-arginine, and CO2 were generated using Gauss View 6.0.20 The optimized geometries of the isolated molecules were obtained at B3LYP/def2-TZVP level of theory in Gaussian-09 with the CPCM solvation model for water and the GD3BJ dispersion correction included.21–23 The molecular charges of those structures were taken from the restrained electrostatic potential (RESP) method and used as forcefield parameters for the MD simulations. The optimized structures were parameterized using the general amber force field (GAFF) via the ANTECHAMBER module.24 The generated topology files were then converted to GROMACS format using the ACPYPE code.25 All molecular dynamics (MD) simulations were performed using the Gromacs-2020.3 software package.25 Structures of L-arginine and glycerol and their atom definitions are shown in Fig. 1. The GAFF parameters of each component in the mixture for the MD simulation, including CO2, arginine, and glycerol are shown in Tables S2–S5, ESI.† To test the validity of the forcefield parameters, we ran test calculations on a pure glycerol liquid using the GAFF and Lennard-Jones refined GAFF forcefields,24,26 and calculated densities of 1272 and 1199 kg m−3, respectively. As such the GAFF forcefield gives a density that is closer to the experimental value of 1260 kg m−3,27 and hence was used in this work.For models A and B, the energy was minimized, and a 1 ns simulation under the NVT ensemble conditions was performed to equilibrate the system temperature to the predefined value of 298 K. Thereafter, a 10 ns (model A) and 100 ns (model B) MD simulation under NPT ensemble conditions with a pressure of 1 bar was conducted. During the final 2 ns of the production simulation, the hydrogen bonding analysis was performed on the interactions between the arginine and its surrounding glycerol molecules. Hydrogen bonds were defined based on geometric criteria: molecules were considered hydrogen-bonded if the donor–acceptor distance was within 3.5 Å and the donor-hydrogen-acceptor angle was less than or equal to 30°. The velocity Verlet algorithm with a step size of 1 fs was used to obtain the trajectory of atoms in the whole system.28 Periodic boundary conditions were applied in all three spatial dimensions. The cut-off radius for both van der Waals and electrostatic interactions was set to 1.3 nm. For model C the energy was minimized and the system was equilibrated to 298 K for 1 ns and then an MD simulation was carried out under the NVT ensemble for 100 ns.
Quantum mechanics calculations
All quantum chemical calculations were performed using Density Functional Theory (DFT) with the unrestricted B3LYP-GD3BJ method21 in combination with the def2-TZVP basis set.22 The software used for the quantum chemical calculations was the Gaussian-09 software package.23 Structures containing a hydrogen bond donor and acceptor were taken from the MD snapshots and their interaction energy calculated through single-point calculations.Results and discussion
Hydrogen bond interactions between one arginine molecule with glycerol
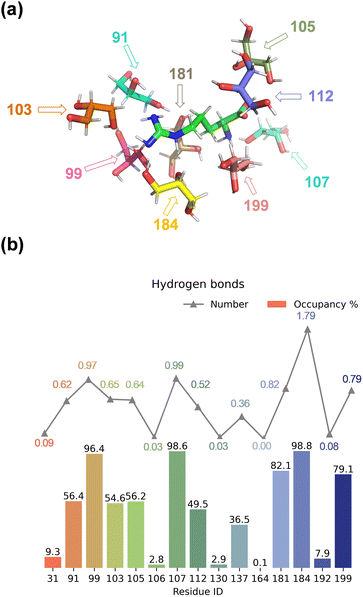
We started the work with a detailed computational analysis on a solution of L-Arg in glycerol and created a simulation box containing one L-Arg molecule and 200 glycerol molecules and ran an MD simulation for 10 ns. The MD simulation equilibrated rapidly and based on the individual snapshots from the MD simulation, we analysed the solvation characteristics of the L-Arg molecule. In particular, we measured hydrogen bonding distances between glycerol solvent molecules and L-Arg and display a histogram with statistics in Fig. 2. As highlighted in Fig. 2, as many as 15 glycerol molecules were able to form hydrogen bonding interactions with the central arginine molecule and eight of those have an occupancy of larger than 50%. Notably, the glycerol molecule with residue ID 184 formed an average of 1.79 hydrogen bonds with the arginine (see Table S7, ESI†), while the glycerol molecules with residue IDs 99 and 107 formed an average of 0.97 and 0.99 interactions during the MD run. Since a single glycerol molecule may form multiple hydrogen bonds with an arginine molecule, a high count of hydrogen bonds does not necessarily imply stability in the formed bonds. Thus, the occupancy of the aforementioned 15 glycerol molecules shown in Fig. 2 was computed (occupancy calculated as the ratio of frames forming hydrogen bonds to total frames).The nine glycerol molecules mentioned above not only formed an average of more than 0.5 hydrogen bond each but also exhibited an occupancy exceeding 50% (see Fig. 2), indicating stability in the formed hydrogen bonds. Indeed, most of the hydrogen bonds stayed intact during the full MD simulation. Specifically, the glycerol molecules with residue IDs 99, 107, and 184 formed hydrogen bonds with the arginine in more than 95% of all MD frames. Additionally, the residue IDs corresponding to the four glycerol molecules with the highest occupancy match those that formed more than 0.8 hydrogen bonds in Fig. 2. Moreover, despite similar occupancy for glycerol molecules between the residues with ID 184 and 107 (98.8% and 98.6%, respectively, see Table S7, ESI†), the difference in the number of hydrogen bonds formed is nearly twofold (1.79 and 0.99, respectively, see Table S6, ESI†). Residue 107 forms a hydrogen bond between atom O2 of glycerol with atom N1 of arginine, while residue 99 and 184 interact with atom N3 of L-Arg, although through O2 and O3, respectively (Fig. 2(a) and Table S6, ESI†). Residue 184 is positioned in such a way that multiple hydrogen bonding interactions are possible between O1 and O3 of glycerol with the N2 and N3 positions of L-Arg. Indeed, a large occupancy approaching a value of two is found that reflects the fact that in most frames it forms multiple hydrogen bonding interactions. In summary, the nine residue IDs—91, 99, 103, 105, 107, 112, 181, 184, and 199—strongly interact with arginine and display a large occupancy of hydrogen bonding interactions. In particular, the glycerol molecules with residue IDs 99, 107, and 184 form hydrogen bonds with the arginine in nearly all frames (occupancy well above 96%).
Subsequently, we varied the molar ratio of arginine to glycerol in our models ranging from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to 1
3 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 and ran MD simulations for each mixture using the model B approaches. The MD simulations converge rapidly and the total energy stabilizes for the system within a few fs. Thereafter, the density of the mixture was calculated from the MD simulation and compared to the tabulated values from the literature.29Table 1 summarizes the obtained results for model B. As can be seen from Table 1, the difference between the simulated and experimental densities of the NaDES systems is less than 8% and in all cases, the computation overestimates the experimental results. Therefore, the computational modelling has a systematic error and the simulation parameters used have high accuracy. These values compare well with previously reported calculations of the density of a mixture of polar compounds.30
9 and ran MD simulations for each mixture using the model B approaches. The MD simulations converge rapidly and the total energy stabilizes for the system within a few fs. Thereafter, the density of the mixture was calculated from the MD simulation and compared to the tabulated values from the literature.29Table 1 summarizes the obtained results for model B. As can be seen from Table 1, the difference between the simulated and experimental densities of the NaDES systems is less than 8% and in all cases, the computation overestimates the experimental results. Therefore, the computational modelling has a systematic error and the simulation parameters used have high accuracy. These values compare well with previously reported calculations of the density of a mixture of polar compounds.30
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to 1
3 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 of L-Arg
9 of L-Arg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerola
glycerola
| Modela | 1A3G | 1A4G | 1A5G | 1A6G | 1A7G | 1A8G | 1A9G |
|---|---|---|---|---|---|---|---|
a Ratio of L-argine![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol (or A glycerol (or A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G) given, i.e. 1A3G represents a ratio of 1 G) given, i.e. 1A3G represents a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 for arginine 3 for arginine![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol.
b Density in g cm−3.
c Experimental data from ref. 29.
d Deviation between experiment and theory (Δ) in %. glycerol.
b Density in g cm−3.
c Experimental data from ref. 29.
d Deviation between experiment and theory (Δ) in %.
|
|||||||
| ρ (MD)b | 1.313 | 1.309 | 1.304 | 1.307 | 1.307 | 1.306 | 1.302 |
| ρ (exp)bc | 1.213 | 1.220 | 1.225 | 1.229 | 1.231 | 1.233 | 1.235 |
| Δd | 7.6 | 6.8 | 6.1 | 6.0 | 5.8 | 5.6 | 5.2 |
Thereafter, we analysed the nature of the hydrogen bonding interactions and attempted to establish the most favourable interactions between arginine and glycerol. Detailed hydrogen bonding information for five glycerol molecules exhibiting the highest number of hydrogen bonds is provided in Table S7, ESI.† As mentioned previously the glycerol molecule with residue ID 184 can form two hydrogen bonds with arginine. From the table, the two hydrogen bonds are clear: one involving O3 in glycerol as the hydrogen bond donor and N3 in arginine as the acceptor, and the other involving N2 in arginine as the donor and O1 in glycerol as the acceptor. Furthermore, we quantified the occupancy of all hydrogen bonds within the system, and present only those with an occupancy that exceeds 50% in Table 2; more details are given in Table S7, ESI.† Analysis of the data in Table 2 reveals a propensity for glycerol to function as a hydrogen bond donor, while L-arginine exhibits a preference for accepting hydrogen bonds. Notably, O2 and O3 in glycerol emerge as robust hydrogen bond donors compared to O1, potentially attributed to the limited accessibility of atom O1 to L-arginine due to a significant steric hindrance effect. This observation elucidates why O1 is more inclined to act as a hydrogen bond acceptor than O2 and O3.
| Type | Donor | Acceptor | Occupancy (%) |
|---|---|---|---|
| 1 | Gly-side-02 | Arg-side-N1 | 100.0 |
| 2 | Gly-side-03 | Arg-side-N3 | 99.9 |
| 3 | Gly-side-02 | Arg-side-N3 | 99.9 |
| 4 | Arg-side-N1 | Gly-side-O1 | 96.1 |
| 5 | Arg-side-N2 | Gly-side-O1 | 88.4 |
| 6 | Arg-side-N4 | Gly-side-O2 | 88.0 |
| 7 | Arg-side-N1 | Gly-side-O2 | 86.2 |
| 8 | Arg-side-N3 | Gly-side-O2 | 78.3 |
| 9 | Gly-side-O1 | Arg-side-O1 | 69.0 |
| 10 | Gly-side-O2 | Arg-side-C6 | 64.4 |
| 11 | Arg-side-O2 | Gly-side-O2 | 64.3 |
| 12 | Arg-side-N4 | Gly-sideO3 | 51.8 |
The nitrogen atoms of L-arginine are more favourable than the oxygen atoms to participate in hydrogen bond formation as donors. While all nitrogen atoms demonstrate the capacity to serve as both donors and acceptors of hydrogen bonds, it is noteworthy that only a minimal percentage (5.6%) of hydrogen bonds involve N2 as the acceptor (see Table S7, ESI†). This stands in stark contrast to the robust occupancy of N1, N3, and N4 as hydrogen bond acceptors, with the former two exceeding 99% and the latter surpassing 30%. Further elucidation is warranted to expound upon this disparity. Additionally, beyond oxygen and nitrogen, carbon atoms within both molecules are also found to participate in hydrogen bond formation, acting as both donors and acceptors (Table S7, ESI†).
Independent gradient model for hydrogen bonding interactions analysis
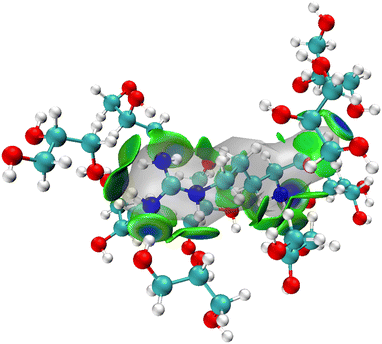
The MD simulations show that upon dissolving L-arginine into a glycerol solution will lead to strong hydrogen bonding interactions between L-arginine and solvent molecules, whereby at least nine glycerol molecules interact in specific orientations and conformations with L-arginine as depicted in Fig. 2(a). Although hydrogen bonding interactions are considered weak intermolecular interactions, recent computational studies have shown that there are considerable orbital interactions in the second-coordination sphere that influence the interactions between the donor and acceptor groups.31 As such we applied the independent gradient model for hydrogen bonding interactions (IGMH) and analysed weak intermolecular interactions between L-arginine and glycerol molecules.31 The IGMH approach takes the electron density gradient to describe regions of weak quantum mechanical interactions. We, therefore, took key structures from the MD simulation and ran a DFT single point calculation was to obtain the electron density gradients and obtained the IGMH surface between L-arginine and glycerol. The IGMH surface for the interaction between arginine and glycerol molecules is shown in Fig. 3 as colour-coded isosurfaces, whereby the colour gradation reflects the strength of the hydrogen bonds, with bluer hues indicating stronger interactions.32 Most of the hydrogen bonding interactions in the isosurface plots are in the dark green/dark blue shades and signify strong intermolecular interactions between the donor and acceptor groups, where strong orbital overlap between the two groups leads to increased electron density. It is worth mentioning that the presence of two flat isosurfaces (dark blue) between glycerol with residue ID 184 and arginine in the middle, indicates notably strong hydrogen bonding. This observation suggests that the interaction between glycerol with residue ID 184 and arginine can be ascribed to the formation of two robust hydrogen bonds.Bond dissociation energy analysis
To gain further insight into the strength of the hydrogen bonding interactions, we calculated individual diabatic bond dissociation energies (BDE) of the nine glycerol molecules around arginine. These computed values should give an indication of the strength of the hydrogen bonding interactions formed between glycerol and arginine. The BDEs were calculated by taking a structure from the MD simulation containing arginine and the nearest nine glycerol molecules and a UB3LYP/def2-TZVP single point calculation was performed. Subsequently, one glycerol molecule was removed from the model and a single point calculation done on the two fragments with the energy difference with respect to the full system the hydrogen bond BDE. The obtained BDEs of the arginine-glycerol interactions and the hydrogen bond distances are shown in Table 3. At least seven hydrogen bonds are shorter than 2 Å. Not surprisingly, the interactions with the shortest hydrogen bond distances give large BDE values, although no linear correlation is seen. This may be the result of secondary effects of long-range repulsion contributions.The calculated BDEs follow the ordering from large to small: 184 > 105 > 99 > 181 > 199 > 112 > 91 > 107 > 103. Thus, glycerol residue 184 interacts with the nitrogen atom of the guanidinium group of arginine, whereas the glycerol residue 105 is positioned on the other side of arginine and forms a hydrogen bond with its carboxylate group. The glycerol residues 99 and 181 also form hydrogen bonding interactions with the guanidinium group of arginine. Notably, the first five rankings roughly mirror the order of occupancy and quantity. Discrepancies in the rankings beyond the top five are primarily attributed to the neglect of the effect of the remaining six glycerol molecules on the nine under investigation.
ESP analysis
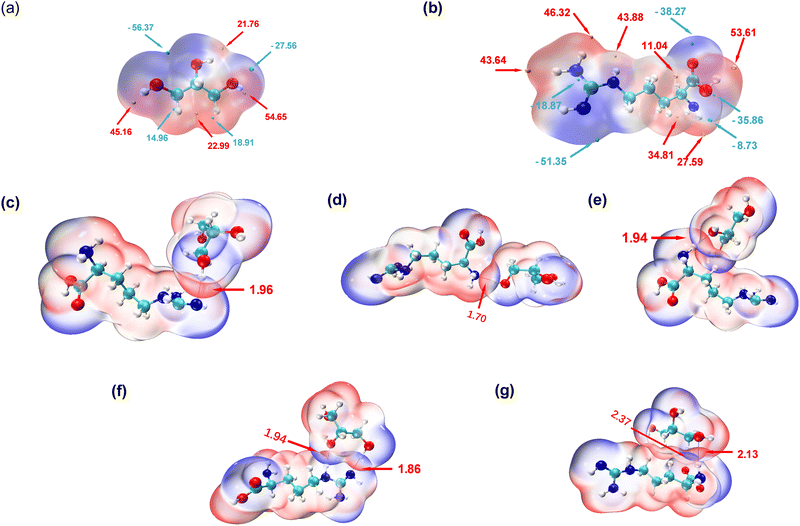
To explore the intricate atomic interactions between arginine and glycerol, the electrostatic potential (ESP) energy surfaces of arginine, glycerol and the arginine-glycerol dimer were individually constructed. This was achieved through the utilization of the wave function analysis software, Multiwfn,33 and visualization software, VMD.34 These tools enabled the generation of electrostatic potential energy surfaces for arginine and glycerol, as well as penetration maps depicting the interactions between their respective surfaces. Specifically, a cube file of electron density and electrostatic potential is generated using Multiwfn, loaded into the VMD, and the data for the electrostatic potential is mapped in different colours onto the electron density equivalent surface as shown in Fig. 4. In this study, the van der Waals surface refers to Bader's definition, where the isosurface of electron density at 0.001 a.u. is considered as the van der Waals surface.35By scrutinizing these electrostatic potential energy surfaces, a more intuitive comprehension of the spatial distribution of ESP surrounding the molecules was obtained. This analysis provided insights into the nature of electrostatic interactions between the two molecules. Fig. 4 illustrates the electrostatic potential energy surfaces of arginine, glycerol and arginine-glycerol. As the electrostatic potential increases gradually, the colour transitions in the sequence of “blue-white-red”, where the orange and cyan spheres in Fig. 4(a) and (b) represent the ESP maximum and ESP minimum, respectively. Fig. 4(a) illustrates that the glycerol molecule exhibits a maximum value point near O2 (54.7 kcal mol−1), indicative of a pronounced hydrogen bond acceptor capacity, notably superior to other atoms. This suggests a facile binding potential with other molecules through hydrogen bond interactions. The occupancy of O2 as a hydrogen bond donor with N1 and N3 in arginine was demonstrated to be nearly 99.9% in Table S7, ESI,† whereas the maximum occupancy as a hydrogen bond acceptor was 88%. Also, in glycerol there is an electrostatic potential (ESP) minimum (−56.4 kcal mol−1) in proximity to the oxygen atoms O1 and O3 in the upper region of the molecule, and an electron-rich acceptor site (−27. 6 kcal mol−1) near O2. This facilitates effective hydrogen bond interactions with arginine. Moreover, since the highest point near O1 is lower than that near O3 (21.8 kcal mol−1 and 45.2 kcal mol−1, respectively), O1 is more inclined to participate in hydrogen bond formation as an acceptor compared to O3. As illustrated in Table S7, ESI,† the maximum occupancy of O1 as a hydrogen bond acceptor is 96.1%, compared to 51.8% for O3. Furthermore, all three carbon atoms in glycerol can function as both hydrogen bond acceptor and donor due to the presence of red electron-deficient regions and blue electron-rich regions in their vicinity. Table S7, ESI,† indicates that the maximum occupancy of C1, C2, and C3 as hydrogen bond donor is 6.0%, 6.3%, and 20.5%, respectively, while as hydrogen bond acceptor it is 4.5%, 0.1%, and 23.6%, respectively.
In Fig. 4(b), a maximum point (53.6 kcal mol−1) is observed near O2 in arginine, indicating a high hydrogen bond capacity compared to other atoms. Table S7 (ESI†) reveals that the maximum occupancy of O2 as hydrogen bond donor is 64.3%, compared to 16.2% for hydrogen bond acceptor. Moreover, the minimum point in arginine occurs at N3 (−51.4 kcal mol−1), attributed to the lone pair of electrons on the N3 atom. The electron-rich N3 is more inclined to participate in hydrogen bonding as a hydrogen bond acceptor, with Table S7 (ESI†) showing its maximum occupancy as acceptor is 99.9% and as donor is 78.3%. Additionally, large and small value points near N1 suggest its potential to act as both hydrogen bond donor and acceptor, with corresponding maximum occupancies exceeding 95% (see Table S7, ESI†).
In the results shown above we indicated that N2 can serve as a hydrogen bond donor but not as an acceptor in hydrogen bond formation, as evidenced by the electrostatic potential energy surface. Specifically, N2 is surrounded by red electron-deficient regions and lacks blue electron-rich regions, making it more prone to participate as a donor. N4 is predominantly encircled by red regions, indicating the dominance of electron-absorption-induced effects. This effect can attract electrons from the hydrogen atom connected to N4, resulting in a decrease in electron density near the hydrogen atom and a notable increase in electrostatic potential. Therefore, N4 primarily contributes to hydrogen bond formation as an hydrogen bond donor, as indicated by Table S7 (ESI†), where the maximum occupancy of N4 as donor is 88%, while as acceptor it is 30.4%. Furthermore, O1 is surrounded by blue colour in Fig. 4 with minimal value points nearby, signifying its role as a hydrogen bond acceptor, which is inevitable as there is no hydrogen atom on O1 to act as a donor. Lastly, the carbon atom in arginine can also participate in hydrogen bond formation. Specifically, C2, is surrounded by red colour in Fig. 4 with a significant value point nearby, and therefore it participates as a hydrogen bond donor. Table S7 (ESI†) shows that its maximum occupancy as hydrogen bond donor is 1.5% and no evidence is seen that it acts as an acceptor. Conversely, C6, is surrounded by blue colour in Fig. 4 with very small value points nearby, and contributes to hydrogen bond formation as a hydrogen bond acceptor. Table S7 (ESI†) shows that its maximum occupancy as hydrogen bond acceptor is 64.4% and there is no data as donor.
As shown in Fig. 4(c)–(g), the penetration of van der Waals surfaces is conspicuous within the region of hydrogen bond formation, where red and blue colours interpenetrate, reflecting the complementary nature of electrostatic potentials and the electrostatic attraction interactions characteristic of hydrogen bonds. Both glycerol molecules with residue IDs 184 and 199 form two hydrogen bonds with arginine. However, a notable difference is observed in their stability: both hydrogen bonds (with N or O as hydrogen bond donors) in residue ID 184 exhibit stable existence, with an average number formed per frame >0.75 and occupancy > 80%, as detailed in Table S7, ESI.† Conversely, the hydrogen bond with N as the hydrogen bond donor in residue ID 199 demonstrates stable existence, with an average number of hydrogen bonds formed per frame of 0.8, as indicated in Table S7 (ESI†). However, the stability of hydrogen bonds formed by carbon as the hydrogen bond donor is comparatively poorer, with an occupancy rate of only 20% (as shown in Table S7 (ESI†), glycerol-C3 as hydrogen bond donor and arginine-O1 as hydrogen bond acceptor).
The interpenetration of van der Waals surfaces offers insight into the sites and strength of interactions between molecules. It is widely acknowledged that larger overlap regions signify stronger interactions, as increased overlap of van der Waals surfaces results in a larger contact area between molecules, facilitating stronger electron cloud interactions.36 This augmentation in attractive forces can influence molecular behaviour, such as adsorption and aggregation. Since the penetration of van der Waals surfaces is within the hydrogen bond formation region, in this study, we have quantified and ranked the bond lengths of hydrogen bonds. The hydrogen bond lengths studied in descending order, are 1.7 Å < 1.86 Å < 1.94 Å < 1.96 Å < 2.13 Å < 2.37 Å. Smaller bond lengths correspond to greater stability, thus the hydrogen bond stability, ranked from strongest to weakest, is as follows: residue ID 107 > 184 > 181 > 99 > 199. Glycerol residue ID 184 forms two stable hydrogen bonds with arginine, exhibiting the highest stability; thus, the actual hierarchy of hydrogen bond stability, based on hydrogen bond lengths, therefore, is from strongest to weakest, is residue ID 184 > 107 > 181 > 99 > 199. This pattern closely resembles that depicted by the metrics of number and occupancy of hydrogen bonds in Fig. 2 above. In addition, as mentioned earlier, carbon can be involved in the formation of hydrogen bonds, but the strength and stability of the hydrogen bonds it forms are weaker due to the longer hydrogen bond length of 2.37 Å. In contrast, the bond lengths of the hydrogen bonds formed with the participation of N or O are less than 2.15 Å.
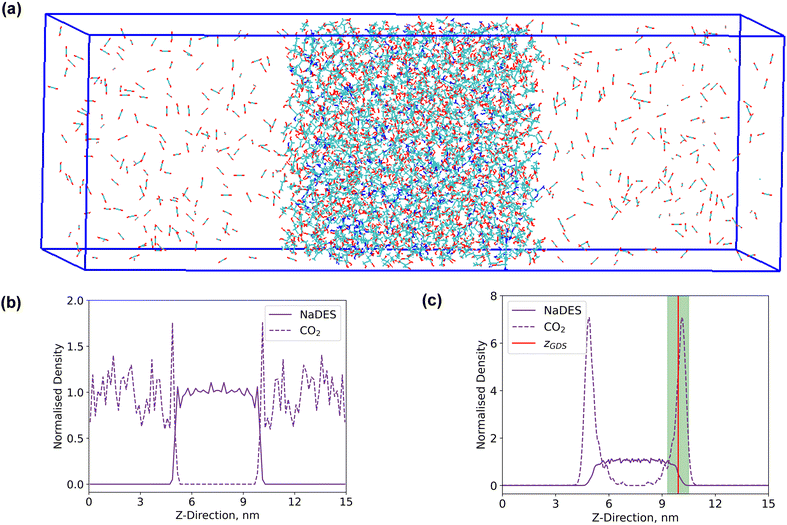
Interfacial system
A rectangular box, as depicted in Fig. 5(a), was constructed for interface analysis (model C), with dimensions of 15 nm along the z-axis and 5 nm along the x- and y-axis. Within the box, NaDESs were positioned at the centre, while CO2 was situated on both ends. Due to the central symmetry of the entire system, subsequent analysis was only conducted on one side of the box. The normalized density profile is illustrated in Fig. 5(b). Fitting the density profile with a tangent hyperbolic function allows for determination of the interface thickness and the position of the Gibbs dividing surface (GDS) (denoted by the green area and red line in Fig. 5(c), respectively).The density profile as a function of the z-direction, ρ(z), is expressed by the following equation:
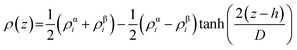 | (1) |
CO2 adsorption
In Table 4, the Gibbs dividing surface is consistently positioned around 10 nm in all systems. Surface excess analysis indicates positive values across all systems, indicating CO2 adsorption at the interface compared to NaDESs. The proportion of arginine to glycerol in NaDESs shows no significant impact on surface excess, indicating that CO2 is insensitive to NaDES compositions. However, with increased pressure, there was a gradual rise in surface excess, attributed to the heightened pressure serving as a driving force for CO2 uptake, facilitating its entry into the liquid phase through the interface. Conversely, an increase in temperature leads to adverse effects on surface excess. This is primarily due to the greater kinetic energy of CO2 at high temperatures, causing it to predominantly exist in the gas phase (NaDESs are in the liquid phase). Additionally, at elevated temperatures, the weakening of hydrogen bonds impedes the binding of CO2 to NaDESs.| Systema | GBS (nm) | Surface excess, kg m−2 | CO2 adsorbed number | CO2 adsorbed rate, % |
|---|---|---|---|---|
| a The nomenclature used for the systems, e.g., 1A3G_200C_25 °C, is as follows: the first four digits represent the molar ratio of arginine (A) to glycerol (G) in NaDES, the middle number represents the total number of molecules of CO2 in the gas phase at the start of the simulation, and the final number is the adsorption temperature in degrees Celsius. | ||||
| Different molar ratio of arginine to glycerol | ||||
| 1A3G_200C_25 °C | 9.86 | 440 | 63 | 31.5 |
| 1A4G_200C_25 °C | 9.94 | 440 | 59 | 29.5 |
| 1A5G_200C_25 °C | 9.88 | 343 | 59 | 29.5 |
| 1A6G_200C_25 °C | 9.85 | 366 | 75 | 37.5 |
| 1A7G_200C_25 °C | 10.11 | 481 | 71 | 35.5 |
| 1A8G_200C_25 °C | 9.98 | 431 | 70 | 35 |
| 1A9G_200C_25 °C | 10.06 | 312 | 115 | 57.5 |
| Different number of CO2 molecules (pressure) | ||||
| 1A6G_50C_25 °C | 9.91 | 67.3 | 28 | 56 |
| 1A6G_100C_25 °C | 9.89 | 110 | 52 | 52 |
| 1A6G_200C_25 °C | 9.85 | 366 | 75 | 37.5 |
| 1A6G_300C_25 °C | 10.02 | 780 | 79 | 26.3 |
| 1A6G_400C_25 °C | 10.01 | 1116 | 78 | 19.5 |
| Different temperature | ||||
| 1A6G_200C_25 °C | 9.85 | 366.2 | 75 | 37.5 |
| 1A6G_200C_40 °C | 10.00 | 268.6 | 116 | 58 |
| 1A6G_200C_50 °C | 10.09 | 203.0 | 121 | 60.5 |
| 1A6G_200C_60 °C | 10.02 | 186.8 | 117 | 58.5 |
| 1A6G_200C_70 °C | 10.21 | 141.8 | 148 | 74 |
Investigation into CO2 adsorption reveals minimal influence from varying NaDES molar ratios and highlights pressure and temperature as significant factors. High pressure intensifies CO2 adsorption through heightened driving forces, mirroring the increased surface excess. Conversely, higher temperatures weaken hydrogen bonds within NaDESs, disrupting the bonding network and facilitating CO2 movement and adsorption between NaDESs. A higher quantity of CO2 adsorbers does not necessarily translate to a higher adsorption rate. Analysis of CO2 adsorption rates suggests minimal effects from NaDES composition changes, while pressure and temperature exert notable influences. Specifically, CO2 uptake decreases with rising pressure, whereas temperature exhibits a positive correlation with uptake. Despite increased CO2 adsorbed numbers at higher pressures, the adsorption rate declines, indicating the limited driving force of pressure. Conversely, the substantial CO2 adsorbed numbers and uptake rate at elevated temperatures imply high temperatures are favourable for CO2 uptake in the temperature range studied. As CO2 adsorption progresses, an increasing number of CO2 molecules form hydrogen bonds with NaDESs. Consequently, the variation in the system's hydrogen bond count was initially investigated.
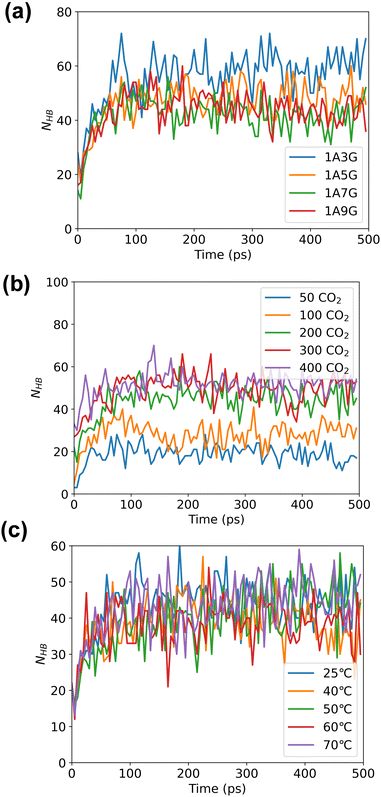
Following energy minimization, the evolution of hydrogen bond counts involving CO2 in the system over time was recorded, see Fig. 6. As follows, different NaDES compositions and systems temperatures have minimal effect on the number of hydrogen bonding interactions nor is the pressure significant. During the MD simulations, the hydrogen bond count reaches equilibrium for all trajectories, although more hydrogen bonds are counted under high-pressure conditions. This suggests that under high pressure, more CO2 can be adsorbed by NaDESs.
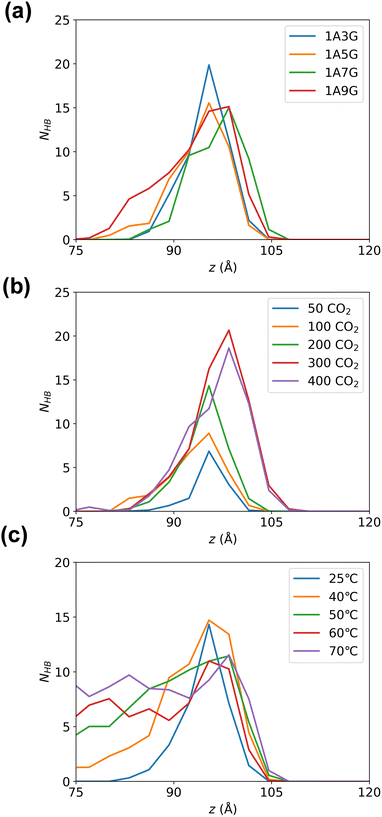
Subsequently, hydrogen bonding interactions that include CO2 participation in the equilibrated system were further analysed. As the system is symmetric along the z-axis, only the right-hand-side compartment was examined. The number of hydrogen bonds were calculated along the z-direction in 3 Å bins. Fig. 7 illustrates the peak of hydrogen bonding in all systems occurs near the Gibbs dividing surface at 10 Å, signifying the highest CO2 concentration at the interface, where CO2 is heavily adsorbed. While varying glycerol percentages in NaDESs have minimal impact on hydrogen bond distribution in the z-direction, pressure exerts a notable influence. To be more specific, the peak of hydrogen bonding increased with increasing pressure. This reflects that the high pressure provides a driving force for CO2 adsorption, which promotes the aggregation of CO2 at the interface and subsequently enters the liquid phase through hydrogen bonding. The effect of temperature is also significant, with a pronounced increase in hydrogen bonds in the liquid-phase region as temperature rises. The higher quantity of hydrogen bonds in the liquid phase reflects a larger amount of CO2 in the liquid phase, as CO2 is primarily adsorbed into the liquid phase through hydrogen bonding with NaDESs. Therefore, this observation reflects that high temperatures in the temperature range studied are favourable for CO2 diffusion and adsorption into the liquid phase.
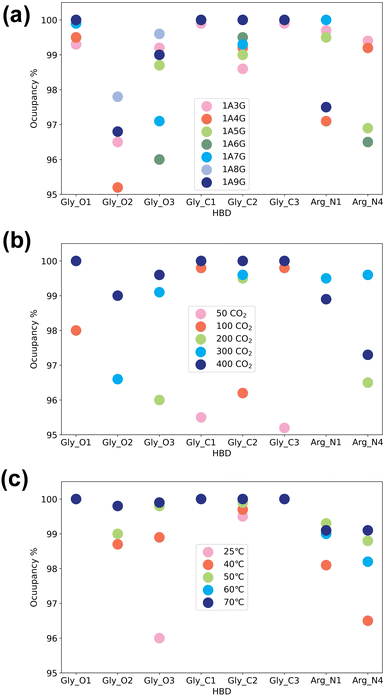
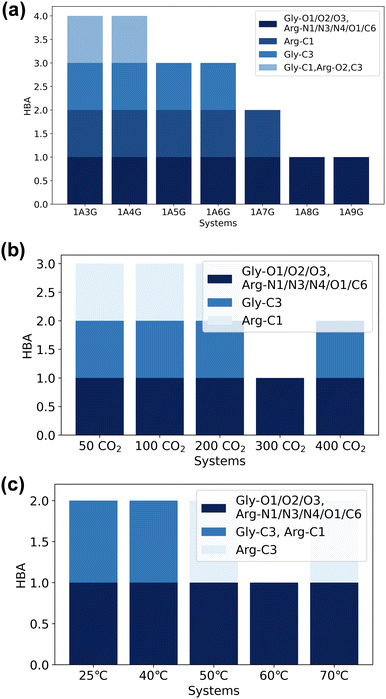
Next, the study focused on the types of atoms forming hydrogen bonds with CO2. CO2 can only serve as a hydrogen bond acceptor, whereas arginine and glycerol can act as hydrogen bond donors in interactions with CO2. Fig. 8 illustrates the types and occupancy of hydrogen bond donors across different systems, with only occupancies exceeding 95% considered. As depicted in Fig. 8 all oxygen and carbon atoms in glycerol, along with nitrogen atoms N1 and N4 in arginine, form stable hydrogen bonds with CO2 as hydrogen bond donors in all systems. Notably, glycerol primarily engages in hydrogen bonding with CO2, which is understandable given that NaDESs contain a significantly higher proportion of glycerol compared to arginine—glycerol content, namely at least three times that of arginine. Consequently, L-arginine is largely bound by glycerol and thus plays a lesser role in interactions with CO2.
Fig. 8(a) delves into the atomic types of hydrogen bond donors involved in CO2 hydrogen bond formation across different NaDES components. All aforementioned atom types in various NaDES components participate in hydrogen bond formation as hydrogen bond donors (HBDs). Moreover, with increasing glycerol proportion, a greater number of glycerol atoms form stable hydrogen bonds with CO2, evidenced by the rising occupancy of glycerol-involved atom types and the declining occupancy of arginine-involved atom types. This trend arises from glycerol's tendency to bind with arginine via hydrogen bonding, thereby limiting arginine's capacity to act as a hydrogen bond donor to interact with CO2.
Fig. 8(b) presents the impact of CO2 concentrations. At low CO2 concentrations, hydrogen bonding donor interaction primarily involves C1 and C3 atoms in glycerol; as CO2 levels rise, O1 and C2 atoms in glycerol also engage in CO2 binding. With further CO2 increases, O2 and O3 atoms in glycerol, as well as N1 and N4 atoms in arginine, contribute to CO2 binding. This phenomenon suggests that the carbon atoms of glycerol are initially dominant in bonding due to their stronger hydrogen bond donor characteristics, as indicated by the prominent red area surrounding these atoms in Fig. 4(a). As the CO2 concentration increases, all non-hydrogen atoms in glycerol become involved, while at higher CO2 concentrations, also the N1 and N4 atoms in L-arginine participate as hydrogen bond donors.
The temperature's influence on hydrogen bond donor type is substantial, as shown in Fig. 8(c). As temperature rises, both the types and occupancy of HBDs involved in bonding increase. This suggests that within the studied temperature range, elevated temperatures prompt more atoms in arginine and glycerol to engage in CO2 bonding, resulting in the formation of more stable hydrogen bonds.
Several atoms within L-arginine and glycerol are implicated in direct binding to CO2 and assist with its solvation patterns, potentially altering the types of atoms involved in hydrogen bond formation within NaDESs. Consequently, the subsequent analysis delves into the atom types of these two substances engaged in hydrogen bonding across different systems, as depicted in Fig. 9. Here, the examination focuses solely on hydrogen bonding between two substances, excluding bonding in the same species. Moreover, given the robustness of the hydrogen bonding network between arginine and glycerol, only stable hydrogen bonding compositions with occupancies of 100% are discussed.
As illustrated in Fig. 9, O1, O2, and O3 in glycerol, along with N1, N3, N4, O1, and C6 in arginine, participate as hydrogen bond acceptors in the formation of stable hydrogen bonds across all systems. Notably, unlike glycerol, where all oxygen atoms can act as both hydrogen bond donors and hydrogen bond acceptors, N2 and O2 in arginine solely function as hydrogen bond donors, while O1 and C6 exclusively act as hydrogen bond acceptors to form stable hydrogen bonds. This distinction is corroborated by the data in Table S7, ESI†: without N2 as a hydrogen bond acceptor and without O1 and C6 as hydrogen bond donors, the maximum occupancy of O2 as a hydrogen bond donor is 64.3%, while its maximum occupancy as a hydrogen bond acceptor is only 16.2%. This highlights the limited ability of O1 and C6 to function as hydrogen bond donors, N2 as hydrogen bond acceptors, and O2 as weak hydrogen bond acceptors. Furthermore, predominantly nitrogen and oxygen atoms serve as hydrogen bond donors or hydrogen bond acceptors in both substances. However, C6 in arginine can also act as a hydrogen bond acceptor in stable hydrogen bond formation, primarily due to the presence of an ESP minimum (−18.9 kcal mol−1) in its vicinity.
Fig. 9(a) demonstrates that the varying components of NaDESs exert a more pronounced effect on hydrogen bonding types in L-arginine and glycerol than pressure and temperature. As the percentage of glycerol in NaDESs increases, the diversity of stable hydrogen bonds formed between arginine and glycerol diminishes. This occurs because at low glycerol concentrations, the surrounding glycerol is limited, and both large and small ESP atoms participate in bonding. Additionally, the aforementioned involvement of O2 atoms in arginine in stable hydrogen bond formation as hydrogen bond acceptors when the glycerol content is low. The type of atoms involved decreases as glycerol content rises, as only large ESP atoms in glycerol take part in bonding due to the high glycerol concentration surrounding arginine.
In Fig. 9(b), the types of stable hydrogen bonds formed remain nearly constant as CO2 increases. Notably, the stability of hydrogen bonds formed with the participation of C1 in arginine decreases with rising CO2 concentration, with only C6 as a hydrogen bond acceptor involved in stable hydrogen bond formation at 300 °C and 400 °C. The influence of temperature on the types of hydrogen bonds in arginine and glycerol is also limited. This is because elevated temperatures weaken hydrogen bond strength uniformly, as hydrogen bonds are inherently weak interaction forces.
O–C–O angle in adsorbed CO2 solutions
Although CO2 is a linear molecule in the gas-phase, often upon binding to metal centres or surfaces the O–C–O angle becomes bent.38 Similarly, when CO2 is adsorbed into DESs, the oxygen atoms of CO2 can participate in hydrogen bonding, which also may influence the O–C–O bond angle. In particular, a recent DFT study of Zolghadr et al.39 on CO2 adsorption into DESs found that the bond angle of CO2 is slightly bent with values ranging between 175° and 178°. We, therefore, performed a statistical analysis of the O–C–O bond angles of all CO2 molecules over the final 5 ns of the MD simulations across of the various systems. Specifically, we checked whether the geometric structure of CO2 changes due to the presence of hydrogen bonds after the adsorption equilibrium has been achieved. As can be seen from Fig. 10, regardless of the composition of the DES, the selected temperatures or pressure, the O–C–O bond angles are slightly distorted from linearity. Thus, the O–C–O bond angle of the adsorbed CO2 is approximately 175° on average and indicates that the CO2 molecule is activated during the adsorption process.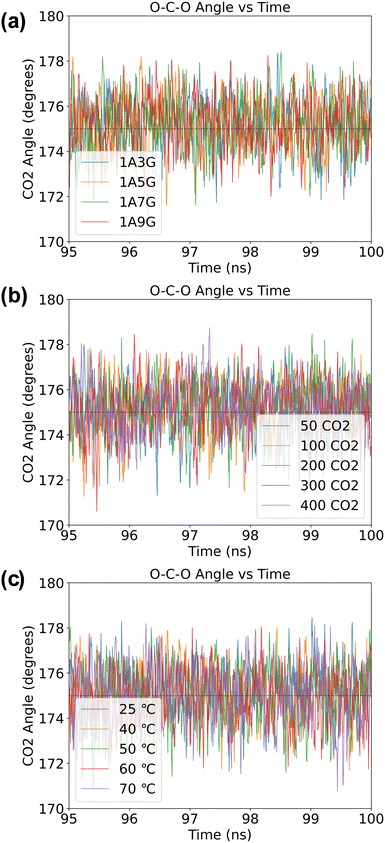 | ||
| Fig. 10 The O–C–O angle (in °) of CO2 molecules obtained in a NaDES systems: (a) under variable NaDES composition, (b) under different pressure conditions, and (c) under diverse temperature settings. | ||
Radial distribution function analysis
To gain further insight into the structure and properties of the NaDES compounds, we calculated the radial distribution function (RDF) for the interactions between different species using the TRAVIS software package.40 In particular, the RDF in a system composed of a DES formed by arginine and glycerol at a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 that contains 200 CO2 molecules was investigated. The distribution function of the DES atoms around the oxygen atoms of CO2 is shown in Fig. 11. As follows from Fig. 11, the RDF peak positions of the oxygen atoms in both arginine and glycerol are similar and located at less than 0.35 nm. By contrast, the RDF peak for nitrogen atoms in arginine appears around 0.4 nm. This suggests that the interactions between the oxygen atoms in DES and CO2 are stronger than those between the nitrogen atoms and CO2. It is well known that peak positions between 0.26 nm and 0.35 nm indicate hydrogen bonding, while positions between 0.35 nm and 0.5 nm suggest van der Waals interactions.41 As such, the RDF patterns indicate that CO2 primarily interacts with the oxygen atoms of DES via hydrogen bonding.
6 that contains 200 CO2 molecules was investigated. The distribution function of the DES atoms around the oxygen atoms of CO2 is shown in Fig. 11. As follows from Fig. 11, the RDF peak positions of the oxygen atoms in both arginine and glycerol are similar and located at less than 0.35 nm. By contrast, the RDF peak for nitrogen atoms in arginine appears around 0.4 nm. This suggests that the interactions between the oxygen atoms in DES and CO2 are stronger than those between the nitrogen atoms and CO2. It is well known that peak positions between 0.26 nm and 0.35 nm indicate hydrogen bonding, while positions between 0.35 nm and 0.5 nm suggest van der Waals interactions.41 As such, the RDF patterns indicate that CO2 primarily interacts with the oxygen atoms of DES via hydrogen bonding.
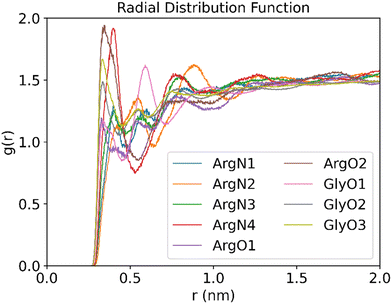 | ||
Fig. 11 RDFs between the O atom of CO2 and the O or N atoms of DES (molar ratios of arginine versus glycerol is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, temperature is 25 °C, 200 CO2 molecules are used to be adsorbed). 6, temperature is 25 °C, 200 CO2 molecules are used to be adsorbed). | ||
Further analysis of the RDF reveals that the peak for atom O2 of arginine is the highest, which implicates that the atom acts as a strong hydrogen bond donor in arginine. This is consistent with the analysis discussed above in Fig. 4(b), where atom O2 is associated with a large electrostatic potential with a value of 53.6 kcal mol−1. As such, atom O2 in L-arginine interacts as a strong hydrogen bond donor. On the other hand, for glycerol the O3 peak is the highest, which suggests that it contributes significantly to CO2 adsorption. As shown in Fig. 4(a), although the maximum value of the electrostatic potential of 54.65 kcal mol−1 occurs nearby atom O2, it can also act as a strong hydrogen bond acceptor (−27.56 kcal mol−1). Therefore, atom O3 will be preferred as hydrogen bond donor over atom O2 in glycerol-CO2 mixtures, as it interacts more effectively with CO2.
Analysis of the RDF for the nitrogen atoms of arginine shows that the N4 atom of arginine gives the highest peak in the RDF spectrum among the nitrogen atoms and is the second highest overall. This implies that the N4 atom of arginine will form a strong hydrogen bond as donor. The conclusion is in line with the electrostatic potential analysis reported above in Fig. 4(b), where two electrostatic potential maxima are observed near N4, and the entire N4 region is surrounded by red electron-deficient areas, which gives further support on its strong hydrogen bond donor ability.
Conclusions
In this study, we conducted a comprehensive investigation into the role of hydrogen bonding in carbon dioxide uptake in NaDES through molecular dynamics and quantum mechanics simulations. Our results reveal that both arginine and glycerol contain multiple atoms that can serve as hydrogen bond donors and hydrogen bond acceptors, with arginine mainly acting as the hydrogen bond acceptor and glycerol as the hydrogen bond donor. During the CO2 capture process, the role of atoms in NaDES as hydrogen bond acceptors is influenced more by the molar ratio of the substances than by the system's temperature and pressure, whereas the hydrogen bond donors are unaffected by molar ratio, temperature, or pressure. Additionally, both arginine and glycerol provide hydrogen bond donors for CO2 adsorption, with glycerol being the predominant contributor. The type of hydrogen bond donor atom is primarily influenced by the CO2 concentration (expressed as system pressure in the NVT ensemble), with limited impact from the system's composition or temperature. In summary, our study provides new insights into the role of hydrogen bonding in NaDES for CO2 uptake, contributing to their understanding, which can boost design and development of these systems as effective CO2 capture solutions.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.References
- (a) L. Fu, Z. Ren, W. Si, Q. Ma, W. Huang, K. Liao, Z. Huang, Y. Wang, J. Li and P. Xu, J. CO2 Util., 2022, 66, 102260 CrossRef CAS; (b) N. Thonemann, Appl. Energy, 2020, 263, 114599 CrossRef; (c) C. W. Jones, JACS Au, 2023, 3, 1536 CrossRef CAS PubMed; (d) W. D. Jones, J. Am. Chem. Soc., 2020, 142, 4955 CrossRef CAS PubMed; (e) F. Nocito and A. Dibenedetto, Curr. Opin. Green Sustainable Chem., 2020, 21, 34 CrossRef CAS; (f) L. Lombardo, Y. Ko, K. Zhao, H. Yang and A. Züttel, Angew. Chem., Int. Ed., 2021, 60, 9580 CrossRef CAS PubMed; (g) B. Yoon and G. A. Voth, J. Am. Chem. Soc., 2023, 145, 15663 CrossRef CAS PubMed; (h) X. Kang, A. Sheveleva, X. Han, J. Li, L. Liu, F. Tuna, E. J. L. McInnes, B. Han, S. Yang and M. Schröder, Nat. Commun., 2020, 11, 5464 CrossRef CAS PubMed; (i) J. Han, X. Bai, X. Xu, X. Bai, A. Husile, S. Zhang, L. Qi and J. Guan, Chem. Sci., 2024, 15, 7870 RSC.
- (a) W. Sun, M. Wang, Y. Zhang, W. Ding, F. Huo, L. Wei and H. He, Green Energy Environ., 2020, 5, 183 CrossRef; (b) A. J. Greer, J. Jacquemin and C. Hardacre, Molecules, 2020, 25, 5207 CrossRef CAS PubMed; (c) M. Zanatta, N. M. Simon and J. Dupont, ChemSusChem, 2020, 13, 3101 CrossRef CAS PubMed; (d) D. Hospital-Benito, J. Lemus, C. Moya, R. Santiago and J. Palomar, Chem. Eng. J., 2020, 390, 124509 CrossRef CAS; (e) J. Avila, L. F. Lepre, C. C. Santini, M. Tiano, S. Denis-Quanquin, K. C. Szeto, A. A. H. Padua and M. Costa Gomes, Angew. Chem., Int. Ed., 2021, 60, 12876 CrossRef CAS PubMed.
- S. K. Singh and A. W. Savoy, J. Mol. Liq., 2020, 297, 112038 CrossRef CAS.
- J. Flieger and M. Flieger, Int. J. Mol. Sci., 2020, 21, 6267 CrossRef CAS PubMed.
- (a) B. B. Hansen, S. Spittle, B. Chen, D. Poe, Y. Zhang, J. M. Klein, A. Horton, L. Adhikari, T. Zelovich and B. W. Doherty, Chem. Rev., 2020, 121, 1232 CrossRef PubMed; (b) F. P. Pelaquim, A. M. Barbosa Neto, I. A. L. Dalmolin and M. C. D. Costa, Ind. Eng. Chem. Res., 2021, 60, 8607 CrossRef CAS; (c) V. Alizadeh, L. Esser and B. Kirchner, J. Chem. Phys., 2021, 154, 094503 CrossRef CAS PubMed.
- (a) D. Yu, Z. Xue and T. Mu, Cell Rep. Phys. Sci., 2022, 3, 100809 CrossRef CAS; (b) H. Ren, S. Lian, X. Wang, Y. Zhang and E. Duan, J. Cleaner Prod., 2018, 193, 802 CrossRef CAS.
- (a) A. P. Abbott, R. C. Harris, K. S. Ryder, C. D’Agostino, L. F. Gladden and M. D. Mantle, Green Chem., 2011, 13, 82 RSC; (b) C. D’Agostino, L. F. Gladden, M. D. Mantle, A. P. Abbott, E. I. Ahmed, A. Y. M. Al-Murshedi and R. C. Harris, Phys. Chem. Chem. Phys., 2015, 17, 15297 RSC; (c) F. M. Perna, P. Vitale and V. Capriati, Curr. Opin. Green Sustainable Chem., 2020, 21, 27 CrossRef CAS; (d) C. Velez and O. Acevedo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1598 CAS; (e) A. Kovács, E. C. Neyts, I. Cornet, M. Wijnants and P. Billen, ChemSusChem, 2020, 13, 3789 CrossRef PubMed; (f) Y. Liu, H. Yu, Y. Sun, S. Zeng, X. Zhang, Y. Nie, S. Zhang and X. Ji, Front. Chem., 2020, 8, 82 CrossRef PubMed; (g) Y. Gu, Y. Hou, S. Ren, Y. Sun and W. Wu, ACS Omega, 2020, 5, 6809 CrossRef CAS PubMed.
- (a) J. Wu, Q. Liang, X. Yu, Q. F. Lü, L. Ma, X. Qin, G. Chen and B. Li, Adv. Funct. Mater., 2021, 31, 2011102 CrossRef CAS; (b) K. A. Omar and R. Sadeghi, J. Mol. Liq., 2022, 360, 119524 CrossRef CAS.
- (a) A. Gutiérrez, S. Rozas, P. Hernando, R. Alcalde, M. Atilhan and S. Aparicio, J. Mol. Liq., 2022, 366, 120285 CrossRef; (b) C. Mukesh, S. G. Khokarale, P. Virtanen and J. P. Mikkola, Sustainable Energy Fuels, 2019, 3, 2125 RSC; (c) Y. Xu, R. Zhang, Y. Zhou, D. Hu, C. Ge, W. Fan, B. Chen, Y. Chen, W. Zhang and H. Liu, Chem. Eng. J., 2023, 463, 142298 CrossRef CAS.
- (a) S. Sarmad, Y. Xie, J.-P. Mikkola and X. Ji, New J. Chem., 2017, 41, 290 RSC; (b) H. Yan, L. Zhao, Y. Bai, F. Li, H. Dong, H. Wang, X. Zhang and S. Zeng, ACS Sustainable Chem. Eng., 2020, 8, 2523 CrossRef CAS; (c) B. Jiang, J. Ma, N. Yang, Z. Huang, N. Zhang, X. Tantai, Y. Sun and L. Zhang, Energy Fuels, 2019, 33, 7569 CrossRef CAS.
- Y. H. Choi, J. van Spronsen, Y. Dai, M. Verberne, F. Hollmann, I. W. Arends, G.-J. Witkamp and R. Verpoorte, Plant Physiol., 2011, 156, 1701 CrossRef CAS PubMed.
- (a) G. Siani, M. Tiecco, P. Di Profio, S. Guernelli, A. Fontana, M. Ciulla and V. Canale, J. Mol. Liq., 2020, 315, 113708 CrossRef CAS; (b) H. Ren, Y. Liu, R. Zhang, T. Zhao, J. Han, Z. Zheng and E. Duan, Process Saf. Environ. Prot., 2023, 172, 136 CrossRef CAS.
- (a) R. Qin, Z. Wang, C. Wei, F. Zhou, Y. Tian, Y. Chen and T. Mu, Phys. Chem. Chem. Phys., 2024, 26, 7042 RSC; (b) Y. Chen, X. Hu, W. Chen, C. Liu, K. Qiao, M. Zhu, Y. Lou and T. Mu, Phys. Chem. Chem. Phys., 2021, 23, 2193 RSC.
- D. Shi, F. Zhou, W. Mu, C. Ling, T. Mu, G. Yu and R. Li, Phys. Chem. Chem. Phys., 2022, 24, 26029 RSC.
- (a) Y. Chen, W. Chen, L. Fu, Y. Yang, Y. Wang, X. Hu, F. Wang and T. Mu, Ind. Eng. Chem. Res., 2019, 58, 12741 CrossRef CAS; (b) R. Stefanovic, M. Ludwig, G. B. Webber, R. Atkin and A. J. Page, Phys. Chem. Chem. Phys., 2017, 19, 3297 RSC; (c) C. Fan, Y. Liu, T. Sebbah and X. Cao, Global Challenge, 2021, 5, 2000103 CrossRef PubMed.
- (a) Z. Wang, Z. Wang, J. Chen, C. Wu and D. Yang, Molecules, 2021, 26, 7167 CrossRef CAS PubMed; (b) I. Cichowska-Kopczyńska, B. Nowosielski and D. Warmińska, Molecules, 2023, 28, 5293 CrossRef PubMed; (c) Z. Wang, M. Chen, B. Lu, S. Zhang and D. Yang, ACS Sustainable Chem. Eng., 2023, 11, 6272 CrossRef CAS; (d) A. Klemm, S. P. Vicchio, S. Bhattacharjee, E. Cagli, Y. Park, M. Zeeshan, R. Dikki, H. Liu, M. K. Kidder, R. B. Getman and B. Gurkan, ACS Sustainable Chem. Eng., 2023, 11, 3740 CrossRef CAS; (e) R. Dikki, V. Khokhar, M. Zeeshan, S. Bhattacharjee, O. K. Coskun, R. Getman and B. Gurkan, Green Chem., 2024, 26, 3441 RSC.
- H. Ren, S. Lian, X. Wang, Y. Zhang and E. Duan, J. Cleaner Prod., 2018, 193, 802 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157 CrossRef PubMed.
- Z. Zhang, X. Liu, D. Yao, Z. Ma, J. Zhao, W. Zhang, P. Cui, Y. Ma, Z. Zhu and Y. Wang, J. Mol. Liq., 2021, 322, 114665 CrossRef CAS.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 6.1, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed; (c) S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157 CrossRef CAS PubMed.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701 CrossRef CAS PubMed.
- A. Chaumont, E. Engler and R. Schurhammer, J. Phys. Chem. B, 2020, 124, 7239 CrossRef CAS PubMed.
- A. Volk and C. J. Kähler, Exp. Fluids, 2018, 59, 75 CrossRef.
- L. Verlet, Phys. Rev. A, 1967, 159, 98 CrossRef CAS.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton (USA), 76th edn, 1996 Search PubMed.
- Z. Wei, J. D. Elliott, A. A. Papaderakis, R. A. W. Dryfe and P. Carbone, J. Am. Chem. Soc., 2024, 146, 760 CrossRef CAS PubMed.
- (a) S. P. de Visser, Chem. – Eur. J., 2020, 26, 5308 CrossRef CAS PubMed; (b) Y. Cao, S. Hay and S. P. de Visser, J. Am. Chem. Soc., 2024, 146, 11726 CrossRef CAS PubMed; (c) S. P. de Visser, H. P. H. Wong, Y. Zhang, R. Yadav and C. V. Sastri, Chem. – Eur. J., 2024, 30, e202402468 CrossRef CAS PubMed.
- T. Lu and Q. Chen, J. Comput. Chem., 2022, 43, 539 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed.
- (a) R. G. A. Bone and R. F. W. Bader, J. Phys. Chem., 1996, 100, 10892 CrossRef CAS; (b) J. Zhang and T. Lu, Phys. Chem. Chem. Phys., 2021, 23, 20323 RSC.
- (a) R. Zhu, S. Huang, C. Gui, G. Li and Z. Lei, Chem. Eng. Sci., 2022, 258, 117745 CrossRef CAS; (b) B. Gao, Q. Chang and H. Yang, Sci. Total Environ., 2021, 765, 144427 CrossRef CAS PubMed.
- (a) E. A. Muller, Å. Ervik and A. Mejía, Living J. Comput. Mol. Sci., 2020, 2, 21385 Search PubMed; (b) M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford (UK), 2017 CrossRef; (c) H. O. Wood, H. M. Burnett, R. A. W. Dryfe and P. Carbone, Faraday Discuss., 2024, 253, 212 RSC.
- (a) P. A. Davethu and S. P. de Visser, J. Phys. Chem. A, 2019, 123, 6527 CrossRef CAS PubMed; (b) C. Zhu, C. D’Agostino and S. P. de Visser, Chem. – Eur. J., 2023, 29, e202302832 CrossRef CAS PubMed; (c) C. Zhu, C. D’Agostino and S. P. de Visser, Inorg. Chem., 2024, 63, 4474 CrossRef CAS PubMed.
- M. H. Dokoohaki and A. R. Zolghadr, J. Phys. Chem. B, 2021, 125, 10035 CrossRef PubMed.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007 CrossRef CAS PubMed.
- (a) J. R. Durig, W. N. Kar, C. Zheng and S. Shen, Struct. Chem., 2004, 15, 149 CrossRef CAS; (b) T. Steiner and G. R. Desiraju, Chem. Commun., 1998, 891 RSC; (c) X. Fu, X. Fan, X. Ju, X. Qi, J. Li and H. Yu, RSC Adv., 2015, 5, 52844 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Tables and figures with the full set of data obtained in this work. See DOI: https://doi.org/10.1039/d4cp03865g |
| This journal is © the Owner Societies 2025 |