A Zn₂-supported B₇ wheel structure for the global minimum of the B₇Zn₂ cluster

Abstract

In this work, we employ density functional theory (DFT) to explore the structure of boron clusters doped with two zinc atoms (B₇Zn₂ or Zn₂B₇). The results show that the most stable structure is a Zn₂ motif standing over a B₇ wheel, which is 0.89 eV lower in energy compared to the classical inverse-sandwich structure for B₇TM₂ (TM = transition metal) clusters. The characteristics of these systems are evaluated by the IR spectra to guide plausible experimental realization. In addition, density of states, and bonding characteristics were evaluated. Our results denote the formation of an intermediate Zn–Zn bond order given by the key electron-acceptor nature of the B₇ motif, leading to a depopulation of antibonding Zn–Zn orbitals and population of the respective bonding orbitals. Thus, the evaluation and use of more electron-deficient supporting ligands may trigger a quest for the design of plausible structures featuring larger Zn–Zn elusive bond orders in stable species.

---

1. Introduction

In the last decade, extensive theoretical and experimental research has been devoted to boron clusters. These clusters possess distinctive structural and electronic properties, as well as unique chemical bonding, which have attracted significant attention from the scientific community.^1,2 Due to their electron-deficient nature, boron clusters are a focal point in materials science and nanotechnology. This electron deficiency enables them to form a wide range of stable and metastable structures, making them highly versatile building blocks for various applications. Introducing dopants into these clusters with other elements can greatly alter their electronic, magnetic, and chemical properties, opening up possibilities for a wide range of applications.³ While significant advances have been achieved in the experimental and theoretical investigation of transition-metal-doped boron clusters in recent years, studies on boron clusters doped with two transition metals are still in their early stages.⁴ In 2006, Zhai et al. studied the electronic structure and chemical bonding of a binary Au₂B₇⁻ cluster and found that the ground-state structure of B₇Au₂⁻ (B₇H₂⁻) can be viewed as adding two Au (H) atoms to the terminal B atoms of a higher-lying planar isomer of B₇⁻. In 2014, Li and coworkers reported a joint experimental and theoretical study on the Ta₂B₆^−/0 clusters and found that the most stable structures of both the neutral and anion are D_6h bipyramidal structures.⁵ Wang and colleagues studied lanthanide-doped boron clusters, Ln₂B_n (n = 7, 9) and discovered inverse sandwich motifs within this series of chemical elements.⁶ In particular, studies on M₂-doped boron clusters M₂B₇ involving alkaline earth metals (M = Be, Mg, Ca) as well as first-row transition metals (M = Sc, V, Fe, Co, Ni) also showed similar structures including enhanced reactivities.^7–10 Moreover, boron clusters and alloys have been proposed for various potential applications, such as building blocks for supramolecular assemblies, hydrogen storage, hydrophilic substances, and protective coatings against corrosion, among others.^10–13

Recently, Yue et al. investigated the fluxional and dynamic behavior of the Al₂B₈ cluster, which was determined by two isolated Al atoms situated above and below the B₈ wheel.¹⁴ Subsequently, Rodríguez–Kessler studied the Al₂B₇ cluster and identified the classical inverse sandwich structure, which contrasts with the Al₂-supported B₈ wheel structure pattern observed in Al₂B₈.¹⁵ In addition, Merino et al. discussed the exploration of TM₂B₇⁻ and TM₂B₈ (TM = Zn, Cd, Hg), denoting a boron centered wheel, involving a fluxional behavior of the TM₂ motif ascribed as molecular stirrers.¹⁶ In order to complete the series of TM₂ doped B₇ cluster, in this work, we have calculated the structure and stability of the Zn₂B₇ cluster. The results show that B₇Zn₂ is formed by two metals lying above a boron centered B₇ wheel, depicting a similar structure to related anionic clusters.¹⁶ In particular, the Zn–Zn distance is in striking contrast to the 4.680 Å in the isolated neutral dimer,^17,18 where the formation of highly elusive Zn–Zn bonds has been realized only after the report by Resa et al. in 2004,¹⁹ triggering efforts to understand and increase the libraries of species featuring Zn–Zn direct bonds.^18,20 In this report, we set out to explore the structural, vibrational, and electronic properties of neutral B₇Zn₂, providing insights into the requirements to induce the formation of a direct Zn–Zn bond and the role of the B₇ wheel acting as a ligand. Besides, we evaluated the global minimum and related high-lying isomers by using a modified basin-hopping (MBH) structure search approach, where the bonding characteristics were estimated via energy decomposition analysis (EDA), leading to the characterization of the Zn–Zn bonding scheme. Our results provide a beneficial background encouraging further design of plausible species leading to the formation of Zn–Zn bonds.

2. Computational details

Calculations performed in this work are carried out by using density functional theory (DFT) as implemented in the Orca quantum chemistry package.²¹ The exchange and correlation energies are addressed by the PBE0 functional in conjunction with the Def2TZVP basis set.^22,23 Atomic positions are self-consistently relaxed through a quasi-Newton method employing the BFGS algorithm. The SCF convergence criteria for geometry optimization are achieved when the total energy difference is smaller than 10⁻⁸ a.u., by using the TightSCF keyword in the input. The van der Waals interactions are included in the exchange–correlation functionals with empirical dispersion corrections of Grimme DFT-D3(BJ). The total density of states (DOS) and partial density of states (PDOS) for clusters and complexes were obtained by using the Multiwfn program.²⁴ The IR spectra are obtained by standard diagonalization of the Hessian matrix by using the NumFreq keyword in the input.

3. Results

The structures of the B₇Zn₂ clusters are obtained using a modified basin-hopping (MBH) structure search method over seven generations, as illustrated in Fig. 1. The MBH modified basin-hopping method (MBH) includes random exchanges of atomic species along with standard random perturbations to explore efficiently all possible combinations in the binary alloy.^15,25 The results show that the lowest energy structure for the B₇Zn₂ cluster is a Zn₂-bicapped B₇ wheel 7M2.1. This is in contrast to previous reports on B₇M₂ clusters with early transition metals (M = Sc, Ti, V, Cr), which found inverse sandwich structures like the 7M2.4 isomer, to represent the most stable structure. For 7M2.2, we found a peripheral Zn₂-doped B₇ structure with a relative energy of 0.62 eV (Fig. 2), while the 7M2.3 and 7M2.4 isomers have relative energies of 0.79 and 0.89 eV, respectively.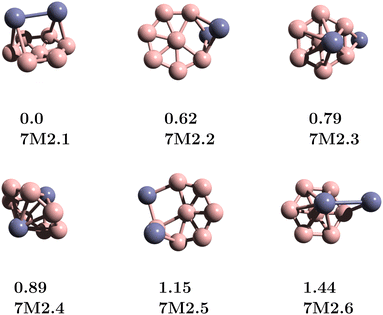

Fig. 1 Potential energy surface obtained by a modified basin hopping (MBH) for B₇Zn₂ clusters.

Fig. 2 Lowest energy structures for the B₇Zn₂ clusters. For simplicity, the isomers are denoted by 7M2.y (y = 1–6).¹⁵ For each structure, the relative energy (in eV) and isomer label are given.

According to the structures found, we explore the thermodynamic stability of the clusters by using molecular dynamics MD simulations as implemented in the Orca code. The default velocity Verlet algorithm in the NVT ensemble at the PBE/def2-SVP level of theory is set. A timestep of 0.5 femtoseconds and initial velocities according to a temperature of 300 K are used. Temperature is maintained at 300 K using a Berendesen thermostat.²⁶ The simulations are performed for a time of 1 ps with 0.5 fs of time step. The behavior of the mean square displacement 〈msd〉 as a function of time allows us to determine the average bond-length variations during MD simulation, which is evaluated as

where r_i(t) is the position vector in the i-th atom at the time t and N is the total number of atoms in the system. The 〈msd〉 parameter allows us to rationalize the dynamical behavior of the clusters.^27,28 In a rigid system, the 〈msd〉 parameter remains constant, where in a non-rigid system the 〈msd〉 shows variations as a function of time. Upon evaluating the 7M2.1 and 7M2.2 structures, we found that the clusters exhibit fluxional behavior, which is more pronounced in 7M2.1 (Fig. 3).

Fig. 3 Temperature (T) and mean square displacement 〈msd〉 during molecular dynamics simulation for 7M2.1 and 7M2.2 clusters at 300 K.

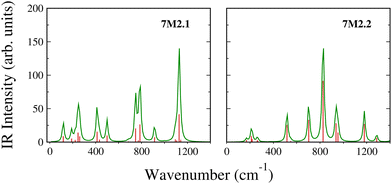
To further characterize the B₇Zn₂ clusters, we have calculated the infrared (IR) spectrum, which serves as a guide for future experimental studies.^29,30 For the most stable configurations 7M2.1 and 7M2.2, we found dispersed peaks in the regions of 57.92–1141.60 cm⁻¹ and 78.81–1428.16 cm⁻¹, respectively, as shown in Fig. 4. However, 7M2.2 presents a more symmetrical spectrum with a main peak in 826.25 cm⁻¹, while in 7M2.1, the main peak is situated at 1127.62 cm⁻¹. The high-intensity peaks correspond to the stretching vibrations of the central B atom toward the B₇ wheel, whereas other vibrational modes represent distortions of the B atoms, as depicted in Table S4 (ESI†).

Fig. 4 IR spectra for 7M2.1 and 7M2.2 clusters obtained at the PBE0/Def2-TZVP level.

To get insight into the electronic properties of the clusters, the total density of states (TDOS) for the 7M2.1 and 7M2.2 clusters is depicted in Fig. S2 (ESI†). For 7M2.1, the PDOS shows more dispersed states, while for 7M2.2 it shows more localization near the HOMO state. The HOMO–LUMO gap for the 7M2.1 and 7M2.2 clusters amounts to 3.43, and 3.75 eV, respectively. The inverse sandwich structure exhibits a smaller gap of 2.07 eV (see Table S3, ESI†). Additionally, the ionization energy of the clusters ranges from 7.40 to 8.27 eV, indicating their exceptional electronic stability. Based on this analysis, the most stable clusters are less reactive compared to the higher-energy isomers.

In order to evaluate the factors governing the stabilization of the global minimum (7M2.1) in relation to high-lying isomers, energy decomposition analysis (EDA) was performed as implemented in the ADF2024 code,³¹ where the relative energy is dissected in different meaningful terms given by the repulsive Pauli (ΔE^relEner_Pauli), orbital interaction (ΔE^relEner_Orb), electrostatic contribution (ΔE^relEner_Elsta), and dispersion term (ΔE^relEner_Disp),³² which accounts for electronic (ΔE^relEner_Elsta + ΔE^relEner_Orb + ΔE^relEner_Disp) and steric (ΔE^relEner_Pauli) contributions (Table 1). The obtained results exhibit several differences between isomers where despite the lesser steric repulsion provided in 7M2.2, a destabilization of the electronic terms, mainly given by the electrostatic character, ensures 7M2.1 as the global minimum. For 7M2.3, the stabilizing electronic contribution is similar to 7M2.1; however, introducing a slightly larger destabilizing steric repulsion. For 7M2.4, 7M2.5, and 7M2.6, the situation is similar to 7M2.2, thus denoting that the decrease in electronic stabilizing contribution is the main factor in determining the global minimum.

Table 1 Energy decomposition analysis of the relative energy (ΔE_relEner) between B₇Zn₂ isomers. Values in eV

	Rel. ene.	ΔE^relEnerPauli	ΔE^relEnerElsta	ΔE^relEnerOrb	ΔE^relEnerDisp	ΔEelectronic	ΔEsteric
7M2.1	0.00	0.00	0.00	0.00	0.00	0.00	0.00
7M2.2	0.62	−16.05	5.91	10.73	0.03	16.67	−16.05
7M2.3	0.79	1.62	−0.81	−0.04	0.02	−0.83	1.62
7M2.4	0.89	−6.62	−0.16	7.67	−0.01	7.51	−6.62
7M2.5	1.15	−19.24	7.19	13.18	0.02	20.39	−19.24
7M2.6	1.44	−1.72	0.28	2.87	0.01	3.16	−1.72

---

For the inverse sandwich isomer, the atomic radii of Zn (1.22 Å)³³ are larger to be placed above the B₇ ring, which involves an available radius of 1.0 Å (B^diameter₇ − B^radii = 1.809 − 0.84 Å = 0.969 Å), which leads to a destabilization of the structure by steric factors (Table 1). In addition, the evaluation of the aromatic properties of 7M2.4 unravels an antiaromatic character (Fig. 5), in line with the electronic destabilization mostly given by the decrease in orbital interactions (Table 1), which are key features to enable electronic delocalization in the overall structure. In this framework, an induced central shielding region is indicative of an aromatic behavior, whereas a central deshielding region accounts for an antiaromatic behavior.^34,35 For 7M2.4, a central deshielding region is found, which is indicative of an antiaromatic behavior, also noted for both bare B₇ structures. In contrast, 7M2.1 exhibits a decrease in the parent antiaromatic behavior of B₇, leading to more aromatic characteristics, as noted by the shielding region at the center of the structure (blue color).

Fig. 5 Induced magnetic field under a perpendicular field (B^ind_z), showing an antiaromatic character for both bare B₇ structures, and the inverse sandwich 7M2.4, given the formation of a deshielding region at the center of the structure. Color code: blue: shielding/red: deshielding. Isosurface values set at ± 3.0 ppm.

The EDA analysis of the Zn₂–B₇ interaction denotes an energy of −2.78 eV, which is mostly provided by the stabilizing contribution of the orbital interaction (55.0%, Table S1, ESI†), and from the electrostatic character (43.8%), which involves a sizable Zn₂ → B₇ net charge transfer of 0.60 e, involving a bonding between Zn₂ and π-orbitals of B₇ (Fig. S1, ESI†). Interestingly, the charge transfer in turn leads to a reorganization of the population of σ-Zn₂ orbitals (Table S2, ESI†), resulting in 1.94 e in σ, 0.81 e in σ*, and population of the initially unoccupied π-Zn₂ of 0.61 e. Such a charge reorganization in the B₇ supported Zn₂ dimer increases the bonding contribution (π-Zn₂) and decreases the antibonding character (σ*-Zn₂), resulting in a Mayer bond order^36,37 of 0.50, denoting the formation of a formal Zn–Zn bond weaker that a single bond. For the related anionic counterpart, Zn₂B₇⁻, the Zn₂–B₇ interaction energy amounts to −2.88 eV, with a Zn₂ → B₇ net charge transfer of 0.33 e, where the incoming electrons reside mainly at the B₇ motif. The population of Zn₂ based orbitals in the anionic species is of σ-Zn₂ 1.92 e, σ*-Zn₂ 0.92 e, π-Zn₂ 0.79 e, denoting a similar situation to the neutral counterpart, with a calculated Zn–Zn Mayer bond order of 0.33. Based on the net bonding electrons of σ- and π-Zn₂ orbitals, the resulting Zn–Zn bond order is given by 64.8% from σ- and 35.2% from π-character in the neutral Zn₂B₇, and of 55.9% and 44.1% respectively, for the anionic counterpart. Thus, the role of B₇ as an electron-acceptor motif acting as a ligand for the Zn₂ dimer ensures the depopulation of the antibonding character, and increases the population of bonding orbitals, leading to the formation of an intermediate Zn–Zn bond, in both neutral and anionic counterparts. Hence, the introduction of more electron-deficient supporting ligands may be able to increase the Zn–Zn bond order, encouraging the quest for the formation of single or larger Zn–Zn bond orders.

4 Conclusions

In this work, we employed density functional theory (DFT) to explore the structure of boron clusters doped with two zinc atoms (B₇Zn₂ or Zn₂B₇). The results showed that the most stable structure is a B₇-supported Zn₂ dimer, which is 0.89 eV lower in energy compared to the classical inverse-sandwich structure adopted in B₇TM₂ (TM = transition metal) clusters. The characteristics of these systems are evaluated by the IR spectra, density of states, and bonding analyses. The formation of the Zn–Zn intermediate bond order is given by the electron-acceptor characteristics of the B₇ motif, leading to a depopulation of antibonding Zn–Zn orbitals, and, population of the respective bonding orbitals, highlighting the role of both σ- and π-Zn₂ orbitals, in the resulting bond order. Interestingly, in the light of such findings, the quest for the design and feasible characterization of Zn–Zn bonded structures may be triggered by the use of more electron-deficient supporting ligands, as a key factor towards obtaining larger Zn–Zn elusive bond orders in stable species.

Data availability

The data supporting the conclusions reached in this study have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

P. L. R.-K. would like to thank the support of IPICyT's National Supercomputing Center under the computational time grant TKII-E-0424-I-080424-4/PR-6. A. M.-C. thanks FONDECYT ANID Regular 1221676.

References

1. E. Oger, N. Crawford, R. Kelting, P. Weis, M. Kappes and R. Ahlrichs, Boron Cluster Cations: Transition from Planar to Cylindrical Structures, Angew. Chem., Int. Ed., 2007, 46, 8503–8506.
2. B. Albert and H. Hillebrecht, Boron: Elementary Challenge for Experimenters and Theoreticians, Angew. Chem., Int. Ed., 2009, 48, 8640–8668.
3. W.-J. Chen, A. S. Pozdeev, H. W. Choi, A. I. Boldyrev, D.-F. Yuan, I. A. Popov and L.-S. Wang, Searching for stable copper borozene complexes in CuB₇⁻ and CuB₈⁻, Phys. Chem. Chem. Phys., 2024, 26, 12928–12938.
4. P.-F. Han, Q. Sun and H.-J. Zhai, Boron-Based Inverse Sandwich V₂B₇⁻ Cluster: Double π/σ Aromaticity, Metal-Metal Bonding, and Chemical Analogy to Planar Hypercoordinate Molecular Wheels, Molecules, 2023, 28(12), 4721.
5. W.-L. Li, L. Xie, T. Jian, C. Romanescu, X. Huang and L.-S. Wang, Hexagonal Bipyramidal [Ta2B6]^−/0 Clusters: B6 Rings as Structural Motifs, Angew. Chem., Int. Ed., 2014, 53, 1288–1292.
6. W.-L. Li, T.-T. Chen, D.-H. Xing, X. Chen, J. Li and L.-S. Wang, Observation of highly stable and symmetric lanthanide octa-boron inverse sandwich complexes, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6972–E6977.
7. J. Jia, X. Li, Y. Li, L. Ma and H.-S. Wu, Density functional theory investigation on the structure and stability of Sc₂B_n (n = 1–10) clusters, Comput. Theor. Chem., 2014, 1027, 128–134.
8. H. T. Pham, M. P. Pham-Ho and M. T. Nguyen, Impressive capacity of the B₇⁻ and V₂B₇ clusters for CO₂ capture, Chem. Phys. Lett., 2019, 728, 186–194.
9. H.-R. Li, C. Zhang, W.-B. Ren, Y.-J. Wang and T. Han, Geometric structures and hydrogen storage properties of M₂B₇ (M = Be, Mg, Ca) clusters, Int. J. Hydrogen Energy, 2023, 48, 25821–25829.
10. D. Olalde-López, P. Rodríguez-Kessler, S. Rodríguez-Carrera and A. Muñoz-Castro, Hydrogen storage properties for bimetallic doped boron clusters M₂B₇ (M = Fe, Co, Ni), Int. J. Hydrogen Energy, 2024 DOI:10.1016/j.ijhydene.2024.05.429.
11. A. Barba-Bon, G. Salluce, I. Lostalé-Seijo, K. I. Assaf, A. Hennig, J. Montenegro and W. M. Nau, Boron clusters as broadband membrane carriers, Nature, 2022, 603, 637–642.
12. P. Álvarez Zapatero, A. Lebon, R. H. Aguilera del Toro, A. Aguado and A. Vega, Why are Zn-rich Zn-Mg nanoalloys optimal protective coatings against corrosion? A first-principles study of the initial stages of the oxidation process, Phys. Chem. Chem. Phys., 2021, 23, 24685–24698.
13. J. Cebula, K. Fink, J. Boratyński and T. M. Goszczyński, Supramolecular chemistry of anionic boron clusters and its applications in biology, Coord. Chem. Rev., 2023, 477, 214940.
14. R.-X. Yue, S.-J. Gao, P.-F. Han and H.-J. Zhai, Chemical bonding and dynamic structural fluxionality of a boron-based Al₂B₈ binary cluster: the robustness of a doubly 6π/6σ aromatic [B₈]²⁻ molecular wheel, RSC Adv., 2023, 13, 1964–1973.
15. P. L. Rodríguez-Kessler, Vibrational and electronic properties of the B₇Al₂ cluster, arXiv, 2024, preprint DOI:10.48550/arXiv.2409.18165.
16. R. Yu, J. Barroso, M.-H. Wang, W.-Y. Liang, C. Chen, X. Zarate, M. Orozco-Ic, Z.-H. Cui and G. Merino, Structure and bonding of molecular stirrers with formula B7M2 and B8M2 (M = Zn, Cd, Hg), Phys. Chem. Chem. Phys., 2020, 22, 12312–12320.
17. J. Hicks, E. J. Underhill, C. E. Kefalidis, L. Maron and C. Jones, A Mixed-Valence Tri-Zinc Complex, [LZnZnZnL] (L = Bulky Amide), Bearing a Linear Chain of Two-Coordinate Zinc Atoms, Angew. Chem., Int. Ed., 2015, 54, 10000–10004.
18. X. Liu, M. Zhang, S. Wu, R. Zhong, Y. Liu, A. M. Arif, Y. Geng and Z. Su, All-Metallic Zn=Zn Double-Bonded Octahedral Zn₂M₄ (M = Li, Na) Clusters with Negative Oxidation State of Zinc, ChemPhysChem, 2020, 21, 459–463.
19. I. Resa, E. Carmona, E. Gutierrez-Puebla and A. Monge, Decamethyldizincocene, a Stable Compound of Zn(I) with a Zn–Zn Bond, Science, 2004, 305, 1136–1138.
20. K. Mayer, L.-A. Jantke, S. Schulz and T. F. Fässler, Retention of the Zn–Zn bond in [Ge₉Zn–ZnGe₉]₆ and Formation of [(Ge₉Zn)(Ge₉)(ZnGe₉)]₈ and Polymeric [(Ge₉Zn)₂], Angew. Chem., Int. Ed., 2017, 56, 2350–2355.
21. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108.
22. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170.
23. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
24. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
25. P. L. Rodríguez-Kessler, A. R. Rodríguez-Domínguez and A. Muñoz-Castro, Systematic cluster growth: a structure search method for transition metal clusters, Phys. Chem. Chem. Phys., 2021, 23, 4935–4943.
26. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690.
27. G. Martínez-Guajardo, J. Luis Cabellos, A. Díaz-Celaya, S. Pan, R. Islas, P. K. Chattaraj, T. Heine and G. Merino, Dynamical behavior of Borospherene: A Nanobubble, Sci. Rep., 2015, 5, 11287.
28. R. A. Murcia-Galán, S. M. Durán, S. M. Leal-Pinto, M. V. Roa-Cordero, J. D. Vargas, L. V. Herrera, A. Muñoz-Castro, D. MacLeod-Carey, T. W. Naranjo, P. L. Rodríguez-Kessler and J. J. Hurtado, Antifungal activity of Co(II) and Cu(II) complexes containing 1,3-bis(benzotriazol-1-yl)-propan-2-ol on the growth and virulence traits of fluconazole-resistant Candida species: synthesis, DFT calculations, and biological activity, BMC Chem., 2023, 17, 135.
29. L. Wen, G. Li, L.-M. Yang and E. Ganz, Structural evolution in boron-based clusters B₅Aln^0/−/+ (n = 1–4): Al atoms transition from the periphery of the planar W-shaped B₅ ring to the vertex of the bipyramid, Eur. Phys. J. D, 2020, 74, 223.
30. P. L. Rodríguez-Kessler, Revisiting the Global Minimum Structure of the Pt₅ V Cluster, arXiv, 2024, preprint, DOI:10.48550/arXiv.2408.03537.
31. ADF 2024.1, SCM , Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2024, https://www.scm.com.
32. S. Ehrlich, J. Moellmann and S. Grimme, Dispersion-Corrected Density Functional Theory for Aromatic Interactions in Complex Systems, Acc. Chem. Res., 2013, 46, 916–926.
33. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Covalent radii revisited, Dalton Trans., 2008, 2832–2838.
34. G. Merino, T. Heine and G. Seifert, The Induced Magnetic Field in Cyclic Molecules, Chem. – Eur. J., 2004, 10, 4367–4371.
35. R. Islas, T. Heine and G. Merino, The Induced Magnetic Field, Acc. Chem. Res., 2012, 45, 215–228.
36. A. J. Bridgeman, G. Cavigliasso, L. R. Ireland and J. Rothery, The Mayer bond order as a tool in inorganic chemistry, J. Chem. Soc., Dalton Trans., 2001, 2095–2108.
37. I. Mayer, Bond order and valence indices: A personal account, J. Comput. Chem., 2007, 28, 204–221.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04444d

---