Elucidating the interplay between entropy-driven and patch-mediated bonding in directing nanoscale assemblies†
Kireeti
Akkunuri‡
 ,
Xiangyu
Zhang‡
and
Thi
Vo
,
Xiangyu
Zhang‡
and
Thi
Vo
 *
*
Chemical and Biomolecular Engineering, Johns Hopkins University, Baltimore, MD 21218, USA. E-mail: tvo12@jhu.edu
First published on 31st October 2024
Abstract
Selective nanoparticle surface patterning presents incredible promise for broadening programmable materials design into a space beyond “close-packed” morphologies. These “patchy” particles impose directional attractions between neighbors that favor the formation of low-coordination, open structures previously inaccessible via their isotropically interacting nanoparticle counterparts. However, unlike patchy colloids, patches on nanoparticles are highly deformable, presenting challenges for their predictive design. Here, we present a multi-faceted approach combining theory and simulation to investigate the underlying forces governing interactions between nanoparticles with flexible patches. We first develop a thermodynamic perturbation theory to fundamentally capture the interplay between patch–patch merging and directional entropic forces in controlling particle organization. We then employ theoretical insights to explicitly consider how monomer geometry synergizes with monomer connectivity in sculpting the equilibrium morphologies for polymeric chains composed of anisotropic monomeric subunits. Theory predictions are then validated using simulations, with excellent agreement across both local and global length scales. Combined, our findings indicate that a large suite of orientational and structural diversity can be attained via precision engineering of how patch–patch and entropic forces between the anisotropic nanoparticles counterbalance each other. These findings on nanoscale patchy interactions offer newer avenues for directing the assembly process of novel polymeric and metamaterials.
Design, System, ApplicationNanoscale building blocks with selective polymer surface patterning represent a class of materials with unprecedented degree of programmability in spatial and orientational orderings. There “patchy” nanoparticles blend the toughness and optical properties of inorganic particles with the flexibility and reconfigurability of polymeric patches, providing a route for fabricating chiral and/or low-coordination multifunctional materials with immediate applications in cargo encapsulation, membrane filtration, sensing, and or optical computing devices. However, due to the similarity in length scales between polymeric patches and the nanoparticle cores, grand challenges in their a priori design lie in a lack of fundamental understanding of how the interplay between flexible patchy interactions and entropic forces associated with particle geometries ultimately influence their hierarchical, mesoscale morphologies. In this work, we combine theory and simulation to explicitly quantify the interplay between enthalpic and entropic forces governing interactions between nanoparticles with flexible patches. We show that these nanoscale-level interactions readily propagate to the mesoscale and present a predictive theoretical framework that can rigorously quantify such effects. Our theory shows that precision engineering of polymeric patchy interactions can produce a diverse suite of symmetry-breaking interactions between nanoparticles, opening newer avenues for designing hybrid organic–inorganic metamaterials. |
Introduction
Recent advances in nanoscale synthesis have resulted in a novel class of polymer functionalized nanoparticles (NPs) exhibiting patch-formation and symmetry breaking surface patterning.1–5 Such “patchy” NPs impose specific spatial and orientational interactions relative to their neighboring particles that disfavor “close-packed” configurations, producing complex and/or low-coordination NP structural orderings.6–16 Typical morphologies include the formation of porous superlattices,8–12,14 host–guest configurations,15–20 and/or chiral supramolecular motifs21–23 – all of which are of interest as they exhibit macroscopic properties ideal for modern day applications. For example, host–guest and/or porous lattices exhibit tunability in cavity sizes, relevant for cargo encapsulation and filtration-based transport processes. Similarly, chiral superstructures exhibit unique optical/photonic responses that make them amenable for use in sensing and optical computing devices. Combined, these findings have enabled access to tunable, open-lattice morphologies using nanoscale synthetic building blocks, expanding both the space of their programmable complexity beyond “close-packed” morphologies as well as their potential for application in previously inaccessible fields.4,24–27A grand challenge hindering the inverse design of patchy, anisotropic NP assemblies, however, lies in understanding how patch–patch interactions between NPs influence their equilibrium spatial and orientational configurations. Unlike colloids whose patch thicknesses are small relative to particle size,13,28–32 NPs possess patch thicknesses with sizes similar to their insphere radius.1,3 This difference in thickness results in patch–patch interactions that are significantly more rigid for colloids as compared to NPs. In fact, recent experimental findings have revealed that patch–patch interactions produce “bonds” between NPs that can twist, relax, and dynamically reconfigure on the seconds timescale,33 in contrast to the hours to days relaxation times observed for colloids.34,35 In short, patchy NP interactions are highly flexible and exhibit bond-like rotational behaviors. This means that predictions of patch-mediated NP assemblies must balance the interplay between entropic forces due to shape anisotropy and NP–NP connectivity resulting from the flexible “bonds” that arise between patch merging.
Through this lens, bonding interactions between patchy NPs are reminiscent of flexible polymers, suggesting that ideas from polymer physics can be employed to provide insights into their equilibrium behaviors. While preliminary works from the polymers community have elucidated the role of anisotropic, ribbon-like monomers on chain conformations,36 a generalized framework capable of accounting for arbitrarily shaped monomer geometries remains elusive. Here, we present one framework capable of predicting the equilibrium spatial and orientational behaviors for systems of anisotropic NPs that accounts for both entropic and bonding interactions. Specifically, we generalize the idea of entropic forces between anisotropic particles37 to account for bonding constraints between different locations on the NP surface, reflecting the high degree of molecular patterning currently accessible in experimental systems.4,5 We then employ our framework to develop a scaling theory that accurately predicts equilibrium chain statistics for systems of polymeric NPs connected via patch–patch merging, validated using simulations. Furthermore, we apply our results to predict previously reported behaviors of patchy triangular prism33 and polymeric “bundlemers”38 in the literature, showcasing our theory's generalizability to experimentally relevant systems. Our work not only provides a fundamental understanding of the underlying forces governing patchy, anisotropic NP interactions, but also presents a generalization of polymer theory to consider the effect of monomer geometry on chain conformations. The former serves as a critical step for inverse design of patchy NP assemblies while the latter generalizes predictions for polymer conformations to complex systems containing polyhedrally shaped (POSS, carborane, fullerene), conjugated, and/or aromatic monomers.39
Theory
Shape anisotropy and entropic bonding theory (EBT)
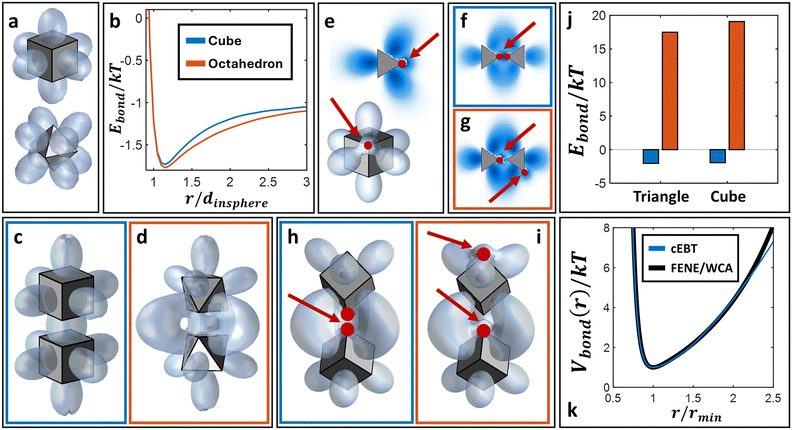
To capture the interplay between inter-NP connectivity and directional entropic forces resulting from particle geometry, we propose a generalization of entropic bonding theory37 (EBT). Here, it is instructive to describe the fundamental concepts of the original theory. Briefly, EBT quantifies the local excluded volume between neighboring NPs to compute their free energy of interactions. Excluded volume quantification employs the ansatz of pseudoparticles (pPs) to define a mean-field interaction potential (eqn (1)) between NPs and pPs that is then coupled with the Smoluchowski equation (eqn (2)) to solve for the free energy (E) of a given set of NP configuration:37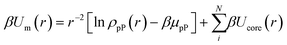 | (1) |
| [∇2 + β∇2Um − (β ∇ Um)2]ρpP = EρpP | (2) |
Connectivity-generalization of entropic bonding theory (cEBT)
To bridge the predictive capabilities of EBT to systems of connected, anisotropic NPs, we first note that shape orbitals (Fig. 1a) are plots of ρpP, which are the general solutions for the pP distribution from eqn (1) and (2). By definition, ρpP, therefore, quantifies the local excluded volume imposed from the reference NP on its neighbors. Our connectivity-generalization to EBT (cEBT) assumes that connectivity imposes an additional excluded-volume constraint with other NPs: that is, the space between two bonded NP locations also cannot be occupied by other NPs. Physically, this assumption captures the fact that polymeric grafts must occupy the space between two merged patches and thus exclude all other NPs from occupying the same space. In a more general sense, even covalent bonding imposes a strong electron density inside the bonding orbitals between atoms that subsequently exclude other subatomic particles. Through this lens, adding effects of connectivity into EBT requires the inclusion of bonding directly in the construction of the shape orbitals for each respective particle geometry.We first define an effective NP composed of a central core whose shape is commensurate with the NP geometry and spherical patches of size σ placed at NP surface locations exhibiting patch–patch merging interactions. The construction of this composite particle captures the physical picture that the patches themselves impose excluded volume constraints and thus directly influences the pP distribution. This approach generalizes eqn (1) to:
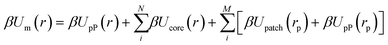 | (3) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) r−2[ln
r−2[ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρpP(r) – βμpP] (for ease of notation). The first two terms in eqn (3) account for the effect of the NP core on the pP distribution and carry over from EBT. The last two terms extend EBT to consider the effect of the patches on the resulting pP distribution. Note that the rp coordinate indicates a relative distance to the patch locations with respect to the NP frame of reference. To account for patch–patch connectivity, we further extend eqn (3) to sum over all pairwise bonding between patches, yielding:
ρpP(r) – βμpP] (for ease of notation). The first two terms in eqn (3) account for the effect of the NP core on the pP distribution and carry over from EBT. The last two terms extend EBT to consider the effect of the patches on the resulting pP distribution. Note that the rp coordinate indicates a relative distance to the patch locations with respect to the NP frame of reference. To account for patch–patch connectivity, we further extend eqn (3) to sum over all pairwise bonding between patches, yielding: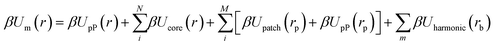 | (4) |
| Uharmonic(rb) = kh(rb − ro)2 | (5) |
Equilibrium chain conformation for polymeric NPs
Results from pairwise calculations between bonded NPs immediately suggest that oligomers/polymers of connected NPs will also experience significant orientational constraints with respect to their equilibrium inter-NP orderings. Motivated by the polymer-like bonding potential between NPs (Fig. 1k), we borrow ideas from polymer physics to develop an analytical theory aimed at predicting the conformational behaviors for long chains of connected patchy NPs. Specifically, it is well known that the equilibrium scaling behavior for chain size (R) is R ∼ N1/2b, where N is the degree of polymerization and b is the size of the Kuhn monomer.43 This classical behavior, however, assumes that monomers are spherical and cannot capture shape-driven orientational orderings that dominate in the limit of anisotropic geometries.44–46 To account for the effects of anisotropy in dictating chain conformation, we first note that the R ∼ N1/2 scaling relationship is obtained via a random-walk derivation. Here, we introduce a variant of a biased random walk model where a step left is different in size than a step right: that is, bleft ≠ bright. This model reflects the idea that different modes of bonding (i.e. vertex–vertex, edge–edge, or face–face) can result in uneven forward/backward steps due to geometric constraints imposed by the underlying particle shapes. Performing a statistical mechanical derivation of the equilibrium chain size for a 3D polymer composed of anisotropic monomers yields (Appendix B†):| R ∼ N(2−Λ)/2bP | (6) |
Experimental validation of cEBT and anisotropic polymer scaling
cEBT for patchy triangular nanoprisms
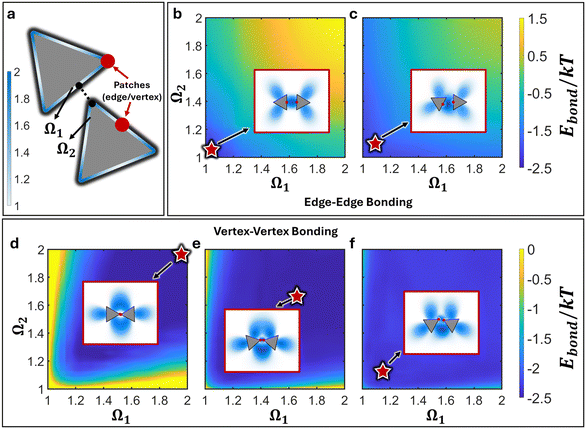
Results from the experimental literature have shown that vertex–vertex connected triangular NPs mediated by patch–patch merging produce an equilibrium motif where edges are slanted towards each other (saw-tooth) as opposed to the expected tip-to-tip configuration (bowtie).33 Furthermore, the emergent inter-NP bonding arising from patch–patch merging are reported to be highly flexible and can freely rotate in solution.33 Here, we employ cEBT (eqn (3)–(5)) to provide a microscopic picture of the underlying driving force governing both the formation of the saw-tooth motif as well as the observed emergent bond flexibility. Fig. 2f shows a free energy surface for vertex–vertex connected NPs as a function of relative NP orientations for a patch size σ equal to 25% of the NP edge length (sNP): that is, 0.25sNP. This patch size is commensurate to the experimentally measured polymeric patches that form on triangular NPs.33 Results from cEBT calculations indicate that the lowest energy configuration between connected NPs is the saw-tooth motif, in agreement with experimental findings (Fig. 2f). The equilibrium configurations are plotted as inset in each of their respective free energy surface in Fig. 2 and their locations on each free energy surface are indicated by red stars. Inspection of the bonding orbitals between NPs clearly indicates that the saw-tooth configuration provides a higher overlap between shape orbitals located at the triangular edges. These edge-localized orbitals are entropic in nature since they arise due to particle geometry and not from patch–patch bonding interactions (Fig. 1). Therefore, the saw-tooth motif is unique to nanoscale patchy NPs and arise due to a direct competition of two counteracting forces: 1). directional entropic forces favoring edge–edge alignment and 2). patch–patch merging favoring vertex–vertex alignment. It is this delicate balance between opposing forces that breaks the symmetry intrinsic to the pre-programmed vertex–vertex patchy interactions.Furthermore, the computed energy difference between different relative NP configurations is on the order of 1kT (Fig. 2f). This means that the bonds between NPs are not orientationally locked but can transition between one state versus another since their energetic differences are on the order of thermal noise. As such, cEBT predicts that the emergent inter-NP bonding resulting from patch–patch merging is highly flexible, which is also congruent with experimental observations.33 Combined, cEBT calculations provide a microscopic understanding of the underlying forces at play that govern both the emergent bond flexibility between NPs as well as their equilibrium saw-tooth configurations.
The critical balance between entropy versus enthalpy in directing orientational ordering between NPs sits in direct contrast to traditional patchy colloids that have been reported in the literature.13,28,30–32,35 In patchy colloids, patch–patch interactions are inflexible and uniquely define the directional interactions between particles: that is, a vertex patchy colloid can only produce vertex–vertex assembly configurations. This is because patches for colloidal particles are small relative to the core size compared to their NP counterparts. As a result, patch–patch bonding in the colloidal limit experience high steric hinderances. Since cEBT is agnostic of scales, decreasing the patch size in our calculations should also capture the behaviors of patchy colloids. Indeed, reduction of the patch size to 0.15sNP shifts the equilibrium structure to the bowtie configuration (Fig. 2e). However, since the patch sizes are still roughly on par with the core size, the difference in energy between bowtie and saw-tooth configurations are still within thermal noise (Fig. 2e). Decreasing patch size further to 0.05sNP show a marked shift in the free energy surface, where the bowtie configuration is now highly energetically favored with energy differences on the order of 3kT (Fig. 2d). In other words, transitions between the bowtie and sawtooth configurations are no longer favorable at this small patch size. This behavior converges cEBT calculations to the limit of patchy colloids where particle sizes are much bigger than patch sizes, indicating that cEBT can accurately model patchy interactions across multiple length scales.
Since entropy-driven interactions favor edge–edge alignments between the triangular NPs, it is natural to expect that patch-mediated edge–edge connected NPs will favor only edge–edge alignments. Indeed, cEBT energy calculations at patch sizes equal to 0.1sNP reveal that only edge-aligned NPs are favored (Fig. 2b). Furthermore, the total free energy between the equilibrium configurations is lower than those observed for vertex–vertex bonded NPs, indicating that entropic effects complement patch–patch connectivity in such edge-aligned cases. However, increasing patch size to 0.3sNP shows a shift away from edge–edge alignments between particles (Fig. 2c). Inspection of the bonding orbitals obtained from cEBT indicates that excluded volume interactions between larger patch sizes push NPs so far apart that a tilted state produces higher shape orbital overlaps relative to the edge-aligned configuration. These equilibrium configurations are shown in the inset for each free energy surface in Fig. 2b and c. In addition to triangular NPs, we computed the potential energy surfaces for several other vertex–vertex connected 2D geometries (Appendix D†) including square (ESI†, Fig. D1a), pentagonal (ESI†, Fig. D1a), and hexagonal (ESI†, Fig. D1a) NPs. Analysis of the equilibrium configurations for patch sizes commensurate with particle edge lengths all reveal that directional entropic forces systematically break tip-to-tip alignments between NPs to favor tilted configurations between NPs at large patch sizes.
cEBT and scaling prediction of peptide bundlemers
To further showcase the generalizability of cEBT and the developed anisotropic chain scaling theory, we apply our calculations to covalently bonded coiled-coil bundles (bundlemers) previously reported in the literature.38 Briefly, each bundlemer is a nanoscale unit constructed from 4 α-helical peptide oligomers that fold into well-defined, anti-parallel coiled-coil bundles roughly 4 nm in length and 2.5 nm in diameter. Each individual α-helix tail contains a maleimide or thiol group that can undergo a thiol-Michael reaction to form covalent bonds between neighboring bundlemers that are typically 0.2 nm in length. Based on the folded coiled-coil geometry, there are two covalent bonding sites at the top and two at the bottom of the long axis for each bundlemer (Fig. 3a). In essence, the effective geometry for this nanoscale building block is that of a cylinder with height h and two patchy sites of size 0.05h: one at the top cylinder face and one at the bottom cylinder face (Fig. 3a, top). Performing cEBT and scaling exponent calculations for these bundlemers reveal a linear, rod-like behavior with ν = 0.97 (Fig. 3a), in excellent agreement with experimentally observed formation of long, rigid rods.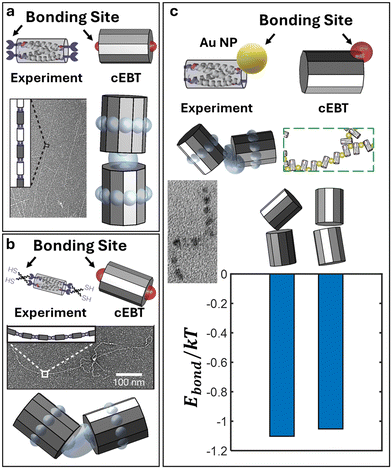 | ||
| Fig. 3 cEBT prediction of polymeric bundlemers. Equilibrium configuration predicted using cEBT sampling across all relative orientations between bundlemers (modelled as cylinders) for a) face–face connection using rigid linkers, b) face–face connection using flexible linkers, and c) edge–edge connection. For each panel, the top indicates how the experimental system is mapped to the cEBT model. All predicted cEBT prediction matches with the experimentally observed bonding motif between bundlemers. In the limit of edge–edge connection, the relative free energy different between tilted and face–face alignment is shown to be on the order of ∼0.1kT, corroborating the mixed motif observed in experiments. All experimental images are reproduced with permission.38 | ||
Furthermore, experiments reported the formation of more flexible bundlemer chains upon transitioning to a PETMP thiol linker between bundlemers. This new PETMP linker corresponds to a new patch size of 0.15h between each NP (Fig. 3b, top). Predictions using the increased bond length in cEBT reveal a shift the equilibrium pairwise configuration to a tilted alignment between cylinders (Fig. 3b), which corresponded to a new scaling exponent of ν = 0.88. Combined, these results indicate that increasing bond flexibility shifts chain conformation from that of a rigid rod to a semiflexible chain, which matches experimental observations. Lastly, experiments also enabled a lateral bonding mode between bundlemers mediated via 2 nm gold NPs functionalized with maleimide (Fig. 3c, top). This new lateral bonding mode results in a mix between lateral and face–face aligned bundlemers in experiments (Fig. 3c). Within our cEBT model, the new NP linker corresponds to a 0.5h patch size located at the rim of the cylinder. Performing calculations for this new patchy motif and visualizing the lowest energy configuration reveal similar relative orientations between bundlemers compared to those observed in experiments (Fig. 3c). More specifically, cEBT calculations indicate that the energy differences are on the order of 0.1kT, indicating that both motifs are thermodynamically favorable, providing a microscopic understanding of the emergent bonding behaviors. We additionally predict that the scaling exponents drops to ν = 0.75. This means that chains formed via lateral bonding between bundlemers are much more flexible compared to their face–face bonded counterparts, in agreement with the experimentally reported chain conformations being more flexible and random relative to the above two cases. Not only do these findings provide additional validations of cEBT, but they also emphasize the universality of our theories by showing that both cEBT (eqn (3)–(5)) and anisotropic chain scaling (eqn (6)) applies to both inorganic NP monomers as well as biological, peptide-based polyhedral monomers.
Simulation methods
While comparison with established literature provide validation testbeds for specific limits of cEBT and anisotropic scaling predictions, we further seek to showcase the broad generalizability of our developed theory to arbitrary monomer geometry as well as bonding modes. Along this vein, we perform simulations for polymer chains consisting of anisotropic monomeric units using the HOOMD-blue package.47 Specifically, we consider two different types of bonding potentials – harmonic and FENE. These potentials are selected due to their usage across a wide range of coarse-grained polymer simulations. For example, the FENE potential is the model of choice for traditional bead-spring polymer simulation and has recently been shown to accurately capture the dynamics of bonded patchy NPs observed in simulations.33 Common force fields such as CHARMM,48 AMBER,49 and MARTINI50,51 readily fit parameters to the harmonic potential to capture the behaviors of traditional polymers such as those containing conjugated and/or charged moieties. As such, validating predictions across these common coarse-grained models will ensure that our theory can be readily applied to a diverse range of both nano/colloidal as well as traditional polymeric systems.Anisotropic polymers bonded via the FENE potential
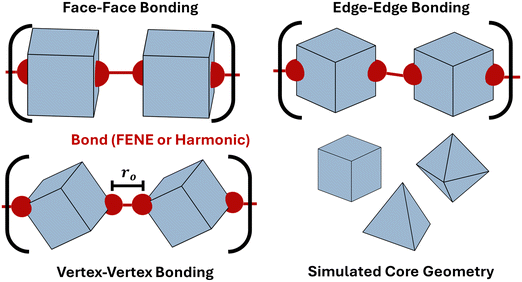
We employ molecular dynamics (MD) to characterize the equilibrium scaling behavior of polymeric chains made of anisotropic building blocks bonded via the FENE potential. Each system is set up on HOOMD-blue as a single chain of bonded anisotropic particles immersed in an implicit-solvent with chain lengths varying from 40 to 200. Simulations are carried out using an NVT ensemble at a temperature of kT = 0.9 and employ the Nosé–Hoover thermostat and the MTK equations.52,53 We perform simulations for both spherical monomers as well as three different monomer geometries: cube, octahedron, and tetrahedron. Anisotropic particles are bonded together edge–edge, face–face, or vertex–vertex using patches that are rigidly attached to the core particle at each respective bonding location (Fig. 4). Bonds between patches use the FENE potential: βV(r) = −0.5kro2 ln(1 − (r/ro)2) + VWCA(r) where VWCA(r) is the Weeks–Chandler–Andersen repulsive interaction.54 The parameters employed in simulations are k = 30 and ro = 1.5α, with α = 10. The core monomers are treated as repulsive hard-particles using the anisotropic Lennard–Jones potential.55 A typical FENE bond has an equilibrium bond length of 0.89α. This translates to effective patch sizes of 10% of the insphere diameter (σin) of the cube and octahedron, and 20% of the insphere diameter (σin) of the tetrahedron. The step-size is dt = 5 × 10−4 for octahedra and cubes, and 2.5 × 10−4 for tetrahedra. All systems are run for 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation time units.
000 simulation time units.
Anisotropic polymers bonded via harmonic potential
We perform Monte Carlo simulations for four different types of particles – patchy spheres, tetrahedron, cube, and octahedron – bonded using the harmonic potential. For each shape, two different modes of bonding are performed: vertex–vertex and face–face. For vertex–vertex bonding, connection sites are placed along the polyhedron's diagonal (Fig. 4). For face–face bonding, connection sites are positioned at the center of opposing faces for each respective shape (Fig. 4). The bonding potential employed for the Metropolis algorithm is:56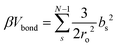 | (7) |
Computational validation of cEBT and anisotropic polymer scaling
Connections between FENE and harmonic potential simulation and cEBT
For clarity, we note that simulations using the FENE potential have effectively identical patch sizes to those for harmonic potential with ro = 0.1σin, where σin is the anisotropic particle's insphere diameter. We define this as the “small patch” limit to connect to theoretical cEBT and scaling calculations for the same patch size of σ = 0.1σin. Similarly, harmonic potential simulations with ro = 0.5σin are defined as the “medium patch” limit to enable a direct comparison with theory calculations for patch size of σ = 0.5σin. Lastly, the “large patch” limit refers to harmonic potential simulations with ro = 5.0σin, which corresponds to theory calculations for patch size of σ = 5.0σin. For ease of notation, we use FE and HR to indicate FENE and harmonic bonding, respectively. These connections are summarized in Table 1. Scaling exponents showing that our patchy bonding models reproduces known behaviors for traditional polymers with spherical subunits are reported in Appendix C of the ESI.†| Patch size | Simulation | cEBT |
|---|---|---|
| r o: equilibrium bond length, σin: monomer insphere diameter, σ: patch size. FE: FENE bonding, HR: harmonic bonding. | ||
| Small (S) | r o = 0.1σin | σ = 0.1σin |
| Medium (M) | r o = 0.5σin | σ = 0.5σin |
| Large (L) | r o = 5.0σin | σ = 5.0σin |
Equilibrium configurations and chain scaling for cubic monomer geometry
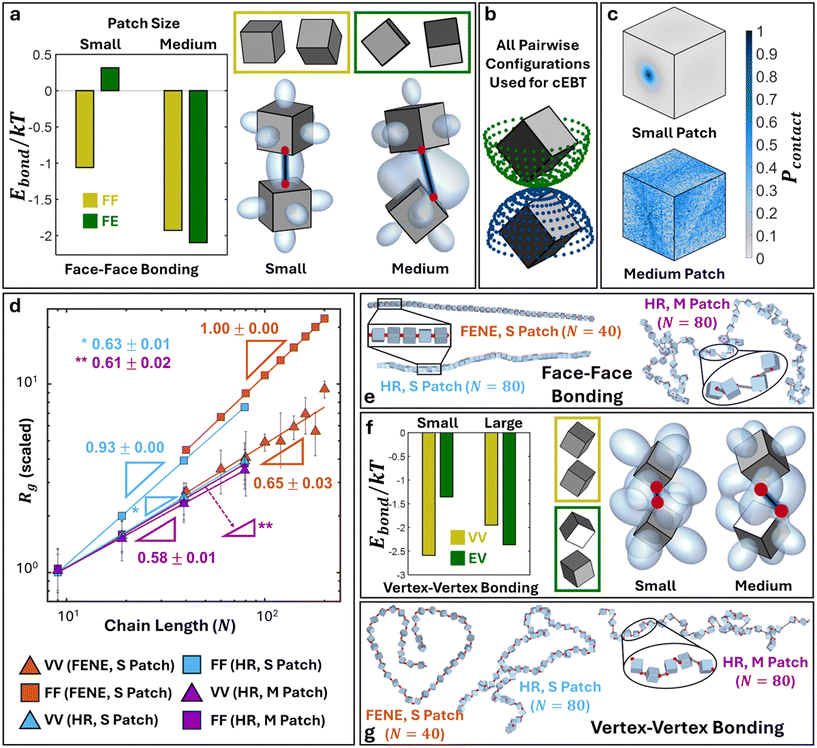
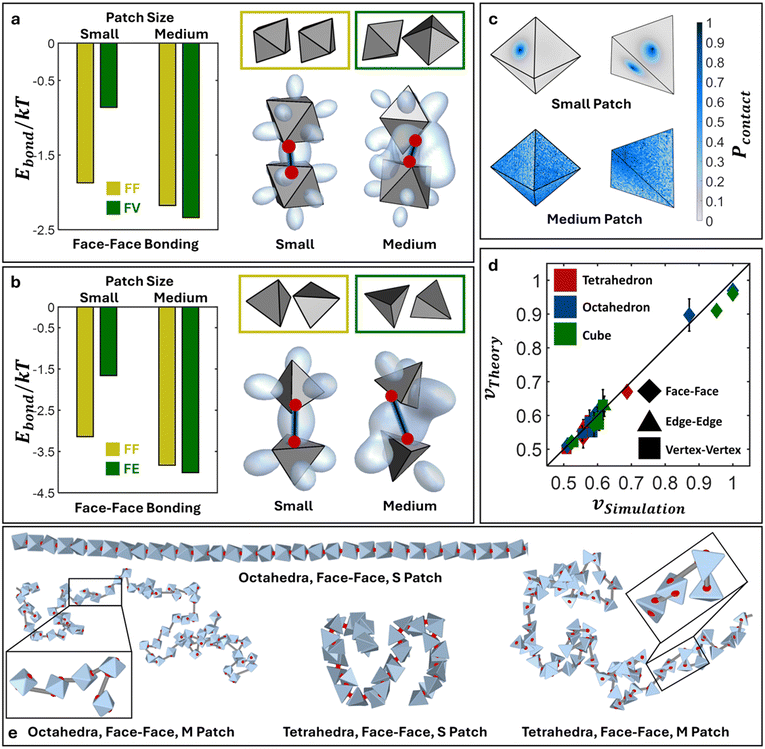
We first discuss results for cubic monomer geometry. Here, we employ cEBT (eqn (3)–(5)) to compute the free energy between vertex–vertex and face–face connected cubes. Across all bonding modes, analysis of the lowest energy configuration reveals the formation of symmetry breaking orientational ordering between NPs. Similar to their 2D counterparts (Fig. 2), visualization of the bonding orbitals of the equilibrium NP configurations reveals that maximization of shape orbital overlaps serves as the dominant driving force underpinning the observed symmetry breakage in NP relative orientation (Fig. 5a and f).Starting with face–face bonded cubes, we employ cEBT (eqn (3)–(5)) to compute the bonding free energy (Ebond) for all pairwise relative orientations between cubes indicated in Fig. 5b. This large sweep ensures that we have properly sampled all possible orientations between cubes. Due to the high dimensionality of this phase space, we chose to compare the computed Ebond between the two identified lowest energy configurations (face–face and face-edge) for small medium patches mediating face–face connections. Specifically, we plot the computed Ebond for face–face and face-edge configurations in the limit of small patches (left, Fig. 5a) and the same two configuration energy but in the limit of medium patches (right, Fig. 5a). Colors for each energy plot correspond to the color of the boxed relative orientations in Fig. 5a. Results indicate that face–face aligned cubes are only favored in for small patches where the short bond length restricts bond flexibility, thereby preventing the system from rotating to seek additional shape orbital overlaps. Indeed, Ebond computed for face-edge oriented cubes in the limit of small patches shows that the total free energy is significantly higher compared to that of face–face alignment, indicating that it is less thermodynamically favored. Consequently, shifting to medium patches enhances bond flexibility and thus Ebond for face–face aligned cubes is now higher compared to face-edge aligned cubes due to additional overlaps between shape orbitals protruding from the cubes' other faces.
To compare simulations to cEBT pairwise calculations, we first compute the set of closest surface points between bonded monomers along the polymer backbone from simulations and plot their distribution on the surface of a reference monomer shape. Fig. 5c (top) shows the computed closest surface point distribution from simulations for face–face bonded cubes in the limit of small patches. Results indicate that the face–face alignment is the most dominant motif across all monomer-monomer relative orientations. These findings are in excellent agreement with pairwise cEBT energy calculations for small patches (Fig. 5a), where face–face aligned configurations are thermodynamically favored. To bridge pairwise calculations to the polymer limit, we measure the end-to-end scaling exponent v (Rg ∼ Nv) for polymer chains constructed from face–face bonded cubic monomers from simulations. Fig. 5d shows an Rgvs. N scaling exponent plot for simulation results using both harmonic and FENE bond potentials for cubic systems. For face–face bonding, small patches yield a scaling exponent of v = 1.00 ± 0.00 and v = 0.93 ± 0.00 for the FENE and harmonic potentials, respectively. These values suggest that chains are extended and experience a high degree of orientational constraints between neighbors. Indeed, theory prediction of the scaling exponent for face–face bonded cubes in the limit of small patches (eqn (6)) gives v = 1, in agreement with simulations. Physically, a scaling exponent of v = 1 indicates that chains exhibit rigid, rod-like behaviors. Visualizations of chain conformation in this limit additionally confirm this interpretation as we only observe straight chains of face–face aligned cube across both FENE and harmonic potential simulations for small patch sizes (Fig. 5e).
Increasing to the medium patch size limit for cubes yields scaling exponents of v = 0.61 ± 0.02 from simulations (Fig. 5d), which closely matches the theoretically predicted value of v = 0.57. Similar to the small patch limit, we compare simulations to cEBT by computing closest surface points distribution between neighboring cubes and plotting the results on a reference particle (Fig. 5c, bottom). Results indicate a shift away from face–face aligned orientations to show a strong signature for face-edge alignments between neighboring monomers, in exact agreement with theory calculations from cEBT (Fig. 5a). Through the lens of increased rotational freedom between neighboring cubes, monomers effectively behave akin to overlapping spherical monomers whose radii are equal to the shape's midsphere radii. This means that connected cubes partially feel the effect of sterically-driven excluded volume interactions for all relative orientations where the shape sits outside the volume occupied by its midsphere. By definition, this is a self-avoiding walk and thus the chain scaling matches the classically known exponent of v = 0.6 for such systems. Visualization of chain conformation for face–face connected cubes in the limit of medium patch sizes further confirms the predictions from theory, where chains exhibit worm-like features intrinsic to self-avoiding conformations (Fig. 5e). Lastly, shifting further to the large patch size limit results in a scaling exponent of v = 0.5 ± 0.003 for face–face bonded cubes (Appendix I†), which is congruent with theory prediction for v = 0.5. In this limit, the large patch size forces monomers so far apart that they do not feel the presence of their neighbors, enabling an unrestricted degree of rotational freedom between bonded cubes. In other words, particles lose knowledge of both their core geometry as well as bonding constraints with their neighbors and behave akin to highly overlapping spherical monomers. This is analogous to a traditional random walk and thus the scaling exponents converge to the well-known gaussian scaling statistics.43
Fig. 5f shows an analogous analysis of cEBT pairwise calculations for vertex–vertex bonding between cubes, where we observe an orbital overlap driven shift from a vertex–vertex to an edge-vertex motif with a corresponding increase from small to medium patch size. Unlike face–face bonding, the measured scaling exponents for both small and medium patch sizes yield similar values of v ∼ 0.6 (Fig. 5d), indicating that chains behave akin to self-avoiding walks between neighboring monomers. This difference relative to their face–face bonded counterparts arises due to the bonding location between neighboring cubes. If we trace the vertex of a cube spinning about its center of mass, the effective geometry that the vertex sweeps out is a sphere whose diameter is equal to the cube's circumsphere. As a result, each cube perceives its neighbor not as a cube but rather as a sphere whose effective diameter is equal to the circumsphere diameter of its neighboring cube. However, since the cubes take up less space than their circumsphere, the neighboring circumspheres are not orientationally locked into a linear, vertex–vertex aligned motif, but can partially overlap with each other. This behavior is also akin to a self-avoiding walk, which is known to exhibit scaling exponent of v = 0.6. Visualization of the equilibrium chain conformation for vertex–vertex bonded cubes for both small and medium patch sizes all reveal worm-like chain conformations, further corroborating the predicted self-avoiding walk scaling statistics (Fig. 5g). Similar to face–face bonding, the large patch limit for vertex–vertex bonding yields the trivial gaussian limit where monomer lose knowledge of both their geometry and bonding constraints. Analogous results are also obtained for edge–edge bonding between cubes and are reported in Table I1 and Appendix H of the ESI.†
Polymeric chains with octahedral and tetrahedral monomer geometries
Additionally, we perform the same cEBT calculation for octahedra (ESI†, Fig. E1b and c) and tetrahedra (ESI†, Fig. E1d and e) for all connectivity – face–face, edge–edge, and vertex–vertex (Appendix E†). Across all shapes and connectivity, the consistent cEBT prediction is that connectivity only locks particle configurations in the limit of small patches. Medium patches allow for higher bond flexibility, resulting in a complex interplay between connectivity constraints and directional entropic interactions to give rise to symmetry breaking orientations such as edge-vertex, face-edge, and face-vertex motifs. Similar to cubes, we compare cEBT pairwise calculations with the closest surface point distribution between bonded monomers measured from simulations. Fig. 6c shows the computed distribution for face–face bonded octahedra and tetrahedra in the limit of small and medium patches. Octahedral monomers transition from face–face dominated to a face-vertex dominated distribution with increasing patch size. Similarly, tetrahedral monomers shift from a face–face dominated to a face-edge dominated motif. Both results are in agreement with cEBT predictions for each respective monomer geometry (Fig. 6a and b). Visualization of the shift in chain conformation with increasing patch sizes are shown for both octahedral and tetrahedral monomers in Fig. 6e. Measured scaling exponents for such systems also progressively shift from rigid rod to self-avoiding walk to gaussian statistics as the patch size increases from small to medium to large, respectively. Analogous results are also obtained for vertex–vertex and edge–edge bonding between both octahedra and tetrahedra and are reported in Appendices F, G, and I of the ESI.† All the measured scaling exponents from simulations are accurately predicted using theory (eqn (6)). Fig. 6d encapsulates and compares all the scaling exponents from FENE and harmonic potential simulations against theory prediction, numerical values are tabulated in Table I1 of the ESI.† The tight agreement across theory and simulation indicates that the interplay between directional entropic forces and flexible patch–patch bonding between anisotropic monomers readily propagates to the oligomeric and polymeric scales and plays a critical role in controlling the equilibrium chain conformation. These findings highlight the success of our theory in illuminating the intricate balance between shape-driven and bond-driven interactions and how they work together to sculpt both local monomer-monomer ordering as well as global chain conformational statistics.Conclusion
In summary, we elucidate how the interplay between patch–patch connectivity and shape-driven entropic interactions sculpts the spatial and orientational orderings between anisotropic building blocks. We show that emergent entropic forces can break the symmetry of the pre-programmed directional patchy (bonding) interactions between particles, especially in cases where patch sizes are more commensurate with NP core sizes. These results indicate that emergent entropic forces must be explicitly considered when designing patchy particles at the nanoscale as they can alter (or even break) the as-synthesized directional, patchy inter-NP interactions. Failure to consider such effects can produce situations where competing forces undermine the desired pre-programmed directional interactions and result in kinetically arrested and/or disordered assemblies. Our proposed cEBT development provides a theoretical framework for a priori prediction of this emergent symmetry breaking by explicitly accounting for both monomer geometry and connectivity constraints between particles. We validate cEBT by showing that it reproduces known behaviors from established experimental systems: patchy triangular nanoprisms and peptide bundlemers. Additionally, we rigorously validate cEBT against simulations for polymer chains containing different particle geometries with different inter-NP bonding modes. Our analysis shows that cEBT not only captures the correct local ordering between NPs but also their macroscopic mesoscale ordering. In short, our work shines light on the complex forces at play with respect to patchy nanoscale building blocks with anisotropic geometries. The excellent agreement across theory, simulation, and validation against the experimental literature indicate that cEBT has the potential to expand the applicability of shape as a handle for directing self-assembly into the space of patchy NPs as well as molecular and colloidal polymers, opening newer doors for designing the self-assembly of novel soft, porous, and metamaterials.Data availability
Numerical data and results for structure and characterizations performed and shown in the main text are provided in the accompanying ZIP file with sample analysis scripts. Sample simulation scripts to perform both MC and MD simulations are included in the zip file. These analysis and simulation scripts will reproduce the data presented in all figures throughout the main text. We also provide sample simulation trajectory data (GSD file format) that represent the data/results that should come back from running the included files. All codes can also be found on our repository: https://github.com/VoGroupJHU/Anisotropic_Chain.git.Author contributions
K. A., X. Z., and T. V. designed and carried out the simulations. T. V. developed theory and directed the research. All authors contributed to the data analysis and writing of the manuscript.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work is supported by start-up AFOSR Award Number FA9550-24-1-0100 and start-up funding provided by Johns Hopkins University. Simulation performed for this research used resources of the Advanced Research Computing Facility at Johns Hopkins University.References
- G. Chen, K. J. Gibson, D. Liu, H. C. Rees, J. H. Lee, W. Xia, R. Lin, H. L. Xin, O. Gang and Y. Weizmann, Nat. Mater., 2018, 18, 169–174 Search PubMed.
- Y. Xiong, S. Yang, Y. Tian, A. Michelson, S. Xiang, H. Xin and O. Gang, ACS Nano, 2020, 14, 6823–6833 Search PubMed.
- A. Kim, T. Vo, H. An, P. Banerjee, L. Yao, S. Zhou, C. Kim, D. J. Milliron, S. C. Glotzer and Q. Chen, Nat. Commun., 2022, 13, 1–14 Search PubMed.
- T. Vo, MRS Bull., 2024, 49, 330–339 Search PubMed.
- S. Ravaine and E. Duguet, Curr. Opin. Colloid Interface Sci., 2017, 30, 45–53 CAS.
- A. W. Long and A. L. Ferguson, Mol. Syst. Des. Eng., 2018, 3, 49–65 RSC.
- G. Doppelbauer, E. G. Noya, E. Bianchi and G. Kahl, Soft Matter, 2012, 8, 7768–7772 RSC.
- D. F. Tracey, E. G. Noya and J. P. K. Doye, J. Chem. Phys., 2019, 151, 224506 CrossRef PubMed.
- E. Bianchi, J. Largo, P. Tartaglia, E. Zaccarelli and F. Sciortino, Phys. Rev. Lett., 2006, 97, 168301 CrossRef.
- C. Karner, C. Dellago and E. Bianchi, Soft Matter, 2020, 16, 2774–2785 RSC.
- F. Romano, J. Russo, L. Kroc and P. Šulc, Phys. Rev. Lett., 2020, 125, 118003 CrossRef CAS PubMed.
- H. Liu, M. Matthies, J. Russo, L. Rovigatti, R. P. Narayanan, T. Diep, D. McKeen, O. Gang, N. Stephanopoulos, F. Sciortino, H. Yan, F. Romano and P. Šulc, Science, 2024, 384, 776–781 CrossRef CAS.
- Y. J. Kim, J. H. Kim, I. S. Jo, D. J. Pine, S. Sacanna and G. R. Yi, J. Am. Chem. Soc., 2021, 143, 13175–13183 CrossRef CAS.
- Y. Tian, J. R. Lhermitte, L. Bai, T. Vo, H. L. Xin, H. Li, R. Li, M. Fukuto, K. G. Yager, J. S. Kahn, Y. Xiong, B. Minevich, S. K. Kumar and O. Gang, Nat. Mater., 2020, 19, 789–796 CrossRef CAS PubMed.
- W. D. Piñeros, M. Baldea and T. M. Truskett, J. Chem. Phys., 2016, 145, 54901 Search PubMed.
- B. A. Lindquist, R. B. Jadrich, W. D. Piñeros and T. M. Truskett, J. Phys. Chem. B, 2018, 122, 5547–5556 CAS.
- S. Lee, T. Vo and S. C. Glotzer, Nat. Chem., 2023, 15, 905–912 CAS.
- T. C. Moore, J. A. Anderson and S. C. Glotzer, Soft Matter, 2021, 17, 2840–2848 CAS.
- T. Dwyer, T. C. Moore, J. A. Anderson and S. C. Glotzer, Soft Matter, 2023, 19, 7011–7019 RSC.
- N. Pakalidou, J. Mu, A. J. Masters and C. Avendanõ, Mol. Syst. Des. Eng., 2020, 5, 376–384 Search PubMed.
- R. Guo, J. Mao, X. M. Xie and L. T. Yan, Sci. Rep., 2014, 4, 1–7 Search PubMed.
- P. Kumar, T. Vo, M. Cha, A. Visheratina, J. Y. Kim, W. Xu, J. Schwartz, A. Simon, D. Katz, V. P. Nicu, E. Marino, W. J. Choi, M. Veksler, S. Chen, C. Murray, R. Hovden, S. Glotzer and N. A. Kotov, Nature, 2023, 615, 418–424 CrossRef CAS PubMed.
- D. Sahoo, M. R. Imam, M. Peterca, B. E. Partridge, D. A. Wilson, X. Zeng, G. Ungar, P. A. Heiney and V. Percec, J. Am. Chem. Soc., 2018, 140, 13478–13487 CrossRef CAS.
- M. A. Boles, M. Engel and D. V. Talapin, Chem. Rev., 2016, 116, 11220–11289 CrossRef CAS.
- D. Samanta, W. Zhou, S. B. Ebrahimi, S. H. Petrosko and C. A. Mirkin, Adv. Mater., 2022, 34, 2107875 CrossRef CAS PubMed.
- C. A. Mirkin and S. H. Petrosko, ACS Nano, 2023, 17, 16291–16307 CrossRef CAS PubMed.
- J. S. Kahn and O. Gang, Angew. Chem., Int. Ed., 2022, 61, e202105678 CrossRef CAS.
- É. Ducrot, M. He, G. R. Yi and D. J. Pine, Nat. Mater., 2017, 16, 652–657 CrossRef PubMed.
- J. A. A. Diaz, J. S. Oh, G. R. Yi and D. J. Pine, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 10645–10653 CrossRef CAS.
- M. He, J. P. Gales, É. Ducrot, Z. Gong, G. R. Yi, S. Sacanna and D. J. Pine, Nature, 2020, 585, 524–529 CrossRef CAS PubMed.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55 CrossRef CAS PubMed.
- T. Hueckel, G. M. Hocky and S. Sacanna, Nat. Rev. Mater., 2021, 6, 1053–1069 CrossRef CAS.
- A. Kim, K. Akkunuri, C. Qian, L. Yao, K. Sun, Z. Chen, T. Vo and Q. Chen, ACS Nano, 2024, 18, 939–950 CrossRef CAS.
- S. Stuij, J. Rouwhorst, H. J. Jonas, N. Ruffino, Z. Gong, S. Sacanna, P. G. Bolhuis and P. Schall, Phys. Rev. Lett., 2021, 127, 108001 CrossRef CAS.
- P. J. M. Swinkels, R. Sinaasappel, Z. Gong, S. Sacanna, W. V. Meyer, F. Sciortino and P. Schall, Phys. Rev. Lett., 2024, 132, 78203 CrossRef CAS PubMed.
- W. Michaels, A. J. Spakowitz and J. Qin, Macromolecules, 2023, 56, 8359–8368 CrossRef CAS.
- T. Vo and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2116414119 CrossRef.
- D. Wu, N. Sinha, J. Lee, B. P. Sutherland, N. I. Halaszynski, Y. Tian, J. Caplan, H. V. Zhang, J. G. Saven, C. J. Kloxin and D. J. Pochan, Nature, 2019, 574, 658–662 CrossRef CAS.
- Z. Su, R. Zhang, X. Y. Yan, Q. Y. Guo, J. Huang, W. Shan, Y. Liu, T. Liu, M. Huang and S. Z. D. Cheng, Prog. Polym. Sci., 2020, 103, 101230 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- S. Lehtola, Int. J. Quantum Chem., 2019, 119, e25968 CrossRef.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1998, 92, 5057 CrossRef.
- Z. G. Wang, Macromolecules, 2017, 50, 9073–9114 CrossRef CAS.
- P. F. Damasceno, M. Engel and S. C. Glotzer, Science, 2012, 337, 453–457 CrossRef CAS.
- U. Agarwal and F. A. Escobedo, Nat. Mater., 2011, 10, 230–235 CAS.
- S. Torquato and Y. Jiao, Nature, 2009, 460, 876–879 CAS.
- J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363 Search PubMed.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CAS.
- D. A. Case, T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688 Search PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 Search PubMed.
- P. Vainikka, S. Thallmair, P. C. T. Souza and S. J. Marrink, ACS Sustainable Chem. Eng., 2021, 9, 17338–17350 CAS.
- J. Cao and G. J. Martyna, J. Chem. Phys., 1996, 104, 2028–2035 CAS.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 Search PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 Search PubMed.
- V. Ramasubramani, T. Vo, J. A. Anderson and S. C. Glotzer, J. Chem. Phys., 2020, 153, 084106 CAS.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4me00153b |
| ‡ Equal contributions. |
| This journal is © The Royal Society of Chemistry 2025 |