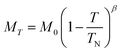Investigation of the magnetic spin correlations in the layered molybdenates, Mn₂Mo₃O₈ and MnAMo₃O₈ (A = Fe, Co, Zn)

Abstract

An exotic range of magnetic (and other) properties have been observed in A₂Mo₃O₈ materials (where A is a single or mix of transition metals) making understanding their chemistry and physics timely. We have investigated the structural–property relationships in Mn₂Mo₃O₈ and the related materials, MnFeMo₃O₈, MnCoMo₃O₈ and MnZnMo₃O₈. We report a detailed powder diffraction analysis confirming ferrimagnetic structures for Mn₂Mo₃O₈ and MnFeMo₃O₈. Differing rates of spin ordering on crystallographically distinct sites (tetrahedral or octahedral) gives rise to magnetic hysteresis, which abruptly disappears in 2 K data. This appears to be correlated with ion displacement and/or electrostriction effects, which also relax at 2 K. We confirm an antiferromagnetic structure type for MnCoMo₃O₈ and no discernible magnetic ordering within the temperature range studied for MnZnMo₃O₈. For MnZnMo₃O₈ we suggest a small amount of site disorder acts to suppress magnetic ordering. This suggests that magnetic properties can be tuned both through A-site cation order and choice of A-site cations.

---

Introduction

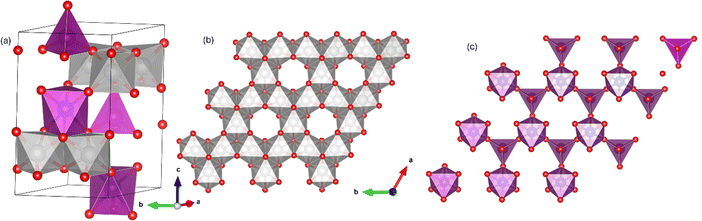
The A₂Mo₃O₈ family of materials (where A = Mn²⁺, Fe²⁺. Co²⁺ or Ni²⁺) have been attracting recent attention due to their exotic magnetic properties and magnetoelectric coupling^1–5 and potential applications for renewable energy technologies (batteries,^6–9 supercapacitors^10,11 and in water splitting^12–15). These materials exhibit a complex layered arrangement, which crystallizes with a hexagonal structure in the P6₃mc space group (#186). The structure consists of Kagomé-type MoO₆ layers which are separated by two-dimensional honeycomb layers stacked in the lattice c-direction (Fig. 1). The AO layer comprises two crystallographically distinct tetrahedral (AO₄) and octahedral (AO₆) corner shared sites which alternate in the lattice a/b plane to form a bipartite buckling honeycomb layer.¹⁶ No magnetic contribution (as might be expected from Mo⁴⁺) arises from the Mo₆ layer due to an orbital driven Peierls effect which gives rise to a trimerization of MoO₆ resulting in a shared electronic ground state and no unpaired electrons. Instead, magnetic order arises from magnetic A²⁺ ions situated within the honeycomb layer.⁶ Computational studies have demonstrated the lack of Mo contribution to the magnetic ground state in A₂Mo₃O₈ (A = Fe, Co and Mn) materials.¹⁶ At room temperature, the materials are considered pyroelectric, arising as a result of the presence of the AO₄ tetrahedra, with the polarisation vector directed along the crystallographic c-direction.^17–19 Below the magnetic transition, type 1 multiferroic character is realised owing to the coexistence of spontaneous polarisation and magnetic ordering and large linear magnetoelectric coupling in both the a/b plane and lattice c-direction have been reported.²⁰

Fig. 1 Schematic representation of the A₂Mo₃O₈ structure where (a) shows the stacking of the MoO₆ Kagomé and AO honeycomb lattices in the lattice c-direction, (b) shows the MoO₆ layer in the lattice a/b plane showing the trimerization of the Mo ions and (c) shows the alternating honeycomb connectivity of AO₆ octahedra and AO₄ tetrahedra. The pink polyhedra and triangles represent the A-site octahedra and tetrahedra respectively, the grey polyhedral the MoO₆ octahedra and the red sphere the oxygen atoms respectively.

By far the most studied members of the family are Fe₂Mo₃O₈ and Co₂Mo₃O₈, with both compounds reported to exhibit antiferromagnetic ordering at Néel temperatures (T_N) of 59.5 K and 40.8 K respectively.²¹ Fe²⁺ ions in Fe₂Mo₃O₈ are antiferromagnetically coupled between tetrahedral and octahedral sites in the a/b plane with a long range colinear antiferromagnetic structure realised through antiferromagnetic coupling of tetrahedral or octahedral units across layers.²² Additionally, Fe₂Mo₃O₈ has been shown to exhibit exciting electronic and magnetic properties such as giant magnetoelectric effect,^2,4,23 optical magnetoelectric effect,²⁴ strong magnon-phonon coupling²² and distinct electric field and terahertz magnetic excitations.²⁰ Co₂Mo₃O₈ shows a sharp transition in temperature dependent susceptibility consistent with antiferromagnetic ordering.⁵ Neutron diffraction demonstrated the magnetic Bragg peaks identifiable at 10 K could be indexed with k = (0,0,0) with similar magnitudes for the magnetic moments for Co²⁺ observed on both the tetrahedral (3.44μ_B) and octahedral (3.35μ_B) sites and C-type connectivity similar to that observed for Fe₂Mo₃O₈.⁵ However, in contrast Fe₂Mo₃O₈, shows no evidence for a magnetic field induced transition to a ferrimagnetic state as is observed in Co₂Mo₃O₈.⁵ This is suggested to be as a result of the small differences in magnitude of the magnetic moments in Co₂Mo₃O₈ when compared to Fe₂Mo₃O₈.⁵ Recently, the dependence of the magnetoelectric effect up to fields of 60 T in Co₂Mo₃O₈ has been studied.²⁵ These authors reported at high applied fields of 27 T and 31 T spin-flop transitions (towards canted antiferromagnetically ordered states) were observed at 1.7 K which result in colossal changes of the electric polarisation.²⁵

In contrast, no magnetic order down to 2 K was initially reported for Ni₂Mo₃O₈ from both computational and experimental studies.²¹ Recent computational studies have suggested that the magnetic order in Ni₂Mo₃O₈ is far more complex with strong antiferromagnetic coupling expected within layers whilst weak interlayer coupling is expected due to the small magnetic moment of Ni²⁺¹⁶. More recently, it has been reported that Ni₂Mo₃O₈ orders non-collinearly with a T_N ≈ 5.5 K with the magnetic moments lying in the a/b plane rather than the crystallographic c-direction as observed for both Fe₂Mo₃O₈ and Co₂Mo₃O₈.¹ Initially the magnetic structure was reported to exhibit a zig-zag-type magnetic ordering such that pairs of antiferromagnetically connected ferromagnetic zig-zag chains are formed within the a/b plane²⁶ or as a complex mixture between zig-zag and stripy structures.²⁷ More recently, powder neutron diffraction data has shown the magnetic structure to be stripy (whereby order with in these chains is antiferromagnetic rather than ferromagnetic and connectivity between the chains is ferromagnetic).¹ In high magnetic fields metamagnetic phase transitions have also been reported for Ni₂Mo₃O₈.²⁸

Comparatively, very little has been reported on the magnetic behaviour of Mn₂Mo₃O₈. Both computational and experimental studies have suggested that Mn₂Mo₃O₈ exhibits ferrimagnetic order with a transition temperature of approximately 40 K.^16,21 In real terms the picture is far more complex. Typically, ferrimagnetic behaviour arises as a result of the coexistence of species with very different magnetic moments on a magnetic lattice such that antiferromagnetic ordering of these species does not result in the complete cancellation of the magnetic moment, leading to a net magnetic moment in a particular crystallographic direction. Neutron diffraction studies performed by Bertrand et al. at 4.5 K suggest that the magnetic moments in Mn₂Mo₃O₈ are ordered along the crystallographic c-axis.²⁹ The authors proposed four different magnetically ordered states, C-type antiferromagnetic, A-type antiferromagnetic, ferrimagnetic (where connections between a particular site (octahedral or tetrahedral) are ferromagnetic whilst those across sites are antiferromagnetic) and ferromagnetically ordered. From the magnetic Bragg peak line strength the authors proposed that the magnetic moments associated with Mn²⁺ on the tetrahedral and octahedral sites have different magnitudes leading to ferrimagnetic ordering.²⁹ However, it is now more commonly accepted (from SQUID magnetometry studies) that below T_N the magnetic moments associated with the octahedral and tetrahedral sublattices cancel out completely (giving rise to antiferromagnetic ordering) at zero temperatures but not at finite temperatures where ferrimagnetic ordering is observed.¹⁸ However, the mechanism for this remains unclear. Given the plethora of exciting magnetic states that can be realised in this family of materials it can be expected that the magnetic behaviour of Mn₂Mo₃O₈ is perhaps not as simplistic as has been reported thus far, warranting more detailed structural and magnetic studies.

Furthermore, many studies have looked at cooperative doping on the lattice A-site since the presence of both octahedral and tetrahedral A-sites provides a versatile playground to study interesting magnetic phenomenon and control magnetic behaviour.^30–38 For example, giant thermal Hall effects have been reported in Fe_2−xZn_xMo₃O₈ materials.³⁰ The magnetoelectric effect has been shown to be tuneable with the transition between antiferromagnetically and ferrimagnetically ordered states with Zn doping in Fe₂Mo₃O₈^31,33,34 and Co₂Mo₃O₈.³⁹ However, as with the parent materials comparatively few studies have been performed with manganese despite the potential for site preference leading to exotic behaviour. Recently, Chang et al., prepared single crystals of (Mn_1−xCo_x)₂Mo₃O₈ (0 ≤ x ≤ 1).¹⁷ Magnetic data have been collected using SQUID magnetometry with the applied magnetic field aligned along the crystallographic c direction (magnetic easy axis). At x values below 0.35 (corresponding to Mn_1.3Co_0.7Mo₃O₈) these materials exhibit ferrimagnetic ordering owing to the differences in magnetic moment between Co²⁺ and Mn²⁺ with suppression of T_N on increasing Co²⁺ contents. Above x = 0.35 there is an abrupt change from ferrimagnetic to antiferromagnetic ordering whereby T_N increases with increasing Co²⁺ contents.¹⁷ Kurumaji et al., have also looked at the variation of the magnetoelectric response in Mn_2−xFe_xMo₃O₈.¹⁸ At x = 0 they report a negative correlation of the spin-induced modulation of the pyroelectric current. They also demonstrated that increasing Fe²⁺ incorporation results in a change from ferrimagnetic to antiferromagnetic ordering at x ≈ 1.2 and significant changes to the pyroelectric current, which in turn “tunes” magnetoelectric coupling in these materials.¹⁸ In addition, spin-flop behaviour has been reported for Mn₂Mo₃O₈ films (∼140 nm) when a 0.5% tensile strain is applied suggesting that further exotic magnetic states might be realised on doping Mn₂Mo₃O₈ materials.⁴⁰

Despite extensive work in the area, there remains a lack of fundamental understanding of the structure–property correlations in the manganese material in particular. In this paper, we report a comprehensive powder neutron diffraction study of Mn₂Mo₃O₈ and MnAMo₃O₈ (where A is Co, Fe and Zn). We have determined the magnetic structures of these materials and importantly correlate our findings with temperature dependent structural behaviour and magnetic property measurements. This work highlights that the magnetic behaviour of Mn₂Mo₃O₈ is not a simplistic ferrimagnet. We see clear correlations between the spin behaviour on the tetrahedral site and ionic displacement/electrostriction behaviour in Mn₂Mo₃O₈. In contrast the octahedral site remains largely unchanged as a function of temperature. These data provide new in sight into the complex magnetic behaviour in these materials. Magnetic structure determination from powder neutron diffraction studies for MnCoMo₃O₈ and MnFeMo₃O₈ favour antiferromagnetic and ferrimagnetic spin arrangements respectively. Furthermore, A-site cation order is important in the MnZnMo₃O₈ material for stabilising magnetic states with a small amount of A-site disorder resulting in no magnetic correlations over the temperature range studied. More work needs to be done in order to understand the role of order/disorder in magnetic co-doped materials.

Experimental

Polycrystalline Mn₂Mo₃O8 and MnAMo₃O₈ (A²⁺ = Fe, Co, Zn) were synthesised using the ceramic method in an evacuated, sealed quartz tube.²⁹ Stoichiometric amounts of MnO, ZnO, FeO or CoO (all Sigma Aldrich, >99%) and MoO₂ (Alfa Aesar, >99%) were mixed in an agate mortar and sealed in evacuated quartz tubes. The tubes were heated at 1223 K for 16 hours at a heating rate of 10 K min⁻¹. The tubes were subsequently cooled to 1073 K and quenched to room temperature. X-ray diffraction data were collected for these materials at room temperature and 12 K using the PANalytical Empyrean diffractometer (Cu kα λ = 1.5406 Å) fitted with an Oxford Instruments PHENIx cryostat. Data were collected over a 2θ range of 10° to 70° with a step size of 0.05° (total run time 10 hours).

Magnetic property measurements were performed using a Quantum Design MPMS SQUID magnetometer. Temperature dependent data were collected between 2 K and 300 K in both zero field cooled (ZFC) and field cooled (FC) environments with an applied magnetic field (H) of 0.1 T or 5 T. Field dependent susceptibility data were collected at discrete temperatures of 2 K, 30 K, 60 K and 100 K applying magnetic fields between −5 T and 5 T. Heat capacity measurements were performed using a Quantum Design Physical Properties Measurement System (PPMS). Data were collected with the materials pressed into small pellets (Mn₂Mo₃O₈ = 3.2 mg, MnCoMo₃O₈ = 3.2 mg, MnFeMo₃O₈ = 2.7 mg, MnZnMo₃O₈ = 3.0 mg) over a temperature range of 2 K to 150 K in zero applied fields.

Powder neutron diffraction data for Mn₂Mo₃O₈, MnCoMo₃O₈ and MnFeMo₃O₈ were collected on the WISH diffractometer at the ISIS Neutron and Muon user facility.^41,42 Samples were loaded into 3 mm vanadium cans (265 mg Mn₂Mo₃O₈, 731 mg MnCoMo₃O₈, 312 mg MnFeMo₃O₈) and data were collected across 12 temperature points between 2 K and 200 K for the Mn₂Mo₃O₈ material. Data were collected for 15 minutes except for temperatures of 2 K and 200 K where data were collected for 2 hours. Data for MnFeMo₃O₈ and MnCo₂Mo₃O₈ were collected at 2 K and 200 K for 2 hours. Powder neutron diffraction data for MnZnMo₃O₈ (618 mg) were collected using the GEM diffractometer at the ISIS Neutron and Muon user facility at 200 K and 5 K for 6 hours and at temperatures of 150 K, 100 K and 50 K for 2 hours with the sample loaded into a 3 mm vanadium can.^43,44

Results and discussion

Powder diffraction data collected for Mn₂Mo₃O₈ confirmed the formation of the expected hexagonal phase. A small amount of second phase is identified as MnMoO₄ (∼5%). Rietveld refinements of the data collected at both room temperature (298 K) and 12 K were performed using the GSAS suite of programs^45,46 in the proposed P6₃mc space group.⁴⁷ Refinements were performed for 26 variables which included lattice parameters, atomic positions, zero point, 12 shifted Chebyshev background terms and peak shape fitted using a pseudo-Voigt function. The refinement also included the MnMoO₄ (C2/m) phase.⁴⁸ Good agreement between the model and the data was observed as shown in Fig. 2 with no perceivable change in structure between room temperature and 12 K, consistent with reported studies for other A₂Mo₃O₈ analogues.^1,5,27,29 We see no evidence for symmetry lowering (P6₃mc → P6₃) as has recently been reported for Fe₂Mo₃O₈ by spectroscopic studies.⁴⁹ Full refinement details and refined parameters are given in Table S1 in the ESI.†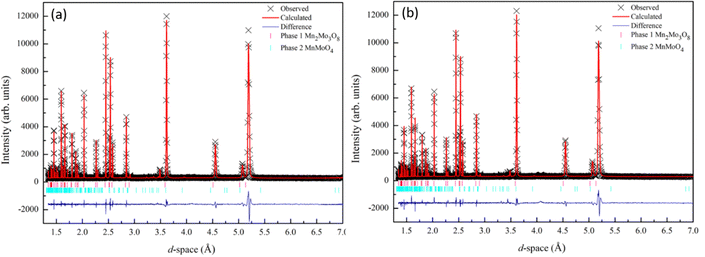

Fig. 2 Rietveld refinement of the X-ray diffraction data collected for Mn₂Mo₃O₈ and fitted to the P6₃mc model⁴⁷ at (a) 298 K (wRp = 7.5%, Rp = 5.74, χ² = 2.7) and (b) 12 K (wRp = 8.6%, Rp = 6.3%, χ² = 3.5). Black crosses represent observed data, red line represents the calculated model and the blue line represents the difference between the observed and calculated data. Mn₂Mo₃O₈ is represented by the magenta tick marks (top) and MnMoO₄ by the cyan tick marks (bottom).

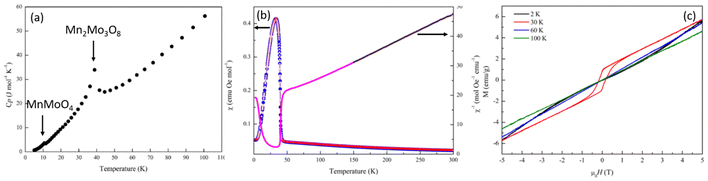
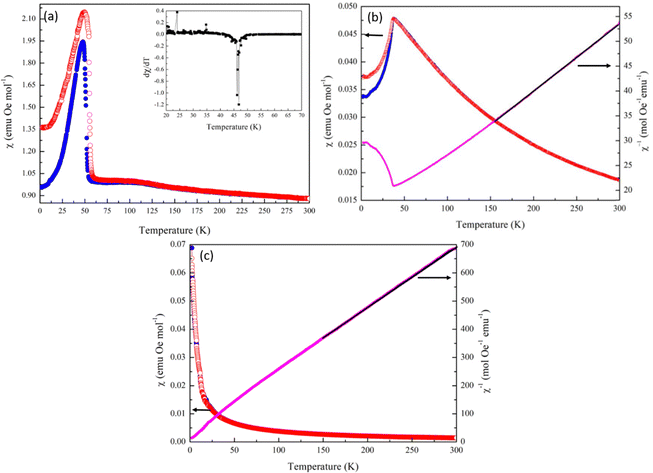
Heat capacity measurements were carried out in order to look at potential magnetic phase transitions in Mn₂Mo₃O₈ (Fig. 3(a)). As expected, the molar heat capacity (C_p) decreases with decreasing temperature until ∼40 K where a sharp peak is observed. This is consistent with the magnetic Néel temperature (T_N) reported for Mn₂Mo₃O₈.^50,51 A second weak peak in C_p is observed at ∼10 K and is associated with the expected magnetic transition in the secondary phase, MnMoO₄.⁵² Magnetic susceptibility data shows a more complex magnetic behaviour. Zero field cooled (ZFC) and field cooled (FC) temperature dependent data collected in an applied magnetic field of 0.1 T are shown in Fig. 3(b). A peak in the susceptibility at 39.6(4) K is observed (extracted from a plot of dχ/dT shown in Fig. S1(a) in the ESI†) with no deviation between ZFC and FC data consistent with long range antiferromagnetic (AFM) ordering. Whilst the shape of the magnetic curve is consistent with previous reported literature,^7,17,21,47 it is neither suggestive of a sharp phase transition to long-range AFM order nor low dimensional magnetic order (which typically show broader transitions).⁵³ It has been suggested previously that the magnetic anisotropy observed in the magnetic susceptibility data originates from differences in the magnitude of the magnetic moments associated with the tetrahedral and octahedral sites.²⁹ However, the differences in energies associated with the crystal field splitting of each of these sites is expected to be small with spin only values on each site predicted to be almost identical potentially ruling out more traditional origins of ferrimagnetism in this material. Another study has suggested the possibility of mixed valence states (+2 and +3) across the octahedral and tetrahedral sites presumably arising as a result of structural defects such as oxygen vacancies which subsequently leads to ferrimagnetic character.⁴⁷ In these cases, we would expect to see divergence between ZFC and FC magnetometry data as a result of large differences in the magnitude of the magnetic moment failing to cancel and resulting in a net magnetic moment in a single crystallographic direction, which we do not see in our studies. It has also been suggested that the magnetic moments associated with the octahedral and tetrahedral sublattices do not cancel each other out over finite temperatures.¹⁸ That is, there is possibly a transition from a partially ordered (ferrimagnetic) to a fully ordered (antiferromagnetic state) such that one or both magnetic sites remain dynamic until well below T_N or there is an intermediate canted antiferromagnetic spin state (below T_N). The shape of the temperature dependent susceptibility curve is, however, consistent with a Néel ferrimagnetically ordered state whereby equal magnitude spins are ordered antiferromagnetically across crystallographically distinct sites but where saturation of the spin state has different time scales (temperature) dependencies leading to ferrimagnetic behaviour.²¹

Fig. 3 Physical property data collected for Mn₂Mo₃O₈ showing (a) molar heat capacity (C_p) data indicating a sharp increase in C_p at approximately 40 K consistent with T_N for Mn₂Mo₃O₈ and a weaker inflection at ∼10 K attributable to the magnetic transition in MnMoO₄, (b) Zero field cooled (blue) and field cooled (red) data measured at 0.1 T and inverse ZFC susceptibility data where the black line shows the fit to the Curie–Weiss law and (c) field (H) dependent magnetisation data collected at 2 K (black), 30 K (red), 60 K (blue) and 200 K (green).

At temperatures between 150 and 300 K Mn₂Mo₃O₈ obeys Curie–Weiss behaviour (Fig. 3(b)). A total effective magnetic moment per formula unit is calculated as 8.52μ_B consistent with that calculated (8.35μ_B) using the spin only formula. A negative Weiss constant (θ) of −132.5(2) K is determined consistent with antiferromagnetic ordering. Calculation of the frustration index, f (f = −T_N/θ) gives a value of 3.2 suggesting some level of magnetic frustration in Mn₂Mo₃O₈ and is consistent with what we have observed in similarly layered materials.⁵³ Magnetic hysteresis loops collected at temperatures of 60 K and 100 K show a linear relationship of the magnetisation as a function of applied field consistent with paramagnetic behaviour. At 2 K we see no hysteric behaviour with the data exhibiting a slight “s” shape as would be expected for long-range antiferromagnetic ordering consistent with our temperature dependent susceptibility measurements and previous literature.^7,17,21,47 However, at 30 K we see distinct hysteric behaviour with a clear opening of the hysteresis loop at low fields consistent with observations by Das et al. who reported similar hysteresis in data collected at 20 K.⁷ This indicates that there is a net magnetic moment in these materials, consistent with formation of the ferrimagnetic state (arising from different spin orientations or spin magnitudes on the octahedral and tetrahedral sites) or a transition from a weakly ferromagnetic to antiferromagnetic state within a relatively short temperature range.

In order to shed further insight into the magnetic behaviour of Mn₂Mo₃O₈ we collected ZFC cooled magnetic susceptibility data at an applied field of 5 T (Fig. S1(b) in the ESI†). These data indicated that at 5 T a sharper magnetic transition is observed, consistent with that expected for antiferromagnetic ordering. This is further confirmed by the negative Weiss constant (θ) of −121.5 K extracted from fitting the Curie–Weiss law between 150 and 300 K at 5 T. The magnetic moment per formula unit (8.83(1)μ_B) is also consistent with that expected for Mn₂Mo₃O₈ and that observed at 0.1 T and with data published previously for Mn₂Mo₃O₈.²¹ It can be suggested that increased field strengths enables the simultaneous long-range order and saturation of the magnetic moments on both tetrahedral and octahedral sites resulting in no net magnetic moment being observed. Equally, this could suggest a field driven phase transition to an antiferromagnetically ordered state similarly to those seen for Fe₂Mo₃O₈ and Co₂Mo₃O₈ but we have not considered this further here.^25,31 Lastly, we see no evidence of low temperature spin-flop behaviour, which may have been expected, based on previous studies.¹⁸ However, our data has been collected at the lower limits of both the expected temperature and applied magnetic field range previously reported and we cannot confidently rule this out from our data.¹⁸

To further investigate the magnetic spin relationships and understand the temperature dependence observed in magnetometry measurements in Mn₂Mo₃O₈ we performed neutron powder diffraction experiments on the WISH diffractometer at the ISIS neutron and muon user facility (UK).⁴¹ Data were refined using the FULLPROF suite of programs to enable determination of both the nuclear and magnetic structures.⁵⁴ At temperatures above T_N the data can be readily be fitted to P6₃mc Mn₂Mo₃O₈ phase with a small contribution from the MnMoO₄ secondary phase (∼5%). Refinements were performed as detailed in the ESI.† The refinement profiles for data collected at 200 K and 2 K are shown in Fig. 4 with refinement profiles and refined parameters for all temperature points given in Fig. S2–S4 and Tables S2 through S5 in the ESI† respectively. With decreasing temperature, we see no change in the P6₃mc nuclear structure consistent with the observations from our powder X-ray diffraction study discussed above. Temperature dependence of the lattice parameters are shown in Fig. S5 in the ESI.† We see that generally the lattice parameters and cell volume decrease with decreasing temperature as expected. However, the a and c lattice parameters show slightly different behaviour. The c lattice parameter plateaus at approximately 60 K. This is consistent with what has been seen in Fe₂Mo₃O₈⁵⁵ and other layered systems⁵³ and is suggestive of the onset of short-range magnetic correlations. In the a/b plane the lattice parameters show a slight kink at ∼40 K and a change in slope consistent with the onset of magnetic order at T_N before reaching a plateau at ∼25 K. At T_N we also see an increase in the Mn_tet–O–Mn_oct bond angle (∼1.76%) with decreasing temperature. These observations are consistent with ionic displacements, which occur in tandem with ferroelectricity,⁵⁶ and suggest the onset potentially of either switchable behaviour or symmetric exchange striction^57,58 at T_N within Mn₂Mo₃O₈. In order to investigate this further we have considered temperature driven changes in the MnO₄ tetrahedral and MnO₆ octahedral units. Previous work has suggested that the pyroelectric (above T_N) and ferroelectric (below T_N) behaviour is linked to the AO₄ tetrahedra, with the polarisation vector directed along the crystallographic c-direction.^17–19 If we first consider the tetrahedral site, we can see that the bond length between the central Mn ion (Mn1) and the oxygen at the apex of the tetrahedron (O2) steadily increases (∼2.9%) as temperature decreases below ∼60 K until we reach T_N (Fig. S6 in the ESI†). This is consistent with the onset of the invariant behaviour in the c lattice parameter and ionic displacement in the lattice c-direction. The (Mn1–O2) bond length is then fairly consistent until 2 K where we see a sudden drop to values more consistent with those observed above T_N. The origin of this behaviour is not well understood and may signify the loss of ferroelectric character at low temperature. This could be related to the loss of hysteric behaviour observed in the field dependent magnetometry data and be driven by saturation of the magnetic moments on both the tetrahedral and octahedral sites resulting in an equalisation of the observed moment and loss of ferrimagnetic ordering. This is interesting as it would suggest that evolution of any possible ferroelectric state is linked to the temperature dependence of the magnetic spin dynamics as opposed to static magnetic order. Alternatively, this may arise as a result of complexities of the refinements at this temperature with two nuclear and two magnetic phases present due to the magnetic ordering of the impurity phase, although we believe this to be unlikely. The bond lengths at the base of the tetrahedron (Mn1–O3) decrease slightly at T_N. In contrast the bond lengths in the MnO₆ octahedra vary only slightly (less than 1%) with temperature (Fig. S6 in the ESI†) consistent with thermal effects and isotropic compression of the octahedra with decreasing temperature. This confirms that the onset of multiferroic behaviour is primarily linked to the tetrahedral sites which is consistent with displacements reported for Fe₂Mo₃O₈.^17–19 Moreover, Tang et al., suggested that the ferroelectric behaviour is correlated to the ferromagnetic coupling in Co₂Mo₃O₈.⁵ As such it is important to understand the magnetic spin state in Mn₂Mo₃O₈.

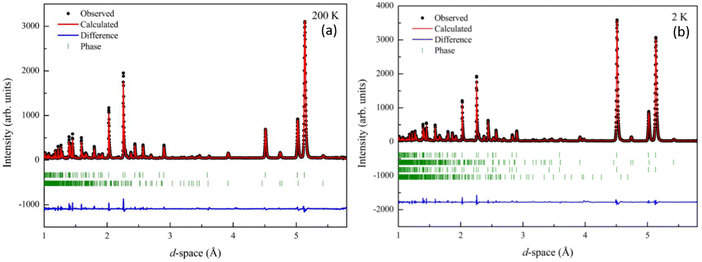Fig. 4 Rietveld refinement of the powder neutron diffraction (WISH) data collected for Mn₂Mo₃O₈ and fitted to the P6₃mc model⁴⁷ at (a) 200 K (wR_p = 13.9%, R_p = 11.5, χ² = 0.8) and (b) 2 K (wR_p = 11.9%, R_p = 8.65%, χ² = 0.92). Black crosses represent observed data, red line represents the calculated model and the blue line represents the difference between the observed and calculated data. From top to bottom the tick marks represent the Mn₂Mo₃O₈ (nuclear phase), MnMoO₄ (nuclear phase), Mn₂Mo₃O₈ (magnetic phase) and MnMoO₄ (magnetic phase) respectively.

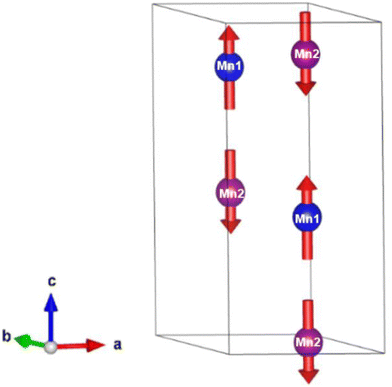
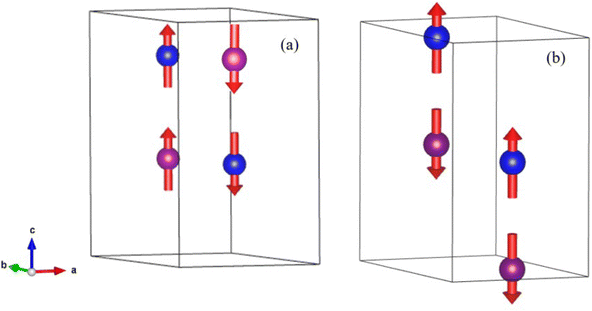
Below 40 K we see the clear onset of increased peak intensity which can be linked to magnetic order on the (101), (103), (201) and (211) reflections. Below this temperature, all data were fit using both the nuclear (P6₃mc) structure and a Mn₂Mo₃O₈ magnetic phase discussed below. Additionally, below 10 K we also see the evolution of additional magnetic Bragg peaks which are attributable to the magnetic structure of the MnMoO₄ phase⁵⁹ and at 2 K we have refined this phase alongside the Mn₂Mo₃O₈ (magnetic and nuclear) phases. For Mn₂Mo₃O₈ the magnetic reflections were indexed using a commensurate propagation vector, k = (0,0,0) in the hexagonal unit cell. Irreducible representations and their corresponding magnetic space groups were determined using the ISODISTORT suite.⁶⁰ Four common irreducible representations (IR) and their corresponding magnetic space groups and numbers were determined (as shown in Table 1) alongside the direction (↑ or ↓) of the magnetic moment relative to the crystallographic site and axes. Previous reports have suggested that the magnetic moments aligning along the lattice c-direction are favoured in hexagonal crystal systems.^21,29 However, in Ni₂Mo₃O₈ the complex magnetic order has been shown to give rise to spins which lie in the lattice a/b plane.¹ Refinements performed using the magnetic structures determined from the Γ(5) and Γ(6) IRs (where the magnetic moments are orientated within the lattice a/b plane) failed to provide magnetic intensity in the correct places leading to unstable refinements. This allows us to rule out both of these models. This leaves structures associated with Γ(2) where the magnetic moments are orientated in the so called ferrimagnetic order such that coupling across the two different sites (tetrahedral and octahedral) is AFM whilst between magnetic cations on the same site (either tetrahedral – tetrahedral or octahedral – octahedral) coupling is ferromagnetic and Γ(3) where all interactions are antiferromagnetic. We have evaluated both spin structures using data collected at 10 K (since this data is free from the magnetic impurity phase) using the SARAh⁶¹ and FULLPROF suite of programs⁵⁴ (as described in the ESI†). The Γ(3) model resulted in an unstable refinement such that convergence was never achieved whilst refinements using the Γ(2) model resulted in a stable refinement which exhibited an excellent fit to the data (Fig. S3, ESI†). This, confirms that Mn₂Mo₃O₈ exhibits a (TT-OO, ↑↑↓↓) antiferromagnetic (ferrimagnetic) spin order as shown in Fig. 5(a) and as has been suggested in previous computational^16,49 and magnetometry work^21,62 and by peak indexing.²⁹ Refinements performed allowing the magnetic moments to be refined independently on the tetrahedral and octahedral sites results in unstable refinements for both the Γ(2) and Γ(3) models. Since both sites are expected to have the same d⁵ electron configuration the magnetic moments across the sites were constrained to have the same value in all refinements. At 2 K the same magnetic structure fit consistently with the data as shown in Fig. 2(b). This suggests that no magnetic phase transition occurs at low temperature. The magnetic moment was also determined as 4.2μ_B on each of the Mn²⁺ sites at 2 K consistent with what is expected in neutron diffraction for S = 5/2 ions. We have further evaluated the critical exponent (β) extracted from the refined magnetic moments (M) in our powder neutron diffraction data as a function of temperature (T) and given by the equation below (using T_N = 39.6 K) and shown in Fig. S7 in the ESI.† This gives β = 0.31(1) which is indicative of a 3D Ising antiferromagnetic consistent with both the SQUID magnetometry and powder neutron diffraction data. Furthermore, the fit is robust over a wide temperature range suggesting that the there are no new interactions emerging at the lowest temperature measured consistent with the absence of a secondary magnetic phase transition.

Table 1 Irreducible representations (IRs) and corresponding magnetic space groups generated for Mn₂Mo₃O₈ within the parent P6₃mc space group and k = (0,0,0) using the ISODISTORT suite. Information related to spin direction and orientation is also provided for each IR. Note TTOO relates to tetrahedral–tetrahedral–octahedral–octahedral spin coupling and 0000 denotes that the spins lie perpendicular to the lattice c-direction

IR	Magnetic space group	Space group number	Moment parallel to lattice c-direction TTOO	a/b Plane moment allowed
Γ(2)	P63m′c	186.207	↑↑↓↓	No
Γ(3)	P63m′c′	186.205	↑↓↑↓	No
Γ(5)	Cmc21	36.172	0000	Yes
	Cm′c′21	36.176	↑↑↓↓	Yes
	P21	4.7	↑↑↓↓	Yes
Γ(6)	Cmc′21′	36.175	0000	Yes
	Cm′c21′	36.174	↑↓↑↓	Yes
	P21′	4.9	↑↓↑↓	Yes

---

Fig. 5 Magnetic spin structure (red arrows) determined for Mn₂Mo₃O₈ within the unit cell (black outline) at 10 K form the Rietveld refinement of powder neutron diffraction data. The blue and pink spheres represent manganese on the Mn1 (tetrahedral) and Mn2 (octahedral) crystallographic sites respectively.

Given the ferrimagnetic spin structure we note that the model for ferroelectric ordering may also be distinct in Mn₂Mo₃O₈. In contrast with both Fe₂Mo₃O₈ and Co₂Mo₃O₈ where the ferromagnetic component is coupled inter-site (i.e. oct–tet) to form ferromagnetic chains, the ferromagnetic coupling in Mn₂Mo₃O₈ is intra-site (i.e. tet–tet or oct–oct). As such Mn₂Mo₃O₈ may show exciting magnetoelectric behaviour and this warrants further investigation.

Doping the A-site in Fe₂Mo₃O₈ and Co₂Mo₃O₈ have been shown to be an effective route for tuning the magnetic properties of these materials.^30–38 We have prepared materials, MnAMo₃O₈, where Mn²⁺ is replaced with Fe²⁺, Zn²⁺ or Co²⁺ in order to investigate A-site cation dependence (tetrahedral versus octahedral) and the role this plays in magnetic ordering. Rietveld refinement of powder X-ray diffraction data collected at 298 K using the GSAS suite of programs^45,46 confirmed the formation of the expected primary hexagonal phase (P6₃mc) for all three MnAMo₃O₈ materials. Refinement profiles and full details are given in Table S6 and Fig. S8 the ESI.† We found no evidence for secondary phases in the MnCoMo₃O₈ material but small amounts of MnMoO₄ were evident in the X-ray diffraction data collected for MnFeMo₃O₈ (4.2(1)%) and MnZnMo₃O₈ (3.4(1)%) and were included in our refinements. Lattice parameters extracted for these materials show the expected relationships with atomic size when compared with the end members of the solid solutions (Zn₂Mo₃O₈, Co₂Mn₃O₈ and Fe₂Mo₃O₈) and are consistent with what is expected from previous literature.^29,47

Heat capacity data collected for both MnCoMo₃O₈ and MnFeMo₃O₈ show a sharp feature at temperature points 35.7(4) K and 49.5(5) K respectively consistent with what we observed for Mn₂Mo₃O₈ and are suggestive of the onset of a magnetically ordered phase (Fig. S9 in ESI†). There are clear shifts in temperature on doping which increases Co < Mn < Fe. In contrast no features are seen in the C_p data collected for MnZnMo₃O₈, suggesting that no magnetically ordered state is realised in this material over the temperature range studied. For both MnFeMo₃O₈ and MnZnMo₃O₈ we see small contributions in the C_p data at ∼10 K consistent with the magnetic ordering associated with the secondary phase. Temperature dependent SQUID magnetometry data collected for these materials in an applied field of 0.1 T clearly demonstrates that the type of magnetic ordering is critically dependent upon the transition metal, which are doped on to the A-site (Fig. 6). Similarly, to Mn₂Mo₃O₈, MnFeMo₃O₈ shows a humped shaped transition at T_N = 46.8(K) (as extracted from a plot of dχ/dT vs. temperature shown in the inset of Fig. 6(a)) and is consistent with observations from heat capacity data showing an increase in T_N on incorporating Fe²⁺. We see clear deviation between ZFC and FC data potentially as a result of small differences between the expected magnetic moments for Mn²⁺ d⁵ (5.91μ_B spin only) and Fe²⁺ d⁶ (4.90μ_B spin only) electronic configurations. These data suggest that the ferrimagnetic structure is still favoured for MnFeMo₃O₈ consistent with work performed on the Fe₂Mno₃O₈ – Mn₂Mo₃O₈ solid solution, which suggests the Fe²⁺ doping leads to an increase in T_N with the ferrimagnetic structure stable to x ≈ 1.2 (in Mn_2−xFe_xMo₃O₈).¹⁸ We also see a broad feature in the susceptibility data at approximately 100 K this is consistent with the Verwey transition in Fe₃O₄.^63–65 Whilst we did not observe any iron oxide based secondary phases in our diffraction data for MnFeMo₃O₈, it is well known that very small (below the limits of detection in conventional diffraction experiments) iron oxide phases can have a large impact on magnetometry data. Since T_C for Fe₃O₄ is expected to be 856 K⁶⁶ we have not been able to extract meaningful data from the Curie–Weiss fits of the inverse susceptibility. Field dependent data (Fig. S10(a) in ESI†) showed pinched hysteric behaviour characteristic of Fe₃O₄ and no further information can be inferred from these data. However, it would be expected that we would see the same low temperature closure of the hysteresis loops as we observed for Mn₂Mo₃O₈ and which is characteristic of the complex interplay between tetrahedral and octahedral sites in these materials.

Fig. 6 Zero field cooled (blue) and field cooled (red) SQUID magnetometry data collected at 0.1 T and inverse ZFC susceptibility data where the black line shows the fit to the Curie–Weiss law for (a) MnFeMo₃O₈ inset shows the dχ/dT data highlighting T_N at ≈ 46 K, (b) MnCoMo₃O₈ showing T_N ≈ 35 K and (c) MnZnMo₃O₈ showing paramagnetic character.

In contrast with Mn₂Mo₃O₈ we see a sharp antiferromagnetic transition in the magnetic susceptibility in MnCoMo₃O₈ at T_N = 36.2(1) K consistent with what is typically observed for Co₂Mn₃O₈.⁵ This suggests that there is a transition away from the ferrimagnetic structure determined from Mn₂Mo₃O₈ towards the antiferromagnetic spin structure expected for Co₂Mo₃O₈ which is consistent with the expected transition at x ≈ 0.7 (in Mn_2−xCo_xMo₃O₈) recently reported by Cheng et al.¹⁷ Again we see a some divergence between the ZFC and FC data collected for MnCoMo₃O₈ consistent with some traditional ferrimagnetic behaviour (net magnetic moment) arising as a result of the differences in magnetic moments between Mn²⁺ d⁵ (5.91μ_B spin only) and Co²⁺ d⁷ (3.87μ_B spin only) electronic configurations. This may also be suggestive of some magnetic behaviour arising as a result of incomplete trimerization of the Mo sub-lattice, clustering effects or glassy behaviour. Between 150 K and 300 K we are able to fit the inverse susceptibility to the Curie–Weiss law giving θ = −100.1(1) K confirming antiferromagnetic order with an effective magnetic moment of 7.69 μ_B per formula unit consistent with what would be expected from the spin only calculation (7.08 μ_B). Calculation of the frustration index gives a value of f = 2.8 in line with the value observed for Mn₂Mo₃O₈ and suggestive of some weak geometric frustration in MnCoMo₃O₈. We see no hysteric behaviour at either 300 K or 12 K in MnCoMo₃O₈ consistent with type A antiferromagnetic order as is described by Co₂Mo₃O₈ (Fig. S10(b) in ESI†).⁵

Finally, we see no evidence of any magnetic order within the measured temperature range in the susceptibility data collected for MnZnMo₃O₈. Previous work investigating Zn doping in Fe₂Mo₃O₈ suggests that FeZnMo₃O₈ is ferrimagnetic with an expected transition to a paramagnetic phase at a composition of approximately Fe_0.75Zn_1.25Mo₃O₈.³⁴ Gao et al., have predicted that CoZnMo₃O₈ (where Zn²⁺ occupies the tetrahedral sites and Co²⁺ the octahedral sites) would be expected to exhibit a striped magnetic order.⁶⁷ It therefore, seems reasonable to expect that MnZnMo₃O₈ could have been predicted to show long-range magnetic order. However, Gao et al. suggested that intersite mixing leads to the suppression of magnetic order in CoZnMo₃O₈ materials.⁶⁷ This suggests that in MnZnMo₃O₈ there may be intersite mixing too, which results in the observation of paramagnetic behaviour on the level of our measurements. At high temperatures MnZnMo₃O₈ follows Curie–Weiss behaviour with fits to the inverse susceptibility providing values for θ = −21.6(1) K) and a magnetic moment of 5.4μ_B consistent with the magnetic moment on Mn²⁺. The negative Weiss constant may suggest a weakly AFM ordered state with T_N below 2 K but equally these may relate to the small amount of MnMoO₄ impurities present in this material. Likewise, field dependent data (Fig. S10(c) in ESI†) collected at 300 K shows paramagnetic behaviour. In contrast, we see a slight “s” shape to data collected at 2 K. This again may be suggestive of weak (short-range) magnetic order in this material or be related to the small amount of MnMoO₄. Either way, these data provide no evidence for magnetic order in MnZnMo₃O₈ over the temperature range studied.

In order to explore cation (dis)order and magnetic structure in these materials we have performed powder neutron diffraction experiments on the WISH (MnFeMo₃O₈ and MnCoMo₃O₈)⁴¹ and GEM (MnZnMo₃O₈)⁴³ diffractometers at the ISIS Neutron and Muon User facility. As expected, the 100 K data for MnFeMo₃O₈ and MnCoMo₃O₈ and 298 K data MnZnMo₃O₈ show excellent fits to the P6₃mc model.⁴⁷ Refinement profiles (Fig. S11 and S12), parameters (Tables S7–S9) and details are given in the ESI.† Refinements were performed with secondary phases refined as observed in our powder X-ray diffraction study discussed above. We noted a small amount of MoO₂ in the MnCoMo₃O₈ sample, which was not detectable in our powder X-ray diffraction data. Additionally, for MnFeMo₃O₈ it was necessary to include both the Fe₃O₄ nuclear and magnetic phases⁶⁸ in our refinements. In order to explore A-site cation (dis)order all refinements were performed with Mn²⁺ and the dopant A-site cation situated on both tetrahedral (Mn1) and octahedral (Mn2) sites and allowed to refine. For both MnFeMo₃O₈ and MnCoMo₃O₈ we determined that both A-site cations are randomly distributed across both tetrahedral and octahedral sites. This may explain some of the differences observed in previous studies within SQUID magnetometry data which were performed on single crystals and assumed to exhibit A-site order. This suggests that the magnetic phases obtainable (and thus other properties such as magnetoelectric coupling) can be further tuned through order and/or disorder and more complex cation doping regimes. Refinements performed for MnZnMo₃O₈ suggests that there is a strong preference for Zn²⁺ to adopt the tetrahedral site with Mn²⁺ on the octahedral site. However, we do see a small amount of intersite mixing (approximately 10%) which may be enough to destabilise the expected magnetic ordering in this material as has been reported by Gao et al.⁶⁷

At low temperature, we see no change in symmetry with all materials readily refined to the P6₃mc model.⁴⁷ Refinement details, full refinement profiles (Fig. S11 and S12) and parameters (Tables S7–S9) are given in the ESI.† On visual inspection of the 2 K powder neutron diffraction data collected for MnFeMo₃O₈ and MnCoMo₃O₈ there are clear differences between the magnetic phases observed, as expected from SQUID magnetometry data. For MnFeMo₃O₈ additional magnetic Bragg intensity is observed on the (101), (103), (201) and (211) reflections similarly to those observed for Mn₂Mo₃O₈. In contrast, MnCoMo₃O₈ shows additional magnetic Bragg intensity on the (100), (101), (200), (210) and (204) reflections. For MnZnMo₃O₈ no magnetic Bragg contributions were observed as expected from the SQUID magnetometry measurements. Furthermore, we see no ion displacement or exchange striction effects in either the tetrahedral or octahedral bond lengths which remain reasonably constant over the temperature range studied (as shown in Fig. S13 in the ESI†). This confirms the lack of both magnetic and multiferroic character in MnZnMo₃O₈. Following the same procedure, we outlined for Mn₂Mo₃O₈ using ISODISTORT⁶⁹ and k = (0,0,0), gives the same IRs shown in Table 1. Refinements were subsequently performed using the Γ(2) and Γ(3) models since those models derived using IRs Γ(5) and Γ(6) failed to successfully account for the magnetic intensity observed for both MnFeMo₃O₈ and MnCoMo₃O₈. For MnFeMo₃O₈ we only achieved a stable refinement using the Γ(2) model whilst the opposite was true for MnCoMo₃O₈ as expected from our previous discussions for Mn₂Mo₃O₈ and our SQUID magnetometry data. The extracted magnetic structure for MnFeMo₃O₈ is identical to the ferrimagnetic model determined for Mn₂Mo₃O₈ (as shown in Fig. 7) where the magnetic spins are antiferromagnetically coupled across the crystallographically distinct A-sites (tetrahedral – octahedral) and ferromagnetically coupled across the same site (tetrahedral – tetrahedral or octahedral – octahedral). The average magnetic moment on both sites was determined to be 4.20(1)μ_B which is consistent with what we have observed for Mn₂Mo₃O₈ although perhaps a little bit higher than might be expected in a mixed system. However, we note that in the 2 K refinement of the MnFeMo₃O₈ data, we have a small amount of intensity, which is unaccounted for. Refinements for this phase were complex containing five phases, MnFeMo₃O₈ nuclear and magnetic phases, MnMoO₄ nuclear phase and Fe₃O₄ nuclear and magnetic phases. It is likely that this is either an artefact due to correlations of the fitting parameters across phases or it may be some magnetic intensity we have not accounted for in these refinements. Alternatively, we have considered that this may arise as a result of the Mo trimers not fully compensating. Previous computational studies have suggested that Mo does not contribute to the magnetic ground state.¹⁶ Chen et al. investigated the possibility of spin liquid magnetic ground states in A₂Mo₃O₈ materials (where A is non-magnetic ions, Mg, Sc and Zn).⁷⁰ They observed weak (low magnetic moment) magnetic ordering in these materials at approximately 15 K using SQUID magnetometry. However, they were unable to determine between ferromagnetic and canted antiferromagnetic ground states with neutron diffraction data demonstrating no discernible magnetic Bragg scattering.⁷⁰ Sheckelton et al. looked at disrupting the Mo trimers through the addition of lithium in the material, LiZn₂Mo₃O₈.⁷¹ They suggest that ⅔ of the Mo magnetic spins condense into singlet states below 96 K. However, no long-range static magnetically ordered state is observed with no magnetic Bragg peaks observed in powder neutron diffraction data.⁷¹ This suggests that whilst small contributions to SQUID magenetometry data may arise as a result of incomplete trimerization of the Mo sub-lattice it is unlikely to be observeable within our powder neutron powder diffraction study as either resolveable magnetic Bragg character or additional intensity. Lastly, given that a transition to the antiferromagntic state is expected at x ∼ 1.2, it is plausible that a mixed magnetically ordered state is observed with both ferrimagnetic and antiferromagnetic order present within our sample potentially as a result of cation inhomogenity.¹⁸ However, due to the complexity of these refinements we have not been able to investigate this further. Additionally, since that the magnetic structure we have derived for this material is consistent with the SQUID magnetometry data we are confident in our structural solution. Additionally, we did not see any contribution from the magnetic phase of MnMoO₄ presumably because the signal from this component is too weak to detect. Likewise, for MnCoMo₃O₄ we also see no evidence of magnetic contributions from MnMoO₄ in our data. Refinement of the magnetic structure (shown schematically in Fig. 7) indicates antiferromagnetic coupling both across crystallographically distinct sites (tetrahedral and octahedral) and importantly between crystallographically identical sites (tetrahedral – tetrahedral and octahedral – octahedral) consistent with what is expected for Co₂Mo₃O₈.⁵ Magnetic moments were calculated to be 3.38(1)μ_B consistent with what is expected for a mixed Co²⁺/Mn²⁺ material.

Fig. 7 Magnetic spin structure (red arrows) determined for (a) MnCoMo₃O₈ and (b) MnFeMo₃O₈ within the unit cell (black outline) at 2 K form the Rietveld refinement of powder neutron diffraction data. The blue and pink spheres represent manganese on the Mn1 (tetrahedral) and Mn2 (octahedral) crystallographic sites respectively.

Conclusions

We have investigated the structure–property correlations in Mn₂Mo₃O₈, MnFeMo₃O₈, MnCoMo₃O₈ and MnZnMo₃O₈ using powder neutron diffraction and magnetic property measurements. For Mn₂Mo₃O₈ we confirm the ferrimagnetic model for the magnetic structure such that magnetic moments are coupled antiferromagnetically across crystallographically distinct A-sites (tetrahedral–octahedral) and ferromagnetically coupled for individual sites (tetrahedral – tetrahedral or octahedral – octahedral) Interestingly, ionic displacements and/or exchange striction behaviour on the tetrahedral site appears to be critically dependent on the spin behaviour on the tetrahedral site with a sudden drop in the Mn–O bond length at the apex of the tetrahedral unit at 2 K. This is important, as it is coincident with the loss of hysteric behaviour and the realisation of a compensated antiferromagnetic state. The driving forces behind this are not known. It remains undetermined if a switchable ferroelectric state is achieved at T_N with some kind of re-entrant non-switchable or alternative state realised at 2 K or if a fully switchable ferroelectric state is not obtainable until 2 K. We note that whilst the ferroelectric state has been shown to exist in both Fe₂Mo₃O₈ and Co₂Mo₃O₈ it has yet to be confirmed in Mn₂Mo₃O₈.^5,72 This warrants further investigation to fully understand any electronic behaviour and potential magnetoelectric coupling (as has been reported for Fe₂Mo₃O₈, Ni₂Mo₃O₈ and Co₂Mn₃O₈^5,23,28,72) in this material.

The magnetic structures for MnFeMo₃O₈ and MnCoMo₃O₈ have been determined as ferrimagnetic and antiferromagnetic respectively. In contrast MnZnMo₃O₈ shows no long range magnetic order down to 2 K. Our data suggests that these materials are cation disordered with A²⁺ and Mn²⁺ distributed randomly on both tetrahedral and octahedral sites in both the Co and Fe analogues whilst some site preference is shown in the Zn material (∼90% site order for Mn on the octahedral site and Zn on the tetrahedral site). Further work is required to understand the roles of cation (dis)order in these systems for tuning the magnetic character in these materials^34,67

Overall, this work demonstrates that there is still much to unravel with respect to the structure–property correlations in Mn₂Mo₃O₈ and related systems. This is a magnetically rich family of materials with the potential for careful property tuning leading to many exciting and technologically important applications.

Data availability

ESI† includes all refinement details (including information about which refinement software has been used, what has been refined and how the data has been treated) and refined data alongside supporting magnetic property data for all materials presented in this work. Powder neutron diffraction raw data is available through the ISIS data gateway with https://doi.org/10.5286/ISIS.E.RB222055 and https://doi.org/10.5286/ISIS.E.XB2390084 for the WISH and GEM data respectively.^41,43

Conflicts of interest

We report no conflicts of interest.

Acknowledgements

DCA, SR, HLM are grateful for the award of a Leverhulme Research grant (RPG_2019_220). We are grateful for the provision of beamtime RB2220551⁴¹ and XB2390084⁴³ at the ISIS Neutron and Muon Source (UK). We are also grateful for access to the Materials Characterisation laboratory (MCL) at the ISIS Neutron and Muon Source (UK) for access to magnetic property measurements.

References

1. P. Yadav, S. Lee, G. L. Pascut, J. Kim, M. J. Gutmann, X. Xu, B. Gao, S. W. Cheong, V. Kiryukhin and S. Choi, Phys. Rev. Res., 2023, 5, 033099.
2. I. V. Solovyev and S. V. Streltsov, Phys. Rev. Mater., 2019, 3, 114402.
3. S. Reschke, D. G. Farkas, A. Strinić, S. Ghara, K. Guratinder, O. Zaharko, L. Prodan, V. Tsurkan, D. Szaller, S. Bordács, J. Deisenhofer and I. Kézsmárki, npj Quantum Mater., 2022, 7, 1–7.
4. M. Eremin, K. Vasin and A. Nurmukhametov, Materials, 2022, 15(22), 8229.
5. Y. S. Tang, S. M. Wang, L. Lin, C. Li, S. H. Zheng, C. F. Li, J. H. Zhang, Z. B. Yan, X. P. Jiang and J. M. Liu, Phys. Rev. B, 2019, 100, 134112.
6. J. Ding, Y. Huang, Z. Liu, X. Wang, Y. Zhang, Y. Guo, R. Sheng, D. Jia, X. Tang and L. Wang, Chem. Eng. J., 2022, 431(1), 133984.
7. B. Das, M. V. Reddy, C. Krishnamoorthi, S. Tripathy, R. Mahendiran, G. V. S. Rao and B. V. R. Chowdari, Electrochim. Acta, 2009, 54, 3360–3373.
8. S. Gao, Y. Tang, Y. Gao, L. Liu, H. Zhao, X. Li and X. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 7006–7013.
9. S. Petnikota, S. K. Marka, V. V. S. S. Srikanth, M. V. Reddy and B. V. R. Chowdari, Electrochim. Acta, 2015, 178, 699–708.
10. O. R. Ankinapalli, B. N. V. Krishna, Y. Hua and J. S. Yu, J. Alloys Compd., 2022, 928, 167063.
11. A. M. Patil, N. R. Chodankar, E. Jung, S. Roy, D. P. Dubal, G. Guan, Y. K. Han and S. C. Jun, J. Mater. Chem. A, 2021, 9, 26135–26148.
12. T. Ouyang, X. T. Wang, X. Q. Mai, A. N. Chen, Z. Y. Tang and Z. Q. Liu, Angew. Chem., Int. Ed., 2020, 59, 11948–11957.
13. L. J. Xie, C. F. Li, J. W. Zhao, L. F. Gu, J. Q. Wu, Y. Wang and G. R. Li, Chem. Eng. J., 2022, 430(4), 133119.
14. W. Hu, Q. Shi, Z. Chen, H. Yin, H. Zhong and P. Wang, ACS Appl. Mater. Interfaces, 2021, 13, 8337–8343.
15. R. Nadarajan, A. V. Gopinathan, N. P. Dileep, A. S. Sidharthan and M. M. Shaijumon, Nanoscale, 2023, 15, 15219–15229.
16. L. Wen, J. Zhai, J. Song, H. Jiang, R. Cui, Y. Xu, K. Sun and X. Hao, J. Solid State Chem., 2022, 308, 122910.
17. Y. Chang, B. You, Y. Xie, Y. Liu, R. Xiong, C. Lu and J. M. Liu, Appl. Phys. Lett., 2023, 123, 102402.
18. T. Kurumaji, S. Ishiwata and Y. Tokura, Phys. Rev. B, 2017, 95, 045142.
19. M. V. Eremin, K. V. Vasin and A. R. Nurmukhametov, J. Exp. Theor. Phys., 2023, 137, 506–519.
20. T. Kurumaji, Y. Takahashi, J. Fujioka, R. Masuda, H. Shishikura, S. Ishiwata and Y. Tokura, Phys. Rev. B, 2017, 95, 020405(R).
21. S. P. Mcalister and P. Strobel, Magnetic order in M2M030 S Single crystals (M = Mn, Fe, Co, Ni), North-Holland Publishing Company, 1983, vol. 30.
22. S. Bao, Z. L. Gu, Y. Shangguan, Z. Huang, J. Liao, X. Zhao, B. Zhang, Z. Y. Dong, W. Wang, R. Kajimoto, M. Nakamura, T. Fennell, S. L. Yu, J. X. Li and J. Wen, Nat. Commun., 2023, 14, 6093.
23. Y. Chang, Y. Weng, Y. Xie, B. You, J. Wang, L. Li, J. M. Liu, S. Dong and C. Lu, Phys. Rev. Lett., 2023, 131, 136701.
24. K. V. Vasin, A. Strinić, F. Schilberth, S. Reschke, L. Prodan, V. Tsurkan, A. R. Nurmukhametov, M. V. Eremin, I. Kézsmárki and J. Deisenhofer, Phys. Rev. B, 2024, 110, 054401.
25. Y. S. Tang, G. Z. Zhou, L. Lin, R. Chen, J. F. Wang, C. L. Lu, L. Huang, J. H. Zhang, Z. B. Yan, X. M. Lu, X. K. Huang, X. P. Jiang and J. M. Liu, Phys. Rev. B, 2022, 105, 064108.
26. S. Li, M. D. Le, V. Loganathan and A. H. Nevidomskyy, Phys. Rev. Mater., 2022, 6, 014405.
27. J. R. Morey, A. Scheie, J. P. Sheckelton, C. M. Brown and T. M. McQueen, Phys. Rev. Mater., 2019, 3, 014410.
28. Y. S. Tang, J. H. Zhang, L. Lin, R. Chen, J. F. Wang, S. H. Zheng, C. Li, Y. Y. Zhang, G. Z. Zhou, L. Huang, Z. B. Yan, X. M. Lu, D. Wu, X. K. Huang, X. P. Jiang and J. M. Liu, Phys. Rev. B, 2021, 103, 014112.
29. D. Bertrand and H. Kerner-Czeskleba, J. Phys., 1975, 36(5), 379.
30. T. Ideue, T. Kurumaji, S. Ishiwata and Y. Tokura, Nat. Mater., 2017, 16, 797–802.
31. T. Kurumaji, S. Ishiwata and Y. Tokura, Phys. Rev. X, 2015, 5, 031034.
32. W. Wang, C. Wang, P. Li, J. Li, J. Xian, K. Cheng, C. M. Leung and M. Zeng, Ceram. Int., 2022, 48, 24326–24331.
33. W. Wang, P. Z. Li, Y. T. Chang, M. F. Liu, C. L. Lu, X. B. Lu, M. Zeng and J. M. Liu, Appl. Phys. Lett., 2021, 118, 112901.
34. S. Nakayama, R. Nakamura, M. Akaki, D. Akahoshi and H. Kuwahara, J. Phys. Soc. Jpn., 2011, 80, 104706.
35. C. Zhang, Y. Zhao, H. Nie, C. Zheng, F. Li, D. Zhou, R. Gao, H. Shen, S. Jiang, L. Zhang and J. Sun, Phys. Status Solidi B, 2023, 260, 2200558.
36. B. Csizi, S. Reschke, A. Strinić, L. Prodan, V. Tsurkan, I. Kézsmárki and J. Deisenhofer, Phys. Rev. B, 2020, 102, 174407.
37. J. Yang, D. Su, J. He, Y. Ji, Q. Guo, Y. Meng, X. Li, L. Wang, X. Shen, Y. Yao, Y. Long, Y. Sun and R. Yu, Phys. Rev. B, 2023, 107, 104408.
38. Z. Yu, H. Ding, K. Zhai, C. Mu, A. Nie, J. Cong, J. Huang, H. Zhou, Q. Wang, F. Wen, J. Xiang, B. Wang, T. Xue, Z. Zeng and Z. Liu, Phys. Rev. B, 2024, 109, 024442.
39. L. Prodan, I. Filippova, A. O. Zubtsovskii, S. Shova, S. Widmann, A. A. Tsirlin, I. Kézsmárki and V. Tsurkan, Phys. Rev. B, 2022, 106, 174421.
40. S. Mo, T. Katayama, A. Chikamatsu, M. Kitamura, K. Horiba, H. Kumigashira and T. Hasegawa, Chem. Mater., 2021, 33, 7713–7718.
41. Neutron data ISIS Neutron and Muon Beamtime award DOI:10.5286/ISIS.E.RB2220551.
42. L. C. Chapon, P. Manuel, P. Radaelli, C. Benson, L. Perrot, S. Ansell, N. J. Rhodes, D. Raspino, D. Duxbury, E. Spill and J. Norris, Neutron News, 2011, 22, 22–25.
43. Neutron data ISIS Neutron and Muon Beamtime award DOI:10.5286/ISIS.E.XB2390084.
44. A. C. Hannon, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 551, 88–107.
45. A. C. Larson and R. B. von Dreele, Los Alamos Natl. Rep. LAUR, 1994, 96, 86.
46. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213.
47. H. Abe, A. Sato, N. Tsujii, T. Furubayashi and M. Shimoda, J. Solid State Chem., 2010, 183, 379–384.
48. S. C. Abrahams and J. M. Reddy, J. Chem. Phys., 1965, 43, 2533–2543.
49. T. N. Stanislavchuk, G. L. Pascut, A. P. Litvinchuk, Z. Liu, S. Choi, M. J. Gutmann, B. Gao, K. Haule, V. Kiryukhin, S. W. Cheong and A. A. Sirenko, Phys. Rev. B, 2020, 102, 115139.
50. T. Kurumaji, Y. Takahashi, J. Fujioka, R. Masuda, H. Shishikura, S. Ishiwata and Y. Tokura, Phys. Rev. B, 2017, 95, 020405(R).
51. V. G. Bessergenev, Y. A. Kovalevskaya, I. E. Paukov, M. A. Starikov, H. Oppermann and W. Reichelt, J. Chem. Thermodyn., 1992, 24, 85–98.
52. G. Lautenschlager, H. Weitzel, H. Fuess and E. Ressouche, Z. Kristallogr., 1994, 209, 936–940.
53. L. J. Vera Stimpson, E. E. Rodriguez, C. M. Brown, G. B. G. Stenning, M. Jura and D. C. Arnold, J. Mater. Chem. C, 2018, 6, 4541–4548.
54. J. Rodriguez Carvajal, Phys. B, 1993, 192, 55–69.
55. S. Reschke, A. A. Tsirlin, N. Khan, L. Prodan, V. Tsurkan, I. Kézsmárki and J. Deisenhofer, Phys. Rev. B, 2020, 102, 094307.
56. S.-W. Cheong and M. Mostovoy, Nat. Mater., 2007, 6, 13–20.
57. J. A. McAllister and J. P. Atfield, J. Mater. Chem., 1998, 8, 1291–1294.
58. M. Eremin, K. Vasin and A. Nurmukhametov, Materials, 2022, 15(22), 8229.
59. G. Lautenschlager, H. Weitzel, H. Fuess and E. Ressouche, Z. Kristallogr., 1994, 209, 936–940.
60. B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607–614.
61. R. Grethe, K. J. W. Etherdo-Sibley, C. Tang, S. Day, D. C. Arnold and E. Schofield, J. Cult. Herit., 2022, 55, 221–227.
62. D. Szaller, K. Szász, S. Bordács, J. Viirok, T. Rõõm, U. Nagel, A. Shuvaev, L. Weymann, A. Pimenov, A. A. Tsirlin, A. Jesche, L. Prodan, V. Tsurkan and I. Kézsmárki, Phys. Rev. B, 2020, 102, 144410.
63. M. S. Senn, I. Loa, J. P. Wright and J. P. Attfield, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 125119.
64. E. J. W. Verwey, Nature, 1939, 144, 327–328.
65. R. Zierold, C. Le Lann, J. Dendooven and F. Walz, J. Phys.:Condens. Matter, 2002, 14, R285.
66. D. Levy, R. Giustetto and A. Hoser, Phys. Chem. Mater., 2012, 39, 169–176.
67. B. Gao, T. Chen, C. L. Huang, Y. Qiu, G. Xu, J. Liebman, L. Chen, M. B. Stone, E. Feng, H. Cao, X. Wang, X. Xu, S. W. Cheong, S. M. Winter and P. Dai, Phys. Rev. B, 2023, 108, 024431.
68. M. E. Fleet, Acta Crystallogr., Sect. B, 1981, 37, 917–920.
69. B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607–614.
70. Q. Chen, R. Sinclair, A. Akbari-Sharbaf, Q. Huang, Z. Dun, E. S. Choi, M. Mourigal, A. Verrier, R. Rouane, X. Bazier-Matte, J. A. Quilliam, A. A. Aczel and H. D. Zhou, Phys. Rev. Mater., 2022, 6, 044414.
71. J. P. Sheckelton, J. R. Neilson, D. G. Soltan and T. M. McQueen, Nat. Mater., 2012, 11, 493–496.
72. Y. Wang, G. L. Pascut, B. Gao, T. A. Tyson, K. Haule, V. Kiryukhin and S. W. Cheong, Sci. Rep., 2015, 5, 12268.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03777d

---