The effect of solvent on the α-effect: C[double bond, length half m-dash]O, P[double bond, length half m-dash]O and SO₂ centers

Abstract

The α-effect for the reaction of a sulfonyl ester exhibits a bell-shaped dependence of the α-effect on solvent composition as do the corresponding reactions with a carbonyl and a phosphinyl ester, and the magnitude of the α-effect is found to be dependent on the magnitude of the β_nuc value, suggesting TS stabilization as the cause of the α-effect.

---

Since the α-effect term was given by Edwards and Pearson in 1962 to the abnormally enhanced reactivity shown by nucleophiles having a pair of unshared electrons adjacent to the nucleophilic center,¹ numerous studies have been performed to account for this phenomenon.^2–11 However, the cause of the α-effect has not been clearly understood.^2–11 One of the intriguing aspects in α-effect studies has been the finding that the magnitude of the α-effect is dependent on the nature of the electrophilic center, generally increasing as sp³ < sp² < sp for carbon centers,^2–4 though some exceptions exist.⁵ Equally interesting, as well as controversial, has been the effect of solvent on the α-effect.^6–9

In order to shed light on the effect of solvent on the α-effect, we initiated systematic studies and in 1986, we investigated the reaction of p-nitrophenyl acetate (PNPA) with butane-2,3-dione monoximate (Ox⁻) and p-chlorophenoxide (ClPhO⁻), as the α- and corresponding normal-nucleophile, respectively, in DMSO–H₂O mixtures of varying compositions.^6a We found, unexpectedly, a bell-shaped dependence of the α-effect (k^Ox−/k^{ClPhO −}) on solvent composition.^6a A similar bell-shaped trend was observed for the corresponding reaction of p-nitrophenyl diphenylphosphinate (PNPDPP).^6b However, Moss reported that the reaction of PNPA with o-iodosylbenzoate (IBO⁻) and ClPhO⁻ in DMSO–H₂O mixtures shows no maximum α-effect but exhibits a decreasing α-effect trend.⁷ More surprisingly, a contrasting solvent behaviour was found recently:⁸ the reaction of PNPA with Ox⁻ and ClPhO⁻ in MeCN–H₂O mixtures exhibits an increasing α-effect trend as the mol% MeCN in the medium is increased.^8a Similarly, the α-effect for the reaction of PNPA with benzohydroxamates and m-chlorophenoxide in MeCN–H₂O mixtures also resulted in an increasing α-effect behaviour as the concentration of MeCN in the reaction medium was increased.^8b

It appeared to us as potentially highly informative, in investigation of the α-effect, to vary the electrophilic center systematically and to couple that with variation of solvent. We report herein such a study for the reaction of a sulfur centered substrate, p-nitrophenyl benzenesulfonate (PNPBS), with Ox⁻ and ClPhO⁻ in DMSO–H₂O mixtures as shown in eqn. (1), and compare the results with the data for the corresponding reactions of PNPA and PNPDPP. 

C₆H₅SO₂-OC₆ H₄NO₂-p + Nu⁻ →C₆H₅SO₂Nu + ⁻OC₆H₄NO₂-p   Nu⁻ = CH₃C(O)C(CH₃)[double bond, length half m-dash]NO⁻ (Ox⁻), an α-nucleophilep-ClC₆H₄O⁻ (ClPhO⁻), a normal nucleophile (1)

As shown in Fig. 1, the second-order rate constant increases as the mol% of DMSO in the medium increases for both Ox⁻ and ClPhO⁻ systems: the rate enhancement upon solvent change from 10 to 90 mol% of DMSO is 2190 and 3330 for Ox⁻ and ClPhO⁻, respectively. Interestingly, the plot of log k^Ox−vs. mol% of DMSO shows downward curvature, while that of log k^ClPhO−vs. mol% DMSO exhibits upward curvature. As a result, the difference in rate constant between Ox⁻ and ClPhO⁻ increases up to ca. 50 mol% DMSO but decreases beyond this point. Such a differential solvent effect on rates leads to the solvent dependent α-effect profile, shown in Fig. 2; i.e. the sulfonyl system exhibits maximum α-effect at ca. 50 mol% DMSO, as do the carbonyl and phosphinyl systems. Therefore, the bell-shaped α-effect behaviour has been found to be general for the reactions of the three different electrophiles with Ox⁻ and ClPhO⁻ in DMSO–H₂O mixtures.

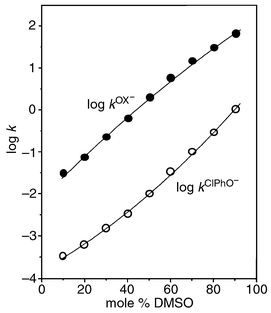Fig. 1 Plots showing the effect of solvent on second-order rate constants for the reaction of PNPBS with Ox⁻ and ClPhO⁻ in DMSO–H₂O mixtures at 25.0 ± 0.1 °C.

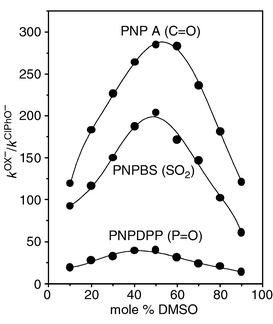Fig. 2 Plots showing the effect of solvent on the α-effect for the reaction of PNPA, PNPDPP and PNPBS with Ox⁻ and ClPhO⁻ in DMSO–H₂O mixtures at 25.0 ± 0.1 °C.

Moreover, interestingly, the magnitude of the α-effect is strongly dependent on the electrophilic center; i.e. the α-effect in 50 mol% is ca. 300, 40 and 200 for the carbonyl, phosphinyl and sulfonyl systems, respectively. The small α-effect for the phosphinyl system compared to the carbonyl and sulfonyl systems is striking. Bruice showed that the magnitude of the α-effect is dependent on the magnitude of the β_nuc value for reactions of a variety of substrates with hydrazine and glycylglycine: the α-effect decreases with decreasing β_nuc value.¹⁰ Similarly, Bernasconi observed no α-effect for the addition reaction of primary amines including hydrazine and o-methylhydroxylamine to Meldrum’s acid, a system for which β_nuc = 0.22.^11a

The β_nuc values for the reactions of PNPA with substituted phenoxides in various DMSO–H₂O mixtures are available,¹² but the ones for the reaction of the phosphinyl and sulfonyl systems have not been reported. Therefore, we performed the reaction of PNPDPP and PNPBS with a series of substituted phenoxides in 50 mol% DMSO, in which the maximum α-effect is observed. The plots of log k^{ZC₆H₄O−}vs.pK_a (ZC₆H₄OH) exhibit good Brønsted type correlation: β_nuc values are 0.64, 0.21 and 0.54 for the carbonyl, phosphinyl and sulfonyl systems, respectively. Thus, the β_nuc value for the phosphinyl systems is much smaller than for the carbonyl and sulfonyl systems, and, moreover, the β_nuc value follows the same order as the α-effect in magnitude. Therefore, one can suggest that the small β_nuc value is responsible for the small α-effect exhibited by the phosphinyl system. This argument is consistent with our recent report that the reaction for an sp hybridized carbon center exhibited an unexpectedly small α-effect in which the β_nuc value was 0.32.⁵

As demonstrated in Fig. 2, the effect of solvent on reactivity is significant. Such a solvent effect on rate can be achieved by destabilizing the ground-state (GS) and/or stabilizing the transition-state (TS). We recently found that the GS of Ox⁻ and ClPhO⁻ becomes destabilized upon addition of DMSO to the reaction medium,^6c however, the GS energy difference between Ox⁻ and ClPhO⁻ is constant for the three systems. Therefore, if the GS energy difference between Ox⁻ and ClPhO⁻ were mainly responsible for the α-effect, the magnitude of the α-effect should be about the same, regardless of the nature of the electrophilic center. However, our results show that this is not the case. Therefore, the present results clearly suggest that the difference in the GS energy is not solely responsible for the α-effect.

The magnitude of the β_nuc value has been understood as a measure of bond formation between the nucleophile and the substrate in the TS of the rate-determining step; hence the TS structures of the carbonyl, phosphinyl and sulfonyl systems would vary according to the different β_nuc values. One can expect that the TS stabilizing effect would be smaller for the reaction system in which the degree of bond formation between nucleophile and substrate in the TS is less advanced (reactant-like TS), and vice versa. Accordingly, one can suggest that the TS stabilizing effect would be developed to a lesser extent for the phosphinyl system compared with the carbonyl and sulfonyl systems, based on the smaller β_nuc value obtained for the former, which would explain the small α-effect observed for the phosphinyl system.

More systematic studies are underway including theoretical investigation for better understanding of solvent effect on the α-effect.

Acknowledgements

The authors are grateful for the financial support from KOSEF of Korea (1999-2-123-003-5 and 2000-123-02-2) and E. B. also thanks NSERC of Canada for a research grant.

Notes and references

1. J. O. Edwards and R. G. Pearson, J. Am. Chem. Soc., 1962, 84, 16.
2. Reviews: (a) E. Buncel and S. Hoz, Isr. J. Chem., 1985, 26, 313; (b) A. P. Grekov and V. Y. Veselov, Usp. Khim., 1978, 47, 1200; (c) N. J. Fina and J. O. Edwards, Int. J. Chem. Kinet., 1973, 5, 1.
3. (a) G. Moutiers, E. Guevel, L. Villien and F. Terrier, J. Chem. Soc., Perkin Trans. 2, 1997, 710; (b) F. Terrier, G. Moutiers, L. Xiao, E. Guevel and F. Guir, J. Org. Chem., 1995, 60, 1748; (c) K. R. Fountain, D. B. Tad-y, T. W. Paul and M. V. Golynskiy, J. Org. Chem., 1999, 64, 6547.
4. (a) E. Buncel, C. Chuaqui and H. Wilson, J. Am. Chem. Soc., 1982, 104, 4896; (b) S. Oae and Y. Kadoma, Phosphorus, Sulfur Silicon Relat. Elem., 1997, 123, 293.
5. I. H. Um, J. S. Lee and S. M. Yuk, J. Org. Chem., 1998, 63, 9152.
6. (a) E. Buncel and I. H. Um, J. Chem. Soc., Chem. Commun., 1986, 595; (b) R. M. Tarkka and E. Buncel, J. Am. Chem. Soc., 1995, 117, 1503; (c) I. H. Um and E. Buncel, J. Org. Chem., 2000, 65, 577.
7. R. A. Moss, S. Swarup and S. Ganguli, J. Chem. Soc., Chem. Commun., 1987, 860.
8. (a) I. H. Um and E. Buncel, J. Chem. Soc., Chem. Commun., 2000, 1917; (b) I. H. Um, H. W. Yoon, J. S. Lee and H. J. Moon, J. Org. Chem., 1997, 62, 5939.
9. (a) G. Moutiers, E. Guevel, L. Villien and F. Terrier, J. Chem. Soc., Perkin Trans. 2, 1997, 7; (b) C. A. Bunton, N. D. Gillitt and A. Kumar, J. Phys. Org. Chem., 1997, 10, 221; (c) M. Laloi-Diard, J. F. Verchere, P. Gosselin and F. Terrier, Tetrahedron Lett., 1984, 25, 1267.
10. H. J. Dixon and T. C. Bruice, J. Am. Chem. Soc., 1972, 94, 2052.
11. (a) C. F. Bernasconi and C. Murray, J. Am. Chem. Soc., 1986, 108, 5251; (b) D. Herschlag and W. P. Jencks, J. Am. Chem. Soc., 1990, 112, 1951; (c) L. E. Fikes, D. T. Winn, R. W. Sweger, M. P. Johnson and A. W. Czarnik, J. Am. Chem. Soc., 1992, 114, 1493.
12. E. Buncel, I. H. Um and S. Hoz, J. Am. Chem. Soc., 1989, 111, 971.

---

Footnote

† Electronic supplementary information (ESI) available: Tables of rate constants. See http://www.rsc.org/suppdata/cc/b0/b007000i/

---