Chiral quantification of D-, L-, and meso-tartaric acid mixtures using a mass spectrometric kinetic method

Abstract

Accurate quantification of the optical isomers in a ternary mixture of D-, L-, and meso-tartaric acids is achieved using electrospray ionization tandem mass spectrometry for in-situ metal complex formation and a three-point calibration method to quantify the dissociation kinetics.

---

In a previous communication¹ we showed that fragmentation rates of metal complexes in the mass spectrometer, treated by a kinetic method, permit rapid enantiomeric determination of α-hydroxy acids. Now we report the first use of mass spectrometry for optical isomer quantification of a ternary mixture. This novel method should be applicable to ternary and higher mixtures of optical isomers. As such, it may provide a solution to the challenging problem of how to perform chiral quantification of multiple chiral-center drugs and their metabolites rapidly and accurately, a requirement imposed by national pharmaceutical regulatory bodies and a topic of great interest in pharmacology.² It may be also useful in developing chiral morphing techniques,³ which allow utilization of the spatial diversity of multiple chiral centers to produce drug candidates with improved efficiency, stability, membrane permeability, and oral availability, as well as decreased toxicity and side effects.

Several mass spectrometric methods for chiral analysis have already been developed, including guest–host adducts formation,⁴ ion/molecule reactions,^5,6 collision-induced dissociation of diastereomeric adducts,⁷ and solution-phase kinetic resolution followed by mass spectrometry.⁸ However, none of them aims at chiral ternary mixture analysis. The kinetic method⁹ as used for chiral analysis distinguishes optical isomers via their transition metal (M^II)-bound trimeric cluster ions by investigating the dissociation kinetics.^10,11 In general, singly-charged cluster ions [M^II(ref*)₂(A) − H]⁺ are mass-selected and dissociated in an ion trap mass spectrometer to form the dimeric cluster ions [M^II(ref*)(A) − H]⁺ and [M^II(ref*)₂ − H]⁺ by competitive loss of the neutral reference compound ref* and the analyte A, respectively. The difference in stability of the diastereomeric ions [M^II(ref*)(A) − H]⁺ due to the two configurations of the analyte A, results in a relative abundance ratio (R, eqn. 1) that depends on the isomeric composition of the analyte A:

R = [M^II(ref*)(A) − H]⁺/[M^II(ref*)₂ − H]⁺ (1)

In this first study of ternary optical isomers, tartaric acid was chosen as the analyte because of its historical importance as the first molecule to be optically resolved¹² and also because it has been used as a model compound to explore such new topics as heterogeneous enantioselectivity on copper surfaces.¹³ As a matter of definition, when the analyte tartaric acid is in any of the optically pure D-, L-, or meso-forms, R in eqn. 1 becomes R_D, R_L, or R_meso, respectively. Experimentally, a transition metal-bound trimeric cluster ion is generated by electrospraying a solution comprised of the analyte (A, referring to D-, L-, or meso-tartaric acid) (100 μM), a chiral reference ligand (100 μM), and a transition metal chloride (25 μM), and the experiments are performed using a commercial ThermoFinnigan LCQ instrument. The sensitive nature of the methodology (1 kJ mol⁻¹ in energy differences between diastereomeric cluster ions are distinguishable) and the linear relationship between the logarithm of the fragment ion abundance ratio and the optical purity, are both intrinsic to the kinetic method.⁹ With such a linear relationship, a two-point calibration allows quantitative analysis in the binary mixture of D/L-tartaric acid.^1,14 However, if a third isomer such as meso-tartaric acid is present, it will also contribute to the branching ratio. Based on the extensive property of free energy change, for a ternary mixture with molar fractions of α_D (D-tartaric acid), α_L (L-tartaric acid), and (1 − α_D − α_L) (meso-tartaric acid), respectively, one can write eqn. 2 for the difference in free energy changes for competitive loss of the neutral reference compound ref* and tartaric acid from a cluster ion generated from a mixture containing the chiral reference and any combination of the D-, L-, and meso-forms of tartaric acid. Eqn. 3 describes the measured branching ratio for such a dissociation.

Δ(ΔG) = α_D*Δ(ΔG)_D + α_L*Δ(ΔG)_L + (1 − α_D − α_L)_*Δ(ΔG)_meso (2)

ln R = α_D*lnR_D + α_L*lnR_L + (1 − α_D − α_L)_*lnR_meso (3)

If the same analyte is also measured under a second set of conditions, a second set of equations is obtained and the system of two unknowns can be solved. Note that small changes in conditions are less useful than changes to both the nature of the reference and the choice of metal ion. The latter (more ‘orthogonal’ systems) gives relatively larger distinctions for all three optical isomers. In previous work on α-hydroxy acids,¹⁴ we identified two candidate orthogonal systems: (i) Co^II as the central metal ion and L-DOPA as the reference ligand; (ii) Ni ^II as the central metal ion and N-acetyl-L-Phe as the reference ligand. These systems were therefore selected for the analysis of the ternary tartaric acid mixtures and typical mass spectra showing the differentiation of D-, L-, and meso-tartaric acid using system (ii) are illustrated in Fig. 1. Data for system (i) is not shown but the measured branching ratios for both systems (i) and (ii) were obtained. To illustrate the additional contribution from meso-tartaric acid, three-point calibration curves constructed using the measured branching ratios are displayed versus the molar fraction of D-tartaric acid (α_D) (Fig. 2). Using Cartesian coordinates, the measured R values can be converted into two groups of points: D1(100, −1.61), L1(0, −2.27), meso1(0, −1.90) for system (i) shown as open-diamond symbols and D2(100, 0.0770), L2(0, −0.728), meso2(0, −0.442) for system (ii), shown as filled-triangle symbols. Note that the points D, L, and meso correspond to cases in which the analyte is pure D, pure L, and pure meso, respectively. For the pure enantiomeric D/L-tartaric acid pair, the two-point calibration curves for the two experimental conditions mentioned above are represented by Curve(D1-L1) and Curve(D2-L2), respectively. With the additional contributions of meso-tartaric acid, these two curves shift upwards, by an amount that depends on the mole fraction of meso-compound in the sample. For all possible compositions, the logarithmic value of each measured ratio, ln R, will fall into the area of the triangle(D1–L1–meso1, dotted line) or triangle(D2–L2–meso2, solid line). This three-point calibration relationship is described using eqn. 3, which takes the forms shown in eqns. 4 and 5 when substituting the actual measured values of R_D, R_L, and R_meso for these two systems.

ln R(i) = (−1.61)*α_D + (−2.27)*α_L + (−1.90)*(1 − α_D − α_L) (4)

ln R(ii) = (0.08)*α_D + (0.728)*α_L + (0.442)*(1 − α_D − α_L) (5)

Fig. 1 MS/MS product ion spectra of [Ni^II(N-Acetyl-L-Phe)₂(A) − H]⁺: A = (a) D-tartaric acid; (b) meso-tartaric acid; and (c) L-tartaric acid using helium CID at an activation level of 275 mV in an ion trap.

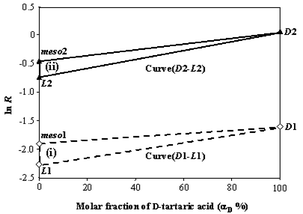Fig. 2 Three-point calibration diagram for chiral quantification of a ternary mixture of tartaric acid using two separate systems: (i) Co^II as the central metal ion and L-DOPA as the reference ligand; (ii) Ni^II as the central metal ion and N-Acetyl-L-Phe as the reference ligand. Values corresponding to each point are averages based on triplicate measurements made on separate occasions with less than ca. 2% error.

Chiral quantification of ternary mixtures of tartaric acid was performed using samples with several representative compositions, the results being summarized in Table 1. The experimentally measured molar fractions are consistent with the actual compositions and they show that less than 1% mole fraction for each form of tartaric acid can be determined with relative errors that range from 0.5% to 6.0%. The average relative errors for D-tartaric acid, L-tartaric acid, and meso-tartaric acid are 1.8%, 2.4%, 2.8%, respectively. The present results show that the kinetic method allows quantitative chiral analysis of a ternary mixture of multiple chiral-center molecules.

Table 1 Chiral quantification of a ternary mixture of tartaric acids^a

	Measured R		Actual			Experimental			Relative error(%)
Entry	Co/L-DOPA	Ni/N-Acetyl- L-Phe	%D	%L	%meso	%D	%L	%meso	D	L	meso
a CID activation time and energy is optimized and kept constant when the same transition metal and reference ligand are used.
1	0.177	0.851	65	30	5	65.3	29.5	5.2	0.5	1.7	4.0
2	0.191	1.01	90	5	5	89.5	5.3	5.2	0.6	6.0	4.0
3	0.143	0.639	10	20	70	9.6	19.7	70.7	4.0	1.5	1.0
4	0.109	0.509	5	90	5	4.9	90.3	4.9	2.0	0.3	2.0
								Average:	1.8	2.4	2.8

---

When choosing two suitable systems (two different sets of the central metal ions and the reference ligands), the kinetic method offers sensitivity and accuracy for chiral quantification of a ternary mixture similar to that reported for binary mixtures.^1,14 It is important to note that the use of pure calibration samples of the three isomers is not needed: one simply requires that three samples of known isomeric composition be available. In addition, the quotient ratio method¹⁵ in which multiple experiments are done using enantiomeric reference ligands could be advantageous. This procedure reduces the requirement for analytes of known composition from three to two. Extension of the procedures described in this paper to mixtures of four optical isomers using a four-point calibration kinetic method should be straight forward.

This work was supported by the U.S. DOE, Office of Basic Energy Sciences and the National Science Foundation (CHE 97-32670). L.W. thanks fellowship support from Merck & Co.

Notes and references

1. W. A. Tao, L. Wu and R. G. Cooks, Chem. Commun., 2000, 20, 2023.
2. S. C. Stinson, Chem. Eng. News, 2000, 78, 55.
3. J. C. Fromme and G. L. Verdine, Nature Struct. Biol., 2002, 9, 544.
4. M. Shizuma, H. Imamura, Y. Takai, H. Yamada, T. Takeda, S. Takahashi and M. Sawada, Int. J. Mass Spectrom., 2001, 210–211, 585.
5. Y. J. Liang, J. S. Bradshaw, R. M. Izatt, R. M. Pope and D. V. Dearden, Int. J. Mass Spectrom., 1999, 187, 977.
6. J. Ramirez, F. He and C. B. Lebrilla, J. Am. Chem. Soc., 1998, 120, 7387.
7. T. T. Dang, S. F. Pedersen and J. A. Leary, J. Am. Soc. Mass Spectrom., 1994, 5, 452.
8. J. Guo, J. Wu, G. Siuzdak and M. G. Finn, Angew. Chem., Int. Ed., 1999, 38, 1755.
9. R. G. Cooks and P. S. H. Wong, Acc. Chem. Res., 1998, 31, 379.
10. A. Filippi, A. Giardini, S. Piccirillo and M. Speranza, Int. J. Mass Spectrom., 2000, 198, 137.
11. M. G. Finn, Chirality, 2002, 14, 534.
12. L. C. R. Pasteur, Hebd. Seance Acad. Sci. Paris, 1848, 26, 535.
13. M. O. Lorenzo, C. J. Baddeley, C. Muryn and R. Raval, Nature, 2000, 404, 376.
14. 14 L. Wu, W. A. Tao and R. G. Cooks, Anal. Bioanal. Chem., 2002, 373, 618.
15. 15 W. A. Tao, R. L. Clark and R. G. Cooks, Anal. Chem., 2002, 74, 3783.

---