Configuration assignment in small organic molecules via residual dipolar couplings†
Alfonso
Mangoni
,
Veronica
Esposito
and
Antonio
Randazzo
*
Dipartimento di Chimica delle Sostanze Naturali, Università degli Studi di Napoli “Federico II”, via D. Montesano 49, I-80131, Napoli, Italy. E-mail: antranda@unina.it; FAX: +39-081-678552; Tel: +39-081-678514
First published on 5th December 2002
Abstract
Here we propose a new method to assign relative configurations of stereocenters in small organic molecules by using residual dipolar couplings; the main advantage of this method is that spatial proximity of the stereocenters is not required.
Structure elucidation of unknown organic compounds is largely based on NMR. Modern NMR techniques allow the determination of the planar structure of virtually any molecule of a reasonable size, provided that a few milligrams of sample are available. Stereochemical assignments by NMR, however, are by far more difficult, and unassigned configurations are commonly encountered in the literature, particularly in the field of natural products. Yet, configuration assignment is crucial in order to understand, for example, the interaction of the metabolites with their biopolymeric receptors, and to provide information for the total synthesis of the compounds.
Configurational assignment by NMR is generally accomplished using NOEs, vicinal 1H–1H and, more recently, 1H–13C (2,3J) coupling constants.1 All these methods, however, require the stereocenters, whose relative configuration has to be assigned, to be close to each other. Fortunately, a new powerful tool based on a well-known NMR parameter, namely dipolar coupling, has recently occupied a very important place in the field of NMR,2 and provides a way to overcome this problem.
In solution state NMR, the measured dipolar coupling between the nuclei m and n is described3 by the average (denoted by the angle brackets 〈〉) of the dipolar interaction over all orientations [eqn. (1)]:
| Dmn = −γmγnμ0h/8π3 〈(3cos2θmn − 1)/r3mn 〉 | (1) |
An obvious method to determine the unknown configuration at one stereocenter is the construction of a model of the two possible epimers, and the comparison of the measured RDCs with those expected for either epimer. In particular, the RDCs for C–H vectors whose orientation are very different in the two epimers (typically, but not exclusively, the C–H bond at the stereocenter itself) should be compared.
Eqn. (1) cannot be used directly to calculate RDCs, because the anisotropic motion of each bond vector is not known a priori. However, for a molecule (or part of a molecule) in a fixed conformation, RDCs themselves can provide information on the molecular motion. In fact, RDCs can be expressed in terms of (a) the time-independent orientation of the internuclear vector between the nuclei to a fixed molecular frame, and (b) a 3 × 3 matrix Sij, called order matrix or alignment tensor, describing the orientational averaging of the whole rigid unit [eqn. (2)]:3
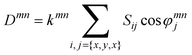 | (2) |
Once the order matrix is known, any RDC can be easily calculated provided that the conformation of the molecule is known or that it can be predicted in some way.
Since the order matrix has five independent elements, it can only be determined if five C–H RDCs are known. When studying small molecules, this is not a simple requirement, especially because the five C–H bonds must not be parallel, and moreover must be located in a region which is more or less conformationally fixed. Therefore, the possibility of decreasing the minimum number of RDC required would greatly increase the usefulness of this method.
A useful approximation for this purpose is to assume the anisotropic motion of the molecule to be axially symmetric (i.e.Sxx = Syy and Szx = Syz). This approximation decreases the minimum number of RDC from 5 to 3, which can be measured in many cases.4
It can be easily demonstrated that, under this assumption and in a suitable molecular frame, RDCs are only dependent on the constant Dax = kmnSzz/2 and on the angle θmn of the CH vector relative to z axis. Therefore, the expression of RDC reduces to eqn. (3):5
| Dmn = Dax (3cos2θmn − 1) | (3) |
To test the feasibility of using RDCs for determination of unknown configurations in small organic molecules, we measured RDCs of the methines of sodium cholate (1) (Fig. 1). Compound 1 was weakly oriented by using strained cross-linked polyacrylamide gels.6 This method, also known as SAG (strain-induced alignment in a gel), is effective over a wide range of temperature, pH, and ionic strength. Moreover, this method allows the sample to be recovered from the gel by diffusive dilution into exterior solution and this has an enormous importance, especially in the field of natural products.
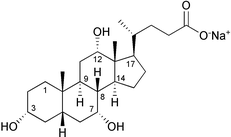 | ||
| Fig. 1 Sodium cholate (1). | ||
The gel was cast at room temperature in the form of a rod (3.8 mm diameter), using a 15% water solution of acrylamide/ bisacrylamide 29∶1. The gel was cut to 30 mm length, washed with water and dried down. 500 μl of 30 mM solution of 1 were used to swell up the gel. The gel was placed in a Shigemi tube (Allison Park, PA, USA). Upon application of pressure by means of the inner piston, the gel achieved the maximum compression in length at 22 mm. Two dimensional {1H; 13C}-HSQC spectra were recorded without 1H decoupling in the 1H dimension and with and without gel compression. For two nuclei with scalar coupling, the presence of RDC translates into a modification of the magnitude of the spin–spin coupling. Therefore, the difference between the splitting observed under anisotropic (with gel compression) and isotropic (without gel compression) conditions provided the value for the RDC. Measured RDCs for the 8 methines of 1 are reported in Table 1. It is important to note that the bonds between C8/H8, C9/H9, C14/H14, and C17/H17 are nearly parallel, as those between C3/H3 and C5/H5. Therefore, the RDCs in Table 1 actually refer to only 4 orientations of the C–H bond, not enough to determine the order matrix without the axial approximation.
| Unknown conf. at C-3 | Unknown conf. at C-7 | Unknown conf. at C-12 | |||||
|---|---|---|---|---|---|---|---|
| Position | Exp. DCH | 1 | 3-epi-1 | 1 | 7-epi-1 | 1 | 12-epi-1 |
| a The experimental RDCs of the methines 3, 7 and 12 were not used for fitting in scenario I, II and III, respectively, because the orientation of the relevant bonds were considered to be unknown. | |||||||
| 3 | +1.5a | +0.81 | −6.93 | +1.24 | +1.26 | +1.22 | +1.34 |
| 5 | +0.9 | +0.66 | +0.83 | +1.08 | +0.97 | +1.10 | +1.18 |
| 7 | +2.5a | +2.32 | +2.77 | +1.71 | −7.89 | +2.57 | +2.57 |
| 8 | −7.8 | −7.36 | −7.11 | −7.22 | −7.17 | −7.37 | −7.30 |
| 9 | −7.5 | −7.39 | −7.31 | −7.28 | −7.60 | −7.50 | −7.48 |
| 12 | +1.6a | +1.14 | +1.60 | +1.34 | +1.46 | +0.54 | −7.4 |
| 14 | −6.6 | −7.14 | −6.94 | −7.15 | −6.90 | −7.10 | −7.12 |
| 17 | −6.0 | −6.20 | −6.50 | −6.37 | −6.34 | −5.93 | −5.97 |
| D ax (RMS) | −3.73 (0.09) | −3.75 (0.10) | −3.64 (0.10) | −4.00 (0.09) | −3.81(0.08) | −3.77 (0.08) | |
We supposed three different scenarios (Table 1), in which the stereochemistry at C3, C7 and C12 was, one by one, unknown. In the first calculation (scenario I—unknown stereochemistry at C3) three-dimensional models of sodium cholate (1) and its epimers at C3 (3-epi-1) were generated using CS Chem3D and minimized in the MM2 force field. The principal axis frame and the parameter Dax needed to apply eqn. (3) were determined for 1 and 3-epi-1 using the program RDC_AX (see electronic supplementary information†). The measured RDCs for all methines, except the one measured for C3/H3, were used in the calculations. RDC_AX performed a grid search over all the possible orientations of the molecule in the frame.7 For each orientation, Dax and its RMS error were determined by least square fitting of experimental RDCs; the orientation with the smallest RMS error was selected. Then, RDCs (including that for C3/H3) were calculated using eqn. (3) and compared with the measured ones. As shown in Table 1, there is a good agreement between the measured and calculated RDCs of compound 1; in contrast, the expected value for C3/H3 of 3-epi-1 is completely different, suggesting that the structure of 3-epi-1 contains the wrong stereochemistry at C3.
Similar results (Table 1) were obtained repeating the calculation with 1 and 7-epi-1 (scenario II—unknown stereochemistry at C7), and 1 and 12-epi-1 (scenario III—unknown stereochemistry at C12), using all measured RDCs for all methines except C7/H7 and C12/H12, respectively. Also in these cases, the whole of the data would allow confident assignment of the correct configuration at the unknown stereocenter.
In conclusion, we showed that RDCs can be used to assign relative configurations of stereocenters in small organic molecules. The main advantage of RCDs over NOE and 1H–1H and 1H–13C coupling constants is that with the former method spatial proximity of the stereocenters is not required. Further work is in progress to test the method with a number of different compounds, as well as to extend the method to solvents other than water.
This work is supported by Italian M.U.R.S.T. (P.R.I.N. 2001). The authors are grateful to ‘Centro Ricerche Interdipartimentale di Analisi Strumentale’, C.R.I.A.S., for supplying NMR facilities. The authors are very grateful to Piero Andrea Temussi for his assistance in preparing the gels and for valuable suggestions.
Notes and references
- N. Matsumori, D. Kaneno, M. Murata, H. Nakamura and K. Tachibana, J. Org. Chem., 1999, 64, 866–876 CrossRef CAS.
- E. de Alba and N. Tjandra, Prog. Magn. Reson. Spectrosc., 2002, 40, 175–197 Search PubMed.
- J. A. Losonczi, M. Andrec, M. W. F. Fischer and J. H. Prestgard, J. Magn. Res., 1999, 138, 334–342 Search PubMed.
- Of course, this approximation also introduces an error in the estimation of RDCs. However, here RDCs are used to chose between two very different orientation of a CH vector, and calculated RDCs for the two epimers are likely to be very different,
so that this error can be tolerated (using caution when the calculated coupling for the two epimers happen to be similar).Dmn = Dax (3cos2θmn − 1) + 3/2 Dr (sin2θmn cos2φmn) - Eqn. (3) is obtained from the usual expression of dipolar coupling in the principal axis frame (Ref. 3) setting the rhombic component Dr to zero.
- R. Tycko, F. J. Blanco and Y. Ishii, J. Am. Chem Soc., 2000, 122, 9340–9341 CrossRef CAS.
- Only two angles need to be considered, because in the axial approximation a rotation along the z axis is irrelevant.
Footnote |
| † Electronic supplementary information (ESI) available: Listing of the C program RDC_AX, tridimensional models of compounds 1, 3-epi-1, 7-epi-1, and 12-epi-1 in PDB format, and the command files for 1, 3-epi-1, 7-epi-1, and 12-epi-1. See http://www.rsc.org/suppdata/cc/b2/b210454g/ |
| This journal is © The Royal Society of Chemistry 2003 |
