The prediction of inorganic crystal framework structures using excluded regions within a genetic algorithm approach
Scott M.
Woodley
*a,
C. Richard A.
Catlow
a,
Peter D.
Battle
b and
Julian D.
Gale
c
aDavy-Faraday Research Laboratory, The Royal Institution of Great Britain, 21 Albemarle Street, London, UK W1S 4BS. E-mail: smw@ri.ac.uk
bInorganic Chemistry Laboratory, University of Oxford, South Parks Road, Oxford, UK OX1 3QR
cNanochemistry Research Institute, Department of Applied Chemistry, PO Box U1987, Perth 6845, Australia
First published on 20th November 2003
Abstract
We have developed a new technique, which is complementary to other procedures, that will have wide applicability for generating new feasible framework structures with defined microporous architectures from the knowledge of only the unit cell dimensions, constituent elements and by defining forbidden regions within the unit cell.
There is a considerable incentive for the development of techniques for the generation and prediction of crystal structures. In some cases it may be difficult to solve structures from available crystallographic data; in others the aim may be to generate new structures with specific topological or other feature. There have been many successful studies in which inorganic and molecular crystal structures have been predicted or solved using either a genetic algorithm (GA) or simulated annealing approach.1–9 The case of framework structures is of particular interest. Here microporous structures have been generated on the basis of topological principles10,11 or by assembling building blocks (SBUs).1 We advance a different and complementary approach in which structures are generated corresponding to a predefined pore architecture. The approach we adopt is an adaptation of one that we have used previously12 in which we combine GA methods with lattice energy minimisation techniques.
A GA approach is based on ideas taken from Darwin's theory of evolution. A “population” of candidate structures is created; these may be different random atomic/ionic coordinates. Then, within a defined environment, competition to “procreate” in the population is simulated. That is, information from the better candidate structures of the current population is statistically more likely to be chosen to create candidate structures for a new population. The new population then replaces the current population and the process is repeated. Thus, candidate structures containing “good” features will prosper and those with “bad” features will diminish such that, eventually, a candidate structure should evolve which best fits the target criteria.
In our simulations the dimensions and contents of the unit cell, as well as the definition of the cost function (used to assess the “fitness” of the candidate structures), form the environment and a binary representation of the unknown coordinates forms the basis of our analogue of DNA. To form the latter, we first define and number a linear grid, of 2n points, over the unit cell. A unique concatenated series of binary numbers can be assigned to each different candidate structure if the ions are restricted to grid points and the order of the ions is kept fixed. This binary representation, or series of 0's and 1's, the length of which is determined by the number of unknown coordinates, the required accuracy of the coordinates and size of the unit cell, is used in the procreation process. Further details are given in references 9 and 12.
We employ a multistage method that has been shown to be an efficient method for generating a large range of ionic crystal structures.12 As before, a different cost function is used in each stage. A genetic algorithm with a robust cost function, is used in stage 1 to generate plausible candidate structures, which are subsequently refined (in stage 2) by minimising the lattice energy based on the Born model – a more accurate measure of fitness. Thus, the GA is only required to find an approximate structure that will relax to a more accurate model.
Following the success of this method in generating dense structures12 we now address the more challenging case of microporous materials. We define exclusion zones (EZs – regions within the unit cell where ions are forbidden), which is necessary because microporous materials, such as zeolites, are metastable with respect to their denser parent phase. More importantly, the procedure also allows us to predefine the size and dimensions of desired pores, or channels, and to generate stable structures that correspond to the desired topology.
The GA can of course be used with different sized EZs, which can be either ellipsoidal (or spherical), elliptical cylinders (channels, Fig. 1) or planar. EZs can contain, for example, known parts of layered crystal structures. The EZs were integrated into our method using two different procedures: directly by using a grid where no points are within the EZ or indirectly by adapting the definition of the cost function. In the indirect method, when an ion is found within the EZ, the candidate structure is heavily penalised such that it is unlikely to be selected for procreation and so will vanish from the population. Variations to this method could include a soft boundary whereby the penalty is weighted with respect to how deep the ion penetrates into the EZ. When the direct method is used in the procreation process, the points on the linear grid within the EZs are not numbered. This has the advantage, compared with the indirect method of EZs, of reducing the length of the binary representation of the structure. The disadvantage is that some grid points may be represented twice (as it is not always possible to have 2m grid points outside the EZ) and the mapping between fractional coordinates and the binary representation is more expensive to compute.
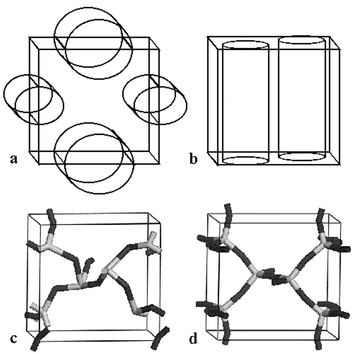 | ||
| Fig. 1 Orthorhombic cell with a, two ellipsoidal channel EZs b, two cylindrical channel EZs c, the best candidate generated from our GA after 2000 iterations and d, the structure of siliceous zeolite JBW. | ||
Whether the direct or indirect approach to EZs is more efficient will depend on the volume of the EZ compared to the unit cell volume. For the indirect approach, an increase in the EZ volume will result in more candidate structures being generated with ion(s) within the EZ. Whereas for the direct approach the number of different possible candidate structures is reduced as the EZ volume increases.
The cost function used for stage 2, is the lattice energy created by the two body potential (Coulomb and short range Buckingham terms),
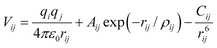 | (1) |
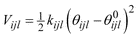 | (2) |
The cost function used in stage 1 (optimisation using the genetic algorithm) consists of a linear combination of terms,
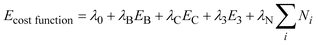 | (3) |
To demonstrate the viability of our approach, we have used the direct approach to EZs, within our multistage approach, to generate the siliceous form of Zeolite JBW (Fig. 1d) within the orthorhombic unit cell (a = 7.93061 Å, b = 7.66355 Å, c = 5.19639 Å) containing 6 Si4+ cations and 12 O2− anions. The structure of JBW presents a system of interpenetrating channels. Note, if we were to make use of asymmetric unit cells, considerably larger systems could be modelled. For example, 6 unique atoms are required for the framework of Faujasite, which contains 576 atoms in the full cell.
We defined four EZs, which reduced the number of grid points from 643 to 47398. Two EZs are ellipsoidal channels, as shown in Fig. 1a, where the cross-section of one cylinder has a width that ranges from 5 to 6 Å and the other from 3 to 4 Å. The other EZs are cylindrical channels, as shown in Fig. 1b, each with a circular cross-section, 2 Å radius. The GA used a population of 100 candidate structures. Other GA parameters were set to values similar† to those given in reference 12. When the ionic coordinates of the best candidate from stage 1, shown in Fig. 1c, were relaxed, the framework structure of JBW, shown in Fig. 1d, was generated in stage 2. As is typically the case, the improvement in the cost function for the best candidate structure is quite rapid in the earlier iterations. In fact there was very little improvement after about the 1350th and none after the 1700th population.
To summarise, we have shown that we can predict framework structures by adapting our GA/lattice energy procedure that was previously designed to predict dense ionic structures from the knowledge of the unit cell dimensions and ionic contents. In the first stage, exclusion zones – regions of the unit cell where ions are forbidden – were employed to drive the procedure to specific pore architectures, which in the case chosen here successfully generates the structure of JBW. This was the first microporous framework structure to be successfully generated by our new algorithm. The generation of other siliceous framework structures is currently in progress, and to date we have successfully generated Sodalite and Chabazite. Details of the efficiency of using this direct approach to exclusion zones, compared with an indirect approach (cost function includes the exclusion zones in its definition), within a genetic algorithm will be reported in subsequent publications.
We thank EPSRC for financial support (grant GR/N14569). We are grateful to Dr A. A. Sokol, Dr A. Simperler and Dr R. G. Bell for useful discussions.
Notes and references
- C. Mellot-Draznieks, S. Girard, G. Férey, J. C. Schön, Z. Cancarevic and M. Jansen, Chem. Eur. J, 2002, 8, 4102 CrossRef CAS.
- J. Pannetier, J. Bassas-Alsina, J. Rodriguez-Carvajal and V. Caignaert, Nature, 1990, 346, 343 CrossRef CAS.
- M. M. J. Treacy, K. H. Randall, S. Rao, J. A. Perry and D. J. Chadi, Z. Kristallogr., 1997, 212, 768 CAS.
- L. Reinaudi, E. P. M. Leiva and R. E. Carbonia, J. Chem. Soc. Dalton Trans., 2000, 23, 4258 RSC.
- J. C. Schön and M. Jansen, Z. Kristallogr., 2001, 216, 307 CAS.
- J. C. Schön and M. Jansen, Z. Kristallogr., 2001, 216, 361 CAS.
- W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Dzyabchenko, P. Erk, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, J. P. M. Lommerse, W. T. M. Mooij, S. L. Price, H. Scheraga, B. Schweizer, M. U. Schmidt, B. P. van Eijck, P. Verwer and D. E. Williams, Acta Crystallogr., Sect. B, 2002, B58, 647 CrossRef.
- K. D. M. Harris, R. L. Johnston, G. W. Turner, E. Tedesco, E. Y. Cheung and B. M. Kariuki, Mol. Cryst. Liq. Cryst., 2002, 389, 123 Search PubMed.
- S. M. Woodley, Prediction of crystal structures using evolutionary algorithms and related techniques,Structure and Bonding, 110, Springer-Verlag, Heidelberg, 2004 Search PubMed.
- J. Klinowski, Curr. Opin. Solid State Mater. Sci., 1998, 3, 79 CrossRef CAS.
- M. D. Foster, O. D. Friedrichs, R. G. Bell, F. A. A. Paz and J. Klinowski, Angew. Chem., Int. Ed., 2003, 42, 3896 CrossRef CAS.
- S. M. Woodley, P. D. Battle, J. D. Gale and C. R. A. Catlow, Phys. Chem. Chem. Phys., 1999, 1, 2535 RSC.
- M. J. Sanders, M. J. Leslie and C. R. A. Catlow, J. Chem. Soc., Chem. Commun., 1984, 19, 1271 RSC.
Footnote |
| † Default parameters were chosen except for the crossover probability and the tournament probability parameters where we used Pc = 0.4 and Pt = 0.8. |
| This journal is © The Royal Society of Chemistry 2004 |
