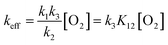Photochemistry of 1,3,2,4-benzodithiadiazines: formation and oxidation of 1,2,3-benzodithiazolyl radicals
Nina P.
Gritsan
*ab,
Stanislav N.
Kim
ac,
Alexander Yu.
Makarov
d,
Eugenii N.
Chesnokov
a and
Andrey V.
Zibarev
*bd
aInstitute of Chemical Kinetics and Combustion, Siberian Branch of the Russian Academy of Sciences, 630090, Novosibirsk, Russia. E-mail: gritsan@ns.kinetics.nsc.ru; Fax: +7 383 330 7350; Tel: +7 383 333 3053
bPhysics Department, Novosibirsk State University, 630090, Novosibirsk, Russia
cDepartment of Natural Sciences, Novosibirsk State University, 630090, Novosibirsk, Russia
dInstitute of Organic Chemistry, Siberian Branch of the Russian Academy of Sciences, 630090, Novosibirsk, Russia. E-mail: zibarev@nioch.nsc.ru; Fax: +7 383 330 9752; Tel: +7 383 330 9664
First published on 11th November 2005
Abstract
Photolysis of 1,3,2,4-benzodithiadiazine and its derivatives in hydrocarbon solutions yields dinitrogen and stable 1,2,3-benzodithiazolyls (Herz radicals) whose interaction with dioxygen leads finally to O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-substituted diphenyl disulfides via a self termination-like process with an effective second-order rate constant depending linearly on the concentration of dissolved O2.
N-substituted diphenyl disulfides via a self termination-like process with an effective second-order rate constant depending linearly on the concentration of dissolved O2.
Introduction
Recently1 we have established that a mild thermolysis (110–150 °C) of 1,3,2,4-benzodithiadiazine (1a) and a number of its derivatives, including the tetrafluoro derivative (1b), results in stable 1,2,3-benzodithiazolyls (Herz radicals, 2) in quantitative yields (Scheme 1). The photolysis1 of 1a in hydrocarbon solvents at ambient temperature also results in the formation of radical 2a in the yield close to 100% (Scheme 1). The quantum yield of this reaction is equal to 0.08 upon 313 nm photolysis and drops significantly at longer wavelength irradiation.1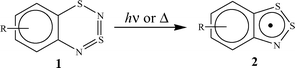 | ||
| Scheme 1 | ||
The transformation of 1 into 2 is a nontrivial process which demands ring contraction and a loss of a nitrogen atom. Evidently, it includes several steps. Indeed, the formation of a thiazyl-like intermediate (3a,b) was revealed upon the photolysis of 1a,b in an argon matrix at cryogenic temperature (Scheme 2).2
 | ||
| Scheme 2 | ||
Thiazyl 3 is an isomer of dithiadiazine 1 and contains the same hetero ring as the final radical product 2. Intermediate 3 differs from 2 only by an exocyclic nitrogen atom, which most reasonably would be released as dinitrogen in a bimolecular process. No attempts were made to detect this by-product.
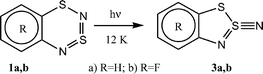
The discussed 1,2,3-benzodithiazolyls are of interest for contemporary materials science as potential building blocks in the design and synthesis of molecular magnets or/and molecular conductors.3,4 However, the instability of these radicals toward dioxygen, especially in solution, is a serious challenge. Despite the fact that several research groups have observed a fast transformation of radicals into diamagnetic species in solution upon the contact with air,1,3,5 only recently, the products have been identified unambiguously.6 It was established that the interaction between 4,6-di(tert-butyl)-1,2,3-benzodithiazolyl (2c) and O2 in hydrocarbon solution leads to the correspondingly substituted N,N′-disulfinyl-2,2′-diaminodiphenyl disulfide 4c in quantitative (∼100%) yield (Scheme 3).6
 | ||
| Scheme 3 | ||
The inhibition of radical oxidation based on the understanding of its chemistry is very important for the potential applications of 1,2,3-benzodithiazolyls in the materials science.
This work was performed both to confirm the formation of dinitrogen upon the photolysis of 1,3,2,4-benzodithiadiazines and to analyze a detailed mechanism of 1,2,3-benzodithiazolyls oxidation using the results of kinetic experiments and quantum chemical calculations. The aforementioned radical 2c was chosen as an object for detailed kinetic studies.
Experimental and computational details
Materials
1,3,2,4-Benzodithiadiazine (1a) and its 4,6-di(tert-butyl) (1c) derivative were synthesized as described in ref. 6 and 7.Methods
The ESR spectra were recorded on a Bruker EMX spectrometer (MW power 0.64 mW, modulation frequency 100 KHz, modulation amplitude 0.01 mT). The spectra were integrated and simulated using the Winsim v.1.0 program. The g-factors of radicals were measured using DPPH as a standard. The yields of radicals were determined to within ±10% by comparing the radical curve integrals with the curve integral of a single crystal of CuCl2·2H2O standard containing the known number of paramagnetic species.The thermolysis of the 10−3 M solutions of 1c in absolute squalane (2,6,10,15,19,25-hexamethyltetracosane) was performed in an ESR Teflon valve-equipped quartz ampoule degassed by three freeze–pump–thaw cycles. It was carried out in a glycerol thermostat in a temperature range of 110–150 °C with a temperature accuracy of ±0.5 °C. After exposure for some time at fixed temperature the sample was cooled to 20° and the ESR spectrum was measured.
The photolysis of the (5–10) × 10−4 M solutions of 1a,c in hexane was performed in a cylindrical quartz ampoule with a Teflon stopcock (for the detection of ESR and mass-spectra) degassed by the freeze–pump–thaw procedure repeated for 3–5 times. The electronic absorption spectra (EAS) were recorded in 2–10 mm quartz cells and oxygen was removed by bubbling argon through the solution for 20 min. The individual line (313 nm) of an Hg lamp (DRSh-500) equipped with a water filter was used. To isolate this line, a combination of glass filters (UVS-2 and ZhS-3) was employed. The EAS of photolysis products were collected by means of a Shimadzu UV-2401PC spectrophotometer. The ESR spectra of the photolysis products were recorded as described above.
To perform the oxidation of radicals 2, the preliminary deoxygenated and photolysed samples of 1 were saturated with dioxygen by intense bubbling of either air or O2 through solution for 3 min.
The dinitrogen by-product was detected by mass-spectrometry. After irradiation and detection of ESR spectrum, the ampoule (∼4 cm3) was connected to the evacuated volume of ca. 200 cm3. The reaction solution (1 cm3) was frozen with liquid nitrogen, thereafter the stopcock was opened and gases were passed to the intermediate evacuated volume. The procedure of melting and freezing was repeated 2–3 times to remove all gaseous products dissolved in the sample. The gas mixture in the intermediate volume was analyzed using a MX-1303 mass-spectrometer. The lines with m/z = 32 and m/z = 28 were used to measure O2 and N2, respectively. The sensitivity of the spectrometer was calibrated using the known amount of air in the intermediate volume.
Calculations
The DFT calculations8 on geometries and electronic structures of compounds of interest were performed at the (U)B3LYP9,10 level of theory with either 6-31G* or 6-311G** basis sets.11 All the structures were ascertained to be either minima or transition states (TS) on the potential energy surface (PES) by second derivative calculations. For Herz radicals (2), peroxyl radicals (5), and peroxide (6), the geometries were also optimized at the UHF/6-311G** level of theory. The single point energy calculations were carried out at the UMP2 level using the 6-311G** basis set (for radicals, also at the UMP3 and UMP4 levels). The EAS were calculated using the time-dependent DFT12,13 at the TD-B3LYP/6-311 + G** level. The GAUSSIAN-98 suit of programs14 was used in the calculations.Results
Detection of the gaseous by-products of photolysis
The formation of dinitrogen by photolysis of 1,3,2,4-benzodithiadiazines was tested as described in the experimental section. The kinetics of 1a photodecomposition was monitored by ESR spectroscopy and the yield of dinitrogen was measured after reaching a plateau on the kinetics.As already shown,1 the chemical yield of 2a radical upon photolysis of 1a precursor is close to unity (about 0.9). Taking into account this value and the experimentally measured amount of evolved dinitrogen, we estimated the chemical yield of N2 to be 0.29 ± 0.03. It is somewhat smaller than the expected value of 0.5 (Scheme 4). One of the reasons for this could be overestimation of the extent of 1a photodecomposition due to the low accuracy of the ESR method. Nevertheless, it is evident that the yield of dinitrogen is high enough to describe the main channel of the 1,3,2,4-benzodithiadiazines photodecomposition by Scheme 4. Most probably, the thermolysis of 1 can also be described in a similar way.
 | ||
| Scheme 4 | ||
Generation and characterization of Herz radical 2c
The sterically hindered 4,6-di(tert-butyl)-1,2,3-benzodithiazolyl 2c is the most appropriate object for an accurate kinetic study of Herz radicals oxidation. As in the case of parent 1,3,2,4-benzodithiadiazine 1a and a number of its derivatives,1 the thermolysis and photolysis of 4,6-di(tert-butyl)-1,3,2,4-benzodithiadiazine 1c release radical 2c in quantitative yield. The formation of radical 2c and its yield were evidenced by ESR spectroscopy (Fig. 1). The experimental hfc constants of the ESR spectrum of 2c are very close to those reported previously3,15,16 and agree fairly well with the values calculated at the UB3LYP/6-311G** level of theory (Fig. 1). The calculated molecular structure of 2c is shown in Fig. 2. Earlier, the radical 2c was detected by ESR in the course of mild thermolysis of 4,6,7a-tri(tert-butyl)-7aH-1,2,3-benzodithiazole15 or the reaction between 2,4,6-tri(tert-butyl)aniline and S2Cl2.16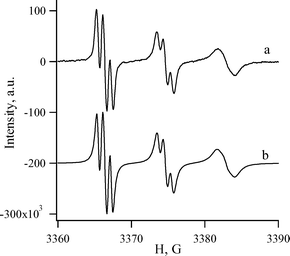 | ||
| Fig. 1 ESR spectrum of Herz radical 2c: (a) detected after 1 h heating of compound 1c at 145 °C in squalane, (b) simulated. Experimental (calculated by UB3LYP/6-311G**, S2 = 0.767 and S2 = 0.750 after annihilation) hfc constants (G) and g-factor: aN3 8.19 (6.26), aH5 0.71 (1.25), aH7 0.98 (1.50); g = 2.0077. Previously reported: aS1 3.69, aS2 4.51, aN3 8.21, aH5 0.75, aH7 0.95; g = 2.0076.3 | ||
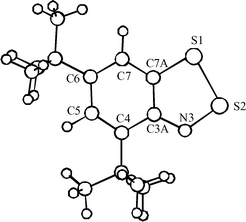 | ||
| Fig. 2 B3LYP/6-311G** geometry of Herz radical 2c (cf. parent 1,2,3-benzodithiazolyl 2a).1 Selected bond lengths (Å) and bond angles (°): C7A–S1 1.766, S1–S2 2.150, S2–N3 1.630, N3–C3A 1.350, C3A–C7A 1.420; C7A–S1–S2 89.9, S1–S2–N3 98.6, S2–N3–C3A 116.2. The hetero ring is perfectly planar. | ||
Fig. 3 displays changes in the EAS of compound 1c upon photolysis. Absorption in the long-wavelength spectral region decreases, and an intense sharp band with a maximum at 344 nm appears, which agrees well with the published EAS of the parent 1,2,3-benzodithiazolyl 2a.1,16 The calculated spectrum of 2a (solid bars) is in a very good agreement with the experimental spectrum (Fig. 3). Note that the time-dependent DFT reproduces well the experimental spectrum of the parent 1,3,2,4-benzodithiadiazine 1a too.1
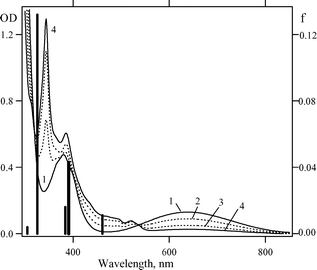 | ||
| Fig. 3 EAS of compound 1c (0.17 mM) in hexane (1) and its changes upon 313 nm photolysis for 5 min (2), 20 min (3) and 40 min (4). Positions and oscillator strengths (f) of the absorption bands of the unsubstituted 2a radical calculated by the time-dependent DFT (B3LYP/6-311 + G*) are depicted as solid bars. | ||
Kinetics of the reaction of Herz radical 2c with dioxygen
Previously,6 it was shown that radical 2c at room temperature in a concentrated (∼0.15 M) benzene solution reacts with dissolved O2 to give the correspondingly substituted N,N′-disulfinyl-2,2′-diaminodiphenyl disulfide 4c, i.e. a highly rearranged product of a 2 : 1 addition, in high yield (Scheme 3). The structure of 4c was confirmed by XRD,6 the obtained data were in full agreement with those published for 4c.17The kinetics of the decay of radical 2c was measured using EAS and ESR spectroscopies. In both cases the photolysis of the compound 1c was performed to generate radicals. The kinetics of the decay of 2c was recorded mainly using EAS at the maximum of a sharp absorption band of 2c (344 nm).
Fig. 4A shows that the kinetics of the decay of the Herz radical 2c can be described by eqn (I).
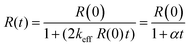 | (I) |
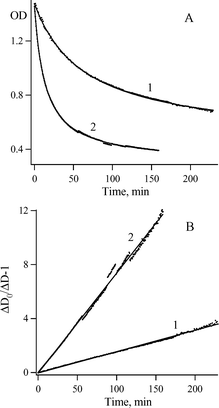 | ||
| Fig. 4 (A) Kinetics of the decay of radical 2c absorption at 344 nm (points) in hexane at ambient temperature and O2 concentration of 3.28 × 10−3 M (1) and 1.56 × 10−2 M (2), and their fitting (solid lines) to the equation: D(t) = D∞ + ΔD/(1 + αt). (B) Linear plots of ΔD0/ΔD(t) − 1 versus time. | ||
In eqn (I), R(0) and R(t) are the concentrations of 2c just after and at the moment t after dioxygen (or air) bubbling. In turn, Fig. 4B demonstrates the linear dependence in corresponding co-ordinates. Therefore, the decay of radical 2c is formally described by eqn (II) as the second-order self-termination reaction.
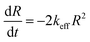 | (II) |
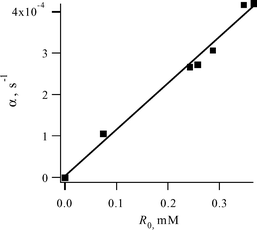 | ||
| Fig. 5 Concentration dependence of the fitting parameter α = 2keffR0 on the initial radical concentration R0 (solutions saturated with air). | ||
It was found (Fig. 4B) that the parameter α and the effective rate constant (keff) are proportional to the concentration of dissolved dioxygen. We used solutions saturated with both O2 (dioxygen concentration 1.56 × 10−2 M)18 and air (dioxygen concentration 4.8 times lower). Similar results were obtained (however with lower accuracy) by ESR recording of the radical decay kinetics.
All the peculiarities of the radical 2c decay can be reproduced assuming it to obey Scheme 5, with the equilibrium between 2c and the corresponding peroxyl (5c) shifted significantly to 2c. Under our experimental conditions, namely with significant excess of radical 2c, peroxyl 5c will react mainly with 2c giving the correspondingly substituted peroxide (6c) (Scheme 5, reaction (3)).
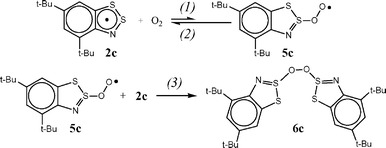 | ||
| Scheme 5 | ||
Under a quasi-stationary approximation for the concentration of peroxyl 5c (d[5c]/dt = 0), the kinetics of the decay of radical 2c will be described by eqn (III).
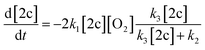 | (III) |
Therefore, if
| k2 ≫ k3[2c], | (IV) |
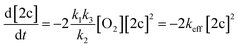 | (V) |
From the experimental value of keff/[O2], we determine k3K12 to be (1.7 ± 0.2) × 102 L2 mol−2 s−1. Assuming that the k3 rate constant of radical recombination is close to a typical value of ∼109 L mol−1 s−1, the equilibrium constant K12 could be estimated to be as low as ∼2 × 10−7 L mol−1. Therefore, reaction (1) (Scheme 5) is endothermic. In the case of normal pre-exponential factors for monomolecular reaction (2) (k20 ∼ 1013 s−1) and bimolecular reaction (1) (k10 ∼ 1011 L mol−1 s−1), the enthalpy of reaction (1) could be estimated very roughly as ∼7 kcal mol−1.
Note, that if k3 ∼ 109 L mol−1 s−1, eqn (IV) will turn into k2 ≫ 3 × 105 s−1. It is a reasonable assumption for the exothermic monomolecular reaction.
Discussion
Thus, according to our experimental results, the primary step in the oxidation of 1,2,3-benzodithiazolyls 2 is the formation of peroxyls 5 which is followed by their recombination with initial 2. The formation of 5 is endothermic and the equilibrium of this reaction is shifted significantly to the starting 2. This is the reason for the sufficiently long lifetime of the Herz radicals even in oxygenated solutions.This mechanism has analogy in the literature19–22 for related thiyl radicals. It is known that the interaction between the thiyl radicals RS˙ and O2 starts with a reversible formation of peroxyl radicals RSOO˙.19–22 The self-termination reaction resulting in the formation of short-lived tetroxides and reaction with initial thiyl radicals were accepted for peroxyl radicals.19,20 Under our experimental conditions, namely with significant excess of radical 2c, peroxyl radical 5c will react mainly with 2c to give the peroxide 6c (Scheme 5, reaction (3)). The latter is an isomer of the final product 4c.
To confirm our experimental findings and to propose the entire mechanism, we performed the quantum chemical calculations of the stationary points (intermediates and the TS) on the potential energy surface (PES) for the parent radical 2a oxidation. Since reaction (1) is a limiting stage of the Herz radical oxidation and its equilibrium is shifted significantly to the starting radicals, it is impossible to detect intermediates of the oxidation process experimentally, and calculations are the only way to support the mechanism proposed.
It was established that the DFT calculations8 with the B3LYP hybrid functional adequately reproduce many properties of the polysulfur-nitrogen heterocyclic systems including the geometries of free molecules (as compared with gas electron diffraction experiments),23,24 ESR and EAS spectra,1,2,5,25–28 as well as the IR spectra of matrix-isolated reaction intermediates.2 In the case of the conformationally flexible compounds 4 and 6, the reliability of B3LYP calculations is confirmed by the reasonable agreement between the calculated bond lengths and bond angles of 4a (Fig. 6A), and those from the experimental geometry of 4c.17 Therefore, the B3LYP method with 6-31G* basis set was used mainly to test the oxidation mechanism.
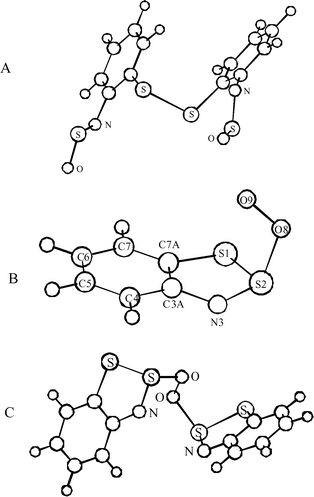 | ||
| Fig. 6 (A) Structure of N,N′-disulfinyl-2,2′-diaminodiphenyl disulfide 4a optimized at the B3LYP/6-31G* level. Selected calculated and experimental (for 4c, in parenthesis) bond lengths (Å) and bond angles (°): C–S 1.789 (1.784), S–S 2.140 (2.046), C–N 1.398 (1.430), N–S 1.555 (1.506), S–O 1.477 (1.448); C–S–S 105.0 (104.0), C–N–S 122.4 (129.3), N–S–O 112.4 (120.6). (B) Structure of the peroxyl radical 5a optimized at the UHF/6-311G** level (S2 = 0.763 and S2 = 0.750 after annihilation). Selected bond lengths (Å) and bond angles (°): C7A–S1 1.770, S1–S2 2.085, S2–N3 1.520, N3–C3A 1.390, C3A–C7A 1.390; O9–O8–S2 115.3, O8–S2–N3 111.5, S1–S2–N3 100.2, S2–N3–C3A 115.5, S1–S2–C7A 99.5. (C) Structure of the peroxide 6a optimized at the B3LYP/6-31G* level. Selected bond lengths (Å) and bond angles (°): C–S 1.768, S–S 2.154, S–O 1.826, O–O 1.426, N–S 1.561, C–N 1.394; C–S–S 89.8, S–S–N 99.6, N–S–O 114.3, S–S–O 111.3. | ||
However, at this level of theory, we were unable to optimize the structure of the key intermediate of Scheme 5, i.e. peroxyl radical 5a. The approach of the Herz radical 2a and O2 leads to a monotonous growth of the electronic energy (Eel), and at the typical S–O bond distance (∼1.7 Å) the Eel of the adduct is about 26 kcal mol−1 higher than that of the isolated species.
The structure of 5a was, however, optimized at the UHF level and found to have a typical S–O bond length of 1.74 Å (Fig. 6, B). According to these calculations, the spin density of 5a is localized mainly on the terminal oxygen atom (0.94) with only a small amount (0.09) associated with the O atom bonded to the sulfur atom. Reaction (1) was found to be endothermic, although the calculated enthalpy of this reaction seems to be unreasonably overestimated (62.8 kcal mol−1). Indeed, the single point energy calculations at UMP2, UMP3 and UMP4 levels with the 6-311G** basis set, at geometries optimized by the UHF method, reduced the calculated enthalpy to 26.5, 38.9, and 28.6 kcal mol−1, respectively. The latter values are in better agreement with the experiment.
The proposed product of the recombination of radicals 2a and 5a (peroxide 6a) is the isomer of the final product 4a. The structure of peroxide 6a (Fig. 6, C) was optimized at both the HF and B3LYP levels of theory. The calculated structures were found to be similar. However, the O–O, S–O and S–S bonds are noticeably longer for a structure optimized by the B3LYP method, than that optimized by the HF (1.426, 1.82, 2.15 Å and 1.379, 1.68, 2.08 Å, respectively).
To calculate the enthalpy of the reaction (3), we have performed geometry optimization and frequency calculation at the HF/6-311G** level, while the difference in electronic energy was calculated at the MP2 level. The calculated enthalpy of reaction (3) was found to be −58.3 kcal mol−1. Therefore reaction (3) is predicted to be strongly exothermal and the assumption that the rate constant of this reaction is typical of radical recombination is reasonable.
Two possible mechanisms can be considered for the transformation of intermediate peroxide 6a into the final product 4a (Scheme 6).
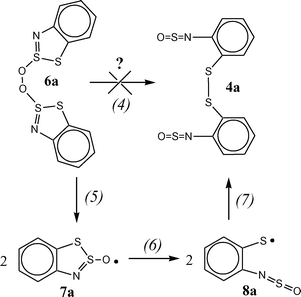 | ||
| Scheme 6 | ||
The first proposed pathway (4) is the [3,3] sigmatropic shift resembling the Cope rearrangement.29 The possibility of concerted reaction is supported by a qualitative analysis based on the frontier MO theory.30 For the cyclic TS of the Cope-like rearrangement of peroxide 6a into disulfide 4a, the [4 + 2] all-suprafacial process is allowed with the O–O σ-bond as 2-electron component and two degenerate S–S σ-bonds as 4-electron component. With this TS, the bonding σ-HOMO (O–O)–σ*-LUMO (S–S) interaction transforms the O–O single bond of 6a into the S–S single bond of 4a. However, our computational attempts to optimize the discussed TS have failed, which does not mean that reaction (4) is really impossible.
Nevertheless, we consider the second pathway (Scheme 6, reactions (5)–(7)) to be more plausible because it is similar to the previously studied reactions and all the steps proposed are thermodynamically favorable. In particular, the recombination of RS˙ and RSOO˙ radicals followed by the formation of RSO˙ radicals was proposed to rationalize the photooxidation of dimethylsulfide.19
The (U)B3LYP/6-31G* method was used to analyze the latter pathway. The O–O bond splitting in peroxide 6a with the formation of two 7a radicals (Scheme 6, reaction (5)) was predicted to be exothermal (ΔH = −32.7 kcal mol−1). The TS for reaction (5) was localized, and the enthalpy (ΔH#) and free energy (ΔG#) of activation were calculated to be 7.9 and 7.8 kcal mol−1, respectively, at 298 K. The predicted rate constant of this reaction, ∼107 s−1, is very high and consistent with the fact that no intermediates were detected for the radical 2c oxidation.
The unpaired electron in radical 7a is delocalized over both rings, heterocyclic and carbocyclic, and the spin density at the oxygen atom is negligibly small (Fig. 7). It is seen that the S–S bond in 7a is noticeably longer (2.37 Å) than that predicted for radical 2a (2.15 Å).
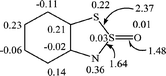 | ||
| Fig. 7 UB3LYP/6-31G* spin density distribution for the radical 7a (selected bond lengths (in Å) are also shown). | ||
The dissociation of this weak bond (Scheme 6, reaction (6)) leads to radical 8a with the reaction enthalpy being 7.8 kcal mol−1 only. In contrast to 7a, in isomeric 8a the unpaired electron is localized mainly on the sulfur atom (Fig. 8).
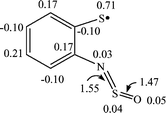 | ||
| Fig. 8 B3LYP/6-31G* spin density distribution for the radical 8a (selected bond lengths (in Å) are also shown). | ||
Recombination of the S-centered radicals 8a (Scheme 6, reaction (7)) yields the final product 4a. This self-termination reaction is exothermal (ΔH = −34.5 kcal mol−1) and its rate constant is likely to be close to a typical value of ∼109 L mol−1 s−1.
Conclusions
Thus, the photolysis of 1,3,2,4-benzodithiadiazines in hydrocarbon solutions yields dinitrogen and 1,2,3-benzodithiazolyls (Herz radicals). These radicals are stable in the absence of dioxygen. In the presence of dioxygen the Herz radicals undergo oxidation to the corresponding N,N′-disulfinyl-2,2′-diaminodiphenyl disulfides.The reaction between Herz radicals and dioxygen starts with a reversible formation of peroxyl radicals. A subsequent recombination of the latter with the initial Herz radicals affords peroxides which are isomers of the final disulfides. Most likely, the peroxide O–O bond dissociation followed by hetero ring-opening isomerization leads to the S-centered radicals of thiyl type whose recombination gives the final disulfides.
Intriguingly, the –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se
Se![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O function is still unknown despite the numerous attempts to prepare R–N
O function is still unknown despite the numerous attempts to prepare R–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se
Se![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O derivatives. These failures seem to reflect the function high instability. Generally, the Se–O bond is weaker (i.e. thermodynamically less attractive) than the S–O bond. Based on this, one can believe that it might be possible to suppress or at least to weaken the discussed interaction with dioxygen of the 2-Se counterparts of the Herz radicals (i.e. 1,2,3-benzothiaselenazolyls) little studied nowadays.3
O derivatives. These failures seem to reflect the function high instability. Generally, the Se–O bond is weaker (i.e. thermodynamically less attractive) than the S–O bond. Based on this, one can believe that it might be possible to suppress or at least to weaken the discussed interaction with dioxygen of the 2-Se counterparts of the Herz radicals (i.e. 1,2,3-benzothiaselenazolyls) little studied nowadays.3
Acknowledgements
The authors are grateful to Prof. Yuri N. Molin and Dr Viktor A. Bagryansky for helpful discussions. The financial support of this work by the Russian Foundation for Basic Research (project 04-03-32259), and the Division of Chemistry and Material Sciences of the Russian Academy of Sciences is also gratefully acknowledged.References
- I. V. Vlasyuk, V. A. Bagryansky, N. P. Gritsan, Yu. N. Molin, A. Yu. Makarov, Yu. V. Gatilov, V. V. Shcherbukhin and A. V. Zibarev, Benzodithiazolyl radicals formed by thermolysis and photolysis of 1,3,2,4-benzodithiadiazines, Phys. Chem. Chem. Phys., 2001, 3, 409–415 RSC.
- N. P. Gritsan, V. A. Bagryansky, I. V. Vlasyuk, Yu. N. Molin, A. Yu. Makarov, M. S. Platz and A. V. Zibarev, Intermediates of photolysis of 1,3,2,4-benzodithiadiazines studied by matrix isolation spectroscopy and quantum chemistry, Russ. Chem. Bull., 2001, 50, 2064–2070 CrossRef CAS.
- J. M. Rawson and G. D. McManus, Benzo-fused dithiazolyl radicals: from chemical curiosities to materials chemistry, Coord. Chem. Rev., 1999, 189, 135–168 CrossRef CAS.
- J. M. Rawson and F. Palacio, Magnetic properties of thiazyl radicals, Struct. Bonding, 2001, 100, 93–128 CAS.
- V. A. Bagryansky, I. V. Vlasyuk, Yu. V. Gatilov, A. Yu. Makarov, Yu. N. Molin, V. V. Shcherbukhin and A. V. Zibarev, Formation of stable 1,2,3-benzodithiazolyl radicals by thermolysis of 1,3,2,4-benzodithiadiazines, Mendeleev Commun., 2000, 5–7 CrossRef.
- A. Yu. Makarov, S. N. Kim, N. P. Gritsan, I. Yu. Bagryanskaya, Yu. V. Gatilov and A. V. Zibarev, Interaction of 1,2,3-benzodithiazolyls (Herz radicals) with dioxygen, Mendeleev Commun., 2005, 14–16 Search PubMed.
- A. W. Cordes, M. Hojo, H. Koenig, M. C. Noble, R. T. Oakley and W. T. Pennington, Aromatic and antiaromatic thiazyl heterocycles. Comparison of the structural, spectroscopic and cycloaddition properties of 1,3,2,4-benzodithiadiazine, C6H4S2N2, and 1,3,5,2,4-benzotrithiadiazepine, C6H4S3N, Inorg. Chem., 1986, 25, 1137–1145 CrossRef CAS.
- P. Geerlings, F. De Proft and W. Langenaeker, Conceptual density functional theory, Chem. Rev., 2003, 103, 1793–1873 CrossRef CAS.
- A. D. Becke, Density-functional thermochemistry: III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B., 1988, 37, 785–789 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Influence of polarization functions on MO hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–217 CrossRef CAS.
- M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, Molecular excitation energies to high-lying bound states from time-dependent density-functional response theory: characterization and correction of the time-dependent local density approximation ionization threshold, J. Chem. Phys., 1998, 108, 4439–4445 CrossRef CAS.
- K. B. Wiberg, R. E. Stratmann and M. J. Frisch, A time-dependent density functional theory study of the electronically excited states of formaldehyde, acetaldehyde and acetone, Chem. Phys. Lett., 1998, 297, 60–64 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98 (Revision A.9), Gaussian, Inc., Pittsburgh, PA, 1998 Search PubMed.
- Y. Inagaki, R. Okazaki and N. Inamoto, Chemistry of N-thiosulfinylanilines. I. Reactions of sterically hindered anilines with sulfur chlorides. Preparation of N-thiosulfinylanilines, Bull. Chem. Soc. Jpn., 1979, 52, 1998–2001 CAS.
- R. Mayer, G. Domschke, S. Bleisch, J. Fabian, A. Bartl and A. Stasko, 1,2,3-Dithiazolyle, eine neue Klasse persistenter Radicale, Collect. Czech. Chem. Commun., 1984, 49, 684–703 CAS.
- H. W. Roesky, K. L. Weber, M. Noltemeyer and G. M. Sheldrick, Ring Cleavage of a benzodithiazolium-chloride and X-ray structure analysis of 3,3′,5,5′-tetrakis-tert-butyl-2,2′-bissulfinylamino-1,1′-diphenyl-disulfide, Z. Naturforsch., B: Anorg. Chem. Org. Chem., 1984, 39, 163–166.
- A. N. Terenin, Photochemistry of Dyes and Related Organic Compounds, AN USSR, Moscow, 1947, pp. 128–129, in Russian Search PubMed.
- M. Tamba and G. Simone, and Quintiliani, Interaction of thiyl free radicals with oxygen: pulse radiolysis study, J. Radiat. Biol., 1986, 50, 595–600 Search PubMed.
- X. Zhang, N. Zhang, H.-P. Schuchmann and C. von Sonntag, Pulse radiolysis of 2-mercaptoethanol in oxygenated aqueus solution. Generation and reaction of the thiylperoxy radical, J. Phys. Chem., 1994, 98, 6541–6547 CrossRef CAS.
- E. Banchereau, S. Lacombe and J. Ollivier, Solution reactivity of thiyl radicals with molecular oxygen: unsensitized photooxidatiom of dimethyldisulfide, Tetrahedron Lett., 1995, 36, 8197–8200 CAS.
- Yu. Razskazovskii, A.-O. Colson and M. D. Sevilla, Nature of the thiyl peroxyl radical: ESR and ab initio MO evidence for intermolecular stabilization of the charge transfer state, RS+OO˙, J. Phys. Chem., 1995, 99, 7993–8001 CrossRef.
- F. Blockhuys, S. L. Hinchley, A. Yu. Makarov, Yu. V. Gatilov, A. V. Zibarev, J. D. Woollins and D. W. H. Rankin, Planar 1,3,2,4-benzodithiadiazine and its non-planar 5,6,7,8-tetrafluoro derivative: gas-phase structures studied by electron diffraction and ab initio calculations, Chem.–Eur. J., 2001, 7, 3592–3602 CrossRef CAS.
- A. R. Turner, F. Blockhuys, C. Van Alsenoy, H. E. Robertson, S. L. Hinchley, A. V. Zibarev, A. Yu. Makarov and D. W. H. Rankin, Causes of nonplanarity in fluorinated 1,3,2,4-benzopdithiadiazines: gas-phase electron diffraction, ab initio and DFT structures, Eur. J. Inorg. Chem., 2005, 572–581 CrossRef CAS.
- P. Kaszynski, Theoretical analysis of heteroaromatic thioaminyl radicals. Part 1: A comparison of ab initio and density functional methods in calculations of molecular geometry and isotropic hyperfine coupling constants, J. Phys. Chem. A, 2001, 105, 7615–7625 CrossRef CAS.
- P. Kaszynski, Theoretical analysis of heteroaromatic thioaminyl radicals. Part 2: A comparison of ab initio and density functional methods in the description of the redox processes, J. Phys. Chem. A, 2001, 105, 7626–7633 CrossRef CAS.
- Zienkiewicz, P. Kaszynski and V. G. Young, Experimental and theoretical studies of fused-ring persistent [1,2,4]thiadiazinyl radicals, J. Org. Chem., 2004, 69, 7525–7536 CrossRef CAS.
- J. Gassmann and J. Fabian, A density functional theory study of hyperfine structures of neutral S,N-heterocycles, Magn. Reson. Chem., 1996, 34, 913–920 CrossRef CAS.
- V. N. Staroverov and E. R. Davidson, The Cope rearrangement in theoretical retrospect, J. Mol. Struct. (THEOCHEM), 2001, 573, 81–89 CrossRef CAS.
- I. Fleming, Frontier Orbitals and Organic Chemical Reactions, Wiley, London, 1978, pp. 87–109 Search PubMed.
| This journal is © The Royal Society of Chemistry and Owner Societies 2006 |