Remotely powered distributed microfluidic pumps and mixers based on miniature diodes†
Suk Tai
Chang
a,
Erin
Beaumont
b,
Dimiter N.
Petsev
b and
Orlin D.
Velev
*a
aDepartment of Chemical & Biomolecular Engineering, North Carolina State University, 911 Partners Way, Raleigh, USA. E-mail: odvelev@ncsu.edu; Fax: +1-919-515-3465; Tel: +1-919-513-4318
bDepartment of Chemical & Nuclear Engineering and Centre for Biomedical Engineering, University of New Mexico, Albuquerque, USA
First published on 8th November 2007
Abstract
We demonstrate new principles of microfluidic pumping and mixing by electronic components integrated into a microfluidic chip. The miniature diodes embedded into the microchannel walls rectify the voltage induced between their electrodes from an external alternating electric field. The resulting electroosmotic flows, developed in the vicinity of the diode surfaces, were utilized for pumping or mixing of the fluid in the microfluidic channel. The flow velocity of liquid pumped by the diodes facing in the same direction linearly increased with the magnitude of the applied voltage and the pumping direction could be controlled by the pH of the solutions. The transverse flow driven by the localized electroosmotic flux between diodes oriented oppositely on the microchannel was used in microfluidic mixers. The experimental results were interpreted by numerical simulations of the electrohydrodynamic flows. The techniques may be used in novel actively controlled microfluidic–electronic chips.
Introduction
Manipulation of fluids, colloidal particles, or biomolecules on the microscale can be performed in integrated devices for sample pre-treatment and analyte detection. Such systems integrated in a single chip are known as micro-Total Analysis Systems (µTAS) or lab-on-a-chip devices.1–6 In comparison to conventional laboratory techniques, these miniaturized analysis systems are more flexible, allow easy automation and require significantly reduced samples sizes and analysis times. The precise control of fluid and particle transport inside the microfluidic channels is of paramount importance for the progress in their design and utilization.Reducing the channel dimensions to the micrometer scale results in a laminar flow, characterized by low Reynolds numbers (Re = Ud/ν, where U is the average flow velocity, d is the characteristic width of the channel and ν is the kinematic viscosity of the liquid). This means that the viscous forces dominate the fluid behaviour, while the inertial contribution is negligible.6,7 The laminar fluid motion makes operations like fluid pumping and solute mixing very challenging. Laminar flows normally lead to low Péclet number (Pe = Ud/D, where D is the molecular diffusivity), indicating that the solute transport is predominantly due to molecular diffusion.3,6–10 Hence, new tools for microfluidic flow control, manipulation and stirring are needed.
Mechanical pumps are not the best solution to overcome the viscous resistance of fluid flow in microchannels. A large external pump defies miniaturization and low energy consumption, which are among the main advantages of microfluidic devices.11,12 Alternatively, microfluidic flows have been driven by electroosmosis,13–15 piezoelectrics,11 internal pressure difference of liquid drops,12 thermal gradients,16,17 optically actuated pumps,18,19 or catalytic micropumps.20,21 Some of these micropumps, however, are difficult to fabricate because of their complex structures, whereas others are limited to a specific chemical solution. Alternating current (AC) field micropumps have been reported that create net flow over asymmetric electrode structures.22–27 An important advantage of using AC field is the minimization of electrolysis, which may occur during direct current (DC) electroosmosis.28AC electrohydrodynamic pumps, however, need complicated electrode micropatterns and can only operate in a limited range of AC frequencies.
Microfluidic mixing may be accomplished by passive or active mixers. The passive mixers guide the fluid flow through specially designed channels, where it is subjected to repeated splitting and recombination,29,30 chaotic advection in staggered herringbones9 or three-dimensional serpentine channels,31,32 and Dean flows in curvilinear or spiral channels.10,33 Passive mixers, however, require complex channel geometries and more importantly cannot be turned on and off on demand. In the active mixers the fluid is actuated using external energy, by miniature magnetic stirrers,34 ultrasonic actuation,35 electrowetting of droplets,36,37 and electrohydrodynamic flows.38–43 The moving components in some active mixers are difficult to fabricate and integrate into a microfluidic chip. A disadvantage of the electrohydrodynamic mixers is the difficulty of patterning complex electrode structures and heterogeneously charged surfaces inside the microchannels.
In our previous work,44 we demonstrated how diodes suspended in liquid can self-propel by local electroosmotic flow. We suggested on this basis a new approach for pumping liquids and controlling flow pattern in microchannels based on miniature diodes. These diodes are powered by an external AC field that is locally rectified into a DC field across the diode electrodes. This DC field gives rise to an electroosmotic flow in the liquid adjacent to the diode surface. The DC voltage (Vd) induced between the electrodes of the floating diode as a result of rectification of the external AC field (Eext) can be evaluated as
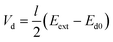 | (1) |
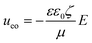 | (2) |
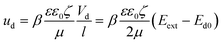 | (3) |
In this report, we present detailed results and discussion of the fluid pumping and flow pattern control using semiconductor diodes with an externally applied AC electric field. The diodes are immobilized alongside the channel walls and depending on their mutual orientation can operate as pumps or mixers. The parameters that govern the fluid flow are identified and their effects are analyzed quantitatively and modelled numerically.
Experimental
Fabrication of microfluidic channels
The microfluidic channels were fabricated in poly(dimethylsiloxane) (PDMS, Sylgard 184, Dow Corning) using soft lithography.47,48Channel masters were created by coating SU-8 2050 photoresist (MicroChem, Inc.) on a silicon wafer to a thickness of ca. 200 µm using a spin-coater (Model P6700, Specialty Coating Systems, Inc.). Then, the wafer was soft-baked on a hot plate. The procedure was repeated twice on the same wafer to obtain thicknesses of ca. 570 µm for the rectangular loop channel and ca. 590 µm for the Y-shaped mixer channel. The transparency photomasks with the channel printout were brought into contact with the SU-8 photoresist followed by a UV exposure (Model B-100A, BLAK-RAY). After a post-baking, the UV-exposed wafers were developed in an SU-8 developer solution (MicroChem, Inc.) and hard-baked.Two 1 mm-long silicon switching diodes (Part no. 1N4448HWTDICT-ND, Digi-key, Co.) were attached to the side wall of the channels using a 500 µm thick sticky rubber patch (Fig. 1). The PDMS was then cast on the masters and cured at 70 °C. Two holes were punched at the centre of the short channel sections in the PDMS layer containing the rectangular loop channel using a 16-gauge needle to inject fluids and connect electrodes. Similar inlet and outlet ports were also punched in the PDMS layer containing the Y-shaped channel. Finally, the polymerized PDMS replicas with the embedded diodes were irreversibly sealed to a PDMS film coated on the glass slides after pre-treatment by an air-plasma cleaner (Model PDC-32G, Harrick Plasma).
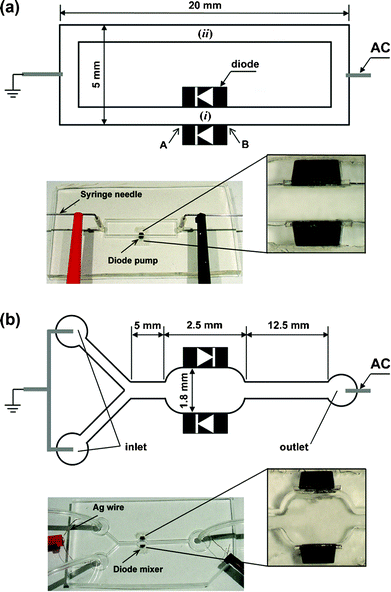 | ||
| Fig. 1 (a) Microfluidic device for diode pumping. Two 1 mm-long diodes were attached on the channel wall facing in the same direction for the diode pump. The electroosmotic flow driven by the diodes was monitored at point (i) between the diodes. The flow velocity of the pump was measured at the centre of the longer channel without diodes (ii), using tracing microspheres. (b) Microfluidic device for diode mixing. The two diodes were attached on the chamber wall facing in opposite directions. Milli-Q water and fluorescent dye solution were injected continuously into each inlet by a syringe pump. The mixing efficiency after applying the external AC field was monitored using a confocal microscope. The microchannels and diodes in both schematics are not to scale. | ||
Microfluidic pumping using diodes
Arranging two diodes in parallel orientation on both sides of the channel creates a micropump that is powered by the global AC field [Fig. 1(a)]. The resultant fluid motion was monitored by tracing a dispersion of 0.002 wt% 2 µm fluorescent sulfate-stabilized latex (Molecular Probes) in Milli-Q water at various pH values. The solutions also contained 10–4 wt% Tween-20 and 10–5 M NaCl. The rectangular loop channel of width ca. 300 µm was used for pH 5.0 and 7.3 solutions, while the pumping experiment at pH 6.0 was performed in a ca. 600 µm wide channel. The trace particle suspensions were injected into the chip through two syringe needles inserted in the access holes at the short channel sections. The AC electric field generated by a function generator (Model 33120A, Agilent) and amplifier (PZD 700, Trek) was applied through the syringe needles. The tracer particles' motion was monitored (i) between the two diodes and (ii) at the centre of the longer channel without diodes using an Olympus BX-61 microscope in reflection and fluorescence mode [Fig. 1(a)]. Time-lapse micrographs were taken using a 50× objective and high resolution Olympus DP-70 digital CCD camera. Two frames of the images were superimposed in Adobe Photoshop and then the distances travelled by each tracer particle were measured from their coordinates in the image.4 The particle velocities were then calculated by dividing the particle displacement by the time span between the two frames.Microfluidic mixing using diodes
The mixing chamber is created by embedding the diodes in an anti-parallel orientation in the walls of the microchannel [Fig. 1(b)]. Silver wire electrodes were placed into the ports of the Y-shaped channel. Rubber tubing (Norton Co.) was inserted into the inlet and outlet ports. The efficiency of microfluidic mixing in the diode chamber was characterized with a neutral fluorescent dye (Texas Red dye-labelled dextran conjugate) obtained from Molecular Probes. Milli-Q water and 10–4 M Texas Red solution, which were adjusted to pH 5.4 also containing 10–4 wt% Tween-20 and 10–5 M NaCl, were flowed into each of the inlet ports using a syringe pump (Model NE 1800, New Era Pump Systems, Inc.). The distribution of dye in the flows was measured by confocal microscopy using an FV 300 scanner attached to the Olympus BX-61 system.Results and discussion
Diode pumping
Macroscopic circulation in the closed rectangular channel was not observed in the absence of diodes on the wall under AC or DC fields because of the symmetry of the channel and the electrode placement – the electroosmotic force in the upper half of the rectangular channel loop is exactly balanced by the one in the lower half [see Fig. 1(a)]. The liquid in the loop channel far from the diodes, however, began circulating upon application of external AC electric fields of square wave-form, frequency 1 kHz and magnitude 20–80 V cm–1. The rectified DC field in the diode section leads to electroosmotic pumping. The equivalent circuit diagram is presented in our earlier publication.44 Intensive circulation is visible in the diode section, including the formation of two vortices between the diodes (see Movies 1 and 2 in the ESI†). These vortices are a result of the backpressure of the viscous liquid in the channel loop. As the electroosmotic force is present only at the diode surfaces, the bulk liquid between the diodes shows some degree of recirculation.The liquid in the closed rectangular loop began circulating through the channel once the external field applied was larger than the diode offset voltage (Fig. 2). The direction of the macroscopic circulation was the same as the direction of the local electroosmotic flows at the diode surfaces. The formation of bubbles by electrolysis at the diode electrodes was not observed under these experimental conditions. All flows driven by the diodes had a linear dependence on the applied AC electric fields (Fig 2). This flow direction depends on the pH and diode orientation. The effect of pH near the isoelectric point of the diode surface (pI ≈ 6.4, as estimated in our earlier work44) can be attributed to the change of the sign of the zeta potential at the diode–solution interface. The local electroosmotic motion on the diode surfaces at lower pH values (pH 5.0 and 6.0) was directed from the anode to the cathode of the diode [that is, from position B to A in Fig. 1(a)]. The liquid in the remaining part of the channel circulated in a clockwise direction [that is, from position A to B in Fig. 1(a)]. At a higher pH value (pH 7.3), however, the direction of the electroosmotic flow between the two diodes reversed, and the resulting circulation changed direction, shown as the negative velocities in Fig. 2.
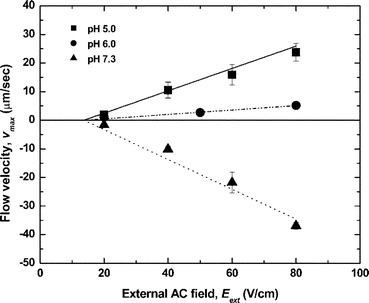 | ||
| Fig. 2 Flow velocities measured in the microfluidic loop channel at different pH values as a function of AC external field. The lines are plotted by the analytical solution of eqns (6) and (7) below with the zeta potential as the fitting parameter (ζ = +60 mV, +25 mV, –80 mV for pH = 5.0, 6.0, 7.3, respectively). | ||
The maximal experimental velocity of ca. 40 µm s–1 was obtained at an AC field of 80 V cm–1 at pH 7.3 (Fig. 2). The fluid velocity in the two vortices between the diodes also increased as the applied voltage increased (compare Movies 1 and 2 in the ESI†). The motion of tracer particles in the loop due to the macroscopic hydrodynamic flow driven by the diode pump is shown in Movie 3 in the ESI.†
Theoretical analysis of the diode pump
The interpretation of the data for the diode pump is based on a separate theoretical analysis of the pump region and the rest of the rectangular loop channel [see Fig. 1(a)]. In the following section, we first consider the electroosmotic vortex generation between the diodes and then the resulting macroscopic circulation in the remaining channel section.The diode pump with electroosmotic flow between a pair of the parallel-oriented diodes in low pH solutions is sketched in Fig. S1.† The electroosmotic flow between the two diodes is opposed by the viscous resistance of the fluid in the rest of the channel, which induces a counterpressure gradient across the diodes' ends. This results in the backflow in the middle of the channel between the diodes and the complex shape of the fluid velocity profile. This flow pattern is broadly similar to the electroosmotic flow combined with pressure-driven flow such as in closed tube electroosmosis.49–51
The counterpressure, ΔP, compensating for electroosmotic flow in a capillary is given by a balance of viscous and electrical body forces,50
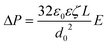 | (4) |
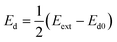 | (5) |
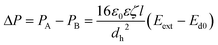 | (6) |
The pressure drop across the diode pump also creates pressure gradients through the whole channel, which give a rise to fluid motion. The fully developed velocity profile in a microchannel with rectangular cross-section is given by53,54
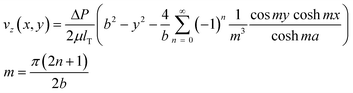 | (7) |
Introducing eqn (6) into eqn (7), we obtain a formula for the macroscopic flow profiles pumped by the diodes, which linearly depends on the external AC electric field. After substituting the physical parameters of the liquid phase, we plot the maximum velocity vz(0,0) with one fitting parameter – the zeta potential for each experimental condition (Fig. 2). The fitted zeta potential values are reasonable, as typical magnitudes of ζ are of the order of 100 mV or lower. The macroscopic flow velocities measured experimentally at position (ii) in Fig. 1(a) can be considered as fully developed because channel entrance effects are negligible. The theoretical calculations of the macroscopic flow induced by the diode pump are in good agreement with the experimental data (Fig. 2). The velocity of the liquid pumped by the diodes decreases as pH increases. Once pH exceeds the pI of the diode surface, the sign of the zeta potential reverses. The electroosmotic pressure gradient through the channel is in the opposite direction at this higher pH, resulting in the pumping in the reverse direction.
The efficiency of the diode pump presented here does not depend on the AC frequency. This was already verified in the study of self-propelling semiconductor diodes whose motility showed no correlation with the AC field frequency in the range from 10 Hz to 40 kHz. This is a major difference with the AC electrohydrodynamic pumps, which have an optimal range of frequencies (5–17 kHz for the maximum flow rate).23–27,44,55 The integration of our diode pumps into devices with microchannels may be simple and straightforward. Single miniature diodes can be used to locally pump and control fluids at specific positions in the chip, while multiple diodes in organized arrays with large surfaces may increase the power of the AC-driven pumps.
Numerical simulation of fluid flows in diode pumping
The diode-driven flow velocity distribution in the two-dimensional (2D) rectangular loop channel as shown in Fig. 1(a) was simulated to compare to the experimentally observed profile using the COMSOL Multiphysics 3.3 package (COMSOL, Burlington, MA) (see ESI† for details of the simulation).The computed flow profiles between the diodes at the channel wall for ζ = +60 mV and Eext = 80 V cm–1 are shown in Fig. S2(a).† The velocity vectors near the diode surfaces are oriented in the same direction, toward the cathodes of the diodes. The flow in the middle of the channel is in the reverse direction due to the loop channel counterpressure, which is in good agreement with the experimental flow pattern. However, there is a net flow in the direction of the electroosmotic flow since the flux at the diode walls is greater than the back flux in the centre. This net flow is conserved along the loop channel due to the fluid incompressibility and is exactly equal to the bulk flow rate far from the diodes. We observed a faster rate of vortex rotation between the diodes at the larger external fields during the pumping experiments. Similarly, the velocity of the reverse electroosmotic flow between the diodes in the simulations also increased with the magnitude of external AC field [Fig. S3(a)†].
The simulation results for the liquid motion in other channel sections confirm the presence of macroscopic circulation through the closed rectangular channel in the direction of the electroosmotic flow on the diode surfaces [Fig. S2(b)†]. The velocity of the circular flow pumped by the diodes obtained in the simulations is plotted as a function of the external electric field in Fig. S3(b).† The simulated velocity of the circulation also shows a linear dependence on the external AC field, in correlation with our experimental measurements, with slightly lower values than the experimental data. This discrepancy of the velocities might come from the restriction of this simulation to 2D domains. Nevertheless, the simulation results are in a good agreement with the experimental data and support the mechanism of pumping driven by the localized electroosmotic flow engendered by the diodes.
Diode mixing experimental results
The flow that developed down the Y-shaped channel in Fig. 1(b) was laminar in the absence of AC field and only subject to mixing by molecular diffusion across the interface. When an AC electric field was applied, the two streams between the diodes formed a vortex that led to intensive mixing. The origin of the transverse flow within the diode mixing chamber is schematically shown in Fig. 3(a). The combination of pressure and electroosmotic flows creates a vortex inside the diode mixer, dramatically improving the mixing efficiency. The active stirring flow led to larger interfacial area between two laminar flows, which reduced the mixing time for a given fluid volume.9,34 A series of typical confocal microscope images of fluid motion inside the diode mixer under the AC field is presented in Fig. 3(b). The dynamics of the process is well visualized in Movie 4 in the ESI.†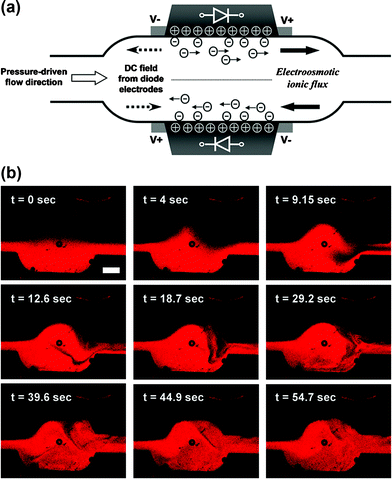 | ||
| Fig. 3 Microfluidic mixing in the channel with two oppositely oriented embedded diodes. (a) Schematic of the generation of the localized electroosmotic flow in the diode mixer. Two oppositely directed ionic fluxes on the diode surfaces create crossover flows leading to mixing inside the chamber. The diodes and channel geometry are not to scale. (b) Typical confocal micrographs of the microfluidic flows in the diode mixer, after an AC external field was applied through the channel at t = 0 s. See also Movie 4 in the ESI.† The AC external field applied was 133 V cm–1 and 1 kHz. The scale bar in (b) is equal to 500 µm. | ||
The efficiency of the diode mixer was characterized from the confocal micrographs collected in the microchannel downstream of the Y-junction. The channel cross-sectional images were converted into grayscale, representing the concentration distributions of the fluorescent dye in the channel. The fluorescence intensities were analyzed using image analysis software supplied with the confocal microscope. The micrographs at a distance of 2.5 mm after the diode mixer showed that the two streams in the channel were clearly separated before applying the AC external field, while the red fluorescent colour was almost uniformly distributed through the channel after the AC field was turned on. The fluorescence intensity averaged across the channel width obtained from the confocal micrographs confirmed that the vortex flow induced by the diodes increased the mixing of two laminar flows, as shown in Fig. 4(a).
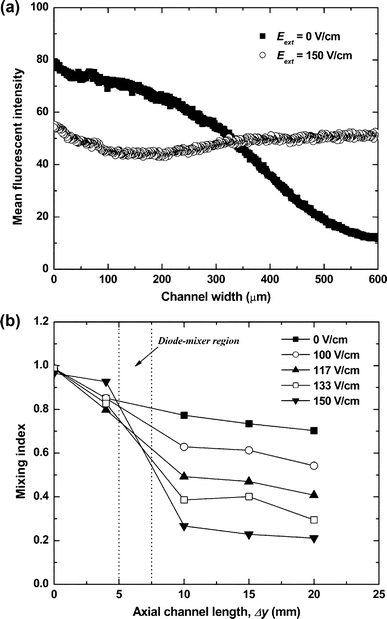 | ||
| Fig. 4 (a) Mean fluorescence intensity of the confocal images for the distribution of neutral fluorescent dye in the cross-section of the channel at a distance of 2.5 mm from the diode mixer at Eext = 0 and 150 V cm–1. (b) Mixing index at different AC fields calculated as a standard deviation of fluorescence intensity in cross-sectional confocal images as a function of the distance from the Y-shaped channel junction. All experimental conditions are the same as in Fig. 3. | ||
The degree of mixing was evaluated with a mixing index calculated as the standard deviation of the fluorescence intensity in the experimental confocal images,34
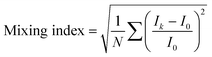 | (8) |
The channel length necessary to obtain the same mixing index by pure diffusion only (Pe ≈ 1.2 × 103 for the molecular diffusivity of fluorescent dye, D ≈ 10–10 m2 s–1 from the literature34,41), would be Δymix ≈ Pe × l = 68 cm. The experimental data in Fig. 4(b) demonstrate nearly complete mixing within 2 cm from the position of the diode mixer. The diode-driven microfluidic mixing is strongly dependent on the overall flow rate through the device. As the pressure-driven flow velocity increased, the mixing efficiency decreased (Fig. S4†). This is not surprising because at higher flow rates the fluid spends less time in the mixing chamber. The present diode mixer is very effective for laminar flows with a low Péclet number (Pe < 2.2 × 103). For comparison, most passive mixers operate well at high Péclet number flows (Pe > 104).9,10,41 The diode mixer efficiency can be improved at high flow speeds by fabricating a series of diode mixers on the channel or reducing the channel dimensions. All mixers can be conveniently and rapidly turned on and off remotely, but switching on and off the AC field.
Numerical simulation of the diode mixing process
The electroosmotic flow from diodes with opposite orientation leading to the mixing was also studied by numerical simulations using the COMSOL software (see the ESI† for details of the simulation). The concentration distributions of uncharged species and the flow profiles were calculated in the 2D projection of the microchannel [see Fig. 1(b)].The simulated concentration distributions and stirring flow profile within the diode mixer at an external AC field of 133 V cm–1 are shown in Fig. 5. Movies of a dynamic simulation for mixing driven by the diodes along the whole length of the channel and in the mixing chamber are available in the ESI† (Movies 5 and 6). The well homogenized solutions flow downstream from the diode mixer [top image of Fig. 5(a)]. At early mixing times, transverse fluid components arise at the diode mixer driven by the up-cross flow toward accelerated flow region [bottom images of Fig. 5(a)]. The resulting vortex leads to mixing within the diode chamber. The velocity vectors in the diode mixer provide further details of the oppositely directed electroosmotic flows on each diode surface and the convective mass transfer across the interface of the two laminar flows in Fig. 5(b). The images and movies of the experiment and simulation for the mixing are well correlated and confirm that the miniature diodes can significantly enhance the micromixing in a simple device that operates on demand under an external AC field, without any additional moving components or complex channel structures. The mixing efficiency can be increased further by using multiple diodes generating flows with different directions, dimensions and intensities, resulting in chaotic-like flow patterns.
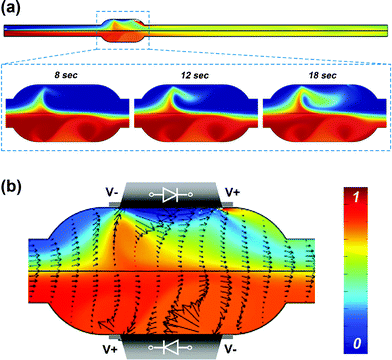 | ||
| Fig. 5 Simulations of the mixing process in a microchannel with oppositely oriented diodes. (a) Concentration distribution in the whole microchannel (top); a series of mixing images within the diode chamber after initial times (bottom). (b) Computed steady-state flow profile and concentration distribution within the diode mixer at 300 s. The magnitudes of the velocity vector are represented by the length of the arrows. Colours show the concentration distribution. The results confirm the creation of crossover flows resulting in enhancement of microfluidic mixing. See also ESI Movie 5 for the mixing in the whole channel and Movie 6 for the mixing inside the diode mixer.† | ||
Conclusions
The new class of electrohydrodynamic techniques presented here allows manipulation of fluids on the microscale by on-chip integration of microfluidic and electronic components. The results prove that oriented diodes placed at specific locations in a microfluidic network enable facile and controllable pumping or mixing under an external AC field. The theoretical model and the numerical simulations for the electrohydrodynamic flows and material transportation in the microchannel systems were in good agreement with the experimental data. The technique and the results from the theoretical and numerical analysis can be used to design and operate new types of microfluidic chips and µTAS devices for injection, mixing and separation of colloidal particles, proteins, DNA, or cells. The miniature diodes can de used in distributed local pumps and mixers in dynamically reconfigurable chips. They can be easily combined with detection and analysis components and simultaneously powered by a global AC electric field.Acknowledgements
The authors acknowledge the support of this study from the Defence Advanced Research Projects Agency (DARPA/AFSOR), NSF-CAREER (CTS-0238636), NSF/NIRT (CTS-0404124 and CBET-0609087), NSF/PREM (DMR 0611616) and the W. M. Keck Foundation. We thank Yong-Jae Choi and Dr Tzy-Jiun Mark Luo for access to the plasma cleaner for microchannel fabrication.References
- D. R. Reyes, D. Iossifidis, P.-A. Auroux and A. Manz, ‘Micro Total Analysis Systems. 1. Introduction, Theory, and Technology’, Anal. Chem., 2002, 74, 2623–2636 CrossRef CAS.
- S. C. Jakeway, A. J. de Mello and E. L. Russell, ‘Miniaturized total analysis systems for biological analysis’, Fresenius’ J. Anal. Chem., 2000, 366, 525–539 CrossRef CAS.
- A.-L. Liu, F.-Y. He, K. Wang, T. Zhou, Y. Lu and X.-H. Xia, ‘Rapid method for design and fabrication of passive micromixers in microfluidic devices using a direct-printing process’, Lab Chip, 2005, 5, 974–978 RSC.
- K. H. Bhatt, S. Grego and O. D. Velev, ‘An AC electrokinetic technique for collection and concentration of particles and cells on patterned electrodes’, Langmuir, 2005, 21, 6603–6612 CrossRef CAS.
- G. M. Whitesides, ‘The origins and the future of microfluidics’, Nature, 2006, 442, 368–373 CrossRef CAS.
- T. M. Squires and S. R. Quake, ‘Microfluidics: Fluid physics at the nanoliter scale’, Rev. Mod. Phys., 2005, 77, 977–1026 CrossRef CAS.
- J. Atencia and D. J. Beebe, ‘Controlled microfluidic interfaces’, Nature, 2005, 437, 648–655 CrossRef CAS.
- N.-T. Nguyen and S. T. Wereley, Fundamentals and Applications of Microfluidics, Artech House, Boston, 2002, ch. 2 Search PubMed.
- A. D. Stroock, S. K. W. Dertinger, A. Ajdari, I. Mezić, H. A. Stone and G. M. Whitesides, ‘Chaotic mixer for microchannels’, Science, 2002, 295, 647–651 CrossRef CAS.
- A. P. Sudarsan and V. M. Ugaz, ‘Multivortex micromixing’, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7228–7233 CrossRef CAS.
- H. Andersson, W. Wijingaart, P. Nilsson, P. Enoksson and G. Stemme, ‘A valve-less diffuser micropump for microfluidic analytical systems’, Sens. Actuators, B, 2001, 72, 259–265 CrossRef.
- G. M. Walker and D. J. Beebe, ‘A passive pumping method for microfluidic devices’, Lab Chip, 2002, 2, 131–134 RSC.
- D. C. Duffy, O. J. A. Schueller, S. T. Brittain and G. M. Whitesides, ‘Rapid prototyping of microfluidic switches in poly(dimethyl siloxane) and their actuation by electro-osmotic flow’, J. Micromech. Microeng., 1999, 9, 211–217 CrossRef CAS.
- D. Ross, T. J. Johnson and L. E. Locascio, ‘Imaging of electroosmotic flow in plastic microchannels’, Anal. Chem., 2001, 73, 2509–2515 CrossRef CAS.
- C.-H. Chen and J. G. Santiago, ‘A planar electroosmotic micropump’, J. Microelectromech. Syst., 2002, 11, 672–683 CrossRef CAS.
- M. A. Burns, C. H. Mastrangelo, T. S. Sammorco, F. P. Man, J. R. Webster, B. N. Johnson, B. Foerster, D. Jones, Y. Fields, A. R. Kaiser and D. T. Burke, ‘Microfabricated structures for integrated DNA analysis’, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 5556–5561 CrossRef CAS.
- D. E. Kataoka and S. M. Troian, ‘Patterning liquid flow on the microscopic scale’, Nature, 1999, 402, 794–797 CrossRef CAS.
- A. Terray, J. Oakey and D. W. M. Marr, ‘Microfluidic control using colloidal devices’, Science, 2002, 296, 1841–1844 CrossRef CAS.
- J. Leach, H. Mushfique, R. Leonardo, M. Padgett and J. Cooper, ‘An optically driven pump for microfluidics’, Lab Chip, 2006, 6, 735–739 RSC.
- T. R. Kline, W. F. Paxton, Y. Wang, D. Velegol, T. E. Mallouk and A. Sen, ‘Catalytic micropumps: Microscopic convective fluid flow and pattern formation’, J. Am. Chem. Soc., 2005, 127, 17150–17151 CrossRef CAS.
- W. F. Paxton, P. T. Baker, T. R. Kline, Y. Wang, T. E. Mallouk and A. Sen, ‘Catalytically induced electrokinetics for motors and micropumps’, J. Am. Chem. Soc., 2006, 128, 14881–14888 CrossRef CAS.
- A. Ajdari, ‘Pumping liquids using asymmetric electrode arrays’, Phys. Rev. E, 2000, 61, R45–R48 CrossRef CAS.
- A. B. D. Brown, C. G. Smith and A. R. Rennie, ‘Pumping of water with ac electric fields applied to asymmetric pairs of microelectrodes’, Phys. Rev. E, 2000, 63, 016305.
- S. Debesset, C. J. Hayden, C. Dalton, J. C. T. Eijkel and A. Manz, ‘An AC electroosmotic micropump for circular chromatographic applications’, Lab Chip, 2004, 4, 396–400 RSC.
- V. Studer, A. Pépin, Y. Chen and A. Ajdari, ‘An integrated AC electrokinetic pump in a microfluidic loop for fast and tunable flow control’, Analyst, 2004, 129, 944–949 RSC.
- M. Z. Bazant and T. M. Squires, ‘Induced-charge electrokinetic phenomena: Theory and microfluidic applications’, Phys. Rev. Lett., 2004, 92, 066101 CrossRef.
- M. Z. Bazant and Y. Ben, ‘Theoretical prediction of fast 3D AC electroosmotic pumps’, Lab Chip, 2006, 6, 1455–1461 RSC.
- I. Rodríguez and N. Chandrasekhar, ‘Experimental study and numerical estimation of current changes in electroosmotically pumped microfluidic devices’, Electrophoresis, 2005, 26, 1114–1121 CrossRef CAS.
- N. Schwesinger, T. Frank and H. Wurmus, ‘A modular microfluid system with an integrated micromixer’, J. Micromech. Microeng., 1996, 6, 99–102 CrossRef CAS.
- C.-C. Hong, J.-W. Choi and C. H. Ahn, ‘A novel in-plane passive microfluidic mixer with modified Tesla structures’, Lab Chip, 2004, 4, 109–113 RSC.
- R. H. Liu, M. A. Stremler, K. V. Sharp, M. G. Olsen, J. G. Santiago, R. J. Adrian, H. Aref and D. J. Beebe, ‘Passive mixing in a three-dimensional serpentine microchannel’, J. Microelectromech. Syst., 2000, 9, 190–197 CrossRef.
- D.-S. Kim, S.-H. Lee, T.-H. Kwon and C. H. Ahn, ‘A serpentine laminating micromixer combining splitting/recombination and advection’, Lab Chip, 2005, 5, 739–747 RSC.
- A. P. Sudarsan and V. M. Ugaz, ‘Fluid mixing in planar spiral microchannels’, Lab Chip, 2006, 6, 74–82 RSC.
- K. S. Ryu, K. Shaikh, E. Goluch, Z. Fan and C. Liu, ‘Micro magnetic stir-bar mixer integrated with parylene microfluidic channels’, Lab Chip, 2004, 4, 608–613 RSC.
- J. C. Rife, M. I. Bell, J. S. Horwitz, M. N. Kabler, R. C. Y. Auyeung and W. J. Kim, ‘Miniature valveless ultrasonic pumps and mixers’, Sens. Actuators, A, 2000, 86, 135–140 CrossRef.
- P. Paik, V. K. Pamula and R. B. Fair, ‘Electrowetting-based droplet mixers for microfluidic systems’, Lab Chip, 2003, 3, 253–259 RSC.
- F. Mugele, J. C. Baret and D. Steinhauser, ‘Microfluidic mixing through electrowetting-induced droplet oscillations’, Appl. Phys. Lett., 2006, 88, 204106 CrossRef.
- A. D. Strook, M. Weck, D. T. Chiu, W. T. S. Huck, P. J. A. Kenis, R. F. Ismagilov and G. M. Whitesides, ‘Patterning electroosmotic flow with patterned surface charge’, Phys. Rev. Lett., 2000, 84, 3314–3317 CrossRef CAS.
- D. Erickson and D. Li, ‘Influence of surface heterogeneity on electrokinetically driven microfluidic mixing’, Langmuir, 2002, 18, 1883–1892 CrossRef CAS.
- J.-K. Chen and R.-J. Yang, ‘Electroosmotic flow mixing in zigzag microchannels’, Electrophoresis, 2007, 28, 975–983 CrossRef CAS.
- N. Sasaki, T. Kitamori and H.-B. Kim, ‘AC electroosmotic micromixer for chemical processing in a microchannel’, Lab Chip, 2006, 6, 550–554 RSC.
- M. H. Oddy, J. G. Santiago and J. C. Mikkelsen, ‘Electrokinetic instability micromixing’, Anal. Chem., 2001, 73, 5822–5832 CrossRef CAS.
- A. O. E. Moctar, N. Aubry and J. Batton, ‘Electro-hydrodynamic micro-fluidic mixer’, Lab Chip, 2003, 3, 273–280 RSC.
- S. T. Chang, V. N. Paunov, D. N. Petsev and O. D. Velev, ‘Remotely powered self-propelling particles and micropumps based on miniature diodes’, Nat. Mater., 2007, 6, 235–240 CrossRef CAS.
- B. G. Streetman, Solid State Electronic Devices, Prentice Hall, New Jersey, 3rd edn, 1990, ch. 6 Search PubMed.
- R. J. Hunter, Foundations of Colloid Science, Oxford University Press, New York, 2001, ch. 8 Search PubMed.
- D. C. Duffy, J. C. McDonald, O. J. A. Schueller and G. M. Whitesides, ‘Rapid prototyping of microfluidic systems in poly(dimethylsiloxane)’, Anal. Chem., 1998, 70, 4974–4984 CrossRef CAS.
- J. C. McDonald, D. C. Duffy, J. R. Anderson, D. T. Chiu, H. Wu, O. J. A. Schueller and G. M. Whitesides, ‘Fabrication of microfluidic systems in poly(dimethylsiloxane)’, Electrophoresis, 2000, 21, 27–40 CrossRef CAS.
- P. Dutta and A. Beskok, ‘Analytical solution of combined electroosmotic/pressure driven flows in two-dimensional straight channels: Finite Debye layer effects’, Anal. Chem., 2001, 73, 1979–1986 CrossRef CAS.
- R. J. Hunter, Zeta Potential in Colloid Science: Principles and Applications, Academic Press, London, 1981, ch. 3 Search PubMed.
- P. M. Reppert and F. D. Morgan, ‘Frequency-dependent electroosmosis’, J. Colloid Interface Sci., 2002, 254, 372–383 CrossRef CAS.
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport Phenomena, John Wiley & Sons, Inc., New York, 2nd edn, 2002 Search PubMed.
- R. K. Shah and A. L. London, Laminar Flow Forced Convection in Ducts, Academic Press, London, 1979 Search PubMed.
- G. M. Walker, in Encyclopedia of Medical Devices and Instruments, ed. J. G. Webster, Wiley, Hoboken, 2nd edn, 2006 Search PubMed.
- O. D. Velev and K. H. Bhatt, ‘On-chip micromanipulation and assembly of colloidal particles by electric fields’, Soft Matter, 2006, 2, 738–750 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Movies of tracer particle motion in a diode pump system and of microfluidic mixing driven by diodes. Figures of flow velocity obtained from numerical simulations for diode pumping and mixing index at various pressure-driven flow rates. See DOI: 10.1039/b712108c |
| This journal is © The Royal Society of Chemistry 2008 |
