Luminescent boracite-like metal–organic frameworks constructed by Cu-centered CuCu₄ tetrahedra and CuCu₃ triangles with an acentric cubic superlarge cell

Abstract

Solvothermal treatment of copper halides and 3-amino-5-mercapto-1,2,4-triazole (H₂amtz) produced three isostructural complexes [Cu₃₁X₄(H_1.55amtz)₂₄](SO₄)₈·xDMF [X = Cl, Br and I, x ∼ 32], which show 3-D networks with bor topology constructed by Cu-centered CuCu₄ tetrahedra and CuCu₃ triangles with an acentric cubic superlarge cell.

---

Metal–organic frameworks (MOFs) have attracted much attention due to their potential as functional materials.¹ One of the main aims in this field is to mimic topological types of natural minerals via replacement of elements and bonds with molecular building blocks and organic linkers, respectively. Up to now, most structural prototypes such as 4-connected diamond, NbO, PtS, and 6-connected α-Po have been successfully imitated in MOFs.^2,3 Compared to above structural types, boracite-like topological type is rarely found in 3-D frameworks,⁴ even though its uncommon (3,4)-connected net, in which triangular nodes and tetrahedral nodes are alternately arranged with ratio of triangular to tetrahedral nodes being 4 : 3, has been known. To our knowledge, only one boracite-like (bor in RCSR) topological metal–organic framework [Cu₃(tpt)₄](ClO₄)₃ (tpt = 2,4,6-tri(4-pyridyl)1,3,5-triazine) has been reported, which shows a twofold interpenetrated structure.^4a The reason for limited bor topological structure in MOFs could be attributed to the difficulty in not only the requirement for geometries of 3-and 4-connected nodes but also the control over the alternative arrangement of 3-and 4-connected nodes.⁵ For example, if the 3-connected node is connected not to three 4-connected nodes but to a 4-connected node and two 3-connected nodes, this will result in the network with jph topology;^5d while the alternative arrangement of 3-connected triangles and 4-connected square nodes will result in the network with twist boracite topology.^5a

On the other hand, metal cluster entities as secondary building units (SBUs) have been proved to be an effective and powerful synthetic strategy in constructing novel MOFs,⁶ especially those with highly connected topologies.⁷ The SBUs, as structural and functional carriers, are responsible for unique properties of MOFs. i.e. luminescence, magnetism and catalysis. For example, polynuclear Cu(I) halides that often show brightly luminescence even at ambient temperature affected by structure and environment, relating to closed-shell copper(I)⋯copper(I) interactions,^1d,8 have been widely chosen as SBUs to construct luminescent high-dimensional coordination networks.⁹ In particular, by using this strategy, we have reported 12-connected face centered cubic (fcu)^10a and 14-connected body centered cubic (bcu) metal–organic frameworks via the assembly of the 4-pyridine thione and Cu(I) halides,^10b in which Cu₆S₄ and nanosized chiral Cu₁₉I₄S₁₂ clusters act as nodes, respectively. What is more, the latter crystallizes in the cubic chiral space group and shows strong red emission at ambient temperature. Evoked by the coordination chemistry of 1,2,4-triazole,¹¹ the ligand 3-amino-5-mercapto-1,2,4-triazole (H₂amtz) has been chosen to generate novel Cu(I)-cluster based MOFs with mineral prototypes and functionalities. Herein, we report the syntheses and structures of three isostructural and luminescent MOFs with bor topology constructed by Cu-centered CuCu₄ tetrahedra and CuCu₃ triangles.

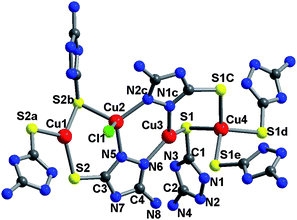
The reaction of H₂amtz with copper halides in N,N′-dimethylformamide (DMF) solution yields yellow cubic crystals of [Cu₃₁X₄(H_1.55amtz)₂₄](SO₄)₈·xDMF [X = Cl, Br, I in 1, 2, and 3, x ∼ 32]. Single-crystal X-ray diffraction analysis‡ reveals that 1 crystallizes in acentric cubic space group F4̄3c, and there are crystallographically independent four Cu(I) sites, one chloride and two Hamtz groups (Fig. 1). All atoms localize in general positions except for Cu(1), Cu(4) and Cl(1). Charge balance indicates that each H₂amtz group deprotonates 0.45 hydrogen atom. The Cu(1) and Cl(1) localize at the three-fold axis with site occupancy of 1/3 while the Cu(4) lies at fourfold inversion axis with site occupancy of 0.25. Cu(1) adopts a triangular coordination geometry, coordinated by three S(2) atoms from three different Hamtz groups with Cu(1)–S(2) distance of 2.2869(16) and 2.2869(17) Å and S–Cu(1)–S bond angles of 119.222(17)°. The Cu(2) shows a distorted CuN₂SCl tetrahedral geometry; Cu(3) adopts a CuN₂S trigonal geometry. Cu(4) closely shows a perfect tetrahedron geometry, ligated by four S(1) atoms with Cu(4)–S(1) distance of 2.4065(15) Å and S–Cu(4)–S angles of 108.24(7) and 110.09(3)°. The Cl(1) atom in 1 adopts a μ₃-mode to connected three Cu(2) with Cu(2)–Cl(1) distance of 2.6015(18) Å and Cu(2)–Cl(1)–Cu(2) angles of 94.92(7)°.

Fig. 1 The coordination environment of Cu(I) sites in 1.

The SBUs in 1 are tetranuclear cuprous clusters (Cu₄Cl) and pentanuclear clusters (Cu₅) (Fig. 2). The former is constructed by triangular shell of three Cu(2) and centered Cu(1) while the latter is built of tetrahedral shell of four Cu(3) and centered Cu(4). The Cu(1)⋯Cu(2) and Cu(4)⋯Cu(3) distances are 2.7858(13) and 2.7175(9) Å, respectively, which are smaller than twice the van der Waals radius of Cu(I) (2.8 Å),¹² indicating the existence of Cu⋯Cu interactions. Each Cu₄Cl cluster is connected to three Cu₅ clusters via six Hamtz groups while each Cu₅ cluster is linked to four Cu₄Cl clusters via eight Hamtz groups, which results in a 3-D MOF (Fig. S2†).

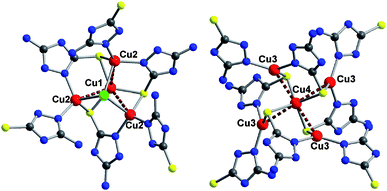Fig. 2 The representation of a tetranuclear cuprous cluster (left) and a pentanuclear cluster (right).

Better insight into the structure of 1 can be achieved by topological analysis. As shown in Fig. 3a, Cu₄Cl and Cu₅ clusters are simplified as a Cu-centered triangle and a tetrahedron, respectively. This results in an infinite (3,4)-connected three-dimensional non-interpenetrating network with bor topology and Schläfli symbol of (6².8⁴)₃(6³)₄. Generally, to achieve the (3,4)-connected net, one of the best approaches is to choose triangular organic ligands as the triangular nodes and metal carboxylate molecular building blocks (MBBs) or metal centers with a low coordination number such as Zn(II), Cu(I) and Co(II) as 4-connected nodes.^4,5 In 1 Cu₄Cl and Cu₅ clusters act as triangular nodes and 4-connected nodes, respectively, which is uncommon in (3,4)-connected networks and has not been documented prior to this work.^4,5 As the character of bor net, the cage [(Cu₅)₆(Cu₄)₄] shows a regular octahedral geometry (Fig. 3b), in which six tetrahedra localize at corners of an octahedron while four triangles are situated on alternate triangular faces of the octahedron. The cage is filled in situ generated sulfate ions that are formed through the desulfurization of H₂amtz followed by an oxidation process.^10,13 If octahedral [(Cu₅)₆(Cu₄)₄] cages are used as supramolecular building blocks,¹⁴ the structure of 1 will become an α-Po topological network with 3D intersected channels that have large internal surface area but small window. Sulfates and DMF molecules are filled inside the channels.

Fig. 3 The simplified 3-D network with bor topology (a), and the [(Cu₅)₆(Cu₄)₄] cage with octahedral geometry (b). Red tetrahedra and blue triangles represent Cu₅ and Cu₄Cl clusters, respectively.

The total potential solvent area volume is 19 779.3 ų per unit cell, or 40.4% of the total volume calculated using the PLATON routine.¹⁵ However, no sorption–desorption isotherm curves could be obtained, possibly because all windows of channels are blocked by the sulfate anions that prevent the removal of DMF molecules. The thermogravimetric analysis (TGA) of 1 shows no weight loss up to 250 °C, indicating the difficulty in removing DMF, which is in agreement with small window of channels. There are two weight losses observed: 29.5% in the range of 250–330 °C and 36.2% in the range of 330–790 °C, which correspond to the consecutive loss of 32 DMF (calc. 29.3%), and removal of chlorides, C, H, N atoms of Hamtz groups and 29 S atoms (calc. 36.4%), respectively. The followed slight weight increase indicates addition of oxygen. Upon further heating, the unstable intermediate (a mixture of CuO and CuSO₄) gradually decomposes into the final residue Cu₂O (28.6%, calc. 27.9%) (Fig. S3†).

The second-order nonlinear optical effects were examined to confirm the physical properties deriving from an acentric space group (F4̄3c). Compounds 1–3 show comparable second harmonic generation (SHG) intensities of about 2.6 relative to that of potassium dihydrogen phosphate (KDP).¹⁶ These observations confirm that compounds 1–3 crystallize in the acentric space group, consistent with the structural analyses.

The room temperature emission spectra of complexes 1–3 (λ_ex = 365 nm) are shown in Fig. 4. As can be seen, 1, 2 and 3 show a strong blue emission centered at 470 nm (τ = 5.05 μs), 468 nm (τ = 6.28 μs), and 469 nm (τ = 6.87 μs), respectively. Besides, a weak lower energy emission band is also observed in 1–3 at 548 nm (τ = 6.05 μs), 544 nm (τ = 9.24 μs) and 543 nm (τ = 7.26 μs), respectively.

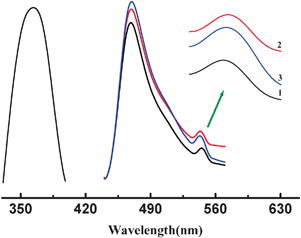Fig. 4 Solid-state photoluminescence spectra of 1–3.

The time-dependent-DFT calculations have been widely used to facilitate better understanding of the assignment of the origin of the luminescence. The Cu₄Cl(Hamtz)₆ and Cu₅(Hamtz)₈ ground-state building-blocks of 1, adapted from the X-ray data, have been used as models for calculations¹⁷ at the B3LYP level (Fig. S4†). The results indicate that the excited energy for the lowest singlet excitation is 3.3404 eV (371.17 nm) in the pentacopper unit and 2.9030 eV (427.09 nm) in the tetracopper unit, where the former is comparable to the excited wavelength (365 nm). The lowest singlet excitation in pentacopper unit is dominated by the combination of HOMO → LUMO and HOMO–6 → LUMO transitions, in which both HOMO and HOMO–6 are mainly composed of d orbitals of central Cu(I) and π orbitals of Hamtz groups, and the LUMO mainly consists of d-orbitals of peripheric Cu(I) and π* orbitals of Hamtz groups (Fig. 5). The lowest singlet excitation in tetracopper unit is dominated by the HOMO → LUMO transition, in which HOMO is mainly composed of d orbitals of Cu(I) and LUMO mainly consists of π* orbitals of Hamtz ligands and d orbitals of central Cu(I). Accordingly, the origin of the phosphorescence at 470 nm for 1 can be ascribed to the intraligand transition, probably involved with metal-centered transitions of the type 3d¹⁰ → 3d⁹4s and 3d¹⁰ → 3d⁹4p on the copper(I) centers modified by copper-copper interactions. While for the origin of the phosphorescence at 548 nm can be ascribed to metal-to-ligand transition (MLCT) and metal-centered transitions of the type 3d¹⁰ → 3d⁹4s and 3d¹⁰ → 3d⁹4p on the copper(I) centers modified by copper–copper interactions. The calculated result is consistent with the previous reports on Cu(I)/halide/thiolate compounds.^13,8a,8b

Fig. 5 Electron-density distribution of the 245 HOMO and 246 LUMO frontier orbitals calculated for [CuCu₃] unit, and 304 HOMO-6, 310 HOMO and 311 LUMO for [CuCu₄] unit.

In summary, three novel 3-D MOFs with bor topology have been constructed from Cu-centered CuCu₃ and CuCu₄ clusters. At ambient temperature, 1–3 show interesting emissions: a weak yellow emission and a strong higher energy blue emission band. The SHG measurements confirm that three complexes crystallize in the acentric space group, indicating they may be suitable candidates for non-linear optical (NLO) materials.

We thank Prof. G.-C. Guo for measuring the second harmonic generation (SHG) and Dr. J.-R. Li for effort in sorption-desorption experiment. This work was financially supported by the NSFC (20771069), Fok Ying Tung Education Foundation (111015), NSF of Shanxi (200801107) and Novelty Project of Shanxi Graduates (20081019).

Notes and references

1. (a) J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1477; (b) M. Kurmoo, Chem. Soc. Rev., 2009, 38, 1353; (c) O. R. Evans and W.-B. Lin, Acc. Chem. Res., 2002, 35, 511; (d) M. D. Allendorf, C. A. Bauer, R. K. Bhakta and R. J. T. Houk, Chem. Soc. Rev., 2009, 38, 1330; (e) S. R. Batten, S. M. Neville and D. R. Turner, Coordination Polymers: Design, Analysis and Application, RSC, Australia, 2009.
2. (a) O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705; (b) N. W. Ockwig, O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2005, 38, 176.
3. RCSR and EPINET, two sources of crystalline networks. The associated websites are as follows: http://rcsr.anu.edu.au and http://epinet.anu.edu.au.
4. (a) B. F. Abrahams, S. R. Batten, H. Hamit, B. F. Hoskins and R. Robson, Angew. Chem., Int. Ed. Engl., 1996, 35, 1690; (b) Q. C. Zhang, Y. Liu, X. H. Bu, T. Wu and P. Y. Feng, Angew. Chem., Int. Ed., 2008, 47, 113.
5. (a) S. S. Y. Chui, S. M. F. Lo, J. P. H. Charmant, A. Gay Orpen and I. D. Williams, Science, 1999, 283, 1148; (b) B. Chen, M. Eddaoudi, S. T. Hyde, M. O'Keeffe and O. M. Yaghi, Science, 2001, 291, 1021; (c) D. N. Dybtsev, H. Chun and K. Kim, Chem. Commun., 2004, 1594; (d) Z. G. Zhao, J. Zhang, X. Y. Wu, Q. G. Zhai, L. J. Chen, S. M. Chen, Y. M. Xie and C. Z. Lu, CrystEngComm, 2008, 10, 273; (e) Z. Q. Wang, V. Ch. Kravtsov and M. J. Zaworotko, Angew. Chem., Int. Ed., 2005, 44, 2877.
6. (a) M. Eddaoudi, D. B. Moler, H. Li, B. Chen, T. M. Reineke, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2001, 34, 319; (b) M. H. Zeng, M. X. Yao, H. Liang, W. X. Zhang and X. M. Chen, Angew. Chem., Int. Ed., 2007, 46, 1832.
7. (a) Q. R. Fang, G. S. Zhu, Z. Jin, M. Xue, X. Wei, D. J. Wang and S. L. Qiu, Angew. Chem., Int. Ed., 2006, 45, 6126; (b) D. Li, T. Wu, X. P. Zhou, R. Zhou and X. C. Huan, Angew. Chem., Int. Ed., 2005, 44, 4175; (c) X. M. Zhang, Y. Z. Zheng, C. R. Li, W. X. Zhang and X. M. Chen, Cryst. Growth Des., 2007, 7, 980; (d) X. L. Wang, C. Qin, Y. Q. Lan, K. Z. Shao, Z. M. Su and E. B. Wang, Chem. Commun., 2009, 410 and references therein.
8. (a) V. W. W. Yam and K. K. W. Lo, Chem. Soc. Rev., 1999, 28, 323; (b) P. C. Ford, E. Cariati and J. Bourassa, Chem. Rev., 1999, 99, 3625.
9. (a) M. H. Bi, G. H. Li, Y. C. Zou, Z. Shi and S. H. Feng, Inorg. Chem., 2007, 46, 604; (b) T. Wu, M. Li, D. Li and X. C. Huang, Cryst. Growth Des., 2008, 8, 568; (c) J. Wang, S. L. Zheng, S. Hu, Y. H. Zhang and M. L. Tong, Inorg. Chem., 2007, 46, 795.
10. (a) X. M. Zhang, R. Q. Fang and H. S. Wu, J. Am. Chem. Soc., 2005, 127, 7670; (b) Z. M. Hao, R. Q. Fang, H. S. Wu and X. M. Zhang, Inorg. Chem., 2008, 47, 8197.
11. (a) J. P. Zhang, Y. Y. Lin, X. C. Huang and X. M. Chen, J. Am. Chem. Soc., 2005, 127, 5495; (b) J. G. Haasnoot, Coord. Chem. Rev., 2000, 200–202, 131.
12. (a) P. C. Ford and A. Vogler, Acc. Chem. Res., 1993, 26, 220; (b) J. Strähle and J. Beck, Angew. Chem., Int. Ed. Engl., 1985, 24, 409.
13. J. K. Cheng, Y. G. Yao, J. Zhang, Z. J. Li, Z. W. Cai, X. Y. Zhang, Z. N. Chen, Y. B. Chen, Y. Kang, Y. Y. Qin and Y. H. Wen, J. Am. Chem. Soc., 2004, 126, 7796.
14. A. J. Cairns, J. A. Perman, L. Wojtas, V. Ch. Kravtsov, M. H. Alkordi, M. Eddaoudi and M. J. Zaworotko, J. Am. Chem. Soc., 2008, 130, 1560.
15. A. L. Spek, PLATON, A Multipurpose Crystallographic Tool, Utrecht University, The Netherlands, 1999; A. L. Spek, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, C34.
16. S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798.
17. (a) R. Bauemschmitt, R. Ahlrichs, F. H. Hennrich and M. M. Kappes, J. Am. Chem. Soc., 1998, 120, 5052; (b) X. Liu, G. C. Guo, A. Q. Wu, L. Z. Cai and J. S. Huang, Inorg. Chem., 2005, 44, 4282.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental details, XPRD patterns for 1–3 and additional figures. CCDC reference numbers 731918–731920. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/b918159h

‡ X-ray data for 1: C₄₈H₇₂Cl₄Cu₃₁N₉₆O₃₂S₃₂ (298 K), M_r = 5643.48, cubic, F4̄3c, a = 36.577(7) Å, U = 48936(17) ų, Z = 8, ρ = 1.532 g cm⁻¹, μ = 3.005 mm⁻¹, F(000) = 22 136, GOF = 1.106. A total of 84 715 reflections were collected, 4019 of which were unique (R(int) = 0.1247). R1 (I > 2σ(I)) = 0.0501, wR₂ = 0.1035. For 2: C₄₈H₇₂Br₄Cu₃₁N₉₆O₃₂S₃₂ (298 K), M_r = 5821.32, cubic, F4̄3c, a = 36.3997(5) Å, U = 48227.4(11) ų, Z = 8, ρ = 1.603 g cm⁻¹, μ = 3.668 mm⁻¹, F(000) = 22 712, GOF = 1.066. A total of 75 603 reflections were collected, 3952 of which were unique (R(int) = 0.0689). R1 (I 2σ(I)) = 0.0333, wR₂ = 0.0854. For 3: C₄₈H₇₂I₄Cu₃₁N₉₆O₃₂S₃₂ (298 K), M_r = 6009.28, cubic, F4̄3c, a = 36.6289(11) Å, U = 49144(3) ų, Z = 8, ρ = 1.624 g cm⁻¹, μ = 3.452 mm⁻¹, F(000) = 23 288, GOF = 1.065. A total of 86 447 reflections were collected, 4039 of which were unique (R(int) = 0.0480). R1 (I > 2σ(I)) = 0.0316, wR₂ = 0.0847. The contribution of the DMF molecules to the diffraction pattern was subtracted from the observed data by the SQUEEZE method implemented in PLATON.¹⁵ Flack parameters in 1–3 cannot be determined due to disordered sulfates and sovlent DMF molecules.

---