Nanoscale interface of metals for withstanding momentary shocks of compression†
Fenying
Wang
,
Yunhong
Liu
,
Tiemin
Zhu
,
Yajun
Gao
and
Jianwei
Zhao
*
Key Laboratory of Analytical Chemistry for Life Sciences, Ministry of Education, School of Chemistry and Chemical Engineering, Nanjing University, Nanjing, 210008, P. R. China. E-mail: zhaojw@nju.edu.cn; Fax: +86-25-83596523; Tel: +86-25-83596523
First published on 14th October 2010
Abstract
The failure of the nanoscale metallic interface has raised concerns owing to the effect interfacial amalgamation has on its application in nanoelectronic devices. Single crystal copper [110] and [100], which are set as two components of [110]‖[100] nanocrystalline copper, are used to simulate the interfacial properties using molecular dynamics simulations. Repeated tension and compression cycles show that the two components of the interface can come into contact and separate without interfacial amalgamation. The [110]‖[100] interface could withstand momentary shocks of compression and heat produced by the momentary shocks. This property of the [110]‖[100] interface is dominated by crystalline orientations of interfacial structure, in comparison with [111]‖[100] and [111]‖[110] interfaces under the same conditions.
1. Introduction
Nanocrystalline metals have been a focus of intense research primarily owing to their potential as the basic building blocks of microelectromechanical systems (MEMS) and nanoelectromechanical systems (NEMS).1–3 One of the major issues for the functionality and reliability of such building blocks is the property of the interface in MEMS and NEMS. For example, when micro- or nanoscale solid components form the interface with a momentary contact, compression or impact during mechanical processes, whether the mechanical shock leads to interfacial amalgamation or not would have a significant influence on fatigue or failure of the nanoelectronic device. For the contacting solid components with different crystalline orientations, grain boundary (GB) in such specially formed interfaces plays a prominent role in mechanical processes,4–6 such as interface mobility, corrosion, crack nucleation resistance and ductility.7–9Over the last decades, considerable efforts have been devoted to developing suitable methods to research the property of GB effects.10–12 Molecular dynamics (MD) simulation, which is promising, has been used widely to describe the fundamental mechanical properties of nanocrystalline materials.8,13–15 Wang et al.14 studied the influence of defects on mechanical properties of the copper grain boundary interface, and they showed the interfacial behaviors subjected to tensile or shear strain were sensitive to crystalline defects. Spearot et al.15 used MD simulation to study the tensile strength of <100> and <110> tilt copper interfaces, which indicated that the two critical attributions of the interface structure were crystalline in orientation and certain structural units. Meanwhile, Heino et al.16 reported that the presence of a grain boundary reduced the elastic modulus and yield strain during the tensile deformation. Previous MD simulation works have studied the failure processes of the nanoscale metallic materials. However, the durability of the interface and the heat effect produced by the momentary impacts are not well known.
Considering the fact that metallic interface subjected to various shocks could show a flexible feature during mechanical deformation, a stable interface applied in micro- or nanodevice would require a strong ability of withstanding momentary shocks, such as contact, compression or impact. To be truly reliable, such ability should be based on the two components of the interface. However, how to prevent such shocks from inducing the fatigue or failure of the interface has not been clearly identified owing to the difficulty of coating or lubricating the interface in such small devices. Here, we attempt to address why the special interface has an ability to withstand momentary mechanical shocks using MD simulation.
2. Computational details
To simulate the shock behaviors of metallic interface which are similar to the ones in MEMS and NEMS, such as the transmitting rotational motion of two meshing gears, we simplify the interfacial interaction into contact, separation and compression of two components, and the model of the interface (Fig. 1) was constructed by contacting the single crystal copper with different crystalline orientations. The nanocrystalline copper was relaxed firstly under zero traction (xy-plane) and zero stress (z-direction) to reach a metastable equilibrium state. In general, when the recorded average potential energy per atom reached a stable state and the stress was fluctuating slightly around 0.0 GPa with the relaxation time increasing, we confirmed that equilibration of the system was achieved. After that, the system was subjected to uniaxial strain by uniformly moving the top and bottom fixed layers in the z-direction. The strain (ε) was defined as: ε = (l − l0)/l0, where l was the current stretching length and l0 was the length just after relaxation. The strain rate in this work had been fixed at 0.16% ps−1, corresponding to 46.3 m s−1. This was a high strain rate for any materials and structures from macroscopic viewpoint. However, this region of strain rate could be considered as quasi-static state for the nanoscale materials, and it could avoid the strain rate effects as much as possible. In all MD simulations, the free boundary condition was adopted. The Verlet leapfrog algorithm was used for the integration of motion equations to obtain velocity and trajectories of atoms with a simulation time step of 1.6 fs.17 The temperature of the system was kept constant using the Nośe-Hoover thermostat18–20 as a velocity rescaling method.![The schematic model of nanocrystalline copper. Schematic models of (a) the [110]‖[100] interface, and (b) one section of the atomic arrangement. The model was set as 20a × 20a × 80a (a stands for lattice constant, 0.362 nm for copper), corresponding to about 128,000 atoms. In detail, the whole length (z-direction) was 28.96 nm with two-half different crystallographic directions, except for the fixed layers with three lattices at the ends, the cross-section (xy-plane) is square, corresponding to 52.42 nm2.](/image/article/2010/NR/c0nr00333f/c0nr00333f-f1.gif) | ||
| Fig. 1 The schematic model of nanocrystalline copper. Schematic models of (a) the [110]‖[100] interface, and (b) one section of the atomic arrangement. The model was set as 20a × 20a × 80a (a stands for lattice constant, 0.362 nm for copper), corresponding to about 128,000 atoms. In detail, the whole length (z-direction) was 28.96 nm with two-half different crystallographic directions, except for the fixed layers with three lattices at the ends, the cross-section (xy-plane) is square, corresponding to 52.42 nm2. | ||
The interaction between copper atoms was described through embedded-atom method (EAM) potential function,21–23 which could provide an effective description of the transitional metals with the face-centered cubic (FCC) structure,24–28 such as Cu, Ag, Au, Ni, Pt, Pd and their alloy materials. Moreover, this EAM potential function was not only suitable for single crystal interfacial systems, but also for the polycrystalline systems. The total energy was given by:
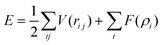 | (1) |
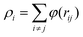 | (2) |
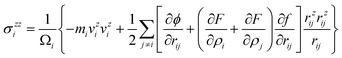 | (3) |
3. Results and discussion
The relaxation and tension of the constructed models in simulations correspond to the contact and separation of the interface, respectively. Fig. 2(a) shows the temperature effects on the behaviors of [110]‖[100] nanocrystalline copper subjected to the uniaxial tension. As expected, the grain boundary between [100] and [110] crystallographic orientations could hinder interfacial atoms from slipping to a certain extent. After the initial elastic deformation, cracks appear quickly in the region of interface with only a slight elongation of nanocrystalline copper. With an increase in tensile strain, the cracks propagate fast along the interface until the overall rupture happens eventually. As shown in Fig. 2(a), the cracks are firstly observed at ε = 0.149, 0.198 and 0.215 (ε is the tensile strain), then the cracks continue to expand until rupture at ε = 0.189, 0.248 and 0.262, corresponding to 4, 300 and 600 K, respectively. Here, the speed of crack propagation is so fast that it is comparable to the speed of sound. However, the discussion of crack propagation is beyond the scope of this paper. The main point is that, from the phenomena that strains are close to that of elastic deformation when cracks appear and propagate fast at different temperatures, we find that single crystal copper [110] and [100] can contact and separate perfectly during mechanical processes. Moreover, temperature hardly affects the breaking in the interface.![The deformation behavior of [110]‖[100] nanocrystalline copper. (a) Deformation behavior of [110]‖[100] subjected to uniaxial strain at 4, 300 and 600 K (a stands for lattice constant of copper, 0.362 nm). In detail, the strain ε from <1> to <5> at 4 K is 0.000, 0.065, 0.149, 0.169 and 0.189; ε at 300 K is 0.000, 0.040, 0.150, 0.223 and 0.248; ε at 600 K is 0.000, 0.033, 0.167, 0.251 and 0.262. Radial distribution function (RDF) of [110]‖[100] at (b) 4, (c) 300 and (d) 600 K. Stress distribution of [110]‖[100] at (e) 4, (f) 300 and (g) 600 K.](/image/article/2010/NR/c0nr00333f/c0nr00333f-f2.gif) | ||
| Fig. 2 The deformation behavior of [110]‖[100] nanocrystalline copper. (a) Deformation behavior of [110]‖[100] subjected to uniaxial strain at 4, 300 and 600 K (a stands for lattice constant of copper, 0.362 nm). In detail, the strain ε from <1> to <5> at 4 K is 0.000, 0.065, 0.149, 0.169 and 0.189; ε at 300 K is 0.000, 0.040, 0.150, 0.223 and 0.248; ε at 600 K is 0.000, 0.033, 0.167, 0.251 and 0.262. Radial distribution function (RDF) of [110]‖[100] at (b) 4, (c) 300 and (d) 600 K. Stress distribution of [110]‖[100] at (e) 4, (f) 300 and (g) 600 K. | ||
From the radial distribution function (RDF) in Fig. 2(b)–2(d), we also find that [110]‖[100] nanocrystalline copper retains perfect crystalline structure in the interfacial separation process. The sharp peaks of the RDF indicate the presence of lattice order in the tensile process. With strain increasing, peak height in the near neighbor distance is slightly reduced, and the peaks still keep sharp feature. Temperature effect on the lattice order can be seen obviously from the RDF of [110]‖[100] nanocrystalline copper at the broken points (see Supplementary Fig. S1†). The peak at 4 K behaves sharp and is the highest one. With temperature increasing, the peak in the near neighbor distance broadens.32 It indicates that temperature could affect the order degree of [110]‖[100] nanocrystalline copper during the process of contact and separation, but [110]‖[100] could always preserve perfect crystalline structure under such momentary shocks due to the GB effect.
The GB effect on the property of [110]‖[100] nanocrystalline copper can be given an explicit interpretation using an averaged stress distribution along the uniaxial tensile direction at 4, 300 and 600 K (Fig. 2(e)–2(g)), respectively. At ε = 0.0 of all temperatures, the stress fluctuating slightly around 0.0 GPa is distributed symmetrically to the middle point (grain boundary interface), then stress distribution behaves like a V-shape with the strain increasing. The stress just at grain boundary interface remains a high level and forms a stress peak at the point of final disconnection, and the phenomena indicate the presence of stress concentration. Moreover, the stress vibrates acutely with the largest amplitude at 600 K indicating that the increasing entropy makes the crystal lattice vibrate acutely at their equilibrium position. However, heat movement of atoms cannot rearrange the atoms to a lower energy state in the interface region, and the interface is difficult to amalgamate owing to stress concentration, so that [110]‖[100] nanocrystalline copper tends to crack rather than deform at 4, 300 and 600 K during the tensile processes.
The effective characterization to the mechanical property of metallic materials in uniaxial strain is using stress-strain relationship, yield stress and Young's modulus,4,13 which may provide more insights into the mechanical breaking, material failure and operation of nano-sized devices. In the following, the stress-strain relationships of [110]‖[100] nanocrystalline copper under uniaxial tension at the temperatures from 4 to 600 K are shown in Fig. 3(a), in comparison with [110] and [100] single crystal copper at the same conditions (Fig. 3(b)–3(c)). Before the first yield point (the critical point of elastic deformation), stress displays a linear response to strain, which accords with elastic law (That is σ1 = Yε1, σ1 and ε1 are strain and stress at the first yield point, respectively. Y is Young's modulus.). After the first yield point, stress decreases abruptly indicating that nanocrystalline copper undergoes an irreversible structural deformation. Subsequently, the decreasing trend of the stress in the whole yielding cycle shows nanocrystalline copper experiences plastic deformation with increasing strain. When the system has no ability to reconstruct a stable configuration, the yield cycle is over. The stress–strain behaviors show that the presence of the GB reduces the breaking strain compared with the single crystal copper [100] and [110]. Moreover, for [110]‖[100], [110] and [100], σ1 and Y both decrease gradually with increasing temperature. It indicates that the temperature effect on mechanical strength of [110]‖[100] nanocrystalline copper is the same as the single crystal copper [110] and [100].
![The mechanical behavior of [110]‖[100] nanocrystalline copper. The stress-strain relationship of (a) [110]‖[100], (b) [110] and (c) [100] from 4 to 600 K. (d) The first yield stress plotted against temperature and (e) Young's modulus plotted against temperature.](/image/article/2010/NR/c0nr00333f/c0nr00333f-f3.gif) | ||
| Fig. 3 The mechanical behavior of [110]‖[100] nanocrystalline copper. The stress-strain relationship of (a) [110]‖[100], (b) [110] and (c) [100] from 4 to 600 K. (d) The first yield stress plotted against temperature and (e) Young's modulus plotted against temperature. | ||
However, the first yield stress and Young's modulus have complex characters as a function of temperature (see Fig. 3(d) and 3(e)). With temperature increasing, the first yield stress of [110]‖[100] is transferred from the region between [100] and [110] (before 300 K) to the one below of them (600 K). Whereas, Young's modulus of [110]‖[100] only distributes in the region between [100] and [110] around 300 K. Y are smaller than those of single crystal copper at lower (4 K) and higher (450 and 600 K) temperatures.
Temperature effects on mechanical strength of [110]‖[100] are attributed to the GB interface of [110]‖[100] nanocrystalline copper. Comparing with the single crystal copper, atoms within [110]‖[100] interface are less mobile, and tend to crack rather than deform at low temperature. Thus, once cracks appear in the interface, cracks will grow quickly. Whereas, around 300 K, nanocrystalline grains within the interface resist crack propagation and provide strength under tensile deformation. This behavior around 300 K is similar to the Hall–Petch effect which describes the hardness and yield stress of polycrystalline materials typically increase with grain size decreasing.33,34 When temperature increases to 600 K, the reduction of σ1 and Y, named as a similar inverse Hall–Petch effect, is expedited by the relative instability of crystal grains owing to a larger magnitude of atomic oscillation around its equilibrium configuration, and this thermally activated process decreases mechanical strength of [110]‖[100] nanocrystalline copper. The similar transformation from Hall–Petch effect to inverse Hall–Petch effect not only shows that temperature can affect the mechanical strength of [110]‖[100] nanocrystalline copper, but also can affect the deformation behavior. However, the temperature effects do not dominate the behavior of [110]‖[100] nanocrystalline copper.
The deformation behaviors of [110]‖[100] nanocrystalline copper at different temperatures show that the special behaviors of [110]‖[100] interface result from the nature of the GB interface. When single crystal copper [110] and [100] are applied in MENS and NEMS, the reliability of the formed interface results from its durability. Here, the tension–compression cycles are applied in the [110]‖[100] interface. It is noted that single crystal copper [110] and [100] can come into contact and separate without interfacial amalgamation. Deformation behaviors of [110]‖[100] nanocrystalline copper subjected to ten tension and compression cycles at 300 K is shown in Video S1 (Supplementary Video S1†). In the tensile process, the grain boundary in the interface dominates the deformation behaviors. Cracks grow and propagate fast with the uniaxial tensile strain increasing, which finally results in completely separation between the two components of the interface. In the process of compression, all the simulation parameters except strain direction are the same as the process of tension. The GB region of the interface exhibits dislocation nucleation when two components come into contact, and the atoms in the two components of [110]‖[100] interface gradually present proper arrangement again with the compression strain increasing.
From above investigations, it is shown that the two components of [110]‖[100] interface can come into contact and separate under repeated cycles of tension and compression. Fig. 4(a) shows the order of crystalline structure in the repeated cycles using histogram of the RDF peaks of the first, third and fifth neighbor distances at the critical point of elastic deformation. The peak values only varying within a narrow range in each neighbor distance, revealing that [110]‖[100] nanocrystalline copper retains perfect order of crystalline structure in the processes of repeated tension and compression. It is consistent with the ability of [110]‖[100] to withstand momentary shocks and to inhibit the interfacial amalgamation. In the following, from the maximum stored potential energy per cycle in Fig. 4(b), we can evaluate that, for [110]‖[100] nanocrystalline copper, the ability of storing energy would decrease gradually with an increase in the tension and compression cycle. Moreover, the decreasing trend may be obvious at the beginning cycle of tension and compression, and then be become less so with the cycle increasing within the region of the failure. This is attributed to the fact that the stored elastic energy is known to promote reverse transformation of crystalline structure under repeated tension and compression.35 On the other hand, dislocation nucleation in the GB interface also relieves the stored energy to get a metastable state. So [110]‖[100] nanocrystalline copper can retain the relatively stable crystalline structure with increasing cycles. From this point it can be seen that the [110]‖[100] interface has the ability to withstand repeated momentary shocks such as tension, compression and impact.
![The property of [110]‖[100] nanocrystalline copper under tension and compression cycles. (a) The values of the RDF peaks are at the first yield point of each stretching process. (b) The maximum stored potential energy per stress-induced strain during the tension–compression process, (the above point is in tension process and the below point is in compression process), the inserted schematic model is the cycle process.](/image/article/2010/NR/c0nr00333f/c0nr00333f-f4.gif) | ||
| Fig. 4 The property of [110]‖[100] nanocrystalline copper under tension and compression cycles. (a) The values of the RDF peaks are at the first yield point of each stretching process. (b) The maximum stored potential energy per stress-induced strain during the tension–compression process, (the above point is in tension process and the below point is in compression process), the inserted schematic model is the cycle process. | ||
The perfect interface separation of [110]‖[100] exhibits a special property of the [110]‖[100] nanocrystalline copper. These phenomena stimulate us to investigate the interaction mechanism in the [110]‖[100] interface through the deformation behaviors of [111]‖[100] and [111]‖[110].
It is interesting that the interface separation of [110]‖[100], [111]‖[100] and [111]‖[110] show completely different behaviors under the same conditions. [111]‖[100] nanocrystalline copper (Fig. 5(a)) inclines to make the interface amalgamate. With increasing strain, a few atoms that originally belong to the [100] crystalline orientation are transferred to [111] crystalline orientation during the tensile process, and the final broken position of [111]‖[100] nanocrystalline copper is in the [100] region, but near to the GB interface. Moreover, from the breaking points at Fig. 5(a), we could find that the transferred atoms in the GB region increase obviously with increasing temperature. In detail, [111]‖[100] at 4 K shows two components of the interface can contact and separate with only a few transferred atoms. However, at 300 and 600 K, [111]‖[100] nanocrystalline copper tends to break in [100] region with much more transferred atoms. Fig. 5(b) gives the atomic arrangements in the interface region at the broken position, and it shows the separated interface with obvious GB at 4 K is transformed into interfacial amalgamation at 300 and 600 K (see Supplementary Fig. S2† for the stress distribution of [111]||[100] at 4, 300 and 600 K). For [111]‖[110] nanocrystalline copper (Fig. 5(c)), the deformation behavior at 4 K is similar to [110]‖[100] nanocrystalline copper, but when temperature increases to 300 or 600 K, the interfacial amalgamation resists crack propagation during the tensile process, then [111]‖[110] nanocrystalline copper breaks in the [111] region with larger tensile strain. The atomic arrangement at the broken position (Fig. 5(d)) shows that the [111]‖[110] interface is an incoherent interface at 4 K, but at 300 and 600 K, the crystalline structural reconstruction results in interfacial amalgamation with increasing temperature (see Supplementary Fig. S3† for the stress distribution of [111]||[110] at 4, 300 and 600 K). In our previous work,36,37 we have given some special samples of the interface-effect-induced the breaking failure with the analysis of a Fourier transformation method.
![The deformation behavior of [111]‖[100] and [111]‖[110] nanocrystalline copper. Deformation behavior of (a) [111]‖[100] subjected to uniaxial strain at 4, 300 and 600 K. In detail, for [111]‖[100], the strain ε from <1> to <6> at 4 K is 0.000, 0.083, 0.368, 0.532, 0.688 and 0.733; ε at 300 K is 0.000, 0.102, 0.313, 0.489, 0.693 and 0.764; ε at 600 K is 0.000, 0.115, 0.323, 0.516, 0.738 and 0.797. (b) Atomic arrangement of [111]‖[100] in GB interface at the broken point for 4, 300 and 600 K. (c) Deformation behavior of [111]‖[110] subjected to uniaxial strain at 4, 300 and 600 K. For [111]‖[110], ε from <1> to <7> at 4 K is 0.000, 0.093, 0.392, 0.623, 0.586, 0.698 and 0.872; ε at 300 K is 0.000, 0.102, 0.256, 0.398, 0.688, 0.955 and 1.110; ε at 600 K is 0.000, 0.201, 0.369, 0.589, 0.736, 1.010 and 1.200. (d) Atomic arrangement of [111]‖[110] in GB interface at the broken point for 4, 300 and 600 K. (a in fig. 5(a) and 5(c) both stand for lattice constant of copper, 0.362 nm).](/image/article/2010/NR/c0nr00333f/c0nr00333f-f5.gif) | ||
| Fig. 5 The deformation behavior of [111]‖[100] and [111]‖[110] nanocrystalline copper. Deformation behavior of (a) [111]‖[100] subjected to uniaxial strain at 4, 300 and 600 K. In detail, for [111]‖[100], the strain ε from <1> to <6> at 4 K is 0.000, 0.083, 0.368, 0.532, 0.688 and 0.733; ε at 300 K is 0.000, 0.102, 0.313, 0.489, 0.693 and 0.764; ε at 600 K is 0.000, 0.115, 0.323, 0.516, 0.738 and 0.797. (b) Atomic arrangement of [111]‖[100] in GB interface at the broken point for 4, 300 and 600 K. (c) Deformation behavior of [111]‖[110] subjected to uniaxial strain at 4, 300 and 600 K. For [111]‖[110], ε from <1> to <7> at 4 K is 0.000, 0.093, 0.392, 0.623, 0.586, 0.698 and 0.872; ε at 300 K is 0.000, 0.102, 0.256, 0.398, 0.688, 0.955 and 1.110; ε at 600 K is 0.000, 0.201, 0.369, 0.589, 0.736, 1.010 and 1.200. (d) Atomic arrangement of [111]‖[110] in GB interface at the broken point for 4, 300 and 600 K. (a in fig. 5(a) and 5(c) both stand for lattice constant of copper, 0.362 nm). | ||
According to these deformation behaviors and structure characters in the grain boundary interfaces, it is obvious that, because of the high coordination number of the (111) facet, grain boundaries (GBs) including the (111) crystalline plane are necessary for the interfacial amalgamation and the ductility of nanocrystalline copper, which is also affected by the increasing temperature. For the GBs among (111), (100) and (110) planes,4,38 according to their large interplanar spacing parallel to the GB plane, GBs on the two densest planes of the FCC lattice, (111) and (100), have low and intermediate energies, respectively; while GB on the (110) plane has high energy, and is also the representative of the highest energy GBs in FCC metals. The GB energy is decided by the average atomic coordination and atomic density in the core of the GB. So for the lower energy planes, rearrangement of crystal structure in the interface can be achieved without crack growth and crack propagation, then makes the GB interface amalgamate in the tensile process. Whereas, for the higher energy plane, the force and temperature are not enough to rearrange the crystal structure in the GB interface and reduce the level of GB energy during stretching. Thus, once a crack grows in the interface, the crack will propagate fast. However, this property of [110]‖[100] interface is just helpful for preventing the interface failure in MENS and NEMS, owing to its ability to withstand momentary shocks and warmth produced by such momentary shocks.
4. Conclusions
In summary, with MD simulation, single crystal copper [110] and [100] are used to investigate the property of [110]‖[100] interface. Comparing with the interfaces of [111]‖[100] and [111]‖[110], we conclude that the two components of [110]‖[100] interface can come into contact and separate freely, which results from the nature of the interface. This process is hardly affected by temperature. Repeated tension and compression of [110]‖[100] nanocrystalline copper show that the interface could undergo more than one mechanical shock. So [110]‖[100] interface has the ability to resist momentary mechanical shocks and withstand heat produced by mechanical shocks, indicating the high reliability of [110]‖[100] interface applied in MENS and NEMS. Through the above investigation, it not only enriches our understanding of how to prevent the failure of interface, but also provides a possible way of optimizing the material capability through GB engineering.39–41Acknowledgements
This project was supported by the National Natural Science Foundation of China (Grant Nos. 20821063, 20873063 and 51071084), National Basic Research Program of China (973 Program, Grant No. 2007CB936302 and 2010CB732400), the Natural Science Foundation of Jiangsu Province (BK2010389) and the Open Project of The State Key Laboratory of Physical Chemistry of Solid Surfaces (Xiamen University).References
- H. G. Craighead, Science, 2000, 290, 1532–1535 CrossRef CAS.
- K. L. Ekinci and M. L. Roukes, Rev. Sci. Instrum., 2005, 76, 061101 CrossRef.
- G. Yun and H. S. Park, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195421 CrossRef.
- D. Wolf, V. Yamakov, S. R. Phillpot, A. Mukherjee and H. Gleiter, Acta Mater., 2005, 53, 1–40 CrossRef CAS.
- A. Hasnaoui, H. Van Swygenhoven and P. M. Derlet, Science, 2003, 300, 1550–1552 CrossRef CAS.
- D. E. Spearot, K. I. Jacob, D. L. McDowell and S. J. Plimpton, J. Eng. Mater. Technol., 2005, 127, 374–382 CrossRef CAS.
- H. Van Swygenhoven, Science, 2002, 296, 66–67 CrossRef CAS.
- J. Schiotz and K. W. Jacobsen, Science, 2003, 301, 1357–1359 CrossRef CAS.
- H. Zhang, D. J. Srolovitz, J. F. Douglas and J. A. Warren, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 115404 CrossRef.
- K. J. Hemker, Science, 2004, 304, 22.
- R. Valiev, Nat. Mater., 2004, 3, 511–516 CrossRef CAS.
- Z. Budrovic, H. Van Swygenhoven, P. M. Derlet, S. Van Petegem and B. Schmitt, Science, 2004, 304, 273–276 CrossRef CAS.
- M. A. Meyers, A. Mishra and D. J. Benson, Prog. Mater. Sci., 2006, 51, 427–556 CrossRef CAS.
- L. Wang, H. W. Zhang and X. Deng, J. Phys. D: Appl. Phys., 2008, 41, 135304 CrossRef.
- D. E. Spearot, M. A. Tschopp, K. I. Jacob and D. L. McDowell, Acta Mater., 2007, 55, 705–714 CrossRef CAS.
- P. Heino, H. Hakkinen and K. Kaski, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 641–652 CrossRef CAS.
- G. M. Finbow, R. M. LyndenBell and I. R. McDonald, Mol. Phys., 1997, 92, 705–714 CrossRef CAS.
- S. Nośe, Mol. Phys., 1984, 52, 255–268 CAS.
- S. Nośe, J. Chem. Phys., 1984, 81, 511–519 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- R. A. Johnson, Phys. Rev. B: Condens. Matter, 1988, 37, 3924–3931 CrossRef.
- R. A. Johnson, Phys. Rev. B: Condens. Matter, 1988, 37, 6121–6125 CrossRef.
- R. A. Johnson, Phys. Rev. B: Condens. Matter, 1989, 39, 12554–12559 CrossRef.
- Y. H. Liu, F. Y. Wang, J. W. Zhao, L. Y. Jiang, M. Kiguchi and K. Murakoshi, Phys. Chem. Chem. Phys., 2009, 11, 6514–6519 RSC.
- Y. H. Liu, J. W. Zhao and W.F.Y, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115417 CrossRef.
- D. X. Wang, J. W. Zhao, S. Hu, X. Yin, S. Liang, Y. H. Liu and S. Y. Deng, Nano Lett., 2007, 7, 1208–1212 CrossRef CAS.
- J. W. Zhao, K. Murakoshi, X. Yin, M. Kiguchi, Y. Guo, N. Wang, S. Liang and H. Liu, J. Phys. Chem. C, 2008, 112, 20088–20094 CrossRef CAS.
- A. R. Setoodeh, H. Attariani and M. Khosrownejad, Comput. Mater. Sci., 2008, 44, 378–384 CrossRef CAS.
- H. A. Wu, Eur. J. Mech. A, 2006, 25, 370–377 CrossRef.
- J. W. Zhao, X. Yin, S. Liang, Y. H. Liu, D. X. Wang, S. Y. Deng and J. Hou, Chem. Res. Chin. Univ., 2008, 24, 367–370 Search PubMed.
- L. Y. Jiang, X. Yin, J. W. Zhao, H. M. Liu, Y. H. Liu, W.F.Y and J. J. Zhu, J. Phys. Chem. C, 2009, 113, 20193–20197 CrossRef CAS.
- S. K. R. S. Sankaranarayanan, V. R. Bhethanabotla and B. Joseph, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 134117 CrossRef.
- E. O. Hall, Proc. Phys. Soc., London, Sect. B, 1951, 64, 747–753 CrossRef.
- N. J. Petch, J. Iron Steel Inst., 1953, 174, 25–28 Search PubMed.
- J. S. Juan, M. L. No and C. A. Schuh, Nat. Nanotechnol., 2009, 4, 415–419 CrossRef.
- J. Zhao, F. Wang, L. Jiang, X. Yin and Y. Liu, Acta Phys. Chim. Sin., 2009, 25, 1835–1840 Search PubMed.
- J. W. Zhao, J. Hou, T. M. Zhu, F. Y. Wang, Y. H. Liu and X. Yin, Comput. Mater. Sci., 2010, 47, 962–967 CrossRef CAS.
- P. Keblinski, D. Wolf, S. R. Phillpot and H. Gleiter, Scr. Mater., 1999, 41, 631–636 CrossRef CAS.
- V. Randle, Scr. Mater., 2006, 54, 1011–1015 CrossRef CAS.
- A. J. Detor and C. A. Schuh, Acta Mater., 2007, 55, 371–379 CrossRef CAS.
- C. C. Koch, K. M. Youssef, R. O. Scattergood and K. L. Murty, Adv. Eng. Mater., 2005, 7, 787–794 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Radial distribution function and stress distribution of [110]‖[100] copper. See DOI: 10.1039/c0nr00333f |
| This journal is © The Royal Society of Chemistry 2010 |
