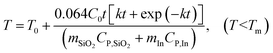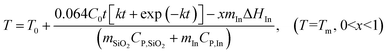DOI:
10.1039/C0NR00585A
(Paper)
Nanoscale, 2010,
2, 2790-2797
Encapsulated nano-heat-sinks for thermal management of heterogeneous chemical reactions
Received
11th August 2010
, Accepted 7th September 2010
First published on
22nd October 2010
Abstract
This paper describes a new way to control temperatures of heterogeneous exothermic reactions such as heterogeneous catalytic reaction and polymerization by using encapsulated nanoparticles of phase change materials as thermally functional additives. Silica-encapsulated indium nanoparticles and silica encapsulated paraffin nanoparticles are used to absorb heat released in catalytic reaction and to mitigate gel effect of polymerization, respectively. The local hot spots that are induced by non-homogenous catalyst packing, reactant concentration fluctuation, and abrupt change of polymerization rate lead to solid to liquid phase change of nanoparticle cores so as to avoid thermal runaway by converting energies from exothermic reactions to latent heat of fusion. By quenching local hot spots at initial stage, reaction rates do not rise significantly because the thermal energy produced in reaction is isothermally removed. Nanoparticles of phase change materials will open a new dimension for thermal management of exothermic reactions to quench local hot spots, prevent thermal runaway of reaction, and change product distribution.
Introduction
The thermal runaway of an exothermic chemical reaction refers to a situation, in which increases in temperature will change reaction condition in such a way that temperature increases further.1–3 The thermal runaway affects the yield, selectivity and safety of many reactions including heterogeneous catalytic reaction, free radical polymerization, electrochemical energy conversion, etc. The thermal runaway of heterogeneous catalytic reactions can cause side reactions, catalyst deactivation, and loss in productivity or selectivity, and leads to explosion if released reaction heat cannot be removed quickly.4–8 A similar effect in polymerization is also called auto-acceleration or gel effect, in which positive feedback will speed up polymerization, and results in heat accumulation due to increased viscosity.9,10 In the case of electrochemical reaction, thermal runaway is the major cause of battery explosion due to temperature rise. A common feature in these exothermic reaction systems is the existence of hot spots induced by non-uniformities of catalyst packing, reactant concentration, as well as heating and cooling effects.11–13
The temperature of heterogeneous reactions is often controlled by proportional–integral–derivative (PID) unit, where temperature around or inside a reactor will be monitored continuously. Once the measured temperature is higher than the designed value, cold air or liquid will be circulated to remove extra heat, or reactant feeding rate will be reduced to limit reaction heat. However, the performance of temperature control depends on the locations and sizes of thermocouples, and heating/cooling units, which cannot be distributed uniformly in the reactor or made sufficiently small to detect or quench microsize hot spots. For heterogeneous catalytic reactions, the reactions take place inside micropores, where the temperatures are higher than those around the reactor. It takes some time for reaction heat transferring to thermocouple from hot spots to activate control units. Such response delay causes temperature increase and leads to ineffectiveness in temperature control.14–16 The thermal runaways of polymerizations cannot be controlled readily using PID units as well, because high viscosity products prevent efficient heat transfer from hot spots. A small quantity of inhibitor is often added into the reactor at early stage of runaway, or polymerization is carried out in water to absorb the reaction heat.
Single phase substances in either liquid or solid phases have small heat capacity and cannot take much thermal energy. As a result, significant temperature rises occur even if small amounts of thermal energy are absorbed by solids or liquids. An effective way to enhance the heat capacity of a pure substance is to add materials that undergo phase change at certain temperature where the latent heat of fusion will contribute significantly to the heat capacity of mixture.17 The solid–liquid phase change material (PCM) involves small volume change, and sufficient heat energy, and has been added into single phase fluid in order to enhance its heat capacity.18,19 Dissipating heat into PCM results in a nearly isothermal heat sink during melting and the operating temperature can be adjusted by using different PCMs so that melting does not occur until needed. A variety of PCM materials such as paraffin waxes, inorganic salt hydrates, or metal eutectic alloys have been used to maintain desired temperature and reduce the fluctuation of temperature.20–23 However, bulk PCMs are not very useful for many applications such as temperature controls of heterogeneous chemical reactors for several reasons. (1) In order to exploit latent heats of fusion for heat absorbing, PCMs should be sufficiently small so that it melts rapidly. It has been shown that if the radius of PCM is reduced by 10 times, the time required for complete melting reduces by 100 times.24 (2) To work in a heterogeneous reactor, the PCM should be encapsulated inside a shell with good sealing and stability to prevent leakage or agglomerate. (3) PCM should form homogeneous mixture with reactants or catalysts in order to quench local microsized hot spots.
Instead of using inert solid (sand) to support catalytic species or liquid (water) to reduce gel effect of polymerization reaction, the advent of nanostructured materials provides a new approach for thermal managements of exothermic reactions. This article describes the use of a new nanostructured material, encapsulated phase change nanoparticles (nano-PCM), to control the thermal runaway of catalytic reactions and polymerizations, where nano-PCMs can absorb reaction heat, and change phases from solid to liquid. The core materials are metal nanoparticles or paraffin wax nanoparticles, which change phases at suitable temperature. The non-melting shells are made of silica or polymer, and are stable at operating conditions to prevent the leakage or oxidization of core material.25 Due to their small sizes, inert surfaces, and large heat-absorbing capabilities, nano-PCMs can be mixed homogeneously with solid catalysts or monomers to quench local hot spots before accumulation of heat energy at a large scale, thus breaking the positive feedback loop between the reaction rate and temperature, and postponing onset of thermal runaway by absorbing reaction heat (Fig. 1). Nano-PCMs do not increase the size of catalytic reactor, because active species can be supported at shells of nano-PCMs; in addition, polymers can be dissolved in its good solvent, and separated from nano-PCM after polymerization. Two highly exothermic reactions, platinum catalyzed methanol oxidation and polymerization of methyl methacrylate (MMA), have been used as examples to prove the generality of this approach.26,27
Experimental procedures
Chemicals such as tetraethoxysilane, ethanol, methanol, tetrahydrofuran, and polyethylene-block-polyethylene glycol at molecular weight of 1400 were obtained from Aldrich and used as received. Poly-α-olefin with boiling point of 250 °C is from Air Force Research Laboratory. Indium, methyl methacrylate (MMA), azoisobutyronitrile (AIBN), toluene and acetic acid are from Alfa Aesar. Polyethylene wax (POLYWAX 1000, melting temperature of 110 °C) is provided by Baker Hughes.
Metallic phase change nanoparticles are made by directly boiling metal powders. 1.0 g of indium powders (−100 mesh) is boiling in poly-α-olefin (PAO) at ∼200 °C at a stirring rate of 800 rpm for 12 h.17 After cooling down to room temperature, nanoparticles are separated by centrifugation, washed with ethanol for three times, and dried in nitrogen. Sol–gel method is used to encapsulate nanoparticles with silica after removing nanoparticles by centrifuging and washing by ethanol. The nanoparticles are encapsulated in silica by decomposing tetraethoxysilane (TEOS) at 70 °C as below. 0.1 g of nanoparticles is dispersed into ethanol and sonicated for 10 min, 1 ml TEOS is added into the solution and sonicated for 1 h, which is followed by adding ammonia hydroxide as catalyst for formation of silica. The thickness of silica shell is controlled by changing TEOS concentration and TEOS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nanoparticle ratio.28,29
Silica encapsulated polyethylene (paraffin wax) nanoparticles are made as following. 1.0 g of polyethylene, 1.0 g of TEOS and 0.25 g polyethylene-block-polyethylene glycol are dissolved in 4 ml of toluene at 100 °C. 50 ml of water are added in 250 ml of three-neck flask equipped with mechanic stirrer, and heated to 95 °C, and toluene solution is poured into three-neck flask, stir vigorously for 60 min to form white emulsion. 0.4 g of acetic acid solution (10 wt%) are added into the above mixture, and cool down to 55 °C and stir at 300 rpm for 3 h to ensure complete hydrolysis and condensation of TEOS. The product is separated by centrifuging at 8500 rpm for 10 min and wash with water for three times, dry in oven at 60 °C for 24 h.
nanoparticle ratio.28,29
Silica encapsulated polyethylene (paraffin wax) nanoparticles are made as following. 1.0 g of polyethylene, 1.0 g of TEOS and 0.25 g polyethylene-block-polyethylene glycol are dissolved in 4 ml of toluene at 100 °C. 50 ml of water are added in 250 ml of three-neck flask equipped with mechanic stirrer, and heated to 95 °C, and toluene solution is poured into three-neck flask, stir vigorously for 60 min to form white emulsion. 0.4 g of acetic acid solution (10 wt%) are added into the above mixture, and cool down to 55 °C and stir at 300 rpm for 3 h to ensure complete hydrolysis and condensation of TEOS. The product is separated by centrifuging at 8500 rpm for 10 min and wash with water for three times, dry in oven at 60 °C for 24 h.
Characterization
The structures, compositions, and thermal properties of these nanoparticles have been studied by using a variety of techniques. Transmission electron microscopy (TEM) images are acquired on a JEOL 1011 TEM operating at 100 kV, and high resolution image is collected on a TECNAI F30 TEM. X-Ray diffraction (XRD) analysis is carried out on Rigaku X-ray diffractometer with CuKα radiation (40 kV, 30 mA). Energy-dispersed X-ray spectroscopy is performed using a Zeiss Ultra 55 scanning electron microscopy (SEM). A PerkinElmer differential scanning calorimetry (DSC 7) is used to measure the fusion enthalpy and melting temperature of nanoparticles.
Supported Pt/SiO2 catalyst is made by impregnating SiO2 (200 m2 g−1) with an aqueous solution of tetraammineplatinum nitrate at 25 °C for 4 h. The impregnated support is dried in ambient air at 125 °C and heated at 500 °C for 4 h. The obtained precursor is reduced in H2/He (10% v/v) mixture at 500 °C for 2 h. 10 mg of the catalyst are then mixed with 1 g of silica encapsulated indium nanoparticles, and the mixture is loaded into a quartz reactor to form a 1 cm column. A nickel–chromium thermocouple of 1 mm diameter is inserted in the reactor to measure the temperature of the catalyst. Before the catalysis experiments, the reactor is heated at 120 °C in a flow of helium gas for 0.5 h. A mixture gas of He, O2, and methanol (87/9/4, p/p/p) at 100 ml min−1 is switched into the reactor. Two on-line chromatograph systems are used to analyze products: a Porapak Q packed column with thermal conductivity detector for carbon dioxide and a methyl-silicone capillary column with flame ionization detector for organic products.
Methyl methacrylate (MMA) monomer is polymerized under isothermal batch condition in a 10 ml glass bottle at 80 °C. The reaction is initiated by adding 0.1 g of azoisobutyronitrile (AIBN) into 2 ml of MMA monomer. Different amounts of silica encapsulated paraffin nanoparticles have been added to prevent thermal runaway. A thermocouple is inserted into the solution, and the reaction temperature is recorded by using an Agilent (34970A) data acquisition unit. The molecular weight of polymer product is measured by gel permeation chromatography (GPC) in tetrahydrofuran (THF).
Results and discussions
1. Structure and composition of silica encapsulated indium nanoparticles
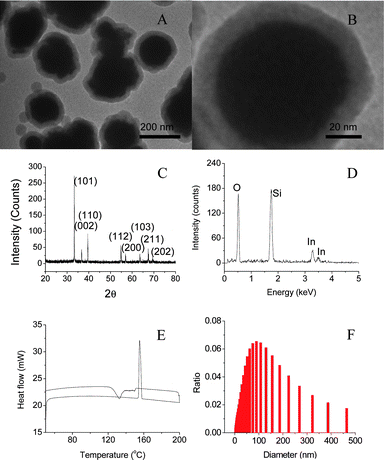
This direct boiling and sol–gel method can produce nano-PCMs of indium with core diameter of ∼150 nm and shell thickness of 10–20 nm as shown in Fig. 2A. High resolution TEM image shows crystallized core and amorphous shell (Fig. 2B). XRD pattern shows that body-centered tetragonal indium is formed in amorphous silica shells (Fig. 2C). The composition of nanoparticles has been confirmed by EDX analysis (Fig. 2D), where the signals of indium and silicon can be identified clearly. Fig. 2E is the DSC curve of nanoparticles collected at ramp rate of 10 °C min−1, where the melting and solidifying of indium nanoparticles occur at 156 and 130 °C, respectively. Fig. 2F shows size distribution of the encapsulated indium nanoparticles, where the mean diameter of nanoparticles is determined as 150 nm by using dynamic light scattering. The core diameter can be controlled in the range from 10 to 200 nm by changing reaction conditions including reaction time and precursor concentration. The thickness of silica shell has been controlled in a range of 10 and 30 nm by changing the molar ratio of nanoparticle and TEOS.
2. Structure and composition of encapsulated paraffin nanoparticles
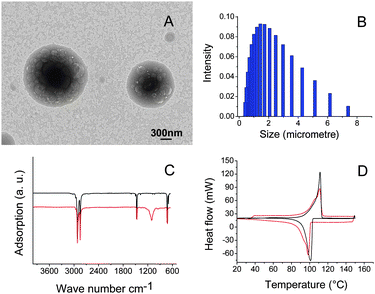
Interfacial polycondensation method has been used to produce silica encapsulated polyethylene nanoparticles. Fig. 3A shows a TEM image, where dark polyethylene core and light silica shell can be seen clearly. The core diameter and shell thickness are approximately 1000 and 500 nm, respectively. The mean size of particles derived from DLS is about 2 µm (Fig. 3B). Fig. 3C shows Fourier transform infrared (FT-IR) spectra of polyethylene and encapsulated polyethylene nanoparticles, where the characteristic peaks of polyethylene can be observed (Fig. 3C, red). The two absorption peaks at 2916 and 2848 cm−1 are characteristic peaks of aliphatic C–H stretching vibration; the peak at 1464 cm−1 is assigned to C–H bending vibration; the peak at 721 cm−1 is associated with in-plane rocking vibration of CH2 group. The absorption peaks at 941 and 3430 cm−1 are assigned to the stretching of hydroxyl group in Si–OH and residual water and 1111 cm−1 is assigned to the asymmetrical stretching of siloxane bond Si–O–Si. The thermal property of nanoparticles has been studied by DSC. Fig. 3D shows DSC curves of polyethylene and silica encapsulated polyethylene nanoparticles. The melting and solidifying points of polyethylene are at 110 and 100 °C, respectively. The latent heats of fusion of paraffin and silica encapsulated paraffin nanoparticles are derived from DSC to be 200 and 160 J g−1, respectively, from which the ratio of PCM in core–shell structure is determined to be approximately 80 wt%.
3. Preventing thermal runaway of catalytic reaction using silica-encapsulated indium nanoparticles
Encapsulated indium nanoparticles are used to prevent thermal runaway of methanol oxidation on supported platinum catalyst. Fig. 4 shows the relation between measured temperature and time after feeding methanol in vapor form, where the temperature control unit is set at 120 °C. In the control experiment with 10 mg of catalyst and 1 g silica as dilutor, the measured temperature quickly rises from 120 to 320 °C and remains constant at 320 °C due to strong heat liberation of the reaction. From the distribution of products as listed in Table 1, CO2 is the main product, suggesting burning of methanol. Instead of using low thermal conductivity silica (1.3 W m−1 K−1) as dilutor in catalyst bed, silicon carbide with high thermal conductivity (∼360 W m−1 K−1) to conduct reaction heat has also been used in the control experiment. However, for the strong exothermal reaction of methanol oxidation catalyzed by Pt/SiO2, silicon carbide cannot eliminate thermal runaway, and the highest and steady temperatures reach 351 °C and 310 °C respectively. When 10 mg of catalyst and 1 g of nano-PCM are packed in the reactor, the reaction temperature is constant at ∼120 °C, meaning effective control of thermal runaway. Although the conversion is as low as 0.6% because of the low reaction temperature, the trend of methanol burning at initial stage of reaction is efficiently controlled. The large latent heat of indium (28.52 J g−1 K−1) takes heat from hot spots of reaction. The ramp rate of temperature at the initial stage of runaway is dependent on the relative mass ratio of nano-PCMs to Pt/SiO2 catalyst as shown in Fig. 4 inset. The highest ramp rate (29.5 °C min−1) is achieved in the cases when there are no nano-PCMs (silica or silicon carbide as dilutor). The ramp rate decreases as the relative amounts of nano-PCMs increases. In the case of 30 mg catalyst and 1 g nano-PCMs, the temperature rises to 140 °C. Increasing the catalyst to 50 mg and keeping PCMs at 1 g leads to a further temperature increases to 165 °C, which is higher than the melting temperature of indium (156 °C), and the temperature of catalyst bed can still be controlled. It implies that local hot spots can melt encapsulated indium nanoparticles due to their high temperature, and the phase change of indium nanoparticles adsorbs reaction heat, quenches local hot spots, and prevents thermal runaway of reaction.
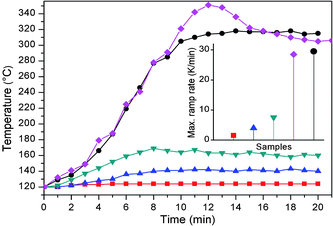 |
| | Fig. 4 Reaction time dependent temperature at different amount of nano-PCM and Pt/SiO2 catalyst: 0 g of nano-PCM and 10 mg of catalyst diluted in 1 g of SiO2 (circle) or 1 g SiC (diamond); 1 g of nano-PCM and 50 mg of catalyst (down triangle), 1 g of nano-PCM and 30 mg of catalyst (up-triangle), 1 g of nano-PCM and 1 mg of catalyst (square). The ramp rates at different amount of nano-PCM and catalyst (inset). | |
| Samplesa |
Steady temp./°C |
Conv. (%) |
Selectivitya (%) |
| HCHO |
MF |
CO2 |
DMM |
DMOH |
|
In@SiO2 denotes silica encapsulated indium PCMs; MF, DMM and DMOH mean methyl formate, dimethoxy methane and methoxymethanol.
|
| 10 mg Pt/SiO2 1 g SiO2 |
320 |
98.2 |
— |
12.1 |
83.2 |
4.7 |
— |
| 10 mg Pt/SiO2 1 g SiC |
310 |
99.3 |
— |
11.2 |
87.7 |
1.1 |
— |
| 10 mg Pt/SiO2 1 g In@SiO2 |
120 |
0.6 |
97.3 |
2.6 |
— |
— |
0.1 |
| 30 mg Pt/SiO2 1 g In@SiO2 |
140 |
5.5 |
75.2 |
21.3 |
3.1 |
0.2 |
0.2 |
| 50 mg Pt/SiO2 1 g In@SiO2 |
165 |
32.5 |
32.5 |
52.3 |
14.8 |
0.3 |
0.1 |
Controlling thermal runaway affects the distribution of the product as shown in Table 1. The conversion of methanol on 10 mg catalyst and 1 g silica is highest (98.2%), but the major product is carbon dioxide. Adding nano-PCM reduces conversion yield and amount of carbon dioxide. At the same load of nano-PCMs (1 g), the conversion yield increases from 0.6 to 32.5% as catalyst increases from 10 to 50 mg. The selectivity to HCHO decreases from 97.3 to 32.5%, and selectivity to methyl formate increases from 2.6 to 52.3%. Due to suppression of runaway, the selectivity to carbon dioxide in methanol oxidation is reduced and the selectivity to partial oxidation products increases. The selectivity to methyl formate (MF) increases to 52.3% when the amount of catalyst is 50 mg. In the mild condition, the reaction rate is decreased, but the yield of methyl formate is increased. Therefore, nano-PCMs can be used to control thermal runaway and promote the yield of products of strong exothermic reaction.
4. Preventing thermal runaway of polymerization using silica-encapsulated polyethylene nanoparticles
The polymerization of methyl methacrylate (MMA) monomer is a strong exothermic reaction. DSC has been used as isothermal calorimeter to determine adiabatic thermal energy release from polymerization, which starts at 80 °C and reaches a maximum at 125 °C as shown in Fig. 5A (red curve). The heat-releasing peak corresponds to reaction enthalpy of −1717.8 mJ for 3 mg of MMA. The melting of polyethylene is endothermic with peak temperature of 110.3 °C and peak area of 202.1 J g−1 (black curve). When 2.5 mg of silica encapsulated polyethylene nanoparticles containing 2 mg polyethylene is added into 2 mg MMA, the exothermic heat decreases to 460.3 mJ (green curve). Doubling the amount of encapsulated polyethylene nanoparticles to 5 mg while keeping amount of MMA (2 mg) leads to reduction of heat to 94.2 mJ (blue curve). Adding silica encapsulated polyethylene nanoparticles in polymerization leads to reduction of exothermic heat due to suppression of local hot spots. When the measured temperature is between 80 and 105 °C, heat released from the polymerization is less than the fusion enthalpy of polyethylene, and a small endothermic peak appears in green and blue curves. (The polyethylene melts due to hot spots, even if the measured temperature is lower than its melting point.) When the measured temperature is increased, the polymerization rate is increased, and the released heat is absorbed by melting polyethylene. The excessive heat gives a small exothermic peak.
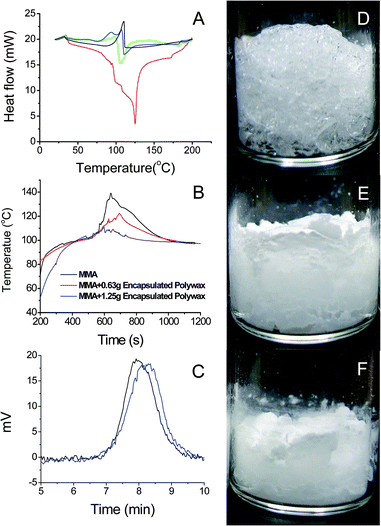 |
| | Fig. 5 DSC curves of polyethylene (black); adiabatic polymerization of 2 mg MMA (red), 2 mg MMA with 2.5 mg (green) or 5.0 mg (blue) silica encapsulated polyethylene nanoparticles; the temperature rises of 1 g MMA (black), 1 g MMA with 0.63 g (red) or 1.25 g (blue) silica encapsulated polyethylene nanoparticles when temperature is maintained at 80 °C (B); the molecular weights of PMMA with (black) and without (blue) silica encapsulated polyethylene nanoparticles from gel permeation chromatography (C); morphologies of products from three reactions, where the images from left to right correspond to no nanoparticles (D), 0.63 (E) and 1.25 g (F) nanoparticles, respectively. | |
In order to further confirm the suppression of thermal runaway of polymerization, encapsulated polyethylene nanoparticles are added into monomer of methyl methacrylate. The temperature is controlled at 80 °C in a water bath, and a thermocouple is inserted into the monomer to record reaction temperature. Fig. 5B shows the magnitudes of measured temperature as functions of time. In the absence of phase change nanoparticles, when polymerization is initiated, the measured temperature increases to 100 °C and the temperature increases abruptly to 140 °C after 600 s, which is presumably because of viscosity increase and thermal runaway. When 0.63 g of silica encapsulated polyethylene nanoparticles are added into monomer, the temperature increases to 120 °C after 700 s. Adding 1.25 g of encapsulated polyethylene nanoparticles leads to smooth reaction, where the highest temperature measured by thermocouple is 110 °C, which is close to the melting point of polyethylene. The molecular weights of generated PMMAs are derived from gel permeation chromatography. The permeation time of PMMA made without silica encapsulated polyethylene nanoparticles is 7.92 min, corresponding to molecular weight of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; the permeation time of PMMA made with encapsulated polyethylene particles is 8.25 min, corresponding to molecular weight 15
000; the permeation time of PMMA made with encapsulated polyethylene particles is 8.25 min, corresponding to molecular weight 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 (Fig. 5C). It is understandable that polymer made at high polymerization temperature normally has higher molecular weight. Fig. 5D–F show the morphologies of polymer produced in the three polymerization reactions. In the absence of polyethylene nanoparticles, polymerization is more acute, which generates bubbles in polymethyl methacrylate (PMMA); adding encapsulated polyethylene particles makes polymerization stable.
800 (Fig. 5C). It is understandable that polymer made at high polymerization temperature normally has higher molecular weight. Fig. 5D–F show the morphologies of polymer produced in the three polymerization reactions. In the absence of polyethylene nanoparticles, polymerization is more acute, which generates bubbles in polymethyl methacrylate (PMMA); adding encapsulated polyethylene particles makes polymerization stable.
5. Thermophysical characteristics of encapsulated phase change nanoparticles
The effect of nano-PCM on preventing thermal runaway can be derived by comparing heat capacities of silica particles and silica encapsulated indium nanoparticles. The specific heat of silica is 0.7 J g−1 K−1, and the latent heat of indium is 28.52 J g−1. If the melting range of indium nanoparticles is taken as 10 °C (151 to 161 °C), the heat that can be taken by 1 g of indium nanoparticles (ignore contribution of shell) will be four times the heat that can be taken by 1 g of silica in the same temperature range. The heat capacity of 1 g of indium nanoparticles will be ∼80 times higher than that of the catalyst, meaning temperature rise of the catalyst due to hot spots can be effectively lowered to avoid heat accumulation.
In order to exploit the latent heat of fusion, nano-PCMs have to melt rapidly during reaction. The heat absorption of nanoparticles depends on characteristics of heat conduction in nanoparticles, which in turn depends upon particle size and material properties. The heat transfer from environment into particles is determined by the difference between environment temperature and surface temperature of particles.
| | 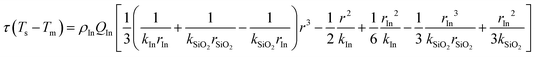 | (1) |
where
τ is the melting time when the solid radius is
r,
ρl is the density of
nanoparticles, and
Ql is the latent heat of fusion of the
nanoparticles,
Ts and
Tm are the surface temperature and melting point of
nanoparticles, respectively,
rp is the
nanoparticle radius before melting, and
kl is thermal conductivity of
nanoparticles.
kIn and
kSiO2 are 81.8 and 1.3 W m
−1 K
−1, respectively,
rIn and
rSiO2 are 100 and 120 nm, respectively,
QIn is 28.52 J g
−1 and
ρIn is 7.3 g cm
−3. Replace all symbols with numbers, and let
r equal to 0 nm, the
eqn (1) is rewritten as
| | | τ(Ts − Tm) = 0.92 × 10−7 s K | (2) |
Fig. 6A shows the melting time as the function of temperature difference between surface temperature (hot spot) and melting temperature for indium nanoparticles. The melting time τ is 0.92 µs when Ts − Tm = 0.1 K. In case of silica encapsulated polyethylene nanoparticles, kWax and kshell are taken as 0.15 and 1.3 W m−1 K−1, rWax and rshell are 500 nm and 1 µm, respectively, QWax is 232 J g−1 and ρWax is 0.7 g cm−3. The melting equation can be written as:
| | | τ(Ts − Tm) = 1.49 × 10−5 s K | (3) |
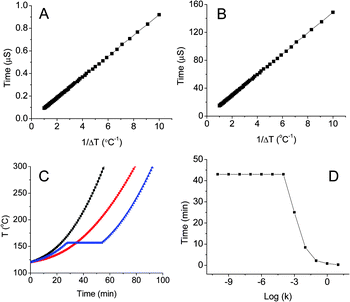 |
| | Fig. 6 Calculated melting times of 200 nm indium nanoparticles with 40 nm silica shell (A); melting times of 1 µm paraffin nanoparticles with 500 nm silica shell (B); simulated temperature rises as functions of time when the mass ratio of silica and indium is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 (square), 2 0 (square), 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 (circle), and 1 0 (circle), and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (triangle) (C); melting delay as a function of rate constant (D). 1 (triangle) (C); melting delay as a function of rate constant (D). | |
Fig. 6B shows the melting time as a function of temperature difference for polyethylene nanoparticles. The melting time of silica encapsulated paraffin is 148.7 µs when Ts − Tm = 0.1 K. Thus, the phase change nanoparticles can response rapidly to local hot spots to remove thermal energy.
6. Kinetics of nano-PCM in prevention of thermal runaway
The contribution of phase change materials to prevent thermal runaway is studied for a general reaction aA + bB ↔ cC, in which heat flow can be expressed as30| | 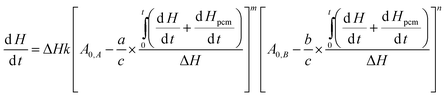 | (4) |
where dH/dt is the instant heat flow of reaction at a certain time, 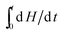 is the corresponding accumulated heat, ΔH is the total heat generation from the reaction, k is the rate constant, C0,A and C0,B are the initial concentrations of reactants, a, b, and c are stoichiometric constants, m and n are orders of the reaction, and Hpcm is the fusion enthalpy of phase change nanoparticles. For methanol oxidation, m is 1 and n is 0, and eqn (4) is thus simplified to:
is the corresponding accumulated heat, ΔH is the total heat generation from the reaction, k is the rate constant, C0,A and C0,B are the initial concentrations of reactants, a, b, and c are stoichiometric constants, m and n are orders of the reaction, and Hpcm is the fusion enthalpy of phase change nanoparticles. For methanol oxidation, m is 1 and n is 0, and eqn (4) is thus simplified to:| | 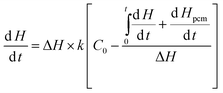 | (5) |
Solving the differential eqn (5) yields:
| | 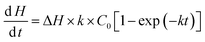 | (6) |
Integrating eqn (6) gives
| | | H = ΔHC0[kt + exp (−kt)] | (7) |
The released heat is absorbed by the catalyst, and phase change nanoparticles, if the mass of the catalyst (10 mg) is negligible; the heat released from the reaction is absorbed by silica and indium as a discrete function of temperature:
| | 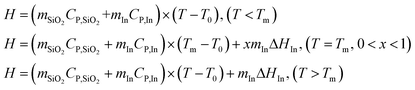 | (8) |
The complete oxidation process of methanol generates water and carbon dioxide:
| CH3OH + 3/2O2 = 2H2O + CO2 |
The enthalpy change of the reaction is ΔH* = −676.5 J g−1.31 Since the amount of methanol that is oxidized is a function of time, the total heat generation from the reaction can be described as ΔH = 0.064t J. Thus, the temperature of the system is written as:
| | 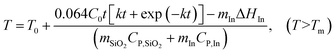 | (9) |
where
C0 = 0.17,
CP,SiO2 = 0.7 J g
−1 K
−1,
CP,In = 0.23 J g
−1 K
−1, Δ
HIn = 28.58 J g
−1,
T0 = 120 °C,
Tm = 156.7 °C,
mSiO2 = 1 g, and
mIn = 1 g. Inputting these values into
eqn (9) gives
| | 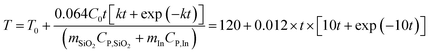 | (10) |
When the temperature reaches the melting point of indium, the temperature will be maintained until all indium melts. Then the temperature will continue to increase as shown in eqn (11):
| | 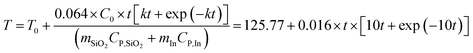 | (11) |
where
k =
Aexp (−
Eact/
RT),
32 and
k is dependent on temperature and
activation energy.
32–34Fig. 6C shows the relation between temperature and time, where the temperature of 1 g of silica increases faster than that of 2 g of silica due to low thermal mass; the temperature of 1 g of silica with 1 g of
indium nanoparticles shows a 25 min delay. The length of delay is dependent on the mass of
indium nanoparticles and the rate constant of the reaction. If the mass of
indium nanoparticles is constant, the delay time will decrease as the rate constant increases (
Fig. 6D). The delay time does not change for log (
k) < −4 S
−1, but decreases rapidly from 43 to 3 min when log (
k) increases from −4 to −1 S
−1. For log (
k) = 1 S
−1, the delay lasts 16 s.
The temperature rise delay demonstrated in these experiments efficiently restricts thermal runaway of the catalytic reactions, and can provide one additional application benefit—temperature stabilization of pulsed or interrupted reactions. One broad technological application would be stabilization of electrode temperatures inside rechargeable ionic battery cells. All modern battery technologies incorporate nanostructure surfaces of electrodes to increase ionic exchange areas and achieve a high density of the electrical energy storage. With such technologies, there is an increased risk of the temperature spikes during rapid charging and discharging event, which may lead to the battery thermal runaway with significant degradation of properties, as well as an occasional catastrophic failure by explosion and fire. The discussed here encapsulated PCM nanoparticles can efficiently be applicable for battery electrochemical reaction temperature runaway mitigation. Particle dielectric shell can provide for a reduced interference with the electrical current flow, while the small size will allow for a rapid response time and reliable response in multiple thermal cycles expected during the battery life.
Conclusions
Adding encapsulated phase change nanoparticles into exothermic reaction systems such as catalytic and polymerization reactions can effectively quench local hot spots, prevent thermal runaway, and change product distribution. A rational design of nano-heat-sinks with different core materials and shell materials can extend the use of this method to a broad range of exothermic reactions. By using different phase change materials, the operating range of nano-heat-sinks can be changed. In particular, silica encapsulated phase change nanoparticles can be used as new multifunctional catalyst support with thermal management capability, which is critical for multiple chemical processes ranging from high quality polymer manufacturing to battery applications.
Acknowledgements
This work is supported by National Science Foundations (CTET 0828466) and Air Force Research Laboratory (AFRL). Some of characterizations are done at Materials Characterization Facilities (MCF) at the University of Central Florida (UCF).
References
- P. K. Shukla and S. Pushpavanam, Ind. Eng. Chem. Res., 1994, 33, 3202 CrossRef CAS
 .
.
- M. Surianarayanan, R. Vijayaraghavan, G. Swaminathan and P. G. Rao, Curr. Sci., 2001, 80, 738 CAS
 .
.
- T. Ohgushi, S. Komarneni and A. S. Bhalla, J. Porous Mater., 2001, 8, 23 CrossRef CAS
 .
.
- J. Verhoeff and P. J. Vandenberg, J. Therm. Anal., 1984, 29, 533 CrossRef CAS
 .
.
- A. N. R. Bos, L. Vandebeld, J. B. Overkamp and K. R. Westerterp, Chem. Eng. Commun., 1993, 121, 27 CrossRef CAS
 .
.
- V. Balakotaiah, D. Kodra and D. Nguyen, Chem. Eng. Sci., 1995, 50, 1149 CrossRef CAS
 .
.
- B. K. Mandal, A. K. Padhi, Z. Shi, S. Chakraborty and R. Filler, J. Power Sources, 2006, 161, 1341 CrossRef CAS
 .
.
- R. Vijayaraghavan, M. Surianarayanan, V. Armel, D. R. MacFarlane and V. P. Sridhar, Chem. Commun., 2009, 6297 RSC
 .
.
- J. Albert and G. Luft, Chem. Eng. Process., 1998, 37, 55 CrossRef CAS
 .
.
- A. Maider, R. L. Jose and M. A. Jose, Macromol. Mater. Eng., 2005, 290, 242 CrossRef
 .
.
- D. Vanhove, Appl. Catal., A, 1996, 138, 215 CrossRef CAS
 .
.
- R. Henda, A. Machac and B. Nilsson, Chem. Eng. J., 2008, 143, 195 CrossRef CAS
 .
.
- N. Frikha, E. Schaer and J. L. Houzelot, Thermochim. Acta, 2006, 449, 47 CrossRef CAS
 .
.
- E. Velo, C. M. Bosch and F. Recasens, Ind. Eng. Chem. Res., 1996, 35, 1288 CrossRef CAS
 .
.
- S. Bashir, T. Chovan, B. J. Masri, A. Mukherjee, A. Pant, S. Sen, P. Vijayaraghavan and J. M. Berty, Ind. Eng. Chem. Res., 1992, 31, 2164 CrossRef CAS
 .
.
- M. M. J. Quina and R. M. Q. Ferreira, Ind. Eng. Chem. Res., 1999, 38, 4615 CrossRef CAS
 .
.
- Y. Hong, S. Ding, W. Wu, J. Hu, A. A. Voevodin, L. Gschwender, E. Snyder, L. Chow and M. Su, ACS Appl. Mater. Interfaces, 2010, 2, 1685 Search PubMed
 .
.
- Z.-X. Gong and A. S. Mujumdar, Appl. Therm. Eng., 1996, 16, 807 CrossRef CAS
 .
.
- Z. H. Han, F. Y. Cao and B. Yang, Appl. Phys. Lett., 2008, 92, 243104 CrossRef
 .
.
- H. Marc, D. W. Randy, J. P. Stephen, M. P. Jason, M. Lou and C. Calvin, J. Electron. Packag., 2002, 124, 419 CrossRef
 .
.
- M. J. Vesligaj and C. H. Amon, IEEE Trans. Compon. Packag. Technol., 1999, 22, 541 CrossRef
 .
.
- S. Ahmet, K. Ali and K. Kamil, Int. J. Energy Res., 2008, 32, 154 CrossRef
 .
.
- H. W. Ryu, S. W. Woo, B. C. Shin and S. D. Kim, Sol. Energy Mater. Sol. Cells, 1992, 27, 161 CrossRef CAS
 .
.
- T. Yokota, M. Murayama and J. M. Howe, Phys. Rev. Lett., 2003, 91, 265504 CrossRef
 .
.
- W. Welnic, A. Pamungkas, R. Detemple, C. Steimer, S. Blugel and M. Wuttig, Nat. Mater., 2006, 5, 56 CrossRef CAS
 .
.
- A. Wan and C.-t. Yeh, Catal. Today, 2007, 129, 293 CrossRef CAS
 .
.
- R. Tesser, M. Di Serio and E. Santacesaria, Catal. Today, 2003, 77, 325 CrossRef CAS
 .
.
- C. Graf, D. L. J. Vossen, A. Imhof and A. V. Blaaderen, Langmuir, 2003, 19, 6693 CrossRef CAS
 .
.
- L. Ma, Y. Hong, Z. Ma, C. Kaittanis and J. M. Perez, Appl. Phys. Lett., 2009, 95, 043701 CrossRef
 .
.
- X.-R. Li and H. Koseki, J. Loss Prev. Process Ind., 2005, 18, 460 CrossRef
 .
.
- B. E. Traxel and K. L. Hohn, Appl. Catal., A, 2003, 244, 129 CrossRef CAS
 .
.
- J. W. Tester, P. A. Webley and H. R. Holgate, Ind. Eng. Chem. Res., 1993, 32, 236 CrossRef CAS
 .
.
- R. W. McCabe and D. F. McCready, J. Phys. Chem., 1986, 90, 1428 CrossRef CAS
 .
.
- K. W. Frese and C. Chen, J. Phys. Chem., 1995, 99, 6074 CrossRef CAS
 .
.
Footnote |
| † M. Zhang, Y. Hong and S. Ding have contributed equally to this work |
|
| This journal is © The Royal Society of Chemistry 2010 |
Click here to see how this site uses Cookies. View our privacy policy here. 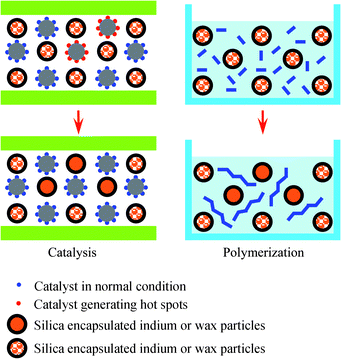
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nanoparticle ratio.28,29
nanoparticle ratio.28,29


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; the permeation time of PMMA made with encapsulated polyethylene particles is 8.25 min, corresponding to molecular weight 15
000; the permeation time of PMMA made with encapsulated polyethylene particles is 8.25 min, corresponding to molecular weight 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 (Fig. 5C). It is understandable that polymer made at high polymerization temperature normally has higher molecular weight. Fig. 5D–F show the morphologies of polymer produced in the three polymerization reactions. In the absence of polyethylene nanoparticles, polymerization is more acute, which generates bubbles in polymethyl methacrylate (PMMA); adding encapsulated polyethylene particles makes polymerization stable.
800 (Fig. 5C). It is understandable that polymer made at high polymerization temperature normally has higher molecular weight. Fig. 5D–F show the morphologies of polymer produced in the three polymerization reactions. In the absence of polyethylene nanoparticles, polymerization is more acute, which generates bubbles in polymethyl methacrylate (PMMA); adding encapsulated polyethylene particles makes polymerization stable.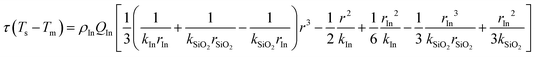

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 (square), 2
0 (square), 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 (circle), and 1
0 (circle), and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (triangle) (C); melting delay as a function of rate constant (D).
1 (triangle) (C); melting delay as a function of rate constant (D).
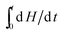 is the corresponding accumulated heat, ΔH is the total heat generation from the reaction, k is the rate constant, C0,A and C0,B are the initial concentrations of reactants, a, b, and c are stoichiometric constants, m and n are orders of the reaction, and Hpcm is the fusion enthalpy of phase change nanoparticles. For methanol oxidation, m is 1 and n is 0, and eqn (4) is thus simplified to:
is the corresponding accumulated heat, ΔH is the total heat generation from the reaction, k is the rate constant, C0,A and C0,B are the initial concentrations of reactants, a, b, and c are stoichiometric constants, m and n are orders of the reaction, and Hpcm is the fusion enthalpy of phase change nanoparticles. For methanol oxidation, m is 1 and n is 0, and eqn (4) is thus simplified to: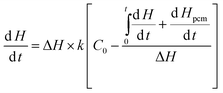
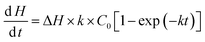
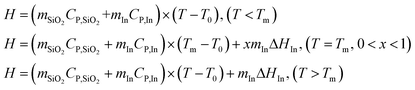
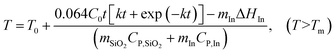
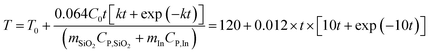
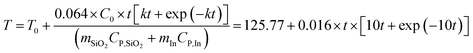
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.