Determination of the propagation rate coefficient of acrylonitrile

Abstract

For the first time, the propagation rate coefficient k_p of acrylonitrile has been determined in a broad temperature range in propylene carbonate solution via the pulsed laser polymerization–size exclusion chromatography technique employing a high frequency pulsed laser system. k_p was determined to fit the Arrhenius relation ln(k_p/L mol⁻¹ s⁻¹) = 14.42 − 1855K/T.

---

Introduction

The model-based development of novel synthesis strategies or the refinement of existing procedures employing radical polymerization requires exact knowledge over the individual rate coefficients for the initiation, propagation, termination and transfer reaction. Among these parameters, the propagation rate coefficient k_p is perhaps the most important one as the determination of all other rate coefficients is often carried out relative to the propagation reaction. Accurate k_p can be accessed via the IUPAC-recommended Pulsed Laser Polymerization–Size Exclusion Chromatography (PLP–SEC) technique.¹ Since its development in the late eighties,² a large number of monomers has been investigated, both commodity and specialty monomers,³ and benchmark values for the most important compounds have been published, among those are the most relevant monomers from an industrial point of view.⁴ However, to date no PLP-data have been provided for the monomer acrylonitrile (AN) despite its importance in academia and industry for commodity (co)polymers. The reason for such limited progress was that no satisfying results could be obtained so far for AN from PLP–SEC (or any other technique) mostly due to the low solubility of polyacrylonitrile in its own monomer solution. Other complications arise from the fast termination reaction in acrylonitrilepolymerizations that have so far prevented successful PLP–SEC experiments at the routinely applied laser frequencies (for a discussion of the effect of laser frequency on PLP and acrylonitrile specifically see below).

Recently, we introduced a PLP–SEC setup that allows for laser pulsing at 500 Hz repetition rate (see reference for details on the setup and the PLP methodology in general).⁵Via the rapid pulsing (compared to the 100 Hz laser systems that were in use before), we were able to overcome the limitations that beset acrylatepolymerizations when going to elevated temperatures (where PLP–SEC measurements are constrained due to significant transfer-to-polymer reactions).^6,7 In addition, we were able to demonstrate that by the use of high laser frequencies, the measurement of fast terminating monomers such as vinyl acetate could be significantly improved.⁸ As the quality of the data could readily be increased via the application of a 500 Hz pulsing rate, it seemed mandatory to apply high frequency PLP towards acrylonitrile to overcome the high termination limitation and provide—for the first time—reliable propagation rate coefficients for this monomer.

Results and discussion

Typically, PLP experiments are carried out in bulk solutions only containing monomer and initiator. Via such a procedure, solvent effects on the propagation rate can be largely excluded and easily comparable data are thus obtained. It is, however, noteworthy that—while a solvent can have an influence on k_p⁹—its presence does usually not compromise the quality of the PLP experiment. However, in order to perform a reliable PLP experiment of AN, a solvent must be chosen that allows for good solubility of the monomer and the polymer to prevent precipitation during polymerization (and hence disruption of the chain length–time correlation). Suitable solvents for AN are the polar dimethyl sulfoxide or dimethylacetamide; for technical applications, ethylene carbonate is often employed. The latter solvent is not overly suitable for PLP due to its melting point above ambient temperature. The first two solvents can unfortunately also not be used due to their instability towards laser irradiation. When PLP of AN is tried in such solvents, the solutions turn yellow after only a few laser pulses and no satisfying polymer distributions are obtained. After testing a variety of solvents, propylene carbonate (PC) was identified as a reasonable choice. PC is liquid even below 0 °C and allows for good solubility of polyAN, at least at low polymer concentrations (in PLP, as low as possible monomer conversions are targeted). Connected with the solubility issue is the determination of absolute molecular weight distributions viasize exclusion chromatography. The main experimental error of PLP–SEC arises from uncertainties of the exclusion chromatography. In the present case, all polymer samples were characterized on a SEC system employing dimethylacetamide as the liquid phase. Fortunately, literature Mark–Houwink parameters are available for polyAN in dimethylacetamide, so that the principle of universal calibration can be applied and no specialized equipment is required (see ESI† for details on the molecular weight analysis).

In PLP, the propagation rate coefficient k_p is determined via the relation:

L_i = k_p × c_M × i × t₀, where i = 1, 2, 3… (1)

where L denotes the chain length at the characteristic inflection points of the molecular weight distribution (MWD) (identified by picking the maxima of the first derivative of the distributions), c_M the monomer concentration and t₀ the dark time between two consecutive laser pulses. For many systems up to four points of inflection can be observed; the presence of two characteristic points in the MWD is, however, sufficient to obtain reliable k_p (technically, if other criteria are fulfilled, even the second point of inflection is not strictly required).¹ From these two characteristic points two rate coefficients can be obtained that ideally are identical. As the second point of inflection is, however, often not as easily determined, usually L₁ is used and L₂ only serves as an affirmation. Other experiments that may be performed to check for the reliability of the results are how dependent the result is on experimental parameters such as initiator concentration and pulse frequency. If no interfering effect exists (such as for example with acrylate monomers),⁵ a variation of these reaction parameters should not change the resulting k_p. For AN, especially the initiator concentration is of interest. The radical polymerization of AN is most likely associated with a relatively high termination rate coefficient, thus the radical concentration decay after a single laser pulse is rapid, preventing the formation of higher order inflection points due to only an insufficient number of radicals surviving more than one dark time period. Faster laser pulsing can overcome this problem to some extent by reducing the dark time between two laser pulses. Yet, experiments with different initiator (2,2-dimethoxy-2-phenylacetophenone, DMPA) concentrations must be performed. Fig. 1 depicts the derivatives of MWDs obtained from PLP at 50 °C where all experimental parameters were kept constant except the initiator concentration. c_DMPA was varied between 2.1 × 10⁻³ and 2.1 × 10⁻² mol L⁻¹. All derivatives exhibit two maxima, M₁ and M₂, with M_i = L_i × M_AN and M_AN being the monomer molecular weight. The first maximum is almost identical in all cases and for the second maxima almost the same molecular weight is observed in all cases. Both characteristic points are spaced by roughly 0.3 logarithmic units, which corresponds well to the factor of two that these values should be associated with following eqn (1). (It should be noted that the molecular weight axis in Fig. 1 is based on a polystyrene calibration for technical reasons, for absolute values of M₁ and M₂ see Table S1†.)

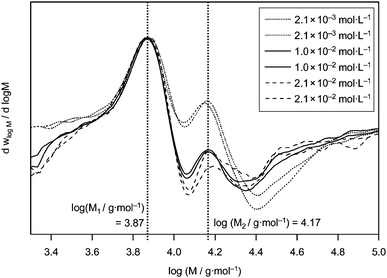Fig. 1 Derivatives of the molecular weight distributions of PLP samples generated under variation of the DPMA concentration at 50 °C. The vertical lines indicate the average molecular weight at the characteristic inflection points (based on a direct polystyrene calibration).

All derivatives in Fig. 1 are scaled to the first maximum M₁. As can be readily seen, the curves obtained from the low-initiator concentration experiments display the most pronounced second maxima. This better distinction arises from the lower overall termination rate directly after application of the laser pulse (and thus instantaneous generation of small radicals). Comparatively larger amounts of polymer in the sample that was terminated by the action of the next laser pulse rather than conventional dark time termination are thus found, because the absolute rate of termination is lower. Generation of fewer radicals with each laser pulse results in improved structuring of the resulting MWD. Regardless, within the tested concentration range, no significant variation of the first inflection point can be observed and it can therefore be safely concluded that the concentration of DMPA has virtually no influence on the resulting k_p values. Thus, all following experiments have been performed at constant c_DMPA = 5 × 10⁻³ mol L⁻¹.

In contrast, the choice of the pulse frequency has a significant impact on the k_p determination. At 50 °C, when the frequency is varied between 500 and 300 Hz, no large deviation from the average value is seen. If, however, the pulse frequency is further lowered to 100 Hz, a successive reduction of the apparent k_p by about 25% is obtained. Remarkably, a very similar result was obtained when studying the frequency dependence of the apparent k_p in vinyl acetatepolymerization.⁸ All MWDs obtained from the samples generated at different pulse frequencies exhibited second inflection points, hence it can be assumed that the experiments themselves did not fail. The deviation between k_p,1 and k_p,2 is above 10% (see Table S1†), but still within reasonable limits. A possible explanation for the change in the apparent result could be that AN—similar to acrylate monomers—undergoes significant transfer reactions that cause a blurring of the time–chain length relation. If transfer occurs, the (close to) monodisperse growth of radicals is disturbed. PLP may thus yield false rate coefficients that do not represent the true k_p, but a somewhat decreased average rate coefficient, which is influenced by the transfer reaction.¹⁰ If such interference of transfer is the case, a frequency dependence should only be observed in a certain range. Above a critical repetition rate, almost no variation of the resulting k_p can be expected. The data obtained herein thus suggest that ANpolymerization is at least to some degree influenced by transfer reactions, either transfer to monomer or (intramolecular) transfer to polymer reactions. AN and acrylates are structurally similar and analogous formation of so-called midchain radicals during radical chain growth appears likely. Midchain radicals are radicals that are formed upon intramolecular radical transfer by which the secondary radical chain terminus is converted into a more stable tertiary radical on the polymer backbone.¹¹ These radicals are significantly more stable and undergo chain propagation at a reduced rate. As a consequence, the polymer product carries chain branches of various lengths and the average propagation rate is somewhat decreased. Regardless, further proof for such a hypothesis is necessary and at the present stage it cannot be concluded to what extent transfer to polymer reactions plays a role as—alternatively—qualitatively similar results from PLP could be obtained when extensive transfer to monomer occurs. The question of the extent of branching occurring in these systems has further relevance as chain branches cause changes in the hydrodynamic volume of chains in solution and thus the SEC analysis might be affected.^6,7,12

The frequency variation has shown that reliable k_p values can be obtained for AN as long as sufficiently high pulse rates are employed. Hence, in what follows, always the maximum frequency, i.e. 500 Hz, was applied. By doing so, relatively small molecular weights are obtained which makes the chromatographic analysis slightly less reliable. However, this seems to be an acceptable compromise, compared to the apparent reduction of k_p at lower frequencies.

PLP experiments were carried out in the temperature range from close to 1 °C up to 76 °C (the boiling point of AN is 77 °C). The monomer concentration was (as in the experiments discussed above) relatively low at close to 5.3 mol L⁻¹. However, a higher monomer concentration is difficult to employ as the solubility of the polyAN decreases strongly with increasing AN content in the reaction mixture.

Fig. 2 shows the Arrhenius plot for k_p in the full temperature range. It should be noted that not all samples, especially at lower temperatures, exhibited a clear second point of inflection. Often, only a shoulder could be observed and thus no k_p,₂ could be obtained to test the primary result from the first inflection point (see Table S2† for a collation of all experimental results). Generally, the quality of the characteristic PLP pattern improved with reaction temperature. Such an improvement can be rationalized by considering the usually low overall activation energy of the termination reaction. Thus, similar radical decay rates after a laser pulse can be assumed for all temperatures. In consequence, a comparatively high amount of low molecular weight material is produced in the PLP experiment. Only with increasing temperature do the propagating radicals grow sufficiently fast to higher molecular weight which makes the typical PLP pattern more visible on the log M weighted SEC distribution. Additionally, the lack of a clearly distinguishable second inflection point can also be attributed—at least in parts—to the generally lower resolution of the employed SEC columns at lower molecular weight. Regardless, an overall good linearity of the Arrhenius plot is obtained. Should the determination of k_p at lower temperatures have been compromised by the separation of the SEC (or any other reason), a significantly different slope of the plot should be seen for this region. Thus all data can be considered reliable, despite the lack of clearly distinguishable second inflection points. k_p increases from about 2200 L mol⁻¹ s⁻¹ at 2.6 °C to 9400 L mol⁻¹ s⁻¹ at 76 °C. Within 95% confidence, the data are best fitted by the following expression:

ln(k_p/L mol⁻¹ s⁻¹) = (14.4 ± 0.3) − (1855 ± 90)/T

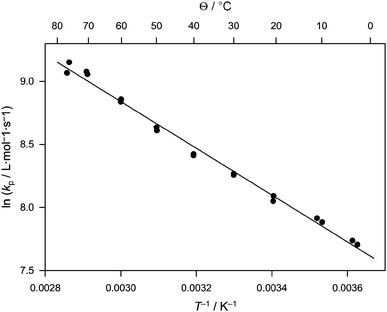Fig. 2 Arrhenius plot for the propagation rate coefficient of acrylonitrile in propylene carbonate solution (c_M = 5.3 mol L⁻¹) in the temperature range from 0 to 77 °C.

The slope corresponds to an activation energy of (15.4 ± 0.8) kJ mol⁻¹ and the y-axis intercept to a frequency factor of 1.79 × 10⁶ L mol⁻¹ s⁻¹. The activation energy is in the range typical for acrylate monomers. The frequency factor, however, is significantly lower than for an acrylate, where A is often close to an order of magnitude higher. The absolute rate coefficients compare well to vinyl acetate with k_p(25 °C) = 3560 L mol⁻¹ s⁻¹ for AN and 4140 L mol⁻¹ s⁻¹ for vinyl acetate. As mentioned above, only little experimental data were available to date for the propagation rate coefficient of AN. Zetterlund et al. used a nitroxide-trapping technique with subsequent quantitative product analysis viaHPLC/ESI-MS to estimate propagation rate coefficients for acrylonitrile oligomers.¹³ These authors estimated k_p to be approximately 4800 L mol⁻¹ s⁻¹ at 75 °C which is in good agreement with our PLP data considering the accuracy of the methods applied. Other literature data are available from quantum mechanical calculations, as various groups have attempted to estimate AN propagation rates from theory.^14–16 Interestingly, all calculations predicted a somewhat larger activation energy than experimentally determined with, however, similar absolute k_p in the covered temperature range. Nevertheless, experiment and theory are in remarkably good agreement if one considers the high dependence of the calculated activation energy on the choice of the level of theory in the calculations. A critical assessment of the theoretical calculations would, however, go far beyond the scope of the present work, especially considering that the calculated data were obtained for reactions in the gas phase or for different solvents, which might also affect the propagation rate coefficient to some extent.

Conclusions

For the first time, the propagation rate coefficient of AN was determined via the PLP–SEC technique. k_p data were obtained in the temperature range between 2 and 76 °C and an activation energy of 15.4 kJ mol⁻¹ and a frequency factor of 1.79 × 10⁶ L mol⁻¹ s⁻¹ were obtained. No significant influence of the initiator concentration on the outcome of the experiments could be detected. The variation of the pulse repetition frequency indicated that the result is, however, somewhat dependent on the pulse rate, which can be overcome by using an as high as possible pulse repetition rate. Transfer to polymer reactions might be responsible for this effect, yet further experiments are required to underpin this hypothesis.

Acknowledgements

C.B.-K. acknowledges financial support from the Karlsruhe Institute of Technology (KIT) within the Excellence Initiative for leading German Universities supporting the current project. T.J. is grateful for additional support from the Fonds der Chemischen Industrie.

References

1. M. Buback, R. G. Gilbert, R. A. Hutchinson, B. Klumpermann, F. D. Kuchta, K. F. O'Driscoll, G. T. Russell and J. Schweer, Macromol. Chem. Phys., 1995, 196, 3267–3280.
2. O. F. Olaj, I. Bitai and F. Hinkelmann, Makromol. Chem., 1987, 188, 1689–1702.
3. Y. Ming, C. Barner-Kowollik, J. P. A. Heuts and T. P. Davis, Macromol. Rapid Commun., 2001, 22, 1035–1040.
4. (a) S. Beuermann, M. Buback, T. P. Davis, R. G. Gilbert, R. A. Hutchinson, O. F. Olaj, G. T. Russell, J. Schweer and A. M. van Herk, Macromol. Chem. Phys., 1997, 198, 1545–1560; (b) S. Beuermann, M. Buback, T. P. Davis, R. G. Gilbert, R. A. Hutchinson, A. Kajiwara, B. Klumpermann and G. T. Russell, Macromol. Chem. Phys., 2000, 201, 1355–1364.
5. C. Barner-Kowollik, F. Günzler and T. Junkers, Macromolecules, 2008, 41, 8971–8973.
6. B. Dervaux, T. Junkers, M. Schneider-Baumann, F. E. Du Prez and C. Barner-Kowollik, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 7090–7095.
7. C. Barner-Kowollik, F. Bennet, M. Schneider-Baumann, D. Voll, T. Rölle, T. Fäcke, M. S. Weiser, F. K. Bruder and T. Junkers, Polym. Chem., 2010 10.1039/b9py00352e.
8. T. Junkers, D. Voll and C. Barner-Kowollik, e-Polym., 2009, 076.
9. S. Beuermann, Macromol. Rapid Commun., 2009, 30, 1066–1088.
10. A. N. Nikitin, P. Castignolles, B. Charleux and J. P. Vairon, Macromol. Rapid Commun., 2003, 24, 778–782.
11. (a) T. Junkers and C. Barner-Kowollik, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 7585–7605; (b) M. Buback, P. Hesse, T. Junkers, T. Sergeeva and T. Theis, Macromolecules, 2008, 41, 288–291.
12. P. Castignolles, Macromol. Rapid Commun., 2010, 30, 1995–2001.
13. P. B. Zetterlund, W. K. Busfield and I. D. Jenkins, Macromolecules, 1999, 32, 8041–8045.
14. D. M. Huang, M. J. Monteiro and R. G. Gilbert, Macromolecules, 1998, 31, 5175–5187.
15. E. I. Izgorodina and M. L. Coote, Chem. Phys., 2006, 324, 96–110.
16. P. Deglmann, I. Müller, F. Becker, A. Schäfer, K.-D. Hungenberg and H. Weiß, Macromol. React. Eng., 2009, 3, 496–515.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental details, tabulated results and selected molecular weight distributions and their derivatives. See DOI: 10.1039/c0py00019a

‡ Current address: Universiteit Hasselt, Agoralaan Gebouw D, B-3590 Diepenbeek, Belgium. E-mail: tanja.junkers@uhasselt.be; Fax: +32 11 268399; Tel: +32 11 268318.

---