DFT investigations on the ring-opening polymerization of cyclic carbonates catalyzed by zinc-{β-diiminate} complexes†
Iker
del Rosal
a,
Pierre
Brignou
b,
Sophie M.
Guillaume
*b,
Jean-François
Carpentier
*b and
Laurent
Maron
*a
aUMR5626 LPCNO (IRSAMC), Université de Toulouse, INSA and CNRS, 135 Avenue de Rangueil, F-31077, Toulouse, France. E-mail: laurent.maron@irsamc.ups-tlse.fr
bUMR 6226 Sciences Chimiques de Rennes, Université de Rennes 1—CNRS, Campus de Beaulieu, 35042, Rennes Cedex, France. E-mail: sophie.guillaume@univ-rennes1.fr; jean-francois.carpentier@univ-rennes1.fr
First published on 8th September 2011
Abstract
The ring-opening polymerizations of trimethylene (TMC) and tetramethylene (7CC) carbonates using [(BDIiPr)Zn(N(SiMe3)2)] (BDIiPr = 2-((2,6-diisopropylphenyl)amido)-4-((2,6-diisopropylphenyl)-imino)-2-pentene) as catalyst precursor, in the presence of benzyl alcohol (BnOH) as co-initiator, have been investigated by means of density functional theory (DFT) calculations. This computational study highlights that the zinc-amido precursor is by itself a poor catalyst whereas the alkoxide analogue, obtained upon alcoholysis of the Zn–N bond by BnOH, is very active. For both TMC and 7CC, the initiation and the first propagation steps have been computed. In each case, the reaction proceeds via two transition states, involving nucleophilic attack of the alkoxide group followed by the ring-opening of the cyclic carbonates. Thus TMC and 7CC undergo a similar ROP process with accessible energy barriers. The analysis of the reaction mechanisms and energy profiles indicates that the relaxation of the growing polymer chain is an important feature, making the overall reaction exergonic (7CC) or athermic (TMC). This exothermicity difference predicts that 7CC is slightly more easily polymerizable than TMC, which is consistent with what is already known in the case of six- and seven-membered related lactones and previous experimental investigations on TMC and 7CC.
1. Introduction
In the past few decades, increasing attention has been dedicated to the study of linear aliphatic polycarbonates. Interest in these polymers arises from their application as valuable alternatives to petrochemical thermoplastics,1–4 especially in the biomedical/pharmaceutical, packaging and microelectronic domains.5–7Ring-opening polymerization (ROP) is the most common, suitable and reliable procedure to synthesize polyesters/polycarbonates with controlled molecular features (expected molecular mass, narrow molecular mass distribution, chain-end fidelity, tuned topology, controlled sequences of different monomer units,…).8,9 In our approach towards environmentally friendly, “green” synthesis of polycarbonates, we have essentially investigated the “immortal” ROP (iROP) of six- and seven-membered ring cyclic carbonates exemplified with trimethylene carbonate (TMC)10–15 and with the one-carbon larger homologuetetramethylene carbonate (7CC) (Fig. 1).16,17 Such iROP procedures involve systems composed of a catalyst/initiator (a metallic or organic species) and a co-initiator (typically a protic nucleophilic source such as an alcohol) used in excess and thus also acting as chain transfer reagent (CTA). The main benefits of such “immortal” ROP processes over “classic” living ones are essentially described in terms of low catalyst loadings, allowing the minimization of possible toxicity issues revolving around catalytic residues, and large amounts of CTA, thus enabling to (i) make the process truly catalyticvs. both the number of monomer units converted and polymer chains produced, and (ii) tune the polymer α-chain end according to the CTA selected.10 | ||
| Fig. 1 Optimized structures of trimethylene (TMC) and tetramethylene (7CC) carbonates. | ||
Among the various metallic, metallo-organic and organic catalytic systems evaluated in the ROP of TMC and 7CC, the zinc β-diiminate catalyst precursor [(BDIiPr)Zn(N(SiMe3)2)] (BDIiPr = 2-((2,6-diisopropylphenyl)amido)-4-((2,6-diisopropylphenyl)-imino)-2-pentene)18,19 proved highly efficient.10–17 In fact, as many as 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 TMC equiv. could be easily converted to poly(trimethylene carbonate) (PTMC) within 2 h at 60 °C from the [(BDIiPr)Zn(N(SiMe3)2)]/BnOH catalytic system, using as little as 20 ppm of zinc complex in the initial loading, under controlled conditions.11,12 The activity (turnover frequency value expressed in molMonomer molCatalyst−1 h−1: TOFmax = 23
500 TMC equiv. could be easily converted to poly(trimethylene carbonate) (PTMC) within 2 h at 60 °C from the [(BDIiPr)Zn(N(SiMe3)2)]/BnOH catalytic system, using as little as 20 ppm of zinc complex in the initial loading, under controlled conditions.11,12 The activity (turnover frequency value expressed in molMonomer molCatalyst−1 h−1: TOFmax = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 h−1; this value is a lower estimate since it is derived from a reaction time that was not necessarily optimized) thus obtained is among the top values thus far reported for the ROP of TMC catalyzed through a coordination-insertion mechanism.
250 h−1; this value is a lower estimate since it is derived from a reaction time that was not necessarily optimized) thus obtained is among the top values thus far reported for the ROP of TMC catalyzed through a coordination-insertion mechanism.
The combination of experimental and computational investigations provides deeper insights and understanding into the mechanism of ROP reactions. As previously demonstrated, valuable rationalization on polymerization pathways—that cannot be easily established experimentally—can be gained from DFT studies.20–30 Following our experimental studies on the iROP of TMC- and 7CC-related carbonates,10–17 we have computationally examined the polymerization mechanism of both monomers. We especially aimed at assessing the differences in reactivity of the zinc β-diiminate complex [(BDIiPr)Zn(N(SiMe3)2)] itself and of the catalytic system based on the combination of this latter complex with an alcohol towards the ROP of TMC and 7CC. Close examination/comparison of the ROP mechanisms has been conducted; in particular, the key initiation step has been considered in details.
2. Methodological details
All DFT calculations were performed with Gaussian 03.31 Calculations were carried out at the DFT level of theory using the hybrid functional B3PW91.32–37 Geometry optimizations were achieved without any symmetry restriction. Calculations of vibrational frequencies were systematically done in order to characterize the nature of stationary points. Stuttgart effective core potentials38 and their associated basis set were used for zinc. Silicon, nitrogen, hydrogen, carbon and oxygen atoms were treated with 6-31G(d,p) double-ζ basis sets.39,40 The electron density and partial charge distribution were examined in terms of localized electron-pair bonding units by using the NBO program.41,42 Through this method, the input atomic orbital basis set is transformed via natural atomic orbitals (NAOs) and natural hybrid orbitals (NHOs) into natural bond orbitals (NBOs), which correspond to the localized one-center (“lone pair”) and two-center (“bond”) elements of the Lewis structure. All possible interactions between “filled” (donor) Lewis-type NBOs and “empty” (acceptor) non-Lewis NBOs, together with their energetic quantification (stabilization energy), were obtained by a second order perturbation theory analysis of the Fock matrix. Only stabilization energy higher than 10 kcal mol−1 was considered.3. Results and discussion
3.1. Ring-opening polymerization of cyclic carbonates by a zinc-disilylamide catalyst/initiator
In the “immortal” ROP of cyclic esters, including carbonates, [(BDIiPr)Zn(N(SiMe3)2)] has been successfully used in association with an alcohol for the in situ formation of the initiating alkoxide species, [(BDIiPr)Zn(O-alkyl)]. Indeed, alcoholysis of the Zn–Namido bond results, upon elimination of HN(SiMe3)2, in the formation of the corresponding zinc-alkoxide species which is the true active species in the ROP process. For the sake of comparison, the reactivity of the zinc-amido precursor was first evaluated.ROP of a cyclic carbonate initiated by [(BDIiPr)Zn(N(SiMe3)2)] is assumed to proceed via a coordination-insertion mechanism.8–10 This mechanism involves first the coordination of the monomer to the electrophilic metal center through the exocyclic carbonyl oxygen. Formation of this adduct activates the carbonyl group of the monomer towards the nucleophilic attack of the active function (X = N(SiMe3)2). This reaction is followed by the cleavage of the acyl-oxygen bond, i.e., a spontaneous ring-opening. Repetition of these elementary steps constitutes propagation and eventually leads to the building up of living (BDIiPr)Zn–{O⋯C(O)}X species. When all of the monomer has been consumed, addition of an acid in the reaction medium deactivates those (BDIiPr)Zn–{O⋯OC(O)}X species to give eventually H–[polymer]–X chains.
The free Gibbs energy profiles determined for the initiation step of the ROP of TMC and 7CC with [(BDIiPr)Zn(N(SiMe3)2)] are presented in Fig. 2. As aforementioned, the first insertion begins, in both cases, by coordination of the carbonatevia the carbonyl oxygen atom (exocyclic oxygen, labelled Oexo) to the zinc center, to form the adduct ITMC (Fig. 3a) and I7CC (Fig. 3d) for TMC and 7CC, respectively. Formation of these adducts is endergonic by 6.1 (TMC) and 7.0 (7CC) kcal mol−1 with respect to the entrance channel, which corresponds more or less to the loss of entropy upon coordination at room temperature. These adducts connect the transition states, TSITMC→IITMC and TSI7CC→II7CC, which lie 44.4 and 45.2 kcal mol−1 above (50.5 and 52.2 kcal mol−1 with respect to the separated reactants) for TMC and 7CC, respectively. This reaction appears thus kinetically very demanding.
![Calculated free-energy profiles of the initiation step in the ROP of TMC (R = (CH2)3) and 7CC (R = (CH2)4) mediated by [(BDIiPr)Zn(N(SiMe3)2)]; all energy values are reported in kcal mol−1.](/image/article/2011/PY/c1py00309g/c1py00309g-f2.gif) | ||
| Fig. 2 Calculated free-energy profiles of the initiation step in the ROP of TMC (R = (CH2)3) and 7CC (R = (CH2)4) mediated by [(BDIiPr)Zn(N(SiMe3)2)]; all energy values are reported in kcal mol−1. | ||
![Optimized structures of complexes involved in the initiation step of the ROP of cyclic carbonates mediated by [(BDIiPr)Zn(N(SiMe3)2)].](/image/article/2011/PY/c1py00309g/c1py00309g-f3.gif) | ||
| Fig. 3 Optimized structures of complexes involved in the initiation step of the ROP of cyclic carbonates mediated by [(BDIiPr)Zn(N(SiMe3)2)]. | ||
These transition states lead to the tetrahedral intermediates IITMC (Fig. 3b) and II7CC (Fig. 3e) for TMC and 7CC, respectively. These intermediates are found to be unstable (+11.8 kcal mol−1 with respect to the separated reactants for TMC and +10.1 kcal mol−1 for 7CC) and connect to the ring-opening transition states. The activation barriers are 9.7 and 10.8 kcal mol−1 for TMC and 7CC, respectively, indicating an easy process. According to this energy profile, the nucleophilic attack of the (SiMe3)2N−group is the rate-determining step of the ROP initiation of TMC and 7CC and is overall a highly demanding process. This is in line with the experimental results reported on the ROP of the TMC with this amido complex that have evidenced an overall slow initiation process.11
3.2. Ring-opening polymerization of cyclic carbonates by a zinc-alkoxide catalyst/initiator
In order to save some computational time, the [(BDIiPr)Zn(OBn)] complex was simplified by replacing the benzyloxy by a methoxy moiety. With either alcohol (i.e., benzyl or methyl alcohol), formation of the corresponding zinc-alkoxide complex [(BDIiPr)Zn(OR)]‡ from the zinc-amido precursor [(BDIiPr)Zn(N(SiMe3)2)] was computed thermodynamically favorable, with alcoholysis energies of −28.4 and −27.2 kcal mol−1 for BnOH and MeOH, respectively. The exergonicity of the exchange reaction is in agreement with the observed rapid and total conversion of the amide to the active alkoxide species.11 Geometrically speaking, replacing BnO by MeO does not significantly influence the structural features of the complex. In particular, all important Zn–ligand bond distances (including the Zn–Oalkoxide, Zn–N1 and Zn–N2 bond distances) in [(BDIiPr)Zn(OMe)] follow the same trends as those observed in [(BDIiPr)Zn(OBn)] (Fig. 4). Likewise, the NPA charges in [(BDIiPr)Zn(OMe)] are similar to those in [(BDIiPr)Zn(OBn)], especially the zinc (+1.34 vs. +1.36), Oalkoxide (−0.95 vs. −0.95), N1 (−0.76 vs. −0.77) and N2 (−0.75 vs. −0.75) charges that are virtually the same in both complexes. Thus, such a modeling strategy did not alter either the nucleophilic character of the alkoxide ligand or the structure of the zinc complex, which suggests that it should not affect the reactivity of the complex.![Comparison of the structural parameters (distances in Å) and of the natural charges in [(BDIiPr)Zn(OMe)] (R = Me) and, in brackets, [(BDIiPr)Zn(OBn)] (R = C7H7).](/image/article/2011/PY/c1py00309g/c1py00309g-f4.gif) | ||
| Fig. 4 Comparison of the structural parameters (distances in Å) and of the natural charges in [(BDIiPr)Zn(OMe)] (R = Me) and, in brackets, [(BDIiPr)Zn(OBn)] (R = C7H7). | ||
For the sake of clarity, the study of the ROP reaction of the two different cyclic carbonates with [(BDIiPr)Zn(OMe)] will be separately analyzed in the following subsections. The ROP mechanism for 7CC is first discussed, followed by that of TMC.
Initiation step of the ROP of 7CC. The initiation step of the ROP of 7CC with [(BDIiPr)Zn(OMe)] takes place via the same two steps defined for [(BDIiPr)Zn(N(SiMe3)2)] that is a nucleophilic attack followed by the ring-opening. An additional step has been included in this study, namely the relaxation of the growing polymer chain in the final product.
The free Gibbs energy profile of the initiation step of the ROP of 7CC is depicted in Fig. 5. The reaction begins by the formation of an endergonic A7CC adduct (Fig. 6a) with a Gibbs-free energy of 10.8 kcal mol−1 with respect to the entrance channel, which corresponds to the loss of entropy upon coordination of free 7CC. For A7CC, the zinc center exhibits a distorted tetrahedral environment with two Zn–N distances of 1.98 and 1.99 Å and two Zn–O distances of 1.89 Å (OMe) and 2.27 Å (7CC). This contrasts with the trigonal planar geometry of [(BDIiPr)Zn(OMe)] which features two Zn–N distances of 1.95 and 1.96 Å, one Zn–OOMe distance of 1.82 Å, and a sum of angles around the metal center of 359°. The coordination of the exocyclic oxygen of 7CC to the metal center results in the polarization of the corresponding C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and makes the carbonyl carbon of the 7CC monomer more electrophilic (natural charges of 1.06 and −0.58 on CC
O bond and makes the carbonyl carbon of the 7CC monomer more electrophilic (natural charges of 1.06 and −0.58 on CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and Oexo for coordinated 7CCvs. 1.13 and −0.67 for free 7CC). Subsequently from A7CC, the nucleophilic attack takes place via the transition state TSA7CC→B7CC (Fig. 6b), yielding a first intermediate (B7CC, Fig. 6c) with the alkoxide group bonded to the carbonyl carbon of 7CC (OOMe–CC
O and Oexo for coordinated 7CCvs. 1.13 and −0.67 for free 7CC). Subsequently from A7CC, the nucleophilic attack takes place via the transition state TSA7CC→B7CC (Fig. 6b), yielding a first intermediate (B7CC, Fig. 6c) with the alkoxide group bonded to the carbonyl carbon of 7CC (OOMe–CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O average distance = 1.41 Å). The activation energy for the nucleophilic attack is calculated to be 16.1 kcal mol−1 above the separated reactants (5.3 kcal mol−1 above the adduct A7CC), which corresponds to a kinetically readily accessible process. The formation of the B7CC intermediate remains endergonic (+7.0 kcal mol−1) with respect to the separated reactants but is slightly exergonic (−3.8 kcal mol−1) with respect to adduct A7CC. From a geometrical point of view, the environment of the metal center changes from the tetrahedral geometry of TSA7CC→B7CC to a distorted trigonal planar geometry of B7CC (sum of angles around Zn = 358°). For B7CC, there is a significant decrease of the Zn–Oexo distance with respect to TSA7CC→B7CC (1.86 Å vs. 2.21 Å). Thus, the ring-opening occurs viaTSB7CC→C7CC (Fig. 6d) and results in the formation of a second intermediate (C7CC, Fig. 6e) in which the 7CC ring is completely opened (CC
O average distance = 1.41 Å). The activation energy for the nucleophilic attack is calculated to be 16.1 kcal mol−1 above the separated reactants (5.3 kcal mol−1 above the adduct A7CC), which corresponds to a kinetically readily accessible process. The formation of the B7CC intermediate remains endergonic (+7.0 kcal mol−1) with respect to the separated reactants but is slightly exergonic (−3.8 kcal mol−1) with respect to adduct A7CC. From a geometrical point of view, the environment of the metal center changes from the tetrahedral geometry of TSA7CC→B7CC to a distorted trigonal planar geometry of B7CC (sum of angles around Zn = 358°). For B7CC, there is a significant decrease of the Zn–Oexo distance with respect to TSA7CC→B7CC (1.86 Å vs. 2.21 Å). Thus, the ring-opening occurs viaTSB7CC→C7CC (Fig. 6d) and results in the formation of a second intermediate (C7CC, Fig. 6e) in which the 7CC ring is completely opened (CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oendo = 2.56 Å) and the intracyclic oxygen atom ensures the coordination to the metal center (Zn–Oendo = 1.87 Å and Zn–Oexo = 2.36 Å). The activation barrier for this process is predicted to be +7.4 kcal mol−1 with respect to the B7CC intermediate (+14.4 kcal mol−1 with respect to the entrance channel). The nucleophilic attack is, as observed previously, the rate-determining step of an overall facile reaction. At TSB7CC→C7CC, the endocyclic oxygen interacts with the metal center (Zn–Oendo distance of 2.01 Å), whereas the exocyclic oxygen moves away (Zn–Oexo = 2.06 Å for TSB7CC→C7CCvs. 1.86 Å for B7CC). These coordination changes lead to the partially opened 7CC ring, as shown by the increase of the CC
O–Oendo = 2.56 Å) and the intracyclic oxygen atom ensures the coordination to the metal center (Zn–Oendo = 1.87 Å and Zn–Oexo = 2.36 Å). The activation barrier for this process is predicted to be +7.4 kcal mol−1 with respect to the B7CC intermediate (+14.4 kcal mol−1 with respect to the entrance channel). The nucleophilic attack is, as observed previously, the rate-determining step of an overall facile reaction. At TSB7CC→C7CC, the endocyclic oxygen interacts with the metal center (Zn–Oendo distance of 2.01 Å), whereas the exocyclic oxygen moves away (Zn–Oexo = 2.06 Å for TSB7CC→C7CCvs. 1.86 Å for B7CC). These coordination changes lead to the partially opened 7CC ring, as shown by the increase of the CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oendo distance from 1.42 Å for B7CC to 1.86 Å for TSB7CC→C7CC. The last step concerns the relaxation of the growing polymer chain that essentially consists in the decoordination of the carbonate arm. This proceeds through transition state TSC7CC→D7CC (Fig. 6f), leading to the final exergonic D7CC product (Fig. 6g), with a Gibbs-free energy of −2.6 kcal mol−1 with respect to the entrance channel. The decoordination of the carbonate arm takes place via a low energy process with an activation barrier calculated to be +1.4 cal mol−1 with respect to the C7CC intermediate (+10.1 kcal mol−1 with respect to the separated reactants). For TSC7CC→D7CC, the NBO analysis revealed that the exocyclic oxygen atom remains in interaction with the metal center (donation from a lone pair of the oxygen atoms towards an empty p orbital of zinc). This transition state connects to the final [(BDIiPr)Zn{OC4H8OC(O)OMe}] product (D7CC) where the exocyclic oxygen is no longer interacting with the metal center. The endocyclic oxygen ensures the coordination of the carbonate arm to the metal center (Zn–Oendo distance of 1.82 Å).
O–Oendo distance from 1.42 Å for B7CC to 1.86 Å for TSB7CC→C7CC. The last step concerns the relaxation of the growing polymer chain that essentially consists in the decoordination of the carbonate arm. This proceeds through transition state TSC7CC→D7CC (Fig. 6f), leading to the final exergonic D7CC product (Fig. 6g), with a Gibbs-free energy of −2.6 kcal mol−1 with respect to the entrance channel. The decoordination of the carbonate arm takes place via a low energy process with an activation barrier calculated to be +1.4 cal mol−1 with respect to the C7CC intermediate (+10.1 kcal mol−1 with respect to the separated reactants). For TSC7CC→D7CC, the NBO analysis revealed that the exocyclic oxygen atom remains in interaction with the metal center (donation from a lone pair of the oxygen atoms towards an empty p orbital of zinc). This transition state connects to the final [(BDIiPr)Zn{OC4H8OC(O)OMe}] product (D7CC) where the exocyclic oxygen is no longer interacting with the metal center. The endocyclic oxygen ensures the coordination of the carbonate arm to the metal center (Zn–Oendo distance of 1.82 Å).
![Calculated free-energy profile of the initiation step of the ROP of 7CC mediated by [(BDIiPr)Zn(OMe)].](/image/article/2011/PY/c1py00309g/c1py00309g-f5.gif) | ||
| Fig. 5 Calculated free-energy profile of the initiation step of the ROP of 7CC mediated by [(BDIiPr)Zn(OMe)]. | ||
![Optimized structures of complexes involved in the initiation step of the ROP of 7CC mediated by [(BDIiPr)Zn(OMe)].](/image/article/2011/PY/c1py00309g/c1py00309g-f6.gif) | ||
| Fig. 6 Optimized structures of complexes involved in the initiation step of the ROP of 7CC mediated by [(BDIiPr)Zn(OMe)]. | ||
First propagation step of the ROP of 7CC. In order to get a better insight into the ROP of 7CC mediated by [(BDIiPr)Zn(OMe)], the first propagation step, namely the second carbonate insertion, was investigated. The energy profile computed for this step is shown in Fig. 7. The geometries and the natural charges of the different minima structures involved in the ROP initiation and the first propagation steps are depicted in Fig. 8.
![Calculated free-energy profile of the first propagation step of the ROP of 7CC mediated by [(BDIiPr)Zn(OMe)].](/image/article/2011/PY/c1py00309g/c1py00309g-f7.gif) | ||
| Fig. 7 Calculated free-energy profile of the first propagation step of the ROP of 7CC mediated by [(BDIiPr)Zn(OMe)]. | ||
![Comparison of the natural charges and the bond distances (in Å) of the minima structures involved in the ROP initiation (R = Me) and, in brackets, the first propagation (R = C4H8OC(O)OMe) step of 7CC mediated by [(BDIiPr)Zn(OR)] species (Ar = 2,6-diisopropylphenyl).](/image/article/2011/PY/c1py00309g/c1py00309g-f8.gif) | ||
| Fig. 8 Comparison of the natural charges and the bond distances (in Å) of the minima structures involved in the ROP initiation (R = Me) and, in brackets, the first propagation (R = C4H8OC(O)OMe) step of 7CC mediated by [(BDIiPr)Zn(OR)] species (Ar = 2,6-diisopropylphenyl). | ||
The energy data for the first propagation step are similar to those obtained for the initiation step (Fig. 7). The reaction begins by the formation of an endergonic 7CC adduct, E7CC, with a Gibbs-free energy of 13.3 kcal mol−1 with respect to the separated reactants (D7CC; product + one 7CC monomer). For E7CC (as for A7CC), the 7CC monomer is coordinated to the zinc atom by its exocyclic oxygen atom (Zn–Oexo distances of 2.27 and 2.23 Å for E7CC and A7CC, respectively; the slightly longer distance in E7CC being explained by steric effects). Nucleophilic attack of the oxygen atom of the growing polymer chain onto the carbonyl carbon of 7CC proceeds through transition state TSE7CC→F7CC. The corresponding activation barrier (+4.7 kcal mol−1 with respect to E7CC adduct) is close to that computed for the initiation step in Fig. 5 (+5.3 kcal mol−1 above the A7CC adduct). For TSE7CC→F7CC, as for TSA7CC→B7CC, the zinc center exhibits a distorted tetrahedral environment, with two Zn–N distances of 1.99 and 1.98 Å (1.98 and 1.98 Å for TSA7CC→B7CC) and two Zn–O distances of 2.13 Å (7CC) and 1.94 Å (growing polymer chain) (2.13 and 1.94 Å for TSA7CC→B7CC, respectively). This transition state leads to adduct F7CC, calculated to be endergonic by 9.3 kcal mol−1 with respect to the separated reactants (D7CC + 7CC and −4.0 kcal mol−1 with respect to adduct E7CC). For F7CC, the oxygen of the open carbonate moiety (first monomer unit introduced) is now bonded to the 7CC carbonyl carbon (CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–O = 1.41 Å). In this case, even if the planarity around the metal center is similar between F7CC and B7CC (sum of angles around Zn = 359° and 358° for F7CC and B7CC, respectively), the steric repulsion between the β-diiminate ligand and the growing polymer chain induces a lateral shift of the ligand. Indeed, although the Zn–Oexo distance remains similar in F7CC with respect to that in B7CC (1.85 Å for B7CCvs. 1.86 Å for F7CC), the Oexo–Zn–N angle twists by ca. 12° to minimize the steric repulsion (from 124° and 134° for B7CC to 112° and 148° for F7CC). The CC
O–O = 1.41 Å). In this case, even if the planarity around the metal center is similar between F7CC and B7CC (sum of angles around Zn = 359° and 358° for F7CC and B7CC, respectively), the steric repulsion between the β-diiminate ligand and the growing polymer chain induces a lateral shift of the ligand. Indeed, although the Zn–Oexo distance remains similar in F7CC with respect to that in B7CC (1.85 Å for B7CCvs. 1.86 Å for F7CC), the Oexo–Zn–N angle twists by ca. 12° to minimize the steric repulsion (from 124° and 134° for B7CC to 112° and 148° for F7CC). The CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oexo distance is also elongated (from 1.22 to 1.34 Å between E7CC and F7CC), which is consistent with a single bond between these two atoms.
O–Oexo distance is also elongated (from 1.22 to 1.34 Å between E7CC and F7CC), which is consistent with a single bond between these two atoms.
This latter adduct connects the ring-opening transition state (TSF7CC→G7CC) which lies +5.8 kcal mol−1 above it (+12.5 kcal mol−1 with respect to the entrance channel). This transition state is kinetically accessible and, as for the initiation step, the nucleophilic attack corresponds to the rate-limiting step of an overall facile reaction. At TSF7CC→G7CC, the ring is already opened (CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oendo distances of 1.86 and 1.44 Å for TSF7CC→G7CC and F7CC, respectively). Moreover, as for TSB7CC→C7CC, the Zn–Oendo distance is now the shortest (Zn–Oendo = 2.01 Å and Zn–Oexo = 2.06 Å), in line with a slightly larger negative charge of Oendo (−0.83) than Oexo (−0.81). This transition state leads to an endergonic G7CC intermediate (−0.2 kcal mol−1 with respect to F7CC and +9.1 kcal mol−1 with respect to the separated reactants). From a geometrical point of view, the metal center in G7CC exhibits a distorted tetrahedral environment with the 7CC monomer fully opened (CC
O–Oendo distances of 1.86 and 1.44 Å for TSF7CC→G7CC and F7CC, respectively). Moreover, as for TSB7CC→C7CC, the Zn–Oendo distance is now the shortest (Zn–Oendo = 2.01 Å and Zn–Oexo = 2.06 Å), in line with a slightly larger negative charge of Oendo (−0.83) than Oexo (−0.81). This transition state leads to an endergonic G7CC intermediate (−0.2 kcal mol−1 with respect to F7CC and +9.1 kcal mol−1 with respect to the separated reactants). From a geometrical point of view, the metal center in G7CC exhibits a distorted tetrahedral environment with the 7CC monomer fully opened (CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oendo = 2.58 Å). The hybridization of the CC
O–Oendo = 2.58 Å). The hybridization of the CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O changes from sp3 back to sp2 as indicated by its planarity (sum of angles around CC
O changes from sp3 back to sp2 as indicated by its planarity (sum of angles around CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = 360°). The CC
O = 360°). The CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oexo distances are shortened (1.23 Å for G7CCvs. 1.34 Å for F7CC), indicating the relocalization of the double bond between these two atoms.
O–Oexo distances are shortened (1.23 Å for G7CCvs. 1.34 Å for F7CC), indicating the relocalization of the double bond between these two atoms.
In a last step, the H7CC product is obtained by decoordination of the carbonate arm via a low energy process, through transition state TSG7CC→H7CC, with an activation barrier calculated to be +1.7 cal mol−1 with respect to the G7CC (+10.8 kcal mol−1 with respect to the entrance channel). For TSG7CC→H7CC, as for TSC7CC→D7CC, the second-order perturbation NBO analysis revealed that, in both cases, the exocyclic oxygen atom remains in interaction with the metal center by donation from an oxygen lone pair towards an empty p orbital of the metal center.
Finally, the system evolves to the final [(BDIiPr)Zn{OC4H8OC(O)}2(OMe)], H7CC, product. The formation of H7CC is predicted to be exergonic (−11.7 kcal mol−1 with respect to G7CC and −2.6 kcal mol−1 with respect to D7CC). From a geometrical point of view, the environment around the metal center in product H7CC is close to that observed in D7CC. Indeed, in both cases, the minimized growing polymer chain is almost linear, with decoordination of the exocyclic oxygen from the metal. The zinc center exhibits a trigonal planar geometry with two Zn–N distances of 1.95 Å (1.95 and 1.96 Å for D7CC), one Zn–O distance of 1.82 Å (1.82 Å for D7CC), two O–Zn–N angles of 126° and 134° (124° and 136° for D7CC) and one N–Zn–N angle of 100° (99° for D7CC). The natural charges are also quite similar for the two products (−0.76 for the nitrogen atoms, −0.96 for Oendo and +1.35 for Zn). These structural and electronic similarities for the two products are coherent with the small energy difference between these two steps.
The polymerization of 7CC catalyzed by [(BDIiPr)Zn(OR)] is thus computed to be a kinetically and thermodynamically favorable process. The rate-determining step is predicted to be the nucleophilic attack of the alkoxide, although the reaction remains really facile. The growing chain relaxation is also found to be important, making the overall reaction thermodynamically favorable. This indicates that the remaining interaction between the exocyclic oxygen and the metal centre induces a steric constraint in the growing polymer chain that overcomes the electronic stabilization due to this extra-interaction.
Initiation Step of the ROP of TMC. A similar theoretical study was carried out with the TMC substrate. The optimized structures of intermediates and transition states relevant for the initiation step of the ROP of TMC are presented in Fig. 9.
![Optimized structures of complexes involved in the initiation step of the ROP of TMC mediated by [(BDIiPr)Zn(OMe)].](/image/article/2011/PY/c1py00309g/c1py00309g-f9.gif) | ||
| Fig. 9 Optimized structures of complexes involved in the initiation step of the ROP of TMC mediated by [(BDIiPr)Zn(OMe)]. | ||
At the transition state TSATMC→BTMC (Fig. 9b), the Zn–OMe distance is elongated by 0.13 Å with respect to ATMC (Fig. 9a) (1.88 Å vs. 2.01 Å), but the methoxy group is still interacting with the metal center, as revealed by the second-order perturbation of the NBO analysis that indicates a donation from an oxygen lone pair towards empty s and p orbitals of zinc. Moreover, a pyramidalization is observed at the TMC carbonyl carbon (sum of angles around the CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = 349°). The empty sp3 orbital of the carbon, resulting from rehybridization from sp2 to sp3 in the carbonyl group, now points towards the oxygen atom of the methoxide ligand (CC
O = 349°). The empty sp3 orbital of the carbon, resulting from rehybridization from sp2 to sp3 in the carbonyl group, now points towards the oxygen atom of the methoxide ligand (CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–OOMe distance = 1.85 Å). Once the trigonal planar complex BTMC (Fig. 9c) is formed, the alkoxide ligand is bonded to CC
O–OOMe distance = 1.85 Å). Once the trigonal planar complex BTMC (Fig. 9c) is formed, the alkoxide ligand is bonded to CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (CC
O (CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–OOMe distance = 1.40 Å). The CC
O–OOMe distance = 1.40 Å). The CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oexo distance is also elongated by 0.11 Å (1.34 Å vs. 1.22 Å) with respect to ATMC, indicating the presence of a single bond between these two atoms, as confirmed by the NBO analysis.
O–Oexo distance is also elongated by 0.11 Å (1.34 Å vs. 1.22 Å) with respect to ATMC, indicating the presence of a single bond between these two atoms, as confirmed by the NBO analysis.
The second step corresponds to the acyl–oxygen bond cleavage (i.e., ring-opening) of the TMC cycle. In the tetrahedral intermediate CTMC (Fig. 9e), TMC is now opened (CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oendo distance of 2.59 Å). The hybridization of the CC
O–Oendo distance of 2.59 Å). The hybridization of the CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ocarbon changes from sp3 to sp2, as indicated by its planarity (sum of angles around CC
Ocarbon changes from sp3 to sp2, as indicated by its planarity (sum of angles around CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = 360°). The CC
O = 360°). The CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oexo distance is also shortened (1.23 Å), which highlights the relocalization of a double bond between these two atoms. For CTMC, it is noteworthy that the coordination to the metal center is ensured by Oendo while Oexo is uncoordinated. Indeed, the Zn–Oendo distance is now the shortest among the two: Zn–Oendo = 1.88 Å and Zn–Oexo = 2.35 Å vs. Zn–Oendo = 2.69 Å for CTMC and Zn–Oexo = 1.87 Å for BTMC. The same trends apply for the natural charges of the two atoms with a negative charge greater for Oendo than for Oexo (−0.96 and −0.70 for CTMC and −0.62 and −0.93 for BTMC, respectively). At the transition state TSBTMC→CTMC (Fig. 9d), the cycle is already opened, with a CC
O–Oexo distance is also shortened (1.23 Å), which highlights the relocalization of a double bond between these two atoms. For CTMC, it is noteworthy that the coordination to the metal center is ensured by Oendo while Oexo is uncoordinated. Indeed, the Zn–Oendo distance is now the shortest among the two: Zn–Oendo = 1.88 Å and Zn–Oexo = 2.35 Å vs. Zn–Oendo = 2.69 Å for CTMC and Zn–Oexo = 1.87 Å for BTMC. The same trends apply for the natural charges of the two atoms with a negative charge greater for Oendo than for Oexo (−0.96 and −0.70 for CTMC and −0.62 and −0.93 for BTMC, respectively). At the transition state TSBTMC→CTMC (Fig. 9d), the cycle is already opened, with a CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oendo distance of 1.84 Å vs. 1.42 Å for BTMC. The NBO analysis revealed that TMC is then equally coordinated to the zinc atom by both its endocyclic and exocyclic oxygen atoms: both Zn–Oendo and Zn–Oexo distances are indeed identical (2.03 Å). Also, the second-order perturbation NBO analysis indicated, in both cases, a donation from a lone pair of the oxygen atoms towards empty s and p orbitals of the zinc, which is similar for Oendo and Oexo.
O–Oendo distance of 1.84 Å vs. 1.42 Å for BTMC. The NBO analysis revealed that TMC is then equally coordinated to the zinc atom by both its endocyclic and exocyclic oxygen atoms: both Zn–Oendo and Zn–Oexo distances are indeed identical (2.03 Å). Also, the second-order perturbation NBO analysis indicated, in both cases, a donation from a lone pair of the oxygen atoms towards empty s and p orbitals of the zinc, which is similar for Oendo and Oexo.
The last step corresponds to the relaxation of the growing polymer chain that leads to the final [(BDIiPr)Zn{OC3H6OC(O)}(OMe)] (DTMC) product (Fig. 9g). The exocyclic oxygen atom does not interact with the metal center in DTMC and the endocyclic oxygen ensures the coordination of the carbonate arm to the metal center (Zn–Oendo = 1.82 Å). In the corresponding transition state, TSCTMC→DTMC (Fig. 9f), the Zn–Oexo distance is elongated by 0.78 Å with respect to CTMC. Nevertheless, the second-order's perturbation of the NBO analysis revealed that Oexo remains in interaction with the metal center via a weak donation from an oxygen lone pair towards an empty p orbital of the zinc.
The overall free energy profile for the TMC ROP initiation step is depicted in Fig. 10. The reaction begins by the formation of the initial adduct ATMC for which the coordination of TMC is computed to be endergonic by 10.3 kcal mol−1 with respect to the separated reactants, due to the loss of entropy associated with coordination of free monomer. The next step corresponds to the nucleophilic attack of the alkoxide ligand onto the TMC carbonyl carbon. The activation barrier for the nucleophilic attack is 7.1 kcal mol−1 with respect to ATMC (17.4 kcal mol−1 with respect to the entrance channel). The newly formed intermediate BTMC is merely lower in energy than the previous intermediate ATMC (−0.8 kcal mol−1). Once the reaction reaches this point, the ring-opening reaction takes place by cleavage of the acyl–Oendo bond (TSBTMC→CTMC). From a kinetic point of view, the activation barrier for this process is predicted to be 6.7 kcal mol−1 with respect to BTMC (16.2 kcal mol−1 with respect to the entrance channel). The two barriers—nucleophilic attack and ring opening—are found to be similar. Following the intrinsic reaction coordinate, TSBTMC→CTMC leads to the thermodynamically unstable intermediate CTMC which lies 0.6 kcal mol−1 above BTMC (10.1 kcal mol−1 with respect to the entrance channel). The last step corresponds to the formation of the final [(BDIiPr)Zn{OC3H6OC(O)}(OMe)] (DTMC) product. This product is 8.9 kcal mol−1 more stable than CTMC and the reaction is almost athermic (slightly endergonic by 1.2 kcal mol−1). The energy barrier for this step is 1.5 kcal mol−1. On the basis of these results, this pathway corresponds to a feasible mechanism for the reaction. Indeed, the reaction is, from a thermodynamic point of view, a nearly athermic process with the highest energy transition state located at 17.4 kcal mol−1 above the entrance channel (7.1 kcal mol−1 above ATMC) leading to an overall facile reaction.
![Calculated free-energy profile of the ROP initiation of TMC mediated by [(BDIiPr)Zn(OMe)].](/image/article/2011/PY/c1py00309g/c1py00309g-f10.gif) | ||
| Fig. 10 Calculated free-energy profile of the ROP initiation of TMC mediated by [(BDIiPr)Zn(OMe)]. | ||
Propagation step of the ROP of TMC. The second ring-opening step was also studied as a representation of the polymer propagation. The resulting reaction profile is shown in Fig. 11. The key geometrical parameters and charges of the different stationary points are gathered in Table 1 and 2.
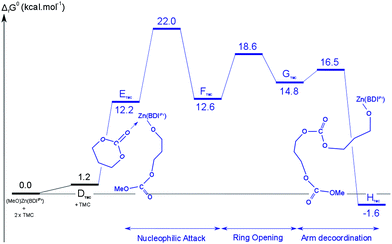 | ||
| Fig. 11 Calculated free-energy profile for the insertion of the second TMC molecule. | ||
| Zn–Oalkoxide | Zn–Oexo | CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oexo O–Oexo |
CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oendo O–Oendo |
Zn–Oendo | CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–Oalkoxide O–Oalkoxide |
|
|---|---|---|---|---|---|---|
| [(BDIiPr)Zn(OMe)] | 1.816 | — | — | — | — | — |
| TMC | — | — | 1.199 | 1.351 | — | — |
| A TMC | 1.883 | 2.269 | 1.223 | 1.326 | 3.251 | 2.713 |
| (ETMC) | (1.879) | (2.218) | (1.224) | (1.322) | (3.285) | (3.252) |
| TS ATMC→BTMC | 2.011 | 2.030 | 1.264 | 1.358 | 3.292 | 1.853 |
| (TSETMC→FTMC) | (2.036) | (2.011) | (1.270) | (1.359) | (3.266) | (1.822) |
| B TMC | 3.439 | 1.865 | 1.400 | 1.425 | 2.695 | 1.401 |
| (FTMC) | (3.429) | (1.865) | (1.340) | (1.422) | (2.741) | (1.403) |
| TS BTMC→CTMC | — | 2.035 | 1.274 | 1.840 | 2.027 | 1.344 |
| TS FTMC→GTMC | — | (2.048) | (1.270) | (1.868) | (2.017) | (1.343) |
| C TMC | — | 2.351 | 1.229 | 2.586 | 1.882 | 1.321 |
| (GTMC) | — | (2.393) | (1.227) | (2.631) | (1.882) | (1.324) |
| TS CTMC→DTMC | — | 3.127 | 1.216 | 2.754 | 1.847 | 1.330 |
| TS GTMC→HTMC | — | (2.890) | (1.217) | (2.765) | (1.856) | (1.331) |
| D TMC | — | 1.206 | — | 1.821 | 1.342 | |
| (HTMC) | — | (1.211) | — | (1.822) | (1.342) |
| Zn | Oalkoxide | Oexo | CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
Oendo | |
|---|---|---|---|---|---|
| [(BDIiPr)Zn(OMe)] | 1.34 | −0.95 | — | — | — |
| TMC | — | — | −0.60 | 1.06 | −0.57 |
| A TMC | 1.34 | −0.97 | −0.67 | 1.12 | −0.54 |
| (ETMC) | (1.39) | (−0.98) | (−0.67) | (1.10) | (−0.52) |
| TS ATMC→BTMC | 1.31 | −0.81 | −0.81 | 1.12 | −0.56 |
| (TSETMC→FTMC) | (1.35) | (−0.80) | (−0.82) | (1.12) | (−0.57) |
| B TMC | 1.33 | −0.60 | −0.93 | 1.14 | −0.62 |
| (FTMC) | (1.36) | (−0.62) | (−0.94) | (1.14) | (−0.62) |
| TS BTMC→CTMC | 1.42 | −0.54 | −0.83 | 1.11 | −0.80 |
| TS FTMC→GTMC | (1.34) | (−0.55) | (−0.82) | (1.13) | (−0.81) |
| C TMC | 1.28 | −0.52 | −0.71 | 1.13 | −0.96 |
| (GTMC) | (1.33) | (−0.53) | (−0.70) | (1.13) | (−0.96) |
| TS CTMC→DTMC | 1.31 | −0.54 | −0.66 | 1.10 | −0.97 |
| TS GTMC→HTMC | (1.35) | (−0.54) | (−0.66) | (1.11) | (−0.97) |
| D TMC | 1.35 | −0.55 | −0.63 | 1.07 | −0.96 |
| (HTMC) | (1.35) | (−0.56) | (−0.66) | (1.07) | (−0.96) |
The insertion of the second TMC molecule is very similar to the initiation step, as discussed in detail in the previous section for 7CC. It is interesting to note that no significant difference is observed concerning the stability of the intermediates and the activation barriers between the initiation and the first propagation steps of the ROP of TMC. The average energy difference between the stability of different intermediates or activation barriers between the initiation and propagation steps is about 3 kcal mol−1. From a geometric point of view, the structures of the different intermediates and transition states are almost identical (maximum deviation of 0.06 Å). The natural charges of the different atoms follow the same trend than the geometric parameters and are virtually identical (within 0.04 u.) between the initiation and the first propagation steps. This was already underlined in the case of 7CC.
It is noteworthy that, in contrast to the endergonic first insertion step (+1.2 kcal mol−1 with respect to ATMC), the second insertion step is exergonic by −2.9 kcal mol−1 (with respect to DTMC). Thus, the polymerization of TMC catalyzed by [(BDIiPr)Zn(OR)] is computed to be a kinetically accessible process. From a thermodynamic point of view, the reaction is predicted to be almost athermic, provided the relaxation of the growing polymer chain is taken into account. This is the main difference between the two monomers considered in the present study.
These computational results support that the initiation and the first propagation steps of the ROP of cyclic carbonates (six- and seven-membered rings) mediated by these [(BDIiPr)Zn(OR)] complexes occur through a classical coordination-insertion mechanism with accessible activation barriers. In both cases, after attack by the nucleophilic alkoxide moiety, ring-opening is followed by relaxation of the oligomeric chain. The rate-determining step to the ROP of 7CC is the nucleophilic attack, whereas for TMC, both the nucleophilic attack and ring-opening barriers are equivalent (the one associated to the nucleophilic attack being slightly higher but close to the uncertainty of the computations). Generally, the activation barrier corresponding to the overall ROP process is slightly lower for 7CC than for TMC, although both are found to be relatively low (17.0 kcal mol−1 for 7CC and 22.0 kcal mol−1 for TMC). The height of the second barrier is associated with the steric constraint introduced by the growing polymer chain that is higher for TMC (6 member-ring) vs. 7CC (7 member-ring). Moreover, the reaction is also thermodynamically more favorable for 7CC (exergonic process) than for TMC (almost athermic). Thus, 7CC is computed to be more easily polymerizable than TMC, which follows well experimental observations made with this catalyst system.10–17 A similar situation is known for the lactones where the larger seven-membered ε-caprolactone is more easily polymerizable than the six-membered δ-valerolactone analogue.43
4. Conclusions
In this study, the first two steps of the ROP of 7CC and TMC mediated by zinc-(β-diiminate) catalysts operating via a coordination-insertion mechanism have been studied using DFT methods. It was possible to show that the zinc-amido precursor is a poor catalyst whereas the alkoxide analogue is quite active, in agreement with the experimental observations previously made on these systems.For both carbonates, it was shown that the initiation and the second insertion proceed at similar rate (i.e., similar energy barriers and reaction energies). Moreover, the reaction occurs according to a two-step process for 7CC and TMC: first, a nucleophilic attack of the alkoxide group followed by the ring-opening of the tetrahedral intermediate. These two steps are predicted to be kinetically accessible, the nucleophilic attack being the rate-determining step although the reaction is really facile (barrier below 22.0 kcal mol−1 at most). From a thermodynamical point of view, the relaxation of the growing polymer chain appears to be an important feature, making the overall polymerization process exergonic (7CC) or almost athermic (TMC). Indeed, breaking residual interactions between the exocyclic oxygen of the carbonate moiety and the metal center allow the steric constraints inside the growing polymer chain to be reduced, eventually leading to a more stable compound.
Finally, the activity of the model alkoxide catalyst [(BDIiPr)Zn(OMe)] in the ROP of 7CC and TMC could be compared. Based on these findings, 7CC was computed to be slightly more easily polymerizable than TMC, as indeed observed experimentally.10–17 This is reminiscent of what is already known in the case of lactones.
Acknowledgements
The Agence Nationale pour la Recherche (ANR) is gratefully acknowledged for financial support of the “BIOPOLYCAT” project (CP2D-08-01). Laurent Maron and Jean-François Carpentier are members of the Institut Universitaire de France (IUF). CINES and CALMIP are also acknowledged for a generous grant of computing time.References and notes
- G. Rokicki, Prog. Polym. Sci., 2000, 25, 259–342 CrossRef CAS.
- S. Mecking, Angew. Chem., Int. Ed., 2004, 43, 1078–1085 CrossRef CAS.
- R. Auras, B. Harte and S. Selke, Macromol. Biosci., 2004, 4, 835–864 CrossRef CAS.
- A. Gandini, Macromolecules, 2008, 41, 9491–9504 CrossRef CAS.
- B. D. Ulery, L. S. Nair and C. T. J. Laurencin, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 832–864 CrossRef CAS.
- D. J. A. Cameron and M. P. Shaver, Chem. Soc. Rev., 2011, 40, 1761–1776 RSC.
- A. P. Dove, Chem. Commun., 2008, 6446–6470 RSC.
- C. M. Thomas, Chem. Soc. Rev., 2010, 39, 165–173 RSC.
- O. Dechy-Cabaret, B. Martin-Vaca and D. Bourissou, Chem. Rev., 2004, 104, 6147–6176 CrossRef CAS.
- N. Ajellal, J.-F. Carpentier, C. Guillaume, S. M. Guillaume, M. Helou, V. Poirier, Y. Sarazin and A. Trifonov, Dalton Trans., 2010, 39, 8363–8376 RSC.
- M. Helou, O. Miserque, J.-M. Brusson, J.-F. Carpentier and S. M. Guillaume, Chem.–Eur. J., 2008, 14, 8772–8775 CrossRef CAS.
- M. Helou, O. Miserque, J.-M. Brusson, J.-F. Carpentier and S. M. Guillaume, Adv. Synth. Catal., 2009, 351, 1312–1324 CrossRef CAS.
- M. Helou, O. Miserque, J.-M. Brusson, J.-F. Carpentier and S. M. Guillaume, Macromol. Rapid Commun., 2009, 30, 2128–2135 CrossRef CAS.
- M. Helou, O. Miserque, J.-M. Brusson, J.-F. Carpentier and S. M. Guillaume, ChemCatChem, 2010, 2, 306–313 CrossRef CAS.
- M. Helou, O. Miserque, J.-M. Brusson, J.-F. Carpentier and S. M. Guillaume, Chem.–Eur. J., 2010, 16, 13805–13813 CrossRef CAS.
- P. Brignou, M. P. Gil, O. Casagrande, J.-F. Carpentier and S. M. Guillaume, Macromolecules, 2010, 43, 8007–8017 CrossRef CAS.
- P. Brignou, J.-F. Carpentier and S. M. Guillaume, Macromolecules, 2011, 44, 5127–5135 CrossRef CAS.
- B. M. Chamberlain, M. Cheng, D. R. Moore, T. M. Ovitt, E. Lobkovsky and G. W. J. Coates, J. Am. Chem. Soc., 2001, 123, 3229–3238 CrossRef CAS.
- L. R. Rieth, D. R. Moore, E. B. Lobkovsky and G. W. J. Coates, J. Am. Chem. Soc., 2002, 124, 15239–15248 CrossRef CAS.
- J. Ling, J. Shen and T. E. Hogen-Esch, Polymer, 2009, 50, 3575–3581 CrossRef CAS.
- E. L. Marshall, V. C. Gibson and H. S. Rzepa, J. Am. Chem. Soc., 2005, 127, 6048–6051 CrossRef CAS.
- A. P. Dove, V. C. Gibson, E. L. Marshall, H. S. Rzepa, A. J. P. White and D. J. Williams, J. Am. Chem. Soc., 2006, 128, 9834–9843 CrossRef CAS.
- H. von Schenck, M. Ryner, A.-C. Albertsson and M. Svensson, Macromolecules, 2002, 35, 1556–1562 CrossRef CAS.
- M. Ryner, K. Stridsberg, A.-C. Albertsson, H. von Schenck and M. Svensson, Macromolecules, 2001, 34, 3877–3881 CrossRef CAS.
- J. Börner, I. dos Santos Vieira, A. Pawlis, A. Dçring, D. Kuckling and S. Herres-Pawlis, Chem.–Eur. J., 2011, 17, 4507–4512 CrossRef.
- N. Barros, M. Schappacher, P. Dessuge, L. Maron and S. M. Guillaume, Chem.–Eur. J., 2008, 14, 1881–1890 CrossRef CAS.
- N. Barros, P. Mountford, S. M. Guillaume and L. Maron, Chem.–Eur. J., 2008, 14, 5507–5518 CrossRef CAS.
- S. M. Guillaume, P. Brignou, N. Susperregui, L. Maron, M. Kuzdrowska and P. W. Roesky, Polym. Chem., 2011, 2, 1728–1736 RSC.
- M. Bouyahyi, N. Ajellal, E. Kirillov, C. M. Thomas and J.-F. Carpentier, Chem.–Eur. J., 2011, 17, 1872–1883 CrossRef CAS.
- Y. Sarazin, B. Liu, T. Roisnel, L. Maron and J.-F. Carpentier, J. Am. Chem. Soc., 2011, 133, 9069–9087 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 03 (Revision B.05), 2003 Search PubMed.
- J. P. Perdew, Chapter Unified Theory of Exchange and Correlation Beyond the Local Density Approximation, in Electronic Structure of Solids, ed. P. Ziesche and H. Eschrig, Akademie, Berlin, 1991 Search PubMed.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter, 1996, 54, 16533–16539 CrossRef CAS.
- K. Burke, J. P. Perdew and Y. Wang, Chapter Derivation of a Generalized Gradient Approximation: the PW91 Density Functional, in Electronic Density Functional Theory: Recent Progress and New Directions, ed. J. F. Dobson, G. Vignale and M. P. Mas, Plenum, New-York, 1998 Search PubMed.
- J. P. Perdew, J. A Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter, 1992, 46, 6671–6687 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter, 1998, 57, 14999 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter, 1993, 48, 4978 CrossRef CAS.
- W. Küechle, M. Dolg, H. Stoll and H. Preuss, Mol. Phys., 1991, 74, 1245–1263 CrossRef.
- P. C. Harihara and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4074 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- W. Saiyasombat, R. Molloy, T. M. Nicholson, A. F. Johnson, I. M. Ward and S. Poschyyachinda, Polymer, 1998, 39, 5581–5585 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Cartesian coordinates and free Gibbs energy for all transition states and intermediates. See DOI: 10.1039/c1py00309g |
| ‡ Note that only monomeric zinc-alkoxide species were considered in this study; [(BDIiPr)Zn(OiPr)] is known to adopt a dimeric structure with μ-bridging alkoxide groups in the solid state and partly in solution as well (see ref. 18 and 19). |
| This journal is © The Royal Society of Chemistry 2011 |
