Retracted article: Enantioselectivity of aza-MBH-type reaction of nitroalkene to N-tosylimine catalyzed by thiourea-tertiary amine: a theoretical study

Abstract

We, the named authors, hereby wholly retract this RSC Advances article.

Signed: Nan Lu, Lin Meng, Dezhan Chen and Guiqiu Zhang, China, February 2012.

Retraction endorsed by Sarah Ruthven, Managing Editor. Retraction published 1st February 2012.

---

Introduction

Carbon–carbon bond formation via the functionalization of sp³ and sp² C–H bonds is considered to be a central part in synthetic chemistry.¹ Devoting to the case of sp² C–H bonds, the aza-Morita–Baylis–Hillman (aza-MBH) reaction is known to involve a Lewis base-catalyzed coupling of activated electron-deficient alkenes with various carbon electrophiles.^2–5 Typically as an important tandem reaction, this method is capable of providing α-functionalized alkenes starting from simple materials with minimal production of waste.⁶ Moreover, the catalytic aza-MBH-type reaction is of great potential in the synthesis of optically active amines.⁷

A wide range of organocatalysts have emerged for aza-MBH-type reactions, such as 1,4-diazabicyclo[2.2.2]octane (DABCO), 1,5-diazabicyclo[4.3.0]non-5-ene (DBU), and phosphine.^8–11 Recently, Pohmakotr has described an asymmetric MBH reaction catalyzed by tributylphosphine in the presence of phenol.¹² Verkade isolated the MBH type adducts employing P(PhCH₂NCH₂CH₂)₃N as an efficient catalyst.¹³ Without Lewis acid or base, the α-acylvinyl anion equivalents could still undergo highly selective addition to imines generating β-substituted aza-MBH-type adducts.¹⁴ However, in the reaction between allenyl ketone and aldehyde,¹⁵ DABCO and 4-dimethylaminopyridine (DMAP) could not lead to the desired products.¹⁶ Challenges also exist in the organocatalytic enantioselective version employing nitro-activated olefins as nucleophiles.

A breakthrough in solving this problem was Xu's enantioselective aza-MBH-type reaction catalyzed by thiourea-tertiary amine.¹⁷ However, there is no report about the detailed mechanistic study currently. In the synthesis of β-nitro-γ-enamines,¹⁸ how are the two substrates activated by catalyst? In the screening of catalysts, why is the best enantioselectivity obtained with the structure incorporating aromatic ring, thiourea and tertiary amine as catalyst? These questions which are inaccessible through experiment can be made clear via density functional theory (DFT), which provides an excellent compromise between computational cost and accuracy of outcome. Generally, the hybrid functions are accurate enough to describe complexes with H bonds. The DFT method is also well-documented for the rationalization and quantitative prediction of stereoselectivity in organocatalysis.^19–21

Computational details

Calculations were carried out by using the B3LYP^22–24 density functional method as implemented in the Gaussian03²⁵ program package. Geometries of all intermediates (Ints) and transition states (TSs) were fully optimized with the 6-31G(d,p) basis set. Frequencies were analyzed at the same level to characterize the nature of stationary points (energy minima or first-order saddle-points) and to provide thermodynamic quantities such as zero-point energy (ZPE) and thermal corrections. Energies were then calculated as single points at B3LYP/6-311++G(d,p) and MP2/6-311++G(d,p) levels^26,27. The intrinsic reaction coordinate (IRC) paths²⁸ were also traced to verify the energy profiles connecting each transition state to the correct associated local minima.

Meanwhile the basis set superposition error (BSSE) corrections for species were estimated using the counterpoise method.²⁹ To illustrate the electronic properties and bonding characters for stationary points, natural bond orbital (NBO) analysis was performed at B3LYP/6-311++G(d,p) level.^30,31 To consider the solvent effect on the reaction, single-point PCM//B3LYP/6-311++G(d,p) calculations were performed with a self-consistent reaction field^32,33 based on the polarizable continuum model (PCM).³⁴ The parameters of xylene (ε = 2.35) and DMF (ε = 36.7) were used to make a comparison, since they were the solvents used in the experiment. For all cited energies, ZPE corrections were taken into account. Since this treatment is somewhat different from the real solution phase condition, our conclusion derived from the present calculation is expected to explain qualitatively the experimental findings.

Results and discussion

The mechanism we suggest for the catalytic aza-MBH-type reaction is outlined in Scheme 1. As a Lewis base, the catalyst activates the nitroalkene 1 by the tertiary amino group to enhance the nucleophilicity of the initial binary complex Int0. The nucleophilic addition of Int0 to N-tosylimine 2 gives Int2. Then the proton transfers from the methyl of 1 to the electronegative nitrogen of 2, which is followed by the generation of β-nitro-γ-enamine 3 and the recovery of catalyst. In researching the reaction process, catalyst 12 in the experiment¹⁷ was simulated by model 4 (Scheme 2) bearing critical elements for catalysis.³⁵ The tosyl group of 2 was also substituted with acetyl (2′) for simplification. Symbols “s” and “a” were used to distinguish species of two paths leading to isomers (3S,4S)-3 and (3S,4R)-3, respectively. When it comes to the enantioselectivity, real system with full catalyst 5 was taken into account (Fig. 1). Key atoms involved in bond cleavage and formation are numbered in one structure of Scheme 2 and Fig. 1. Relative electronic energy profiles of the reaction in the solution phase are depicted in Fig. 2.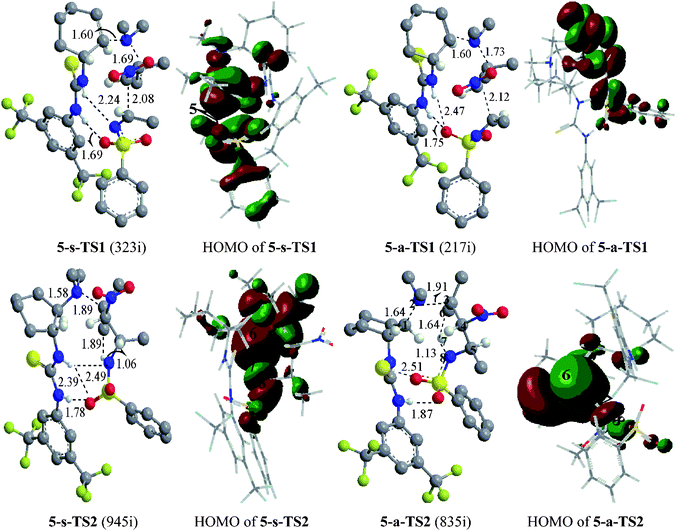

Fig. 1 Optimized geometries (bond length in Å) and HOMOs of four TSs in two steps of the aza-MBH-type reaction with full catalyst 5. In the left column, hydrogen atoms of the methyl and on the ring are omitted for clarity; blue, red, gray, yellow, white and Kelly green balls represent N, O, C, S, H and F atoms, respectively; the imaginary frequency (cm⁻¹) of the TSs are in parentheses. In the right column, different colors are used to identify the phase of the wave functions.

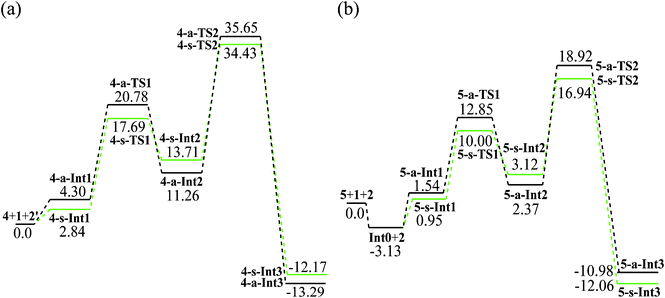Fig. 2 Relative electronic energy profiles (kcal mol⁻¹) of the s-path (green) and a-path (black) in the aza-MBH-type reaction with (a) catalyst 4 and (b) catalyst 5 in the solution phase of xylene.

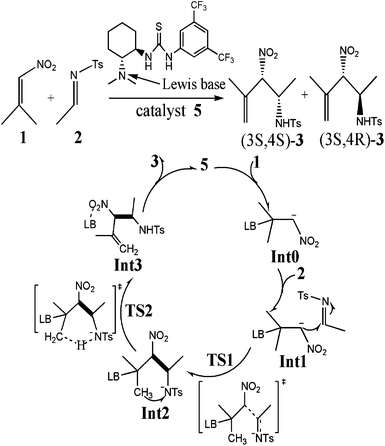Scheme 1 Proposed mechanistic rationale of the thiourea-tertiary amine-catalyzed enantioselective aza-MBH-type reaction.

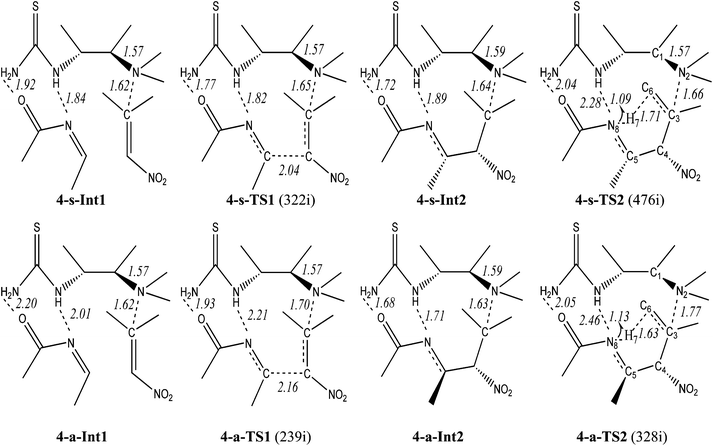Scheme 2 The aza-MBH-type reaction with model catalyst 4. Bond lengths in Å and the imaginary frequency (cm⁻¹) of TS is in parentheses.

Reaction with 4

In the s-path of step 1, the nucleophilic addition of Int0 to N-acetylimine 2′ takes place via4-s-TS1 from a pre-reactive complex 4-s-Int1 yielding an active intermediate 4-s-Int2. This step is endothermic by 10.87 kcal mol⁻¹ with a barrier of 14.85 kcal mol⁻¹. The H bonds between N, O atoms of 2′ and thiourea of 4 in 4-s-Int1 (1.84, 1.92 Å) are stronger than those of 4-a-Int1 (2.01, 2.20 Å). The case is inversed in 4-s-Int2 (1.72, 1.89 Å) and 4-a-Int2 (1.68, 1.71 Å), which advocates the higher energy of 4-s-Int2 (13.71 kcal mol⁻¹) than 4-a-Int2 (11.26 kcal mol⁻¹). Although the distance between N2 and C3 (N2⋯C3) exceeds the length of a normal single C–N bond (1.47–1.55 Å),³⁶ it denotes one type of weak covalent interaction between the catalyst and nitroalkene. The length of N2–C3 is nearly the same in the corresponding Ints. The discrepancy appears in two TSs (4-s-TS1, 1.65 Å; 4-a-TS1, 1.70 Å). The transition vector of 4-s-TS1 (322i cm⁻¹) corresponds to the formation of C4–C5 bond (2.04 Å). In 4-a-TS1 (239i cm⁻¹), length of the C4–C5 bond is 2.16 Å. Along with two H bonds of 4-s-TS1 (1.77, 1.82 Å) which are shorter than those of 4-a-TS1 (1.93, 2.21 Å), the desired C–C bond formation is more readily accessible in the s-path than in the a-path.

The proton transfer proceeds viaTS2 from Int2 yielding a stable intermediate Int3. Two paths are both exothermic (s: −25.88; a: −24.21 kcal mol⁻¹) with energy barriers of 20.72 (s) and 24.39 (a) kcal mol⁻¹, respectively. Obviously, the proton transfer is the rate-limiting step of the catalytic aza-MBH-type reaction. The transition vector of TS2 corresponds to the formation of the N8–H7 bond (s: 1.09 Å; a: 1.13 Å) and cleavage of the C6–H7 bond (s: 1.71 Å; a: 1.63 Å). The interaction between 4 and 1 in 4-a-TS2 (1.77 Å) is weaker than that of 4-s-TS2 (1.66 Å). Moreover the H bonds mentioned above in 4-a-TS2 (2.05, 2.46 Å) are longer than those of 4-s-TS2 (2.04, 2.28 Å). Evidently, 4-s-TS2 (476i cm⁻¹) is more favorable than 4-a-TS2 (328i cm⁻¹) leading to (3S,4S)-3.

To verify the reliability of the B3LYP method, we carried out single-point calculations for species in the rate-limiting step of the two paths with catalyst 4 at two different levels (Table 1). Compared with the case of B3LYP, both electronic energy and relative energy of the species with the MP2 method are lowered at different degrees. The energy barriers of the two paths decrease by 0.68 (s) and 0.82 (a) kcal mol⁻¹, respectively. This discrepancy is small so that its influence could almost be omitted. In the following analysis, the B3LYP method will be applied to replace the time-consuming MP2 method.

Table 1 Relative electronic energy (kcal mol⁻¹) of species in the rate-limiting step 2 with catalyst 4 at two different levels

Species	B3LYP/6-311++G(d,p)		MP2/6-311++G(d,p)
	E (a.u.)^a	δE ^b	E (a.u.)^a	δE ^b
a Real energies (a.u.). b Relative energy considering ZPE and BSSE corrections. c Activation energy barrier.
4-s-Int2	−1486.9015	12.43	−1486.9078	10.32
4-s-TS2	−1486.8685	31.40	−1486.8786	28.61
Ea(s)^c	18.97		18.29
4-a-Int2	−1486.9054	10.01	−1486.9119	6.95
4-a-TS2	−1486.8665	32.67	−1486.8771	28.79
Ea(a)^c	22.66		21.84

---

The detailed mechanism is made clear with the help of model catalyst 4. After the activation of nitroalkene by the tertiary amino group of the catalyst, the catalytic cycle consists of nucleophilic addition and proton transfer. Step 2 is rate-limiting.

Reaction with 5

Structural characteristic of TSs. The optimized geometries of the TSs in the real system with full catalyst 5 are illustrated in the left column of Fig. 1. In step 1, lengths of the forming C4–C5 bond in 5-s-TS1 and 5-a-TS1 are 2.08 and 2.12 Å, respectively. The distances of N2–C3 and two H bonds (5-s-TS1: 1.69, 1.69, 2.24 Å; 5-a-TS1: 1.73, 1.75, 2.47 Å) indicate that 1 and 2 are loosely bonded to 5 in 5-a-TS1 (217i cm⁻¹) in contrast with the compact assembly of 5-s-TS1 (323i cm⁻¹). In particular, there is no H-bonded interaction between the N atom of 2 and the thiourea of 5 in 5-a-TS1 and 5-a-TS2. In step 2, the lengths of the forming N8–H7 and the breaking C6–H7 bonds are 1.06 and 1.89 Å in 5-s-TS2 (945i cm⁻¹); 1.13 and 1.64 Å in 5-a-TS2 (835i cm⁻¹). In 5-a-TS2, not only is the distance of N2–C3 (1.91 Å) longer than that of 5-s-TS2 (1.89 Å), but also the C1–N2 bond elongates remarkably to 1.64 Å. This reveals that the interaction between 5 and 1 in 5-a-TS2 remains weaker even if the catalyst itself experiences a bigger change in structure.

The relationship among atoms directly involved in bond formation and dissociation could be exhibited visually by the highest occupied molecular orbital (HOMO) of the TSs (right column of Fig. 1). In the HOMO of 5-s-TS1, the electropositive parts (+) of the p-orbital of the C4 and C5 atoms overlap with each other to make a bonding interaction, which also exists among most of the adjacent atoms. The superposition turns to the electronegative parts (−) of the p-orbital and is dramatically reduced in the HOMO of 5-a-TS1. Together with the anti-bonding characters surrounding, the disfavored formation of the C–C bond in 5-a-TS1 is rationalized. For TS2, the H7 atom is located exactly at the node between two phases of the wave function, which corresponds to a typical HOMO shape of a proton transfer. In 5-a-TS2, there is a small superposition between the s-orbital of H7 and the (+)p-orbital of N8, as well as a big one between it and the (−)p-orbital of C6. In 5-s-TS2, the former superposition is increased, the latter is decreased and the sign of the p-orbital beside H7 is inversed. It follows that the bonding interaction of N8–H7 is stronger in 5-s-TS2 and the proton transfer from C6 to N8 occurs more readily via5-s-TS2 than 5-a-TS2.

Energetic profiles. To research the effect of active site environment on the catalytic reaction, we chose the parameters of non-polar xylene and polar DMF to estimate the solvation energy of the main Ints and TSs. In general, the energies of the species in the solution phase are decreased compared with those of the gas phase. The decrease is larger in DMF than in xylene, presumably owing to the stronger polarity of DMF than xylene. As can be seen in Table 2, the energy barriers and activation Gibbs free energies in the solution phase are also reduced in the same tendency.

Table 2 Energy barriers, activation Gibbs free energies of two steps and ee values of the aza-MBH-type reaction with full catalyst 5 in the solution phase

	Gas		In xylene		In DMF
	Ea	δG ^≠	Ea	δG ^≠	Ea	δG ^≠
s-Step 1	18.60	19.67	9.05	10.24	8.38	9.54
s-Step 2	23.28	24.83	13.82	15.07	13.03	14.26
a-Step 1	20.02	20.99	11.31	11.73	9.16	9.97
a-Step 2	26.16	27.64	16.55	17.68	13.73	14.59
ee			97.6%		27.2%

---

The binary precursor Int0 is stabilized by 3.13 kcal mol⁻¹ with respect to isolated 5 and 1. In step 1, the s-path proceeds with an energy barrier of 9.05 kcal mol⁻¹versus the barrier of 11.31 kcal mol⁻¹ in the a-path (10.24 and 11.73 kcal mol⁻¹ in free energy). The barrier of the a-path (16.55 kcal mol⁻¹) in step 2 is higher than that of the s-path (13.82 kcal mol⁻¹) (17.68 and 15.07 kcal mol⁻¹ in free energy). The two paths are both endothermic in step 1 (s: 2.17; a: 0.83 kcal mol⁻¹) and exothermic in step 2 (s: −15.18; a: −13.35 kcal mol⁻¹). Since the enantioselectivity is determined in the rate-limiting step, the enantiomer (3S,4S)-3 generated in the s-path is preferential kinetically. In the whole reaction, the exothermic energy of the s-path is 0.49 kcal mol⁻¹ larger than the a-path. Thereby (3S,4S)-3 is also the thermodynamically controlled product.³⁷

Essence of enantioselectivity. As a Lewis base, the tertiary amine nitrogen atom enables the formation of a weak covalent bond between 5 and 1. To study the role of weak covalent interaction on the enantioselectivity of the reaction, we list some vital Wiberg bond indices³⁸ in Table 3. The bond order (BO) value of the C1–N2 bond has almost no change in step 1. The BO value of N2–C3 in 5-s-TS1 (0.68) indicates a stronger interaction of 5 and 1 than that in 5-a-TS1 (0.57). Compared with the BO value of C4–C5 in 5-a-TS1 (0.33), the value in 5-s-TS1 (0.38) verifies the earlier C–C bond formation of the s-path than the a-path. In step 2, the BO value of the C1–N2 bond is increased in 5-s-TS2 (0.83 → 0.90) while decreased in 5-a-TS2 (0.80 → 0.74). Although the BO value of the N2–C3 bond in 5-s-Int2 is smaller than that in 5-a-Int2, it becomes bigger in 5-s-TS2 (0.47) than in 5-a-TS2 (0.42). BO values of C6–H7 and N8–H7 bonds in 5-s-TS2 (0.12, 0.61) demonstrate that the extent of C6–H7 bond dissociation and N8–H7 bond formation is much higher than that of 5-a-TS2 (0.26, 0.47). From the Int to the TS, the less the BO value of N2–C3 bond changes, the easier the reaction proceeds.³⁷ Two steps of the s-path (0.06, 0.21) are both superior to those of the a-path (0.18, 0.32) leading to the favorable (3S,4S)-3. In the activation of nitroalkene by tertiary amine via weak covalent bond, the weak covalent interaction not only stabilizes the TSs in the s-path, but also orients the reaction in the s-path with smaller variations of this bond.

Table 3 Bond orders of major species with full catalyst 5 at B3LYP/6-311++G(d,p) level

Bond order	5-s-Int1	5-s-TS1	5-a-Int1	5-a-TS1
C1–N2	0.83	0.84	0.82	0.84
N2–C3	0.74	0.68	0.75	0.57
C4–C5		0.38		0.33
	5-s-Int2	5-s-TS2	5-a-Int2	5-a-TS2
C1–N2	0.83	0.90	0.80	0.74
N2–C3	0.68	0.47	0.74	0.42
C6–H7		0.12		0.26
N8–H7		0.61		0.47

---

From the steric perspective, we are intrigued by the impact of the π–π stacking between the aromatic rings of 5 and 2 on the enantioselectivity (Supplementary Data†). The extent of π–π stacking relates directly to the efficient packing areas of the aromatic rings, which is identical to the projected area proportional to the cosine value of the angle between the two planes. In a complex, a smaller angle corresponds to a larger extent of π–π stacking. A smaller change of the angle gives rise to an easier reaction process.³⁷ In 5-s-Int1, two aromatic rings are almost parallel to each other. The aromatic ring of 5 tilts upward in 5-s-TS1 to form a 20° angle with the one of 2. In contrast, two aromatic rings are vertical in 5-a-Int1 and the aromatic ring of 2 bends towards the one of 5 to form a 60° angle in 5-a-TS1. Although the extent of π–π stacking in 5-s-Int2 (50°) is downhill from 5-s-TS1, then it is somewhat increased in 5-s-TS2 (40°). However, the angle in 5-a-Int2 comes back to 90° via5-a-TS1. There is still little π–π stacking interaction in 5-a-TS2 ascribed to the aromatic rings stretching in opposite directions with a large angle of 170°. In the activation of N-tosylimine by the aromatic ring via π–π stacking, the non-covalent interaction effectively stabilizes the species of the s-path and prefers the s-path with smaller changes of the efficient packing areas.

The enantiomeric excess (ee) of an isomer is measured by chiral column chromatography or NMR spectroscopy in the experiment. Here, based on the calculation of rate constant (k) in transition state theory,³⁹ ee values (298 K) could be predicted employing the activation Gibbs free energies of the rate-limiting step 2 in different solution phase conditions⁴⁰ (Table 2). With xylene and DMF, the calculated ee values of (3S,4S)-3 are 97.6% and 27.2%, respectively. The results are in accordance with the experiment. It is known that the weak covalent interaction exerted by a Lewis base and non-covalent interactions (H bonds, π–π stacking) would play their roles adequately in non-polar not polar environment. Therefore the fact that the ee value with xylene is much higher than with DMF confirms the cooperative effect of three interactions attributed by different units of catalyst on the domination of enantioselectivity.

Conclusion

Our DFT calculations provide the first theoretical investigation on enantioselective aza-MBH-type reaction of nitroalkene and N-tosylimine catalyzed by thiourea-tertiary amines. The whole process contains two steps: nucleophilic addition of the nitroalkene-catalyst binary precursor to N-tosylimine; proton transfer from methyl of nitroalkene to the electronegative nitrogen of imine; step 2 is rate-limiting.

The research on the real system with full catalyst elucidates the relationship between enantioselectivity and the structural properties of the catalyst. Three functional groups of the catalyst play different roles in the activation process. As a Lewis base, the tertiary amine group activates the nitroalkene via a weak covalent bond. The weak covalent interaction orients the reaction in a major path with smaller variations of this bond. On the other hand, the aromatic ring group activates the N-tosylimine via π–π stacking. The non-covalent interaction selects the major path with smaller changes of the efficient packing areas. The thiourea group donates more compact H-bonded network in species of the major path. The enantioselectivity is dominated by the cooperative effect of non-covalent and weak covalent interactions attributed by different units of the catalyst. This conclusion is supported by the ee value with non-polar xylene (97.6%) which is much higher than that with polar DMF (27.2%).

Acknowledgements

This work was supported by National Basic Research Program of China (973 Program, 2007CB936000), National Natural Science Foundations of China (No. 20975064) and Natural Science Foundation of Shandong Province (No. ZR2009BZ003).

References

1. C. J. Li, Acc. Chem. Res., 2009, 42, 335–344.
2. P. Langer, Angew. Chem., Int. Ed., 2000, 39, 3049–3052.
3. G. Masson, C. Housseman and J. Zhu, Angew. Chem., Int. Ed., 2007, 46, 4614–4628.
4. T. Kataoka and H. Eur. Kinoshita, J. Org. Chem., 2005, 45–48.
5. Y. L. Shi and M. Eur. Shi, J. Org. Chem., 2007, 18, 2905–2916.
6. H. Pellissier, Tetrahedron, 2006, 62, 2143–2173.
7. G. K. Friestad and A. K. Mathies, Tetrahedron, 2007, 63, 2541–2569.
8. M. E. Kraft, T. F. N. Haxell, K. A. Seibert and K. A. Abboud, J. Am. Chem. Soc., 2006, 128, 4174–4175.
9. I. Deb, M. Dadwal, S. M. Mobin and I. N. N Namboothiri, Org. Lett., 2006, 8, 1201–1204.
10. M. Dadwal, S. M. Mobin and I. N. N. Namboothiri, Org. Biomol. Chem., 2006, 4, 2525–2528.
11. M. E. Kraft and J. A. Wright, Chem. Commun., 2006, 2977–2979.
12. M. Pohmakotr, S. Thamapipol, P. Tuchinda, S. Prabpai, P. Kongsaeree and V. Reutrakul, J. Org. Chem., 2007, 72, 5418–5420.
13. K. Wadhwa, V. R. Chintareddy and J. G. Verkade, J. Org. Chem., 2009, 74, 6681–6690.
14. T. E. Reynolds, M. S. Binkley and K. A. Scheidt, Org. Lett., 2008, 10, 5227–5230.
15. G. L. Zhao and M. Shi, Org. Biomol. Chem., 2005, 3, 3686–3694.
16. P. Maity and S. D. Lepore, J. Am. Chem. Soc., 2009, 131, 4196–4197.
17. X. Wang, Y. F. Chen, L. F. Niu and P. F. Xu, Org. Lett., 2009, 11, 3310–3313.
18. V. Singh and S. Batra, Tetrahedron, 2008, 64, 4511–4574.
19. J. H. Lii, B. Ma and N. L. Allinger, J. Comput. Chem., 1999, 20, 1593–1603.
20. K. C. Hunter, L. R. Rutledge and S. D. Wetmore, J. Phys. Chem. A, 2005, 109, 9554–9562.
21. M. Lozynski and D. Rusinska-Roszak, J. Phys. Chem. A, 1998, 102, 2899–2903.
22. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
23. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
24. S. H. Vosko, L. Wilk and M. Can. Nusair, J. Phys., 1980, 58, 1200–1211.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, J. A. Pople, Gaussian 03, Revision A. 1; Gaussian, Inc., Pittsburgh, PA, 2003.
26. A. D. Becke, J. Chem. Phys., 1996, 104, 1040–1046.
27. Y. Zhao, B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 2715–2719.
28. K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163.
29. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–556.
30. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
31. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
32. O. J. Tapia, J. Math. Chem., 1992, 10, 139–181.
33. B. Y. Simkin, I. Sheikhet, Quantum Chemical and Statistical Theory of Solutions—A Computational Approach, Ellis Horwood, London, 1995.
34. J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094.
35. R. X. Zhu, D. J. Zhang, J. Wu and C. B. Liu, Tetrahedron: Asymmetry, 2006, 17, 1161–1164.
36. D. R. Lloyd, Chem. Phys. Lett., 2000, 323, 198–199.
37. N. Lu, L. Meng, D. Z. Chen and G. Q. Zhang, J. Mol. Catal. A: Chem., 2011, 339, 99–107.
38. K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096.
39. D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800.
40. D. Z. Chen, N. Lu, G. Q. Zhang and S. Z. Mi, Tetrahedron: Asymmetry, 2009, 20, 1365–1368.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c1ra00015b

---