A method to determine the recombination and attachment coefficients of atmospheric ions and ultrafine particles in different charge levels
Florian
Mandija
*
Department of Physics,, University of Shkodra, Shkoder, Albania. E-mail: f_mandija@yahoo.com
First published on 20th July 2011
Abstract
Electrostatic interactions among atmospheric particles like cluster ions and aerosols are of great interest nowadays in atmospheric studies. There are several models which describe this interaction. Recombination and attachment coefficients are expressed in terms of many environmental and particle properties. In this study are derived further simplified expressions of recombination and attachment coefficients between cluster ions and ultrafine aerosol particles. These expressions require the knowledge of only the ion and aerosol concentrations as well as the ion production rate. Thus the usage of these coefficients facilitates the elaboration of a balance equation, enabling the prediction of the evolution of ion and aerosol concentrations.
Introduction
One of the most investigated regions of atmosphere is the troposphere. This is because it is the lowest part of the atmosphere, in direct contact with ground surface constituting our living environment.1 In this region the main sources of small ions are cosmic rays, radon, and radioactivity from the ground, and also depend on properties of the ground.2–5 The main sources of primary aerosol particles are volcanic eruptions, sea salts, dust storms, etc. Secondary aerosol particles are formed by binary and ternary nucleation mechanisms. The presence of atmospheric ions enhances the particle formation process by an ion mediated nucleation mechanism.Atmospheric ions and aerosol particles are essential factors which influence atmospheric electricity. Atmospheric ions increase air conductivity; meanwhile aerosol particles have an inverse impact on the global electric circuit, because of their lower electric mobility.6–8 Aerosol particles influence the radiation budget, reducing the atmospheric visibility.9,10
Apart their influence on the electrical parameters of the atmosphere, atmospheric ions has an obvious effect on human health, where relatively high ion concentrations meliorate psychological and physical human conditions. But aerosol particles, especially smaller ones, play the opposite role in human health, primarily influencing the respiratory system.11–22
Concentrations of both atmospheric ions and atmospheric particles are governed by balance equations.23–25 Taking into account only ion–ion and ion–aerosol interactions, the balance equation can be written in its simplest form:
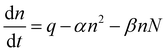 | (1) |
The recombination and attachment coefficients are indicators of the interaction rate between all these particles, and their determination is of great interest in the study of atmospheric ion and aerosol particle behavior, their concentrations and size distributions.28 This affects the electric parameters of atmosphere, like electrical conductivity, and indirectly the air quality of our environment.
Theory and method
It is possible to determine the recombination and attachment coefficients based on the physical properties of atmospheric ions and aerosol particles. There are diverse expressions that can predict the evaluation of recombination and attachment coefficients.29–33 The evaluation procedure of these coefficients is based on relatively complicated calculations. This is because the determination of α and β, requires several physical parameters of the ions and aerosols to be known, like their electric charge and mobility, their size, and other environmental parameters. Knowing these parameters allows us to determine recombination and attachment coefficients.However, another method used to determination of these coefficients can be used efficiently. Here we introduce a method that requires the knowledge of only the concentration of atmospheric ions and aerosol particles, as well as the ion production rate. In this study we are restricted only on the stationary case, where ion and aerosol concentrations can be considered time-constant. Under these conditions the balance equation (1) takes the form:
| αn2 + βnN = q | (2) |
Eqn (2) can be used for the total ion and aerosol concentrations, where
q – ion pair production rate
α – recombination coefficient
β – effective attachment coefficient
n – ion concentration
N – aerosol concentration
In eqn (2)αn2 gives the ion pair loss by the recombination processes (one positive and one negative ion are eliminated instantly), βnN gives the number of ions (of both positive and negative polarity) that are eliminated by the attachment processes. These reduction processes are compensated by the ion pair produced production rate q, which is the number of ion pairs produced by natural sources in unit time and unit volume.
It is well known that aerosol distribution is presented by continuous curves, and although the modes are characterized by their peaks, they are not separated from each other.34–38
Ultrafine particles can be electrically neutral or can carry a maximum of only one electric charge.39 This is due to their small size; we use a Boltzmann charge distribution to evaluate the charged sate of aerosol particles, although this distribution gives certain errors for the nucleation mode.40–44
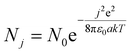 | (3) |
The balance equation in these conditions is:
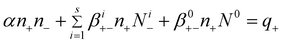 | (4) |
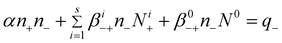 | (5) |
n ± – ion concentrations of both polarities
N i ± – i-charged aerosol concentrations of both polarities
N 0 – neutral aerosol concentrations
q ± – ion production rates of both polarities
α – recombination coefficient
β i +− – attachment coefficients of positive ions to aerosol particles having i negative charges
β i −+ – attachment coefficients of negative ions to aerosol particles having i positive charges
β 0+− – attachment coefficients of positive ions to neutral aerosol particles
β 0−+ – attachment coefficients of negative ions to neutral aerosol particles
In eqn (4)–(5) there are 2s + 3 variables; α, βi+−, βi−+, β0+−, and β0−+ (where i = 1 ÷ s).
In order to obtain the solution for these variables, we must find other equations. These additional equations are retrieved from the below conditions;
The ion production rate of both polarities are assumed to be equal:
| q+ = q− = q | (6) |
In stationary conditions, aerosol concentrations are constant, and we can obtain these additional equations:
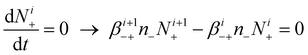 | (7) |
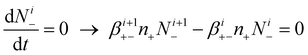 | (8) |
Eqn (7) derives from the fact that the concentration of positively i-charged aerosol particles increases due to the attachment of negative ions to positively (i + 1)-charged aerosol particles, and decreases due to the attachment of negative ions to positively i-charged aerosol particles. The first of these two processes increases number concentration of positively i-charged aerosol particles, and the second one decreases this concentration. Similarly, in eqn (8), the concentration of negatively i-charged aerosol particles is governed by the competition between these two processes; the attachment of positive ions to negatively (i + 1)-charged aerosol particles, which increases concentration of positively i-charged aerosol particles; and the attachment of positive ions to negatively i-charged aerosol particles, which decreases this concentrations. The first process increases number concentration of negatively i-charged aerosol particles, as the second process increases this concentration.
The set of equations (7)–(8), gives additional 2s equations.
Let us retrieve the last equation. This can be done making the following assumptions:
Mono-charhged aerosol particles, in normal atmospheric conditions, can also be considered atmospheric ions, because all these particles are electrically charged. This assumption is justified by the fact that atmospheric ions and charged ultrafine particles are almost mono-charged, although charged ultrafine particles have a greater size than atmospheric ions. So, the attachment process between mono-charged ultrafine particles and atmospheric ions, as well as the recombination between ions, is considered as a recombination process between all these particles.
This approximation gives the last equation:
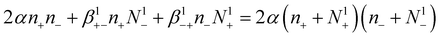 | (9) |
The factor 2 in eqn (9) is due to the fact that the recombination process eliminates two ions (of opposite polarity) at the same time.
From eqn (7)–(8), we can find the terms 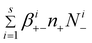 and
and 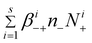 , respectively in eqn (2) and (5). Summing between i = 0 to s in eqn (7)–(8), we obtain:
, respectively in eqn (2) and (5). Summing between i = 0 to s in eqn (7)–(8), we obtain:
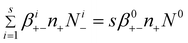 | (10) |
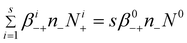 | (11) |
Making these substitutions, eqn (4)–(5) can be transformed:
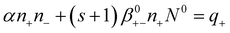 | (12) |
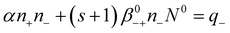 | (13) |
After some relatively easy calculations, we can obtain the expressions for the recombination and attachment coefficients for different aerosol charge levels:
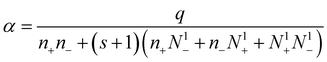 | (14) |
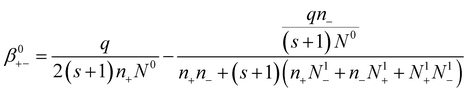 | (15) |
Eqn (15) gives the attachment coefficient between positive ions and neutral aerosols.
By applying eqn (8) to eqn (15), we can obtain the attachment coefficients of positive ions with negatively charged aerosols, in different charging levels.
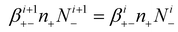 | (16) |
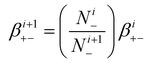 | (17) |
N i − is the concentration of negatively i-charged aerosols
N i+1− is number concentration of negatively (i + 1)-charged aerosols
So, the attachment coefficients of positive ions with negative (i + 1)-charged aerosol particles are:
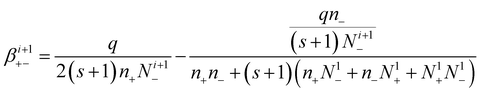 | (18) |
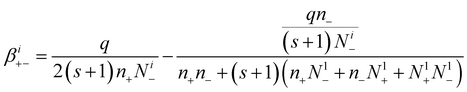 | (19) |
Similarly, the attachment coefficients of negative ions with positively i-charged aerosol particles are:
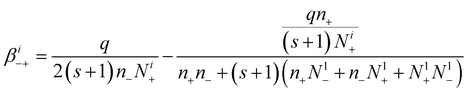 | (20) |
In order to find the expression of the attachment coefficient between negative ions and neutral aerosol particles, we simply use eqn (20) and take i = 0:
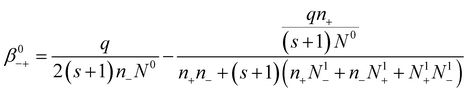 | (21) |
Discussions
This method of determining the recombination and attachment coefficients of atmospheric particles is based on the use of the balance equation in certain conditions. The altitude dependence of the coefficients was not taken into account, because we focused on the lower part of troposphere, near the ground level.45In our study several approximations are made; the ion production rates are equal for different polarities, ion and aerosol concentrations of positive and negative polarities, and, in the case of neutral particles, are considered as time-constant. These stationary conditions are satisfied in normal meteorological conditions.
Ultrafine particles include nucleation mode (dp < 20 nm) and Aitken mode (20 < dp < 90 nm). Based on their charge distribution, ultrafine particles are considered electrically neutral or mono-charged.46 So, the approximation made in eqn (9), where charged ultrafine particles are considered as atmospheric ions, was based on their electrostatic behaviour. In normal meteorological conditions, in an unpolluted region, charged ultrafine particles are mono-charged, like atmospheric ions.
Form the eqn (14), (15), (19) and (20) it can be deduced that the recombination and attachment coefficients, in stationary conditions are inversely proportional to the concentration of atmospheric ions and aerosol particles in a given ion production rate.
Measuring only the concentrations of atmospheric ions of both polarities, i-charged and neutral ultrafine particle concentrations, as well as ion production rate in the same location, we can obtain the values of the recombination and attachment coefficients.
In normal meteorological conditions, near ground concentrations of atmospheric ions are in the order of 102–103 cm−3, concentrations of aerosol particles are in the order of 103–104 cm−3, while the ion production rate is about 10 ions cm−3s−1. All these parameters are dependent on the measurement locations and ground properties.
Conclusions
In order to evaluate the rate of interaction between atmospheric particles, it is necessary to determine the recombination coefficient between atmospheric ions, and the attachment coefficient between atmospheric ions and aerosol particles. Theoretically several expressions of these coefficients have been deduced. But their determination requires the calculation of several physical parameters of the atmospheric particles, and the environmental conditions.The stationary case is used in our calculations for atmospheric ions and aerosol particles of both polarities. Based on the balance equation and on the above mentioned conditions, we have formulated all the necessary equations to determine the recombination and attachment coefficients. According to this method, these coefficients depend only on the concentrations of atmospheric ions and aerosol particles at a given ion production rate.
This method is very convenient, because it simplifies the equations and makes the procedure of determination of these coefficients faster, even though these results are obtained using approximations during our calculations. The treatment of ultrafine aerosol particles is related to the fact that these particles constitute the majority of total atmospheric particles.
References
- H. Lihavainen, M. Kommpula, V.-M. Kerminen, H. Jarvinen, Y. Vissanen, K. Lehtinen, M. Vana and M. Kulmala, Size distributions of atmospheric ions inside clouds and in cloud-free air at remote continental site, Boreal Env. Res., 2007, 12, 337–344 CAS.
- P. Tiitta, P. Miettinen, P. Vaattovaara, J. Joutsenaari, A. Hirsikko, P. Aalto and M. Kulmala, Road-site measurements of aerosol and ion number size distributions: a comparison with remote site measurements, Boreal Env. Res., 2007, 12, 311–321 CAS.
- A. Hirsikko, T. Y-Juuti, T. Nieminen, E. Vertiainen, L. Laakso, T. Hussein and M. Kulmala, Indoor and outdoor air ions and aerosol particles in the urban atmosphere of Helsinki: characteristics, sources and formation, Boreal Env. Res., 2007, 12, 295–310 CAS.
- U. Horrak, Air ion mobility spectrum at a rural area, Dissertationes geophysicales universitatis tartuensis, 2001 Search PubMed.
- L. Laakso Kinetics and dynamics of atmospheric ions, clusters and aerosols, Report Series In Aerosol Science, No. 70 ( 2004). Search PubMed.
- R. G. Harrison a and K. L. Aplin, Water vapour changes and atmospheric cluster ions, Atmos. Res., 2007, 85, 199–208 CrossRef.
- R.G. Harrison and K.L. Aplin, Atmos. Res., 2007, 85(2), 199–208 CrossRef CAS.
- K. Y. Kndratyev, L. S. Ivlev, V. F. Krapivin, C. A. Varotsos, Atmospheric aerosol properties, Formation, Processes and Impacts, Praxis Publishing, 2006. Search PubMed.
- W. N. Chen, S. Y. Chang, C.K. Chou Charles, T. K. Chen, Total Scatter-To-Backscatter Ratio Of Aerosol Derived From Aerosol Size Distribution Measurement, Research Center for Environmental Changes, Academia Sinica, Taipei 115, Taiwan. Search PubMed.
- Radiative Forcing of Climate Change, National Research Council, 2005..
- M. Dall’Osto and R. M. Harrison, Chemical characterization of single airborne particles in Athens (Greece) by ATOFMS, Atmos. Environ., 2006, 40, 7614–7631 CrossRef.
- A. M. Jones and R. M. Harrison, Interpretation of particulate elemental andorganic carbon concentrations at rural, urban and kerbside sites, Atmos. Environ., 2005, 39, 7114–7126 CrossRef CAS.
- K. M. Latha, A. Bennett, E. J. Highwood and G. Harrison R, Retrieval of Global Atmospheric Electrical Activity at a Polluted Urban Site, J. Phys.: Conf. Ser., 2008, 142, 012013 CrossRef.
- J. Yin, A. G. Allen, R. M. Harrison, S. G. Jennings, E. Wright, M. Fitzpatrick, T. Healy, E. Barry, D. Ceburnis and D. McCusker, Major component composition of urban PM10 and PM2.5 in Ireland, Atmos. Res., 2005, 78, 149–165 CrossRef CAS.
- R. G. Harrison and K. L. Aplin, Mid-nineteenth century smoke concentrations near London, Atmos. Environ., 2002, 36, 4037–4043 CrossRef CAS.
- A. Kousa PM2.5 and NO2 exposure assessment of urban population in the Helsinki metropolitan area and other European urban areas, Report Series in Aerosol Science, No 57 ( 2002). Search PubMed.
- C. Oliveira, C. Pio, C. Alves, M. Evtyugina, P. Santos, V. Goncalves, T. Nunes, A. J. D. Silvestre, F. Palmgren, P. Wahlin and S. Harrad, Seasonal distribution of polar organic compounds in the urban atmosphere of two large cities from the North and South of Europe, Atmos. Environ., 2007, 41, 5555–5570 CrossRef CAS.
- X. Wang, T. Sato and B. Xing, Size distribution and anthropogenic sources apportionment of airborne trace metals in Kanazawa, Japan, Chemosphere, 2006, 65, 2440–2448 CrossRef CAS.
- M. Viana, T. A. J. Kuhlbusch, X. Querol, A. Alastuey, R. M. Harrison, P. K. Hopke, W. Winiwarter, M. Vallius, S. Szidat, A. S. H. Prévôt, C. Hueglin, H. Bloemen, P. Wåhlin, R. Vecchi, A.I. Miranda, A. Kasper-Giebl, W. Maenhaut and R. Hitzenberger, Source apportionment of particulate matter in Europe: A review of methods and results, J. Aerosol Sci., 2008, 39, 827–849 CrossRef CAS.
- X. Querol, A. Alastuey, C. R. Ruiz, B. Artinano, H. C. Hansson, R. M. Harrison, E. Buringh, H. M. Brink, M. Lutz, P. Bruckmann, P. Straehl and J. Schneider, Speciation and origin of PM10 and PM2.5 in selected European cities, Atmos. Environ., 2004, 38, 6547–6555 CrossRef CAS.
- P. A. Jaques and C. S. Kim, Measurement of total lung deposition of inhaled ultrafine particles in healthy men and women, Inhalation Toxicol., 2000, 12, 715–731 CrossRef CAS.
- G. Buzorius, Variation of aerosol concentration in ambient air, Report Series in Aerosol Science, No. 46, ( 2000). Search PubMed.
- L. Laakso, T. Petaja, K. E. J. Lehtinen, M. Kulmala, J. Paatero, U. Horrak, H. Tammet and J. Joutsensaari, Ion production rate in a boreal forest based on ion, particle and radiation measurements, Atmos. Chem. Phys. Discuss., 2004, 4, 3947–3973 CrossRef.
- L. Laakso, J. M. Makela, L. Pirjola and M. Kulmala, Model studies on ion-induced nucleation in the atmosphere, J. Geophys. Res., 2002, 107(D20), 4427 CrossRef.
- T. Maruyama and T. Katayama, Transfer of small negative atmospheric ions, J. Appl. Phys., 2003, 94, 11 Search PubMed.
- T. Hussein, A. Karppinen, J. Kukkonen, J. Harkonen, P. P. Aalto, K. Hameri, V. M. Kerminen and M. Kulmala, Meteorological dependence of size-fractionated number concentrations of urban aerosol particles, Atmos. Environ., 2006, 40, 1427–1440 CrossRef CAS.
- W. C. Hinds, Aerosol Technology, Properties, Behavior, and Measurement of Airborne Particles,, Second Edition, John Wiley & Sons, p. 1999. Search PubMed.
- U. Horrak, P. P. Aalto, J. Salm, K. Komsaare, H. Tammet, J. M. Makela, L. Laakso and M. Kulmala, Characterization of positive air ions in boreal forest air at the Hyytiala SMEAR station, Atmos. Chem. Phys. Discuss., 2007, 7, 9465–9517 CrossRef.
- R. J. Wilding and R. G. Harrison, Aerosol modulation of small ion growth in coastal air, Atmos. Environ., 2005, 39, 5876–5883 CrossRef CAS.
- K. E. J. Lehtinen, H. Korhonen, M. Dal Maso and M. Kulmala, On the concept of condensation sink diameter, Boreal Env. Res., 2003, 8, 405–411 Search PubMed.
- T. Hussein, M. Dal Maso, T. Petäjä, I. K. Koponen, P. Paatero, P. P. Aalto, K. Hämeri and M. Kulmala, Evaluation of an automatic algorithm for fitting the particle number size distributions, Boreal Env. Res., 2005, 10, 337–355 Search PubMed.
- T. Hussein, A. Puustinen, P. P. Aalto, J. M. Makela, K. Hameri and M. Kulmala, Urban aerosol number size distributions, Atmos. Chem. Phys., 2004, 4, 391–411 CrossRef CAS.
- M. S. Bae, J. J. Schwab, O. Hogrefe, B. P. Frank, G. G. Lala and K. L. Demerjian, Characteristics of size distributions at urban and rural locations in New York, Atmos. Chem. Phys. Discuss., 2010, 10, 69–108 CrossRef.
- A. Pugatsova, H. Iher and E. Tamm, Modal structure of aerosol particle size spectrum for nucleation burst days in Estonia, Boreal Env. Res., 2007, 12, 361–373 CAS.
- T. Hussein, K. Hameri, P. P. Aalto, P. Paatero and M. Kulmala, Modal structure and spatial–temporal variations of urban and suburban aerosols in Helsinki—Finland, Atmos. Environ., 2005, 39, 1655–1668 CrossRef CAS.
- J. M. Makkela, I. K. Koponen, P. Aalto and M. Kulmala, One-year data of submicron size modes of tropospheric background aerosol In southern Finland, J. Aerosol Sci., 2000, 31(5), 595–611 CrossRef.
- J. Curtuis, Nucleation of atmospheric aerosol particles, C. R. Physique, 2006 Search PubMed.
- M. Kulmala, K. E. J. Lehtinen, L. Laakso, G. Mordas and K. Hämeri, On the existence of neutral atmospheric clusters, Boreal Env. Res., 2005, 10, 79–87 CAS.
- S. N. Tripathi and R. G. Harrison, Enhancement of contact nucleation by scavenging of charged aerosol particles, Atmos. Res., 2002, 62, 57–70 CrossRef CAS.
- S. H. Kim, K. S. Woo, B. Y. H. Liu and M. R. Zachariah, Method of measuring charge distribution of nanosized aerosols, J. Colloid Interface Sci., 2005, 282, 46–57 CrossRef CAS.
- F. Vila and F. Mandija, The altitude profile of atmospheric ion concentration and the determination of recombination and attachment coefficients in suburbs areas, J. Electrost., 2009, 67(2–3), 492–495 CrossRef CAS.
- H. Tammet, U. Horrak, L. Laakso and M. Kulmala, Factors of air ion balance in a coniferous forest according to measurements in Hyytiala, Finland, Atmos. Chem. Phys., 2006, 6, 3377–3390 CrossRef CAS.
- I. K. Koponen, Observations of tropospheric aerosol size distributions, Report Series in Aerosol Science, No. 63 ( 2003). Search PubMed.
- U. Horrak, P. P. Aalto, J. Salm, K. Komsaare, H. Tammet, J. M. Makela, L. Laakso and M. Kulmala, Variation and balance of positive air ion concentrations in a boreal forest, Atmos. Chem. Phys. Discuss., 2008, 8, 655–675 CrossRef CAS.
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics,, Second Edition, John Wiley & Sons, 2006. Search PubMed.
- S. T. Parker, Exploring the interactions between atmospheric ions and micrometre sized aerosols, J. Phys.: Conf. Ser., 2008,(142) Search PubMed.
| This journal is © The Royal Society of Chemistry 2011 |
