Synthesis of a new nanocrystalline titanium aluminum fluoride phase by reaction of Ti₂AlC with hydrofluoric acid

Abstract

A new nanocrystalline phase of titanium aluminum fluoride, with a stoichiometry of Ti₂AlF₉—exact stoichiometry measured herein is Ti_2.1Al_0.9F₉,—was synthesized by the fluorination of Ti₂AlC in anhydrous hydrofluoric acid at 55 °C for 2 h. The results from X-ray diffraction, scanning and high-resolution transmission electron microscopy and selected area diffraction, together with crystal structure solution via simulated annealing, confirmed the formation of a nanocrystalline material with a trigonal structure belonging to the R3 space group. The structure can also be viewed as being comprised of corner-sharing octahedra that are arranged in a distorted simple cubic arrangement. Thermogravimetric analysis, in argon, indicates that this phase is stable up to ≈ 850 °C. Density functional theory calculations estimate the band gap to be ≈ 5 eV and the bulk modulus to be ≈ 109 GPa.

---

1. Introduction

Many properties of metal fluorides differ from related metal oxides or carbides, because of their high Lewis acidities, low refractive indices (1.33–1.60), and a wide wavelength window for light transmission (100–15 000 nm). Metal fluorides find widespread applications as catalysts, optical coatings, transparent ceramics, and high energy-density electrodes in Li ion batteries.^1–4 With the prominent exception of CaF₂—the principal source of HF—all other metal fluorides do not (or no longer) occur in sufficient abundance in nature—especially not the important aluminum flux agent cryolite (Na₃AlF₆).³ However, unlike many metal oxides and carbides,⁵ the synthesis of metal fluorides can usually be carried out at low or even room temperature, which in turn offers unique synthesis routes with relatively low expenditure of energy.⁶ In particular, aluminum fluoride (AlF₃) attracted interest not only because of its use for Al production² and the glass industry,⁷ but also as an anti-caries agent in dentistry.⁸ The most common Ti-ternary fluoride is potassium fluorotitanate, K₂TiF₆, which is used as a flux agent during the forging of Al or Ti.⁹

The main motivation of this study was to evaluate the reactivity of Ti₂AlC with anhydrous HF. The former is a member of the so-called MAX phase family of ternary carbides and nitrides governed by the general formula M_{n + 1}AX_n, where n = 1, 2, or 3, M is an early transition metal, A is an A-group element (mostly groups 13 and 14), and X is carbon and/or nitrogen.¹⁰ The MAX phases are layered hexagonal nanolaminates (space groupP6₃/mmc) with two formula units per unit cell. In the crystal structure, near close-packed M-atom layers are interleaved with layers of group A elements with the X atoms filling the octahedral sites between the M atoms. The MAX phases have attracted much attention recently because some of them combine some of the best attributes of ceramics and metals. Most notably, Ti₂AlC has excellent oxidation resistance, high elastic moduli and strengths, chemical stability, excellent thermal shock resistance, good machinability and a high ratio of fracture toughness to strength.¹¹ As shown in recent studies,^12,13 the layered structure of the MAX phases makes them highly susceptible to selective etching and with the large number of MAX phases with various chemical compositions in mind, this offers the possibility of templated synthesis of a large variety of new compounds.

In this study we report, to the best of our knowledge, for the first time on a new trigonal, nanocrystalline ternary titanium aluminum fluoride phase with an approximate chemistry of Ti_2.1Al_0.9F₉. We exemplify HF treatment on Ti₂AlC as one common member of the vast MAX phase family to illustrate the potential of metal fluoride synthesis viaHF treatment.

2. Experimental

To synthesize this new phase, 10 g Ti₂AlC powder (−325 mesh with average particle size of 17 μm, >92 wt% purity, 3-ONE-2, Voorhees, USA) was fluorinated using 37 g of anhydrous hydrofluoric acid, HF (HF : Ti₂AlC ∼27 : 1 molar ratio) at 55 °C for 2 h. The temperature of 55 °C was determined to be the onset temperature for the reaction and was determined by carefully increasing the temperature from room temperature and monitoring gas formation (the fluorination was done by F2ChemTech, Allentown-PA, USA). Fourier transform infrared spectroscopy—FTIR—(Perkin Elmer Spectrum 100 FTIR, Shelton-CT, USA) was used to analyze the gaseous reaction products during the fluorination reaction. The resultant material was characterized by X-ray diffraction (XRD) using a powder diffractometer (Siemens D500, Bruker AXS, Karlsruhe, Germany) operating with Cu-Kα radiation (step scan 0.02°, 1 s per step). Si powder (99 wt% purity, Alfa Aesar, Ward Hill, USA) was used as an internal standard.

A scanning electron microscope, SEM, (Supra 50VP, Zeiss, Oberkochen, Germany) equipped with an energy-dispersive spectrometer, (EDS; Oxford Inca X-Sight, Oxfordshire, UK) was used to investigate chemical composition and the morphology of the particles formed after the reaction. Differential scanning calorimetry (DSC) analysis was carried out on powder samples in a simultaneous thermogravimetric analysis TGA/DSC unit (Netzsch STA 449C Jupiter, Selb, Germany) in ultrahigh pure Ar (200 ml min⁻¹) in a platinum crucible. The sample was heated at 10 °C min⁻¹ to 1200 °C and held at that temperature for 10 min before cooling to room temperature.

Transmission electron microscopy, TEM, (FEI, Tecnai G2 TF20UT FEG, The Netherlands) operating at 200 kV was used for high-resolution imaging and selected area electron diffraction (SAED). A multi-scan CCD digital camera was used to capture the images. Elemental analysis in the TEM was carried out using an ultra-thin window X-ray energy dispersive spectrometer. The TEM samples were prepared by depositing flakes, suspended in isopropanol, on a lacey-carbon coated copper grid (200 mesh).

The crystal structure was determined using TOPAS4 (Bruker AXS, Karlsruhe, Germany). Based on the fundamental parameter approach (FPA),¹⁴ the instrumental parameters (e.g., broadening, offset) were derived from measurements of a Si reference. From the diffractograms, the peak positions and intensities were extracted via whole-pattern fitting with the Pawley method¹⁵ yielding results in agreement with the LeBail method.¹⁶ Based on the space group identified from indexing, the derived unit cell dimensions and peak intensities were used for structure solutions, based on whole-profile fitting simulated annealing.¹⁷

Ab initio calculations, based on density functional theory (DFT), were performed using the Perdew–Burke–Eruzerhof (PBE) generalized gradient approximation (GGA),¹⁸ with a plane wave cutoff of 400 eV and a 9 × 9 × 9 Γ-centered k-point grid, as implemented in the VASP software. For Ti, the semi-core 3p states were treated as valence electrons. To represent the Ti and Al positions, a unit cell—with one out of the three Al/Ti positions [(⅓, ⅔, z), (0, 0, z + ⅓), or (⅔, ⅓, z − ⅓)] filled with an Al atom—was used. Computations of the electronic properties and structural parameters were carried out with calculations of the total density of states (DOS) and energy minimization through the relaxation of atomic positions and c/a ratio for a range of fixed volumes. The equilibrium volume and bulk moduli were obtained with the modified Morse equation of state fit of the total energy as a function of volume.¹⁹

3. Results and discussion

The XRD patterns (Fig. 1a–b) show a significant diminution of Ti₂AlC-related Bragg peaks after HF treatment and the formation of another crystalline phase. To the best of our knowledge, the powder diffraction pattern of that phase has never been reported before and neither XRD databases (PDF-2/ICSD) nor the thoroughly searched literature yielded a match. Comparison with literature data shows that the peaks do not match the peaks of TiF₂, TiF₃, TiF₄, AlF₃^20–24 or TiOF₂.²⁵ It is thus reasonable to conclude that it is a new phase, with an unknown crystal structure.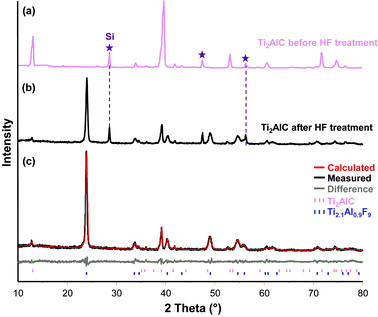

Fig. 1 X-Ray pattern of Ti₂AlC (a) before and, (b) after HF treatment. After fluorination, low intensity peaks belonging to not completely reacted carbide can be seen. Note the peak broadening of the new phase compared to the precursor or the Si reference. (c) Measured and calculated diffraction patterns of Ti_2.1Al_0.9F₉ with <10 wt% residual Ti₂AlC. The lowest line shows the difference between the calculated and measured intensities.

Compared to either the MAX phase precursor or the Si reference, significant peak broadening was observed for this new phase. Deconvolution of the XRD pattern did not indicate the presence of residual strains.²⁶ The broadening of the Bragg reflections can, thus, be explained by a finite domain size; as discussed later, the nanocrystalline nature of this new compound was confirmed by TEM. The broadening corresponds to an average coherence length, or domain size, of ≈ 15 nm calculated from the integral breadth.²⁷

Pawley fitting based on 21 hkl reflections in the angular 2θ range, between 10 and 80° (3501 data points), yielded a profile value of R_wp = 11.14, R_exp = 8.86, and a goodness of fit, GOF, = 1.26 (Table 1; for definitions see ref. 28). The structure was solved via simulated annealing (cf.ref. 29) with 3 degrees of freedom (x, y, z) for all atoms. When the final calculated powder pattern and the measured diffractograms were compared (Fig. 1c) the agreement between them was found to be excellent.

Table 1 Goodness of fit and R-values after Pawley fitting (GOF = goodness of fit, DB = Durbin Watson)

Parameter	Value
GOF	1.42
R exp	8.88
R′exp	12.77
R wp	11.14
R′wp	17.22
R p	8.51
R′p	18.51
DB	1.36

---

As no additional data (e.g., from nuclear magnetic resonance spectroscopy) was available, and despite their great likelihood, not even MF₆ octahedra were assumed at the start of the simulation. All atoms were moved individually starting from 0, 0, 0 = x, y, z. Using more than 1 atom per element (i.e., 1 × Ti, 1 × Al, and 1 × F per unit cell) led to converging atomic positions overlapping on a level smaller than their radii. This is why all further refinement was carried out using a 15 parameter model (3 fractional indexes, 6 Ti/Al–F distances and 6 bond angles) of restrained TiF₆ octahedra, which were within ±2.8% of the unrestrained fit. The results are presented in Fig. 2 and Tables 2–4. The x and y coordinates of the Ti and Al atoms converged on special positions (0.3334 and 0.6657) and were set to ⅓ and ⅔, respectively. Fitting other ternary fluorides, such as ABF₆ (ref. 1, 30, 31), did not yield as good an agreement between calculated and measured patterns.

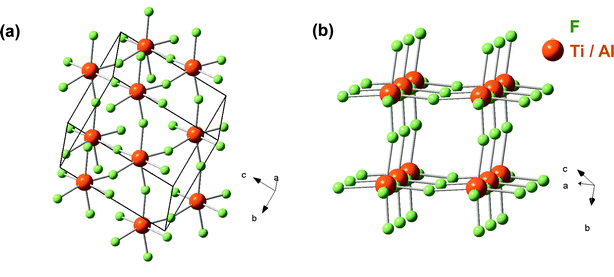Fig. 2 Unit cell of Ti₂AlF₉ (a) and the cellular MF-sublattice (b). Note that Ti and Al atoms occupy the same positions in the structure.

Table 2 Crystallographic data for Ti₂AlC and Ti_2.1Al_0.9F₉. Calculated structural parameters obtained from DFT are also listed and denoted by asterisks

Formula	Ti2AlC	Ti2.1Al0.9F9
Formula weight (g mol^−1)	134.753	295.817
Space group	P63/mmc	R3
Crystal system	Hexagonal	Trigonal
a/(Å)	2.968	5.3190	5.42*
c/(Å)	13.224	6.2609	6.71*
c/a	4.45	1.18	1.24*
V (Å^3)	100.88	153.40	171.31*
Bulk modulus (GPa)	186^40	–	109*
Formula units per unit cell	2	6
Calc. density (g cm^−3)	4.2	3.4	3.04*
Lin. absorption μ (cm^−1)	640.1	239.9

---

Table 3 Atomic positions (SOF = site occupancy factor)

Atom	SOF	x/a	y/b	z/c	U (Å^2)
F1	1	−0.18975	0.18975	−0.08888	1.783
Ti1	0.71	1/3	2/3	0.43142	0.879
Al1	0.29	1/3	2/3	0.43142	0.614

---

Table 4 Calculated atomic distances and angles

Atom 1	Atom 2	Distance 1–2 (Å)	Atom 3	Distance 1–3 (Å)	Angle 2–1–3 (°)
F1	Ti1|Al1	1.7664	Ti1|Al1	1.9738	166.16
	Ti1|Al1	1.7664	F1	2.2912	49.57
	Ti1|Al1	1.7664	F1	2.2912	49.57
	Ti1|Al1	1.9738	F1	2.2912	140.09
	Ti1|Al1	1.9738	F1	2.2912	140.09
	F1	2.2912	F1	2.2912	60.00
Ti1|Al1	F1	1.7664	F1	1.7664	80.87
	F1	1.7664	F1	1.7664	80.87
	F1	1.7664	F1	1.9738	88.63
	F1	1.7664	F1	1.9738	88.63
	F1	1.7664	F1	1.9738	166.16
	F1	1.7664	F1	1.7664	80.87
	F1	1.7664	F1	1.9738	88.63
	F1	1.7664	F1	1.9738	166.16
	F1	1.7664	F1	1.9738	88.63
	F1	1.7664	F1	1.9738	166.16
	F1	1.7664	F1	1.9738	88.63
	F1	1.7664	F1	1.9738	88.63
	F1	1.9738	F1	1.9738	100.18
	F1	1.9738	F1	1.9738	100.18
	F1	1.9738	F1	1.9738	100.18

---

The virtual starting temperature for the simulated annealing (not to be confused with sample temperature; cf.ref. 29) was 100 K. Not surprisingly, the atoms were observed to quickly move in a fashion that formed distorted MF₆ octahedra, where M was either Ti or Al. A good GOF was only obtained after the atomic fractional positions of Al and Ti converged, that is, excluding either Ti or Al to be present in the inter-octahedral positions in-between the MF₆ entities. Refinement was also carried out assuming the site occupancy factor, SOF, of Al plus Ti to unity. After ∼3.2 million moves, the structure was solved and the calculated and measured positions and intensities for Ti_2.1Al_0.9F₉ agreed well. The refined structure, shown in Fig. 2a and b, is built out of slightly distorted MF₆ octahedra with an average Ti/Al–F bonding distance of ∼1.8 Å. The structure can be understood as a distorted simple cubic arrangement of (Ti_{3 −} xAl_x)F₆ octahedra, where x is ≈ 1 (Fig. 2b). Compared to other metal fluorides—especially the stoichiometrically comparable AM₂F₁₁ type structures¹—the structure proposed herein is less densely packed and more reminiscent of the distorted Besenstielpackung-like TiF₄ structure.²¹

Compensating for the shared atomic position of Al and Ti, the Ti_2.1Al_0.9F₉ structure translates into a Ti : Al : F ratio ∼2.3 : 1 : 10, which is close to the stoichiometry derived from EDSviz. 2.1 : 1.0 : 9.0 associated with the TEM. Although it is possible for OH⁻ to substitute for F⁻ in some sites,³² the absence of oxygen in the TEM EDX spectra eliminates this possibility. It is important to note that with the Al and Ti site occupancy factor (SOF) and the temperature factor being refined independently, the calculated Al : Ti ratio may vary by approximately 10–15%, which could, thus, explain the deviation from the measured values.

During the HF treatment, FTIR recorded the evolution of gaseous reaction products and peaks were recorded at 3016, 1305, 1035 and 991 cm⁻¹ (Fig. 3). The peaks at 3016, and 1305 cm⁻¹ correspond to the C–H bond in CH₄;³³ while the two peaks around 1000 cm⁻¹ correspond to a C–F stretching vibration mode.³⁴ When these results are combined with XRD results it is reasonable to assume that the simplified reaction at 55 °C is:

Ti₂AlC + 11HF = Ti₂AlF₉ + 1/2CH₄ + 1/2CF₄ + 4.5H₂ (1)

At low resolution, SEM micrographs show that the layered nature of the initial MAX grains is preserved to some extent (Fig. 4a,c). At higher resolution (Fig. 4b,d) it becomes clear that the fluoride phase is not perfectly conformal but is associated with the formation of small cuboids. EDX analysis of the cubes is in agreement with the spectrum shown in Fig. 6e. Tellingly, the uncovered part in Fig. 4d, labeled X, shows in addition to Ti, Al and F also C. Since EDS in the TEM corroborates cubes to be devoid of C, we conclude that the C signal is coming from an unreacted Ti₂AlC core below the new phase. This behavior is similar to what which was observed during the fluorination of TiC, where a C–Ti–F shell formed around a TiC core.³⁵

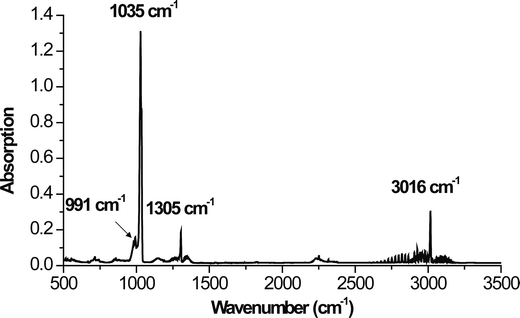Fig. 3 In situ FTIR spectrum of gases that evolved during the fluorination of Ti₂AlC.

Fig. 4 SEM images of the new phase. (a) At low magnification the particle shows the layered morphology, (b) the same as (a) but at higher magnification showing Ti₂AlF₉ cuboids, (c) another particle with part of it not covered with cuboids, and (d) the same as (c) but at higher magnification focusing on the circled part. X denotes Ti₂AlC substrate below the Ti₂AlF₉ cuboids

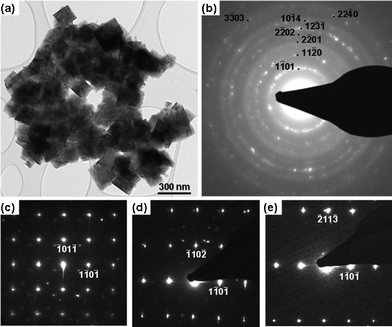Fig. 5 (a) A low magnification TEM image of Ti_2.1Al_0.9F₉ grains. (b) The corresponding SAED patterns, (c–e) are a series of SAED patterns from the Ti_2.1Al_0.9F₉ phase.

Low magnification TEM (Fig. 5a) and SAED (Fig. 5b) confirmed the nanocrystalline character of the new phase, also the indexed rings in the Fig. 5b and SAED patterns (Fig. 5c–e) are in good agreement with the XRD results and confirms the trigonal structure. The angle between (1̄011̄) and (11̄01̄) reflections (Fig. 5c) is ≈ 89°, which is in excellent agreement with the angle obtained from crystal structure obtained by simulated annealing (88.5°). It follows that both the XRD and TEM support the conclusion that R3 is the best-fitting space group, with a GOF of 32.35; followed by P31c with a GOF of 28.79. EDS analysis (Fig. 6d) shows that all grains contained Al, Ti, and F with a ratio of Ti : Al : F ∼2.1 : 0.9 : 9. A bright-field image for a single crystal is shown in Fig. 6a and Fig. 6bHRTEM along [112̄0] direction, SAED (Fig. 6c) and EDS (Fig. 6d) results. The grain boundaries are, within the resolution limitations of our TEM, free of secondary phases.

Fig. 6 (a) A bright field image of a Ti_2.1Al_0.9F₉ grain. (b) HRTEM image along [112̄0] direction, (c) EDS pattern of Ti_2.1Al_0.9F₉ (d) the copper signal originates from the use of a copper grid for sample mounting.

The TGA results (Fig. 7a) show that the new phase is stable up to 850 °C in Ar, above which it starts to dissociate. The weight loss, after heating to 1200 °C for 10 min under Ar and cooling down to room temperature, was found to be ∼70 wt%, which suggest that decomposition resulted in products with sublimation points less than 1100 °C. Among the titanium fluoride phases, TiF₄ has the lowest sublimation temperature (∼284 °C) and gaseous AlF was observed around 777 °C.³⁶ It is thus reasonable to assume that around 850 °C the following simplified reaction,

Ti₂AlF₉ = 2TiF₄ + AlF (2)

is occurring. XRD of the powder remaining after the TGA cycle consists mainly of TiC_xO_y (Fig. 7b). SEM of the same powder (Fig. 7c) showed the presence of exfoliated layered particles—but no cuboids such as those shown in Fig. 5a and 6—which contain only Ti, C and O, but no Al or F. The source of the oxygen is unclear at this time but, most probably, was initially adsorbed by the powder before heating and or was inadvertently introduced by leaks in the TGA system. The exfoliated particles are very similar in morphology and chemistry to those obtained when Ti₂AlC is immersed in molten LiF.³⁷ It follows when the fluorinated particles are heated in Ar in the TGA furnace, the following reaction—between the unreacted Ti₂AlC core and the gases generated in reaction 2—occurred:

0.3Ti₂AlC + 0.4TiF₄ + 0.15O₂ = TiC_0.3O_0.3 + 0.3AlF + 0.65F₂ (3)

It is only by assuming that some of the Ti₂AlC remains unreacted, and that reactions 2 and 3 are occurring, that the 70 wt% loss can be accounted for. Said otherwise had the fluorinated sample been totally comprised of the new phase, the weight loss—according to reaction 2—would have been 100%. The 30 wt% remaining implies that the unreacted fraction was approximately 35%.

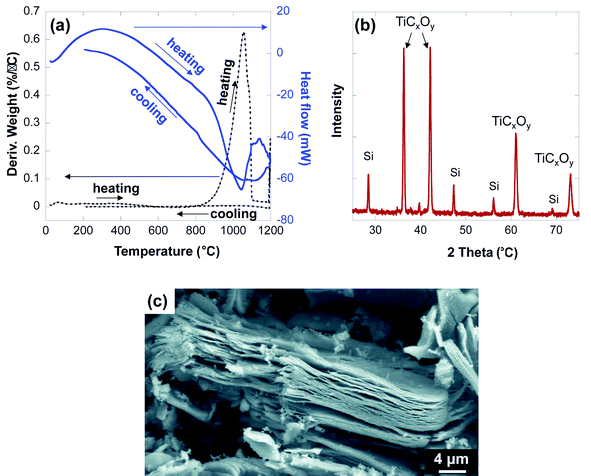Fig. 7 TGA results after heating from room temperature to 1200 °C, (a) Derivative weight and heat flow, (b) XRD of the remaining powder after TGA, (c) SEM image for a particle after the thermal cycle.

The equilibrium unit cell parameters and bulk modulus determined from ab initio calculations based on DFT are listed in Table 2. The equilibrium volume and c/a ratio obtained from total energy calculations based on DFT are slightly higher than the volume obtained from XRD peak-fitting. The theoretical a and c lattice parameter values are 1.9% greater 7.1% greater than the experimental values, respectively. These discrepancies are relatively high for DFT calculations, however, it should be noted that the ab initio calculations model an ordered Ti/Al arrangement, when in reality, the compound is most probably disordered, nanocrystalline, and non-stoichiometric. Another possible factor is that the DFT models stoichiometric Ti₂AlF₉, whereas the exact chemistry is slightly Al-deficient. Clearly more theoretical work using larger supercells, to model the disorder of the arrangement of Ti and Al atoms is needed, but this aspect is beyond the scope of this paper.

The calculated full, and partial, density of states (Fig. 8a–b) suggest that the new phase is not conductive, as indicated by the band gap at the Fermi level, E_F, from −3 to 2 eV. Above the Fermi level, the bonding is dominated by the 3d Ti states; below it, the F states dominate from −7 to −3 eV. In Ti₂AlC, the hybridization of the strong Ti–C bonds is responsible for its high stiffness, while its substantial density of states at E_F is responsible for its metallic-like electrical conductivity.^38,39 In this new phase, the lack of strong Ti–C bond leads to a lower bulk modulus determined from the volume–energy curve from ab initio calculations.

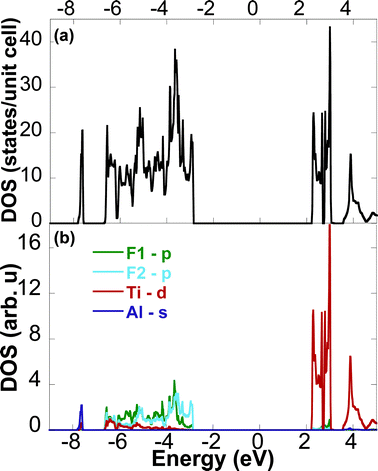Fig. 8 Calculated density of states showing (a) total density of states for Ti₂AlF₉ and (b) site-projected density of states for Ti, Al, F1 and F2 atoms.

4. Conclusions

A new, nanocrystalline titanium aluminum fluoride phase with a formal stoichiometry of Ti₂AlF₉ and an approximate composition of Ti_2.1Al_0.9F₉ was produced by reacting Ti₂AlC with anhydrous HF at 55 °C. The structure of this new phase was found to be trigonal with an R3 space group. The structure can also be viewed as being comprised of corner-sharing octahedra, arranged in a distorted simple cubic arrangement. This phase is stable up to 850 °C under Ar. The band gap is estimated to be ≈ 5 eV; the bulk modulus is ≈ 109 GPa. With this simple reaction route employing HF and a MAX phase, prospective applications of ternary fluorides tuned in composition, crystallinity and size, for catalytic, electric, or optical applications can be envisioned.

Acknowledgements

This work was supported by the Assistant Secretary for Energy Efficiency and Renewable Energy, Office of Vehicle Technologies of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, subcontract No. 6951370, under the Batteries for Advanced Transportation Technologies (BATT) Program. Also supported by the Commonwealth of Pennsylvania's Ben Franklin Technology Development Authority through the Ben Franklin Technology Partners of Southeastern Pennsylvania. VP acknowledges financial support by the Alexander von Humboldt foundation. NL acknowledges funding by the Integrated Graduate Education and Research Traineeship (IGERT) under NSF grant number DGE-0654313. The authors also thank SSF for the International Strategic Recruitment Grant. Use of the equipment of the Centralized Research Facility (Drexel University) is acknowledged.

References

1. Z. Mazej and R. Hagiwara, J. Fluorine Chem., 2007, 128, 423–437.
2. S. Rüdiger, U. Groβ and E. Kemnitz, J. Fluorine Chem., 2007, 128, 353–368.
3. S. Rüdiger and E. Kemnitz, Dalton Trans., 2008, 1117–1127.
4. G. G. Amatucci and N. Pereira, J. Fluorine Chem., 2007, 128, 243–262.
5. Y. G. Gogotsi, R. A. Andrievski, ed., Materials Science of Carbides, Nitrides and Borides, Kluwer, Dordrecht, NL, 1999.
6. K. R. Muddukrishna, R. N. Singh and D. K. Padma, J. Fluorine Chem., 57, 155–158.
7. V. K. Bogdanov, W. E. K. Gibbs, D. J. Booth, J. S. Javorniczky, P. J. Newman and D. R. MacFarlane, Opt. Commun., 1996, 132, 73–76.
8. L. Li, Crit. Rev. Oral Biol. Med., 2003, 14, 100–114.
9. K. V. S. Prasad, B. S. Murty, P. Pramanik, P. G. Mukunda and M. Chakraborty, Mater. Sci. Technol., 1996, 12, 766–770.
10. M. W. Barsoum, Prog. Solid State Chem., 2000, 28, 201–281.
11. M. W. Barsoum, M. Radovic, in Encyclopedia of Materials: Science and Technology, ed. K. H. J. Buschow, W. C. Robert, C. F. Merton, I. Bernard, J. K. Edward, M. Subhash and V. Patrick, Elsevier, Oxford, 2004, pp. 1–16.
12. M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. Barsoum, Adv. Mater., 2011, 23, 4248–4253.
13. M. W. Barsoum, T. El-Raghy, L. Farber, M. Amer, R. Christini and A. Adams, J. Electrochem. Soc., 1999, 146, 3919–3923.
14. R. W. Cheary, A. A. Coelho and J. P. Cline, J. Res. Nat. Inst. Stand. Technol., 2004, 109, 1–25.
15. G. S. Pawley, J. Appl. Crystallogr., 1981, 14, 357–361.
16. A. Le Bail, H. Duroy and J. L. Fourquet, Mater. Res. Bull., 1988, 23, 447–452.
17. A. Coelho, J. Appl. Crystallogr., 2000, 33, 899–908.
18. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
19. P. M. Morse, Phys. Rev., 1929, 34, 57–64.
20. H. Sowa and H. Ahsbahs, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 578–584.
21. H. Bialowons, M. Müller and B. G. Müller, Z. Anorg. Allg. Chem., 1995, 621, 1227–1231.
22. N. Morita, T. Endo, T. Sato and M. Shimada, J. Mater. Sci. Lett., 1987, 6, 859–861.
23. J. A. A. Ketelaar, Nature, 1931, 128, 303.
24. A. Le Bail, C. Jacoboni, M. Leblanc, R. De Pape, H. Duroy and J. L. Fourquet, J. Solid State Chem., 1988, 77, 96–101.
25. K. Vorres and J. Donohue, Acta Crystallogr., 1955, 8, 25–26.
26. R. L. Snyder, J. Fiala and H. J. Bunge, Defect and Microstructure Analysis by Diffraction, Oxford University Press, Oxford, 1999.
27. R. A. Young, The Rietveld Method, Oxford University Press, Oxford, 1993.
28. R. E. Dinnebier and S. J. L. Billinge, Powder Diffraction: Theory and Practice, Royal Society of Chemistry, Cambridge, 2008.
29. R. E. Dinnebier, P. Sieger, H. Nar, K. Shankland and W. I. F. David, J. Pharm. Sci., 2000, 89, 1465–1479.
30. R. Hagiwara, K. Kitashita, Y. Ito and O. Tamada, Solid State Sci., 2000, 2, 237–241.
31. R. D. W. Kemmitt, D. R. Russell and D. W. A. Sharp, J. Chem. Soc., 1963, 4408–4413.
32. A. Demourgues, N. Penin, D. Dambournet, R. Clarenc, A. Tressaud and E. Durand, J. Fluorine Chem., 2011 DOI:10.1016/j.jfluchem.2011.02.006.
33. L.-T. Hsieh, W.-J. Lee, C.-Y. Chen, M.-B. Chang and H.-C. Chang, Plasma Chem. Plasma Process., 1998, 18, 215–239.
34. A. Hamwi, M. Daoud and J. C. Cousseins, Synth. Met., 1988, 26, 89–98.
35. N. Batisse, K. Guérin, M. Dubois and A. Hamwi, Carbon, 2011, 49, 2998–3009.
36. J. M. Dyke, C. Kirby, A. Morris, B. W. J. Gravenor, R. Klein and P. Rosmus, Chem. Phys., 1984, 88, 289–298.
37. M. Naguib, V. Presser, D. Tallman, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, J. Am. Ceram. Soc. , 2011, accepted and in publication process.
38. M. Magnuson, O. Wilhelmsson, J. P. Palmquist, U. Jansson, M. Mattesini, S. Li, R. Ahuja and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 195108.
39. Y. C. Zhou and Z. M. Sun, Phys. Rev. B: Condens. Matter, 2000, 61, 12570–12573.
40. B. Manoun, F. X. Zhang, S. K. Saxena, T. El-Raghy and M. W. Barsoum, J. Phys. Chem. Solids, 2006, 67, 2091–2094.

---

Footnote

† CCDC reference number 88372. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c1ra00390a

---