Nanoscale spectroscopy with optical antennas
Palash
Bharadwaj†
,
Ryan
Beams†
and
Lukas
Novotny
*
Institute of Optics, University of Rochester, Rochester, New York 14627, USA Web: www.nano-optics.org
First published on 15th October 2010
Abstract
Optical antennas made of gold nanoparticles are used to enhance the spectroscopic response of single molecules. With a scannable optical half-wave antenna in the form of a gold nanorod we achieve a spatial resolution of 20nm in fluorescence imaging. We explore simultaneous fluorescence and Raman enhancement of dye molecules in the junction of two gold nanoparticles and find similar enhancements as a function of interparticle distance for both fluorescence and Raman scattering. We compare our results with theoretical predictions and provide possible explanations.
1 Introduction
In the microwave and radio frequency regime, electromagnetic fields are commonly manipulated on the sub-wavelength scale by means of antennas and electronic circuitry. On the other hand, at optical frequencies, electromagnetic fields are controlled by redirecting the wavefronts of optical radiation. This is accomplished with elements such as lenses, mirrors, and diffractive elements, and relies on the wave nature of electromagnetic fields. As a consequence, the smallest volume to which propagating optical radiation can be localized is limited by diffraction to roughly (λ/2)3, with λ being the wavelength of radiation. This limit imposes a limitation not only on spatial resolution in microscopy, but also on the signal-to-noise ratio in spectroscopic measurements. Therefore, to boost the resolution and the sensitivity of optical spectroscopy it is necessary to exploit concepts for subwavelength control of fields, as developed in the radio and microwave technology.Here, we use the emerging concept of optical antennas to enhance the sensitivity of both photoluminescence spectroscopy and vibrational spectroscopy. Analogous to its radio wave and microwave counterparts, we define an optical antenna as a device designed to efficiently convert free propagating optical radiation to localized energy, and vice versa.1 In the context of microscopy and spectroscopy, an optical antenna replaces a conventional focusing lens or objective, thereby enabling the concentration of external laser radiation to dimensions smaller than the diffraction limit. The antenna concept at optical frequencies provides an opportunity for enhancing absorption cross-sections and quantum yields in photovoltaics, for efficient release of energy from light-emitting devices, and for boosting the efficiency of photochemical or photophysical detectors.
Fig. 1 illustrates the optical antenna concept in the context of optical spectroscopy. A molecule irradiated by radiation of frequency ν1 gives rise to scattered radiation at frequency ν2. The optical antenna improves the coupling between the molecule and the radiation field thereby enhancing the scattered intensity (Fig. 1b). Notice, that the antenna enters the light-matter interaction twice, i.e. it influences the in-coupling of radiation and the out-coupling of radiation. In the following we will discuss antenna-coupled fluorescence and Raman scattering. We will consider optical antennas of simple geometry, namely gold nanoparticles and nanorods. These geometries are experimentally reproducible and allow for a quantitative comparison with theoretical model calculations.
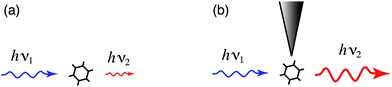 | ||
| Fig. 1 Enhancing the light-matter interaction with an optical antenna. (a) Incident radiation of frequency ν1 gives rise to scattered radiation at frequency ν2. (b) An optical antenna improves the coupling between the radiation field and the molecule and enhances the intensity of the scattered radiation. | ||
2 Antenna-enhanced fluorescence
In our experiments we attach a single colloidal gold nanoparticle of diameter 80 nm to the end of a sharply pointed dielectric fiber.2–5 As shown in Fig. 2, this ‘model antenna’ is used to locally influence the fluorescence from single molecules (Nile Blue) dispersed on a glass coverslip. A thin layer (<5 nm) of polymer (PMMA) is deposited on top of the molecules to reduce the photobleaching rate and to orient the molecules into different directions. The molecules are excited by a focused radially polarized excitation laser of wavelength λ1 = 637 nm and the emitted fluorescence is recorded with a single-photon counting detector. Radially polarized excitation yields a longitudinal field in the laser focus and is favorable for fluorescence excitation of molecules with transition dipoles oriented perpendicular to the sample surface.4 The nanoparticle antenna is positioned into the focus using a shear-force feedback mechanism.6 We can either generate a fluorescence rate image by raster-scanning the particle at a controllable but constant distance (typically ∼5 nm) over the sample surface, or we can position the particle over a selected molecule and record the fluorescence rate as a function of the particle–sample distance. Single molecules are identified based on their characteristic fluorescence pattern, which represents the molecule's transition dipole axis,4,5 and their discrete photoblinking and photobleaching behavior.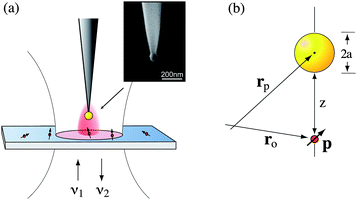 | ||
| Fig. 2 Configuration of single molecule fluorescence experiments. (a) A single gold nanoparticle (80 nm) supported by a sharpened dielectric fiber is brought close to a single molecule dispersed on a transparent glass cover slip. Sample and antenna are excited with a laser of frequency ν1. The emitted fluorescence at frequency ν2 is recorded as a function of molecule–antenna separation. The inset shows an electron micrograph of a fabricated gold nanoparticle antenna. (b) Geometry and coordinates used in the theoretical analysis. | ||
Fig. 3 summarizes the results of our antenna-enhanced single molecule fluorescence experiments. Fig. 3 (a) shows a confocal fluorescence rate image of the single molecule sample recorded in absence of the antenna. Each fluorescence spot corresponds to a map of the intensity of the excitation laser according to I(x,y) ∝ |p·Eexc(x,y)|2, with p being the molecular transition dipole and Eexc the focal field of the excitation laser. The fluorescence patterns in the image are not identical because each molecule has a different dipole orientation. Fig. 3 (b) shows a corresponding near-field fluorescence rate image recorded with a single gold nanoparticle antenna. The resolution is improved from ∼300 nm to ∼60 nm. Furthermore, the fluorescence intensity is enhanced by a factor of 10. The fluorescence enhancement can be visualized by recording the fluorescence intensity as a function of antenna–molecule separation (Fig. 3c). For short distances quenching sets in and the fluorescence counts do not increase further.3,5 The PMMA layer used in the experiments ensures a minimum distance between antenna and molecule and limits the amount of fluorescence quenching.
 | ||
| Fig. 3 Single molecule fluorescence enhancement with a gold nanoparticle antenna. (a) Confocal fluorescence excitation rate image recorded in absence of the antenna by raster scanning the sample through the stationary excitation focus. Scale bar: 1 μm. (b) Near-field fluorescence image recorded with a 80 nm gold nanoparticle antenna. The antenna enhances the fluorescence intensity by a factor of 10 and improves the resolution to ∼60 nm. Scale bar: 200 nm. (c) Fluorescence enhancement as a function of molecule–antenna separation. | ||
The spherical antenna geometry allows for a quantitative comparison with theory. For weak excitation intensities the fluorescence emission process can be treated as a two-step process, involving the excitation from ground state to excited state followed by a radiative transition back to the ground state. In this limit the fluorescence rate γem can be written as
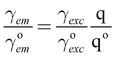 | (1) |
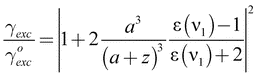 | (2) |
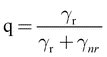 | (3) |
Here γr and gammanr are the radiative and nonradiative transition rates, respectively. In terms of the intrinsic quantum yield qo (quantum yield in absence of antenna) the quantum yield can be expressed as
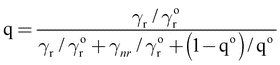 | (4) |
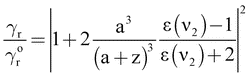 | (5) |
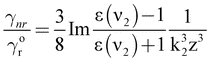 | (6) |
According to eqn (1), the fluorescence rate can be improved by enhancing the excitation rate through the local field E or by enhancing the quantum yield q. However, for efficient molecules with qo ≈ 1 the quantum yield cannot be enhanced further and the excitation rate becomes the only fluorescence enhancement mechanism. On the other hand, for molecules with low intrinsic quantum yield (qo ≪ 1) an optical antenna is able to boost both the excitation rate and the quantum yield.7 For example, it has been shown that the photoluminescence quantum yield of carbon nanotubes having qo ≈ 0.001 can be enhanced by more than tenfold.8 The ability to enhance the quantum efficiency of low-qo systems holds promise for improving the performance of solid state and organic light emitting devices.
The analysis outlined above also predicts that maximum fluorescence enhancement is obtained for emission frequencies ν2 that are red-shifted from the surface plasmon resonance of the gold nanoparticle. It is therefore important to design an optical antenna such that it matches the spectral properties of the emitter. For high-qo systems the analysis yields a maximum fluorescence enhancement of ∼10 for visible excitation and emission frequencies. To achieve higher enhancement factors we need to turn to more favorable antenna geometries, such as gold nanorods discussed in the following.
A gold nanorod excited at its fundamental surface plasmon resonance corresponds to an optical half-wave antenna.9–11 Compared to a spherical nanoparticle, a gold nanorod exhibits lower damping, a sharper resonance, and a stronger local field enhancement factor.12–14Fig. 4 shows the results of electromagnetic calculations based on the multiple multipole (MMP) method15 for a 20 nm × 60 nm gold nanorod placed half way into a glass substrate. The nanorod is excited by a radially polarized laser beam of variable wavelength. Fig. 4 (b) shows the computed real and imaginary parts of the local field enhancement factor at the surface of the nanorod and Fig. 4 (c) renders the corresponding intensity enhancement factor. On resonance, the gold nanorod provides clearly much stronger excitation enhancement compared with a spherical nanoparticle. A challenge, however, is associated with the shift of the resonance towards the red part of the spectrum and the fact that molecules are typically less photostable in the near infrared. The red-shift of the resonance can be minimized by small nanorod dimensions.10,16
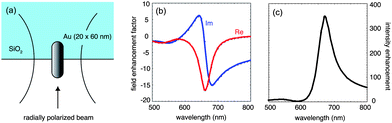 | ||
| Fig. 4 Electromagnetic calculations for a gold nanorod excited by a radially polarized beam and supported by a dielectric substrate. (a) Geometry used in the computations. (b) Real and imaginary parts of the field enhancement factor evaluated at the surface of the nanorod. (c) Corresponding intensity enhancement showing a resonance at λ ∼ 650 nm, red-shifted with respect to a spherical gold nanoparticle. | ||
To fabricate an optical half-wave antenna we first synthesized a sample of monodisperse gold nanorods by seed-mediated colloidal chemistry17,18 (cf.Fig. 5a) and then used a sharply pointed quartz capillary to trap a single nanorod into the opening of the pipette.19 A quartz nanopipette was pulled using a Sutter P-2000 Micropipette Puller to give an end opening comparable to the short axis of the synthesized nanorods (20 nm). The nanopipette was then dipped in a concentrated solution (10−7 M) of gold nanorods and 1 atm of suction was applied for two hours in order to capture a single nanorod. Fig. 5 (b) shows an electron micrograph of a completed half-wave antenna. The supporting capillary was fixed to a quartz tuning fork, similar to the case of the gold nanoparticle antenna described previously. A representative near-field fluorescence image recorded with the half-wave antenna is shown in Fig. 5 (c). The image shows four isolated molecules. The curve in the inset is a cross-section through the lower left fluorescence spot. The full-width-at-half-maximum (FWHM) of 20 nm indicates a resolution comparable to the width of the nanorod. Approach curves, similar to the one shown in Fig. 3 (c), yield a maximum fluorescence enhancement factor of ≃20. This number is twice the enhancement observed for spherical gold nanoparticles but it is lower than what the peak in the spectrum of Fig. 4 (c) predicts. The lower enhancement is largely due to the off-resonant excitation at λ1 = 637 nm.
 | ||
| Fig. 5 Optical half-wave antennas made of gold nanorods. (a) Colloidal synthesis of gold nanorods. (b) A single gold nanorod placed in the aperture of a nanoscale quartz pipette. (c) Near-field fluorescence image recorded with the optical half-wave antenna. The curve in the inset shows a cross-section through one of the fluorescence spots. Scale bar: 100nm. | ||
The fabrication of optical half-wave antennas is a tedious process since it not only involves the capture of a nanorod but also its orientation with respect of the pipette. Furthermore, the resonances of the nanorods are narrow, which makes them susceptible to slight geometrical variations. Indeed, we observed that the enhancement factors vary from nanorod to nanorod. These variations are likely due to size variations generated during colloidal synthesis. Improved growth procedures will likely eliminate this uncertainty and make the experiments more predictable. Notice that only the very end of the nanorod is exposed to the outside. Thus, once a nanorod is trapped in the opening of a nanopipette, it is largely protected from chemical and mechanical perturbations.
3 Antenna-enhanced raman scattering
The fluorescence rate of a molecule with high intrinsic quantum yield can only be enhanced by the excitation rate γexc. Below saturation γexc∝|p·Eexc|2 and hence the fluorescence enhancement depends on the square of the local field enhancement factor. The situation is different for the enhancement of Raman scattering since no real excited state is involved. Instead, Raman scattering involves a virtual state whose lifetime is limited only by uncertainty.20 This means that the antenna does not influence the lifetime, but changes the radiative rate.‡ As a consequence, Raman enhancement turns out to be the product of excitation rate enhancement and emission rate enhancement, i.e.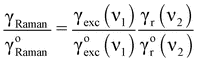 | (7) |
Thus, in Raman scattering the optical antenna acts both as a receiving antenna and as a transmitting antenna. For ν1 ≈ ν2 we find that the enhancement of Raman scattering depends on the fourth power of the local field enhancement factor21–25 and not on the second power as in the case of fluorescence. Thus, if we were to simultaneously measure Raman scattering and fluorescence from a single molecule as a function of molecule–antenna separation we would expect to find a considerably steeper curve for Raman scattering than for fluorescence.
To test this prediction we prepared a sample of Atto532 dye molecules attached to isolated 80nm gold nanoparticlesvia a cysteamine linker. The gold nanoparticles were then dispersed on a glass coverslip. A 80 nm gold nanoparticle antenna is then used to map out the distribution of functionalized gold nanoparticles on the surface and to select single nanoparticles for subsequent distance measurements. The sample was excited with 1 μW of focused radially-polarized light of wavelength λ1 = 532 nm, as schematically shown in Fig. 1 (a). Fig. 6 (a–c) shows the topography, near-field fluorescence image, and the near-field Raman image recorded for one selected sample particle. These images were recorded by using a nanoparticle antenna as a local probe for raster scanning to record the full spectrum of emitted radiation from each pixel. The contrast in the images results from integrating the spectrum for every image pixel over a chosen spectral range. For the Raman image in Fig. 6 (c) we first subtracted the broad fluorescence background and then integrated over the strongest Raman band centered at λ2 = 585 nm (∼1650 cm−1).
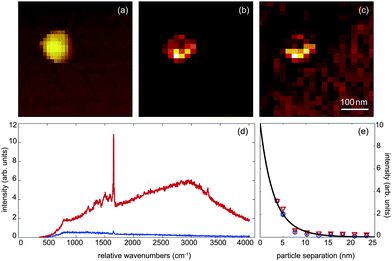 | ||
| Fig. 6 Simultaneous Raman and fluorescence enhancement measurements. (a) Topography of a single 80 nm gold nanoparticle covered with Atto532 dye. (b) Near-field fluorescence image and (c) near-field Raman scattering image of the same particle. (d) Spectrum of detected radiation recorded in absence of a nanoparticle antenna (blue) and in presence of a nanoparticle antenna (red). (e) Intensity of fluorescence (red triangles) and Raman scattering (blue circles) as a function of particle–particle separation. | ||
Typical spectra are shown in Fig. 6 (d) where the red curve was recorded for a small separation between the two gold nanoparticles (antenna and sample particles) and the blue curve for a large separation. It is evident that the nanoparticle antenna enhances both the fluorescence intensity and the Raman scattering intensity. We observe an enhancement of a factor of 27 for the Raman peak. Generally, Raman enhancement for SERS is defined as the ratio between the Raman signal on the SERS substrate and the signal from the molecules in solution, correcting for the difference in the number of molecules in the interaction volume.26,27 In our case, Raman enhancement is defined as the signal from the dimer (small particle separation) divided by the signal for the single particle (large particle separation). This normalization results in a more modest Raman enhancement due to enhancement from the single particle itself. We note that a Raman signal from single spheres has often not been observed in literature because of the excitation wavelength being significantly shifted from the plasmon resonance.28,29 Our excitation is close to the plasmon resonance for gold, which makes the enhancement for the single nanoparticle case significant. Notice, that the surface plasmon resonance of a nanoparticle pair shifts to the red as the interparticle distance is reduced.30–32 This red shift has to be taken into account for an accurate theoretical prediction of distance-dependent enhancement factors.
In Fig. 6 (e) we show the dependence of Raman enhancement and fluorescence enhancement on the interparticle separation. The data points have been extracted from spectra that were recorded for different vertical positions of the nanoparticle antenna. The red triangles correspond to fluorescence enhancement and the blue circles to Raman enhancement. The solid line is a fitting curve. Interestingly, we observe similar enhancements for fluorescence and Raman scattering, which contradicts the hypothesis that fluorescence enhancement should depend on the square local field enhancement factor and Raman enhancement of the fourth-power of the local field enhancement factor.
The reason for the contradiction between our experiments and the theoretical predictions likely lies in the experimental limitations. First, it was experimentally not possible to reduce the separation between the gold nanoparticles below ≈4 nm. Shorter separations result in strong forces and cause the sample particles to jump on the nanoparticle antenna. Second, the quantum yield of dye molecules deposited on the nanoparticle surface is likely lower than the corresponding quantum yield in solution and hence, as discussed previously, it is possible that the nanoparticle antenna not only enhances the excitation rate but also the fluorescence quantum yield. Third, the dye coverage on the nanoparticle surface is not homogeneous giving rise to brighter and darker regions on the nanoparticle surface as seen in Fig. 6 (b,c). Fourth, fluorescence bleaching affects the recorded signals during data acquisition. All four limitations can be greatly reduced by more sophisticated sample preparation techniques. For example, a uniform molecular coverage can be achieved by self-assembly33 and the effect of photobleaching can be minimized by the use of more photostable molecules. Notice that Hartschuh et al. have performed simultaneous photoluminescence and Raman scattering experiments on single-walled carbon nanotubes8 and observed stronger photoluminescence enhancement than Raman enhancement, contrary to the hypothesis in this paper. The reason for the stronger photoluminescence enhancement has been assigned to the low intrinsic quantum yield (qo ∼ 0.001) of nanotubes deposited on a glass surface. Distance dependent SERS measurements have also been performed by Pettinger et al.34 The authors compared the enhancement of gold photoluminescence with the enhancement of Raman scattering from coadsorbed guanine and ClO4 molecules in the junction between a gold tip and a gold surface. They observed similar enhancements for photoluminescence and Raman scattering as a function of tip–sample distance, in agreement with our observations for molecules in the junction of a gold nanoparticle pair.
4 Conclusions
We have used an optical antenna to enhance the spectroscopic response of single molecules. The fluorescence of a single molecule can be enhanced by more than a factor of 10 by a simple model antenna consisting of a single gold nanoparticle. This simple antenna geometry makes it possible to derive analytical formulas for the fluorescence enhancement. The theoretical calculations are in good agreement with our experiments and predict that fluorescence enhancement is the product of excitation enhancement and quantum yield enhancement. For a molecule with high intrinsic quantum yield the antenna is not able to further enhance the quantum yield. As a consequence, the fluorescence enhancement scales with the square of the local field enhancement. By using gold nanorods instead of spherical nanoparticles we are able to mimic an optical half-wave antenna and to boost the local field enhancement factor. This geometry makes it possible to improve the resolution in near-field optical imaging without loss of sensitivity. On the other hand, the nanorod enhancement factor is susceptible to geometrical variations.While fluorescence enhancement of a high-qo molecule depends on the square of the local field enhancement, theory predicts that Raman scattering depends on the fourth power of the local field enhancement. Based on this difference, one expects that Raman scattering exhibits a stronger dependence on antenna–molecule separation than fluorescence. However, our experiments were not able to demonstrate this effect. We have discussed several possible reasons for the discrepancy between theory and experiments, such as nonuniform coverage, photobleaching and low quantum yield. Future experiments based on self-assembled monolayers will be able to resolve the difference between fluorescence enhancement and Raman enhancement in more detail.
The local control of the light-matter interaction with optical antennas of well-defined geometry holds promise not only for various applications, such as chemical and biological sensing, but also for resolving open questions in the field of surface enhanced Raman scattering and fluorescence.
Acknowledgements
The authors are grateful for financial support by the National Science Foundation (CBET-0930074 and ECCS-0651079). They thank Shanlin Pan and Lewis Rothberg for help with colloidal nanoparticle synthesis.References
- P. Bharadwaj, B. Deutsch and L. Novotny, Advances in Optics and Photonics, 2009, 1, 438–483 Search PubMed.
- S. Kühn, U. Hakanson, L. Rogobete and V. Sandoghdar, Phys. Rev. Lett., 2006, 97, 017402 CrossRef.
- P. Anger, P. Bharadwaj and L. Novotny, Phys. Rev. Lett., 2006, 96, 113002 CrossRef.
- P. Bharadwaj, P. Anger and L. Novotny, Nanotechnology, 2007, 18, 044017 CrossRef.
- P. Bharadwaj and L. Novotny, Opt. Express, 2007, 15, 14266–14274 CrossRef CAS.
- K. Karrai and R. D. Grober, Appl. Phys. Lett., 1995, 66, 1842–1844 CrossRef CAS.
- A. Wokaun, H.-P. Lutz, A. P. King, U. P. Wild and R. R. Ernst, J. Chem. Phys., 1983, 79, 509–514 CrossRef CAS.
- A. Hartschuh, H. Qian, A. J. Meixner, N. Anderson and L. Novotny, Nano Lett., 2005, 5, 2310 CrossRef CAS.
- F. Neubrech, T. Kolb, R. Lovrincic, G. Fahsold, A. Pucci, J. Aizpurua, T. W. Cornelius, M. E. Toimil-Molares, R. Neumann and S. Karim, Appl. Phys. Lett., 2006, 89, 253104 CrossRef.
- L. Novotny, Phys. Rev. Lett., 2007, 98, 266802 CrossRef.
- G. W. Bryant, F. J. G. de Abajó and J. Aizpurua, Nano Lett., 2008, 8, 631–636 CrossRef CAS.
- C. Sönnichsen, T. Franzl, T. Wilk, G. von Plessen, J. Feldmann, O. Wilson and P. Mulvaney, Phys. Rev. Lett., 2002, 89, 77402 CrossRef.
- L. Rogobete, F. Kaminski, M. Agio and V. Sandoghdar, Opt. Lett., 2007, 32, 1623–1625 Search PubMed.
- A. Mohammadi, V. Sandoghdar and M. Agio, New J. Phys., 2008, 10, 105015 CrossRef.
- L. Novotny and B. Hecht, Principles of Nano-Optics, Cambridge University Press, Cambridge, 2006 Search PubMed.
- P. K. Jain, K. S. Lee, I. H. El-Sayed and M. A. El-Sayed, J. Phys. Chem. B, 2006, 110, 7238–7248 CrossRef CAS.
- B. Nikoobakht and M. A. El-Sayed, Chem. Mater., 2003, 15, 1957–1962 CrossRef CAS.
- N. R. Jana, L. Gearheart and C. J. Murphy, J. Phys. Chem. B, 2001, 105, 4065–4067 CrossRef CAS.
- Y. Kawata, S. Urahama, M. Murakami and F. Iwata, Appl. Phys. Lett., 2003, 82, 1598–1600 CrossRef CAS.
- A. Long, The Raman Effect, John Wiley and Sons, LTD, West Sussex, England, 2002 Search PubMed.
- J. Gersten and A. Nitzan, J. Chem. Phys., 1980, 73, 3023–3037 CrossRef CAS.
- M. Moskovits, Rev. Mod. Phys., 1985, 57, 783–826 CrossRef CAS.
- G. W. Ford and W. H. Weber, Phys. Rep., 1984, 113, 195–287 CrossRef CAS.
- K. Kneipp, Y. Wang, H. Kneipp, I. Itzkan, R. R. Dasary and M. S. Feld, Phys. Rev. Lett., 1997, 78, 1667 CrossRef CAS.
- E. C. Le Ru and P. G. Etchegoin, Chem. Phys. Lett., 2006, 423, 63–66 CrossRef CAS.
- N. Félidj, J. Aubard, G. Lévi, J. R. Krenn, M. Salerno, G. Schider, B. Lamprecht, A. Leitner and F. R. Aussenegg, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 0754193–0754199.
- E. C. Le Ru, E. Blackie, M. Meyer and P. G. Etchegoin, J. Phys. Chem. C, 2007, 111, 13794–13803 CrossRef CAS.
- C. E. Talley, J. B. Jackson, C. Oubre, N. K. Grady, C. W. Hollars, S. M. Lane, T. R. Huser, P. Nordlander and N. J. Halas, Nano Lett., 2005, 5, 1569–1574 CrossRef CAS.
- W. Li, P. H. C. Camargo, X. Lu and Y. Xia, Nano Lett., 2009, 9, 485–490 CrossRef CAS.
- T. Atay, J.-H. Song and A. V. Nurmikko, Nano Lett., 2004, 4, 1627 CrossRef CAS.
- I. Romero, J. Aizpurua, G. W. Bryant and F. J. Garcia de Abajo, Opt. Express, 2006, 14, 9988 CrossRef.
- M. Danckwerts and L. Novotny, Phys. Rev. Lett., 2007, 98, 026104 CrossRef.
- D. K. Schwartz, Annu. Rev. Phys. Chem., 2001, 52, 107–137 CrossRef CAS.
- B. Pettinger, K. F. Domke, D. Zhang, R. Schuster and G. Ertl, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 113409 CrossRef.
Footnotes |
| † These authors contributed equally to this work. |
| ‡ In fluorescence, the expression |p·Eexc|2 involves a fixed dipole p (the transition dipole matrix element), whereas in Raman scattering p is an induced dipole (p ∝ Eexc) |
| This journal is © The Royal Society of Chemistry 2011 |
