Normal and inverted redox potentials and structural changes tuned by medium effects in [M₂Mo(η⁵-C₅Me₅)₂(S₂C₆H₄)₂(CO)₂] (M: Co, Rh)

Abstract

Redox potential inversion was observed during the two-electron (2e⁻) reduction of two novel heterometal trinuclear complexes, [Co₂Mo(η⁵-C₅Me₅)₂(S₂C₆H₄)₂(CO)₂] (1) and [Rh₂Mo(η⁵-C₅Me₅)₂(S₂C₆H₄)₂(CO)₂] (2), the metalladithiolenes of which were found to communicate electronically via a Mo(CO)₂ moiety through two Co/Rh–Mo bonds. The redox properties and structural changes associated with each complex were investigated. 1 showed both two-step one-electron (1e⁻) reductions with a normal-order redox potential difference and a one-step 2e⁻reduction with a redox potential inversion that depended on the solvent and electrolyte. The size of the counter cation was found to significantly influence the reduction behaviour of 1. In contrast, 2 showed only a one-step 2e⁻reduction that didn't depend on the solvent–electrolyte conditions. The CO coordination mode in each reduction underwent a reversible structural reorganization upon reduction, from a semibridging configuration between the Co/Rh atoms and the Mo atom in the neutral form to a bridging configuration in the reduced form. The local coordination structure of the metal atoms in the dianion 2²⁻2− was experimentally determined for the first time. The interactions between Co and CO in 1 were weaker than the interactions between Rh and CO in 2, and differences in the interaction strengths, together with the influence of the solvent–electrolyte medium, were found to determine the redox processes available to the complexes.

---

Introduction

Multi-electron transfer reactions are a fundamental class of electron transfer reactions^1,2 and are key to the functionality of many important materials, including biological redox complexes,^3,4catalysts,^5,6 conjugated organic polymers or metallopolymer materials,^7,8 and photovoltaic cells.^9,10 The importance of multi-electron transfer reactions has been widely recognized, and comprehensive studies of such redox processes and accompanying structural changes have been undertaken to understand the nature of these reactions. Most organic oligomers and transition metal multinuclear complexes, which include several redox sites that electronically communicate through π-conjugation or metal–metal bonds, exhibit multi-step 1e⁻redox reactions with a positive redox potential difference (ΔE^0′_i > 0, where ΔE^0′_i = E^0′_i + 1 − E^0′_i, i is the number of redox sites). Such one-electron redox reactions proceed through thermodynamically favorable mixed-valence states.^11–18 The factors that influence ΔE^0′_i, such as the statistical, electrostatic, magnetic, inductive, and electronic coupling effects, have been extensively studied.^19–23 Recently, the solvent and the electrolyte medium were found to influence ΔE^0′_i.^24–30 In contrast, several organic compounds and multinuclear transition metal complexes that undergo single-step multi-electron redox reactions with a negative potential difference (ΔE^0′_i < 0, where ΔE^0′_i = E^0′_i + 1 − E^0′_i) have been reported, even though the redox sites may be linked by π-conjugated organic spacers or metal–metal bonds.^31–45 This phenomenon is called redox potential inversion, or simply, ‘potential inversion’. In such cases, dramatic structural changes induced by a first redox reaction can facilitate the subsequent redox reaction by making it favorable.^46–50

In this context, we have studied several pioneering examples of unique metalladichalcogenolene complexes that exhibit redox reactions characterized by either ΔE^0′_i > 0 or ΔE^0′_i < 0. A trinuclear complex [Co₃(η⁵-C₅H₅)(S₆C₆)] in which three cobaltadithiolenes were fused to a π-conjugated phenyl ring exhibited successive multi-step 1e⁻redox reactions with a positive redox potential difference (ΔE^0′_i > 0). The absolute value of ΔE^0′_i was found to depend on the solvent–electrolyte system.^24,25 The heterometal trinuclear complex [Co₂Mo(η⁵-C₅H₅)₂(S₂C₆H₄)₂(CO)₂], which contains two metalladithiolene units bridged by Mo(CO)₂ through Co–Mo–Co bonds, showed two-step 1e⁻reductions with a positive redox potential difference (ΔE^0′ > 0) in Bu₄NClO₄–MeCN.⁵¹ Another heterometal trinuclear complex [Rh₂Mo(η⁵-C₅Me₅)₂(S₂C₆H₄)₂(CO)₂] with Rh–Mo–Rh bonds showed a one-step 2e⁻reduction with a negative redox potential difference (ΔE^0′ < 0), that is, potential inversion, under the same solvent–electrolyte conditions.⁵² The structural changes of the two carbonyl groups (CO groups) during the reduction process, from semibridging to bridging, were described previously in a communication.⁵² These complexes provided the first demonstrations of the novel redox properties of late transition metal metalladithiolenes, which have unique physical and chemical properties that arise from quasi-aromaticity, an unsaturated electronic structure, and the good donor properties of the five-membered ring.^53–57 These compounds have uncovered a new field of ‘heterometal bond formation’,^{51,52,58–68} which complements the well-studied fields of molecular conductors and magnetic materials^53,69–73 in metalladithiolene chemistry.

Here, we report a new heterometal trinuclear complex, [Co₂Mo(η⁵-C₅Me₅)₂(S₂C₆H₄)₂(CO)₂], 1‡, which is analogous to [Co₂Mo(η⁵-C₅H₅)₂(S₂C₆H₄)₂(CO)₂].⁵¹ We investigated the redox properties and associated structural changes of 1 in comparison with [Rh₂Mo(η⁵-C₅Me₅)₂(S₂C₆H₄)₂(CO)₂], 2.⁵² The neutral forms were characterized by single crystal X-ray diffraction analysis, XPS, FT-IR, NMR spectroscopy, and cyclic voltammetry, and the reduced forms were characterized by in situinfrared reflection absorption spectroscopy (IRAS), EPR, XAFS, and DFT calculations. We found that 1 underwent both two-step 1e⁻reductions and a one-step 2e⁻reduction, depending on the solvent and electrolyte, whereas 2 underwent a one-step 2e⁻reduction without a dependence on the solvent or electrolyte. The alternating CO coordination mode, between semibridging and bridging modes, caused reversible structural changes in both complexes during the reduction processes. The interaction between Co and CO in 1 was found to be weaker than the interaction between Rh and CO in 2. This interaction strength determined the redox processes available to each compound in different combinations of solvents and electrolytes.

Results and discussion

Structures of the neutral complexes 1 and 2, and the valence states of the metal atoms

1 was synthesized by the reaction of [Co(η⁵-C₅Me₅)(S₂C₆H₄)] (3) with [Mo(CO)₃(py)₃] in the presence of BF₃·OEt₂ in toluene (Scheme 1). The structure of 1, determined by single crystal X-ray diffraction analysis (Fig. 1(a) and Table S1†), was similar to that of 2.⁵² Both complexes showed direct metal–metal single bonds, and the average Co–Mo bond length in 1 was 2.6459 Å, similar to the bond length reported in the trinuclear complex [Co₂Mo(η⁵-C₅H₅)₂(S₂C₆H₄)₂(CO)₂].⁵¹ The structural similarities between 1 and 2 were also confirmed by FT-IR spectroscopy, the spectra of which displayed similar peak positions in the fingerprint region (500–1500 cm⁻¹) and in the C–H stretching vibration region (2700–3200 cm⁻¹) (Fig. S1(a,c)†). The average Co–S–C bond angle (101.85°) in 1 and the average Rh–S–C bond angle (103.49°) in 2 were far from 180° (Table 1), indicating that the metalladithiolene rings lost their planarity after metal–metal bond formation. The UV-vis-NIR spectra of 1 and 2 showed several absorption peaks in the visible region (606 nm and 481 nm for 1, and 535 nm for 2, respectively, in THF, Table S2 and Fig. S2†), which were ascribed to MMCT transitions based on TD-DFT calculations.⁵² The peak positions of these spectra were not solvent-dependent, which indicated a loss of planarity in the metalladithiolene rings after formation of the metal–metal bonds.

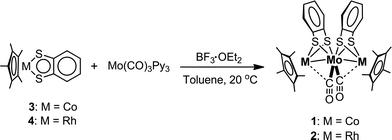Scheme 1 Syntheses of 1 and 2.

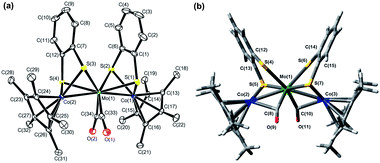Fig. 1 (a) ORTEP diagram of 1 with thermal ellipsoids set at the 50% probability level. Hydrogen atoms were omitted for clarity. (b) Optimized structure of 1²⁻2− from DFT calculations (C₂ symmetry, triplet state).

Table 1 Selected bond lengths (Å) and bond angles (°) for 1 and 2

Bond or angle^a	1	2 ^b
a 1: M = Co, 2: M = Rh. b Data from ref. 52.
M(1)–Mo(1)	2.6567(6)	2.7621(7)
M(2)–Mo(1)	2.6351(6)	2.7184(7)
Mo(1)–C(33)	1.975(2)	1.966(3)
Mo(1)–C(34)	1.961(2)	1.944(3)
C(33)–O(1)	1.158(2)	1.164(4)
C(34)–O(2)	1.165(2)	1.171(4)
M(1)–S(1)	2.1978(6)	2.3200(9)
M(1)–S(2)	2.2391(7)	2.3564(9)
M(2)–S(3)	2.2635(9)	2.3807(9)
M(2)–S(4)	2.1918(6)	2.3124(9)
Mo(1)–S(1)	2.4838(8)	2.5048(10)
Mo(1)–S(2)	2.5350(7)	2.5434(9)
Mo(1)–S(3)	2.5324(7)	2.5599(9)
Mo(1)–S(4)	2.4761(9)	2.4805(10)
M(1)⋯C(34)	2.718	2.692
M(2)⋯C(33)	2.683	2.647
M(1)–Mo(1)–M(2)	169.01(1)	162.14(1)
Mo(1)–C(33)–O(1)	169.06(14)	169.1(3)
Mo(1)–C(34)–O(2)	167.89(14)	166.3(3)
M(1)–S(1)–C(1)	102.43(6)	103.67(11)
M(1)–S(2)–C(6)	101.69(6)	103.52(11)
M(2)–S(3)–C(7)	101.32(6)	102.75(11)
M(2)–S(4)–C(12)	101.94(5)	104.02(11)

---

The coordination modes of the CO groups were investigated by single crystal X-ray diffraction analysis, FT-IR, ¹³C NMR, and DFT calculations. The X-ray crystal structure of 1 revealed that the average O–C–Mo bond angle was 168.5°, the average Mo–C (CO) bond length was 1.968 Å, and the average Co⋯C (CO) distance was 2.701 Å, indicating that the CO groups were not bound to Mo only in the terminal coordination mode, but were bent toward Co (Table 1). Similar trends were observed in 2 (the average O–C–Mo bond angle was 167.7°, the average Mo–C (CO) bond length was 1.955 Å, and the average Rh⋯C (CO) distance was 2.670 Å, Table 1).⁵² The CO groups in both 1 and 2 were classified as semibridging but closer to terminal, according to an analysis of the asymmetric parameter α (α (1) = 0.38 and α (2) = 0.37).^74,75 However, the CO groups in 1 and 2 displayed significant differences in their bonding characteristics. The average C≡O bond length in 1 (1.162 Å) was shorter than that in 2 (1.168 Å), the average Mo–C bond length in 1 (1.968 Å) was longer than that in 2 (1.955 Å), and the average Co–C length (2.701 Å) in 1 was much longer than that in 2 (Rh–C: 2.670 Å) (Table 1). Two strong bands corresponding to the stretching vibrations of the CO groups (asymmetric and symmetric vibration of the CO groups, 1876 cm⁻¹ and 1809 cm⁻¹ in a KBr pellet and 1879 cm⁻¹ and 1821 cm⁻¹ in a 0.1 M NaBPh₄–THF solution, respectively) were observed in the FT-IR spectra of 1, and these values were larger than those in 2 (1862 cm⁻¹ and 1797 cm⁻¹ in KBr and 1864 cm⁻¹ and 1806 cm⁻¹ in a 0.1 M NaBPh₄–THF solution, respectively) (Table 2 and Fig. S1(b)†). These results suggested that the electron donation from Mo to CO was weaker in 1 than in 2. The interactions between Co and the CO groups, ascribed to π back-donation from Co to CO, were much weaker than the interactions between Rh and the CO groups in 2. This observation was further supported by the ¹³C NMR spectrum of 1, in which the chemical shift (δ_C) of the CO group (243.63 ppm) was shifted down-field relative to the corresponding peak in 2 (239.61 ppm) (Fig. S3†). This shift indicated that the C atom in 1 was more deshielded due to weaker π back-donation from Co to CO. DFT calculations of 1 and 2 satisfactorily reproduced the structures determined by single crystal X-ray diffraction analysis and identified several structural differences in the metal–metal bonds, semibridging coordination structures of the two CO groups, and the interactions between Co/Rh and CO (Table S3 and Fig. S4†). The spatial distributions of the d orbitals on the Co and Rh atoms were most likely responsible for the differences in π back-donation in the two structures. Spatially smaller Co 3d orbitals interacted less strongly with the π* orbitals of CO, whereas the larger Rh 4d orbitals produced stronger π back-donation, which resulted in shorter Rh–CO distances and a larger shift in ν(CO) frequencies to lower wavenumbers.

Table 2 ν(CO) frequencies for the compounds

	ν(CO) /cm^−1
	In 0.1 M NaBPh4–THF	In 0.1 M Bu4NClO4–THF	In KBr	Calcd. ^a
a The original calculated values were multiplied by the scale factor ω = 0.9614 for B3LYP/6-31G(d) (ref. 76). b Triplet state. c Data from ref. 52.
1	1879, 1821	1880, 1825	1876, 1809	1852, 1804
1^−−		1815, 1694
1^2−2−	1686, 1613	1709, 1655		1731, 1683 ^b
2 ^c	1864, 1806		1862, 1797	1839, 1792
2^2−2− ^c	1682, 1617			1705, 1664 ^b

---

The formal valence states of the metal atoms in 1 and 2 were analyzed by XPS spectroscopy. A curve fit of the spectrum of 1 gave six peaks: 794.3 eV [Co(2p_1/2)] and 779.3 eV [Co(2p_3/2)] for Co(2p), small peaks at 783.7 eV, 231.4 eV [Mo(3d_3/2)], and 228.1 eV [Mo(3d_5/2)] for Mo(3d), and 226.8 eV for S(2s). A curve fit of the spectrum of 2 gave five peaks: 312.8 eV [Rh(3d_3/2)] and 308.2 eV [Rh(3d_5/2)] for Rh(3d), 231.2 eV [Mo(3d_3/2)] and 228.0 eV [Mo(3d_5/2)] for Mo(3d), and 226.7 eV for S(2s) (Fig. S5†). The binding energies of Co, Rh, and Mo to the mononuclear metalladithiolenes, 3 (794.9 eV [Co(2p_1/2)] and 779.8 eV [Co(2p_3/2)] for Co(2p), and 226.4 eV for S(2s)), 4 (313.3 eV [Rh(3d_3/2)], 308.6 eV [Rh(3d_5/2)], and 226.3 eV for S(2s)), and the reported Mo⁰ complexes,^77,78 respectively, were quite similar, indicating that the valence states of the Co atoms in 1 and the Rh atoms in 2 were three, and the valence states of the Mo centers in 1 and 2 were zero. The validity of this attribution was supported by the EPR spectra of the reduced forms of 1 (vide infra) and 2,⁵² which showed that reductions occurred at two Co or Rh atoms. Thus, the formal valence states of the metal atoms in 1 and 2 could be expressed as Co^IIIMo⁰Co^III and Rh^IIIMo⁰Rh^III, respectively, suggesting that the oxidation states of the metal atoms in the mononuclear complexes did not change significantly upon formation of Co–Mo or Rh–Mo bonds.

Electrochemical reduction behaviour and structural changes in 1 and 2 under various solvent–electrolyte conditions

We previously described the two-step 1e⁻reductions of [Co₂Mo(η⁵-C₅H₅)₂(S₂C₆H₄)₂(CO)₂] in Bu₄NClO₄–MeCN and the contrasting one-step 2e⁻reduction of 2 (the number of electrons were determined to be 2.01 by coulometry) to form the dianion form of 2²⁻2−.^51,52 The electrochemical behaviour of 1 in Bu₄NClO₄–MeCN/toluene (1 : 1 v/v) was similar to that of [Co₂Mo(η⁵-C₅H₅)₂(S₂C₆H₄)₂(CO)₂],⁵¹ that is, a cyclic voltammogram (CV) of 1 at 253 K showed two reversible redox waves at E^0′₁ = −1659 mV and E^0′₂ = −1941 mV vs.ferrocenium/ferrocene (Fc⁺/Fc) (Table 3 and Fig. 2(a)) with peak separations (ΔE_p, where ΔE_p = E_pa − E_pc)⁷⁹ of 58 mV and 65 mV, respectively. Note that the decomposition pathway of 1²⁻2− to the initial cobaltadithiolene 3 was suppressed at low temperatures, for example, at 253 K. The CVs were simulated according to the following equations:

1 ([Co^IIIMo⁰Co^III]) + e⁻ ⇄ 1⁻− ([Co^IIIMo⁰Co^II]¹⁻) E^0′₁, (1-1)

1⁻− ([Co^IIIMo⁰Co^II]¹⁻) + e⁻ ⇄ 1²⁻2− ([Co^IIMo⁰Co^II]²⁻) E^0′₂. (1-2)

Table 3 E ^0′ ₁, E^0′₂, and ΔE^0′ values obtained from cyclic voltammograms of 1 and 2

	Electrolyte–solvent	E ^0′ 1 /mV	E ^0′ 2 /mV	ΔE^0^′ /mV
a Data were obtained from Fig. 3. E^0′1 and E^0′2 are reported with respect to Fc^+/Fc. ΔE^0′ = (E^0′2 − E^0′1). b Data were obtained by digital simulation of CVs (see Table 4). c Data from ref. 52.
1 ^a	Bu4NClO4–MeCN/toluene (1 : 1 v/v)	–1659	–1941	282
1 ^a	Bu4NClO4–THF	–1757	–1978	221
1 ^a	NaBPh4–MeCN/toluene (1 : 1 v/v)	–1665	–1775	110
1 ^b	NaBPh4–THF	–1740	–1730	–10
1 ^a	NaBPh4/18-crown-6–THF	–1784	–1979	195
2 ^b ^, ^c	Bu4NClO4–MeCN/toluene (1 : 1 v/v)	–1891	–1851	–40
2 ^b ^, ^c	NaBPh4–THF	–1920	–1730	–190

---

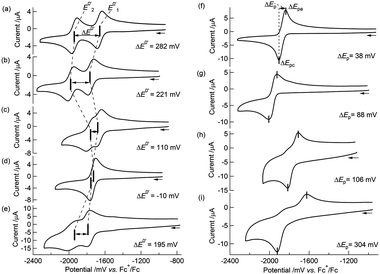Fig. 2 Cyclic voltammograms of (a) 1 in 0.1 M Bu₄NClO₄–MeCN/toluene (1 : 1 v/v) at 253 K; (b) 1 in 0.1 M Bu₄NClO₄–THF at 258 K; (c) 1 in 0.1 M NaBPh₄–MeCN/toluene (1 : 1 v/v) at 258 K; (d) 1 in 0.1 M NaBPh₄–THF at 258 K; (e) 1 in 0.1 M 18-crown-6/NaBPh₄–THF at 298 K; (f) 2 in 0.1 M Bu₄NClO₄–MeCN/toluene (1 : 1 v/v) at 253 K; (g) 2 in 0.1 M Bu₄NClO₄–THF at 258 K; (h) 2 in 0.1 M NaBPh₄–MeCN/toluene (1 : 1 v/v) at 258 K; (i) 2in 0.1 M NaBPh₄–THF at 258 K. Scan rate: 100 mV s⁻¹.

The simulated CVs accurately predicted the difference between the redox potentials (ΔE^0′ = E^0′₂ − E^0′₁, experimental: 282 mV, simulated: 280 mV, Table 4 and Fig. 3(a)).

Table 4 Digital simulation parameters for the electrochemical processes of 1 and 2^a

	1		2 ^b
a Scan rate (v) = 100 mV s^−1, concentration (c) = 5 × 10^−4 mol dm^−3, surface area (A) = 7.065 × 10^−2 cm^2. b Data from ref. 52.
Electrolyte–solvent	Bu4NClO4–MeCN/toluene (1 : 1 v/v)	NaBPh4–THF	Bu4NClO4–MeCN/toluene (1 : 1 v/v)	NaBPh4–THF
E ^0′ 1 /mV	−1662	−1740	−1891	−1920
k s1 /cm s^−1	10	5.0 × 10^−3	0.85	8.0 × 10^−3
α 1	0.50	0.50	0.50	0.50
E ^0′ 2 /mV	−1942	−1730	−1851	−1730
k s2 /cm s^−1	0.012	5.0 × 10^−3	0.10	2.0 × 10^−4
α 2	0.50	0.50	0.50	0.42
ΔE^0^′ /mV	280	−10	−40	−190
Diffusion constant (D) /cm^2s^−1	1.8 × 10^−6	1.1 × 10^−6	1.7 × 10^−6	1.2 × 10^−6
Resistance (R) /Ω	1.5 × 10^3	1.63 × 10^3	1.64 × 10^3	1.62 × 10^3
Capacitance (Cdl) /F	5 × 10^−6	—	5 × 10^−6	—
Temperature (T) /K	253	258	253	258

---

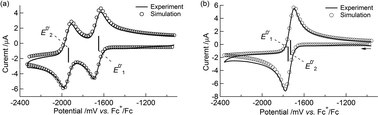Fig. 3 (a) A cyclic voltammogram of 1 at 100 mV s⁻¹ in 0.1 M Bu₄NClO₄–MeCN/toluene (1 : 1 v/v) at 253 K and its simulated voltammogram. (b) A background-corrected cyclic voltammogram of 1 at 100 mV s⁻¹ in 0.1 M NaBPh₄–THF at 258 K and its simulated voltammogram.

Interestingly, the CVs and redox potentials of 1 depended on the solvent and electrolyte, as shown in Table 3 and Fig. 2(a–d). The CVs of 1 in Bu₄NClO₄–THF or NaBPh₄–MeCN/toluene (1 : 1 v/v) showed two reversible redox waves, although the ΔE^0′ values were smaller: ΔE^0′ = 221 mV and ΔE^0′ = 110 mV, respectively. The CV of 1 in NaBPh₄–THF at 258 K showed only one reversible redox wave, and the simulated CV at 258 K gave ΔE^0′ = −10 mV (E^0′₁ = −1740 mV and E^0′₂ = −1730 mV vs. Fc⁺/Fc, respectively) (Table 4 and Fig. 3(b)), indicating a one-step 2e⁻reduction with potential inversion. These results strongly suggested that the electrolyte cation played an important role in the dramatic changes in ΔE^0′.^24–30 The effects of cation size were tested by measuring the CV of 1 in a NaBPh₄ (0.1 M)–THF solution with stoichiometric amounts of 18-crown-6 (0.1 M), which can capture Na⁺. The single redox wave split into two waves, and ΔE^0′ became positive, 195 mV (Table 3 and Fig. 2(e)). This result confirmed that the cation size strongly dominated the redox behaviour of 1. The valence state changes of the Co atom, as described in eqn (1-1) and (1-2), were confirmed by EPR spectroscopy of 1²⁻2−, which was generated by the chemical reduction of 1 with Na in 2-MeTHF under high vacuum (Fig. S6†). The EPR spectrum of 1²⁻2− exhibited peaks attributed to Co^II in the ΔM_s = 1 region, with a hyperfine structure corresponding to Co (I = 7/2) at 9.2 K, supporting the reduction from Co^III to Co^II (Fig. S7(a)†). In addition, a signal in the “spin-forbidden” ΔM_s = 2 region was clearly observed at 4.2 K (Fig. S7(b)†), implying that 1²⁻2− displayed a triplet ground state similar to that observed in 2²⁻2−.⁵²

In contrast, 2 underwent a one-step 2e⁻reduction with potential inversion under all solvent–electrolyte conditions in which 1 was tested. When a less polar solvent was used (MeCN → THF) and the electrolyte cation was smaller (Bu₄N⁺ → Na⁺), the reversibility of the CV decreased and ΔE_p became larger (Fig. 2(f–i)). CV simulations of 2 in both Bu₄NClO₄–MeCN/toluene (1 : 1 v/v) and NaBPh₄–THF based on eqn (1-3) and (1-4) predicted negative ΔE^0′ = E^0′₂– E^0′₁ values (−40 mV and −190 mV, respectively) for the reactions (Table 4).

2 ([Rh^IIIMo⁰Rh^III]) + e⁻ ⇄ 2⁻− ([Rh^IIIMo⁰Rh^II]¹⁻) E^0′₁, (1-3)

2⁻− ([Rh^IIIMo⁰Rh^II]¹⁻) + e⁻ ⇄ 2²⁻2− ([Rh^IIMo⁰Rh^II]²⁻) E^0′₂. (1-4)

We previously reported that the coordination mode of the CO groups changed during the 2e⁻reduction of 2 from semibridging to bridging, and this change was crucial for the potential inversion, as observed by in situIRAS and EPR spectroscopies and by DFT calculations of the 2²⁻2− structure.⁵² CV simulations based on the redox reactions listed in eqn (1-1) and (1-2) predicted structural changes during the reduction of 1, consistent with the fitting parameters associated with the small electron transfer rate constants (Table 4).^49,50,79,80 Based on these results, we investigated the structural changes during the reduction of 1 under different solvent–electrolyte conditions through in situIRAS measurements and DFT calculations. When a potential of −1.9 V vs. Fc⁺/Fc was applied to a Bu₄NClO₄–THF solution of 1 to produce 1⁻−, the two ν(CO) peaks for 1, originally at 1880 cm⁻¹and 1825 cm⁻¹, shifted to lower frequencies. One of the ν(CO) peaks remained in the region corresponding to the semibridging CO (1815 cm⁻¹), and the other shifted to significantly lower frequencies (1694 cm⁻¹, Table 2 and Fig. 4(a)). These results indicated that one semibridging CO converted to a bridging CO, and the other remained semibridging. When a potential of −2.1 V was applied to produce 1²⁻2−, the two peaks shifted to 1709 cm⁻¹ and 1655 cm⁻¹ (Table 2 and Fig. 4(a)), which corresponded to bridging CO coordination modes. This result indicated that two bridging CO groups were formed. When a potential of −1.75 V was applied to the NaBPh₄–THF solution of 1 to produce 1²⁻2− in one step, the two peaks shifted to 1686 cm⁻¹ and 1613 cm⁻¹ (Table 2 and Fig. 4(b)), which corresponded to bridging CO, indicating the direct formation of two bridging CO groups. These results show that the size of the counter cation strongly affected the reduction mechanism. Reduction proceeded by either two-step 1e⁻reductions with successive CO structural changes or by a one-step 2e⁻reduction with simultaneous double CO structural changes. Reoxidation from 1²⁻2− to 1 recovered the original spectrum in both cases, indicating that the CO coordination mode reversibly switched between semibridging and bridging conformations. The optimized structure of 1²⁻2− was calculated using DFT methods, in which all geometric parameters were optimized and the solvent effects were modelled using the CPCM method. The triplet state structure was found to be the most stable structure, as determined experimentally by EPR spectroscopy. The triplet state included two CO groups that bridged between the Co and Mo atoms (Fig. 1(b)), as was observed in 2²⁻2−.⁵² A structural analysis revealed that the O–C–Mo angle was 159.73°, the Mo–C bond length was 1.959 Å, and the Co–C (CO) length was 2.330 Å (Table S3†). Moreover, the FT-IR frequencies of the two CO groups in 1²⁻2− were found to be 1731 cm⁻¹ and 1683 cm⁻¹ (Table 2), which strongly supported the experimental evidence for the presence of bridging CO groups.

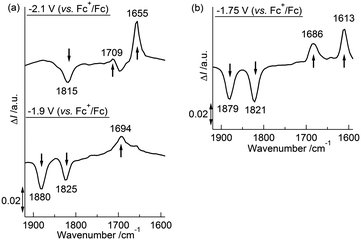Fig. 4 (a) Differential in situIRAS spectra of 1 with applied potentials of −1.9 V and −2.1 V (vs. Fc⁺/Fc) in 0.1 M Bu₄NClO₄–THF at 293 K. (b) Differential in situIRAS spectra of 1 with an applied potential of −1.75 V (vs. Fc⁺/Fc) in 0.1 M NaBPh₄–THF at 293 K.

The unique redox behaviour and structural changes arose from the joint effects of the electrostatic interactions between the electrochemically produced anions and counter cations and variations in the interaction strength of the Co/Rh atoms and the CO groups. The size of the counter cation apparently governed the redox behaviour and coordination mode of the CO groups in 1 (Fig. 5(a)). To elucidate the counter cation size effect, the relative position of the counter cation and the dianion 1²⁻2− was modelled using DFT calculations of 1²⁻2− in the presence of two Na⁺ ions (denoted 1²⁻2−·2Na⁺). The optimized structure of 1²⁻2−·2Na⁺, in which both CO groups were bridging, showed that the two Na⁺ ions were located between the Co atoms and the O atoms of the bridging CO group, indicating the presence of strong cation–anion electrostatic interactions (Fig. 5(b)). The stability of this ion pair produced the one-step 2e⁻reduction of 1 without the formation of the monoanion 1⁻− in 0.1 M NaBPh₄–THF. If the size of the cation increased due to solvation by a polar solvent (e.g., MeCN) or due to trapping by 18-crown-6, the Na⁺ ion could no longer closely associate with the complex. As a result, the ion pair was expected to be less stable and to suppress the direct formation of 1²⁻2− through changes in the CO coordination mode. The two-step 1e⁻reductions would, therefore, dominate via the intermediate monoanion 1⁻− in a mixed-valence form (Fig. 5(c)). This behaviour was derived from the fact that the Co atom interacted more weakly with CO in 1 than with Rh in 2 (determined by comprehensive structural analysis of single crystal X-ray diffraction results, FT-IR and NMR spectra, vide supra), which affected the redox behaviour and associated structural changes. In contrast, 2 was more likely to undergo structural changes in the CO coordination mode due to stronger π back-donation to CO. The larger 4d orbitals caused a semibridging-to-bridging transition in the CO groups, irrespective of the outer-sphere counter cation environment, as determined by the polarity of the solvent and the size of the counter cation.

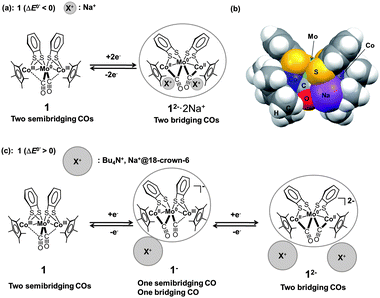Fig. 5 (a) Schematic diagram of the CO group coordination mode transition between 1 and 1²⁻2− upon one-step 2e⁻redox reaction. (b) Optimized structure of 1²⁻2−·2Na⁺ (triplet state) (C₂ symmetry) in the CPK model. (c) Schematic diagram of the CO group coordination mode transitions between 1, 1⁻−, and 1²⁻2− upon two-step 1e⁻redox reactions.

Structure of 2²⁻2− determined by Rh K-edge and Mo K-edge EXAFS

We reported previously that the CO coordination mode transition from semibridging to bridging during the 2e⁻reduction of 2 was crucial, based on in situIRAS and EPR spectroscopy and DFT models of the dianion 2²⁻2−.⁵² However, experimental support for the local coordination structure of 2²⁻2− was not conclusive. We investigated the local coordination structure of 2²⁻2− in 2-MeTHF by Rh K-edge and Mo K-edge EXAFS in an attempt to corroborate the expected structure from in situIRAS measurements and DFT calculations. Although single crystals of the dianion 2²⁻2− were difficult to prepare due to the complex's high reactivity in air, its thermal stability, which was much higher than that of 1²⁻2−, was sufficient to allow EXAFS measurements at 20 K.

Prior to the analysis of 2²⁻2−, EXAFS results from 2 in the solid state were analyzed by curve fitting (Fig. 6). The Rh K-edge EXAFS oscillation was successfully fitted using three contributions: Rh–Mo at 2.76 ± 0.01 Å (coordination number, CN = 1.1 ± 0.1), Rh–S at 2.38 ± 0.01 Å (CN = 2.1 ± 0.1), and Rh–C (C₅Me₅) at 2.19 ± 0.01 Å (CN = 5.4 ± 0.2). The Mo K-edge EXAFS oscillation was successfully fitted with four contributions: Mo–Rh at 2.75 ± 0.01 Å (CN = 1.9 ± 0.1), Mo–S at 2.52 ± 0.01 Å (CN = 3.9 ± 0.1), Mo–C (CO) at 1.96 ± 0.01 Å (CN = 2.2 ± 0.1), and Mo⋯O (CO) at 3.07 ± 0.02 Å (CN = 2.2) (Table 5). These results reproduced the data of the single crystal X-ray diffraction analysis of 2. An independent analysis of the Rh K-edge and Mo K-edge EXAFS oscillations showed identical values for the Rh–Mo bonds, indicating the validity of the EXAFS analysis of 2. The EXAFS oscillations of 2²⁻2− were analyzed based on the fitting results of 2 (Fig. 6). The Rh K-edge EXAFS oscillation of 2²⁻2− in 2-MeTHF was successfully fitted with five contributions: Rh–Mo at 2.69 ± 0.01 Å (CN = 1.4 ± 0.1), Rh–S at 2.38 Å (CN = 1.2 ± 0.1), Rh–C (C₅Me₅) at 2.20 ± 0.01 Å (CN = 4.8 ± 0.3), Rh–C (CO) at 1.94 ± 0.02 Å (CN = 1.3 ± 0.1), and Rh⋯O (CO) at 2.82 ± 0.06 Å (CN = 1.3). The Mo K-edge EXAFS oscillation was fitted with four contributions: Mo–Rh at 2.69 ± 0.01 Å (CN = 2.1 ± 0.1), Mo–S at 2.47 ± 0.01 Å (CN = 3.7 ± 0.1), Mo–C (CO) at 1.97 ± 0.01 Å (CN = 2.0 ± 0.3), and Mo⋯O (CO) at 2.84 ± 0.03 Å (CN = 2.0) (Table 5). An independent analysis of the Rh K-edge and Mo K-edge EXAFS oscillations of 2²⁻2− showed identical values for the Rh–Mo bonds, and the R_f factor determined by Rh K-edge EXAFS analysis was larger when the contribution of Rh–C (CO) was not included in the curve-fitting analysis. These factors suggested that the curve-fitting analysis of 2²⁻2− described above was appropriate. Two new Rh–C (CO) bonds (CN = 2) emerged and two out of four Rh–S bonds were cleaved (CN decreased from 4 to 2), indicating that the experimental results agreed with the DFT calculated results for 2²⁻2− (Table S3†). Summarizing the results of the Rh K-edge and Mo K-edge EXAFS for both 2 and 2²⁻2−, two CO groups bridged the Rh and Mo atoms and two Rh–S bonds were cleaved during the 2e⁻reduction of 2 (Fig. 7).

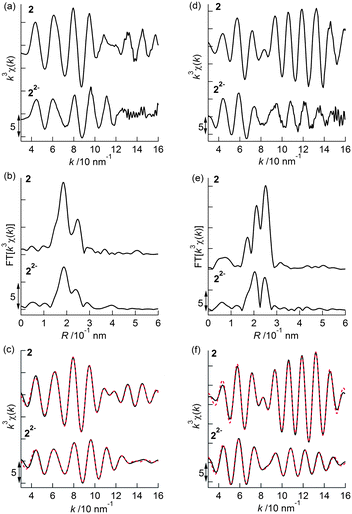Fig. 6 (a) k³-Weighted Rh K-edge EXAFS oscillations, (b) their Fourier transforms, and (c) their curve-fitted oscillations (black: observed data, red: curve-fitted data) for 2 (solid state) and 2²⁻2−(solution of 2-MeTHF). (d) k³-Weighted Mo K-edge EXAFS oscillations, (e) their Fourier transforms, and (f) their curve-fitted oscillations (black: observed data, red: curve-fitted data) for 2 (solid state) and 2²⁻2− (solution of 2-MeTHF).

Table 5 Structural parameters estimated by curve-fitting analysis of the Rh K-edge and Mo K-edge EXAFS measured at 20 K

	2 (Rh K-edge)^a				2^2−2− (Rh K-edge)^b
a k = 3–16 Å^−1, R = 1.38–2.70 Å, Rf = 0.6%. b k = 3–16 Å^−1, R = 1.44–2.85 Å, Rf = 0.9%.
Shell	CN	Distance /Å	ΔE0	σ /Å	CN	Distance /Å	ΔE0	σ /Å
Rh–Mo	1.1 ± 0.1	2.76 ± 0.01	7.2 ± 0.7	0.048 ± 0.004	1.4 ± 0.1	2.69 ± 0.01	7.2	0.086 ± 0.005
Rh–S	2.1 ± 0.1	2.38 ± 0.01	6.8 ± 0.6	0.048 ± 0.004	1.2 ± 0.1	2.38	6.8	0.048
Rh–C (C5Me5)	5.4 ± 0.2	2.19 ± 0.01	3.2 ± 0.7	0.042 ± 0.005	4.8 ± 0.3	2.20 ± 0.01	3.2	0.059 ± 0.005
Rh–C (CO)	—	—	—	—	1.3 ± 0.1	1.94 ± 0.02	2.9 ± 3.7	0.090 ± 0.024
Rh⋯O (CO)	—	—	—	—	1.3	2.82 ± 0.06	2.9	0.090

---

	2 (Mo K-edge)^c				2^2−2− (Mo K-edge)^d
Shell	CN	Distance /Å	ΔE0	σ /Å	CN	Distance /Å	ΔE0	σ /Å
Mo–Rh	1.9 ± 0.1	2.75 ± 0.01	1.3 ± 0.3	0.037 ± 0.002	2.1 ± 0.1	2.69 ± 0.01	1.3	0.087 ± 0.004
Mo–S	3.9 ± 0.1	2.52 ± 0.01	3.5 ± 0.3	0.052 ± 0.003	3.7 ± 0.1	2.47 ± 0.01	3.5	0.066 ± 0.003
Mo–C (CO)	2.2 ± 0.1	1.96 ± 0.01	0.1 ± 1.0	0.025 ± 0.010	2.0 ± 0.3	1.97 ± 0.01	0.3 ± 2.1	0.084 ± 0.014
Mo⋯O (CO)	2.2	3.07 ± 0.02	0.1	0.025	2.0	2.84 ± 0.03	0.3	0.084
c k = 3–16 Å^−1, R = 1.32–2.64 Å, Rf = 1.4%. d k = 3–16 Å^−1, R = 1.53–2.70 Å, Rf = 1.8%.

---

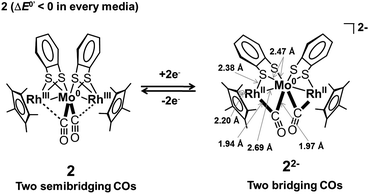Fig. 7 Schematic diagram of the CO group coordination mode transition between 2 and 2²⁻2− upon one-step 2e⁻redox reaction, and the local coordination structure of 2²⁻2− obtained from Rh and Mo K-edge EXAFS.

Conclusions

In the heterometal trinuclear complexes [Co₂Mo(η⁵-C₅Me₅)₂(S₂C₆H₄)₂(CO)₂], 1, and [Rh₂Mo(η⁵-C₅Me₅)₂(S₂C₆H₄)₂(CO)₂], 2, two metalladithiolenes were found to electronically communicate via a bridging Mo(CO)₂ moiety through two Co/Rh–Mo bonds. Multi-electron transfer accompanied the structural changes in the complexes. The neutral forms were found to have structures with similar Co–Mo or Rh–Mo bonds and similar valence states (Co^IIIMo⁰Co^III and Rh^IIIMo⁰Rh^III), and the two CO groups occupied a semibridging conformation between the Co/Rh atoms and the Mo atom. The interaction between Co and CO was weaker than that between Rh and CO, which played a crucial role in distinguishing the electro-reduction properties and structural changes in 1 and 2. Electrochemical reduction of 1 showed a strong solvent–electrolyte dependence. Two-step 1e⁻reductions with positive redox potential differences (ΔE^0′ > 0) were observed in Bu₄NClO₄–MeCN/toluene (1 : 1 v/v), Bu₄NClO₄–THF, and NaBPh₄–MeCN/toluene (1 : 1 v/v), whereas a one-step 2e⁻reduction with a negative redox potential difference (potential inversion, ΔE^0′ < 0) was observed in NaBPh₄–THF. The stepwise change from semibridging to bridging CO occurred during the two-step 1e⁻reduction processes of 1, and the single-step transition from semibridging to bridging CO was accompanied by a one-step 2e⁻reduction process. The size of the counter cation significantly influenced this reduction behaviour and the accompanying structural changes. The reduction of complex 2 did not show any solvent–electrolyte dependence. This could be explained in terms of the strong interaction between Rh and CO, which led to the easy formation of bridging CO. The local coordination structure of 2²⁻2− was characterized for the first time using Rh K-edge and Mo K-edge EXAFS. CO groups were found to bridge the Rh and Mo atoms, and the cleavage of two Rh–S bonds was experimentally confirmed.

Acknowledgements

The authors wish to extend their gratitude to Prof. Manabu Sugimoto at Kumamoto University, Prof. Seiji Miyashita at the University of Tokyo, and Prof. Tatsuhisa Kato at Josai University for their helpful discussions. This work was supported by Grant-in-Aid for Scientific Research from MEXT of Japan (Nos. 20245013 and 21108002, area 2107 (Coordination Programming)), Grand Challenges in Next-Generation Integrated Nanoscience from MEXT, Japan, and by a Research Fellowship from the Japan Society for the Promotion of Science for Young Scientists. XAFS measurements were performed with the approval of PF-PAC (No. 2009G076).

Notes and references

1. R. A. Marcus and N. Sutin, Biochim. Biophys. Acta., 1985, 811, 265–322.
2. V. Balzani, Ed., Electron Transfer in Chemistry, Wiley–VCH, Weinheim, Germany, 2001, Vol. I–IV.
3. T. J. Meyer, M.-H. V. Huynh and H. H. Thorp, Angew. Chem., Int. Ed., 2007, 46, 5284–5304.
4. H. B. Gray and J. R. Winkler, Biochim. Biophys. Acta, Bioenerg., 2010, 1797, 1563–1572.
5. D. V. Yandulov and R. R. Schrock, Science, 2003, 301, 76–78.
6. D. Astruc, Organometallic Chemistry and Catalysis, Springer, Heidelberg, Germany, 2007, Chapters 5, 16, and 19.
7. P. Nguyen, P. Gómez-Elipe and I. Manners, Chem. Rev., 1999, 99, 1515–1548.
8. B. J. Holliday and T. M. Swager, Chem. Commun., 2005, 23–36.
9. B. O'regan and M. Grätzel, Nature, 1991, 353, 737–740.
10. M. Grätzel, J. Photochem. Photobiol., C, 2003, 4, 145–153.
11. R. J. Crutchley, Adv. Inorg. Chem., 1994, 41, 273–325.
12. K. D. Demadis, C. M. Hartshorn and T. J. Meyer, Chem. Rev., 2001, 101, 2655–2685.
13. H. Nishihara, Bull. Chem. Soc. Jpn., 2001, 74, 19–29.
14. H. Nishihara, Adv. Inorg. Chem., 2002, 53, 41–86.
15. G.-L. Xu, R. J. Crutchley, M. C. DeRosa, Q.-J. Pan, H.-X. Zhang, X. Wang and T. Ren, J. Am. Chem. Soc., 2005, 127, 13354–13363.
16. J. C. Salsman, C. P. Kubiak and T. Ito, J. Am. Chem. Soc., 2005, 127, 2382–2383.
17. D. M. D'Alessandro and F. R. Keene, Chem. Rev., 2006, 106, 2270–2298.
18. W. Kaim and G. K. Lahiri, Angew. Chem., Int. Ed., 2007, 46, 1778–1796.
19. D. E. Richardson and H. Taube, Inorg. Chem., 1981, 20, 1278–1285.
20. C. Creutz, Prog. Inorg. Chem., 1983, 30, 1–73.
21. D. E. Richardson and H. Taube, Coord. Chem. Rev., 1984, 60, 107–129.
22. D. M. D'Alessandro and F. R. Keene, Chem. Soc. Rev., 2006, 35, 424–440.
23. P. Aguirre-Etcheverry and D. O'Hare, Chem. Rev., 2010, 110, 4839–4864.
24. H. Nishihara, M. Okuno, N. Akimoto, N. Kogawa and K. Aramaki, J. Chem. Soc., Dalton Trans., 1998, 2651–2656.
25. M. Okuno, K. Aramaki and H. Nishihara, J. Electroanal. Chem., 1997, 438, 79–83.
26. F. Barrière, N. Camire, W. E. Geiger, U. T. Mueller-Westerhoff and R. Sanders, J. Am. Chem. Soc., 2002, 124, 7262–7263.
27. N. A. Macías-Ruvalcaba and D. H. Evans, J. Phys. Chem. B, 2005, 109, 14642–14647.
28. F. Barrière and W. E. Geiger, J. Am. Chem. Soc., 2006, 128, 3980–3989.
29. A. Nafady, T. T. Chin and W. E. Geiger, Organometallics, 2006, 25, 1654–1663.
30. A. K. Diallo, C. Absalon, J. Ruiz and D. Astruc, J. Am. Chem. Soc., 2011, 133, 629–641.
31. J. P. Collman, R. K. Rothrock, R. G. Finke, E. J. Moore and F. Rose-Munch, Inorg. Chem., 1982, 21, 146–156.
32. J. G. Gaudiello, T. C. Wright, R. A. Jones and A. J. Bard, J. Am. Chem. Soc., 1985, 107, 888–897.
33. R. Moulton, T. W. Weidman, K. P. C. Vollhardt and A. J. Bard, Inorg. Chem., 1986, 25, 1846–1851.
34. D. A. Smith, B. Zhuang, W. E. Newton, J. W. McDonald and F. A. Schultz, Inorg. Chem., 1987, 26, 2524–2531.
35. D. Astruc, M. Lacoste and L. Toupet, J. Chem. Soc., Chem. Commun., 1990, 558–561.
36. M. Lacoste, H. Rabaâ, D. Astruc, N. Ardoin, F. Varret, J.-Y. Saillard and A. Le Beuze, J. Am. Chem. Soc., 1990, 112, 9548–9557.
37. T. T. Chin, W. E. Geiger and A. L. Rheingold, J. Am. Chem. Soc., 1996, 118, 5002–5010.
38. A.-J. DiMaio, A. L. Rheingold, T. T. Chin, D. T. Pierce and W. E. Geiger, Organometallics, 1998, 17, 1169–1176.
39. G. A. N. Felton, B. J. Petro, R. S. Glass, D. L. Lichtenberger and D. H. Evans, J. Am. Chem. Soc., 2009, 131, 11290–11291.
40. N. Bellec, K. Boubekeur, R. Carlier, P. Hapiot, D. Lorcy and A. Tallec, J. Phys. Chem. A, 2000, 104, 9750–9759.
41. P. Hapiot, L. D. Kispert, V. V. Konovalov and J.-M. Savéant, J. Am. Chem. Soc., 2001, 123, 6669–6677.
42. T. Nishiumi, Y. Chimoto, Y. Hagiwara, M. Higuchi and K. Yamamoto, Macromolecules, 2004, 37, 2661–2664.
43. N. A. Macías-Ruvalcaba and D. H. Evans, J. Phys. Chem. B, 2006, 110, 5155–5160.
44. N. A. Macías-Ruvalcaba and D. H. Evans, J. Phys. Chem. B, 2006, 110, 24786–24795.
45. S. F. Nelsen, G. Li, K. P. Schultz, H. Q. Tran, I. A. Guzei and D. H. Evans, J. Am. Chem. Soc., 2008, 130, 11620–11622.
46. D. H. Evans and K. Hu, J. Chem. Soc., Faraday Trans., 1996, 92, 3983–3990.
47. M.-H. Baik, T. Ziegler and C. K. Schauer, J. Am. Chem. Soc., 2000, 122, 9143–9154.
48. M.-H. Baik, C. K. Schauer and T. Ziegler, J. Am. Chem. Soc., 2002, 124, 11167–11181.
49. N. A. Macías-Ruvalcaba and D. H. Evans, Chem.–Eur. J., 2007, 13, 4386–4395.
50. D. H. Evans, Chem. Rev., 2008, 108, 2113–2144.
51. M. Nihei, T. Nankawa, M. Kurihara and H. Nishihara, Angew. Chem., Int. Ed., 1999, 38, 1098–1100.
52. S. Muratsugu, K. Sodeyama, F. Kitamura, M. Sugimoto, S. Tsuneyuki, S. Miyashita, T. Kato and H. Nishihara, J. Am. Chem. Soc., 2009, 131, 1388–1389.
53. K. D. Karlin and E. I. Stiefel, Ed., Dithiolene Chemistry; Syntheses, Properties, and Applications. Progress in Inorganic ChemistryVol. 52, John Wiley & Sons, Inc., Hoboken, NJ, 2004.
54. R. Eisenberg, Prog. Inorg. Chem., 1970, 12, 295–369.
55. R. P. Burns and C. A. McAullife, Adv. Inorg. Chem. Radiochem., 1979, 22, 303–348.
56. M. Fourmigue, Coord. Chem. Rev., 1998, 178–180, 823–864.
57. A. Sugimori, T. Akiyama, M. Kajitani and T. Sugiyama, Bull. Chem. Soc. Jpn., 1999, 72, 879–908.
58. N. Nakagawa, T. Yamada, M. Murata, M. Sugimoto and H. Nishihara, Inorg. Chem., 2006, 45, 14–16.
59. M. Murata, S. Habe, S. Araki, K. Namiki, T. Yamada, N. Nakagawa, T. Nankawa, M. Nihei, J. Mizutani, M. Kurihara and H. Nishihara, Inorg. Chem., 2006, 45, 1108–1116.
60. N. Nakagawa, M. Murata, M. Sugimoto and H. Nishihara, Eur. J. Inorg. Chem., 2006, 2129–2131.
61. B.-H. Zhu, Y. Shibata, S. Muratsugu, Y. Yamanoi and H. Nishihara, Angew. Chem., Int. Ed., 2009, 48, 3858–3861.
62. G.-X. Jin, J.-Q. Wang, C. Zhang, L.-H. Weng and M. Herberhold, Angew. Chem., Int. Ed., 2005, 44, 259–262.
63. S. Cai, J.-Q. Wang and G.-X. Jin, Organometallics, 2005, 24, 4226–4231.
64. S. Cai and G.-X. Jin, Organometallics, 2005, 24, 5280–5286.
65. Y.-Q. Chen, J. Zhang, S. Cai, X.-F. Hou, H. Schumann and G.-X. Jin, Dalton Trans., 2007, 749–758.
66. S. Liu, G.-L. Wang and G.-X. Jin, Chem. Soc. Rev., 2007, 36, 1543–1560.
67. J.-S. Zhang, Y.-F. Han and G.-X. Jin, Dalton Trans., 2009, 111–118.
68. X. Meng, F. Wang and G.-X. Jin, Coord. Chem. Rev., 2010, 254, 1260–1272.
69. P. Cassoux, Coord. Chem. Rev., 1999, 185–186, 213–232.
70. H. Tanaka, Y. Okano, H. Kobayashi, W. Suzuki and A. Kobayashi, Science, 2001, 291, 285–287.
71. A. Kobayashi, E. Fujiwara and H. Kobayashi, Chem. Rev., 2004, 104, 5243–5264.
72. R. Kato, Chem. Rev., 2004, 104, 5319–5346.
73. Y. Kosaka, H. M. Yamamoto, A. Nakao, M. Tamura and R. Kato, J. Am. Chem. Soc., 2007, 129, 3054–3055.
74. M. D. Curtis, K. R. Han and W. M. Butler, Inorg. Chem., 1980, 19, 2096–2101.
75. R. H. Crabtree and M. Lavin, Inorg. Chem., 1986, 25, 805–812.
76. J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683–11700.
77. C. D. Wagner, W. M. Riggs, L. E. Davis, J. F. Moulder and G. E. Muilenberg, Handbook of X-ray Photoelectron Spectroscopy, Perkin-Elmer Corp., Physical Electronics Division, Eden Prailie, MI, 1979.
78. W. B. Hughes and B. A. Baldwin, Inorg. Chem., 1974, 13, 1531–1532.
79. A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, 2nd ed., Wiley, Hoboken, NJ, 2001, Chapter 12.
80. A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, 2nd ed., Wiley, Hoboken, NJ, 2001, Chapter 3.

---

Footnotes

† Electronic supplementary information (ESI) available: experimental procedures, FT-IR, UV-vis-NIR and ¹³C NMR spectra of 1 and 2, XPS spectra of 1, 2, 3, and 4, EPR spectra of 1²⁻2−, optimized structure of 1, and a table of selected bond lengths and bond angles for 1 and 2 from DFT calculations. CCDC reference number 822924. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c1sc00272d

‡ Crystal data for 1: C₃₄H₃₈O₂S₄Co₂Mo, Fw = 820.68, monoclinic, space groupP2₁/n, a = 15.450(5), b = 11.362(5), c = 19.951(5) Å, β = 106.933(5)°, V = 3350(2) ų, Z = 4, T = 113 K, μ = 16.27 cm⁻¹, R₁ = 0.0208, wR₂ = 0.0506, GOF = 1.064.

---