Reactivity studies on [Cp′FeI]₂: From iron hydrides to P₄-activation

Abstract

Metathesis of [Cp′FeI]₂ (1) with KHBEt₃ affords the polyhydride iron complexes [Cp′FeH₂]₂ (2) and [Cp′₂Fe₂H₃] (3). The ratio in which both 2 and 3 are obtained correlates to the applied H₂ pressure during synthesis. Complex 2 activates CH- or CD- bonds in aromatic compounds and shows slow H/D exchange in the presence of D₂ at room temperature in cyclohexane solvent. [Cp′FeH₂]₂ acts as a Cp′Fe(I)-synthon when reacted with white phosphorus (P₄) to give [Cp′Fe]₂(μ-P₄) (4) as the only P-containing product. This complex is best described as a triple-decker complex with a planar arrangement of a severely distorted kite-like cyclo-P₄ unit. This distortion persists in solution and solid state as evidenced by a small PP coupling constant in the ³¹P{¹H} NMR spectrum and a long P–P distance of 2.53 Å. Complex 4 is an isomer to the long-known [{Cp′Fe}₂(μ-η⁴:η⁴-P₄)] (5) with a cis-tetraphosphabutadiene moiety and it thermally rearranges to 5, [{Cp′Fe}₂(μ-η³:η³-P₃)] and [Cp′Fe(P₅)]. All complexes described in this paper have been completely characterized including X-ray crystallography, variable temperature NMR studies and DFT calculations. Relaxed force constants (inverse compliance constants) are used as bond strength descriptors.

---

Introduction

The exploration of low-coordinate iron complexes as possible models systems for the active sites in metalloenzymes has been the focus of many groups.¹ A common motif to all these investigations is the stabilization of low-coordinate iron fragments by sterically demanding ligands which allow highly unusual molecules to be synthesized and their chemistry to be explored.^2–10 Despite the fact that ferrocene, (C₅H₅)₂Fe, is one of the iconic complexes in organometallic chemistry, low-coordinate, open-shell mono(cyclopentadienyl) iron complexes have not been explored extensively. One reason is the competitive formation of thermodynamically favored Cp₂Fe. Sterically demanding alkylcyclopentadienyl ligands are a prerequisite for the isolation of high-spin mono(cyclopentadienyl) iron(II) complexes and their kinetic stability results from the effective blocking of the dismutation pathway. In this context the synthesis of [(ⁿCp)FeBr]₂ (⁵Cp = C₅(CH₂Me₂)₅, ⁴Cp = C₅H(CHMe₂)₄ and Cp′ = 1,2,4-C₅H₂(CMe₃)₃) without additional donor ligands has been reported.^11,12 These species can be obtained as stable compounds and react with substituted phenolates to yield monomeric and dimeric complexes depending on the steric bulk of the phenolate ligand.¹² More recently σ/π-rearrangements of aryl ligands connected to the Cp′Fe-fragment have been reported,^13–15 whereas the related ⁵CpFe(C₅H₃-2,6-(iPr)₂) derivative is a single-molecule magnet.¹⁶

The synthesis of organophosphorus compounds directly from elemental phosphorus is a challenging process for chemists and the chemical industry, and involves the hazardous chlorination of P₄ to PCl₃.^17,18 Therefore, it would be environmentally beneficial to develop mild metal-mediated reactions which allow direct P₄ functionalization to form new P–C and/or P–H bonds based on abundant and environmentally benign metals.¹⁹ Hence, iron hydrides might be an intriguing starting material for this transformation. The only example of an iron polyhydride cluster supported exclusively by cyclopentadienyl ligands is [(C₅Me₅)FeH₂]₂ (prepared from (C₅Me₅)FeCl(tmeda) and LiAlH₄),²⁰ which exhibits a rich reaction chemistry with borane,^21,22 silanes^20,23 and phosphines.²⁰ However, the use of sterically demanding ligands such as Cp′ can alter reactivity patterns significantly as previously shown for other metals.^24–29

We have set out investigating the reactivity of [Cp′FeI]₂ (1) focusing on synthetically attractive target molecules. In the course of these studies we have recently shown that 1 is a good synthon for the [Cp′Fe]⁺ fragment which has been successfully transferred to (POCOP)Ir pincer complexes.³⁰ In this contribution the reaction chemistry of 1 with KHBEt₃ is reported to give either [Cp′FeH₂]₂ (2) or [Cp′₂Fe₂H₃] (3) depending on the reaction conditions. Subsequent activation of white phosphorus (P₄) by [Cp′FeH₂]₂ is discussed.

Results and discussions

Iron polyhydrides

The reaction of 1 with KHBEt₃ in a pentane/THF mixture under an Ar atmosphere did not yield the expected molecule possessing “[Cp′FeH]” units, instead a mixture of two different Fe-polyhydrides was isolated and identified as the diamagnetic [Cp′FeH₂]₂ (2) and paramagnetic mixed-valent [Cp′₂Fe₂H₃] (3). The formation of these complexes was rather surprising, and spurred us on to investigate this reaction in more detail.

The ratio in which complexes 2 and 3 are formed strongly depends on the reaction conditions: Under 1 atm of Ar the mixed-valent complex 3 is obtained as the major product (in a 40 : 60 ratio of 3 : 2). However, the product distribution is inverted, when the synthesis is carried out in the presence of H₂ (1 atm), and a nearly complete formation of 2 (∼95%) may be achieved at elevated hydrogen pressures (15 atm pressure of H₂). In general, the reaction proceeds less smoothly under Ar (28% total yield) compared to reactions carried out under H₂ (52% total yield). An isolated mixture of 2 and 3 is stable under an H₂ atmosphere and the relative ratio of 2 and 3 does not change. These observations suggest that “[Cp′FeH]” is formed initially, but it is unstable and converted to 2 and 3.‡ The formation of 2 is a consequence of trapping of the reactive intermediate “[Cp′FeH]” with H₂, while 3 is formed as the major degradation product of “[Cp′FeH]” (in the absence of a suitable trap) (Scheme 1). Fig. 1 shows the linear relationship between the ratio in which complexes 2 and 3 are formed and the applied pressure of H₂. It also reflects the high efficiency with which H₂ traps the unobserved “[Cp′FeH]” intermediate. Complexes 2 and 3 can be isolated independently and are very soluble in all common organic solvents to give deep purple and deep green solutions, respectively. Solutions of both complexes are thermally stable at ambient temperature for an extended period of time, and can be exposed to vacuum without apparent degradation. Variable temperature NMR studies on 2 and 3 have been undertaken (see ESI for details†). The chemical shifts of 3 exhibit a linear temperature dependence consistent with a simple Curie-paramagnet. When heated in C₆D₆ at 65 °C, 3 shows a significantly higher thermal stability than 2, which is probably due to a relatively facile loss of H₂ from this molecule and hence generation of the unstable “CpFeH” fragment. However, this behavior might have interesting synthetic applications (vide infra).

Scheme 1 Reactivity of [Cp′FeI]₂ with KHBEt₃.

Fig. 1 Product ratio of [Cp′FeH₂]₂ and [Cp′₂Fe₂H₃] as a function of applied H₂ pressure during synthesis.

The diamagnetism of 2 facilitates characterization and reactivity studies by NMR spectroscopy, e.g. measurements of the inversion-recovery T₁ relaxation time of the Fe–H resonances (δ −21.9) at variable temperatures are consistent with the description of a classic hydride complex (0.76 ms at −98 °C, 500 MHz). The bonding in 2 is similar to that in [(C₅Me₅)RuH₂]₂ which has been analyzed by ab initio studies on the model complex [(C₅H₅)RuH₂]₂.^31,32 Slow H/D exchange occurs between D₂ and the iron hydride ligands in 2 at ambient temperature in C₆H₁₂ solvent. This exchange was fitted to a pseudo first-order kinetic and the rate constant was determined to be 3.4(4) × 10⁻⁵ s⁻¹ at 298 K which corresponds to a ΔG‡(298 K) = 23.3(2) kcal mol⁻¹ (see Experimental Section and ESI for details†). The exchange is slower than in [(C₅Me₅)FeH₂]₂,²⁰ presumably a consequence of the increased steric bulk of the Cp′ ligand, and consistent with an associative ligand exchange mechanism as proposed for [(C₅Me₅)RuH₂]₂ based on experimental³³ and computational studies.³⁴ In agreement with previous observations for [(C₅Me₅)FeH₂]₂²⁰ no aliphatic C–H bond activation of the solvent or the CMe₃-groups of the Cp′ ligand was observed. However, slow H/D exchange occurs at room temperature between deuterated aromatic solvents such as C₆D₆ and C₇D₈ and the Fe–H functionality, while the exchange is fast at 90 °C. In the case of toluene-d₈ only the less sterically hindered aromatic meta- and para-positions are activated with roughly the same rate (as judged by the amount of H incorporation). The decay of the Fe–H resonance on H/D exchange in C₇D₈ was monitored over time by ¹H NMR spectroscopy and fit to a first-order decay model. The rate constants were determined over a temperature range 62–96 °C; and the values ranged from 3.9(2) × 10⁻⁵ to 7.8(3) × 10⁻⁴ s⁻¹. The Eyring plot for this process is depicted in Fig. 2 and corresponds to ΔH‡ = 21.2(9) kcal mol⁻¹ and ΔS‡ = −17(3) eu (see ESI for details†). The negative sign and large magnitude of ΔS‡ indicate an associative exchange process.

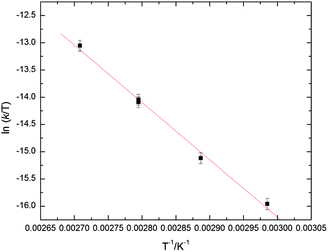Fig. 2 Eyring plot for the H/D exchange in 2 recorded in C₇D₈ (error bars shown at 95% confidence interval) yielding the estimated parameters ΔH‡ = 21.2(9) kcal mol⁻¹ and ΔS‡ = −17(3) eu.

Complex 2 acts as a slow hydrogenation catalyst for 2,2-dimethylbutene (TBE) in the presence of 1 atm of H₂ in C₆D₆ at 65 °C (7 TON after 50 h). However, this reaction is accompanied by significant catalyst degradation to give a mixture of 3 and HCp′. Under an argon atmosphere complete degradation of 2 occurs in the presence of an excess of TBE in C₆H₁₂ at 65 °C within a few hours, while no degradation is observed for 3 under these conditions. This reactivity difference allows the isolation of 3 in pure crystalline form, albeit in low yield. No conversion of 3 to 2 was observed in the presence of a H-radical source such as 9,10-dihydroanthracene. The solution magnetic moment of 2.0(2) μ_B for complex 3 is consistent with one unpaired electron (S = ½) per molecule. The bonding in 3 can be explained by the frontier orbital diagram developed for [(L₃)₂M₂H₃] complexes.^35,36

The molecular structures of 2 and 3 were determined by X-ray crystallography (Table 1) and are shown in Fig. 3 and 4. Selected bond distances and angles are given in the Figure captions. The methodology used for locating metal hydrides in Fourier density maps was previously described by Ibers and Bau.^37,38 In both cases the hydride ligands were located in the Fourier density map as peaks of the expected height and the R₁-factor dropped significantly when the hydrides were included in the least-square refinement cycles and refined isotropically (see ESI for details†). Further trust was gained by the fact that the Fe–H distance in 2 and 3 agree well with M–H bond distances determined by neutron or X-ray diffraction for related molecules.^20,39–41

Table 1 Crystallographic details for 2, 3 and 4

Compound reference	2	3	4
Chemical formula	C34H62Fe2	C34H61Fe2	C34H58Fe2P4
Formula Mass	582.54	581.53	702.38
Crystal system	Tetragonal	Triclinic	Orthorhombic
a/Å	9.0398(2)	10.2629(2)	13.3878(3)
b/Å	9.0398(2)	12.4476(3)	13.7768(3)
c/Å	40.2263(12)	14.5233(3)	19.6471(4)
α (°)	90.00	112.514(2)	90.00
β (°)	90.00	91.655(2)	90.00
γ (°)	90.00	105.741(2)	90.00
Unit cell volume/Å^3	3287.21(14)	1631.16(7)	3623.73(14)
T/K	100(2)	100(2)	100(2)
Space group	P 41212	P1̄	P 212121
No. of formula units per unit cell, Z	4	2	4
Radiation type	Cu-Kα	Mo-Kα	Mo-Kα
Absorption coefficient, μ/mm^−1	7.191	0.908	0.999
No. of reflections measured	22777	12986	51726
No. of independent reflections	3095	6865	7410
R int	0.0375	0.0389	0.0447
Final R1 values (I > 2σ(I))	0.0253	0.0459	0.0388
Final wR(F^2) values (I > 2σ(I))	0.0648	0.0930	0.0845
Final R1 values (all data)	0.0262	0.0839	0.0476
Final wR(F^2) values (all data)	0.0653	0.1076	0.0879
Goodness of fit on F^2	1.055	1.005	1.025

---

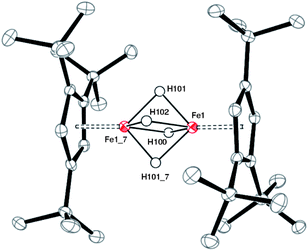Fig. 3 ORTEP diagram of 2. ‘_7’ indicate symmetry related positions. Selected bond distances (Å) and angles (deg): Cp1(cent)-Fe(1) 1.66, Fe(1)⋯Fe(1_7) 2.1989(5), Fe(1)-H(100) 1.61(3), Fe(1)-H(101) 1.57(3), Fe(1)-H(102) 1.63(3), H(100)-H(101) 1.65(4), H(101)-H(102) 1.62(4), H(102)-H(101_7) 1.62(4), H(101_7)-H(100) 1.65(4), H(100)-H(101)-H(102) 93.3, H(101)-H(102)-H(101_7) 87.9, H(102)-H(101_7)-H(100) 93.3.

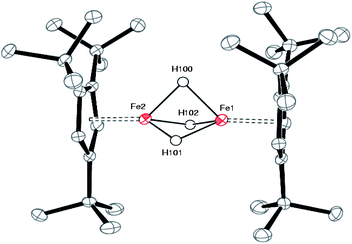Fig. 4 ORTEP diagram of 3. Selected bond distances (Å) and angles (deg): Cp1(cent)-Fe(1) 1.71, Cp2(cent)-Fe(1) 1.71, Fe(1)⋯Fe(2) 2.2205(6), Fe(1)-H(100) 1.64(4), Fe(1)-H(101) 1.54(4), Fe(1)-H(102) 1.56(4), Fe(2)-H(100) 1.66(4), Fe(2)-H(101) 1.57(4), Fe(2)-H(102) 1.49(4), H(100)-H(101) 1.87(6), H(101)-H(102) 1.94(6), H(102)-H(100) 1.96(6), H(100)-H(101)-H(102) 61.8, H(101)-H(102)-H(100) 57.4, H(102)-H(100)-H(101) 60.8.

Reactivity towards P₄

With complexes 2 and 3 in hand, we decided to explore their reactivity toward P₄. Recent studies have mainly focused on the activation of P₄ in the coordination sphere of coordinatively unsaturated metal fragments^42–52 and in the presence of organic substrates,^17–19e.g. the photochemical or thermal conversion of [Cp′Fe(CO)₂]₂ in the presence of P₄ results in a surprisingly broad range of different P_n-containing molecules by successive lose of coordinated CO, such as [{Cp′(OC)₂Fe}₂(μ-η¹:η¹-P₄)], [Cp′Fe(P₅)], [{Cp′Fe}₂(μ-η⁴:η⁴-P₄)], [{Cp′Fe}(μ-η⁴:η¹-P₄){Fe(CO)₂Cp′}], [{Cp′Fe}₂(μ-CO)(μ-η²:η²-P₂)] and [{Cp′Fe}₂(μ-P)₂].^53–55 In a more recent approach low-valent transition metallates are used for P₄ activation.^56,57 For the latest reviews on P₄ activation the reader may refer to refs. 58–60. However, with very few exceptions such as [(triphos)RhH₃]^61,62 and [(C₅Me₅)(C₅H₄tBu)ZrH₂]⁶³ reactions with transition metal hydrides and P₄ have received very little attention. This is rather surprising considering that the reaction of metal hydrides with dinitrogen is known to be a very attractive route to dinitrogen complexes with different levels of N₂ activation.^64,65 It was therefore of interest to explore the reactivity of 2 and 3 toward P₄ and to compare the results with those of [Cp′Fe(CO)₂]₂.

No reaction of 3 was observed with an excess of P₄ at 100 °C in C₇D₈, which is probably related to its inability to act as a Cp′Fe(I)-synthon and its significantly enhanced thermal stability when compared to 2. However, 2 reacts under the same conditions to a single P-containing complex 4, while H₂ is evolved accompanied by a color change from purple to dark red (Scheme 2). No new P–H or Fe–H bonds were formed as shown by ¹H and ³¹P NMR spectroscopy. This suggested that complex 2 can act as a masked Fe(I) synthon which offers interesting perspectives for further transformations.§ Dark red crystals of 4 suitable for a single crystal X-ray diffraction experiment were obtained from a saturated toluene solution at −38 °C (Table 1). Selected bond distances are given in the Figure caption (Fig. 5).

Scheme 2 Reactivity of [Cp′FeH₂]₂ with P₄.

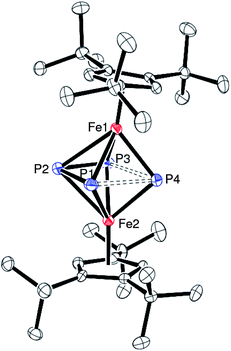Fig. 5 ORTEP diagram of 4 (thermal ellipsoids set at 50% probability). Hydrogen atoms have been omitted for clarity. Selected bond distances (Å) and angles (deg): Cp1(cent)-Fe(1) 1.71, Cp2(cent)-Fe(2) 1.71, Fe(1)-P4(cent) 1.62, Fe(2)-P4(cent) 1.62, Fe(1)-P(1) 2.3167(9), Fe(1)-P(2) 2.4526(10), Fe(1)-P(3) 2.2829(9), Fe(1)-P(4) 2.1913(10), Fe(2)-P(1) 2.2889(9), Fe(2)-P(2) 2.4526(10), Fe(2)-P(3) 2.3201(9), Fe(2)-P(4) 2.1893(10), P(1)-P(2) 2.12311(13), P(2)-P(3) 2.1371(13), P(3)-P(4) 2.5322(12), P(1)-P(4) 2.5314(12), Fe(1)⋯Fe(2) 3.1822(6), Cp1(cent)-Fe(1)-P4(cent) 172.96, Cp2(cent)-Fe(2)-P4(cent) 172.45, Fe(1)-P4(cent)-Fe(2) 157.3.

The ³¹P{¹H} NMR data of 4 confirmed the formation of an A₂MX-spin system (P_A = P(1),P(3); P_M = P(2); P_X = P(4)). The P_A nucleus appears as a doublet of doublets at δ 625.5 (¹J_AM = 380 Hz, ¹J_AX = 126 Hz). The small P_A-P_X coupling constant of ¹J_PP = 126 Hz reflects the long distances between the atoms P_A and P_X observed in the crystal structure. The P_X and P_M resonances are both split into a doublet of triplets and reveal remarkable high-field shifts at δ −163.1 and δ −336.5, respectively (see ESI for details†). The crystal structure of 4 reveals a planar cyclo-P₄ unit capped by two Cp′Fe moieties (Fe⋯Fe distance: 3.1822(6) Å) However, the P₄-unit shows a significant kite-like distortion, and consequently two short 2.13 Å and two long P–P distances (2.53 Å) are observed. The longer distances are intermediate between a P–P bond and a van-der-Waals contact.^66,67 In combination with the very small ¹J_AX coupling constant of 126 Hz the P–P bonding appears to be weak. Interestingly, the isoelectronic [{(C₅H₄CMe₃)Co}₂(μ₂-η⁴-As₄)]²⁺ complex shows a nearly square planar cyclo-As₄ ring.⁶⁸ However, complexes with cyclo-P₄ do exist, and show different degrees of distortion, e.g. a rather small distortion was observed for mononuclear complexes of the second- and third-row transition metals such as (C₅Me₅)M(CO)₂(η-P₄) (M = Nb⁶⁹ and Ta⁷⁰), whereas a severe kite-like distortion was reported for the trimetallic Co-cluster [Cp′′Co(P₄){(Cp′′Co)₂(μ-CO)}] (Cp′′ = 1,3-(Me₃C)₂C₅H₃). Conversely, multi-decker complexes with a cyclo-P₄ middle deck have been elusive.^45,58–60 This is rather surprising considering that Tremel and Hoffmann predicted the existence of triple-decker complexes with μ-cyclo-P₄ middle deck based on frontier orbital argument more than 20 years ago,⁷¹ and showed that the 30/34 electron rule is of special importance for the stability of triple-decker complexes in general.⁷² However, the combined constraints of M–P distance, P–P contacts in the bridge, and M–M separation leaves only a small “window” for possible structures. Cyclo-P₄²⁻ can bridge two uranium fragments in μ₂:η⁴:η⁴-fashion (see (μ₂:η⁴:η⁴-P₄)[U(N[tBu]Ar)₃]₂)⁷³ and μ₂:η²:η²-fashion (see [U(C₅Me₅)(C₈H₆(SiiPr₃)₂−1,4)]₂(μ₂:η²:η²-P₄)),⁷⁴ and Fryzuk and co-workers described an inverse Zr sandwich complex with a formal cyclo-P₄⁴⁻ unit.⁵⁰ Recently, a novel binding mode for cyclo-E₄²⁻ (E = P₄, As₄, AsP₃) has been reported in which it forms terminal E₄-decks bridging two Cr-centers.⁷⁵ However, it was suggested that a kite-like distortion of the cyclo-P₄ might point to a reaction pathway of the tetrahedral P₄ in the coordination sphere of transition metal complexes with an odd number of valence electrons. The first step includes the cleavage of two P–P bonds to give a square-planar cyclo-P₄ unit followed by a kite-like distortion, and finally disproportionation into P₁ and cyclo-P₃ complexes.^44,48 Hence, 4 might be regarded as a “snapshot” of such a disproportionation process.

However, 4 is also an isomer to the long-known [{Cp′Fe}₂(μ-η⁴:η⁴-P₄)] (5). Complex 5 contains a cis-tetraphosphabutadiene moiety (isolobal to the cis-butadiendiyl-fragment) sandwiched by the two Cp′Fe-fragments (Fe⋯Fe distance: 2.6430(8) Å) and should therefore only be considered as a pseudo-triple-decker.⁵³ In addition, dynamic ³¹P{¹H} NMR studies for 5 and [{Cp′′′Fe}₂(μ-η⁴:η⁴-P₄)] revealed that the P-atoms of the cis-tetraphosphabutadiene chain undergo rapid exchange on the NMR time scale at ambient temperature. Therefore only one broad resonance is observed for the AA‘XX’-spin system in 5 (294 K: ν_1/2 = 910 Hz). This interchange process of the different P-atoms in the less-substituted derivative [{Cp′′Fe}₂(μ-η⁴:η⁴-P₄)] can be frozen out at 185 K, whereas 5 shows fast exchange on the NMR time scale at this temperature.^53,54 One possible transition state accounting for this exchange process is the 30VE-triple-decker complex with a cyclo-P₄ middle-deck (closo-octaeder), and this makes isolation and characterization of 4 even more remarkable.

It was therefore of interest to establish the relationship between the two isomers 4 and 5, and also to probe the ability of 4 to act as source for “P₁”/“P₃” fragments. Complex 5 was prepared from [Cp′Fe(CO)₂]₂ and P₄ under rather harsh reaction conditions, i.e. thermolysis at 190 °C for 3 h, and [Cp′Fe(η⁵-P₅)] was also formed as a side-product. In contrast the synthesis of 4 is accomplished under relatively mild conditions (100 °C, 10 min) and obtained as sole P-containing product. Consequently, the thermal stability of 4 was investigated. Complex 4 is stable in solution at ambient temperature for at least a week. However, the thermal behavior of 4 in C₇D₈ solution is very informative. After heating a C₇D₈ solution of 4 for 7 days at 75 °C the ³¹P{¹H} NMR spectrum shows a complete conversion of 4 into 5, [{Cp′Fe}₂(μ-η³:η³-P₃)] and [Cp′Fe(η⁵-P₅)] in an approximate ratio of 12 : 2 : 1 (Scheme 3).¶ The phosphaallyl complex [{Cp′Fe}₂(μ-η³:η³-P₃)] was identified by ³¹P{¹H} and ¹H NMR spectroscopy, and it was previously reported as a side-product in the reaction of [{Cp′(OC)₂Fe}₂(μ-η¹:η¹-P₄)] with tBuC≡P.⁷⁶ The phosphaallyl [η³-P₃] moiety displays an AA′X spin system with a large chemical shift difference between the two resonances P_A,A′ (δ 677.8) and P_X (δ −380.9). These chemical shifts are very similar to the A₂M part of the A₂MX spin system of 4 (P_A: δ 625.5, P_M: δ −336.5) supporting the earlier contention that the bonding between the A₂M and X part in 4 is extremely weak, and it might be more appropriately described as cyclo-P₄²⁻ consisting of an allylic-like μ-[P₃]⁻ anion coordinated to a μ-[P]⁻ anion. However, the major degradation pathway of 4 is the formation of 5 (80%), but the elimination of a P₁-fragment is also feasible as demonstrated by the formation of [{Cp′Fe}₂(μ-η³:η³-P₃)] and [Cp′Fe(η⁵-P₅)]. The addition of a P₁-fragment to 5 would formally give the paramagnetic, 31VE triple-decker complex [{Cp′Fe}₂(μ-η⁵:η⁵-P₅)] with a cyclo-P₅ middle deck, but this species was not detected by ¹H or ³¹P NMR spectroscopy. Interestingly, isolated 5 can be converted to [Cp′Fe(η⁵-P₅)] in the presence of excess P₄ at 190 °C.⁵⁴ This observation might point to an inherent instability of [{Cp′Fe}₂(μ-η⁵:η⁵-P₅)]. In conclusion, this study provides experimental evidence for the original proposal that the kite-like distorted cyclo-P₄ precedes the formation of P₁- and P₃-fragments, but also yields a cis-tetraphosphabutadiene system.

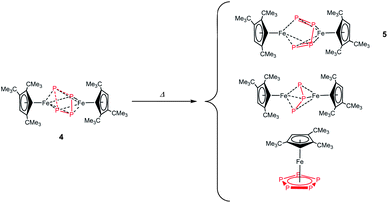Scheme 3 Thermal degradation of 4.

Computational studies

Density functional theory (DFT) calculations in combination with experimental data have become a valuable combination of tools in organometallic chemistry since DFT accounts, in part, for electron correlation effects. Especially for large molecular systems and clusters of low symmetry, the low computational expense in comparison with post-Hartree–Fock methods makes DFT nearly always the only choice when it comes to electronic structure calculations of such complex systems. However, given the fact that the exact functional of the electron density is not known and only approximate expressions are at hand, an exhaustive evaluation of different Density Functionals (DFs) is a prerequisite for computational chemistry studies. Concerning our phosphorus compounds, this is of particular importance: It is known that the potential energy surfaces (PES) involving P₄ are very flat and minute changes in the nature of the surrounding metal fragments —and hence in the nature of the describing DF— can modify the structure of the P₄ unit, which is due to the low lying P–P σ*-orbitals, the number of lone pairs and the ability of phosphorus to assume a large variety of different coordination modes.⁴⁷ We evaluated several DFs with the focus on optimizing the complex geometries and on comparing these results to the available X-ray crystallographic data of 2, 3, 4 and 5. Surprisingly, most of the modern hybrid and hybrid meta DFs such as B3PW91, M05, M052x and M06 did not reproduce the kite-like distortion of the central cyclo-P₄ unit in 4; instead a triple-decker complex with an aromatic, square-planar cyclo-P₄ bridge was also predicted to be thermodynamically more stable than 5. The reason for this inconsistency might be twofold: 1) pronounced packing effects in the solid state, and/or 2) uncertainties and several, in part diametrical, intrinsic problems of the modern DFs. The molecular systems 4 and 5 for example comprise a variety of physical phenomena which until today present test cases for modern computational chemistry methods: steric effects (that means long range dispersion), delocalization vs. localization (that means dynamic correlation) and state mixing (that means static correlation). Several DFT functionals have been employed to rationalize (transition) metal mediated P₄ activation and explain the bonding in P_n-fragment containing complexes.^{48,74,76–80} The best agreement between experimental and calculated structures have been achieved with the dispersion-corrected B97 functional, B97D⁸¹ in combination with the 6-311G(d,p) basis set. Selected experimental and calculated bond angles and distances are compared in Table 2.

Table 2 Calculated vs. experimental bond distances (Å) and angles (deg).

	[2] (exp)	[2] (calc)	[3] (exp)	[3] (calc)	[4] (exp)	[4] (calc)	[4′] (calc)	[5] (exp)	[5] (calc)
Cp1(cent)-Fe1	1.66	1.61	1.71	1.67	1.71	1.65	1.68	1.74	1.71
Cp2(cent)-Fe2	1.66	1.61	1.71	1.67	1.71	1.65	1.68	1.74	1.71
Fe1⋯Fe2	2.1989	2.162	2.2005	2.219	3.1822	3.335	3.266	2.6430	2.568
Fe1–H1	1.61(3)	1.67	1.64(4)	1.65
Fe2–H1	1.61(3)	1.66	1.66(4)	1.65
Fe1–H2	1.57(3)	1.66	1.54(4)	1.66
Fe2–H2	1.57(3)	1.66	1.57(4)	1.64
Fe1–H3	1.63(3)	1.64	1.56(4)	1.66
Fe2–H3	1.63(3)	1.67	1.49(4)	1.65
Fe1–H4	1.61(3)	1.65
Fe2–H4	1.61(3)	1.65
Fe1- P1					2.3167	2.331	2.343	2.2649	2.256
Fe2–P1					2.2889	2.296	2.328	2.2678	2.254
Fe1–P2					2.4526	2.484	2.497	2.3337	2.317
Fe2–P2					2.4526	2.484	2.491	2.3346	2.337
Fe1–P3					2.2829	2.296	2.323	2.3337	2.337
Fe2–P3					2.3201	2.331	2.344	2.3346	2.317
Fe1–P4					2.1913	2.212	2.212	2.2649	2.254
Fe2–P4					2.1893	2.212	2.209	2.2678	2.256
H1⋯H2	1.65(4)	1.77	1.87(6)	2.08
H2⋯H3	1.62(4)	1.77	1.94(6)	2.13
H3⋯H4	1.62(4)	1.77	1.96(6)	2.15
H4⋯H1	1.65(4)	1.77
P1–P2					2.1311	2.188	2.131	2.0877	2.112
P2–P3					2.1371	2.188	2.137	2.368	2.391
P3–P4					2.5322	2.369	2.532	2.0877	2.112
P4–P1					2.5314	2.369	2.531	3.555	3.570
H1-H2-H3	93.3	90.1	61.8	61.3
H2-H3-H4	87.9	90.1	57.4	58.4
H3-H4-H1	93.3	89.8	60.8	60.3

---

However, before discussing the results concerning the P₄ activation product in detail, the iron hydride complexes 2 and 3 were investigated. Experimental and computational geometries are in good agreement (Table 2). As suggested above 2 and 3 are most likely derived from a “[Cp′FeH]” intermediate that could not be isolated, but trapped H₂ to give 2 in good yields. DFT calculations were undertaken to predict a possible structure for the intermediate [Cp′FeH]₂ assuming a diamagnetic ground state (S = 0). Addition of H₂ or H• to [Cp′FeH]₂ is exergonic with ΔG(298 K) = −22.4 and −62.3 kcal mol⁻¹ to give 2 and 3, respectively. This explains the intrinsic instability of [Cp′FeH]₂ with respect to the formation of 2 and 3, but also the enhanced thermal stability of 3 compared to 2. Complex 2 undergoes H/D exchange presumably via an associative reaction mechanism, and the calculated structure of the proposed reaction intermediate [Cp′Fe(H)(η²-H₂)]₂ is shown in Fig. 6. [Cp′FeH(H₂)]₂ lies about 21.8 kcal mol⁻¹ higher in energy than 2, and therefore it is in reasonable agreement with the experimental data.

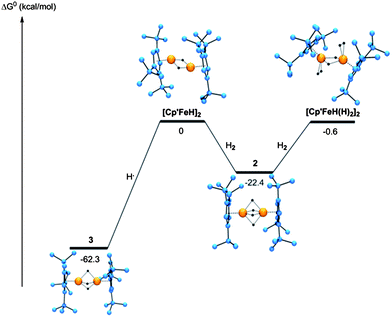Fig. 6 Gibbs Free Enthalpy of Iron Hydride Species.

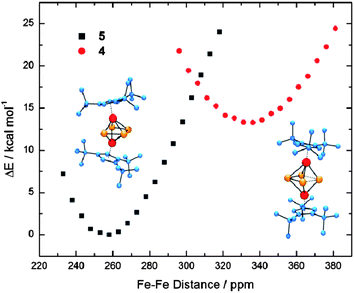Fig. 7 PES Scan along the Fe–Fe coordinate of 4 and 5.

B97D also reproduces the kite-like distortion of the central cylclo-P₄ middle deck and predicts isomer 5 to be more stable than 4 by 10.4 kcal mol⁻¹ (free enthalpy) or 12.6 kcal mol⁻¹ (electronic energy). However, the distortion is less pronounced than observed in solid state.|| Freezing the experimentally observed pronounced kite-like distortion of the cyclo-P₄ middle-deck in the DFT it increases the electronic energy of 4′ relative to 4 by ca. 4.1 kcal/mol. A PES scan along the Fe⋯Fe reaction coordinate for 4 and 5 shows how flat the potential energy surface actually is in the proximity of the calculated minima structures (Fig. 8). Unfortunately, every attempt to locate the transition state between complexes 4 and 5 has been unsuccessful so far.

We also addressed the question if the distortion of the cyclo-P₄ unit is a consequence of the steric demand of the Cp′ ligand. Maybe surprisingly, replacing the Cp′ ligand against C₅H₅ has no effect on the kite-like distortion, but the thermodynamic isomer 5a is significantly stabilized compared to 4a by 15.1 kcal mol⁻¹ (see ESI for details†). We therefore conclude that the kite-like distortion is not a consequence of crystal packing and dispersion effects, but an intrinsic phenomenon for this system.

The long P–P bond distance and the small ¹J_PP coupling constant in the cyclo-P₄ unit in 4 raise the question: How strong are the bonds within the cyclo-P₄ unit or is it more appropriate to describe the distorted cyclo-P₄ middle-deck as a P₁/P₃ moiety? In this context, local bond lengths in complex molecular systems are not necessarily good bond strength descriptors, since secondary interactions may lead to compressed (but weak; see the Ga–Ga discussion⁸²) or elongated (because they are weak; see molecular recognition⁸³) local bonds. Relaxed force constants can answer this type of question by measuring force due to a unit displacement, while all other coordinates are allowed to relax providing unique information about the intrinsic elasticity of bonds.⁸⁴ There are more and more examples in the literature, where the significance of mechanical properties indeed helped to unravel otherwise quite obscure bonding situations.^85–87Inter alia, different types of PP bonds have recently been evaluated by this method applying the DFT and coupled cluster methods. These studies have shown that relaxed force constants for P(III)-P(III) bonds correlate almost linearly to the formal P–P bond order. Furthermore, PP bonds are highly elastic, and can easily be deformed by inter- and intramolecular forces.^88,89 Due to these calculations, the mechanical strength of a typical 2-electron P–P single bond is ∼1.5 N cm⁻¹ while the value for a 4-electron P=P double bond averages out at ∼3.3 N cm⁻¹. Therefore, we expected the value for an aromatic P–P bond to be between 2.1 and 2.4 N cm⁻¹. Interestingly, our calculated P–P relaxed force constant for the isolated D_4h symmetric P₄²⁻ of just 1.50 N cm⁻¹ (B97D/6-311G(d,p)) points to four equal P–P single bonds with no double bond character and therefore no π-contribution. This interpretation is supported by the positive sign of our computed compliance coupling constant between each germinal P–P bonds. Indeed, earlier computational analysis of the bonding in P₅⁻ and P₄²⁻ has clearly shown that the charge is mainly localized via the P lone pairs, and therefore the term “lone-pair aromaticity” was suggested.^90–92 This clearly demonstrates that care has to been taken when the well-established concept of (Hückel) aromaticity in classic hydrocarbons such as benzene, cyclopentadiene anion, C₅H₅⁻, or the cyclobutadiene diananion, C₄H₄²⁻,⁹³ is applied to inorganic compounds of main group elements. Consequently, not only the π-orbitals but also the eight in-plane σ-orbitals of the cyclo-P₄ unit, four radial and four tangential ones, need to be considered in the interaction with the two CpFe fragments (vide infra).

Turning to the bonding situation in complex 4 the P–P interaction seems to become even softer compared to isolated cyclo-P₄²⁻: the kite-like distortion is accompanied by a pronounced weakening of the P–P bonds: The relaxed force constant values of 1.16 N cm⁻¹ (short contact) and only 0.88 N cm⁻¹ (long contact; both are the B97D/6-311G(d,p) values) illuminate the reason for the discrepancies between theory (gas phase) and experiment in terms of P–P distances: the exceptional softness of the P–P potential in 4. In addition, we preclude any pronounced Fe⋯Fe covalency or coupling in 4: the relaxed force constant of 0.80 N cm⁻¹ is far from the value for a typical Fe–Fe two electron bond in, for example, Fe₂(CO)₉ (2.30 N cm⁻¹,⁹⁴). In contrast, the Fe–Fe contact in isomer 5 is characterized by a pronounced coupling: the relaxed force constants of 1.51 N cm⁻¹ is in line with a molecular orbital analysis. To simplify the bonding discussion in 4 and 5 the Cp′ ligand was replaced by C₅H₅ and C_2v symmetry was imposed on both molecules. These two model complexes 4′′ and 5′′ have very different Fe–Fe distances of 3.271 and 2.514 Å, respectively. Increasing the Fe–Fe distance (and decreasing the P–P distance) turns on a significant P–P repulsion. Consequently, two different orbitals react very sensitive to the variations of the Fe–Fe distance, that is the Fe–Fe σ*-orbital (b₂) and the P–P σ*-orbitals (b₁). The relevant Kohn–Sham orbitals are shown in Fig. 8. While the antibonding σ*-orbital is occupied in 4′′ (HOMO-2), it is unoccupied in 5′′ (LUMO) which is consistent with the relaxed force constant analysis. The driving force for the conversion of 4′′ to 5′′ may be traced to the formation of an Fe–Fe bond. Furthermore, the HOMO of 4′′ also suggests that the lone pairs at P will be accessible to electrophiles.

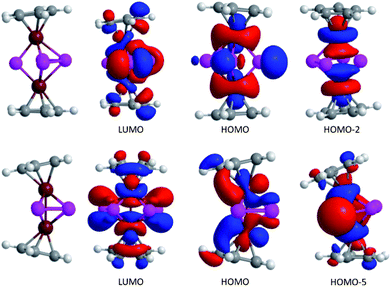Fig. 8 Selected Kohn–Sham orbitals for 4′′ and 5′′.

Conclusions

Iron hydride complexes 2 and 3 were generated on salt metathesis of 1 with KHBEt₃. Interestingly, the product distribution of 2 and 3 is directly proportional to the applied pressure of H₂ during synthesis, suggesting that H₂ is a highly efficient trap for the “[Cp′FeH]”-intermediate. The diamagnetic tetrahydride complex 2 is an excellent Cp′Fe(I)-synthon, and reacts smoothly with P₄ to triple-decker complex 5, in which the two Cp′Fe-fragments are bridged by a severe kite-like distorted [cyclo-P₄] unit. This distortion persists in solution and solid state, however, on prolonged heating 4 converts to the well-known pseudo-triple-decker complex 5 in which the Cp′Fe-units are bridged by a cis-tetraphosabutadiendiyl chain, but also to [{Cp′Fe}₂(μ-η³:η³-P₃)] and [Cp′Fe(η⁵-P₅)]. This established 4 as intermediate in the thermodynamically favored formation of 5, and as a precursor for delivery P₁-fragments. Due to our computations, the interatomic forces within the P₄ moiety are weak and comparable to other P–P two-electron sigma bonds (in the case of isolated P₄) or electron deficient clusters, leading to facile distortions of the quadratic planer D_4h geometry in 4 and 5 without a pronounced energy penalty. The term “aromaticity” might be overstressed in this case, and we predict that the distortion (kite-like or butadiene-like) of the P₄ fragment in triple-decker systems will be observed more frequently in the future. While any coupling in the metastable isomer 4 can be excluded, a considerably Fe–Fe interaction in 5 is observed, leading to a pronounced stabilization of this very isomer.

In summary, the Cp-fragment has once again shown that it allows for much more than only ferrocene formation. These initial studies also suggest that this ligand set might exhibit complementary reactivity patterns to the trisphosphinoborato and β-diketiminato ligands. Therefore we are currently actively pursuing the synthesis of other synthetically attractive target functionalities for low-coordinate Cp′Fe-half-sandwich complexes. Further investigations regarding the reaction chemistry and electronic structure of the molecules presented here, are subject of ongoing work and will be reported in due course. In addition the reactivity of the complex 5 towards electrophiles with the aim to functionalize P₄ in the iron coordination sphere will be evaluated.

Experimental section

General comments

All reactions and product manipulations were carried out under an atmosphere of dry, oxygen free argon using standard high-vacuum, Schlenk, or drybox techniques. Argon was purified by passage through BASF R3-11 catalyst (Chemalog) and 4 Å molecular sieves. Dry, oxygen-free solvents were employed throughout. NMR spectra were recorded on a Bruker DRX 500 MHz, a Bruker DRX 400 MHz, or a Bruker 400 MHz AVANCE spectrometer. All chemical shifts are reported in δ units with reference to the residual protons of the deuterated solvents, which are internal standards, for proton chemical shifts. The elemental analyses were performed by the analytical facilities at the University of California at Berkeley or by Robertson Microlit Laboratories of Madison, NJ.

Materials

All solvents were deoxygenated and dried by passage over columns of activated alumina.^95,96 Tetrahydrofuran dried over sodium/benzophenone and freshly distilled prior to use. Deuterated solvents, C₆D₆, C₇D₈, cyclohexane-d₁₂ and methylcyclohexane-d₁₄, were purchased from Cambridge Laboratories, Inc., dried over sodium metal, vacuum transferred to a Teflon sealable Schlenk flask containing 4 Å molecular sieves, and degassed via three freeze-pump-thaw cycles.

KHBEt₃ (1M in THF) was purchased from Aldrich and used as received. [Cp′FeI]₂ was prepared according to ref. 30. White phosphorus (P₄) was crystallized from toluene prior to use.

Synthesis

[Cp′FeH₂]₂ (2). A pentane solution (20 mL) of [Cp′FeI]₂ (0.42 g, 0.5 mmol) was transferred into a Fisher-Porter bottle equipped with a stirring bar. The pentane solution of [Cp′FeI]₂ was frozen in liquid N₂ while purging with high purity H₂. The potassium superhydride KHBEt₃ (1M in THF, 1 mL, 1 mmol) was added to the frozen pentane solution while cooling the Fisher-Porter bottle at 77 K. The frozen reaction mixture was exposed to 4 atm of H₂ at 77 K and the reaction vessel was sealed. The liquid nitrogen cooling bath was removed and the reaction mixture was allowed to warm slowly to room temperature. During this time the color changed from dark red to purple. (Caution: The reaction had to be performed with appropriate safety precautions, i.e. behind an additional safety shield and in a well-vented fume hood.) After ca. 30 min the H₂ pressure was carefully released and the purple reaction mixture was transferred via cannula into a Schlenk tube. The solvent was removed under dynamic vacuum and the residue was extracted with pentane. The pentane extracts were concentrated to a minimum amount of pentane and cooled to −40 °C. Dark purple crystals of 5 formed within a few days (0.15 g, 0.26 mmol, 52%). M. p. 154–156 °C (dec). The ¹H NMR spectrum revealed the purity of 2 and only small amounts of [Cp′₂Fe₂H₃] (3) (ca. 5%) were present (Fig. 7). ¹H NMR (C₆D₁₂, RT, 400 MHz): δ 3.92 (4H, ring-CH), 1.44 (36H, CMe₃), 1.29 (18H, CMe₃), −22.10 (4H, Fe–H). ¹³C{¹H} NMR (C₆D₁₂, RT, 100.6 MHz): δ 99.8 (1C, ring-C(CMe₃), 99.0 (2C, ring-C(CMe₃), 67.8 (2C, ring-CH), 34.7 (6C, CMe₃), 32.1 (3C, CMe₃), 31.6 (2C, CMe₃), 29.8 (1C, CMe₃). Anal. calcd. for C₃₄H₆₂Fe₂: C, 70.1; H, 10.73. Found: C, 69.9; H, 10.68.

[Cp′₂Fe₂H₃] (3). To a solution of [Cp′FeI]₂ (0.42 g, 0.5 mmol) in pentane (20 mL) potassium superhydride, KHBEt₃ (1M in THF, 1 mL, 1 mmol), was added under an argon atmosphere at ambient temperature. On addition the color changed immediately from red to purple, and then red-brown. The solvent was removed under dynamic vacuum and the residue extracted with pentane. The pentane extracts were filtered, concentrated to a minimum amount of pentane and cooled to −40 °C. Dark crystals formed which contained 2 and 3 in a ratio of 40 : 60 (see ESI for details†) (0.08 g, 28%). These crystals were dissolved in hexane (15 mL) and t-butylethylene (TBE) (2 mL) was added. This mixture was heated to 60 °C for 6 h, and the color changed from purple to olive green. The solvent was removed and the slightly oily residue was extracted with a minimum amount of pentane (ca. 1 mL). Cooling of the pentane extracts to −38 °C yielded green plate like crystals of [Cp′₂Fe₂H₃] in low yield (0.03 g, 0.052 mmol, 10%). ¹H NMR spectrum revealed the purity of 3 (see ESI for details†). ¹H NMR (C₆D₆, RT, 400 MHz): δ 32.9 (2H, ν_1/2∼ 350 Hz), −8.0 (18 H, ν_1/2 = 53 Hz), −9.9 (9 H, ν_1/2 = 53Hz). Anal. calcd. for C₃₄H₆₁Fe₂: C, 70.2; H, 10.57. Found: C, 70.1; H, 10.63.

[{Cp′Fe}₂(μ-P₄)] (4). [Cp′FeH₂]₂ (0.1 g, 0.17 mmol) was added to P₄ (0.05 mg, 0.4 mmol) in a Kontes flask equipped with a stirring bar, followed by toluene (10 mL) to form a purple solution. The purple solution was heated to 100 °C for 10 min, the color changed from purple to red and H₂ evolved. The reaction mixture was filtered, concentrated and cooled to −38 °C to yield dark red crystals (0.08 g, 0.11 mmol, 67%). The same reaction was also performed as an NMR experiment, which confirmed the quantitative conversion of [Cp′FeH₂]₂ to form H₂ and a single phosphorus containing complex. ¹H NMR (C₆D₆, RT, 500.13 MHz): δ 3.93 (4H, ring-CH), 1.37 (36H, CMe₃), 1.32 (18H, CMe₃). ¹³C{¹H} NMR (C₆D₆, RT, 125.77 MHz): δ 107.8 (1C, ring-C(CMe₃), 105.1 (2C, ring-C(CMe₃), 76.0 (2C, ring-CH), 34.1 (6C, CMe₃), 33.6 (2C, CMe₃), 32.0 (1C, CMe₃), 31.7 (3C, CMe₃). ³¹P{¹H} NMR (C₆D₆, RT, 202.45 MHz): δ 625.6 (2P, dd, ¹J_AM = 380 Hz, ¹J_AX = 126 Hz, P_A), −163.1 (1P, dt, ¹J_AX = 126 Hz, ²J_MX = 26 Hz, P_X), −336.5 (1P, dt, ¹J_MX = 380 Hz, ²J_MX = 26 Hz, P_M),. Anal. calcd. for C₃₄H₅₈Fe₂P₄: C, 58.1; H, 8.32. Found: C, 57.9; H, 8.49.

H/D exchange reaction of [Cp′FeH₂]₂ (2) with D₂. [Cp′FeH₂]₂ (15 mg) was dissolved in C₆D₁₂ (0.5 mL) and transferred into a J-Yang NMR tube. The tube was sealed and frozen in liquid N₂. The headspace evacuated and backfilled with D₂ (1 atm). The NMR tube was allowed to slowly warm to ambient temperature and shaken. The ¹H NMR was recorded at room temperature. To ensure proper mixing between the headspace and the C₆D₁₂ solution, the NMR sample was rotated during the exchange experiment. The decay of the Fe–H resonance (corrected against an internal standard) was monitored over a period of 2.5 half-lives by ¹H NMR spectroscopy, and fit to the (pseudo) first-order rate equation I(t)=Ae^−kt + b.

H/D exchange reaction of [Cp′FeH₂]₂ (2) with C₇D₈. [Cp′FeH₂]₂ (15 mg) and C₇D₈ (0.5 mL) were charged in a J-Yang NMR tube. The tube was sealed and inserted in prewarmed NMR probe. The temperature of the probe was verified using an ethylene glycol NMR thermometer before each run. Four- or eight-scan ¹H NMR spectra were collected over a period of 2.5–3 half-lives. The integral of the hydride resonance of 2 (corrected against an internal standard) as a function of time was fit to the (pseudo) first-order rate equation I(t) = Ae^−kt + b. Two runs were performed at each temperature and the error bars presented are at the 95% confidence level. The Eyring fit was performed using the error-weighted least squares regression.

Computational methods

All calculations employed the long-range dispersion-corrected Grimme's functional (B97D).⁸¹ The calculations were carried out with Gaussian 09⁹⁷ and no symmetry restrictions imposed (C₁). C, H, P and Fe were represented by an all-electron 6-311G(d,p) basis set. The nature of the extrema (minima) was established with analytical frequencies calculations. The zero point vibration energy (ZPE) and entropic contributions were estimated within the harmonic potential approximation. The Gibbs free energy, ΔG, was calculated for T = 298.15 K and 1 atm. Geometrical parameters were reported within an accuracy of 10⁻³ Å and 10⁻¹ degrees.

Acknowledgements

We thank the Alexander-von Humboldt Foundation for a Feodor-Lynen Fellowship (MDW), Prof. Maurice Brookhart for providing financial support (through NSF grant CHE-0615704) and laboratory facilities (MDW) during the initial phase of this research program, and Prof. Helmut Sitzmann, Prof. Richard A. Andersen and Prof. Odile Eisenstein for very helpful discussions. MDW gratefully acknowledges the current financial support by Deutsche Forschungsgemeinschaft (DFG) through the Emmy-Noether program (WA 2513/2-1).

References

1. J. C. Peters and M. P. Mehn, in Activation of Small Molecules, ed. W. B. Tolman, Wiley-VCH, Weinheim, 2006, pp. 81–120.
2. P. L. Holland, Acc. Chem. Res., 2008, 41, 905–914.
3. M. P. Hendrich, W. Gunderson, R. K. Behan, M. T. Green, M. P. Mehn, T. A. Betley, C. C. Lu and J. C. Peters, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 17107 , and references cited therein.
4. C. Vogel, F. W. Heinemann, J. Sutter, C. Anthon and K. Meyer, Angew. Chem., Int. Ed., 2008, 47, 2681–2684.
5. J. J. Scepaniak, M. D. Fulton, R. P. Bontchev, E. N. Duesler, M. L. Kirk and J. M. Smith, J. Am. Chem. Soc., 2008, 130, 10515–10517.
6. J. J. Scepaniak, J. A. Young, R. P. Bontchev and J. M. Smith, Angew. Chem., Int. Ed., 2009, 48, 3158–3160.
7. J. J. Scepaniak, C. S. Vogel, M. M. Khusniyarov, F. W. Heinemann, K. Meyer and J. M. Smith, Science, 2011, 331, 1049–1052.
8. J. J. Scepaniak, T. D. Harris, C. S. Vogel, J. Sutter, K. Meyer and J. M. SMith, J. Am. Chem. Soc., 2011, 133, 3824–3827.
9. I. Nieto, F. Ding, R. P. Bontchev, H. Wang and J. M. Smith, J. Am. Chem. Soc., 2008, 130, 2716–2717.
10. F. A. Jové, C. Pariya, M. Scoblete, G. P. A. Yap and K. H. Theopold, Chem.–Eur. J., 2011, 17, 1310–1318.
11. H. Sitzmann, T. Dezember, W. Kaim, F. Baumann, D. Stalke, J. Kärcher, E. Dormann, H. Winter, C. Wachter and M. Kelemen, Angew. Chem., Int. Ed. Engl., 1996, 35, 2872.
12. M. Wallasch, G. Wolmershäuser and H. Sitzmann, Angew. Chem., 2005, 117, 2653.
13. M. W. Wallasch, F. Rudolphi, G. Wolmershäuser and H. Sitzmann, Z. Naturforsch. B, 2009, 64, 11–17.
14. M. W. Wallasch, G. Vollmer, A. Kafiyatullina, G. Wolmershäuser, P. G. Jones, M. Mang, W. Meyer and H. Sitzmann, Z. Naturforsch. B, 2009, 64, 18–24.
15. M. W. Wallasch, D. Weismann, C. Riehn, S. Ambrus, G. Wolmershäuser, A. Lagutschenkov, G. Niedner-Schatteburg and H. Sitzmann, Organometallics, 2010, 29, 806–813.
16. D. Weismann, Y. Sun, Y. Lan, G. Wolmershäuser, A. K. Powell and H. Sitzmann, Chem.–Eur. J., 2011, 17, 4700–4704.
17. M. Perruzini, L. Gonsalvi and A. Romerosa, Chem. Soc. Rev., 2005, 34, 1038–1047.
18. M. Peruzzini, R. R. Abdreimova, Y. Budnikova, A. Romerosa, O. J. Scherer and H. Sitzmann, J. Organomet. Chem., 2004, 689, 4319–4331.
19. B. M. Cossairt and C. C. Cummins, Angew. Chem., Int. Ed., 2008, 47, 8863–8866.
20. Y. Ohki and H. Suzuki, Angew. Chem., Int. Ed., 2000, 39, 3120–3122.
21. M. A. Peldo, A. M. Beatty and T. P. Fehlner, Organometallics, 2003, 22, 3698–3702.
22. M. A. Peldo, A. M. Beatty and T. P. Fehlner, Organometallics, 2002, 21, 2821–2823.
23. Y. Ohki, T. Kojima, M. Oshima and H. Suzuki, Organometallics, 2001, 20, 2654–2656.
24. H. Sitzmann, Coord. Chem. Rev., 2001, 214, 287–327.
25. G. F. Zi, L. Jia, E. L. Werkema, M. D. Walter, J. P. Gottfriedsen and R. A. Andersen, Organometallics, 2005, 24, 4251–4264.
26. F. Jaroschik, F. Nief and L. Ricard, Chem. Commun., 2006, 426–428.
27. E. L. Werkema, E. Messines, L. Perrin, L. Maron, O. Eisenstein and R. A. Andersen, J. Am. Chem. Soc., 2005, 127, 7781–7795.
28. M. D. Walter, F. Weber, G. Wolmershäuser and H. Sitzmann, Angew. Chem., Int. Ed., 2006, 45, 1903–1905.
29. M. D. Walter, D. Bentz, F. Weber, O. Schmitt, G. Wolmershäuser and H. Sitzmann, New J. Chem., 2007, 31, 305–318.
30. M. D. Walter and P. S. White, New J. Chem., 2011 10.1039/c1nj20399a.
31. N. Koga and K. Morokuma, J. Mol. Struct., 1993, 300, 181–189.
32. M.-H. Baik, R. A. Friesner and G. Parkin, Polyhedron, 2004, 23, 2879–2900.
33. H. Suzuki, H. Omori, D. H. Lee, N. Yoshida, M. Fukushima, M. Tanaka and Y. Moro-oka, Organometallics, 1994, 13, 1129–1146.
34. S. Tussupbayev and S. F. Vyboishchikov, Organometallics, 2007, 26, 56–64.
35. A. Dedieu, T. A. Albright and R. Hoffmann, J. Am. Chem. Soc., 1979, 101, 3141–3351.
36. R. H. Summerville and R. Hoffmann, J. Am. Chem. Soc., 1979, 101, 3821–3831.
37. S. J. LaPlaca and J. A. Ibers, J. Am. Chem. Soc., 1963, 85, 3501–3502.
38. S. W. Kirtley, J. D. Olsen and R. Bau, J. Am. Chem. Soc., 1973, 95, 4532–4536.
39. R. G. Teller and R. Bau, Struct. Bonding, 1981, 44, 1–82 , and references cited therein.
40. R. Bau and M. H. Drabnis, Inorg. Chim. Acta, 1997, 259, 27–50 ; and references cited therein.
41. M. Bortz, R. Bau, J. J. Schneider and S. A. Mason, J. Cluster Sci., 2001, 12, 285–291.
42. M. Regitz and O. J. Scherer, ed., Georg Thieme Verlag, Stuttgart, 1990.
43. M. Scheer and U. Becker, Phosphorus, Sulfur Silicon Relat. Elem., 1994, 93–94, 257–260.
44. M. Scheer, K. Schuster and U. Becker, Phosphorus, Sulfur Silicon Relat. Elem., 1996, 109–110, 141–144.
45. O. J. Scherer, Acc. Chem. Res., 1999, 32, 751–762.
46. O. J. Scherer, Chem. Unserer Zeit, 2000, 34, 374–381.
47. M. Ehses, A. Romerosa and M. Perruzini, Top. Curr. Chem., 2002, 220, 107–140.
48. F. H. Stephens, M. J. A. Johnson, C. C. Cummins, O. P. Kryatova, S. V. Kryatov, E. V. R. Rybak-Akimova, J. E. McDonough and C. D. Hoff, Angew. Chem. Int. Ed., 2005, 127, 15191–15200.
49. J. S. Figueroa and C. C. Cummins, Dalton Trans., 2006, 2161–2168.
50. W. W. Seidel, O. T. Summerscales, B. O. Patrick and M. D. Fryzuk, Angew. Chem., Int. Ed., 2009, 48, 115–117.
51. F. Dielmann, M. Sierka, A. V. Virovets and M. Scheer, Angew. Chem., Int. Ed., 2010, 49, 6860–6864.
52. S. Yao, Y. Xiong, C. Milsmann, E. Bill, S. Pfirrmann, C. Limberg and M. Driess, Chem.–Eur. J., 2010, 16, 436–439.
53. O. J. Scherer, T. Hilt and G. Wolmershäuser, Organometallics, 1998, 17, 4110–4112.
54. T. Hilt, Ph.D. Dissertation, Universität Kaiserslautern, 1999.
55. C. Eichhorn, O. J. Scherer, T. Sögding and G. Wolmershäuser, Angew. Chem., Int. Ed., 2001, 40, 2859–2861.
56. E. Urnéžius, W. W. Brennessel, C. J. Cramer, J. E. Ellis, P. von and R. Schleyer, Science, 2002, 295, 832–834.
57. E.-M. Schnöckelborg, J. J. Weigand and R. Wolf, Angew. Chem., Int. Ed., 2011, 50, 6657–6660.
58. B. M. Cossairt and C. C. Cummins, Chem. Rev., 2010, 110, 4164–4177.
59. M. Caporali, L. Gonsalvi, A. Rossin and M. Perruzini, Chem. Rev., 2010, 110, 4178–4235.
60. M. Scheer, G. Balazs and A. Seitz, Chem. Rev., 2010, 110, 4236–4256.
61. M. Peruzzini, J. A. Ramirez and F. Vizza, Angew. Chem., Int. Ed., 1998, 37, 2255.
62. P. Barbaro, A. Ienco, C. Mealli, M. Perruzini, O. J. Scherer, O. Schmitt, F. Vizza and G. Wolmershäuser, Chem.–Eur. J., 2003, 9, 5195–5210.
63. J. A. Pool, E. Lobkovsky and P. J. Chirik, Angew. Chem., Int. Ed., 2002, 41, 3463.
64. J. Ballmann, R. F. Munhá and M. D. Fryzuk, Chem. Commun., 2010, 46, 1013–1025.
65. M. D. Walter, C. D. Sofield and R. A. Andersen, Organometallics, 2008, 27, 2959–2970.
66. D. E. C. Corbridge, The Structural Chemistry of Phosphorus, Elsevier, New York, 1974.
67. M. Scheer, U. Becker, M. H. Chisholm, J. C. Huffman, F. Lemoigno and O. Eisenstein, Inorg. Chem., 1995, 34, 3117–3119.
68. C. von Hänisch, D. Fenske, F. Weigend and R. Ahlrichs, Chem.–Eur. J., 1997, 3, 1494–1498.
69. O. J. Scherer, J. Vondung and G. Wolmershäuser, Angew. Chem., Int. Ed. Engl., 1989, 28, 1355.
70. O. J. Scherer, R. Winter and G. Wolmershäuser, Z. Anorg. Allg. Chem., 1993, 619, 827–835.
71. W. Tremel, R. Hoffmann and M. Kertesz, J. Am. Chem. Soc., 1989, 111, 2030–2039.
72. J. W. Lauher, M. Ellian, R. H. Summerville and R. Hoffmann, J. Am. Chem. Soc., 1976, 98, 3219–3224.
73. F. H. Stephens, Massachusetts Institute of Technology, 2004.
74. A. S. P. Frey, F. G. N. Cloke, P. B. Hitchcock and J. C. Green, New J. Chem., 2011 10.1039/c1nj20163h.
75. C. Schwarzmaier, A. Noor, G. Glatz, M. Zabel, A. Y. Timoshkin, B. M. Cossairt, C. C. Cummins, R. Kempe and M. Scheer, Angew. Chem., Int. Ed., 2011, 50, 7283–7286.
76. M. Scheer, S. Deng, O. J. Scherer and M. Sierka, Angew. Chem., Int. Ed., 2005, 44, 3755–3758.
77. M. Lein, J. Frunzke and G. Frenking, Inorg. Chem., 2003, 42, 2504–2511.
78. J. Frunzke, M. Lein and G. Frenking, Organometallics, 2002, 21, 3351–3359.
79. Y. Peng, H. Fan, H. Zhu, H. W. Roesky, J. Magull and C. E. Hughes, Angew. Chem., Int. Ed., 2004, 43, 3443–3445.
80. N. A. Piro and C. C. Cummins, J. Am. Chem. Soc., 2008, 130, 9524–9535.
81. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
82. J. Grunenberg and N. Goldberg, J. Am. Chem. Soc., 2000, 122, 6045–6047.
83. J. Grunenberg, Phys. Chem. Chem. Phys., 2011, 13, 10136–10146.
84. K. Brandhorst and J. Grunenberg, Chem. Soc. Rev., 2008, 37, 1558.
85. C. A. Pignedoli, A. Curioni and W. Andreoini, ChemPhysChem, 2005, 6, 1795–1799.
86. Y. Xie and H. F. Schaefer, Z. Phys. Chem., 2003, 217, 189–203.
87. P. R. Schreiner, H. P. Reisenauer, J. Romanski and G. Mloston, Angew. Chem., Int. Ed., 2009, 48, 8133–8136.
88. S. Katsyuba and R. Schmutzler, Dalton Trans., 2008.
89. S. Katsyuba, R. Schmutzler and J. Grunenberg, Dalton Trans., 2005, 1701–1706.
90. F. Kraus, J. C. Aschenbrenner and N. Korber, Angew. Chem., Int. Ed., 2003, 42, 4030–4033.
91. F. Kraus and N. Korber, Chem.–Eur. J., 2005, 11, 5945–5959.
92. F. Kraus, T. Hanauer and N. Korber, Inorg. Chem., 2006, 45, 1117–1123.
93. L. Salem, The Molecular Orbital Theory of Conjugated Systems, W.A. Benjamin, Inc., Reading, Massachusetts, 1966.
94. J. Grunenberg, unpublished results.
95. P. J. Alaimo, D. W. Peters, J. Arnold and R. G. Bergman, J. Chem. Educ., 2001, 78, 64.
96. A. B. Pangborn, M. A. Giardello, R. H. Grubbs, R. K. Rosen and F. J. Timmers, Organometallics, 1996, 15, 1518–1520.
97. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision A.1), Gaussian, Inc., Wallingford, CT, 2009.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental and crystallographic details and crystallographic data. CCDC reference numbers 738662–738664. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c1sc00413a

‡ The reaction of 1 with KHBEt₃ was also investigated in methylcyclohexane-d₁₄ under Ar. Immediately upon addition of KHBEt₃ gas evolution was observed accompanied by the formation of a colorless precipitate and a color change from red to purple and then red-brown. Three paramagnetic species 2, 3 and an unidentified paramagnetic complex were detected in solution. The solvent was removed and the residue dissolved in methylcyclohexane-d₁₄ to give a green solution which was filtered. The ¹H NMR spectrum of the crude reaction mixture showed resonances due to 3 (as major product), 2 and HCp′ (consistent with the bulk experiment). This clearly demonstrates the intrinsic instability of “[Cp′FeH]” with respect to formation of 2 and 3. No ²H-incorporation in the Fe–H functionality of 2 was observed. The decomposition of “[Cp′FeH]” is most likely the source of the excess hydride by acting as H₂ and H-radical source. This also explains the low yield when the reaction is carried out under Ar.

§ No reaction of 2 with N₂ was observed under the same conditions.

¶ One should note that [{Cp′Fe}₂(μ-η³:η³-P₃)] slowly decomposes on prolonged heating at this temperature.

|| Changing the basis set from 6-311G(d,p) to TZVP leads to slightly better agreement of calculated and experimental structures (see ESI for details†).

---