Adaptive multiscale regression for reliable Raman quantitative analysis
Da
Chen
a,
Zhiwen
Chen
b and
Edward R.
Grant
b
aState Key Laboratory of Precision Measuring Technology and Instruments, Tianjin University, Tianjin, China 300072
bDepartment of Chemistry, University of British Columbia, Vancouver, BC V6T 1Z1
First published on 28th October 2011
Abstract
This paper presents a novel methodology, adaptive multiscale regression (AMR), to adaptively process Raman spectra for quantitative analysis. The proposed methodology aims to construct an optimal calibration model for a Raman spectrum at hand, regardless of its structural characteristics, thus facilitating the application of Raman spectroscopy as a general tool for analytical chemistry. AMR firstly splits the spectra in a calibration set into frequency components at different scales using adaptive wavelet transform (AWT). Parallel member models constructed at different scales are then fused into a final prediction. The contributions of member models to a fusion model are straightforwardly estimated by a partial least square (PLS) model that emerges from a cross-validation results matrix (X) and reference values (Y). This procedure avoids information leakage by fully utilizing the multiscale nature of the input Raman spectra instead of arbitrarily removing some part of the spectral information by calibrating to selected features. Theoretically, we establish that AMR represents an automatic data-driven strategy that captures the Raman spectral structures adaptively and accurately. Our work tests and refines the AMR method by drawing upon the systematic analysis of spectra formulated to yield challenges representative of those encountered in common Raman analyses. AMR compares favorably with other popular preprocessing methods. Satisfactory calibration results suggest that AMR has the capacity to improve robustness and reliability of Raman spectral analysis, and may well extend to other spectroscopic techniques.
Introduction
Multivariate calibration plays a role of great significance in many qualitative and quantitative applications of analytical chemistry.1–6Raman spectroscopy in particular has come to rely on multivariate calibration models for facile quantitative analysis.7 However, despite the discriminating power of multivariate analysis, overwhelming fluorescence background and varying sources of other spectral interference often combine to limit conventional Raman approaches.8 The presence of spectral interference can limit the prediction precision of a quantitative measurement, and may spoil the reliability of prediction.9,10 For this reason, analysts have developed various preprocessing strategies to improve the reliability of calibration models for Raman spectral analysis.A number of preprocessing methods operate successfully to remove spectral interference in advance of calibration. These fit generally into one of two categories:11 (1) methods that perform geometric spectral preprocessing, such as Multiplicative Signal Correction (MSC),12 first-derivative based on SG-smoothing (SG-1D),13 second-derivative based on SG-smoothing (SG-2D),13 wavelet prism (WP),14 and continuous wavelet transform (CWT),15 and (2) methods that reduce dimensionality by orthogonal projection or variable selection, such as orthogonal signal correction (OSC),16 uninformative variable elimination (UVE),17 stacked partial least square (SPLS).18 However, the design of any given pretreatment method seldom conforms optimally with the requirements of a specific analytical problem, and thus the performance of a method usually varies by case.
This complicates the generalization of any pretreatment strategy, and can raise questions about its impact on the validity of a given calibration model. Moreover, improper signal preprocessing prior to modeling often gives rise to information leakage, owing to the loss of analyte signal,19 which can worsen the performance of a calibration model. These factors combine to limit the degree to which an analysis can rely on conventional methods of pretreatment. For broad utility, a calibration model requires a pretreatment method, tailored to quantitatively extract analyte signatures in the presence of uncontrolled variance, owning to particular sources of spectral interference.
Spectra are inherently multiscale in nature. A spectral signal contains contributions localized differently in both time (wavelength position) and frequency (peak width resolution) domains.20 Present pretreatment methods seldom use these two localization characteristics simultaneously. But, information exists in the time-frequency covariance of localization, and pretreatment strategies that can exploit this will suffer less information leakage and erroneous feature selection.
In this regard, we suggest that a recently developed technique, dual-domain multiscale regression (DDMR),19–21 provides an attractive new way to direct feature selection for the purpose of suppressing the effects of interference in Raman spectra. A strategy employing this method would first decompose spectra into different frequency blocks in the time domain by adopting DWT, and then construct parallel models from which to fuse frequency components into a final model according to a scheme of weights.
At present, the majority of DWT applications select the base wavelet filter from one of the eight standard types of wavelets.22,23 This limitation of fixed wavelets generally yields a suboptimal filter for a given experimental signal.24 The adoption instead of a wavelet filter tailored to the Raman signal at hand offers the potential of significantly improved calibration results. A second-generation, adaptive wavelet transform (AWT) based on a strategy of lifting, facilitates this kind of construction.25 AWT builds a unique wavelet filter adapted to the specific set of Raman spectra, thus improving the wavelet regression performance. This characteristic enables AWT to extract quantitative information in a more efficient way.
The success of dual-domain regression depends on the effectiveness by which it fuses parallel member models. Current dual-domain regression methods19–21,26 fuse member models into a final prediction, weighted by the reciprocal of the prediction residual error sum of squares (PRESS). Although this fusion strategy succeeds, it is somewhat artificial and lacks a fundamental connection between each member model and the corresponding fusion model. It is hard for this relatively fixed strategy to efficiently capture the variations of data structure as presented in different data sets, and usually results in a suboptimal fusion model.
In the present work, we introduce a new data-driven fusion strategy. This new strategy simply constructs a partial least square (PLS) model to estimate the relationship between cross-validation result matrix obtained by member models and reference values. Through PLS projection, corresponding regression coefficients represent the contribution of the member model on each fusion model. We anticipate that this PLS fusion strategy can capture the data structures in data sets adaptively and accurately.
We further propose novel multiscale algorithm, adaptive multiscale regression (AMR). AMR, firstly tailors the wavelet filter to match the spectral structure using an AWT lifting scheme, and then constructs parallel member models with wavelet coefficients at different scales to fuse into a final prediction employing the PLS weighting strategy.
Our work has tested and refined the AMR method by drawing upon the systematic analysis of two Raman data sets formulated to yield challenges representative of those encountered in common Raman spectral analyses. Satisfactory calibration results suggest that AMR has the capacity to improve the robustness and reliability of Raman spectral analysis. In addition, we demonstrate that AMR compares favorably many with other popular preprocessing methods, including MSC, SG-1D, SG-2D, WP, DDPLS and OSC.
Theory
Adaptive wavelet transform
AWT was originally developed to adjust wavelet transforms to complex geometries and irregular sampling,25,27 enabling the simultaneous design of wavelet filters and the completion of wavelet transform calculations. As described in the wavelet literature,25,27 AWT requires a spatial (or time) domain construction of biorthogonal wavelets, based on a process known as lifting, as opposed to convolution, as used in DWT. Lifting enables the design of a more intricate wavelet filter ensuring perfect reconstruction.27 With the flexibility of lifting, AWT allows the development of wavelet filters required in the transform algorithms, custom adaptated to the situation at hand, thus optimizing the quantification or discrimination capability of AWT regression.Two kinds of lifting strategies operate in AWT: primal lifting and dual lifting. The primal lifting strategy lifts the low-pass filter with the help of the high-pass subband, while the dual lifting strategy lifts the high-pass filter with the help of the low-pass subband. Because the Raman spectral background owing to scattered laser light and sample fluorescence oscillates with low frequency, and dominates thħıe uninformative component of the signal, we use only the primal lifting strategy in this work to improve the efficiency of the low-pass filter.
In a primal elementary lifting step (ELS), the biorthogonal quadruplet, ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ,
, ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) and h, g (derived from a mother wavelet filter), yields a new quadruplet,
and h, g (derived from a mother wavelet filter), yields a new quadruplet, ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) new,
new, ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) and h, gnew, via:
and h, gnew, via:
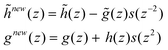 | (1) |
| s(z) = s1zpmax + s2zpmax−1 + … + sendzpmin | (2) |
involving positive and negative integer powers of z. The difference between the maximum and minimum integer power of z, (pmax-pmin) defines the degree, D, of s(z). Eqn (1) and (2), show that the optimization of AWT depends on the selection of appropriate Laurent polynomials.28 Here, we employ the Lawton strategy, as presented by Curran et al. to select optimal Laurent polynomials.29 This requires only one parameter, τ. We adopt a numerical strategy for optimizing τ with a step size of 1/128 in the range of [−1, 1]. We accept the τ corresponding to the minimum RMSECV as the one that produces the optimal wavelet filter.
In contrast with DWT, one does not necessarily propagate wavelets in AWT by translation and dilation, but the transformations produced by lifting still present all of the powerful properties of DWT.27 The strategy of AWT optimization yields an optimized filter that can shape wavelet components to adapt well to a given Raman data structure. AWT splits spectra into multiple frequency components at different scales. A spectrum c0, for example, decomposes into different scale components [D1,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2,
D2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) … ,Dl,Cl], just as with DWT, where D and C are detail and approximation coefficients, respectively, and the scale parameter, l, controls the depth of the decomposition. Increasing l increases the accuracy of the frequency division. Because AWT is a linear transformation, the quantitative information contained in the wavelet coefficients at each scale theoretically equates to their reconstruction. Thus we can use the AWT coefficients directly, instead of their reconstructions, for the purpose of further calibration.
… ,Dl,Cl], just as with DWT, where D and C are detail and approximation coefficients, respectively, and the scale parameter, l, controls the depth of the decomposition. Increasing l increases the accuracy of the frequency division. Because AWT is a linear transformation, the quantitative information contained in the wavelet coefficients at each scale theoretically equates to their reconstruction. Thus we can use the AWT coefficients directly, instead of their reconstructions, for the purpose of further calibration.
Adaptive mutliscale regression
The AMR strategy offers some key advantages for multivariate calibration. (1) Its novel multiscale algorithm prevents information leakage. (2) It uses an automatic data-driven strategy to capture Raman spectral structures adaptively and accurately, regardless of drastic variations from one data set to another. AMR avoids information leakage by reweighting the contributions of frequency components instead of simply removing them. The method adaptively optimizes its parameters according to the data structures at hand, to produce an accurate and reliable calibration model.We perform adaptive multiscale regression after AWT. The procedure constructs parallel member models using AWT coefficients at different scales [D1,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2,
D2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) … ,Dl,Cl], and then fuses them into a final model using a PLS weighting strategy. The procedure can be expressed as following
… ,Dl,Cl], and then fuses them into a final model using a PLS weighting strategy. The procedure can be expressed as following
ŷ = 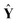 b + e, E(e) = 0, Cov(e) = σ2I b + e, E(e) = 0, Cov(e) = σ2I | (3) |
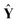 = [ŷ1, ŷ2, …, ŷl, ŷl+1] represents the prediction matrix obtained from all member models in AMR. b is the PLS regression vector between
= [ŷ1, ŷ2, …, ŷl, ŷl+1] represents the prediction matrix obtained from all member models in AMR. b is the PLS regression vector between 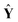 and ŷ. e denotes an m × 1 error vector, where m is the number of samples. E(e) and Cov(e) describe the expectation and covariance respectively. In the matrix
and ŷ. e denotes an m × 1 error vector, where m is the number of samples. E(e) and Cov(e) describe the expectation and covariance respectively. In the matrix 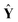 , terms ŷi represent the prediction values obtained from ith member model, as follows,
, terms ŷi represent the prediction values obtained from ith member model, as follows,| ŷi = Xiβi + ei, Xi ∈ [D1, D2, … ,Dl,Cl], 1 ≤ i ≤ l + 1 | (4) |
Combining eqn (3) and (4), we can write the AMR regression model as,
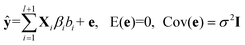 | (5) |
We estimate both regression coefficients, βi and bi in eqn (5), by PLS, which binds the developed AMR fusion model to the structure of data set at hand. Since bi is a scalar, we can express eqn (5) in matrix format,
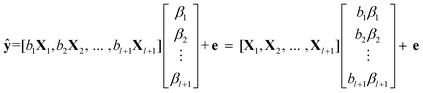 | (6) |
Eqn (6) establishes that the essential difference between AMR and PLS lies in the independent estimation of each block component.
We illustrate AMR by a flowchart in Fig. 1. In summary, an AMR calculation proceeds by means of the following steps:
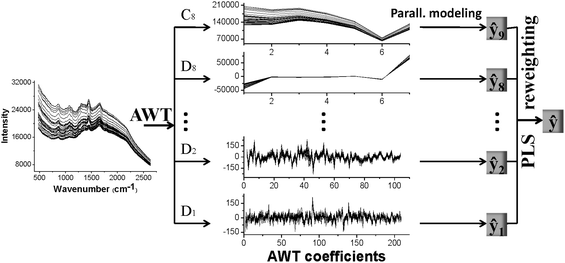 | ||
| Fig. 1 Adaptive multiscale regression flow chart for a scale of 8. | ||
(1) We decompose the signal to scale l using AWT, obtaining the corresponding AWT coefficients [D1, D2, … ,Dl,Cl]. We use the Lawton strategy in combination with MCCV to select the optimal wavelet filter. We set l as the floor integer of (log2(p)), where p is the number of variables.
(2) To calibrate, we construct the ith member PLS model at the scale i of AWT, determining the PLS factors and regression vector βi by MCCV. We then combine the MCCV predicted values, ŷi,t, for each member PLS model to form the training matrix 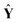 t = [ŷ1,t, ŷ2,t, … ,ŷl,t, ŷl+1,t].
t = [ŷ1,t, ŷ2,t, … ,ŷl,t, ŷl+1,t].
(3) We build up a new PLS model to correlate the matrix  t = [ŷ1,t, ŷ2,t, … ,ŷl,t, ŷl+1,t] with a vector y of predicted values according to eqn (3). We treat the regression coefficients, b, of PLS model as the contribution of each member model to the final prediction model.
t = [ŷ1,t, ŷ2,t, … ,ŷl,t, ŷl+1,t] with a vector y of predicted values according to eqn (3). We treat the regression coefficients, b, of PLS model as the contribution of each member model to the final prediction model.
(4) To apply AMR for prediction, we decompose a set of unknown spectra with AWT. We then predict property value, ŷi,p, with the ith member model, and fuse into a final prediction using [ŷ1,p, ŷ2,p, … ,ŷl+1,p]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b.
b.
Experimental
Raman instrument
We record Raman spectra using a SpectraCode model RP-1 spectrometer. This system integrates a component spectrograph (Acton 150 mm f/4.0) with a thermoelectrically cooled CCD detector (Princeton Instruments 1024 × 256 20 μm pixels) and a backscattering probe that combines interferometric optics with spatial filtering to provide near-total stray light rejection. This probe illuminates the sample with the output of a fiber-coupled 785 nm single-mode diode laser light source that has an output power of 350 mW. It collects the backscattered laser light using an eighteen-around-one bundle of 100 μm i.d. optical fibres, which abuts the 100 μm entrance slit of the spectrograph as a linear array, affording image compression to enhance sensitivity. A 300 groove mm−1 grating blazed at 900 nm disperses this light over an image plane measured in CCD pixels as 189 high by 844 wide. Binning columns of two pixels yields 422 horizontal elements of resolution spanning a Raman shift interval from 250 to 2400 cm−1. For illumination at 785 nm, Raman Stokes shifts larger than 2400 cm−1 fall at wavelengths longer than the detection limit of the CCD.We collect signal recorded by the CCD on a laboratory computer under LabVIEW control, and process the resulting files off-line using multivariate analysis algorithms described above, which we have developed using MATLAB.
Lactic acid in milk
Lactic acid is used as an indicator of milk's hygienic quality and of its state of preservation. We recorded Raman spectra of 64 lactic acid and milk mixture solutions using exposure times of 25 s. For the milk, we used 4 different brands of commercially available 2% milk, and collected 16 samples from each brand to simulate biological matrix interference that may be encountered in practice. Samples consisted of 15 ml milk mixed with 15 ml lactic acid solutions with variant concentrations. The concentrations of lactic acid ranged from 0.44 g L−1 to 2.40 g L−1. After extraction of spectral information by AMR, we divided the data set arbitrarily into two parts, a training set with 32 samples and a validation set with 32 samples to simulate the analysis of unknowns.Pulp data systems
In total, the complete sample set consists of 137 representative sheets together with measurements of Light-scattering Coefficient established separately using standard procedures of the Pulp and Paper Technical Association of Canada. For each sheet sample, we collected fifteen Raman spectra using 5 s exposures taken at different positions on each sheet sample with sample rotation during acquisition, and averaged these to form a final spectrum in each case for processing. Before building a calibration model with our AMR extracted spectra, we set aside the data for 31 sheet samples, selected randomly to simulate the analysis of a batch of real unknown samples. We then used the remaining 106 AMR processed sheet sample spectra as a training set.Results and discussion
Determination of optimal AWT parameters
The lifting scheme, by which we derive a wavelet filter for AWT, relies on the Lawton parameter, τ.29 To optimally determine τ, we use a root mean square error of prediction (RMSEP) criterion. Fig. 2 illustrates the relationship between the parameter τ and the measured RMSEP obtained by MCCV for two data sets. From this determination, we select optimal Laurent parameters with reference to the lactic acid concentration of milk samples and the Light-Scattering coefficient of sheet samples as 27/128 and 18/128, respectively. We regard the corresponding wavelet filters constructed using these coefficients as the best representations.![RMSECV values versus representative Lawton parameter (within [−1,1]) for the prediction of the light-scattering coefficient for pulp sheet samples (top) and lactic acid in milk (bottom), where the star in each case marks the optimal Lawton parameter.](/image/article/2012/AN/c1an15719a/c1an15719a-f2.gif) | ||
| Fig. 2 RMSECV values versus representative Lawton parameter (within [−1,1]) for the prediction of the light-scattering coefficient for pulp sheet samples (top) and lactic acid in milk (bottom), where the star in each case marks the optimal Lawton parameter. | ||
Fusion of member models
After AWT, we construct parallel PLS member models at each scale component of AWT. The connection of PLS member models plays a critical role in our AMR methodology by reflecting the importance of frequency components at each scale. In practice, however, the data structure of different data sets varies drastically, and the importance of each scale component can fluctuate strongly. It is therefore difficult for a conventional, fixed strategy, such as weighting with reciprocal prediction errors, to capture variations, which can often result in a suboptimal fusion model. As mentioned above, PLS modeling encodes data structures of all kinds well, and we exploit this capacity to estimate the relationship between member models and a fusion model with accuracy and reliability. Thus, we treat the regression coefficients of the PLS model as the contribution of scale information to final fusion model.The two spectral data sets investigated here represent two typical data structures encountered in practice. The analysis of lactic acid in milk represents a single component quantification, in which the characteristic features of an analyte are relatively easy to untangle from a highly overlapped matrix. The prediction of Light-Scattering Coefficients in sheet samples presents a much more complicated challenge, because this parameter represents the synergistic effect of a large number of physicochemical properties and no simple spectral feature encodes for it directly. In such a situation, any unguided removal of spectral background or noise can cause information leakage, making a calibration model unreliable. Even in a simple, direct, one-component case, a complex and varying matrix (milk) can swamp the features of an analyte (lactic acid). Removal of information should still be done with caution. In this regard, the reweighting strategy in AMR model can effectively avoid information loss, resulting in a more robust prediction result.
Fig. 3 illustrates the PLS regression coefficients of member models, b, together with their PLS factors. As shown in Fig. 3 (a), the low-frequency and high-frequency blocks, C8, D8, D2 and D1, possess tiny regression coefficients, and the medium-frequency blocks, D3, D4, D5 and D6, have much larger absolute values of regression coefficients. Among these coefficients, some are negative and others are positive, the reason being is that these PLS regression coefficients balance the relative contributions of member models. This provides PLS weighting more flexibility and accuracy in capturing the data structure compared with a conventional weighting strategy. As a result, the larger the absolute value of a coefficient |bi| is, the more important is its member model. As shown in Fig. 3, it is clear that the analytical information here concentrates mainly in the medium-frequency components. This is consistent with the inherent multi-resolution nature of spectra, which is to say that the background and noise are mainly located in low-frequency and high-frequency components, while the analytical information occupies the medium-frequency components.19–21 It is of great interest to find that the sum of all PLS regression coefficients approximately equals 1, confirming that the AMR strategy of combining member PLS models represents a weighting strategy. Similarly, the same conclusion can be reached for Fig. 3 (b).
 | ||
| Fig. 3 Distribution of PLS weighting coefficients, b, and the corresponding PLS factors of the member models for the determination of (a) the concentration of lactic acid in milk and (b) the light-scattering coefficient of pulp sheet samples. | ||
With AMR, it is of great interest to investigate the extracted spectral information after weighting. As indicated in eqn (6), the extracted spectral information can be expressed in the form of [b1X1, b2X2, … ,bl+1Xl+1], although the regression coefficients of block components [β1,β2, … ,βl+1] are estimated independently. Fig. 4 illustrates the extracted information for the prediction of lactic acid and light-scattering coefficients. As shown in Fig. 4 (a), the spectral baseline and noise are greatly suppressed, and a tiny shoulder-peak, present around 825 cm−1 establishes that AMR efficiently isolates the lactic acid from the overlapping interference. In Fig. 4 (b), we find that Raman features extracted by AMR fit well with chemical groups, e.g. C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch, and bending vibrations associated with C–H, C–O–C, C–C, O–H and O–O bonds, providing evidence that AMR extracts informative features in the presence of uncontrolled variance. These groups figure in fibre constituents representing the physicochemical basis of the Light-Scattering Coefficient. The results indicate that the AMR methodology clearly serves as a promising tool for extracting useful information in the presence of uncontrolled interference, and is capable of producing a high-quality calibration model that is robust against spectral interference.
O stretch, and bending vibrations associated with C–H, C–O–C, C–C, O–H and O–O bonds, providing evidence that AMR extracts informative features in the presence of uncontrolled variance. These groups figure in fibre constituents representing the physicochemical basis of the Light-Scattering Coefficient. The results indicate that the AMR methodology clearly serves as a promising tool for extracting useful information in the presence of uncontrolled interference, and is capable of producing a high-quality calibration model that is robust against spectral interference.
![Spectral information extracted by AMR for the determination of (a) the concentration of lactic acid in milk and (b) the light-scattering coefficient of pulp sheet samples, consisting of Raw Raman spectra (top solid line) and extracted information (bottom solid line). Extracted data obtained in each case from sums of coefficients [b1X1, b2X2, …, bl+1Xl+1] using the AMR PLS reweighting strategy. Among PLS coefficients, some are negative, causing negative-going peaks.](/image/article/2012/AN/c1an15719a/c1an15719a-f4.gif) | ||
| Fig. 4 Spectral information extracted by AMR for the determination of (a) the concentration of lactic acid in milk and (b) the light-scattering coefficient of pulp sheet samples, consisting of Raw Raman spectra (top solid line) and extracted information (bottom solid line). Extracted data obtained in each case from sums of coefficients [b1X1, b2X2, …, bl+1Xl+1] using the AMR PLS reweighting strategy. Among PLS coefficients, some are negative, causing negative-going peaks. | ||
Prediction results
Table 1 summarizes the AMR models for the two data sets, and compares the results obtained with different pretreatment methods. We employ MCCV to determine PLS factors.| Methods | PLS factors | RMSEP a | RRMSEP(%) | R |
|---|---|---|---|---|
| a Units of g l−1 for lactic acid in milk, m2 kg−1 for light scattering in paper sheet. | ||||
| (a) lactic acid in milk | ||||
| None | 7 | 0.27 | 19.2 | 0.883 |
| MSC | 6 | 0.30 | 21.1 | 0.870 |
| SG-D1 | 5 | 0.14 | 9.7 | 0.962 |
| SG-D2 | 5 | 0.15 | 10.4 | 0.955 |
| OSC | 4 | 0.26 | 18.6 | 0.893 |
| WP | 4 | 0.13 | 8.8 | 0.959 |
| DWT-UVE | 2 | 0.16 | 11.6 | 0.950 |
| DDPLS | 3,2,2,3,2,7,2,2,1 | 0.13 | 9.1 | 0.954 |
| AMR (9 blocks) | 2,2,3,4,2,5,4,2,1 | 0.10 | 6.9 | 0.981 |
| (b) light-scattering coefficient in paper sheet | ||||
| None | 10 | 1.96 | 8.2 | 0.934 |
| MSC | 9 | 1.99 | 8.3 | 0.930 |
| SG-D1 | 8 | 1.69 | 7.1 | 0.948 |
| SG-D2 | 5 | 1.89 | 7.9 | 0.940 |
| OSC | 5 | 4.67 | 19.6 | 0.877 |
| WP | 8 | 1.87 | 7.8 | 0.942 |
| DWT-UVE | 3 | 2.22 | 9.3 | 0.908 |
| DDPLS | 1,2,2,3,4,5,6,2,1 | 2.50 | 10.5 | 0.950 |
| AMR (9 blocks) | 1,1,1,2,6,6,6,2,2 | 1.31 | 5.48 | 0.968 |
As can be seen in Table 1 (a), the raw Raman spectra require a high number of PLS factors to construct a PLS model that can handle the substantial spectral interference, with poor prediction performance. Perhaps unexpectedly, MSC preprocessing worsens the calibration performance, confirming that an inappropriate preprocessing strategy can cause spectral distortion and give rise to unreliable prediction. SG-1D, SG-2D and OSC all improve the prediction performance compared with the raw PLS model. As expected, WP effectively suppresses the effects of spectral background and noise on calibration, producing a parsimonious model with improved prediction precision. However, the variable selection performed in the wavelet domain using DWT-UVE does not further improve the WP model, on the contrary, the prediction error clearly increases. This shows that a simple variable selection can cause the loss of useful information. Both DDPLS and AMR function to avoid information leakage, and yield more reliable calibration models than those employing conventional pretreatment strategies. The performance of AMR exceeds that of DDPLS, suggesting that the flexibility of AMR in tailoring wavelet filter and fusion weights to the Raman data sets at hand can significantly improve the calibration performance.
Table 1 (b) tells a somewhat different story than Table 1 (a). The structures of these two data sets are quite different. It seems surprising that DDPLS produces a much worse calibration model than WP. This occurs because a fixed weighting strategy based on 1/PRESS2 does not capture the complex data structure well. This underlines the power of PLS weighting, which changes adaptively according to data structure, over 1/PRESS2, for complex situations. With the further advantage of an optimal wavelet filter, AMR is especially suited to encoding complex data sets. We note for the pulp sheet samples in particular that the smooth appearance of the Raman spectrum belies the presence of a great number of individual vibrational bands, representative generally of spectra that can be expected for exceedingly complex materials or mixtures. For both systems, the introduction of biological variance adds a realistic challenge to analysis.
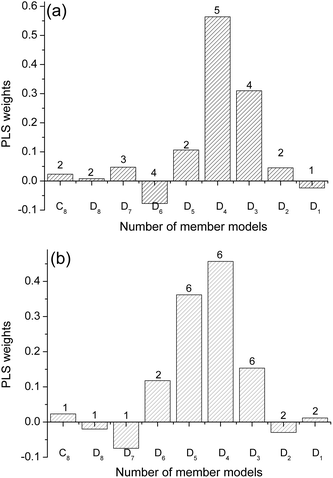
It is of great interest to quantify the calibration performance of models using AMR. Fig. 5 and Fig. 6 compare plots of measured values versus predicted values obtained with PLS and with AMR. Here, R and SD stand for correlation coefficients and standard deviations obtained by least-squares regression between the measured and the predicted values. We can see from the results that AMR preprocessing significantly reduces scatter, and for the case of lactic acid in milk, overcomes a systematic bias evident in the PLS prediction results.
 | ||
| Fig. 5 Measured vs. predicted values of lactic acid concentration for samples in the milk test set as determined by (a) PLS and (b) AMR. | ||
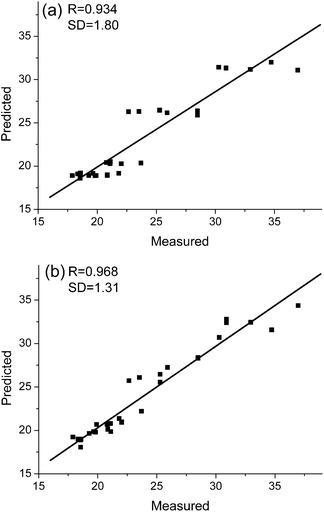 | ||
| Fig. 6 Measured vs. predicted values of light-scattering coefficient for sheet samples in the pulp test sets as determined by (a) PLS and (b) AMR. | ||
Conclusion
In the present work, we have progressed in developing a novel regression method, AMR, for reliable Raman quantitative analysis. We show that a strategy of adaptively utilizing the multiscale nature of spectra, instead of using preprocessing strategies that arbitrarily remove some part of the spectral information, can effectively avoid information leakage. In AMR, parallel, frequency-domain member models adaptively capture the localized variations in the time domain, and a PLS reweighting method accurately measures the relative importance of these parallel models. AMR is thus capable of producing a reliable and high-quality calibration model comparing favorably to PLS models employing other pretreatment methods. Our work has tested and refined the AMR method by applying it to the systematic analysis of two complex Raman data sets formulated to yield real challenges. Satisfactory calibration results suggest that AMR has the capacity to provide a universal tool for reliable modeling for all kinds of spectra, no matter the details of the data structure.Acknowledgements
This work was supported by British Columbia Innovation Council and Natural Sciences and Engineering Research Council of Canada. DC gratefully acknowledges support from the 111 Project (No. B07014) and the Innovation Foundation of Tianjin University (No. 60302048).References
- V. A. Lozano, G. A. Ibanez and A. C. Olivieri, Anal. Chem., 2010, 82, 4510 CrossRef CAS.
- H. Stenlund, E. Johansson, J. Gottfries and J. Trygg, Anal. Chem., 2009, 81, 203 CrossRef CAS.
- M. Daszykowski, M. S. Wrobel, H. Czarnik-Matusewicz and B. Walczak, Analyst, 2008, 133, 1523 RSC.
- N. A. Woody, R. N. Feudale, A. J. Myles and S. D. Brown, Anal. Chem., 2004, 76, 2592 CrossRef.
- B. Lavine and J. Workman, Anal. Chem., 2010, 82, 4699 CrossRef CAS.
- Q. S. Xu, Y. Z. Liang and H. L. Shen, J. Chemom., 2001, 15, 135 CrossRef CAS.
- D. I. Ellis and R. Goodacre, Analyst, 2006, 131, 875 RSC.
- T. Vankeirsbilck, A. Vercauteren, W. Baeyens, G. Van der Weken, F. Verpoort, G. Vergote and J. P. Remon, TrAC, Trends Anal. Chem., 2002, 21, 869 CrossRef CAS.
- Q. Ding, G. W. Small and M. A. Arnold, Appl. Spectrosc., 1999, 53, 402 CrossRef CAS.
- D. Chen, X. G. Shao, B. Hu and Q. D. Su, Anal. Chim. Acta, 2004, 511, 37 CrossRef CAS.
- M. Zeaiter, J. M. Roger and V. Bellon-Maurel, TrAC, Trends Anal. Chem., 2005, 24, 437 CrossRef CAS.
- T. Naes, T. Isaksson and B. R. Kowalski, Anal. Chem., 1990, 62, 664 CrossRef CAS.
- P. A. Gorry, Anal. Chem., 1990, 62, 570 CrossRef CAS.
- H. W. Tan and S. D. Brown, J. Chemom., 2002, 16, 228 CrossRef CAS.
- D. Chen, F. Wang, X. G. Shao and Q. D. Su, Analyst, 2003, 128, 1200 RSC.
- W. D. Ni, S. D. Brown and R. L. Man, Anal. Chem., 2009, 81, 8962 CrossRef CAS.
- V. Centner, D. L. Massart, O. E. de Noord, S. de Jong, B. M. Vandeginste and C. Sterna, Anal. Chem., 1996, 68, 3851 CrossRef CAS.
- W. D. Ni, S. D. Brown and R. L. Man, J. Chemom., 2009, 23, 505 CrossRef CAS.
- Y. Liu and S. D. Brown, Anal. Bioanal. Chem., 2004, 380, 445 CrossRef CAS.
- H. W. Tan and S. D. Brown, J. Chemom., 2003, 17, 111 CrossRef CAS.
- Z. C. Liu, W. S. Cai and X. G. Shao, Analyst, 2009, 134, 261 RSC.
- D. Donald, Y. Everingham and D. Coomans, Chemometr. Intell. Lab. Syst., 2005, 77, 32 CAS.
- L. Eriksson, J. Trygg, E. Johansson, R. Bro and S. Wold, Anal. Chim. Acta, 2000, 420, 181 CrossRef CAS.
- C. J. Coelho, R. K. H. Galvão, M. C. U. Araujo, M. F. Pimentel and E. C. da Silva, Chemometr. Intell. Lab. Syst., 2003, 66, 205 CAS.
- I. Daubechies and W. Sweldens, J. Fourier Anal. Appl., 1998, 4, 247 CrossRef.
- H. W. Tan and S. D. Brown, Anal. Chim. Acta, 2004, 490, 291 CrossRef.
- W. Sweldens, Appl. Comput. Harmon. Anal., 1996, 3, 186 CrossRef.
- X. Q. Jiang, L. Blunt and K. J. Stout, Proc. R. Soc. London, Ser. A, 2000, 456, 2283 CrossRef.
- P. F. Curran and G. McDarby, Wavelet Analysis and Its Applications Second International Conference, Hong Kong, China, 2001 Search PubMed.
- N. M. Faber and R. Rajkó, Anal. Chim. Acta, 2007, 595, 98 CrossRef CAS.
- Q. S. Xu and Y. Z. Liang, Chemom. Intell. Lab. Syst., 2001, 56, 1 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
