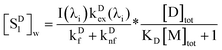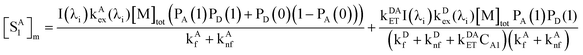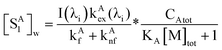DOI:
10.1039/C1AN15805H
(Paper)
Analyst, 2012,
137, 153-162
Application of PARAFAC to a two-component system exhibiting Fluorescence Resonance Energy Transfer: from theoretical prediction to experimental validation†
Received
1st September 2011
, Accepted 20th October 2011
First published on 7th November 2011
Abstract
One of the conventionally accepted requirements for parallel factor analysis (PARAFAC) to handle the fluorescence excitation emission matrices (EEMs) is the independence of each component's absorption and emission spectra in simple mixtures of fluorophores. EEMs of samples in which Förster resonance energy transfer (FRET) occurs between fluorophores seem to fail to meet this requirement. A rigorous theoretical treatment of the steady-state kinetics in the present work indicates that the fluorescence in the presence of FRET, excited by relatively weak excitation light intensity, can be reasonably separated into additive contributions from three parts: donors, acceptors and FRET. This prediction is for the first time verified experimentally in sodium dodecyl sulfate micellar solutions containing biphenyl as the energy donor and 2,5-diphenyloxazole as the energy acceptor. The experimental EEMs were well fitted to three components as predicted. A well accepted diagnostic test called core consistency (CC), specifically designed for modeling simple mixtures of fluorophores with PARAFAC, was found to be negative for the 3-component model in the present study. The simultaneous occurrence of good model fit and significantly negative CC when modeling fluorophore mixtures by conventional PARAFAC would be indicative of the presence of physical/chemical processes (e.g., FRET) that deviate from the conventional working requirements for PARAFAC. The extent of FRET has been independently measured or calculated by three methods: 1) decrease in steady state fluorescence of donor; 2) lifetime measurements with population analysis; and 3) Poisson statistics based on PARAFAC-determined distribution constants. The results of the three methods are consistent. The normalized scores of the three components found by PARAFAC also agree to within a few percent with relative concentrations in aqueous and micelle phases determined from distribution constants for the solutions prepared with nine different combinations of total donor and acceptor concentrations. Our theoretical treatment also for the first time spells out in detail the relationship between the PARAFAC scores and concentrations of components, in terms of photophysical constants of the components and spectral shape factors.
Introduction
As is well known, parallel factor analysis applied to fluorescence excitation-emission matrices (PARAFAC-EEMs) holds great promise as a tool to resolve the contributions of spectrally overlapped non-interacting fluorophores, and this approach has become a popular technique for the analysis of mixtures.1–14 Some complicated photophysical processes, e.g., Förster resonance energy transfer (FRET) or excited-state reactions in complicated samples (e.g., natural organic matter), may introduce interactions among the fluorophores. With three-mode data, it is possible that the patterns generated by the underlying component fluorophores have independent effects in two modes, yet nonetheless are linearly dependent in a third mode. More broadly, this circumstance may arise in many practical examples in multivariate analysis, e.g., the identical elution profile in a chromatogram for two components, the fixed concentrations of interfering fluorophores (co-varying) while spiking a target fluorophore in a standard addition experiment, or the identical spectra (excitation or emission) associated with different fluorophores in the EEMs. As a consequence, column rank-deficiency of the loading matrices in PARAFAC (referred to as A, B and C15) will result. A PARAFAC variant (PARAFAC with linear dependences, referred to as PARALIND) has been proposed16 to deal with these situations, in which case proper constraints are imposed in PARALIND to force certain modes of the data block to be linearly dependent.
When dealing with highly complicated unknown samples such as dissolved organic matter in natural water, the investigators often have no a priori knowledge whether the samples involve component-component interaction leading to linear dependences in modes. Consequently, it is not practical to employ PARALIND with linear dependences imposed on modes. Another issue worth noting is that determining the “similarity” between two components' spectra can be difficult; for example, in a recent paper we found that the spectra of solutes (biphenyl or 2,5-diphenyloxazole (PPO)) in water phase and in micelle phase of sodium dodecyl sulfate were quite similar but not identical.17 Because of the polarity difference in the two phases, the spectra in the two phases are not strictly identical. The very similar spectra in the two phases would be falsely forced to be identical when applying PARALIND in the absence of a priori knowledge. Therefore, the only practical approach for many PARAFAC users facing samples with unknown spectral interactions is to employ conventional PARAFAC with simple constraints such as non-negativity in the modes. We are interested in what the models of PARAFAC-EEMs would look like in the case of linear dependences in modes; in this paper, we investigate the case of two components exhibiting FRET.
Leurgans and Ross for the first time postulated the feasibility of using a trilinear model called Tucker2 rather than PARAFAC to describe the EEMs in the presence of FRET between donors (D) and acceptors (A).18,19 The authors only considered the simple situation under which light absorption by a chromophore (D) transfers energy to a fluorophore (A), from which successive emission occurs; they however did not take into account the likelihood that D could also be a fluorophore and emit fluorescence or the likelihood that A could also get excited by direct absorption of light. These two previously unconsidered situations are practically important, since EEM intensities are measured across a relatively wide excitation/emission wavelength range rather than a specifically chosen excitation/emission pair. In addition, the Tucker2 model, because of the rotation problem, is unable to model FRET-EEM data in a unique way to give chemically meaningful profiles of D and A.19 Harshman suggested forcing a component to have the same excitation pattern as D and the same emission pattern as A in PARAFAC to fix the rotation problem.20 Except for the very preliminary theoretical treatment by Ross and Leurgans,18,19 no theoretical work has rigorously proven that fluorescence intensities in FRET-EEMs would be decomposed by PARAFAC into separate contributions. Experimental work on PARAFAC-EEM in the presence of FRET has been lacking, and even EEMs in the presence of FRET have not been reported, to the best of our knowledge. The difficulty in experimentally measuring and correcting EEMs in the presence of FRET may in part be attributed to the requirement for generating FRET in solutions: high concentrations of D and/or A to make them approach each other closely enough to give considerable FRET. This requirement inevitably results in high absorbance, which gives rise to severe inner filtering effects (IFEs) that are difficult to correct. An alternative approach, taken in this work, is to confine D and A in micelles to make FRET occur, even when the bulk concentrations of D and A are low.
The present work provides the theoretical basis for the applicability of PARAFAC to analysis of EEMs of simple systems containing a single donor and a single acceptor species. It also provides verification by experimental study. The theoretical part is a straightforward analysis of steady-state fluorescence kinetics which includes the necessary terms for FRET.
Experimental design
We chose suitable D = biphenyl and A = PPO molecules based on convenient spectral range and sufficient spectral overlap (see Figure S1) as required for FRET. Both are relatively nonpolar fluorophores with favorable distribution constants that allow us to achieve the required occupancy numbers in SDS micelles in aqueous solution. The design principle was to ensure a detectable amount of FRET from micelles containing exactly one D and one A, and virtually no FRET from bulk solution or from multiply-occupied micelles (D or A >1). In a recent publication17 we used PARAFAC analysis of EEMs of pure A or pure D in aqueous SDS micelle solutions to determine these previously unavailable (PPO) or poorly known (biphenyl) distribution constants. This allowed us to closely achieve the desired conditions described above.
Given these experimental conditions, our theoretical treatment employs the simplifying assumption of a single FRET rate constant, consistent with a single D–A distance R and an average orientation factor κ2. Experimental results provide some justification for the reasonableness of this assumption. We believe that the study of this simple distribution will be a first step toward comprehensive understanding of more complicated situations.
The following content is organized as follows. First, the fluorescence intensities contributed by each underlying component in the simple distribution are derived based on steady-state kinetics and expressed in terms of the PARAFAC model; second, micellar solutions containing low concentrations of donors and acceptors are investigated with EEMs and PARAFAC; and, third, the results are verified by time-resolved experiments and Poisson statistics.
Theoretical
We consider the case of D and A dissolved in a single condensed phase. (If multiple phases are present, the fluorescence intensity, properly corrected for inner filter effects, will be the sum over all phases.) Let CD and CA denote the concentrations of D and A, respectively. The primary photophysical processes are outlined below.
In most cases, molecular fluorescence in condensed matter occurs from the first singlet excited state; we will assume that is the case here for D and A, also that the S0 ↔ S1 transition in each is strongly allowed. At excitation wavelength λi with photon flux density I(λi), steady states of both D and A are achieved. The kinetic equation of singlet state for D can be described by eqn (1):
| | 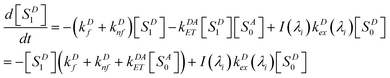 | (1) |
where
kDf and
kDnf are the intrinsic fluorescence and non-fluorescent deactivation rate constants of D, respectively,
kDAET is the FRET rate constant which depends on the D–A distance, spectral overlap and dipole–dipole orientations,
21 and k
Dex(λ
i) is proportional to the conventional molar absorptivity of D at wavelength λ
i, k
Dex(λ
i) = α
εD(
λi). [S
D1] and [S
D0] are concentrations of the first singlet excited state and singlet ground states of D, respectively. [S
A0] denotes the concentration of ground-state acceptors. At steady state,
d[
SD1]/
dt = 0 gives
| | 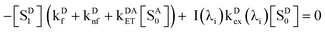 | (2) |
or
| | 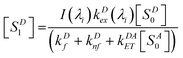 | (3) |
The kinetic equation for acceptors, including a term accounting for resonance energy transfer, which pumps some ground-state acceptors into the excited states, is given by eqn (4),
| | 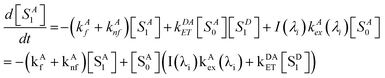 | (4) |
where
kAf and
kAnf are the intrinsic fluorescence and non-fluorescent deactivation rate constants of A, respectively, and
kAex(
λi) is proportional to the conventional molar absorptivity of A at wavelength λ
i,
e.g.,
kAex(
λi) =
αε
A(λ
i). At steady-state,
d[
SA1]/
dt = 0 gives
| | 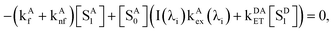 | (5) |
or, solving for [
SA1] in terms of [
SA0] and [
SD1]:
| | 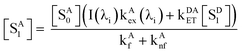 | (6) |
The steady-state concentrations [SD1] and [SA1] are interdependent. In the case of very weak excitation and short natural lifetimes of the excited states, [SA1] ≪ [SA0] ≈ CA, and [SD1] ≪ [SD0] ≈ CD, reducing the eqn (3) and (6) to simplified (7) and (8), respectively. The assumption of weak excitation is justified in the Supplementary Information.
| | 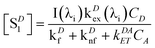 | (7) |
| | 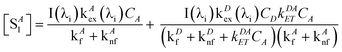 | (8) |
The total fluorescence measured at excitation wavelength λi is
| | 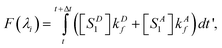 | (9) |
where the concentrations are the steady state values derived above.
Defining the fluorescence quantum yields in the conventional manner,
| | 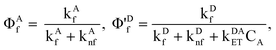 | (10) |
where the prime on Φ'
Df is meant as a reminder that the usual fluorescence quantum yield,
| | 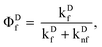 | (11) |
has been diminished by the energy transfer process. Similarly we define
| | 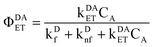 | (12) |
Using eqn (7) and (8) in eqn (9) and carrying out the integration with εA(λi) and εD(λi) replacing kAex(λi) and kDex(λi), we have
| | 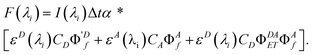 | (13) |
If proper units are chosen for the rate constants, the units of F(λi) are photons emitted. Since the fluorescence is dispersed in an EEM, we need to insert the dependence on emission wavelength λj, into eqn (13). We do so by multiplying the equation by an emission probability distribution function, MA(λj) or MD(λj), normalized so that its integral equals the quantum yield; using finite intervals corresponding to the emission wavelength step size, we have
| | 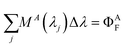 | (14) |
with a similar equation for M
D(λ
j). For each emission wavelength (λ
j), there is also an instrument factor H(λ
j) that includes such considerations as collection efficiency, transmission at wavelength λ
j, and
detector sensitivity.
Including full excitation and emission wavelength dependence into our equation, then, we have
| | 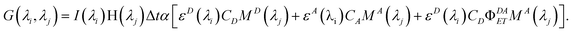 | (15) |
If instrument factors and proportionality constant α are removed for simplicity, this equation
| | | EEM(λi,λj) = G(λi,λj)/(I(λi)ΔtαH(λj)) | (16) |
gives the contributions of the various components to the EEM:
| | 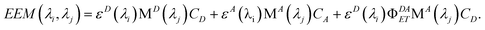 | (17) |
Because a single value of I(λi) is used in the equations above, they are strictly applicable when the condition of optical diluteness (absorbance in 1-cm pathlength ≪ 1) at the excitation wavelength is met, i.e., all molecules contributing to the fluorescence signal are illuminated by the same intensity; similarly, a single value of H(λj) implies optical diluteness at the emission wavelength. When these conditions are not met, the data must be corrected for inner filter effects.22
Further development of the equation above must be preceded by a discussion of the relationship between the PARAFAC spectra (sometimes referred to as “loadings”) and the conventional absorption and emission spectra, i.e., plots of molar absorptivity versus excitation wavelength for absorption and relative fluorescence emission probability versus emission wavelength for fluorescence, the latter scaled as in eqn (14).
PARAFAC assumes that there are several independent components that contribute in each of a collection of EEMs, and the linear superposition of these components gives the experimentally collected EEMs, as follows,23
| | 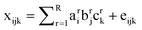 | (18) |
xijk is the intensity of fluorescence for sample
k at excitation wavelength
i and emission wavelength
j. The “score” c
kr is directly proportional to the concentration of the component
r in the
kth sample. A vector a
r of elements
air (
i = 1,2,3,…) denotes the excitation spectrum of component
r, and a vector b
r of elements
bjr (
j = 1,2,3,…) denotes the emission spectrum of component
r. For a given choice of number of components, PARAFAC tries to find proper scores and spectra (emission and excitation) such that the sum of squares of the residual
eijk is minimized. R defines the number of components. The mathematics of PARAFAC is that of vectors and matrices, and the excitation and emission “loadings” for component r, a
r(λ
i) and b
r(λ
j) are commonly normalized as vectors,
i.e., such that the sum of squares of the elements equals unity. Therefore, scaling constants must be used to understand the relationship between PARAFAC scores and concentrations of the fluorescent components. For a given component r, let ε
r(λ
i) = γ
ra
r(λ
i), where γ
r converts the PARAFAC absorption output a
r(λ
i) to molar absorptivity, and let M
r(λ
j) = δ
rb
r(λ
j), where δ
r converts the PARAFAC emission output b
r(λ
j) to normalized emission. It it easy to show that γ
r = ε
rmax/a
rmax, while
Rewriting eqn (17) explicitly in terms of the PARAFAC output gives
| |  | (19) |
Breaking out the PARAFAC output (dropping the subscript k since we are dealing only with one sample), we have
| |  | (20) |
For this system, the total EEM intensity is obtained by summation of three terms whose structure is similar; in PARAFAC terms: (excitation loading) • (emission loading) • (score). If kDAET were zero, the first two terms would be identical in form and the third term would be zero; this corresponds to the situation of two non-interacting fluorophores contributing to the EEM of the mixture. The first term has excitation and fluorescence spectral dependences characteristic of D, and the second term has spectral characteristics of A. When kDAET is nonzero, the first term has a primed fluorescence quantum yield; its numerical value would be reduced from the unprimed value depending on the extent of FRET. The third term now represents the contribution of FRET, and has excitation dependence of D but emission dependence of A. The first two scores are indeed proportional to the concentrations of D and A, respectively, but they contain additional factors that also depend on the properties of D and A. The third score, for the FRET term, contains an explicit factor of CD and an implicit factor of CA embedded in the FRET quantum yield (see eqn (1) and (12)).
If one wishes to compare the concentrations of component A in different samples, the raw scores may be used to give relative concentrations. However, to obtain relative concentrations of two different components, corrections must be made for the other factors in curly brackets above. A brief discussion of this point was given in our article on using PARAFAC to determine distribution constants.17
Results and discussion
1. Appropriateness of D–A pair chosen
a. Förster distance R0.
For our experimental design to succeed, the Förster distance R0 should be comparable to the size of the SDS micelles and much smaller than the distance between D and A in the bulk aqueous solution. The calculation of R0 is detailed in the ESI.† Calculations gave R0 = 27.9 Å and R0 = 26.3 Å using κ2 = 2/3 and κ2 = 0.475, respectively. This range is comparable to the literature value of 28.88 Å for this D–A pair in degassed cyclohexane.24 For comparison, the micelle is approximately spherical with a radius of 20 Å.25 At the highest CA used, the approximate D–A distance in the aqueous phase is >200 Å, too large for FRET to occur. Similarly, donors and acceptors in separate phases or separate micelles are too far apart for FRET to be significant.
b. Absence of ground-state association.
As is well known, a micelle may confine more than one solute, and as such, the solutes may form ground-state complexes. UV-Vis absorption spectra were used to verify whether there was ground-state association between the solutes in the micelles. Absorption at 250 nm, a wavelength associated with the maximum absorption peak of D, was monitored as a function of CD in the micellar solutions. The 250 nm absorption increased linearly with CD, either in the absence of A or in the presence of A (Figure S2). This indicated that there was no D–D or D–A association in the presence of micelles. Similar experiments were also applied to the absorption at 305 nm, the maximum absorption peak of A in the presence of micelles. The 305 nm absorption increased linearly with CA, either in the absence of D or in the presence of D (Figures not shown), and this further indicated that there was no association of D–A or A–A.
2. Evidence of FRET
Steady-state emission of a mixture of D and A in the presence of 8.5 mM SDS was not a simple superposition of the emission of independent D and A in the solution (Fig. 1). Instead, D's emission at 313 nm was depressed while A's emission at 450 nm was increased when D and A were mixed in the micellar solutions. D's 313 nm emission intensity decreased from 280.6 to 276 by a factor of 1.6% ± 0.1% (three replicates), whereas A's emission intensity increased from 4.4 to 8.4 (±1%).
 |
| | Fig. 1
Emission spectrum excited by 250 nm in 8.5 mM SDS micellar solution. IFE was corrected. Concentrations shown in legend refer to convention described in Experimental Details. | |
Fluorescence decay time of D in pure water and in 20 mM SDS micellar solution were almost the same, 10.6 ns.17 We used 20 mM SDS, a relative high concentration of SDS, which gave the total micelle concentration of 1.935 × 10−4 M, calculated based on the partition coefficient of 4.5 × 104 M−1 for D reported previously.17 These conditions correspond to 89% and 11% of D partitioned in micelles and water, respectively. We should have observed different decay times in the presence of 20 mM SDS, if the solute in micelles and in water had showed significantly different decay times. Similarly, we measured the fluorescence lifetimes of the acceptor A, and found the same decay time of 1.8 ns in both solutions (with or without micelles) in the absence of donor.17 These observations established that the environments in micelles and water are not different enough to give rise to detectable differences in lifetimes on our time-resolved instrument with a resolution of nanoseconds. This is consistent with the statement given previously17 that some solutes may preferentially stay close to micelle surfaces and/or fluorescence quenching by oxygen is not significant in micelles.
When D and A were present at the concentration ratio of 4/0.8 (D/A) in the micellar solution of 8.5 mM SDS, an additional shorter decay time of 2.4 ns was observed for D, whereas A's decay time did not vary. The fluorescence decay profile for D was monitored at 313 nm with an excitation wavelength of 250 nm. The lifetime fit and the residual are shown in Fig. 2. We used the exponential series method (ESM) to fit the decay curve, as there might be multiple decay times associated with D in the presence of A and micelles. Strictly speaking, the distance between D and A in micelles as well as the orientation factor may not be a single value but have a distribution, which would result in a distribution of rate constants for energy transfer. However, we only observed two distinct decay times for D (Fig. 3) under these experimental conditions. Besides the intrinsic lifetime of 10.6 ns, the new lifetime of 2.4 ns is attributed to the donor undergoing FRET.
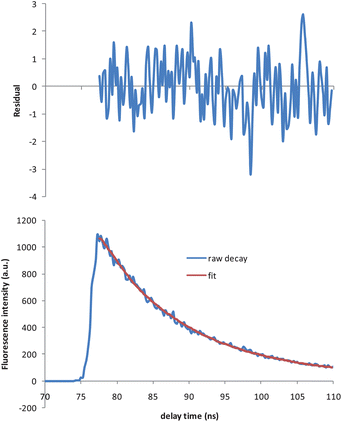 |
| | Fig. 2 Decay trace of D (7.04 μM) in the presence of 1.41 μM of A in 8.5 mM SDS solution (bottom), and its fit using exponential series method (ESM) (top). Excitation: 250 nm. Emission: 313 nm. Goodness-of-fit χ2 = 1.03. | |
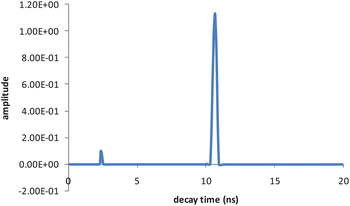 |
| | Fig. 3 Decay time distribution of D (7.04 μM) in the presence of A (1.41 μM) in 8.5 mM SDS solution. | |
The integral under-peak area for 10.6 ns is 37 times that for 2.4 ns, which means that only a small portion of the D molecules are quenched by A to give shorter decay times. If the total integral is normalized to unity, calculation gives that the 2.4 ns band integral is 0.026, which means ∼2.6% of the D population has a FRET decay channel, whereas 97.4% D decays normally. The macroscopic decay is approximated to be a sum of two exponential decays, expressed as IDA(t) = 0.026exp(−t/2.4) + 0.974exp(−t/10.6) with χ2 = 1.05. In contrast, D's decay in the absence of A is only a single exponential, i.e. ID(t) = 1.00*exp(−t/10.6).
The D–A distance R is related to the decay time by21
| | 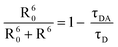 | (21) |
Calculation gives R = 0.81*R0 which ranges between 21.5 Å and 22.7 Å. Since an SDS micelle has radius ∼20 Å (<R),25 our calculated values for R indicate that neither D or A resides at the very center of the micelle cavity, which is agreement with the statement that some hydrophobic solutes preferably stay close to the micelle surface.25
It is possible to examine the steady-state data to verify that ∼2.6% of donors participate in energy transfer. Due to energy transfer, quantum yield (ΦDF) of donors in the absence of energy transfer now decreases to (Φ′DF).
| | 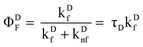 | (22) |
| | 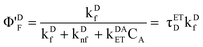 | (23) |
| | 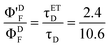 | (24) |
Based on the biexponential decay function given above, the fluorescence decrease of D in steady-state experiments may be predicted to be 0.026 ×(1–2.4/10.6) which is ∼2.0%, a value comparable to the percent decrease of D's emission in the presence of A in micelles (i.e. 1.6%, see above). The pre-exponential factors recovered by time-resolved experiments should be verified by Poisson statistics. We discuss this issue below.
3. The PARAFAC modeling
a. What to expect.
The foregoing discussion may be summarized to suggest that the EEMs should consist of contributions of aqueous D, aqueous A, micellar D, micellar A, and micellar D–A pairs which have a certain probability of undergoing FRET. We might therefore expect to model the EEM data with five components. We need to check these expectations against the expected distribution of D and A in the aqueous and micelle phases.
The distribution constant Keq is defined as25
| | 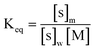 | (25) |
where [s]
m is the concentration of solute in the micellar phase, [s]
w is the concentration of solute in
water, and [M] is the concentration of micelles. (In
ref. 25 it was shown that the solute occupation of the micelles follows a Poisson distribution; therefore [M] in
eqn (25) is the total micelle concentration, not the concentration of “empty” micelles. In this work, the difference is unimportant since the fraction of occupied micelles is small.) According to this definition, [s]
m and [s]
w are the moles of solute per unit of total volume of the micelle-containing solution, not the volumes of the phases. Other conventions are found in the literature.
In our recent work in which we determined the K values, we found that the excitation and emission spectra of D in water and in micelle phase were very similar; the same was found to be true for A. We were able to distinguish the spectra from each other despite these similarities because we used an experimental design in which total solute concentration (summed over both phases) was kept constant but surfactant was increased, which changed the ratio of [s]m and [s]w significantly. PARAFAC can separate components with similar spectra if their concentrations do not covary. However, in the present experiment we held the surfactant concentration constant, which means that the ratio of [s]m and [s]w stays very nearly constant (see section c below). The same solute, e.g., D, would have co-varying concentrations and fluorescence intensities (or excited-state concentrations) in both phases. These two components, Dw and Dm would be combined to become a single component D as PARAFAC is unable to discriminate between two co-varying fluorophores. A similar conclusion is expected for the acceptor, i.e. A. In fact, we show in the ESI† that the spectra recovered for D and A by PARAFAC are the weighted averages of their spectra in the two phases, the weighting factors being the mole fractions. For this reason, it is expected that the PARAFAC analysis will yield one component for D in both phases, one component for A in both phases, and one component for the FRET pair in micelles. Thus, a three-component model is expected to fit the experimental data.
b. PARAFAC results.
The corrected EEMs were fitted to 1 through 5 components, respectively. Core consistency (CC), sum-of-squares of residuals (SSR) and the percentage of explained variation (referred to as RELFIT)15 are listed in Table 1 for comparison.
Table 1 Comparison of core consistency values (CC), sum of squared residuals (SSR) and percentage of explained variations (RELFIT) between various PARAFAC models with 1 through 5 components
| |
1-comp
|
2-comp
|
3-comp
|
4-comp
|
5-comp
|
| CC |
100 |
100 |
-971 |
−7.79E + 4 |
−1.42E + 4 |
|
SSR
|
3.8E + 7 |
1.5E + 5 |
1.4E + 4 |
1.1E + 4 |
1.0E + 4 |
|
RELFIT
|
80 |
99.9211 |
99.9926 |
99.9942 |
99.9947 |
According to conventional interpretation of the core consistency diagnostic, a 2-component model is preferred over a 3-component model, since CC at the 2-component model is 100 whereas the 3-component model gives a negative CC equal to −971. However, the 2-component model gave SSR nearly 10 times as much as the 3-component model. It should be noted that the conventional core consistency is a relatively reliable diagnostic tool only for simple mixtures of non-interacting fluorophores.15 Steady-state and time-resolved experiments in this work both showed that energy transfer occurs in the D/A mixtures. Additionally, at least three components were required to describe the micellar solutions, according to the theoretical analysis. As a result, a 3-component model is preferred over the 2-component model. The scores and loadings for the 3-component model are shown in Fig. 4. A brief discussion of the 4- and 5-component models, which are also rejected in favor of the 3-component model, is given in the ESI.† Also provided are the scores and loadings for these models shown in Figures S3 and S4.
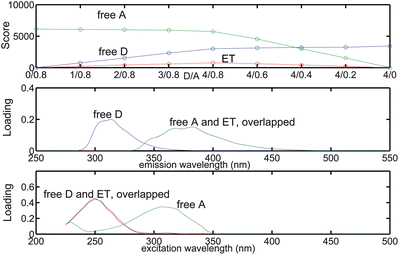 |
| | Fig. 4 Relative concentration and spectral profiles of the components recovered by a 3-component PARAFAC model fitted to the micellar EEMs. | |
c. Verification of the 3-component model.
In order to verify whether the 3-component PARAFAC model really describes the EEMs as predicted above, we first calculated the distribution of D and A in both phases with special attention given to those micelles containing one D and A. The low occupancies of D and A in dilute solutions (cf. the experimental section) makes most of the micelles either contain one solute or no solutes, while a relatively small numbers of micelles contain two solutes (i.e., one D and A), as depicted in Fig. 5. Given the concentration of SDS of 8.5 mM and critical micelle concentration of 8.0 mM as well as the aggregation number of 62,17 the micelle concentration was calculated to be 8.06 × 10−6 M. The reported distribution constants of D and A between SDS micelles and water are KD = 4.5 × 104 M−1 and KA = 8.8 × 105 M−1 respectively.17
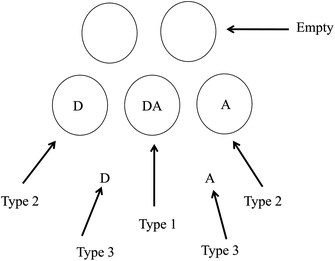 |
| | Fig. 5 Three types of distributions of D and A in a micellar solution containing free solutes in water phase and micelles as well as confined in the same micelles to give FRET. Circular shapes denote micelles of SDS. | |
Assuming the Poisson distribution of solutes justified in ref. 25 (which also assumes the independent distribution of D and A in the case of low occupancy less than one), we used the following equation to calculate the concentrations of D and A confined in the same micelles (type 1, cf.Fig. 5),
| | | CA1 = CD1 = [M]totPA(1)PD(1) | (26) |
where [M]
tot is the concentration of micelles, and P
A(1) and P
D(1) refer to the probability that a micelle contains one D and one A, respectively. The product of P
A(1)P
D(1) therefore refers to the joint probability that a micelle simultaneously contains one A and one D. The excited-state concentration of D (
eqn (7)) in the type 1 distribution is therefore expressed as follows,
| | 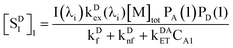 | (27) |
According to Poisson distribution theory, we have
| | | PA(1)PD(1) = μAe−μAμDe−μD | (30) |
where μ
A and μ
D are the occupancy of the acceptor and donor in micelles, respectively. Given the bulk concentrations of D and A (
cf. the experimental section), the concentrations of D and A distributed in micelles (defined as the solute moles in micelles divided by the total volume of the whole micellar solution) can be evaluated by the following equations:
| | 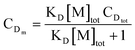 | (31) |
| | 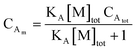 | (32) |
The occupancy of D and A in SDS micelles are calculated as μD = CDm/[M]tot and μA = CAm/[M]tot, and we therefore have
| | 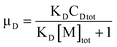 | (33) |
| | 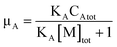 | (34) |
Given [M]tot = 8.06 × 10−6 M, KD = 4.5 × 104 M−1 and KA = 8.8 × 105 M−1, we have
| | | μD = 3.3023 × 104CDtot | (35) |
| | | μA = 1.0874 × 105CDtot | (36) |
Combining eqn (27) through (36) and taking into account the rate constants obtained by time-resolved experiments, the excited-state concentration of D may be calculated. However, the value of I(λi)kDex(λi) in eqn (27), and therefore that of [SD1]1, is not easily obtained. We are only able to obtain the relative value of [SD1]1 in the type 1 distribution.
The concentration of D in the type 2 distribution is
| | | CD2 = [M]tot(1 − PD(0))PA(0), | (37) |
and the excited-state concentration of [
SD1]
2 in this type of distribution is
| | 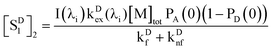 | (38) |
Addition of eqn (27) and (38) gives the total value of [SD1]m in the micelles,
| | 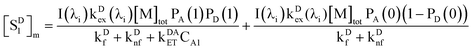 | (39) |
We omit 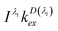 and obtain the relative value of [SD1]m in the micelles. Similarly, we obtain the relative value of [SD1]w in the water phase by omitting I(λi)kDex(λi) from eqn (39),
and obtain the relative value of [SD1]m in the micelles. Similarly, we obtain the relative value of [SD1]w in the water phase by omitting I(λi)kDex(λi) from eqn (39),
| | 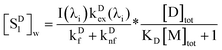 | (40) |
The ratio of eqn (39) to (40) is calculated as a function of CDtot and CAtot (Table 2). It is evident that the excited state concentrations of D in both phases are almost co-varying, because the ratio is narrowly distributed, with a mean 0.304 and standard deviation 0.012 (rsd = 3.9%).
Table 2 Total concentrations of D and A, their occupancies (μD and μA) in the micelles, relative concentrations of excited D and A under steady-state conditions in the micelles that have type 1 and 2 distributions, relative concentrations of excited D and A under steady-state conditions in the water phase as well as the ratios of the two phases for excited D and A. Note: the relative concentrations of excited A generated by FRET are not presented in this table. The relative concentration unit is ns × 10−6 M. [SD1]1 and [SD1]2 are the concentrations of excited D in micelles having the type 1 and type 2 distributions, respectively. [SD1]m = [SD1]1 + [SD1]2. [SA1]1 and [SA1]2 are the concentrations of excited A in micelles having the type 1 and type 2 distributions, respectively. [SA1]m = [SA1]1 + [SA1]2. [SD1]w and [SA1]w are the concentrations of excited D and A in the water phase, respectively. D ratio = [SD1]m/[SD1]w, and A ratio = [SA1]m/[SA1]w. N/A means “not available” for the ratio due to the zero denominators
| total D (μM) |
total A (μM) |
μD |
μA |
[SD1]1 |
[SD1]2 |
[SD1]m |
[SA1]1 |
[SA1]2 |
[SA1]m |
[SD1]w |
[SA1]w |
D ratio (m/w) |
A ratio (m/w) |
| 0 |
1.41 |
0.000 |
0.153 |
0.000 |
0.000 |
0.000 |
2.062 |
0.000 |
2.062 |
0.000 |
0.314 |
N/A |
6.576 |
| 1.76 |
1.41 |
0.058 |
0.153 |
0.140 |
4.138 |
4.278 |
1.946 |
0.105 |
2.050 |
13.690 |
0.314 |
0.312 |
6.538 |
| 3.52 |
1.41 |
0.116 |
0.153 |
0.263 |
8.043 |
8.306 |
1.836 |
0.197 |
2.033 |
27.381 |
0.314 |
0.303 |
6.484 |
| 5.28 |
1.41 |
0.174 |
0.153 |
0.373 |
11.727 |
12.100 |
1.732 |
0.279 |
2.012 |
41.071 |
0.314 |
0.295 |
6.415 |
| 7.04 |
1.41 |
0.232 |
0.153 |
0.469 |
15.203 |
15.672 |
1.634 |
0.352 |
1.986 |
54.762 |
0.314 |
0.286 |
6.333 |
| 7.04 |
1.06 |
0.232 |
0.115 |
0.366 |
15.793 |
16.159 |
1.252 |
0.275 |
1.526 |
54.762 |
0.236 |
0.295 |
6.474 |
| 7.04 |
0.7 |
0.232 |
0.076 |
0.251 |
16.424 |
16.675 |
0.843 |
0.189 |
1.031 |
54.762 |
0.156 |
0.304 |
6.624 |
| 7.04 |
0.35 |
0.232 |
0.038 |
0.131 |
17.061 |
17.191 |
0.429 |
0.098 |
0.527 |
54.762 |
0.078 |
0.314 |
6.774 |
| 7.04 |
0 |
0.232 |
0.000 |
0.000 |
17.722 |
17.722 |
0.000 |
0.000 |
0.000 |
54.762 |
0.000 |
0.324 |
N/A |
We also derived the analogous equations, for the total concentration of excited state A in micelles and in water phases respectively:
| | 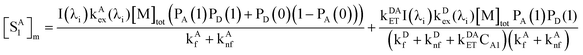 | (41) |
| | 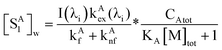 | (42) |
It should be noted that the first term on the right side of eqn (41) is the excited-state concentration of A that does not participate in FRET in micelles; the second term is associated with FRET. The ratio of the first term of eqn (41) to eqn (42) is tabulated as a function of CD and CA (Table 2). It is evident that these ratios are also very narrowly distributed, showing a mean 6.527 and standard deviation 0.135 (rsd = 2.1%), which is indicative of the co-varying relationship between excited state A (generated by direct absorption) in micelles and in water.
We were interested in comparing the PARAFAC scores and predicted scores based on theoretical calculations. Because the PARAFAC scores have absorbed many instrumental factors (e.g., voltage of PMT), we therefore focused on comparing the shapes of the score plots rather than the absolute values. Briefly, the scores of a given component at various D/A values (Fig. 4) are divided by the score at D/A = 4/0.8 (See Experimental Details for convention). Such normalization approach was applied to both PARAFAC-recovered scores and predicted scores, and these normalized scores were then compared (Fig. 6). As can be seen in Fig. 6, the predicted scores and PARAFAC-recovered scores are in good agreement.
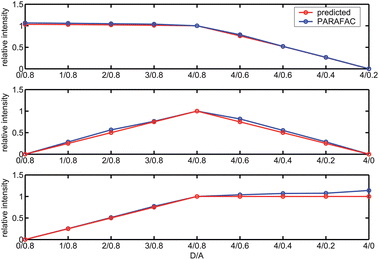 |
| | Fig. 6 Comparison between the predicted scores (in red) and 3-component PARAFAC-recovered scores (in blue) of free acceptors (top), FRET(middle) and free donors (bottom) for the SDS micellar solutions containing biphenyl as energy donors and 2,5-diphenyloxazole as energy acceptors. | |
As discussed above, in Table 2 we report the micelle:water ratios of excited A and excited D. The near constancy of these ratios for the range of concentrations studied in this work resulted in PARAFAC modeling each solute in both phases as a single component. (See Figures S5 and S6). Therefore, there are subtle differences between the PARAFAC-recovered excitation spectrum of free D (a two-phase composite) and that of the D which undergoes FRET in type 1 micelles (Figure S7); similarly for the emission of free A (a two-phase composite) and that of A excited by FRET in type 2 micelles (Figure S8). In a previous study, our experimental design ensured enough variation in the concentrations in the two phases to permit the pure spectra of the solutes in each phase to be determined with PARAFAC.17 The excitation spectrum of D and emission spectrum of A in type 1 micelles were found to be the same as the excitation and emission spectrum of the FRET component in type 1 micelles identified by PARAFAC (Figure S9), which further substantiates the validity of the 3-component model.
4. Verification of time-resolved experiments using Poisson distribution
The pre-exponential factors were also consistent with Poisson statistics, as follows. Steady-state experiments showed that D emission at 313 nm decrease by 1.64% in the presence of A (D/A = 4/0.8). In sample D/A = 4/0.8, D has mean occupancy 0.232 whereas A has mean occupancy 0.153 (Table 2). SDS micelle concentration is 8.06 μM, so the concentration of micelles simultaneously containing one D and one A (a D–A pair) is 8.06 × PA(1) × PD(1), where PA(1) = 0.153exp(−0.153) and PD(1) = 0.232exp(−0.232). Calculation gives that ∼0.1947 μM micelles contain D–A pair. In other words, the concentration of D that participates in FRET is ∼0.1947 μM. Since the total concentration of D is 7.04 μM, 0.1947 μM corresponds to 2.77% of the D population, which is in good agreement with the pre-exponential value of 2.6% recovered by the ESM fitting. It should be emphasized that 2.77% of D participating in FRET does not mean that D's emission decreases by 2.77%; the decrease of D's emission also depends on the FRET efficiency. When this is taken into account, as shown above, the result is a 2% drop in D's emission, which was verified independently by steady state measurements.
Experimental details
1. Materials
Surfactant
sodium dodecyl sulfate (SDS) with purity >99.5% was purchased from Sigma-Aldrich and was used as received. Biphenyl (D) and 2,5-diphenyloxazole (A) were used as received (Sigma-Aldrich, >99.9%). A series of stock solution containing only D or only A or mixed D and A were made by dissolving appropriate quantities of D or A or both in HPLC grade methanol. The concentrations of D in the stock solutions were 14.08, 10.56, 7.04 and 3.52 mM, whereas A's concentration were one fifth of that of D, i.e. 2.82, 2.11, 1.41 and 0.70 mM, respectively. Our preliminary studies indicated that at the same concentrations, A gives much stronger fluorescence than D; one-fifth concentration of A (ca.) ensures comparable fluorescence to that of D. These stock solutions were capped tightly with Teflon tape and stocked in the dark prior to use.
To 1000 ml volumetric flasks were added appropriate volumes of SDS aqueous solution, 0.5 ml of methanol stock solution (neat D or neat A or D–A mixed) and water to bring the total volume close to the mark. The solutions were sonicated for 6 h and allowed to equilibrate for ∼12 h before more water was added to bring the total volume to the mark. The 1000-mL solutions were allowed to equilibrate for another ∼12 h to ensure complete equilibrium. The 0.5 ml of methanol in the total 1000 ml of working solution is negligible. For simplicity when referring to the samples in other parts of this paper, number “4” is used to denote 7.04 μM, and “0.8” is used to denote 1.41 μM, etc. The concentrations of working solutions were expressed as D/A = 0/0.8, 1/0.8, 2/0.8, 3/0.8, 4/0.8, 4/0.6, 4/0.4, 4/0.2, 4/0, the order of which was indicative of first increasing D concentration (0 through 4) at fixed A concentration (0.8), then decreasing A concentration (0.8 through 0) at fixed D concentration (4).
2. Optical measurements
Optical measurements were performed at 20 °C. Absorbance was measured on a Cary 300 spectrometer with double beam mode with wavelength scanned from 225 to 500 nm with nanopure water as blank. Bandwidth was set 5 nm. The maximal absorbance of the samples in the scanned wavelength range was less than 0.2 per cm in this study. EEMs were measured on a Varian Cary Eclipse fluorometer (Varian Inc.) with excitation and emission wavelengths scanned from 225 to 500 nm with 5-nm increments and from 250 to 550 nm with 1-nm increments, respectively. Light scattering in the EEMs was mathematically replaced with not-a-number values (NaN), following the treatment of previous studies. IFE correction was applied.26 The optical geometry parameters for the excitation beam and emission beam in the cuvette were provided by Varian. The time-resolved experimental setup utilized a 10-Hz PTI Time-Master system. A nitrogen laser (NL_3300) operating at 10 pulses per second pumped a dye laser (NL_302) coupled to a frequency doubler crystal (NL_303).
3. Analysis
The scattering-removed, IFEs-corrected EEMs were fitted to PARAFAC models. The PARAFAC routine was provided by commercial software package PLS_Toolbox 3.0.4 (Eigenvector Research, Inc). Orthogonal random initial values were generated by PARAFAC to start the fit. Maximum iteration number and time for the alternating least square (ALS) algorithm in PARAFAC were set to 1000 and 3600 s, respectively. Fit convergence criteria was set to 1E-6, and as such, whenever either absolute or relative change in fit residuals is less than or equal to 1e-6 the ALS procedure stops. Core consistency test was employed to evaluate whether the correct number of components is chosen. Visual check of the fit residuals also helped judge the fit, as the random distribution of the residuals was indicative that the EEMs have been adequately modeled.
Conclusions
We have designed, performed and analyzed an experiment in which FRET donors and acceptors are distributed between aqueous and micelle phases, with jointly occupied micelles satisfying the distance requirement for FRET. Theoretical derivations based on steady-state kinetics indicate that EEMs in the presence of intermolecular energy transfer can be decomposed into separate contributions from three parts: one from donors, one from acceptors and one from FRET. The theory has been verified in sodium dodecyl sulfate micellar solutions containing biphenyl as the donor and 2,5-diphenyloxazole as the acceptor. A 3-component PARAFAC model is shown to be the best for this FRET system in this study. The identified spectra and relative concentrations of each component have been well interpreted by means of Poisson statistics. The extent of FRET has been independently measured or calculated by three methods: 1) decrease in steady state fluorescence of donor; 2) lifetime measurements with population analysis; and 3) Poisson statistics based on PARAFAC-determined distribution constants. The normalized scores of the three components found by PARAFAC also agree to within a few percent with relative concentrations in aqueous and micelle phases determined from distribution constants for the solutions prepared with nine different combinations of total donor and acceptor concentrations. Finally, the relationship between score and concentration for a component determined by PARAFAC has been for the first time developed in detail.
Acknowledgements
This work was supported in part by a Tufts University “New Directions” Faculty Research Award.
Notes and references
- R. Bro, Crit. Rev. Anal. Chem., 2006, 36, 279 CrossRef CAS.
- T. Ohno, A. Amirbahman and R. Bro, Environ. Sci. Technol., 2008, 42, 186 CrossRef CAS.
- T. Ohno, I. J. Fernandez, S. Hiradate and J. F. Sherman, Geoderma, 2007, 140, 176 CrossRef CAS.
- C. A. Stedmon, S. Markager, L. Tranvik, L. Kronberg, T. Slatis and W. Martinsen, Mar. Chem., 2007, 104, 227 CrossRef CAS.
- C. A. Stedmon, D. N. Thomas, M. Granskog, H. Kaartokallio, S. Papadimitriou and H. Kuosa, Environ. Sci. Technol., 2007, 41, 7273 CrossRef CAS.
- Y. Yamashita, R. Jaffe, N. Maie and E. Tanoue, Limnol. Oceanogr., 2008, 53, 1900 CrossRef CAS.
- Y. Yamashita and R. Jaffe, Environ. Sci. Technol., 2008, 42, 7374 CrossRef CAS.
- Z. C. Cui, W. Q. Liu, N. J. Zhao, X. Xiao, Z. G. Wang, Y. J. Zhang, W. C. Sima, J. G. Liu and Q. N. Wei, Spectroscopy and Spectral Analysis, 2008, 28, 1332 CAS.
- J. F. Hunt and T. Ohno, J. Agric. Food Chem., 2007, 55, 2121 CrossRef CAS.
- M. R. Banaitis, H. Waldrip-Dail, M. S. Diehl, B. C. Holmes, J. F. Hunt, R. P. Lynch and T. Ohno, J. Colloid Interface Sci., 2006, 304, 271 CrossRef CAS.
- R. M. Cory and D. M. McKnight, Environ. Sci. Technol., 2005, 39, 8142 CrossRef CAS.
- C. A. Stedmon, S. Markager and R. Bro, Mar. Chem., 2003, 82, 239 CrossRef CAS.
- J. B. Fellman, D. V. D'Amore, E. Hood and R. D. Boone, Biogeochemistry, 2008, 88, 169 CrossRef CAS.
- G. J. Hall, K. E. Clow and J. E. Kenny, Environ. Sci. Technol., 2005, 39, 7560 CrossRef CAS.
- R. Bro and H. A. L. Kiers, J. Chemom., 2003, 17, 274 CrossRef CAS.
- R. Bro, R. A. S. N. D. Harshman and M. E. Lundy, J. Chemom., 2009, 23, 324 CrossRef CAS.
- H. Chen and J. Kenny, Analyst, 2010, 135, 1704 RSC.
- S. Leurgans and R. T. Ross, Stat. Sci., 1992, 3, 289 CrossRef.
- R. T. Ross and S. Leurgans, Methods Enzymol., 1995, 246, 679 CAS.
- R. Harshman, Talk presented to TRIC (Three-way analysis methods in Chemistry) in Epe, Holland, 1993 Search PubMed.
-
J. R. Lakowicz. Principles of fluoresecence spectroscopy, 3rd ed.; Springer: New York, 2006 Search PubMed.
- Q. Gu and J. Kenny, Analytical Chemistry, 2008, 1, 420 Search PubMed.
- R. Bro, Chemom. Intell. Lab. Syst., 1997, 38, 149 CrossRef CAS.
-
I. B. Berlman. Handbook of fluorescence spectra of aromatic molecules, 2nd ed.; Academic Press: New York, 1971 Search PubMed.
- M. Almgren, F. Grieser and J. K. Thomas, J. Am. Chem. Soc., 1979, 101, 279 CrossRef CAS.
- B. C. MacDonald, S. J. Lvin and H. Patterson, Anal. Chim. Acta, 1997, 338, 155 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Includes justification of weak excitation condition, appropriateness of Donor–Acceptor pair, discussion of 4 and 5 component PARAFAC models, and details of PARAFAC-recovered spectra. See DOI: 10.1039/c1an15805h |
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. 
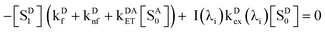
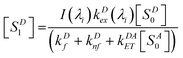
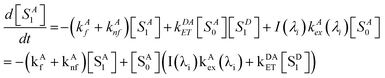
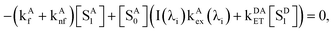
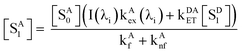
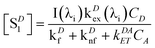
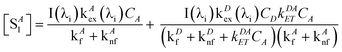
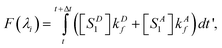
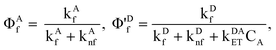
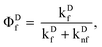
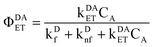
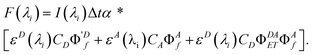
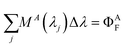
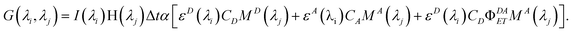
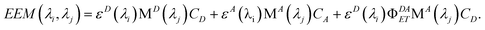
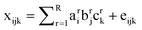
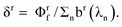
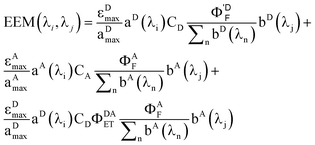
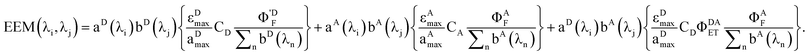



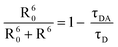
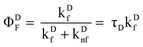
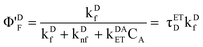
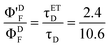
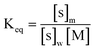


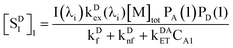
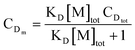
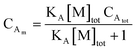
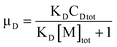
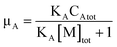
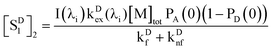
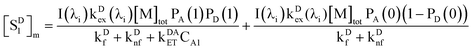
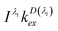 and obtain the relative value of [SD1]m in the micelles. Similarly, we obtain the relative value of [SD1]w in the water phase by omitting I(λi)kDex(λi) from eqn (39),
and obtain the relative value of [SD1]m in the micelles. Similarly, we obtain the relative value of [SD1]w in the water phase by omitting I(λi)kDex(λi) from eqn (39),