Enhanced spectrophotometric methods for trace metal determination in waters: zinc as an example
Juan J.
Pinto
*,
Manuel
García-Vargas
and
Carlos
Moreno
Department of Analytical Chemistry, Faculty of Marine and Environmental Sciences, University of Cádiz, 11510, Puerto Real, Spain. E-mail: juanjose.pinto@uca.es
First published on 23rd November 2011
Abstract
Although spectrophotometric methods seem to be outdated as analytical tools for the analysis of trace metals in waters, there is no doubt that they still present a series of advantages over other advanced techniques (simplicity, speed, low cost and maintenance, portable instrumentation, etc.). Even more, if experimental conditions are strictly controlled, it is possible to develop highly competitive methods. In this sense, method validation turns into a key feature to improve and demonstrate its applicability. Bearing this in mind, a simple and very sensitive spectrophotometric method for the direct determination of μg L−1 levels of zinc in natural waters has been developed and in-house validated. It is based on the reaction of Zn(II) with di-2-pyridyl ketone benzoylhydrazone (dPKBH) under slightly acidic conditions (pH 6.4) and 15% (v/v) ethanol to produce a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (Zn
2 (Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dPKBH) complex (λmax 370 nm). Beer's law is obeyed in the range 6.3–3000 μg L−1Zn(II) with a detection limit of 0.7 μg L−1. Different parameters such as selectivity, recovery, linearity, limits of detection and quantification, precision, and uncertainty of the measurements were evaluated in order to validate the proposed method. Then, the new method was applied to the analysis of different water samples (e.g., tap and river water), demonstrating its applicability to the determination of Zn at environmental levels.
dPKBH) complex (λmax 370 nm). Beer's law is obeyed in the range 6.3–3000 μg L−1Zn(II) with a detection limit of 0.7 μg L−1. Different parameters such as selectivity, recovery, linearity, limits of detection and quantification, precision, and uncertainty of the measurements were evaluated in order to validate the proposed method. Then, the new method was applied to the analysis of different water samples (e.g., tap and river water), demonstrating its applicability to the determination of Zn at environmental levels.
1. Introduction
Zinc is an essential trace metal for humans, animals and plants. It naturally occurs in food, sediments and water, but when it is present in excess it can be toxic.1 High levels of zinc in natural waters can be related to anthropogenic activities such as mining, smelting, water sewage, etc. Therefore, the knowledge of zinc concentration in natural waters may serve to characterise the pollution level of a certain area.2Several analytical techniques may be used for trace zinc determination such as differential pulse anodic stripping voltammetry (dPASV),3,4flame atomic absorption spectroscopy (FAAS),5,6graphite furnace atomic absorption spectroscopy (GFAAS),7inductively coupled plasma atomic emission spectroscopy (ICP-AES),8,9 and inductively coupled plasma mass spectrometry (ICP-MS).10 Besides its well-known advantages, they also present a series of disadvantages such as higher investment cost, complexity, time-consuming or difficulty for in situ application. Moreover, in many cases it has been necessary to carry out a preconcentration step in order to improve the detection limit as well as the selectivity of the method. In environmental monitoring, safe, simple and sensitive analytical methods are needed. In this context, spectrophotometric methods are shown as an alternative, because of their simplicity, speed, low cost, and availability of portable instrumentation to get in situ measurements.
A large number of spectrophotometric methods were developed to evaluate the zinc concentration in different matrices.11–14 All of them were based on the formation of a coloured complex obtained by the reaction of the metallic ion with the suitable chelating organic compound, such as the hydrazone derivatives 2,4-dihydroxy benzaldehyde isonicotinoyl hydrazone,15di-2-pyridyl ketone salicyloylhydrazone,16 or di-2-pyridyl ketone benzoylhydrazone (dPKBH).17 The latter has been previously used for the spectrophotometric determination of iron,18–20palladium,21cobalt,22–24 and nickel25,26 in different matrices. Besides, it has been successfully applied to the direct spectrophotometric determination of copper in natural waters.27,28
In this sense, owing to the ability of dPKBH to react with divalent cations, we have developed a spectrophotometric method to analyse zinc in water samples with a doubled objective. On the one hand, we have optimised a new spectrophotometric method which is capable of quantifying microamounts of zinc in natural waters without a previous preconcentration step. On the other hand, in order to demonstrate reliability of the analytical results, we validated the proposed methodology. Thus, a set of performance characteristics, selected depending on the analytical problem to be solved, must be previously verified in order to guarantee its applicability.29 Usually these are derived by using statistical procedures, being the commonest: trueness, precision, selectivity, sensitivity, linear and working range, limits of detection and quantification and ruggedness.30 Besides, measurement uncertainty and fitness-for-purpose can be added.31 Finally, the purpose and type of method, the type and concentration range of analyte(s) to be measured, the type of matrices or materials for which the method will be applied and an “experimental procedure” must be stated.32
2. Experimental
2.1 Reagents and solutions
All the chemicals used were of analytical-reagent grade and purchased from Merck (Darmstadt, Germany). All the solutions were prepared with MilliQ water (Millipore, USA). The spectrophotometric reagent dPKBH was synthesized according to the procedure outlined by García-Vargas et al.33 Then, stock solutions of dPKBH (0.4% w/v) were prepared by dissolving the synthesized reagent in ethanol, and diluted with MilliQ water as required.Commercial standard solutions of 1000 ± 2 mg L−1Zn(II) were purchased from Merck. Working solutions were prepared daily by appropriate dilution of the standard solution in water.
A 0.2 M stock phosphate buffer solution at pH 6.4 was prepared by dissolving the appropriate amounts of Na2HPO4 and KH2PO4 in water. When required, different working buffer solutions were prepared by dilution.
For selectivity evaluation, anions were added as sodium or potassium salts, while cations were added as nitrates or chlorides.
2.2 Instruments
Spectrophotometric measurements were carried out by using a PU 8750 UV/VIS spectrophotometer (Philips, The Netherlands) equipped with a quartz cell with 10 mm path length (Hellma, Germany).The acidity was measured with a Model 2001 pH-meter provided with a combined glass–Ag/AgCl electrode (Crison, Spain).
2.3 Optimisation
In order to achieve the optimal experimental conditions at which complex formation took place, we studied the chemical variables affecting the behaviour of the system. Therefore, we varied pH of the aqueous solution, concentration of phosphate buffer solution, concentration of dPKBH and concentration of ethanol. The influence of other variables such as the order of reagents addition, the composition of the complex and the reaction time was also studied.All the experiments were carried out with solutions containing 1 mg L−1Zn(II) prepared under different conditions and by measuring the absorbance of the Zn(II)–dPKBH complex against its corresponding blank at 370 nm.
2.4 Validation
In order to check if the method fits for its intended purpose, selectivity, recovery, linearity, limits of detection and quantification, precision, and uncertainty were established.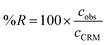 | (1) |
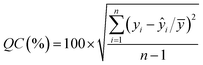 | (2) |
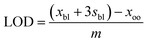 | (3) |
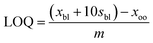 | (4) |
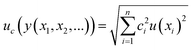 | (5) |
Finally, an expanded uncertainty (U) is established in order to obtain an interval within which the value of the measurand is believed to lie with a higher level of confidence. The value of U is obtained by multiplying uc by a coverage factor (k). Usually, k = 2 for a confidence level of 95%.
3. Procedure
3.1 Determination of zinc(II)
The proposed method was applied to the analysis of two different real samples in order to verify its applicability. In this sense, a tap water sample, collected from the own facilities of the laboratory, and a river water sample were selected. Both samples were previously analysed by FAAS, and significant concentrations for different metals (13.21 μg L−1Cu; 41.07 μg L−1Fe; 146.66 μg L−1Al and 2.56 μg L−1Mn in tap water sample and 542 μg L−1Cu; 604 μg L−1Fe and 63.8 μg L−1Pb in river water sample) were found. Next, both samples were analysed by the proposed method as follows.An aliquot of sample was transferred into a 10 mL volumetric flask, and then 0.2 mL of 0.4 M sodium thiosulfate, 0.4 mL of 0.0085 M dimethylglyoxime, 0.25 mL of 0.2 M phosphate buffer solution, 0.25 mL of 0.013 M dPKBH and 1.25 mL of ethanol were added in this order. Finally, the sample was diluted to the mark with MilliQ water and mixed thoroughly. The absorbance of the yellow complex was measured at 370 nm against the corresponding reagent blank.
4. Results and discussion
4.1 Optimisation of the spectrophotometric system
The absorption spectrum of the Zn(II)–dPKBH complex was obtained by reacting several solutions containing 1 mg L−1Zn(II) with an excess of dPKBH and 10% v/v ethanol, at different acidities. Corresponding blank solutions were prepared in the same way but in the absence of Zn(II). The maximum absorbance obtained for the complex Zn(II)–dPKBH was always found at 370 nm while for blank solution showed negligible. Therefore, all the experiments were carried out at this wavelength.Firstly, the influence of the chemical variables affecting the correct formation of the complex was studied. In Fig. 1a are shown the results obtained when solution pH was varied in the range 3–11. As it can be seen, an increase in the signal with pH up to 6–8 was obtained, indicating the range at which complex formation took place under optimum conditions. As a consequence, a pH value of 6.4 was selected as optimum. Next, a phosphate buffer solution was employed in order to control the pH of the samples. Thus, we varied its concentration in the range 2.5 × 10−3 to 1.0 × 10−2 mol L−1 and the signal was practically independent of the buffer concentration. A 5 × 10−3 mol L−1buffer concentration was selected to ensure the complex formation with acidified samples. The effect of the dPKBH concentration on the complex formation is shown in Fig. 1b. As it can be seen, in the absence of reagent no signal was obtained and it was increasing with reagent concentration until a plateau was reached. Thus, 3.25 × 10−4 mol L−1 was selected for further studies. Finally, to ensure the absence of any precipitates in the solution, the final concentration of ethanol was studied in the range 2.5–50% v/v. A slight increase in the absorbance up to 20% v/v of ethanol was observed, and then it was independent of the concentration. We selected as optimum a final concentration of ethanol in the solution of 15% v/v.
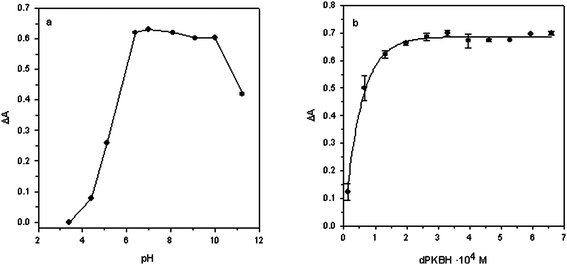 | ||
| Fig. 1 Effect of (a) pH and (b) dPKBH concentration on the complex formation. (a) 1 mg L−1Zn(II); 3.25 × 10−4 mol L−1dPKBH; 10% v/v ethanol and (b) 1 mg L−1Zn(II); pH 6.4; 5 × 10−3 mol L−1phosphate buffer; 10% v/v ethanol. | ||
Once the chemical variables were optimised, we studied other experimental conditions such as the order of reagent addition, the stability of the complex and its stoichiometry. Among the proposed orders of addition, the highest signal was obtained for: Zn2+ + buffer + dPKBH + ethanol.
The composition of the complex was studied by applying Job's method of continuous variations and the molar ratio method. In both of them, the results suggested the formation of a complex with a stoichiometric ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 of Zn(II) to dPKBH. Finally, the stability of the complex was determined by measuring the absorbance as a function of time. The results obtained demonstrated that it remained stable for sixty minutes and then, a decay of about 10% in the signal in the next thirty minutes was observed.
2 of Zn(II) to dPKBH. Finally, the stability of the complex was determined by measuring the absorbance as a function of time. The results obtained demonstrated that it remained stable for sixty minutes and then, a decay of about 10% in the signal in the next thirty minutes was observed.
4.2 Validation of the method
| Ion | Molar ratio |
|---|---|
| Cl −, Br−, F−, I−, NO3−, SO42−, ClO4−, S2O32−, Na+, K+, NH4+, oxalate, acetate | >20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Tartrate, citrate | 5000 |
| NO2− | 1000 |
| Sn(II) | 2 |
| Pb(II), Al(III), Mn(II), Cr(III), Fe(III) | 1 |
| Co(II), Ni(II), Cu(II), Cd(II), Hg(II), Fe(II) | <0.25 |
| n | [Zn]/mg L−1 | a | m | r 2 | (%) QC |
|---|---|---|---|---|---|
| a a.a. = as above. | |||||
| 4 | 0.00–0.03 | 0.0724 | 0.6820 | 0.9896 | 1.55 |
| 5 | a.a. + 0.04 | 0.0724 | 0.6813 | 0.9948 | 1.29 |
| 6 | a.a. + 0.05 | 0.0724 | 0.6838 | 0.9970 | 1.11 |
| 7 | a.a. + 0.06 | 0.0722 | 0.6936 | 0.9980 | 1.02 |
| 8 | a.a. + 0.10 | 0.0750 | 0.5813 | 0.9870 | 3.09 |
| 9 | a.a. + 0.20 | 0.0746 | 0.5917 | 0.9969 | 2.63 |
| 10 | a.a. + 0.50 | 0.0730 | 0.6253 | 0.9993 | 2.51 |
| 11 | a.a. + 1.00 | 0.0735 | 0.6185 | 0.9998 | 1.83 |
| 12 | a.a. + 2.00 | 0.0693 | 0.6497 | 0.9996 | 3.83 |
| 13 | a.a. + 3.00 | 0.0715 | 0.6392 | 0.9998 | 3.12 |
| 14 | a.a. + 4.00 | 0.0837 | 0.5991 | 0.9978 | 9.35 |
| Technique | Reagent | ε a | Precision | LOD/μg L−1 | Reference |
|---|---|---|---|---|---|
| a Molar absorptivity (L mol−1 cm−1) × 104. b Preconcentration factor of 200. c Enrichment factor of 12. | |||||
| FAAS b | Microcrystalline triphenylmethane + malachite green | — | — | 0.05 | 6 |
| GFAAS | — | — | — | 0.247 | 7 |
| ICP-AES c | Iminodiacetate chelating resin | — | — | 0.02 | 9 |
| UV-Vis spectrophotometry | N-Ethyl-3-carbazolecarboxaldehyde-3-thiosemicarbazone | 1.55 | 0.97% | — | 11 |
| UV-Vis spectrophotometry | 1-(2-Pyridylazo)2-naphthol | — | 2.0% | — | 12 |
| UV-Vis spectrophotometry | 4-(2-Pyridylazo)-resorcinol | — | — | 11.0 | 13 |
| UV-Vis spectrophotometry | 2,6-Bis(1-hydroxy-2-naphthylazo)pyridine | 6.00 | 1.0% | — | 14 |
| UV-Vis spectrophotometry | 2,4-Dihydroxybenzaldehyde isonicotinoyl hydrazone | 3.55 | 1.2% | — | 15 |
| UV-Vis spectrophotometry | Di-2-pyridyl ketone salicyloylhydrazone | 4.82 | 2.0% | 4.0 | 16 |
| UV-Vis spectrophotometry | Di-2-pyridyl ketone benzoylhydrazone | 3.64 | 0.5% | 2.29 | 17 |
| UV-Vis spectrophotometry | Di-2-pyridyl ketone benzoylhydrazone | 4.20 | 1.7% | 0.7 | This method |
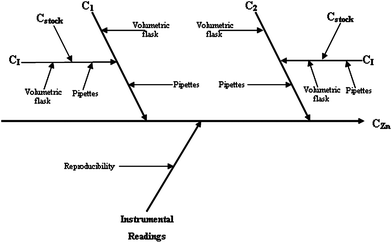 | ||
| Fig. 2 Cause and effect diagram for the spectrophotometric determination of zinc. | ||
The uncertainty related to the instrumental readings was calculated by multiplying the average absorbance (for samples or standards, analysed in triplicate) by the within-laboratory reproducibility.
The zinc concentration in the samples (CZn) was calculated according to the model equation proposed below, in which the absorbance for the sample (As) was related to the corresponding absorbances of the neighbourhood standards (A1 and A2) and its concentration (C1 and C2) as follows:
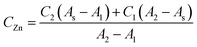 | (6) |
Once the combined uncertainty was calculated, a coverage factor k = 2 was employed in order to obtain the expanded uncertainty. Thus, the concentration of zinc in LGC 6011 and SRM 1643d was calculated as 522 ± 52 μg L−1 and 71.96 ± 9.69 μg L−1, respectively. The certified values of zinc concentrations were 514 ± 25 μg L−1 and 72.48 ± 0.65 μg L−1 for LGC 6011 and SRM 1643d. When comparing these results it was observed that expanded uncertainty overlapped in both cases (see Fig. 3). Therefore, the results have demonstrated the fit for the intended purpose of the proposed method to analyse the zinc concentration in natural waters.
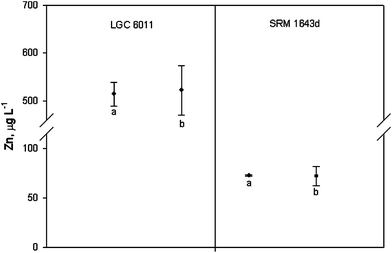 | ||
| Fig. 3 Determination of zinc in the CRMs. Values are expressed as mean ± expanded uncertainty ((a) certified zinc concentration and (b) calculated by the validated method). | ||
5. Application of the proposed method
When a new method is proposed, it is not truly applicable if its validity in the analysis of real samples has not been previously demonstrated. Two different real samples (tap water and river water) were analysed five times and then, the zinc concentration was calculated by using eqn (6). The obtained results were compared with that of FAAS, previously employed to quantify the zinc concentration and some of the interferences, as shown in Table 4. As it can be seen, the relative expanded uncertainty was below 10% in both samples. According to this, the method has demonstrated its applicability for the determination of zinc in natural waters.Furthermore, from the evaluation of methods (Table 3) using reagents different from those of hydrazone derivatives, only 2,6-bis(1-hydroxy-2-naphthylazo)pyridine14 showed higher sensitivity, although a higher percentage of ethanol (50% v/v) was required. The same percentage of ethanol was also employed in two of the methods using hydrazone derivatives, those using di-2-pyridyl ketone salicyloylhydrazone16 and di-2-pyridyl ketone benzoylhydrazone.17 Although the former was slightly more sensitive, it was balanced by the better precision and detection limit in the proposed method. Besides, higher sensitivity and better detection limit than that using the same reagent were obtained.
6. Conclusions
A simple and very sensitive spectrophotometric method has been developed for the direct determination of zinc ions in natural waters without a preconcentration step. A detection limit of 0.7 μg L−1, similar to that of advanced spectroscopic techniques, makes it one of the best spectrophotometric methods for the direct determination of zinc in natural waters.In addition, the method has been in-house validated according to the EURACHEM guide, with the results showing the fitness for the purpose of the proposed method. On the other hand, the study has been completed with the determination of the uncertainty. In this sense, different sources of error were detected and taken into account. Finally, the results obtained when analyzing real water samples of different composition revealed the applicability of the proposed method.
References
- G. F. Nordberg, B. Sandström, G. Becking and R. A. Goyer, Essentiality and Toxicity of Metals, in Heavy Metals in the Environment, Marcel Dekker, New York, 2002, pp. 1–34 Search PubMed.
- V. A. Lemos, W. N. L. dos Santos, J. L. Santos and M. B. de Carvalho, Anal. Chim. Acta, 2003, 481(2), 283 CrossRef CAS.
- K. Tyszczuk, M. Korolczuk and M. Grabarczyk, Talanta, 2007, 71(5), 2098 CrossRef CAS.
- S. Yilmaz, S. Yagmur, G. Saglikoglu and M. Sadikoglu, Int. J. Electrochem. Sci., 2009, 4(2), 288 Search PubMed.
- V. N. Bulut, A. Gundogdu, C. Duran, H. B. Senturk, M. Soylak, L. Elci and M. Tufekci, J. Hazard. Mater., 2007, 146(1–2), 155 CrossRef CAS.
- Q. Li, X. Zhao, Q. Lv and G. Liu, Sep. Purif. Technol., 2007, 55(1), 76 Search PubMed.
- C. Terrés, M. Navarro, F. Martín, R. Jiménez, H. López and M. C. López, Water Res., 2002, 36(7), 1912 Search PubMed.
- H. Zheng, X. Chang, N. Lian, S. Wang, Y. Cui and Y. Zhai, Int. J. Environ. Anal. Chem., 2006, 86(6), 431 Search PubMed.
- R. K. Katarina, N. Lenghor and S. Motomizu, Anal. Sci., 2007, 23(3), 343 CrossRef.
- D. Point, G. Bareille, H. Pinaly, C. Belin and O. F. X. Donard, Talanta, 2007, 72(3), 1207 CrossRef CAS.
- K. J. Reddy, J. R. Kumar, T. Ramachandraiah, T. Thriveni and A. V. Reddy, Food Chem., 2007, 101(2), 585 CrossRef CAS.
- M. Arvand, S. Abolghasemi and M. A. J. J. Zanjanchi, Anal. Chem., 2007, 62(4), 342 Search PubMed.
- Y. Ni, Y. Wang and S. Kokot, Anal. Lett., 2007, 40(6), 1209 CrossRef CAS.
- A. K. Sharma and I. Singh, Food Anal. Methods, 2009, 2(4), 311 Search PubMed.
- S. Sivaramaiah and P. R. J. Reddy, Anal. Chem., 2005, 60(9), 828 Search PubMed.
- I. Gaubeur, M. C. C. Areias, L. H. S. Ávila-Terra and M. E. V. Suárez-Iha, Spectrosc. Lett., 2002, 35(3), 455 Search PubMed.
- L. E. M. Vieira, F. P. Vieira, L. H. S. Ávila-Terra, I. Gaubeur, M. Guekezian and M. E. V. Suárez-Iha, Anal. Lett., 2008, 41(5), 779 CrossRef CAS.
- T. Nakanishi and M. Otomo, Microchem. J., 1986, 33(2), 172 CAS.
- N. A. Zatar, A. Z. Abu-Zuhri, M. A. Al-Nuri, F. M. Mahmoud and A. Abu-Obai, Spectrosc. Lett., 1989, 22(9), 1203 CAS.
- S. O. Pehkonen, Y. Erel and M. R. Hoffmann, Environ. Sci. Technol., 1992, 26(9), 1731 CAS.
- T. Nakanishi and M. Otomo, Anal. Sci., 1985, 1(2), 161 CAS.
- M. A. Al-Nuri, M. Abu-Eid, N. A. Zatar, S. Khalaf, M. Hannoun and M. Khamis, Anal. Chim. Acta, 1992, 259(1), 175 CrossRef CAS.
- N. A. Zatar, M. A. Al-Nuri, M. Abu-Eid, M. Hannoum and A. Z. Abu-Zuhri, Spectrosc. Lett., 1991, 24(9), 1145 Search PubMed.
- M. V. Rossi, M. E. V. Suárez-Iha and M. R. Hoffmann, Spectrosc. Lett., 1995, 28(8), 1153 Search PubMed.
- L. H. S. Ávila-Terra and M. E. V. Suárez-Iha, Spectrosc. Lett., 1997, 30(4), 625 Search PubMed.
- L. H. S. Ávila-Terra, M. C. D. Areias, I. Gaubeur and M. E. V. Suárez-Iha, Spectrosc. Lett., 1999, 32(2), 257 Search PubMed.
- J. J. Pinto, C. Moreno and M. García-Vargas, Anal. Bioanal. Chem., 2002, 373(8), 844 CrossRef CAS.
- J. J. Pinto, C. Moreno and M. García-Vargas, Talanta, 2004, 64(2), 562 CrossRef CAS.
- IUPAC, Harmonised Guidelines for In-house Validation of Methods of Analysis (Technical Report), 1999, http://old.iupac.org/divisions/V/501/draftoct19.pdf Search PubMed.
- EURACHEM/CITAC, Fitness for Purpose of Analytical Methods: a Laboratory Guide to Method Validation and Related Topics, 1998, http://www.eurachem.org/guides/valid.pdf Search PubMed.
- M. Thomson, S. L. R. Ellison and R. Wood, Pure Appl. Chem., 2002, 74(5), 835 CrossRef CAS.
- I. Taverniers, M. De Loose and E. Van Bockstaele, Trends Anal. Chem., 2004, 23(8), 535 CrossRef CAS.
- M. García-Vargas, M. Belizón, M. P. Hernández-Artiga, C. Martínez and J. A. Pérez-Bustamante, Appl. Spectrosc., 1986, 40(7), 1058 CAS.
- P. Vankeerberghen and J. Smeyers-Verbeke, Chemom. Intell. Lab. Syst., 1992, 15(2–3), 195 CrossRef CAS.
- JCGM Guide 100, Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement, 2008 Search PubMed.
- J. Kragten, Analyst, 1994, 119(10), 2161 RSC.
| This journal is © The Royal Society of Chemistry 2012 |
