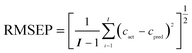DOI:
10.1039/C1AY05388D
(Paper)
Anal. Methods, 2012,
4, 222-229
Measuring estriol and estrone simultaneously in liquid cosmetic samples using second-order calibration coupled with excitation–emission matrix fluorescence based on region selection
Received
29th June 2011
, Accepted 26th October 2011
First published on 23rd November 2011
Abstract
This paper describes a sensitive excitation–emission matrix fluorescence (EEM) method for simultaneously measuring contents of two estrogens, estriol (E3) and estrone (E1), in liquid cosmetic samples with the aid of a second-order calibration method based on a parallel factor analysis (PARAFAC) algorithm. Before processing the obtained three-way data, a better region of the excitation and emission spectra was purposely selected. Then PARAFAC was recommended to acquire the clean spectra and predict the individual concentrations of the analytes of interest even in the presence of uncalibrated interferences. The standard curves of the two analytes are linear within a linear concentration range of 0–0.736 μg mL−1 of E3 and 0–18.000 μg mL−1 of E1 with correlation coefficients typically greater than 0.99. In the analysis of watermelon frost anti-acne toner sold on the internet web site, the limit of detection (LOD) of E3 is 4.7 ng mL−1 with an accuracy of 102.3–113.7%, and for E1, the LOD is 96.1 ng mL−1 with an accuracy of 92.3–111.0%. In the analysis of pagoda flower relaxing lotion from the commercial market in Changsha, the LOD of E3 is 8.9 ng mL−1 with an accuracy of 95.0–107.1%, and for E1, the LOD is 76.9 ng mL−1 with an accuracy of 98.6–119.3%. Generally, a new avenue has been opened up to determine estrogens quantitatively in cosmetic samples. This methodology will achieve greater development and gradually become a more routine approach in cosmetic quality control due to its advantages of high sensitivity, simple pretreatment procedure and non-destructive nature.
1. Introduction
In recent years, a massive amount of substandard cosmetic products have been successively exposed, which has raised extensive concerns about the security of cosmetics. It is reported that in most of the unqualified cosmetics the primary illegal additives are hormones, which can produce adverse effects in consumers. Therefore, monitoring the potential presence of non-allowed hormones in cosmetics is essential to prevent their serious consequences.
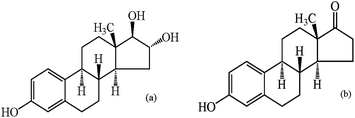
In this paper, we focus on two natural estrogens which are strictly prohibited to exist in cosmetics by China1 and European Commission.2Estriol (E3, Fig. 1a) and estrone (E1, Fig. 1b) are two sorts of more representative steroid hormones produced by the ovary, testis, placenta and adrenal cortex of vertebrates. Due to their stronger physiological activity and clinical applications, such as capability of accumulation of subcutaneous fat, plumping body and promoting secondary sexual characteristics, they have been illegally added in some cosmetics to make skin white and breast plump, eliminate wrinkles, prevent skin from aging as well as fight biochemical signs of hyperandrogenism (hirsutism, acne, male-pattern hair loss).3 However, the long-term use of these cosmetics can cause metabolism disorders of the human body and occurrence of breast cancer and endometrial hyperplasia.4 Hence, for quality control of cosmetic products and protection of consumers' health, it is extremely important to develop simple, effective routine methods for simultaneous determination of the two estrogens in cosmetic products.
Various methods available in the literature for determination of estrogens in different matrices include flow injection analysis (FIA),5enzyme-linked immunosorbent assay (ELISA),6 column partition chromatography,7 radioimmunoassay,8high performance liquid chromatography9–15 with ultraviolet/diode array detection (HPLC-UV/DAD), fluorescence detection (HPLC-FLD) or mass spectrometry (HPLC-MS), and gas chromatography combined with mass spectrometry (GC-MS).6,16,17 For instance, Wang et al.9 have established an efficient avenue for analyzing seven sexual hormones in essential oil by HPLC-DAD tandem FLD. McNamara et al.14 have reported a method for measurement of sex steroids in murine blood and reproductive tissues by LC-MS. Almeida et al.15 have described a procedure for the determination of steroid sex hormones in water and urine matrices by stir bar sorptive extraction and LC-DAD. Among these conventional techniques, HPLC-UV/DAD and HPLC/GC-MS are the primary and most used ones for determination of estrogens in all sorts of fields especially in complicated cosmetic matrices.
In this work, we tried to use a spectrofluorimetry approach to simultaneously measure E3 and E1 contents in liquid cosmetic samples, which had not been reported in the literature so far. Firstly, fluorescence spectroscopy is a versatile analytical technique, which is generally more sensitive than other detection systems such as classical UV absorption and less expensive than MS detection. Secondly, the spectrofluorimetry method has also proved capable of acquiring clean spectra. Finally, unlike HPLC-UV/DAD or HPLC/GC-MS, there is no need of hazardous solvents, complex and time-consuming sample pretreatment procedures, such as derivatization after extraction in order to get rid of interfering substances. However, quantification of E3 and E1 in cosmetics is still difficult to be achieved with a routine spectrofluorimetry method, due to the fact that serious overlapping between the fluorescence spectra of E3 and E1 occurs, and the natural interferences in the complicated backgrounds of cosmetic products remarkably affect the fluorescence signals of the analytes. Fortunately, we can resolve the aforementioned problem by employing an excitation–emission matrix fluorescence (EEM) method coupled with a second-order calibration based on PARAFAC.18 In addition, modern hyphenated instruments combined with second-order calibration methods18–22 have recently been applied in many scientific fields including environment and cosmetic monitoring,23–25 determination of drugs in body fluids,26–28food analysis29–31 and monitoring of bio-processes.32,33
In this study, we proposed a simple, rapid, sensitive, and efficient excitation–emission matrix fluorescence (EEM) method based on region selection34 coupled with a PARAFAC algorithm to simultaneously measure E3 and E1 contents in liquid cosmetic samples. We removed the region in which not only E3 and E1 had serious collinearity, but also the two analytes had lower signals whereas cosmetics had very strong signals. The selected region made the PARAFAC algorithm capable of attaining clean spectra and concentrations of E3 and E1 in complex cosmetics, fully exploiting the idea of “mathematical separation” instead of “physical or chemical separation”. The predicted results acquired were satisfactory. Moreover, the figures of merit involving sensitivity (SEN), selectivity (SEL), limit of detection (LOD) and the statistic parameter of root-mean-square error of prediction (RMSEP) were investigated.
2. Theory
2.1. Trilinear model for second-order calibration
Suppose a given sample produces a data matrix of size I × J, where I and J denote the number of data points in the first and second dimensions, respectively. In the case of the excitation–emission matrix fluorescence (EEM) system, I stands for the number of excitation wavelengths, J is the number of emission wavelengths. If K samples, consisting of calibration and prediction samples, are stacked, a three-way data array ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) is obtained with dimensions I × J × K. A trilinear model for such a three-way array
is obtained with dimensions I × J × K. A trilinear model for such a three-way array ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) can be depicted as follows:
can be depicted as follows:| | 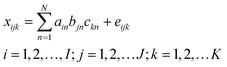 | (1) |
Here xijk, the element of ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) , is the fluorescent intensity of sample k at excitation wavelength i and emission wavelength j, ain is the element (i, n) of an I × N matrix A with relative excitation spectra of the N species; bjn is the element (j, n) of a J × N matrix B with relative emission spectra of the N species; ckn is the element (k, n) of a K × N matrix C with relative concentrations of the N species in K samples; and eijk represents the residual element of an I × J × K three-way residual array,
, is the fluorescent intensity of sample k at excitation wavelength i and emission wavelength j, ain is the element (i, n) of an I × N matrix A with relative excitation spectra of the N species; bjn is the element (j, n) of a J × N matrix B with relative emission spectra of the N species; ckn is the element (k, n) of a K × N matrix C with relative concentrations of the N species in K samples; and eijk represents the residual element of an I × J × K three-way residual array, ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) . N denotes the number of factors, which should be considered as the total number of fluorescing species, including the components of interest and the background as well as uncalibrated interferences.
. N denotes the number of factors, which should be considered as the total number of fluorescing species, including the components of interest and the background as well as uncalibrated interferences.
A typical property of ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) is that it can be uniquely decomposed, which can provide access to spectral profiles (A and B) and the relative concentrations (C) of individual components in the K samples, even in the presence of chemically unknown interferences. The property makes up of the basis of the “second-order advantage”.
is that it can be uniquely decomposed, which can provide access to spectral profiles (A and B) and the relative concentrations (C) of individual components in the K samples, even in the presence of chemically unknown interferences. The property makes up of the basis of the “second-order advantage”.
2.2. PARAFAC algorithm
Different algorithms used to analyze three-way trilinear data arrays emerge ceaselessly and belong to two main groups: (i) the non-iterative methods and (ii) the iterative methods. In our experiments, we chose the most representative iterative algorithm, PARAFAC algorithm, to deal with the three-way data. The PARAFAC model, proposed by Harshman35 and Carroll and Chang,36 has been widely accepted and used in many fields. In 1997, Bro18 reported a paper about tutorials and applications of PARAFAC that explains the multi-way decomposition method PARAFAC and its use in chemometrics. The algorithm solves the trilinear component model on the base of a procedure known as alternating least-squares (ALS) and can uniquely converge into physical and chemical solutions. That is, ALS assumes the loading matrices in two modes known and then estimates the unknown parameters in the last mode, under the condition of minimizing the sum of squares of the residuals eijk. For a more detailed discussion of the technique used, the reader should refer to the ref. 18.
2.3. Core consistency diagnostic (CORCONDIA) test
Accordingly, the traditional PARAFAC algorithm is sensitive to the estimated component number in a system, and either overestimation or underestimation of the underlying factors will lead to erroneous results. Hence, the core consistency diagnostic (CORCONDIA) test37 is used to determine the number of components in the present work, it is based on scrutinizing the “appropriateness” of the structural model based on the data and the estimated parameters of gradually augmented models. The model is appropriate if the fitness does not improve significantly upon adding other combinations of the same components. An appropriate number of components is considered to be obtained when the core consistency drops from a high value (usually above 60%) to a low value.
2.4. Figures of merit and statistic parameter
Figures of merit (FOM) such as sensitivity (SEN), selectivity (SEL), limit of detection (LOD) and the statistic parameter of root-mean-square error of prediction (RMSEP) are very important in developing, comparing and assessing the reliability of analytical methodologies as well as analytical results. In second-order calibration, the idea of FOM is easy to be comprehended by resorting to the useful concept of net analyte signal (NAS),38 which is defined as the part of the signal that relates uniquely to the analyte of interest. Different approaches for the calculation of the FOM have been extensively discussed in the literature.39–42
The SEN is estimated as the NAS at unit concentration, and the SEL is the ratio between the sensitivity and the total signal. The following equations can be obtained to estimate the SEN and SEL in this presently studied case:
| | | SEN = k{[(ATA)−1]nn[(BTB)−1]nn}−1/2 | (2) |
| | | SEL = {[(ATA)−1]nn[(BTB)−1]nn}−1/2 | (3) |
where
nn designates the (
n,
n) element of a matrix and
k is the total signal for component
n at unit concentration, which is also a parameter for converting scores to concentrations.
The LOD is estimated as follows:
where
s(0) is the standard deviation in the predicted concentration for three different background blank samples.
The RMSEP can be calculated in terms of the following formula:
| | 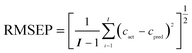 | (5) |
where
I is the number of prediction samples,
cact and
cpred are the actual and predicted concentrations of the analytes, respectively.
3. Experimental
3.1. Reagents and chemicals
Estriol (E3) and estrone (E1), used as chemical reference substances (CRS), were obtained from the National Institute for the Control of Pharmaceutical and Biological Products (Changsha, China). Stock solutions of E3 (46 μg mL−1) and E1 (90 μg mL−1) were prepared in a 100 mL volumetric flask by dissolving with methanol (HPLC grade) and then stored at 4 °C in a refrigerator, remaining stable for at least 2 months. The working solution of E3 was prepared daily by appropriate dilution of the stock solution, and the stock solution of E1 was used as the working solution directly owing to its lower fluorescence intensity. E3 and E1 free cosmetic products bought from commercial markets in Changsha (China) and internet web sites, were stored at room temperature until preparation for recovery experiments.
3.2. Apparatus
Fluorometric measurements were achieved on an F-4500 fluorescence spectrophotometer (Hitachi, Japan) equipped with a 150 W continuous xenon arc lamp, using a 1.00 cm quartz cell. All calculations were implemented on a personal computer under the Windows XP operating system with the help of Matlab Version 6.5 (TheMathWorks, Natick, USA). All glassware were previously soaked in chromate lotion overnight, and then rinsed with doubly distilled water before use.
3.3. Procedure
3.3.1. Analytical methodology.
Prior to quantitative analysis, the linear analytical ranges and how to choose the solvent were investigated for both E3 and E1, respectively. It was found that by linear regression between different concentrations and relative fluorescence intensity, a linear concentration range of 0–0.736 μg mL−1 of E3 and a linear concentration range of 0–18.000 μg mL−1 of E1 were realized. In addition, we used ethanol, methanol of analytical grade and HPLC grade to dissolve E3 and E1 because of their low solubility in water, and we eventually found that methanol (HPLC grade) was the best choice, since it was a pure solvent with few peaks as well as being able to dissolve most cosmetics.
3.3.2. Experimental design.
Eighteen samples including one calibration set and two prediction sets were prepared for the simultaneous determination of E3 and E1 contents in two different sorts of liquid cosmetics. The first seven samples (C1–C7) were built for calibration (see Table 1) by adding appropriate working solutions of the two analytes within their corresponding linear ranges into 10 mL volumetric flask and marking in methyl alcohol, then, six samples (J1–J6) were constructed as a predict set in which an equivalent amount of 10 times diluted watermelon frost anti-acne toner sold on an internet web site and different amounts of E3 and E1 were mixed evenly and diluted to 10 mL with methanol. In addition, another five samples (N1–N5), each 100 μL 10 times diluted pagoda flower relaxing lotion from the commercial market in volume, were spiked with different amount of E3 and E1 diluted to 10.00 mL with methanol in volumetric flasks. The final analytes concentrations are listed in Tables 2 and 3.
Table 1 Concentrations of estriol (E3) and estrone (E1) in calibration samples
| Sample |
Added concentration (μg mL−1) |
| E3 |
E1 |
| C1 |
0.736 |
0.000 |
| C2 |
0.000 |
18.000 |
| C3 |
0.644 |
5.400 |
| C4 |
0.552 |
4.500 |
| C5 |
0.368 |
2.700 |
| C6 |
0.184 |
9.000 |
| C7 |
0.092 |
14.400 |
Table 2 Measured results of estriol (E3) and estrone (E1) in spiked watermelon frost anti-acne toner samples J1–J6 by the PARAFAC algorithm
| Sample |
E3 (μg mL−1) |
E1 (μg mL−1) |
| Real |
Resolved |
Recovery (%) |
Real |
Resolved |
Recovery (%) |
| J1 |
0.575 |
0.609 |
105.9 |
4.950 |
5.494 |
111.0 |
| J2 |
0.437 |
0.447 |
102.3 |
6.750 |
7.353 |
108.9 |
| J3 |
0.299 |
0.340 |
113.7 |
5.850 |
6.221 |
106.3 |
| J4 |
0.207 |
0.217 |
104.8 |
9.450 |
8.723 |
92.3 |
| J5 |
0.161 |
0.175 |
108.7 |
11.250 |
10.996 |
97.7 |
| J6 |
0.115 |
0.126 |
109.6 |
13.050 |
12.351 |
94.6 |
| Average recovery (%) |
107.5 ± 3.2 |
|
101.8 ± 6.9 |
Table 3 Measured results of estriol (E3) and estrone (E1) in spiked pagoda flower relaxing lotion samples N1–N5 by the PARAFAC algorithm
| Sample |
E3 (μg mL−1) |
E1 (μg mL−1) |
| Real |
Resolved |
Recovery (%) |
Real |
Resolved |
Recovery (%) |
| N1 |
0.575 |
0.588 |
102.3 |
4.950 |
5.173 |
104.5 |
| N2 |
0.437 |
0.468 |
107.1 |
6.750 |
7.188 |
106.5 |
| N3 |
0.299 |
0.304 |
101.7 |
5.850 |
6.979 |
119.3 |
| N4 |
0.207 |
0.201 |
97.1 |
9.450 |
10.455 |
110.6 |
| N5 |
0.161 |
0.153 |
95.0 |
11.250 |
11.095 |
98.6 |
| Average recovery (%) |
100.6 ± 3.8 |
|
107.9 ± 5.7 |
The spectra of methanol blank solution were recorded in triplicate during the whole analysis procedure for estimating instrument noise. Each cosmetic blank solution was also determined in triplicate in order to estimate the LODs. All the spectral surfaces were obtained in the excitation wavelength range of 200–300 nm (each 2 nm) and in the emission wavelength range of 280–470 nm (each 3 nm). The excitation and emission monochromator slit widths were 5.0/5.0 nm, and the scanning rate was 2400 nm min−1.
4. Results and discussion
4.1. Spectral characteristics
Fig. 2 displays the three-dimensional EEMs plots of pure E3, E1 and cosmetic samples as well as spiked cosmetic samples (i.e. E3, E1 and cosmetics interference) in the excitation and emission wavelength ranges which avoid Rayleigh and Raman scatterings. E3 presented an emission maxima at 307 nm and two excitation peaks at 228 and 280 nm (Fig. 2a), E1 had similar two excitation peaks at 230 and 282 nm as well as a broad emission band with two peaks value at 307 and 406 nm (Fig. 2b), as for two sorts of cosmetic samples, the fluorescence intensity was very strong and the serious overlapping between the EEMs of E3 and E1 as well as cosmetic samples was experimentally observed, which consequently made the simultaneous determination of the two analytes using traditional fluorescent methods impossible. In such instances, we successfully adopted a PARAFAC algorithm to resolve each of the analyte profiles and predict the concentrations of the components of interest, which yielded satisfactory results, fully exploiting the second-order advantage.
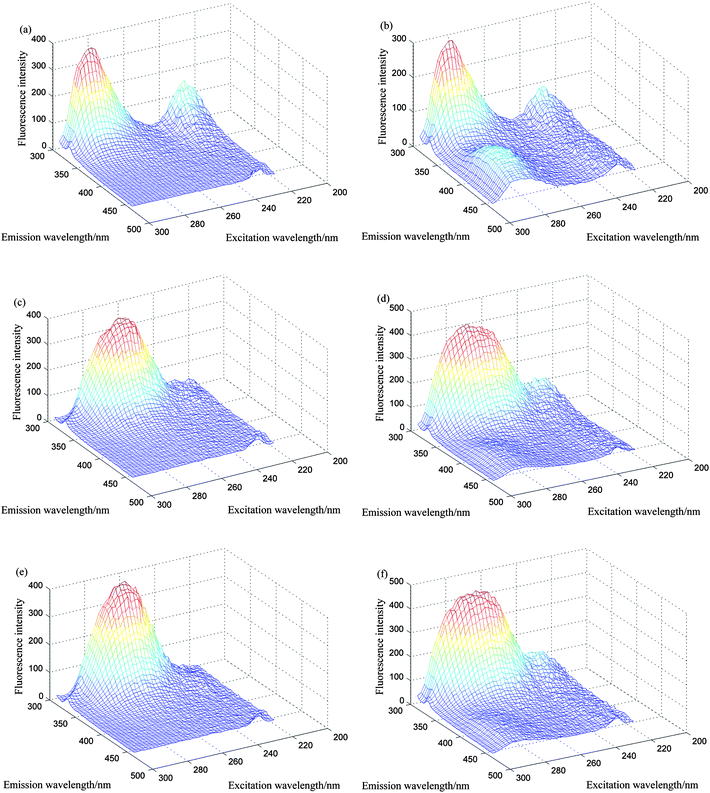 |
| | Fig. 2 Three-dimensional plots of the excitation–emission matrix fluorescence spectra: (a) for 0.736 μg mL−1 of estriol (E3); (b) for 18.0 μg mL−1 of estrone (E1); (c) for 100 μL 10 times diluted watermelon frost anti-acne toner; (d) for 100 μL 10 times diluted watermelon frost anti-acne toner and appropriate amount of E3 and E1; (e) for 100 μL 10 times diluted pagoda flower relaxing lotion; (f) for 100 μL 10 times diluted pagoda flower relaxing lotion and appropriate amount of E3 and E1. | |
4.2. Simultaneous determination of E3 and E1 in liquid cosmetic samples
4.2.1. Region selection.
In the application of a three-dimensional data array resolution, selecting the appropriate excitation and emission wavelength ranges is very important especially in the system with serious collinearity and strong matrix effects. Appropriate wavelength range selection can make successful resolution more possible and help to improve the analysis results. In our experiments, we faced the same question, that is, there existed serious collinearity between E3 and E1 which could be seen visually from Fig. 3. The picture shows the actual excitation and emission spectral profiles of E3, E1 and pure diluted watermelon frost anti-acne toner (a1, b1) as well as E3, E1 and pure diluted pagoda flower relaxing lotion (a2, b2) using singular value decomposition (SVD). Herein the red solid lines and green dash–dot–dot lines represent the actual spectral profiles of E3 and E1, respectively, and the black dotted lines denote the inherent interference deriving from the two cosmetic products. As shown in Fig. 3 (a1, a2), E3 and E1 presented serious collinearity and the spectra of them were seriously overlapped in most excitation wavelength ranges (240–298 nm), in addition, within the middle region of 240–270 nm, the two analytes had lower signals whereas cosmetic samples exhibited very strong fluorescence intensity, that is, the signal-to-noise ratio (SNR) herein was very low which made resolution quite difficult, so we made a preliminary region selection, i.e., got rid of the excitation wavelength region of 240–270 nm. Then, we chose 218–238 and 272–298 nm to analyze the three-way data since the spectra of E3 and E1 had obvious difference (218–238 nm) and the maximum fluorescence intensity of the two analytes are observed in the range of 272–298 nm. As for the emission wavelength region selection, we can see from Fig. 3 (b1, b2) the spectra of the three components in the region of 310–397 nm showed big differences, in the region of 400–457 nm, serious collinearity of E3 and the two sorts of cosmetic samples was observed, but the fluorescence intensity of them within the region was very low, moreover for E1, there existed significant difference among them which allowed for the successful resolution, so we chose the emission wavelength ranges of 310–457 nm for processing of the data. Making such a region selection not only kept as much information as possible, but also made resolution easy to implement.
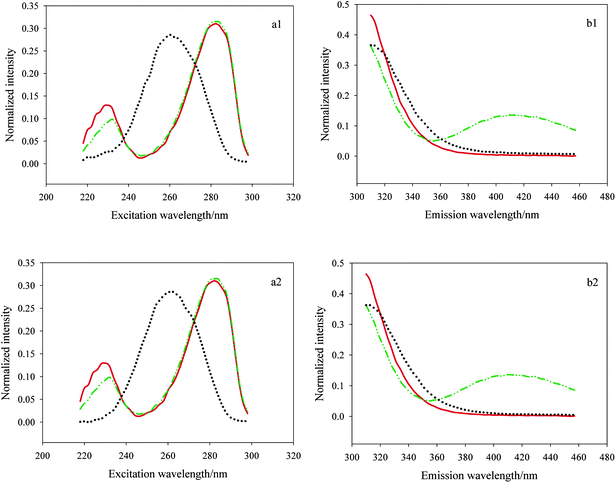 |
| | Fig. 3 Actual excitation and emission spectral profiles of estriol (E3), estrone (E1) and pure diluted watermelon frost anti-acne toner (a1, b1) as well as E3, E1 and pure diluted pagoda flower relaxing lotion (a2, b2) from SVD decomposition. | |
4.2.2. Results from a core consistency diagnostic (CORCONDIA) test.
Subsequently, a CORCONDIA method was applied to estimate the number of components before decomposing the three-way data matrix since as mentioned in part 2, a PARAFAC algorithm is very sensitive to the component number. In Fig. 4, we can find that for two different sorts of cosmetic models three factors are needed since three factors give a CORCONDIA value more than 60%. Chemically, two factors are attributed to the contribution of the analytes, the last one can be considered to the contribution of the background.
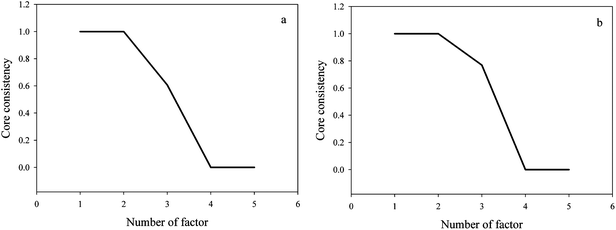 |
| | Fig. 4 Estimating the rank of a three-way data array in watermelon frost anti-acne toner (a) and pagoda flower relaxing lotion (b) using the CORCONDIA method. | |
4.2.3. Decomposing the treated three-way data matrix by PARAFAC.
Ultimately, the PARAFAC algorithm was employed to decompose the treated three-way data matrix. Fig. 5 (a1 and b1) shows the actual spectral profiles and the estimated spectral ones from decomposition of a 25 × 50 × 13 three-way data array including C1–C7 and J1–J6 using the PARAFAC algorithm. Fig. 5 (a2 and b2) describes the actual spectral profiles and the estimated spectral ones from decomposition of a 25 × 50 × 12 three-way data array including C1–C7 and N1–N5 using the same algorithm. Herein the red solid lines and green dash–dot–dot lines represent the actual spectral profiles of E3 and E1, respectively, and the blue dashed lines and dark pink dashed lines represent the loadings of the two analytes, and the black dotted lines denote the inherent interference deriving from the cosmetic products. The figure indicates that these spectral profiles match each other very well, which demonstrates the PARAFAC algorithm coupled with region selection is effective to solve the qualitative problems.
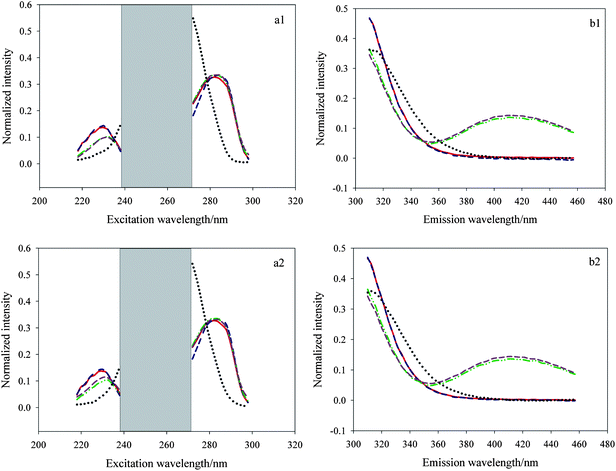 |
| | Fig. 5 Spectral profiles, normalized to unit length, obtained from PARAFAC when the number of factors was chosen as three for the spiked watermelon frost anti-acne toner samples (a1, b1) and the spiked pagoda flower relaxing lotion (a2, b2). | |
Tables 2 and 3 summarise the prediction results for the two sorts of liquid cosmetic samples. As for watermelon frost anti-acne toner, the average recoveries gained from the PARAFAC algorithm are 107.5 ± 3.2 and 101.8 ± 6.9% for E3 and E1, respectively. As for pagoda flower relaxing lotion, the average recoveries are 100.6 ± 3.8 and 107.9 ± 5.7% for E3 and E1, respectively. It highlighted at the same time that the second-order calibration method based on the PARAFAC algorithm combined with region selection is able to quantitatively analyze E3 and E1 in complex cosmetic samples satisfactorily.
4.3. Figures of merit and statistic parameter
Table 4 shows the figures of merit and statistic parameter, including SEN, SEL, LOD and RMSEP for direct determination of E3 and E1 with different concentration magnitudes in two different sorts of liquid cosmetic samples using PARAFAC algorithm. The LODs for E3 in the two cosmetic products are 4.7 and 8.9 ng mL−1, and for E1 are 96.1 and 76.9 ng mL−1, respectively. One can easily find that after an appropriate region selection, the proposed second-order calibration method based on PARAFAC algorithm can yield satisfactory predictive capacity for measuring E3 and E1 contents simultaneously in the two complex cosmetics.
Table 4 Statistic parameter and figures of merit of measuring estriol (E3) and estrone (E1)
| |
E3 |
E1 |
| Watermelon frost anti-acne toner |
Pagoda flower relaxing lotion |
Watermelon frost anti-acne toner |
Pagoda flower relaxing lotion |
|
SEN/mL μg−1 |
72.7 |
50.0 |
7.7 |
5.0 |
|
SEL
|
0.032 |
0.022 |
0.078 |
0.049 |
| LOD/ng mL−1 |
4.7 |
8.9 |
96.1 |
76.9 |
|
RMSEP/μg mL−1 |
0.026 |
0.018 |
0.613 |
0.799 |
|
R
|
0.9990 |
0.9991 |
0.9949 |
0.9944 |
5. Conclusion
A novel method for simultaneously measuring estriol and estrone in liquid cosmetics by using excitation–emission matrix fluorescence based on region selection coupled with parallel factor analysis algorithm is successfully established. Such a chemometrics-based protocol shows several advantages over the traditional methods: simple, rapid, accurate and effective. Besides, it is capable of acquiring clean spectra and accurate concentration prediction even in cases with overlapped profiles of background or interferences. More importantly, it is very well-suited to fast trace analysis of banned compounds as estriol and estrone where the limits of detection are satisfactory. Accordingly, due to its advantages of easy sample pretreatment and non-destructive, it will achieve greater development in cosmetic quality control and gradually become a more routine approach.
Acknowledgements
The authors gratefully acknowledge the National Natural Science Foundation of China (Grant No. 21175041), the National Basic Research Program (Grant No. 2012CB910602) and Program for Changjiang Scholars and Innovative Research Team in University (PCSIRT) for financial support.
References
-
Ministry of Health of China. Hygienic standard for cosmetics. Beijing: Ministry of Health of the people's Republic of China, 2007 Search PubMed.
- European Directive 76/768/EEC, Council Directive 76/768/EEC of 27 July of 1976 on the approximation of the laws of the Member States relating to cosmetic products.
- T. L. Setji and A. J. Brown, Minerva Med., 2007, 98, 175–189 Search PubMed.
- P. D. Darbre, Best Pract. Res., Clin. Endocrinol. Metab., 2006, 20, 121–143 Search PubMed.
- J. C. Bravo, P. Fernández and J. S. Duranda, Analyst, 2005, 130, 1404–1409 RSC.
- C. H. Huang and D. L. Sedlak, Environ. Toxicol. Chem., 2001, 20, 133–139 CAS.
- J. R. K. Preedy and E. H. Aitken, J. Biol. Chem., 1961, 236, 1300–1311 Search PubMed.
- S. T. Wolford and C. J. Argoudelis, J. Dairy Sci., 1979, 62, 1458–1463 Search PubMed.
- X. F. Wang, W. F. Zeng, J. Wang and R. Ren, Chin. J. Chromatogr., 2009, 27, 328–332 Search PubMed.
- Y. Wen, B. S. Zhou, Y. Xu, S. W. Jin and Y. Q. Feng, J. Chromatogr., A, 2006, 1133, 21–28 CrossRef CAS.
- D. De Orsi, M. Pellegrini, S. Pichini, D. Mattioli, E. Marchei and L. Gagliardi, J. Pharm. Biomed. Anal., 2008, 48, 641–648 CrossRef CAS.
- X. X. Lin, Y. Liu, J. H. Zhang and J. M. Lin, Sci. China Ser. B: Chem., 2009, 39, 832–837 Search PubMed.
- X. Xu, L. K. Keefer, D. J. Waterhouse, J. E. Saavedra, T. D. Veenstra and R. G. Ziegler, Anal. Chem., 2004, 76, 5829–5836 CrossRef CAS.
- K. M. McNamara, D. T. Harwood, U. Simanainen, K. A. Walters, M. Jimenez and D. J. Handelsman, J. Steroid Biochem. Mol. Biol., 2010, 121, 611–618 Search PubMed.
- C. Almeida and J. M. F. Nogueira, J. Pharm. Biomed. Anal., 2006, 41, 1303–1311 CrossRef CAS.
- W. Q. Wu, C. Y. Shen, Y. L. Yang and Y. Zhang, Chin. J. Environ. Occup. Med., 2004, 21, 307–309 Search PubMed.
- T. A. Ternes, H. Andersen, D. Gilberg and M. Bonerz, Anal. Chem., 2002, 74, 3498–3504 CrossRef CAS.
- R. Bro, Chemom. Intell. Lab. Syst., 1997, 38, 149–171 CrossRef CAS.
- H. L. Wu, M. Shibukawa and K. Oguma, J. Chemom., 1998, 12, 1–26 CrossRef CAS.
- Z. P. Chen, H. L. Wu, J. H. Jiang, Y. Li and R. Q. Yu, Chemom. Intell. Lab. Syst., 2000, 52, 75–86 CrossRef CAS.
- A. L. Xia, H. L. Wu, D. M. Fang, Y. J. Ding, L. Q. Hu and R. Q. Yu, J. Chemom., 2005, 19, 65–76 CrossRef CAS.
- J. F. Nie, H. L. Wu, S. R. Zhang, Y. J. Yu and R. Q. Yu, Anal. Methods, 2010, 2, 1918–1926 RSC.
- Y. N. Li, H. L. Wu, J. F. Nie, S. F. Li, Y. J. Yu, S. R. Zhang and R. Q. Yu, Anal. Methods, 2009, 1, 115–122 RSC.
- J. A. Porini and G. M. Escandar, Anal. Methods, 2011, 3, 1494–1500 RSC.
- J. F. Nie, H. L. Wu, X. M. Wang, Y. Zhang, S. H. Zhu and R. Q. Yu, Anal. Chim. Acta, 2008, 628, 24–32 CrossRef CAS.
- A. M. de la Peña, A. E. Mansilla, D. G. Gómez, A. C. Olivieri and H. C. Goicoechea, Anal. Chem., 2003, 75, 2640–2646 CrossRef CAS.
- G. M. Escandar, D. G. Gómez, A. E. Mansilla, A. M. de la Peña and H. C. Goicoechea, Anal. Chim. Acta, 2004, 506, 161–170 CrossRef CAS.
- S. F. Li, H. L. Wu, L. Huang, Y. N. Li, J. F. Nie, S. R. Zhang and R. Q. Yu, Anal. Methods, 2010, 2, 1069–1077 RSC.
- Y. Zhang, H. L. Wu, A. L. Xia, Q. J. Han, H. Cui and R. Q. Yu, Talanta, 2007, 72, 926–931 CrossRef CAS.
- M. C. Mahedero, N. M. Díaz, A. M. de la Peña, A. E. Mansilla, D. G. Gómez and D. B. Gil, Talanta, 2005, 65, 806–813 CrossRef CAS.
- J. W. B. Braga, C. B. G. Bottoli, I. C. S. F. Jardim, H. C. Goicoechea, A. C. Olivieri and R. J. Poppi, J. Chromatogr., A, 2007, 1148, 200–210 CrossRef CAS.
- P. P. Mortensen and R. Bro, Chemom. Intell. Lab. Syst., 2006, 84, 106–113 Search PubMed.
- Y. X. Tan, J. H. Jiang, H. L. Wu, H. Cui and R. Q. Yu, Anal. Chim. Acta, 2000, 412, 195–202 CrossRef CAS.
- J. Z. Lu, H. L. Wu, X. Y. Sun, H. Cui, J. Q. Sun and R. Q. Yu, Chin. J. Anal. Chem., 2004, 32, 1278–1282 Search PubMed.
- R. A. Harshman, UCLA Working Papers in Phonetics, 1970, 16, 1–84 Search PubMed.
- J. D. Carroll and J. J. Chang, Psychometrika, 1970, 35, 283–319 CrossRef.
- R. Bro and H. A. L. Kiers, J. Chemom., 2003, 17, 274–286 CrossRef CAS.
- A. Lorber, Anal. Chem., 1986, 58, 1167–1172 CrossRef CAS.
- Y. Wang, O. S. Borgen, B. R. Kowalski, M. Gui and F. Turecek, J. Chemom., 1993, 7, 117–130.
- K. Faber, A. Lorber and B. R. Kowalski, J. Chemom., 1997, 11, 95–109 CrossRef CAS.
- A. C. Olivieri, Anal. Chem., 2005, 77, 4936–4946 CrossRef CAS.
- A. C. Olivieri and N. M. Faber, J. Chemom., 2005, 19, 583–592 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) is obtained with dimensions I × J × K. A trilinear model for such a three-way array
is obtained with dimensions I × J × K. A trilinear model for such a three-way array ![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) can be depicted as follows:
can be depicted as follows: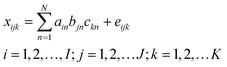
![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) , is the fluorescent intensity of sample k at excitation wavelength i and emission wavelength j, ain is the element (i, n) of an I × N matrix A with relative excitation spectra of the N species; bjn is the element (j, n) of a J × N matrix B with relative emission spectra of the N species; ckn is the element (k, n) of a K × N matrix C with relative concentrations of the N species in K samples; and eijk represents the residual element of an I × J × K three-way residual array,
, is the fluorescent intensity of sample k at excitation wavelength i and emission wavelength j, ain is the element (i, n) of an I × N matrix A with relative excitation spectra of the N species; bjn is the element (j, n) of a J × N matrix B with relative emission spectra of the N species; ckn is the element (k, n) of a K × N matrix C with relative concentrations of the N species in K samples; and eijk represents the residual element of an I × J × K three-way residual array, ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) . N denotes the number of factors, which should be considered as the total number of fluorescing species, including the components of interest and the background as well as uncalibrated interferences.
. N denotes the number of factors, which should be considered as the total number of fluorescing species, including the components of interest and the background as well as uncalibrated interferences.
![[X with combining low line]](https://www.rsc.org/images/entities/b_char_0058_0332.gif) is that it can be uniquely decomposed, which can provide access to spectral profiles (A and B) and the relative concentrations (C) of individual components in the K samples, even in the presence of chemically unknown interferences. The property makes up of the basis of the “second-order advantage”.
is that it can be uniquely decomposed, which can provide access to spectral profiles (A and B) and the relative concentrations (C) of individual components in the K samples, even in the presence of chemically unknown interferences. The property makes up of the basis of the “second-order advantage”.